10 Basic: regular operations

R 中可以执行各式各样的操作，这些操作都是通过使用 operator 或 function 实现。常见的操作有：

基本数学运算
关系和逻辑
筛选和排序
随机抽样
其他

注意：绝大多数 operators 和 functions 都支持 recycling rule（详见7.2.2）。

由于 subsetting operator 进阶用法的第二步是将拆解的步骤（操作）转换成相应的代码，所以本节中将重点演示如何将部分 operator 和 function 运用在 subsetting 中。

10.1 Basic mathematical operations

10.1.1 Arithmetic operators

+ - * / ^ %% %/% %*%

c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10) %% 5  # 求余数

#>  [1] 1 2 3 4 0 1 2 3 4 0

c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10) %/% 5  # 整除

#>  [1] 0 0 0 0 1 1 1 1 1 2

m1 <- matrix(c(1, 2, 3, 4, 5, 6), nrow = 3, ncol = 2)
m1

#>      [,1] [,2]
#> [1,]    1    4
#> [2,]    2    5
#> [3,]    3    6

m2 <- matrix(c(1, 2, 3, 4, 5, 6), nrow = 2, ncol = 3)
m2

#>      [,1] [,2] [,3]
#> [1,]    1    3    5
#> [2,]    2    4    6

m1 %*% m2   # 矩阵乘法

#>      [,1] [,2] [,3]
#> [1,]    9   19   29
#> [2,]   12   26   40
#> [3,]   15   33   51

10.1.2 Functions

10.1.2.1 Extremum and range

max(x)
min(x)
range(x)

m1 <- matrix(c(1, 2, 3, 4), nrow = 2, ncol = 2)
max(m1)

#> [1] 4

min(m1)

#> [1] 1

range(m1)

#> [1] 1 4

10.1.2.2 Sum

sum(x)，连加求和 $\sum_{i=1}^{n}x_i$；
rowSums(x)，行求和；
colSums(x)，列求和。

m1 <- matrix(c(1, 2, 3, 4), nrow = 2, ncol = 2)
m1

#>      [,1] [,2]
#> [1,]    1    3
#> [2,]    2    4

sum(m1)

#> [1] 10

rowSums(m1)

#> [1] 4 6

colSums(m1)

#> [1] 3 7

10.1.2.3 Average

mean(x)，均值 $\frac{\sum_{i=1}^n(x_i)}{n}$；
rowMeans(x)，行均值；
colMeans(x)，列均值。

m1 <- matrix(c(1, 2, 3, 4), nrow = 2, ncol = 2)
m1

#>      [,1] [,2]
#> [1,]    1    3
#> [2,]    2    4

mean(m1)

#> [1] 2.5

rowMeans(m1)

#> [1] 2 3

colMeans(m1)

#> [1] 1.5 3.5

10.1.2.4 Product

prod(x)，连乘求积 $\prod_{i=1}^nx_i=x_1x_2\cdots x_n$：

m1 <- matrix(c(1, 2, 3, 4), nrow = 2, ncol = 2)
prod(m1)

#> [1] 24

10.1.2.5 Round

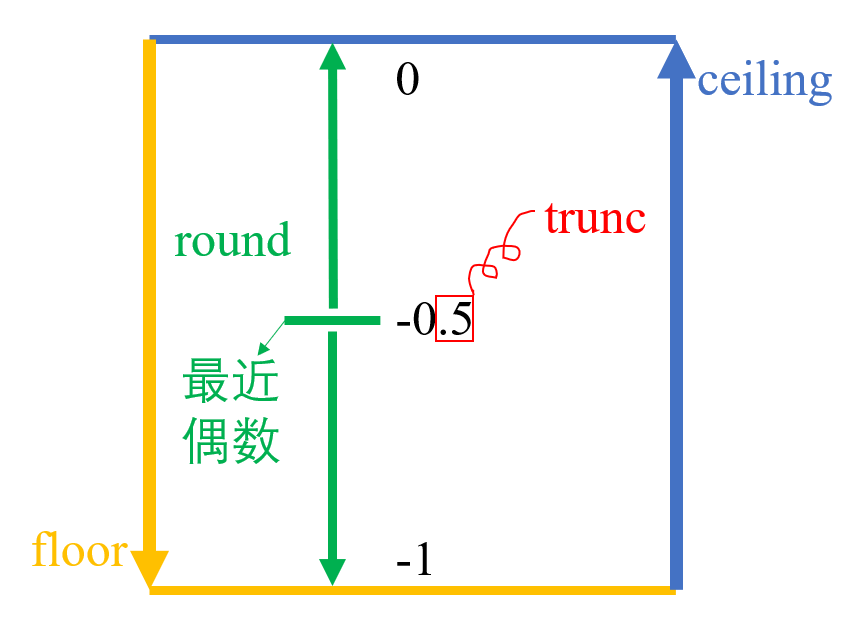
round(x, digits = 0)，取整，规则是 4 舍 6 入，逢 5 成双，即逢 5 时向最近的偶数取整，保留digits位小数，默认为 0；
floor(x)，向下取整；
ceiling(x)，向上取整；
trunc(x)，保留整数部分，舍弃小数部分。

m1 <- matrix(c(-1.1, -2.5, 3.9, 4.6), nrow = 2, ncol = 2)
m1

#>      [,1] [,2]
#> [1,] -1.1  3.9
#> [2,] -2.5  4.6

round(m1)

#>      [,1] [,2]
#> [1,]   -1    4
#> [2,]   -2    5

floor(m1)

#>      [,1] [,2]
#> [1,]   -2    3
#> [2,]   -3    4

ceiling(m1)

#>      [,1] [,2]
#> [1,]   -1    4
#> [2,]   -2    5

trunc(m1)

#>      [,1] [,2]
#> [1,]   -1    3
#> [2,]   -2    4

10.1.2.6 Natrual exponential and logorithm

exp(x)，自然指数 $e^{x}$

exp(0)

#> [1] 1

exp(1)

#> [1] 2.718282

log(x, base = exp(1))，对数 $\log_{base}x$，base的默认值是exp(1)：

log(1)

#> [1] 0

log(10, base = 10)

#> [1] 1

10.1.2.7 Contingency table

table(...)，统计频率，...是一个或多个 objects。

df <- data.frame(
  gender = c("female", "male", "female", "male", "female"),
  pass = c(1, 0, 0, 1, 1)
)
table(df$gender)

#> 
#> female   male 
#>      3      2

table(df$gender, df$pass)

#>         
#>          0 1
#>   female 1 2
#>   male   1 1

10.1.2.8 Others

Square root: sqrt(x)，即$\sqrt{x}$。
Trigonometric Functions: sin(x)，cos(x)，tan(x)
Absolute value: abs(x)，即$|x|$。
Sign:（正数输出 1，负数输出 -1）

sign(x)

sign(c(-1, 2, -sqrt(2)))

#> [1] -1  1 -1

Transpose

t(x)，即$x'$或$x^T$，将x转置（沿主对角线翻转，行列互换），x可以是 matrix 或 data.frame。

a <- matrix(c(1, 2, 3, 4, 5, 6), nrow = 3, ncol = 2)
a

#>      [,1] [,2]
#> [1,]    1    4
#> [2,]    2    5
#> [3,]    3    6

t(a)

#>      [,1] [,2] [,3]
#> [1,]    1    2    3
#> [2,]    4    5    6

例子：数据转换（Skewed Distribution: Definition, Examples）

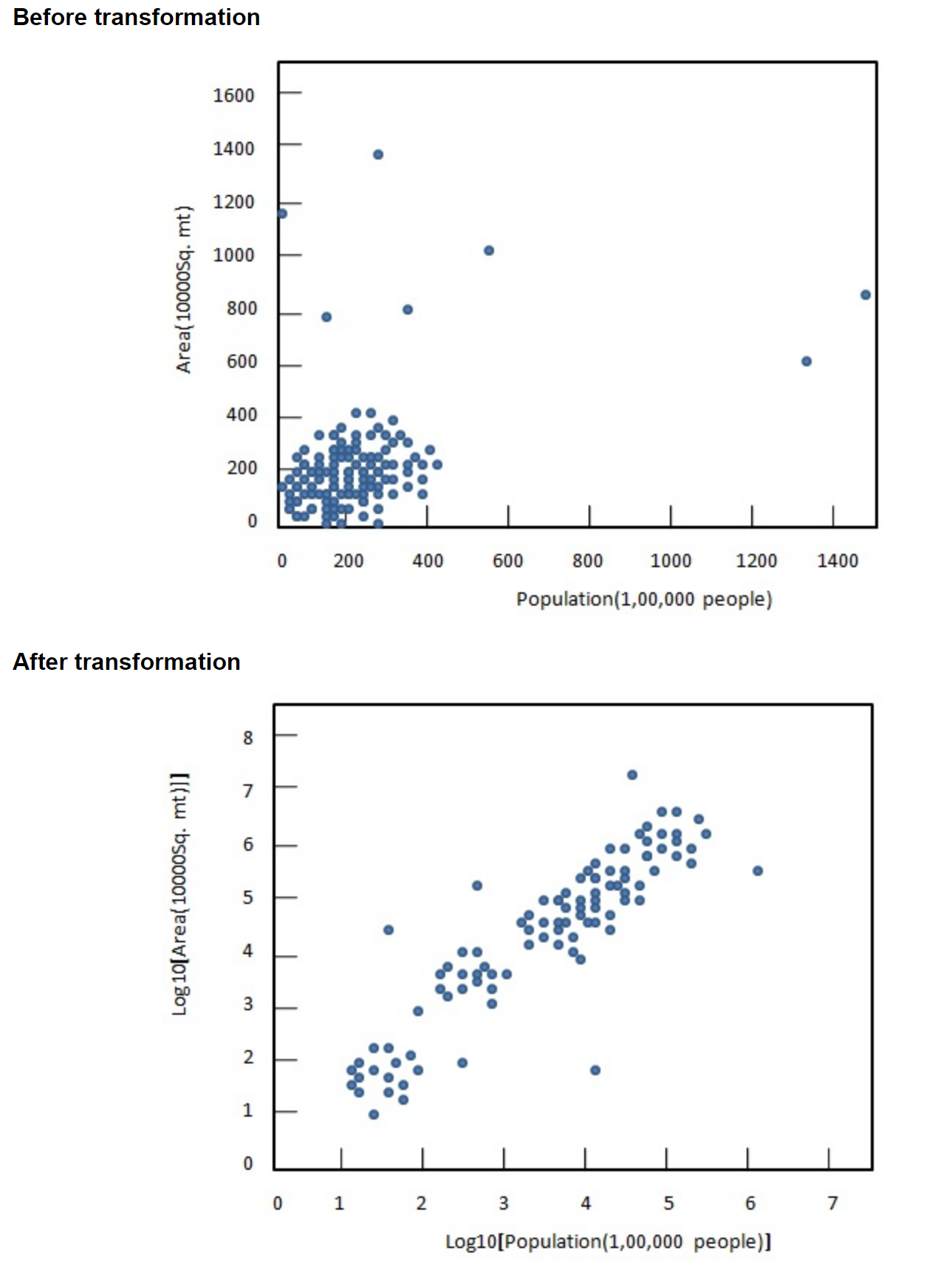
data$Population <- log(data$Population, base = 10)
data$Area <- log(data$Area, base = 10)

10.2 Relational and Logical operators

10.2.1 Relational operators

>，<，>=，<=，==，!=。这些 operators 返回的结果都是 logical：

m1 <- matrix(c(-1, -2, 0, 4), nrow = 2, ncol = 2)
# 以下代码全部都受到 recycling rule 的作用
m1 > 0

#>       [,1]  [,2]
#> [1,] FALSE FALSE
#> [2,] FALSE  TRUE

m1 < 0

#>      [,1]  [,2]
#> [1,] TRUE FALSE
#> [2,] TRUE FALSE

m1 >= 0

#>       [,1] [,2]
#> [1,] FALSE TRUE
#> [2,] FALSE TRUE

m1 <= 0

#>      [,1]  [,2]
#> [1,] TRUE  TRUE
#> [2,] TRUE FALSE

m1 == 0

#>       [,1]  [,2]
#> [1,] FALSE  TRUE
#> [2,] FALSE FALSE

m1 != 0

#>      [,1]  [,2]
#> [1,] TRUE FALSE
#> [2,] TRUE  TRUE

其中，在使用==时需要注意，object == NA、object == NaN，object == NULL都是错误写法：

1 == NA

#> [1] NA

1 == NaN

#> [1] NA

1 == NULL

#> logical(0)

若想要检测某个 object 究竟是不是NA、NaN或NULL，正确的写法应该是：

is.na(c(1, 2, NA))

#> [1] FALSE FALSE  TRUE

is.nan(c(1, 2, NaN))

#> [1] FALSE FALSE  TRUE

is.null(c(1, 2, NULL))

#> [1] FALSE

此外，因为==返回的是各 element 位置上比较的结果，所以：

如果只想知道两个 objects 是否完全相同，即所有 elements 都一样，则需要加all()，或者使用identical()，
如果只想知道两个 objects 是否部分相同，即只要至少有一个位置上的 elements 相同，则需要加any()。

a <- 1:3
b <- a
a == b

#> [1] TRUE TRUE TRUE

all(a == b)

#> [1] TRUE

identical(a, b)

#> [1] TRUE

any(a == b)

#> [1] TRUE

identical和==的工作原理都是比较两个 objects 是否绝对相同，如果想要比较两个 objects 是不是几乎相同需使用all.qual()：

a <- c(0.1111111111, 1, 2, 3)
b <- c(0.1111111112, 1, 2, 3)
a == b

#> [1] FALSE  TRUE  TRUE  TRUE

identical(a, b)

#> [1] FALSE

all.equal(a, b)

#> [1] TRUE

比较两个 numerical objects 时，只要两者的任意一对 elements 的差异不超过1.5e-8，all.equal()就会认为这两个 objects 几乎相同。

Relational operators 在 subsetting 的进阶写法中十分常用。例如，

vec_int <- 1:100
vec_int[vec_int > 50]

#>  [1]  51  52  53  54  55  56  57  58  59  60  61  62  63  64
#> [15]  65  66  67  68  69  70  71  72  73  74  75  76  77  78
#> [29]  79  80  81  82  83  84  85  86  87  88  89  90  91  92
#> [43]  93  94  95  96  97  98  99 100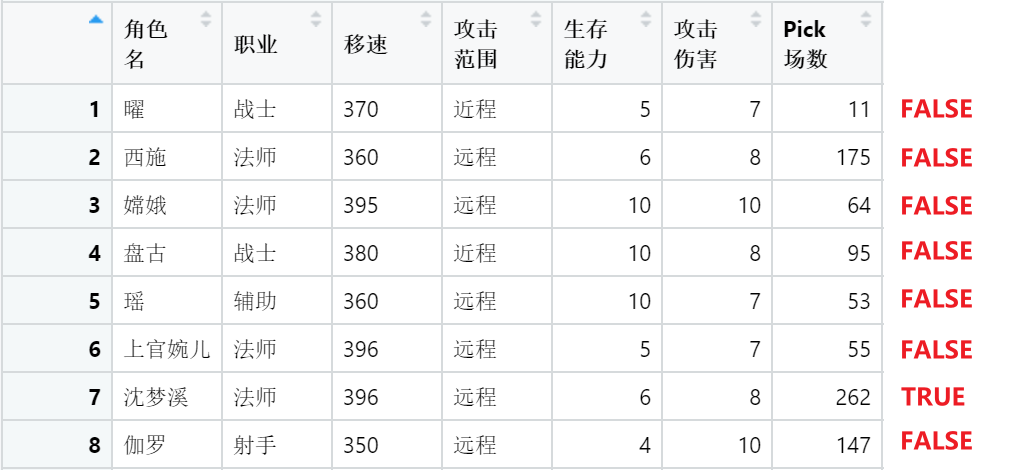

Basic mathematical operations 和 relational operators 的组合也是 subsetting 进阶写法中常用手段。例如，取绝对值最大的数：

a <- c(-0.1, -0.9, 0.2, 0.4)
a[abs(a) == max(abs(a))]

#> [1] -0.9

10.2.2 Logical operator

10.2.2.1 `&` and `&&`

基本结构：LHS & RHS，LHS && RHS。

LHS（left hand side）和RHS（right hand side）的结果是长度为 1 的 logical vector 时，&和&&等价。

`LHS`	`RHS`	结果
`TRUE`	`TRUE`	`TRUE`
`TRUE`	`FALSE`	`FALSE`
`FALSE`	`TRUE`	`FALSE`
`FALSE`	`FALSE`	`FALSE`

a <- 3
a > 2 & a < 4

#> [1] TRUE

a > 2 && a < 4

#> [1] TRUE

LHS和RHS的结果是长度大于 1 的 logical vector 时，&和&&的结果不同。&会比较左右两侧的 logical vector 中每一对 element，&&会从左往右比，直到有结果为止，本质上相当于只会比较第一个位置上的那对 elements，也正是因为如此，从 4.3.0 开始，R 强制要求&&的LHS和RHS的长度只能为1（因为只比第一个位置），否则就报错，这点在&&的帮助页面也有明确说明（详见?`&&`）：

a <- c(1, 2, 3, 4, 5)
a >= 1

#> [1] TRUE TRUE TRUE TRUE TRUE

a <= 3

#> [1]  TRUE  TRUE  TRUE FALSE FALSE

a >= 1 & a <= 3

#> [1]  TRUE  TRUE  TRUE FALSE FALSE

a >= 1 && a <= 3

#> Error in a >= 1 && a <= 3: 'length = 5' in coercion to 'logical(1)'

10.2.2.2 `|` and `||`

基本结构：LHS | RHS，LHS || RHS。

当LHS（left hand side）和RHS（right hand side）的结果是长度为 1 的 logical vector 时，|和||等价。

`LHS`	`RHS`	结果
`TRUE`	`TRUE`	`TRUE`
`TRUE`	`FALSE`	`TRUE`
`FALSE`	`TRUE`	`TRUE`
`FALSE`	`FALSE`	`FALSE`

a <- 6
a < 2 | a > 4

#> [1] TRUE

a < 2 || a > 4

#> [1] TRUE

当LHS和RHS（的结果是长度大于 1 的 logical vector 时，|会比较左右两侧的 logical vector 中每一对 element，||则会报错：

a <- c(1, 2, 3, 4, 5)
a <= 2

#> [1]  TRUE  TRUE FALSE FALSE FALSE

a >= 4

#> [1] FALSE FALSE FALSE  TRUE  TRUE

a <= 2 | a >= 4

#> [1]  TRUE  TRUE FALSE  TRUE  TRUE

a >= 1 || a <= 3

#> Error in a >= 1 || a <= 3: 'length = 5' in coercion to 'logical(1)'

注意，如果&和|的LHS和RHS的长度不一，会触发 recycling rule （详见7.2.2）。

# 等价于 c(T, F, T) & c(T, T, T)
c(T, F, T) | T

#> [1] TRUE TRUE TRUE

# 等价于 c(T, F, T) | c(T, T, T)

10.2.2.3 `!`

基本结构：!expr。若expr的结果是TRUE，则改为FALSE；若FALSE则改为TRUE：

a <- c(1, 2, 3, 4, 5)
a <= 2

#> [1]  TRUE  TRUE FALSE FALSE FALSE

!(a <= 2)

#> [1] FALSE FALSE  TRUE  TRUE  TRUE

!is.na(a)

#> [1] TRUE TRUE TRUE TRUE TRUE

Relational operator 和 logical operator 组合使用，可以非常便捷地完成按照指定条件 subsetting 的任务，尤其是当需要同时满足多个条件时：

m1 <- matrix(c(0.5, 0.1, 0.8, 0.25), nrow = 2, ncol = 2)
m1

#>      [,1] [,2]
#> [1,]  0.5 0.80
#> [2,]  0.1 0.25

m1[m1 > 0.2 & m1 < 0.8]

#> [1] 0.50 0.25

m1[m1 < 0.3 | m1 > 0.7]

#> [1] 0.10 0.80 0.25

m1[!(m1 < 0.3 | m1 > 0.7)]

#> [1] 0.5

10.3 Locate, match and sort

10.3.1 Locate

which(x)，输出x中所有TRUE的位置信息，x必须是一个 logical object。

a <- runif(5)
a

#> [1] 0.10941253 0.05274798 0.17444520 0.24512316 0.25178300

which(a == max(a)) # 等价于which.max(a)，类似的还有which.min(a)

#> [1] 5

which(a > 0.5)

#> integer(0)

which(a > 0.1 & a < 0.9)

#> [1] 1 3 4 5

使用which()通常不是为了将符合条件的 elements 取出，而是为了将这些 elements 的位置找出来，起个名字并保存在 Environment 里，方便后续单独处理这些 elements 的时候可以直接使用位置作为 index 来定位。如果只是需要将符合条件的所有 elements 取出来，只用 relational operator 就足够了。

a <- c(0.5, 0.1, 0.8, 0.25)
a

#> [1] 0.50 0.10 0.80 0.25

a[which(a > 0.5)]

#> [1] 0.8

a[a > 0.5]

#> [1] 0.8

当然，如果x中存在NA，则加上which()会使代码容错率更高，

a <- c(0.5, NA, 0.8, 0.25)
a

#> [1] 0.50   NA 0.80 0.25

a[a > 0.5]

#> [1]  NA 0.8

a[which(a > 0.5)]

#> [1] 0.8

如果x是一个有dim的array或matrix，which(x)可以通过设定arr.ind = TRUE来输出按dim标识的 index：

m1 <- matrix(1:4, 2, 2)
which(m1 == 3, arr.ind = TRUE)

#>      row col
#> [1,]   1   2

10.3.2 Match

%in%: 返回一个和逻辑向量，表示左边的值在右边的依据值中是否有匹配。

x %in% table

x: 被匹配的值。
table: 匹配时依据的值。

vec <- c(1, 2, 3)
vec_all <- c(6, 1, 5, 6, 1, 4, 4, 2, 10, 5)
vec %in% vec_all

#> [1]  TRUE  TRUE FALSE

vec_all %in% vec

#>  [1] FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE  TRUE FALSE
#> [10] FALSE

%in%可以用于挑选数据的指定列，例如：

vars <- c("x", "y", "z")
df <- data.frame(
  x = 1, 
  n = 2, 
  z = 3, 
  m = 4, 
  n = 5, 
  y = 5
)
df_select <- df[names(df) %in% vars]
df_select

%in%对于匹配的定义比==考虑的更完备，对一些特殊的匹配情况做了处理，如NA，只有匹配NA时才会返回TRUE的结果，否则返回FALSE，

c(1, NA, 3) %in% c(1:10)

#> [1]  TRUE FALSE  TRUE

c(1, NA, 3) %in% NA # equivalent to is.na(c(1, NA, 3))

#> [1] FALSE  TRUE FALSE

正是因为%in%考虑更加完备，故%in%可以替代==，用在 subsetting 上，

df <- data.frame(x = c(1, NA, 1, 2, 4), y = c(2, 1, 1, 3, 5))
df$x == 1

#> [1]  TRUE    NA  TRUE FALSE FALSE

df[df$x == 1 & df$y == 1, ]

df[df$x %in% 1 & df$y %in% 1, ]

# or wrap == with which
df[which(df$x == 1 & df$y == 1), ]

10.3.3 Sort

sort(x, decreasing = FALSE)，将x升序排列（默认），输出排列后的x。decreasing是可选 argument。decreasing = TRUE则是按照降序排序列。

a <- c(5, 1, 8, 2.5)
a

#> [1] 5.0 1.0 8.0 2.5

sort(a)

#> [1] 1.0 2.5 5.0 8.0

sort(a, decreasing = TRUE)

#> [1] 8.0 5.0 2.5 1.0

rank(x, na.last = TRUE, ties.method = c("average", "first", "last", "random", "max", "min"))，返回x的排名信息。其中，x是一个 vector，必选 argument；na.last为可选 argument，其为TRUE（默认）时会将x中缺失数据放在最后排名；ties.method也是可选 argument，控制x中相同的 elements 该如何排名，默认是average。注意，rank()只能按照升序输出排名。

set.seed(123)
#相同元素的排名为均值，(1+2+3)/3
rank(c(2, 1, 3, 1, 4, 1))

#> [1] 4 2 5 2 6 2

# 相同元素按照出现的顺序正序赋予排名，1,2,3
rank(c(2, 1, 3, 1, 4, 1), ties.method = "first")

#> [1] 4 1 5 2 6 3

# 相同元素按照出现的顺序倒序赋予排名，3,2,1
rank(c(2, 1, 3, 1, 4, 1), ties.method = "last")

#> [1] 4 3 5 2 6 1

 # 相同元素随机赋予排名，sample(3, 3)
rank(c(2, 1, 3, 1, 4, 1), ties.method = "random")

#> [1] 4 2 5 3 6 1

 # # 相同元素按照最大排名赋予排名，3,3,3
rank(c(2, 1, 3, 1, 4, 1), ties.method = "max")

#> [1] 4 3 5 3 6 3

# 相同元素按照最小排名赋予排名，1,1,1
rank(c(2, 1, 3, 1, 4, 1), ties.method = "min")

#> [1] 4 1 5 1 6 1

order(..., decreasing = FALSE)，...是一个或多个 objects。decreasing是可选 argument，decreasing = TRUE表示按照降序排序列。

order()输出的其实是 object 中元素位置的具体调整方式，根据该方式调整以后就实现了排序（升序或降序）。所以，order()实际上给出的是位置信息。

无重复元素

a <- c(5, 1, 8, 2.5)
order(a)

#> [1] 2 4 1 3

order(a, decreasing = TRUE)

#> [1] 3 1 4 2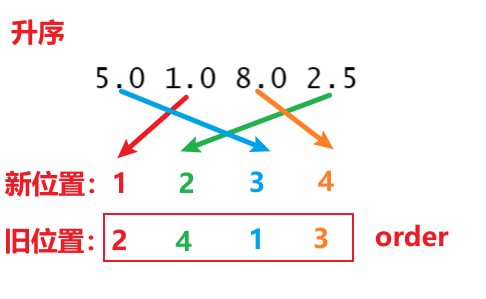

有重复元素

当输入的单个 object 有重复元素（即 ties，表示一个独特的值同时有多个位置索引）时，默认是按照元素出现的先后顺序来排序，

a <- c(5, 1, 8, 1)
order(a)

#> [1] 2 4 1 3

order(a, decreasing = TRUE)

#> [1] 3 1 2 4

如果有额外的线索可以区分重复元素时，order()可以将这些重复元素按照额外线索排序，

score <- c(90, 95, 99, 95)
id <- c(4, 3, 2, 1)
order(score, id)

#> [1] 1 4 2 3

order(score, id, decreasing = TRUE)

#> [1] 3 2 4 1

总结一下，当输入 1 个 object 时，order()排序的是这个object；当输入多个 objects 时（这些 objects 都必须是同样长度），order()排序的依旧是第一个 object，只不过该 object 中的重复元素是以第 2 个 object 中对应位置上的元素大小为依据，若这些元素依旧是重复的，则按照第 3 个 object 中对应位置上的元素大小为依据，依此类推。

order()对字符也有效，默认升序，数字按从小到大，英文按字母，中文按拼音顺序，三者的优先级是数字 > 英文字母 > 中文拼音：

vec_cha <- c("3", "2", "a", "b", "啊", "呀")
order(vec_cha)

#> [1] 2 1 3 4 5 6

vec_cha[order(vec_cha)]

#> [1] "2"  "3"  "a"  "b"  "啊" "呀"

order()常用于根据某一列重新排列整个数据。例如根据score_math降序排列：

data_set1 <- data.frame(
  name = c("小红", "小明", "小白", "小黑"), 
  id = c(1, 4, 2, 3),
  score_math = c(90, 95, 98, 95)
)
data_set1[order(data_set1$score_math, id, decreasing = TRUE), ]

10.4 Randomness

10.4.1 Generating random number following specific distribution

从指定的分布中随机抽取指定数量的数是模拟（simulation）研究中的常见任务，通常都是由生成随机数的函数来完成的。这类函数的命名特点是rxxx()，其中r代表 random，xxx一般都是某种分布的缩写。

runif(n, min = 0, max = 1)生成n个在$(\min,\max)$这个开区间（默认为$(0,1)$）内的均匀（uniform）分布随机数。

runif(5)

#> [1] 0.5281055 0.8924190 0.5514350 0.4566147 0.9568333

rnorm(n, mean = 0, sd = 1)，生成n个服从$N$($\mu=$mean, $\sigma=$sd)的正态（normal）分布（默认是标准正态分布$N(0,1)$）随机数。

vec_rnd <- rnorm(5)
vec_rnd

#> [1] -0.1172420  0.1830826  1.2805549 -1.7272706  1.6901844

mean(vec_rnd)

#> [1] 0.2618619

sd(vec_rnd)

#> [1] 1.340188

vec_rnd <- rnorm(5, mean = 20, sd = 10)
vec_rnd

#> [1] 25.038124 45.283366 25.490967 22.382129  9.511069

mean(vec_rnd)

#> [1] 25.54113

sd(vec_rnd)

#> [1] 12.81555

其他类似的专门用来生成指定分布随机数的常用函数还有：

rt()，生成服从指定$t$分布随机数；
rchisq()，生成服从指定$\chi^2$分布随机数；
rbeta()，生成服从指定$\beta$分布随机数；
rf()，生成服从指定$F$分布随机数。

10.4.2 Other randomness-based sampling functions

以最常用的sample()为例：

sample(x, size, replace = FALSE, prob = NULL)，从x中随机取出size个元素。x可以是一个 vector 或 integer scalar，当x是 integer scalar 时，等价于1:x；size是 integer。可选 argument：

replace = TRUE表示有放回抽样；
prob是一个向量，每一个元素是x中对应元素被抽中的概率。

sample(5, 1)  # 等价于 sample(5, 1, prob = rep(1/5, 5))

#> [1] 3

sample(5, 5)

#> [1] 4 2 1 3 5

sample(5, 5, replace = TRUE)

#> [1] 5 4 2 5 1

sample(
  6, 
  size = 6, 
  replace = TRUE, 
  prob = c(1/6, 1/6, 1/6, 1/6, 1/3, 1/3)
)

#> [1] 5 6 6 2 5 6

随机抽样的一个典型的应用场景是自助法（bootstrap），从样本中随机取出多批和原始数据同样大小的 bootstrap 数据集。以英雄联盟数据集为例：

library(openxlsx)

#> Warning: package 'openxlsx' was built under R version 4.3.3

data_ori <- read.xlsx("F:/Nutstore backup/R/codes/RBA/data/Arena of Valor_midterm dataset.xlsx")
n <- nrow(data_ori)
data_sample <- data_ori[sample(n, size = n, replace = TRUE), ]

10.4.3 Fun fact: everything is `runif()` (optional)

在 R 中，绝大多数生成指定分布随机数的函数本质上都是基于runif()的。下面将以rnorm()为例来讲解。

runif()

首先看下 R 中runif()的源码，如下：

#> function (n, min = 0, max = 1) 
#> .Call(C_runif, n, min, max)
#> <bytecode: 0x0000027badd4d768>
#> <environment: namespace:stats>

C_runif() 在实际执行时是调用 statsR.h 中声明的do_runif()：

SEXP do_runif(SEXP sn, SEXP sa, SEXP sb);

调用do_runif()的代码在 random.c 的第 227 行：

DEFRAND2_REAL(runif)

其中，DEFRAND2_REAL()的定义在 random.c 的第 208-211 行：

#define DEFRAND2_REAL(name) \
  SEXP do_##name(SEXP sn, SEXP sa, SEXP sb) { \
    return random2(sn, sa, sb, name, REALSXP); \
  }

大致意思是执行do_runif(sn, sa, sb)会调用random2(sn, sa, sb, name, REALSXP)，其定义在 random.c 的第 164-223 行，其中sn对应runif(n, min, max)中的n——将生成的随机数的个数，sa对应min，sb对应max，name对应 runif()的底层 C 语言函数。random2(sn, sa, sb, name, REALSXP)本质上是重复调用 C 语言版的runif()，共计sn次（详见 random.c 的第 193-195 行）：

R_xlen_t n = resultLength(sn);
for (R_xlen_t i = 0; i < n; i++) {
  rx = fn(ra[i % na], rb[i % nb]);} 
  // when executing random2, name is fn within the life cycle of random2
}

综上，只要查看 C 语言版的runif()即可，其定义在 runif.c 中，如下：

#include "nmath.h"

double runif(double a, double b)
{
  if (!R_FINITE(a) || !R_FINITE(b) || b < a)    ML_ERR_return_NAN;

  if (a == b)
      return a;
  else {
      double u;
      /* This is true of all builtin generators, but protect against
         user-supplied ones */
      do {u = unif_rand();} while (u <= 0 || u >= 1);
      return a + (b - a) * u;
  }
}

其中，负责最终生成随机数的是另一个 C 语言函数unif_rand()，位于 RNG.c 的第 105 -179 行。

rnorm()

再来看看rnorm()，其中 R 语言中能查看到的源码如下：

#> function (n, mean = 0, sd = 1) 
#> .Call(C_rnorm, n, mean, sd)
#> <bytecode: 0x0000027bad010ae8>
#> <environment: namespace:stats>

与runif()类似，对应do_rnorm()：

SEXP do_rnorm(SEXP sn, SEXP sa, SEXP sb);

这个声明指向DEFRAND2_REAL(rnorm)，本质上也是调用random2()将 C 语言版的rnorm()重复执行sn次。进一步检索，能查到 C 语言版的rnorm()在 rnorm.c 中，定义如下：

#include "nmath.h"

double rnorm(double mu, double sigma)
{
  if (ISNAN(mu) || !R_FINITE(sigma) || sigma < 0.)
    ML_ERR_return_NAN;
  if (sigma == 0. || !R_FINITE(mu))
      return mu; /* includes mu = +/- Inf with finite sigma */
  else
      return mu + sigma * norm_rand();
}

不难发现，核心的随机数生成函数为norm_rand()，依旧是一个 C 语言函数，其定义详见 snorm.c。由于 R 语言中生成服从正态分布随机数的算法有多种，都包含在 norm_rand() 中。但默认算法是inversion（详见?RNG的Details部分），故只截取与之相关的部分，对应的是 snorm.c 的第 265-270 行，如下：

case INVERSION:
#define BIG 134217728 /* 2^27 */
/* unif_rand() alone is not of high enough precision */
u1 = unif_rand();
u1 = (int)(BIG*u1) + unif_rand();
return qnorm5(u1/BIG, 0.0, 1.0, 1, 0);

其中负责生成随机数的核心函数同样是unif_rand()，所以rnorm()是基于runif()的。

sample()

同理，也可查询到sample()是基于runif()的。sample()的 R 语言源码如下：

#> function (x, size, replace = FALSE, prob = NULL) 
#> {
#>     if (length(x) == 1L && is.numeric(x) && is.finite(x) && x >= 
#>         1) {
#>         if (missing(size)) 
#>             size <- x
#>         sample.int(x, size, replace, prob)
#>     }
#>     else {
#>         if (missing(size)) 
#>             size <- length(x)
#>         x[sample.int(length(x), size, replace, prob)]
#>     }
#> }
#> <bytecode: 0x0000027bab4d2c70>
#> <environment: namespace:base>

继续查看sample.int()的 R 语言源码：

#> function (n, size = n, replace = FALSE, prob = NULL, useHash = (n > 
#>     1e+07 && !replace && is.null(prob) && size <= n/2)) 
#> {
#>     stopifnot(length(n) == 1L)
#>     if (useHash) {
#>         stopifnot(is.null(prob), !replace)
#>         .Internal(sample2(n, size))
#>     }
#>     else .Internal(sample(n, size, replace, prob))
#> }
#> <bytecode: 0x0000027bab4d0d08>
#> <environment: namespace:base>

核心函数为.Internal(sample())，对应 random.c 中的do_sample()（第 461-553 行）。以最常见的sample()用法为例，如sampe(1:5, size = 1, replace = FALSE, prob = NULL)，对应执行是do_sample()最后一部分的分支代码（533-547 行）：

int n = (int) dn;
PROTECT(y = allocVector(INTSXP, k));
int *iy = INTEGER(y);
/* avoid allocation for a single sample */
if (replace || k < 2) {
  for (int i = 0; i < k; i++) iy[i] = (int)(dn * unif_rand() + 1);
} else {
    int *x = (int *)R_alloc(n, sizeof(int));
    for (int i = 0; i < n; i++) x[i] = i;
    for (int i = 0; i < k; i++) {
    int j = (int)(n * unif_rand());
    iy[i] = x[j] + 1;
    x[j] = x[--n];
    }
}

其中负责生成随机数的核心函数依旧是unif_rand()。

10.4.4 Control randomness

10.4.4.1 Why do we need and how to control randomness

模拟（simulation）研究常见于方法学研究，这类研究的目的可以是改进某种方法。为了实现这一目的，需要模拟生成很多批数据，且这些数据需具备随机性，这个过程称作是重复实验（replication）。重复实验本质上是在近似实际研究中多次收集数据的过程。

假定一种非常极端的现象，某学者提出了一种新的统计方法，并使用 R 语言实现了该方法。该方法的代码只会在一种特定的条件下才会出错，大约是每生成 1000 批模拟数据才会有 1 批是符合这种特定条件。但由于生成数据是随机的，根本无法预计是哪一次重复实验会出错，也就无法稳定复现错误来 debug。所以，就需要使用控制随机数种子的技巧让随机有迹可循，对应的函数为set.seed()。

set.seed(integer)

integer: a single value, interpreted as an integer.

R 里面所有与随机行为有关的代码（如sample()，rnorm()，runif()）本质上都是伪随机，都是通过激活某种随机数生成器（random number generator， RNG）来实现的。如果把 RNG 理解为一个函数 $y=f(x)$，可以简单地认为每次激活 RNG 都需要给定一个起点$x$，最终的$y$就是随机行为。如果起点一致，那么两次随机行为的结果就是完全一致的。set.seed()就是用来控制每次激活 RNG 时使用的起点——随机数种子（seed）。

# set.seed 之前，结果不同
rnorm(5)

#> [1] -0.6279061  1.3606524 -0.6002596  2.1873330  1.5326106

rnorm(5)

#> [1] -0.2357004 -1.0264209 -0.7104066  0.2568837 -0.2466919

# set.seed 之后，结果相同
set.seed(1)
rnorm(5)

#> [1] -0.6264538  0.1836433 -0.8356286  1.5952808  0.3295078

set.seed(1)
rnorm(5)

#> [1] -0.6264538  0.1836433 -0.8356286  1.5952808  0.3295078

学会了set.seed()，就可以来整点活了

set.seed(2219868)
greeting <- sample(letters, size = 5, replace = TRUE)
set.seed(6024)
year <- sample(0:9, size = 4, replace = TRUE)
cat(paste(greeting, collapse = ""), paste(year, collapse = ""))

#> happy 2023

以上代码改编自 r/statsmemes 中的 Season’s greetings，作者是 brrybk。思考一下，如何令第 2 个 sample() 产生出 [1] 2 0 2 4?

10.4.4.2 A slightly deeper understanding of `set.seed()` (optional)

在 R 中，所有 seeds 都存储在.Random.seed这个 vector 里，不同 RNG 产生的.Random.seed不一样。R 中默认的 RNG 是 Mersenne-Twister。Mersenne-Twister 同时是众多编程语言（R, Python，C++11）的默认 RNG，其本质上是一个算法，可以从数学上理解，但过于复杂。下面将从代码的角度来简单讲解 Mersenne-Twister 是如何在 R 中实现的。

Mersenne-Twister 对应的.Random.seed是一个长度为 626 的 integer vector，第 1 个位置上存储的是代表 RNG 种类的编号，第 2 个位置上储存的是下一次激活 RNG 将使用的 seed 位置序号，第 3-626 个位置上储存的是 624 个 seeds。

.Random.seed[1:5]

#> [1]       10403           4  1044506428 -1557773185
#> [5]  1308604373

length(.Random.seed)

#> [1] 626

在不改变 RNG 种类的情况下，set.seed()只会改变.Random.seed的第 2-626 个位置上的信息——将下一次激活 RNG 将使用的 seed 位置序号重置为 624，并更换所有 624 个 seeds。

set.seed(123)
.Random.seed[1:5]

#> [1]      10403        624 -983674937  643431772 1162448557

set.seed(1)
.Random.seed[1:5]

#> [1]      10403        624 -169270483 -442010614 -603558397

在使用了set.seed()以后，只要是执行含有随机行为的代码，RNG 运用.Random.seed的基本流程就是：

一次随机行为激活一次 RNG，激活时按顺序使用一个 seed，
RNG 激活后更新.Random.seed第 2 个位置上记录的 seed 位置序号。

set.seed(1)
.Random.seed[1:5]

#> [1]      10403        624 -169270483 -442010614 -603558397

runif(1) # 共有 1 次随机行为

#> [1] 0.2655087

.Random.seed[1:5]

#> [1]       10403           1  1654269195 -1877109783
#> [5]  -961256264

runif(2) # 共有 2 次随机行为

#> [1] 0.3721239 0.5728534

.Random.seed[1:5]

#> [1]       10403           3  1654269195 -1877109783
#> [5]  -961256264

runif(3) # 共有 3 次随机行为

#> [1] 0.9082078 0.2016819 0.8983897

.Random.seed[1:5]

#> [1]       10403           6  1654269195 -1877109783
#> [5]  -961256264

但不难看出以上代码的运行结果似乎和前述的基本流程有所出入，.Random.seed在执行runif(1)后会改变，然后就固定不变了。这和 Mersenne-Twister 的算法有关，下面来解释一下背后的原因。

如10.4.3所述，R 中runif(1)本质上是调用 C 语言函数random2() 1 次。在生成随机数前，random2()的第 188 行会先执行GetRNGstate()，该函数的定义详见 RNG.c 的第 397-422 行。其中，第 401-406 行表明GetRNGstate()会先尝试获取已经存在的 seeds（即由set.seed(1)更新的.Random.seed的第 2-626 个元素），如果没有则此时会自动生成一组随机的 seeds：

SEXP seeds;

/* look only in the workspace */
seeds = GetSeedsFromVar();
if (seeds == R_UnboundValue) {
  Randomize(RNG_kind);

后续就会调用unif_rand()，该函数的定义详见 RNG.c 的第 109-183 行。unif_rand()中激活 Mersenne-Twister 的代码在第 136-137 行：

case MERSENNE_TWISTER:
return fixup(MT_genrand());

其中，fixup()函数的定义在 RNG.c 的第 100-106 行，如下：

#define i2_32m1 2.328306437080797e-10/* = 1/(2^32 - 1) */
static double fixup(double x)
{
  /* ensure 0 and 1 are never returned */
  if(x <= 0.0) return 0.5*i2_32m1;
  if((1.0 - x) <= 0.0) return 1.0 - 0.5*i2_32m1;
  return x;
}

不难看出这个函数只是用来保证生成出来的随机数不会恰好是 0 或 1。因此，unif_rand()中负责生成随机数的核心函数是MT_genrand()，其定义在 RNG.c 的第 687-732 行。下面只摘出其中关键的部分并加以注释（//部分）：

static Int32 dummy[628]; // allow for optimizing compilers to read over bound

// dummy is an array, of which the 1st element is the current position, 
// the 2-625 elements are the 624 seeds.
// after set.seed(1), dummy[0] = 624

#define N 624
#define M 397
#define UPPER_MASK 0x80000000 /* most significant w-r bits */
#define LOWER_MASK 0x7fffffff /* least significant r bits */

static Int32 *mt = dummy+1; /* the array for the state vector  */

// mt = dummy with the 1st removed, mt are the 624 seeds, if modified, dummy
// will be updated

static int mti=N+1; /* mti==N+1 means mt[N] is not initialized */

static double MT_genrand(void)
{
  Int32 y;
  static Int32 mag01[2]={0x0, MATRIX_A};
  /* mag01[x] = x * MATRIX_A  for x=0,1 */

  mti = dummy[0]; /**/
  
  // mti = 624, the following if body will be executed

  if (mti >= N) { /* generate N words at one time */
    int kk;

    if (mti == N+1)   /* if sgenrand() has not been called, */
      MT_sgenrand(4357); /* a default initial seed is used   */

    for (kk = 0; kk < N - M; kk++) {
      y = (mt[kk] & UPPER_MASK) | (mt[kk+1] & LOWER_MASK);
      mt[kk] = mt[kk+M] ^ (y >> 1) ^ mag01[y & 0x1];
    }
    // scramble the 1-397 seeds
    for (; kk < N - 1; kk++) {
      y = (mt[kk] & UPPER_MASK) | (mt[kk+1] & LOWER_MASK);
      mt[kk] = mt[kk+(M-N)] ^ (y >> 1) ^ mag01[y & 0x1];
    }
    y = (mt[N-1] & UPPER_MASK) | (mt[0] & LOWER_MASK);
    mt[N-1] = mt[M-1] ^ (y >> 1) ^ mag01[y & 0x1];
    // then scramble the 398-624 seeds
  
    mti = 0; 
    // update the current position
  }

  y = mt[mti++];
  // use the current value of mti, 0, as the index, extract mt[0]
  // then mti = mit + 1
  
  y ^= TEMPERING_SHIFT_U(y);
  y ^= TEMPERING_SHIFT_S(y) & TEMPERING_MASK_B;
  y ^= TEMPERING_SHIFT_T(y) & TEMPERING_MASK_C;
  y ^= TEMPERING_SHIFT_L(y);
  // use mt[0] as the seed to generate 1 random number 
  
  dummy[0] = mti;
  // record the current position

  return ( (double)y * 2.3283064365386963e-10 ); /* reals: [0,1)-interval */
}

所以，当set.seed(1)重置.Random.seed第 2 个位置上记录的 seed 位置序号为 624 后，第一次激活 Mersenne-Twister 时就会把 624 个 seeds 全部重新改变一次。此后再激活 Mersenne-Twister 时就会因为 seed 位置序号不满足条件（mti<=N）自动跳过改变所有 seeds 的语句，seeds 就保持不变。可想而知，set.seed(1)后每激活 Mersenne-Twister 624 次，所有的 624 个 seeds 就会被自动更新：

set.seed(1)
.Random.seed[1:5]

#> [1]      10403        624 -169270483 -442010614 -603558397

do_not_display <- runif(624)
.Random.seed[1:5]

#> [1]       10403         624  1654269195 -1877109783
#> [5]  -961256264

do_not_display <- runif(624)
.Random.seed[1:5]

#> [1]      10403        624 1980538363 -125047968 -820381145

这种周期性自动更新全部 seeds 的设定可以避免 Mersenne-Twister 生成出重复的随机数。不过，由于set.seed(1)的存在，所以相当于人为设定了 seeds 自动更新的起点。因此，只要set.seed(integer)中的integer不变，那后续所有含有随机行为的代码使用的 seed 顺序就是固定的。只要代码的执行顺序不变，即便是随机抽样也是可以完美重复出来：

set.seed(1)
df1 <- iris[sample(nrow(iris), 3), ]
rnd1 <- runif(3)
df1

rnd1

#> [1] 0.62911404 0.06178627 0.20597457

set.seed(1)
df2 <- iris[sample(nrow(iris), 3), ]
rnd2 <- runif(3)
df2

rnd2

#> [1] 0.62911404 0.06178627 0.20597457

需要注意的是，Mersenne-Twister 会在一些特殊的情况下出现大面积重复：

set.seed(0)
seeds_1 <- .Random.seed[-(1:2)]
runif(10)

#>  [1] 0.8966972 0.2655087 0.3721239 0.5728534 0.9082078
#>  [6] 0.2016819 0.8983897 0.9446753 0.6607978 0.6291140

set.seed(1)
seeds_2 <- .Random.seed[-(1:2)]
runif(10)

#>  [1] 0.26550866 0.37212390 0.57285336 0.90820779 0.20168193
#>  [6] 0.89838968 0.94467527 0.66079779 0.62911404 0.06178627

sum(seeds_1 %in% seeds_2)

#> [1] 623

rbind(seeds_1, seeds_2)[, 1:10]

#>               [,1]       [,2]       [,3]       [,4]
#> seeds_1 1280795612 -169270483 -442010614 -603558397
#> seeds_2 -169270483 -442010614 -603558397 -222347416
#>               [,5]       [,6]       [,7]       [,8]
#> seeds_1 -222347416 1489374793  865871222 1734802815
#> seeds_2 1489374793  865871222 1734802815   98005428
#>              [,9]     [,10]
#> seeds_1  98005428 268448037
#> seeds_2 268448037  63650722

由于无法准确预测什么时候会出现这个问题，因此可以考虑：

使用其他 RNG，
在 simulation 自定义一段代码来自动调整integer，以下是一个简单的示例：

seed_old <- .Random.seed[-1]
int <- 0
is_change <- TRUE
while (is_change) {
  set.seed(int)
  seed_new <- .Random.seed[-1]
  if (sum(seed_old %in% seed_new) < 100) {
    is_change <- FALSE 
  } else {
    is_change <- TRUE
    int <- int + 1
  }
}

本节内R内置函数的 C 源码的追踪均是基于: fossies.org。

10.5 Others

10.5.1 Combine

c(...)，将多个 object 合并成一个 vector，...为要合并的 object。
cbind(...)，将多个 objects，视作是 columns，将多个 object 横向合并成一个 object，...为要合并的 object。
rbind(...)，将多个 objects 视作是 rows，纵向合并成一个 object，...为要合并的 object。

a <- c(1, 2, 3)
b <- c(4, 5, 6)
cbind(a, b)

#>      a b
#> [1,] 1 4
#> [2,] 2 5
#> [3,] 3 6

rbind(a, b)

#>   [,1] [,2] [,3]
#> a    1    2    3
#> b    4    5    6

10.5.2 Get the number of

length(x)，返回x中 element 的个数；
nrow(x)或NROW(x)，返回x的行数，如果x没有行数的信息，返回NULL；
ncol(x)或NCOL(x)，返回x的列数，如果x没有列数的信息，返回NULL；
nchar(x)，返回x各 element 的字符个数。

df <- data.frame(number = c(1, 2, 3), letter = c("a", "b", "c"))
length(df)

#> [1] 2

nrow(df)

#> [1] 3

ncol(df)

#> [1] 2

fruits <- c("banana", "apple", "pineapple", "melon")
length(fruits)

#> [1] 4

nrow(fruits)

#> NULL

ncol(fruits)

#> NULL

nchar(fruits)

#> [1] 6 5 9 5

10.5.3 Generate sequence

10.5.3.1 Operator

from:to，生成有序整数数列。from为数列的起点；to为数列的终点。

1:100

#>   [1]   1   2   3   4   5   6   7   8   9  10  11  12  13
#>  [14]  14  15  16  17  18  19  20  21  22  23  24  25  26
#>  [27]  27  28  29  30  31  32  33  34  35  36  37  38  39
#>  [40]  40  41  42  43  44  45  46  47  48  49  50  51  52
#>  [53]  53  54  55  56  57  58  59  60  61  62  63  64  65
#>  [66]  66  67  68  69  70  71  72  73  74  75  76  77  78
#>  [79]  79  80  81  82  83  84  85  86  87  88  89  90  91
#>  [92]  92  93  94  95  96  97  98  99 100

:可以用来生成行索引，在需要分半数据进行统计分析（交叉验证，复本信度等）时快速取出数据子集。以英雄联盟数据集为例：

library(openxlsx)
data_ori <- read.xlsx("F:/Nutstore backup/R/codes/RBA/data/Arena of Valor_midterm dataset.xlsx")
data_subset1 <- data_ori[1:trunc(nrow(data_ori)/2), ]
data_subset2 <- data_ori[(trunc(nrow(data_ori)/2) + 1):nrow(data_ori), ]

10.5.3.2 Functions：

seq(from = 1, to = 1, by = ((to - from)/(length.out - 1)), length.out = NULL)，生成有序数列。from为数列的起点，to为数列的终点。可选 argument：

by为步长，即后一个数和前一个数之差；
length.out为生成数列的长度。

seq()

#> [1] 1

seq(from = 1, to = 100)  # 等价于 1:100

#>   [1]   1   2   3   4   5   6   7   8   9  10  11  12  13
#>  [14]  14  15  16  17  18  19  20  21  22  23  24  25  26
#>  [27]  27  28  29  30  31  32  33  34  35  36  37  38  39
#>  [40]  40  41  42  43  44  45  46  47  48  49  50  51  52
#>  [53]  53  54  55  56  57  58  59  60  61  62  63  64  65
#>  [66]  66  67  68  69  70  71  72  73  74  75  76  77  78
#>  [79]  79  80  81  82  83  84  85  86  87  88  89  90  91
#>  [92]  92  93  94  95  96  97  98  99 100

seq(1, 100, by = 3)

#>  [1]   1   4   7  10  13  16  19  22  25  28  31  34  37  40
#> [15]  43  46  49  52  55  58  61  64  67  70  73  76  79  82
#> [29]  85  88  91  94  97 100

seq(1, 100, length.out = 34)

#>  [1]   1   4   7  10  13  16  19  22  25  28  31  34  37  40
#> [15]  43  46  49  52  55  58  61  64  67  70  73  76  79  82
#> [29]  85  88  91  94  97 100

seq()可以用于快速奇偶分半数据。以英雄联盟数据集为例：

library(openxlsx)
data_ori <- read.xlsx("F:/Nutstore backup/R/codes/RBA/data/Arena of Valor_midterm dataset.xlsx")
data_ori <- cbind(ID = 1:nrow(data_ori), data_ori)
data_subset1 <- data_ori[seq(1, nrow(data_ori), 2), ]
data_subset2 <- data_ori[seq(2, nrow(data_ori), 2), ]

rep(x, times = 1, length.out = NA, each = 1)，生成重复序列。

rep(0, times = 3)

#> [1] 0 0 0

rep(c(1, 2, 3), times = 3)

#> [1] 1 2 3 1 2 3 1 2 3

rep(c(1, 2, 3), times = 3, length.out = 10)

#>  [1] 1 2 3 1 2 3 1 2 3 1

rep(c(1, 2, 3), times = 3, length.out = 30, each = 3)

#>  [1] 1 1 1 2 2 2 3 3 3 1 1 1 2 2 2 3 3 3 1 1 1 2 2 2 3 3 3 1
#> [29] 1 1

rep()可以巧妙地和subsetting的操作相结合，来实现快速复制矩阵。例如以一个 $2\times2$ 的矩阵为最小 element，复制出一个 $2 \times 2$ 的大矩阵：

m1 <- matrix(1:4, nrow = 2, ncol = 2)
m1[rep(1:nrow(m1), times = 2), rep(1:ncol(m1), times = 2)]

#>      [,1] [,2] [,3] [,4]
#> [1,]    1    3    1    3
#> [2,]    2    4    2    4
#> [3,]    1    3    1    3
#> [4,]    2    4    2    4

来源：R中是否有复制平铺矩阵的函数

10.5.4 Concatenate strings

paste(..., sep = " ", collapse = NULL)，将object按照指定方式拼接成字符串。...是一个或多个待拼接的object。可选argument如下：

sep = " "是拼接时用来分隔各项的字符串，默认值是一个英文空格；
collapse = NULL 表示拼接好的各项最后合并成一个字符串，各项间用collapse的值来分隔，默认值是NULL，即不合并成一个字符串。

paste(1:12)  # 等价于 as.character(1:12)

#>  [1] "1"  "2"  "3"  "4"  "5"  "6"  "7"  "8"  "9"  "10" "11"
#> [12] "12"

paste(1:12, "month")

#>  [1] "1 month"  "2 month"  "3 month"  "4 month"  "5 month" 
#>  [6] "6 month"  "7 month"  "8 month"  "9 month"  "10 month"
#> [11] "11 month" "12 month"

paste(1:12, c("st", "nd", "rd", rep("th", 9)), "month")

#>  [1] "1 st month"  "2 nd month"  "3 rd month"  "4 th month" 
#>  [5] "5 th month"  "6 th month"  "7 th month"  "8 th month" 
#>  [9] "9 th month"  "10 th month" "11 th month" "12 th month"

paste(1:12, c("st", "nd", "rd", rep("th", 9)), "month", sep = "")

#>  [1] "1stmonth"  "2ndmonth"  "3rdmonth"  "4thmonth" 
#>  [5] "5thmonth"  "6thmonth"  "7thmonth"  "8thmonth" 
#>  [9] "9thmonth"  "10thmonth" "11thmonth" "12thmonth"

paste(
  1:12, c("st", "nd", "rd", rep("th", 9)), "month", 
  sep = "", collapse = ","
)

#> [1] "1stmonth,2ndmonth,3rdmonth,4thmonth,5thmonth,6thmonth,7thmonth,8thmonth,9thmonth,10thmonth,11thmonth,12thmonth"

paste()可用于自动生成符合要求的文件名：

num_subsets <- 10
filenames <- paste(
  1:num_subsets, 
  ".txt",
  sep = ""
)
filenames

#>  [1] "1.txt"  "2.txt"  "3.txt"  "4.txt"  "5.txt"  "6.txt" 
#>  [7] "7.txt"  "8.txt"  "9.txt"  "10.txt"

write.table(data_subset1, filenames[1])
write.table(data_subset2, filenames[2])

只要是需要按照一定的规律生成字符串，就要想到paste()。

10.5.5 Print to console

有 2 个十分常用的 functions：print()和cat()。

print(x)，将x的 value 输出在 Console。print(x)和x在单独执行时都会输出x的 value，但二者是有几个细微的区别：
1. 通过 Source 的方式执行当前活动脚本中所有的代码时，print(x)会在 Console 输出x的 value，x则不会；
2. 在 function 内部使用print(x)，在执行 function 时会在 Console 输出x的 value，x则不会；
3. 在循环体内部使用print(x)会在 Console 输出x的 value，x则不会（具体例子将在12章节展示）。

cat(..., sep = " ", fill = FALSE, labels = NULL)，将输入的一个或多个 object 拼接后输出在 Console。sep为可选 argument，指定拼接时用来分隔各项的字符串，默认是" "。

cat("The correlation between a and b is", 0.6)

#> The correlation between a and b is 0.6

cat("The correlation between a and b is", 0.6, sep = "_")

#> The correlation between a and b is_0.6

cat("The correlation between a and b is\n", 0.6)

#> The correlation between a and b is
#>  0.6

cat(
  "The correlation between a and b is", 
  rep("+", 100), 
  0.6, 
  rep("+", 100), 
  sep = ""
)

#> The correlation between a and b is++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++0.6++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

10.5.6 Head and tail

head(x, n = 6L)和tail(x, n = 6L)，在 Console 输出x的前 6 或后 6 个元素（x为vector）/行（x为matrix或data.frame）。n为可选argument,表示输出的个/行数，默认是 6。

m1 <- matrix(1:100, nrow = 10, ncol = 10)
head(m1)

#>      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
#> [1,]    1   11   21   31   41   51   61   71   81    91
#> [2,]    2   12   22   32   42   52   62   72   82    92
#> [3,]    3   13   23   33   43   53   63   73   83    93
#> [4,]    4   14   24   34   44   54   64   74   84    94
#> [5,]    5   15   25   35   45   55   65   75   85    95
#> [6,]    6   16   26   36   46   56   66   76   86    96

tail(m1)

#>       [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
#>  [5,]    5   15   25   35   45   55   65   75   85    95
#>  [6,]    6   16   26   36   46   56   66   76   86    96
#>  [7,]    7   17   27   37   47   57   67   77   87    97
#>  [8,]    8   18   28   38   48   58   68   78   88    98
#>  [9,]    9   19   29   39   49   59   69   79   89    99
#> [10,]   10   20   30   40   50   60   70   80   90   100

10.5.7 Uniuqe

unique(x)，输出x中所有不重复的 elements 或 rows，x是必选 argument，可以是 vector，data.frame 或 array。

set.seed(123)
x <- sample(3, size = 10, replace = TRUE)
x

#>  [1] 3 3 3 2 3 2 2 2 3 1

# for vector, keeps unique elements
unique(x)

#> [1] 3 2 1

x <- iris[sample(1:nrow(iris), size = 20, replace = TRUE), ]
rmarkdown::paged_table(x)

# for data.frame, keeps unique rows
rmarkdown::paged_table(unique(x))

10.5.8 Continuous to discrete

cut(x, breaks)

x: a numeric vector which is to be converted to a factor by cutting.
breaks: either a numeric vector of two or more unique cut points or a single number (greater than or equal to 2) giving the number of intervals into which x is to be cut.

cut(1:10, breaks = c(0, 3, 6, 10))

#>  [1] (0,3]  (0,3]  (0,3]  (3,6]  (3,6]  (3,6]  (6,10] (6,10]
#>  [9] (6,10] (6,10]
#> Levels: (0,3] (3,6] (6,10]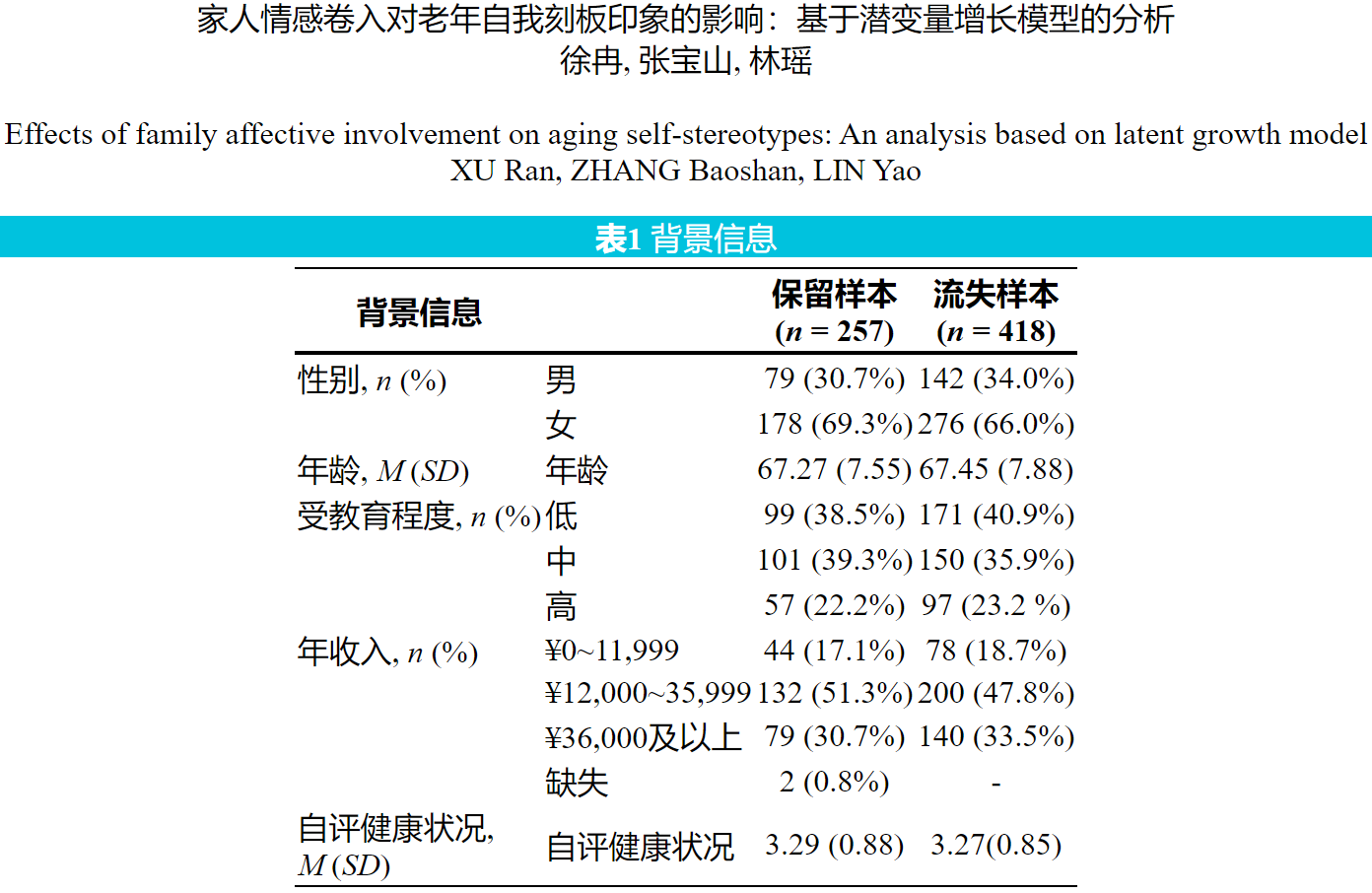

# Simulate the demographic data reported in 
#  http://journal.psych.ac.cn/xlxb/article/2021/0439-755X/0439-755X-53-11-1215.shtml

Income <- c(
  sample(11999, 122), 
  sample(12000:35999, 332),
  sample(36000:100000, 219)
)
Income <- c(Income, NA, NA)
is_lost <- rep(1, length(Income))
is_lost[c(
  sample(122, 78), 
  sample(123:454, 200), 
  sample(456:673, 140)
)] <- 0
is_lost[c(length(Income) - 1, length(Income))] <- NA
data_xb <- data.frame(Income, is_lost)
head(data_xb)

data_xb$Income <- cut(
  data_xb$Income, 
  breaks = c(0, 11999, 35999, 100000), 
  labels = c("￥0-11,999", "￥12,000-35,999", "￥36,000及以上")
)
data_xb$is_lost <- factor(
  data_xb$is_lost, 
  levels = c(1, 0), 
  labels = c("保留样本", "流失样本")
)
as.matrix(table(data_xb))

#>                  is_lost
#> Income            保留样本 流失样本
#>   ￥0-11,999            44       78
#>   ￥12,000-35,999      132      200
#>   ￥36,000及以上        79      140

10.5.9 Built-in constants

R 中内置有如下常量：

pi

#> [1] 3.141593

LETTERS

#>  [1] "A" "B" "C" "D" "E" "F" "G" "H" "I" "J" "K" "L" "M" "N"
#> [15] "O" "P" "Q" "R" "S" "T" "U" "V" "W" "X" "Y" "Z"

letters

#>  [1] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n"
#> [15] "o" "p" "q" "r" "s" "t" "u" "v" "w" "x" "y" "z"

month.abb

#>  [1] "Jan" "Feb" "Mar" "Apr" "May" "Jun" "Jul" "Aug" "Sep"
#> [10] "Oct" "Nov" "Dec"

month.name

#>  [1] "January"   "February"  "March"     "April"    
#>  [5] "May"       "June"      "July"      "August"   
#>  [9] "September" "October"   "November"  "December"

10.6 Precedence of operators (optional)

目前学过的 operators 可以大致归为以下几类：

类	包括	如何查看帮助
`subsetting` （取子集）	`$` `@` `[[]]` `[]`	?`$`（`$`可替换为任意一个`subsetting operator`）或 `?Extract`
`Colon` （分号）	`:`	?`:` 或 `?Colon`
`Arithmetic` （算术）	`+`, `-`, ``, `/`, `^`, `%%`, `%/%`, `%%`	?`+` （`+`可替换为任意一个 Arithmetic operator）或`?Arithmetic`，`?matmult`
`Relational` （关系）	`>`, `<`, `<=`, `>=`, `==`, `!=`	?`>` （`>`可替换为任意一个 Relation operator）或 `?Comparison`
`Logical` （逻辑）	`!`, `&`, `&&`, `\|`, `\|\|`	?`!` （`!`可替换为任意一个 Logical operator）或 `?Logic`
`Assignment` （分配）	`<-`	?`<-` 或 `?assignOps`

注意：` ` 为反单引号，当某个 name 本身是非法字符（如已经定义的 operator）或者违背 name 命名规则时，就需要加反单引号来标识，否则会被当作是语句直接执行。

以上各 operator 在同一个语句中执行时是有优先顺序（precedence）的，就好比是加减乘除运算有优先顺序一样，同一个式子中先算乘除后算加减。 R 中各 operator 的优先顺序如下：

如果没有注意优先顺序，容易出现代码的执行结果和预期不一致的情况，例如：

a <- runif(10)
a
#  把最大值最小值所在位置找出来
position <- 1:length(a)[as.logical(a == max(a) + a == min(a))] 
position

#> Error in parse(text = input): <text>:4:52: unexpected '=='
#> 3: #  把最大值最小值所在位置找出来
#> 4: position <- 1:length(a)[as.logical(a == max(a) + a ==
#>                                                       ^

如果需要保证低优先度的操作被完整执行，不受高优先度代码的影响，需要使用()把低优先度的操作包起来：

a <- runif(10)
a

#>  [1] 0.8735112 0.3628250 0.9456221 0.5583189 0.5126612
#>  [6] 0.9477717 0.1098016 0.8189076 0.3773421 0.5566410

#  把最大值最小值所在位置找出来
position <- (1:length(a))[as.logical((a == max(a)) + (a == min(a)))]
position

#> [1] 6 7

更多有关 operator 优先顺序的内容请使用?Syntax查看。

如果在实际编程过程中，如果不能准确记住各 operator 之间的优先顺序也不要紧。可以在不确定的时候，将不确定的代码单独拿出来执行一下，确保和自己预期的结果一致，如果发现不一致，就说明存在低优先度的操作但没有用()的情况，然后再去查看问题到底出在哪一个操作。

10.7 Recap

常用操作	operators 或 functions
基本数学运算	`operator`：`+` `-` `` `/` `^` `%%` `%/%` `%%` 极值：`max()` `min()` 求和：`sum()` `rowSums()` `colSums()` 均值：`mean()` `rowMeans()` `colMeans()` 求积：`prod()` 取整：`round()` `ceiling()` `floor()` `trunc()` 自然指数和对数：`exp()` `log()` 开根号：`sqrt()` 三角函数：`sin()` `cos()` `tan()` 绝对值：`abs()` 符号：`sign()` 转置：`t()`
关系和逻辑	关系`operator`：`>` `<` `>=` `<=` `==` `!=` 逻辑`operator`：`&` `&&` `\|` `\|\|` `!`
定位、匹配和排序	定位：`which()` 匹配：`%in%` 排序：`sort()` `order()`
其他	合并：`c()` `cbind()` `rbind()` 个数：`length()` `nrow()` 或 `NROW()` `ncol()` 或 `NCOL()` `nchar()` 生成序列：`:` `seq()` `rep()` 随机抽样：`sample()` 拼接字符：`paste()` 输出：`print()` `cat()` “展露头脚”：`head()` `tail()` 内置常量：`pi` `letters` `LETTERS` `month.abb` `month.name` 连续变离散: `cut()`

大多数 operators 和 functions 支持 recycling rule,（详见@ref(byrow-recycling）；
round()的规则是 4 舍 6 入，逢 5 成双；
&（|）和&&（||）的区别是前者匹配所有位置上的元素对，后者只匹配第一个位置；
Relational operator 和 logical operator 常搭配在一起，用于按照指定条件 subsetting；
cbind()和rbind()的默认输出结果是 matrix，只有拼接的 object 中有 data.frame 时，输出结果才是 data.frame；
常用:、seq()、rep()和sample()产生位置索引，实现快速抽取和复制数据的目的；
通过 Source 执行活动脚本的全部代码时，要输出内容至 Console 需使用print()或cat()；
operators 间在执行上有优先顺序，同时使用多种 operators 时要注意检查结果是否符合预期；
使用()包裹住低优先度的代码可以保证这部分代码被完整执行。

9 Basic: subsetting

11 Basic: data analysis