Chapter 26 Surveys
| Sampling | Interviews | Data environment | |
|---|---|---|---|
| 1st era | area probability | face-to-face | stand-alone |
| 2nd ear | random digital dial probability | telephone | stand-alone |
| 3rd era | non-probability | computer-administered | linked |
Total survey error framework (Groves and Lyberg 2010)
Insight:
- Errors can come from bias or variance
- Total survey error = Measurement error + representation error
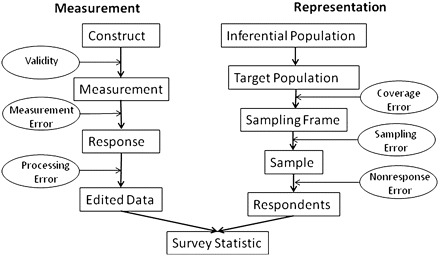
(Groves and Lyberg 2010, Fig. 3)
Probability and Non-probability Sampling
- Probability sample: every unit from a frame population has a known and non-zero probability of inclusion
- With weighting, we can recover bias in your sampling.
- Non-response problem
Horvitz-Thompson estimator (or bias estimator):
\[ \hat{\bar{y}} = \frac{\sum_{i \in s}y_i / \pi_i}{N} \]
where \(\pi_i\) = person i’s probability of inclusion (we have to estimate)
- Create a survey that leverages the power of people
Mass Collaboration
Human Computation: Train People -> Train Lots of People -> Train Machine
Cleaning
De-biasing
Combining
Open Call:
solutions are easier to check than generate
required specialized skills
Distributed Data Collection:
People go out and collect data
quality check
References
Groves, R. M., and L. Lyberg. 2010. “Total Survey Error: Past, Present, and Future.” Public Opinion Quarterly 74 (5): 849–79. https://doi.org/10.1093/poq/nfq065.