Skip to main content

Marketing Research

23 Formative vs. Reflective Measurements

Reflective Formative
Root Common factor model Principal Component Analysis (Weighted Linear Composites)
Direction Construct as causes of measures Measures as causes of construct
Dimensionality

Interchangeable

Measures = reflection of construct in its entirety (Unidimensionality of reflective measures)

Useful redundancy

 Multidimensionality of formative measures (this is a liability because it is analogous to multibarralled items) because the variance of the latent variable is determined by the paths (i.e., strength) from the measures, and variances and covariances of the measures.
Interchangeability

Measures are interchangeable

Dropping one measure should not change the construct

Measures can’t be interchanged

Missing one formative measure can change the meaning of the construct
Internal Consistency Reflective measures should correlate positively

No needs for the formative measures to correlate

Correlation among measures can be problem (multicollinearity).

Higher the correlation (among measures), more unstable the loadings on construct, larger standard errors.

The lack of internal consistency does not provide evidence for a set of measures to be formative.
Identification

identified only when either

  • at least 3 measures, and fix scale variance to 1 or fix a loading to 1.

  • 2 measures, and loadings, are set equal to each other, or latent variable covary with anther latent variables that has at least 2 reflective measures.

are not identified, unless 2 additional reflective measures are added to be caused by the construct- multiple indicator multiple cause (MIMIC) model.

Hence, the choice of reflective measures for identification concern can change the loadings relating the measures to its latent variable, which in turn, change the construct itself. Hence, specifying the reflective measures in MIMIC model is monumental
Measurement Error independent measurement errors No measurement error (i.e., error-free indicators)
Construct Validity construct validity is manifested by the the magnitudes of the loadings relating the measures to the construct, which determined by the covariances among measures (e.g., the higher covariances the stronger correspondence)
  1. strength between construct and its measures
  2. proportion of variance in the construct attributed to the residual \(\zeta\) (smaller better)
  3. In relation to other variables (nomological validity and criterion-oriented validity)
  4. Indirect effect of formative measure on reflective measure via the construct.

Drawbacks:

  • estimates are sensitive to the chose of reflective measures as mentioned in the identification section.

  • Nomological network could not be empirically validated because of the conceptual heterogeneity in the formative measures.
Causality

construct to measures

construct = latent variable

From a realist perspective, construct = real entity (i.e., could influence) (e.g., psychological state), measures = scores

measures to construct

construct = composite variable

From an operationalist or instrumentalist perspective, formative measures define the construct (i.e., composite score)

I’d suggest to think of formative constructs as processes

Under constructivist perspective, constructs can be ascribed theoretical meaning, but would only be a conceptual entity

But the causal thinking is inappropriate (because measures and construct are not 2 distinct entities), they are part-whole correspondence

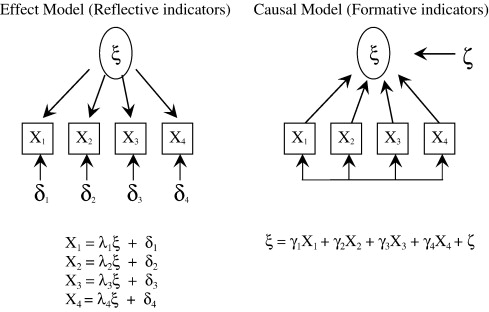
depiction by Coltman et al. (2008)


According to (Edwards 2010),

\[ x_i = \lambda_i \xi + \delta_i \]

where

  • \(x_i\) = reflective measure

  • \(\xi\) = construct

  • \(\lambda_i\) = effect of \(\xi\) on \(x_i\)

  • \(\delta_i\) = uniqueness of the measure (error)

\[ \eta = \gamma_i x_i + \zeta \]

where

  • \(\eta\) = construct

  • \(\gamma_i\) = effect of \(x_i\) on \(\eta\)

  • \(\zeta\) = residual (unexplained part of \(\eta\))

In case that \(\eta\) is a perfect weighted linear combination of \(x_i\), then

\[ \eta = \gamma_i x_i \]

23.1 Alternative to formative model

  • Model with first-order constructs instead of measures, and each with single reflective measures

    • can’t estimate the loadings and unique variances of the reflective measures

  • Model with first-order constructs instead of measure, but each with three reflective measures, and second-order construct also has two reflective measures.

    • sometimes, first-order construct can’t be measured multiple times (e.g., income, age)


Validity

Validity should be be established in the following order:

  1. Construct Validity (also known as face validity, or concept validity): requires concepts and theory is strong

  2. Convergent Validity: (e.g., AVE statistics >.5)

  3. Discriminant/Divergent Validity:

  4. Nomological Validity: (might also involve moderation).

  5. Known Group Validity

Reliability

  • Test-retest reliability

  • Internal consistency reliability: standardized Cronbach \(\alpha\) (> 0.7 if well establish, and .6 if newly developed)

  • Composite construct reliability

Seminar paper in marketing

23.2 Partial Least Squared

The difference between PLS and Principal Components Regression is that Principal Components Regression focuses on variance while reducing dimensionality. PLS focuses on covariance while reducing dimensionality.

Hair Jr. et al. (2017)

  • Partial Least Squared- Structural Equation Modeling vs. Covariance-based Structural Modeling

  • PLS-SEM vs. CB-SEM

CB-SEM PLS-SEM
Base Model Common Factor Model Composite Factor Model


McIntosh, Edwards, and Antonakis (2014)

  • Reflections on Partial least Squares Path Modeling (PLS-PM)

  • There is still a debate to whether

    1. PLS-PM is a SEM method

    2. PLS-PM can reduce the impact of measurement error: yes (increase reliability)

    3. PLS-PM can validate measurement models

    4. PLS-PM provides valid inference on path coefficients

    5. PLS-PM is better than SEM at handling small sample sizes

    6. PLS-PM can be used for exploratory modeling

  • Model fit can be based on

    • global chi-square fit statistic

    • local chi-square fit statistic

    • explained variance