21 Analytical Models

Marketing models consists of

1. Analytical Model: pure mathematical-based research
2. Empirical Model: data analysis.

“A model is a representation of the most important elements of a perceived real-world system”.

Marketing model improves decision-making

• Econometric models

  • Description
  • Prediction
  • Simulation

• Optimization models

  • maximize profit using market response model, cost functions, or any constraints.

• Quasi- and Field experimental analyses

• Conjoint Choice Experiments.

“A decision calculus will be defined as a model-based set of procedures for processing data and judgments to assist a manager in his decision making”(Little 1976):

• simple
• robust
• easy to control
• adaptive
• as complete as possible
• easy to communicate with

		Type of game
		Static	Dynamic
Info Content	Complete	Nash	Subgame perfect
	Incomplete	Bayesian Nash (Auctions)	Perfect Bayesian (signaling)

(K. S. Moorthy 1993)

• Mathematical Theoretical Models

• Logical Experimentation

• An environment as a model, specified by assumptions

  • Math assumptions for tractability

  • Substantive assumptions for empirical testing

• Decision support modeling describe how things work, and theoretical modeling present how things should work.

• Compensation package including salaries and commission is a tradeoff between reduced income risk and motivation to work hard.

• Internal and External Validity are questions related to the boundaries conditions of your experiments.

• “Theories are tested by their predictions, not by the realism of their super model assumptions.” (Friedman, 1953)

(McAfee and McMillan 1996)

• Competition is performed under uncertainty

• Competition reveals hidden information

  • Independent-private-values case: selling price = second highest valuation

  • It’s always better for sellers to reveal information since it reduces chances of cautious bidding that is resulted from the winner’s curse

• Competition is better than bargaining

  • Competition requires less computation and commitment abilities

• Competition creates effort incentives

(Leeflang et al. 2000)

• Types of model:

  • Predictive model

    • Sales model: using time series data

    • Trial rate: using exponential growth.

    • Product growth model: Bass (1969)

  • Descriptive model

    • Purchase incidence and purchase timing : use Poisson process

    • Brand choice: Markov models or learning models.

    • Pricing decisions in an oligopolistic market Howard and Morgenroth (1968)

  • Normative model

    • Profit maximization based on price, adverting and quality (Dorfman and Steiner 1976), extended by (H. V. Roberts, Ferber, and Verdoorn 1964; Lambin 1970)

Later, Little (1970) introduced decision calculus and then multinomial logit model (Peter M. Guadagni and Little 1983)

Potential marketing decision automation:

• Promotion or pricing programs

• Media allocation

• Distribution

• Product assortment

• Direct mail solicitation

(K. S. Moorthy 1985)

• Definitions:

  • Rationality = maximizing subjective expected utility

  • Intelligence = recognizing other firms are rational.

  • Rules of the game include

    • # of firms

    • feasible set of actions

    • utilities for each combination of moves

    • sequence of moves

    • the structure of info (who knows what and when?)

  • Incomplete info stems from

    • unknown motivations

    • unknown ability (capabilities)

    • different knowledge of the world.

  • Pure strategy = plan of action

  • A mixed strategy = probability dist of pure strategies.

  • Strategic form representation = sets of possible strategies for every firm and its payoffs.

  • Equilibrium = a list of strategies in which “no firm would like unilaterally to change its strategy.”

• Equilibrium is not outcome of a dynamic process.

• Equilibrium Application

  • Oligopolistic Competition

    • Cournot (1838): quantities supplied: Cournot equilibrium. Changing quantities is more costly than changing prices

    • Bertrand (1883): Bertrand equilibrium: pricing.

  • Perfect competition

  • Product Competition: Hotelling (1929): Principle of Minimum Differentiation is invalid.

  • Entry:

    • first mover advantage

    • deterrent strategy

    • optimal for entrants or incumbents

  • Channels

• Perfectness of equilibria

  • Subgame perfectness

  • Sequential rationality

  • Trembling-hand perfectness

  • Application

    • Product and price competition in Oligopolies

    • Strategic Entry Deterrence

• Dynamic games

  • Long-term competition in oligopolies

  • Implicit Collusion in practice : price match from leader firms

• Incomplete Information

  • Durable goods pricing by a monopolist

  • predatory pricing and limit pricing

  • reputation, product quality, and prices

  • Competitive bidding and auctions

21.1 Building An Analytical Model

Notes by professor Sajeesh Sajeesh

Step 1: Get “good” idea (either from literature or industry)

Step 2: Assess the feasibility of the idea

• Is it interesting?

• Can you tell a story?

• Who is the target audience?

• Opportunity cost

Step 3: Don’t look at the literature too soon

• Even when you have an identical model as in the literature, it’s ok (it allows you to think)

Step 4: BUild the model

• Simplest model first: 1 period, 2 product , linear utility function for consumers

• Write down the model formulation

• Everything should be as simple as possible .. but no simpler

Step 5: Generalizing the model

• Adding complexity

Step 6: Searching the literature

• If you find a paper, you can ask yourself why you didn’t do what the author has done.

Step 7: Give a talk /seminar

Step 8: Write the paper

21.2 Hotelling Model

(KIM and SERFES 2006): A location model with preference variety

(Hotelling 1929)

• Stability in competition

• Duopoly is inherently unstable

• Bertrand disagrees with Cournot, and Edgeworth elaborates on it.

  • because Cournot’s assumption of absolutely identical products between firms.

seller try to \(p_2 < p_1 c(l-a-b)\)

the point of indifference

\[ p_1 + cx = p_2 + cy \]

• c = cost per unit of time in each unit of line length

• p = price

• q = quantity

• x, y = length from A and B respectively

\[ a + x + y + b = l \]

is the length of the street

Hence, we have

\[ x = 0.5(l - a - b + \frac{p_2- p_1}{c}) \\ y = 0.5(l - a - b + \frac{p_1- p_2}{c}) \]

Profits will be

\[ \pi_1 = p_1 q_1 = p_1 (a+ x) = 0.5 (l + a - b) p_1 - \frac{p_1^2}{2c} + \frac{p_1 p_2}{2c} \\ \pi_2 = p_2 q_2 = p_2 (b+ y) = 0.5 (l + a - b) p_2 - \frac{p_2^2}{2c} + \frac{p_1 p_2}{2c} \]

To set the price to maximize profit, we have

\[ \frac{\partial \pi_1}{\partial p_1} = 0.5 (l + a - b) - \frac{p_1}{c} + \frac{p_2}{2c} = 0 \\ \frac{\partial \pi_2}{\partial p_2} = 0.5 (l - a + b) - \frac{p_2}{c} + \frac{p_1}{2c} = 0 \]

which equals

\[ p_1 = c(l + \frac{a-b}{3}) \\ p_2 = c(l - \frac{a-b}{3}) \]

and

\[ q_1 = a + x = 0.5 (l + \frac{a -b}{3}) \\ q_2 = b + y = 0.5 (l - \frac{a-b}{3}) \]

with the SOC satisfied

In case of deciding locations, socialism works better than capitalism

(d’Aspremont, Gabszewicz, and Thisse 1979)

• Principle of Minimum Differentiation is invalid

\[ \pi_1 (p_1, p_2) = \begin{cases} ap_1 + 0.5(l-a-b) p_1 + \frac{1}{2c}p_1 p_2 - \frac{1}{2c}p_1^2 & \text{if } |p_1 - p_2| \le c(l-a-b) \\ lp_1 & \text{if } p_1 < p_2 - c(l-a-b) \\ 0 & \text{if } p_1 > p_2 + c(l-a-b) \end{cases} \]

and

\[ \pi_2 (p_1, p_2) = \begin{cases} bp_2 + 0.5(l-a-b) p_2 + \frac{1}{2c}p_1 p_2 - \frac{1}{2c}p_2^2& \text{if } |p_1 - p_2| \le c(l-a-b) \\ lp_2 & \text{if } p_2 < p_1 - c(l-a-b) \\ 0 & \text{if } p_2 > p_1 + c(l-a-b) \end{cases} \]

21.3 Positioning Models

Tabuchi and Thisse (1995)

• Relax Hotelling’s model’s assumption of uniform distribution of consumers to non-uniform distribution.

• Assumptions:

  • Equal cost

  • Consumers distributed over [0,1]

  • \(F(x)\) = cumulative distribution of consumers where \(F(1) = 1\) = total population

  • 2 distributions:

    • Traditional uniform density: \(f(x) =1\)

    • New: triangular density: \(f(x) = 2 - 2|2x-1|\) which represents consumer concentration

  • Transportation cost = quadratic function of distance.

Hence, marginal consumer is

\[ \bar{x} = (p_2 - p_1 + x^2_2-x_1^2)/2(x_2-x_1) \]

then when \(x_1 < x_2\) the profit function is

\[ \Pi_1 = p_1 F(\bar{x}) \]

and

\[ \Pi_2 = p_2[1-F(\bar{x})] \]

and vice versa for \(x_1 >x_2\), and Bertrand game when \(x_1 = x_2\)

• If firms pick simultaneously their locations, and then simultaneously their prices, and consumer density function is log-concave, then there is a unique Nash price equilibrium

  • Under uniform distribution, firms choose to locate as far apart as possible (could be true when observing shopping centers are far away from cities), but then consumers have to buy products that are far away from their ideal.

  • Under triangular density, no symmetric location can be found, but two asymmetric Nash location equilibrium can still be possible (decrease in equilibrium profits of both firms)

• If firms pick sequentially their locations, and pick their prices simultaneously,

  • Under both uniform and triangular, first entrant will locate at the market center

Sajeesh and Raju (2010)

• Model satiation (variety-seeking) as a relative reduction in the willingness to pay of the previously purchased brand. also known as negative state dependence

• Previous studies argue that in the presence of variety seeking consumers, firms should enjoy higher prices and profits, but this paper argues that average prices and profits are lower.

  • Firms should charge lower prices in the second period to prevent consumers from switching.

Assumptions:

• Period 0, choose location simultaneously

• Period 1, choose prices simultaneously

• Period 2, firms choose prices simultaneously

K. S. Moorthy (1988)

• 2 (identical) firms pick product (quality) first, then price.

Tyagi (2000)

• Extending Hotelling (1929) Tyagi (1999b) Tabuchi and Thisse (1995)

• Two firms enter sequentially, and have different cost structures.

• Paper shows second mover advantage

KIM and SERFES (2006)

• Consumers can make multiple purchases.

• Some consumers are loyal to one brand, and others consume more than one product.

Shreay, Chouinard, and McCluskey (2015)

• Quantity surcharges from different sizes of the same product (i.e., imperfect substitute or differentiated products) can be led by consumer preferences.

21.4 Market Structure and Framework

Basic model utilizing aggregate demand

• Bertrand Equilibrium: Firms compete on price

• Cournot Market structure: Firm compete on quantity

• Stackelberg Market structure: Leader-Follower model

Because we start with the quantity demand function, it is important to know where it’s derived from Richard and Martin (1980)

K. S. Moorthy (1988)

• studied how two firms compete on product quality and price (both simultaneous and sequential)

21.4.1 Cournot - Simultaneous Games

\[ TC_i = c_i q_i \text{ where } i= 1,2 \\ P(Q) = a - bQ \\ Q = q_1 +q_2 \\ \pi_1 = \text{price} \times \text{quantity} - \text{cost} = [a - b(q_1 +q_2)]q_1 - c_1 q_1 \\ \pi_2 = \text{price} \times \text{quantity} - \text{cost} = [a - b(q_1 +q_2)]q_1 - c_2 q_2 \\ \]

\[\begin{equation} \frac{d \pi_1}{d q_1} = a - 2bq_1 - bq_2-c_1 = 0 (1) \tag{21.1} \end{equation}\] \[\begin{equation} \frac{d \pi_2}{d q_2} = a - 2bq_2 - bq_1-c_2 = 0 \tag{21.2} \end{equation}\]

From (21.1)

\[\begin{equation} q_1 = \frac{a-c_1}{2b} - \frac{q_2}{2} = R_1 (q_2) \tag{21.3} \end{equation}\]

is called reaction function, for best response function

From (21.2)

\[\begin{equation} q_2 = \frac{a-c_2}{2b} - \frac{q_1}{2} = \tag{21.4} \end{equation}\]

\[ q_1 = \frac{a-c_1}{2b} - \frac{a-c_2}{4b} + \frac{q_1}{4} \]

Hence,

\[ q_1^* = \frac{a-2c_1+ c_2}{3b} \\ q_2^* = \frac{a-2c_2 + c_1}{3b} \]

Total quantity is

\[ Q = q_1 + q_2 = \frac{2a-c_1 -c_2}{3b} \]

Price

\[ a-bQ = \frac{a+c_1+c_2}{3b} \]

21.4.2 Stackelberg - Sequential games

also known as leader-follower games

• Stage 1: Firm 1 chooses quantity

• Stage 2: Firm 2 chooses quantity

\[ c_2 = c_1 = c \]

Stage 2: reaction function of firm 2 given quantity firm 1

\[ R_2(q_1) = \frac{a-c}{2b} - \frac{q_1}{2} \]

Stage 1:

\[ \pi_1 = [a-b(q_1 + \frac{a-c}{2b} - \frac{q_1}{2})]q_1 - cq_1 \\ = [a-b( \frac{a-c}{2b} + \frac{q_1}{2}]q_1 + cq_1 \]

\[ \frac{d \pi_1}{d q_1} = 0 \]

Hence,

\[ \frac{a+c}{2} - b q_1 -c =0 \]

The Stackelberg equilibrium is

\[ q_1^* = \frac{a-c}{2b} \\ q_2^* = \frac{a-c}{4b} \]

Under same price (c), Cournot =

\[ q_1 = q_2 = \frac{a-c}{3b} \]

Leader produces more whereas the follower produces less compared to Cournot

\[ \frac{d \pi_W^*}{d \beta} <0 \]

for the entire quantity range \(d < \bar{d}\)

As \(\beta\) increases in \(\pi_W^*\) Firm W wants to reduce \(\beta\).

Low \(\beta\) wants more independent

Firms W want more differentiated product

On the other hand,

\[ \frac{d \pi_S^*}{d \beta} <0 \]

for a range of \(d < \bar{d}\)

Firm S profit increases as \(\beta\) decreases when d is small

Firm S profit increases as \(\beta\) increases when d is large

Firm S profit increases as as product are more substitute when d is large

Firm S profit increases as products are less differentiated when d is large

21.5 More Market Structure

Dixit (1980)

• Based on Bain-Sylos postulate: incumbents can build capacity such that entry is unprofitability

• Investment in capacity is not a credibility threat if incumbents can change their capacity.

• Incumbent cannot deter entry

Tyagi (1999a)

• More retailers means greater competition, which leads to lower prices for customers.

• Effect of \((n+1)\) st retailer entry

  1. Competition effect (lower prices)

  2. Effect on price (i.e., wholesale price), also known as input cost effect

• Manufacturers want to increase wholesale price because now manufacturers have higher bargaining power, which leads other retailers to reduce quantity (bc their choice of quantity is dependent on wholesale price), and increase in prices.

Jerath, Sajeesh, and Zhang (2016)

• Organized Retailer enters a market

• Inefficient unorganized retailers exit

• Remaining unorganized retailers increase their prices. Thus, customers will be worse off.

Amaldoss and Jain (2005)

• consider desire for uniqueness and conformism on pricing conspicuous goods

• Two routes:

  • higher desire for uniqueness leads to higher prices and profits

  • higher desire for conformity leads to lower prices and profits

• Under the analytical model and lab text, consumers’ desire for unique is increased from price increases, not the other way around.

Snob:

\[ U_A = V - p_A - \theta t_s - \lambda_s(n_A) \\ U_B = V - p_B - (1-\theta) t_s - \lambda_s(n_B) \]

where

• \(\lambda_s\) = sensitivity towards externality.

• \(\theta\) is the position in the Hotelling’s framework.

• \(t_s\) is transportation cost.

Conformist

\[ U_A = V - p_A - \theta t_s + \lambda_c(n_A) \\ U_B = V - p_B - (1-\theta) t_s + \lambda_c(n_B) \]

Rational Expectations Equilibrium

If your expectations are rational, then your expectation will be realized in equilibrium

Say, Marginal Snob = \(\theta_s\) and \(\beta\) = number of snob in the market

Snobs

\[ U_A^c \equiv U_B^c = \theta_s \]

Conformists

\[ U_A^c =U_B^c = \theta_c \]

Then, according to rational expectations equilibrium, we have

\[ \beta \theta_s +( 1- \beta) \theta_c = n_A \\ \beta (1-\theta_s) +( 1- \beta) (1-\theta_c) = n_B \]

where

• \(\beta \theta_s\) = Number of snobs who buy from firm A

• \((1-\beta)\theta_c\) = Number of conformists who buy from firm B

• \(\beta(1-\theta_s)\) = Number of snobs who buy from firm B

• \((1-\beta)(1-\theta_c)\) = Number of conformists who buy from firm B

which is the rational expectations equilibrium (whatever we expect happens in reality).

In other words, expectation are realized in equilibrium.

The number of people expected to buy the product is endogenous in the model, which will be the actual number of people who will buy it in the market.

We should not think of the expected value here in the same sense as expected value in empirical research (\(E(.)\)) because the expected value here is without any errors (specifically, measurement error).

• The utility function for snobs is such that overall when price increase for one product, snob will like to buy the product more. When price increases, conformist will reduce the purchase.

Balachander and Stock (2009)

• Adding a Limited edition product has a positive effect on profits (via increased willingness of consumers to pay for such a product), but negative strategic effect (via increasing price competition between brands)

• Under quality differentiation, high-quality brand gain from LE products

• Under horizontal taste differentiation, negative strategic effects lead to lower equilibrium profits for both brands, but they still have to introduce LE products because of prisoners’ dilemma

Sajeesh, Hada, and Raju (2020)

• two consumer segments:

  • functionality-oriented

  • exclusivity-oriented

• Firm increase value enhancements when functionality-oriented consumers perceive greater product differentiation

• Firms decrease value enhancements if exclusivity-oriented perceive greater product differentiation

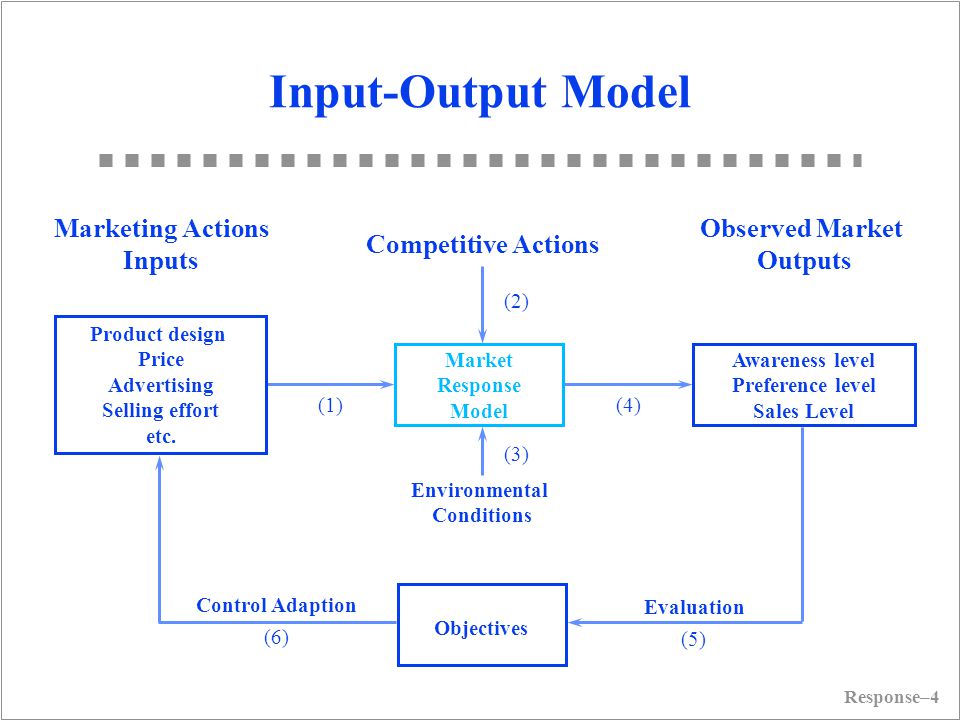
21.6 Market Response Model

Marketing Inputs:

• Selling effort
• advertising spending
• promotional spending

Marketing Outputs:

• sales
• share
• profit
• awareness

Give phenomena for a good model:

• P1: Dynamic sales response involves a sales growth rate and a sales decay rate that are different
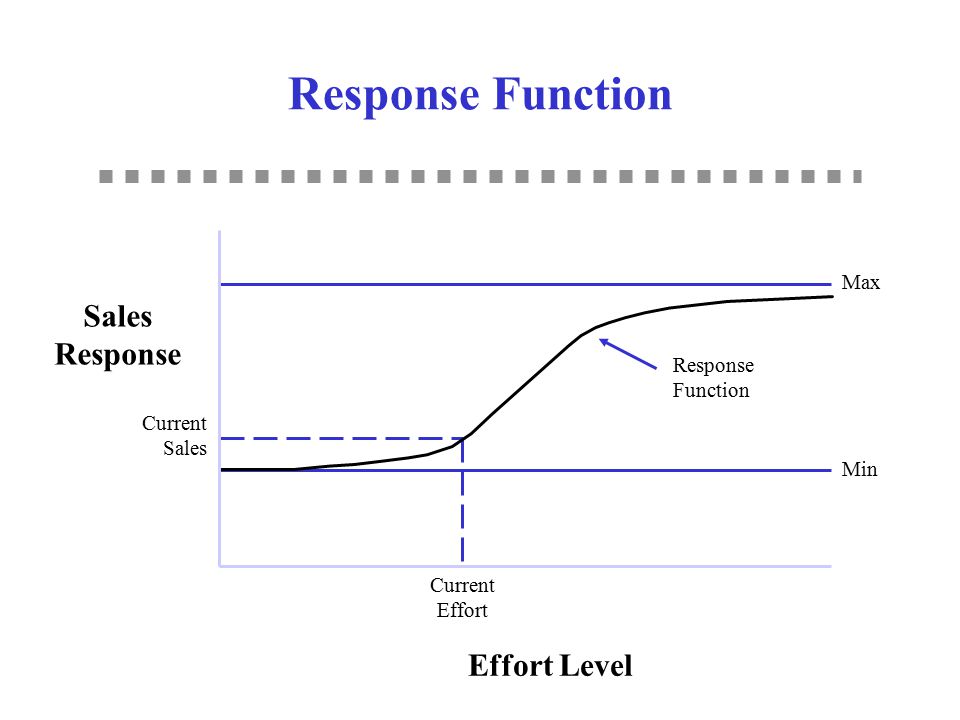
• P2: Steady-state response can be concave or S-shaped. Positive sales at 0 adverting.
• P3: Competitive effects
• P4: Advertising effectiveness dynamics due to changes in media, copy, and other factors.
• P5: Sales still increase or fall off even as advertising is held constant.

Saunder (1987) phenomena

• P1: Output = 0 when Input = 0
• P2: The relationship between input and output is linear
• P3: Returns decrease as the scale of input increases (i.e., additional unit of input gives less output)
• P4: Output cannot exceed some level (i.e., saturation)
• P5: Returns increase as scale of input increases (i.e., additional unit of input gives more output)
• P6: Returns first increase and then decrease as input increases (i.e., S-shaped return)
• P7: Input must exceed some level before it produces any output (i.e., threshold)
• P8: Beyond some level of input, output declines (i.e., supersaturation point)

Aggregate Response Models

• Linear model: \(Y = a + bX\)

  • Through origin

  • can only handle constant returns to scale (i.e., can’t handle concave, convex, and S-shape)

• The Power Series/Polynomial model: \(Y = a + bX + c X^2 + dX^3 + ...\)

  • can’t handle saturation and threshold

• Fraction root model/ Power model: \(Y = a+bX^c\) where c is prespecified

  • c = 1/2, called square root model

  • c = -1, called reciprocal model

  • c can be interpreted as elasticity if a = 0.

  • c = 1, linear

  • c <1, decreasing return

  • c>1, increasing returns

• Semilog model: \(Y = a + b \ln X\)

  • Good when constant percentage increase in marketing effort (X) result in constant absolute increase in sales (Y)

• Exponential model: \(Y = ae^{bX}\) where X >0

  • b > 0, increasing returns and convex

  • b < 0, decreasing returns and saturation

• Modified exponential model: \(Y = a(1-e^{-bX}) +c\)

  • Decreasing returns and saturation

  • upper bound = a + c

  • lower bound = c

  • typically used in selling effort

• Logistic model: \(Y = \frac{a}{a+ e^{-(b+cX)}}+d\)

  • increasing return followed by decreasing return to scale, S-shape

  • saturation = a + d

  • good with saturation and s-shape

• Gompertz model

• ADBUDG model (Little 1970) : \(Y = b + (a-b)\frac{X^c}{d + X^c}\)

  • c > 1, S-shaped

  • 0 < c < 1

    • Concave

    • saturation effect

    • upper bound at a

    • lower bound at b

  • typically used in advertising and selling effort.

  • can handle, through origin, concave, saturation, S-shape

• Additive model for handling multiple Instruments: \(Y = af(X_1) + bg(X_2)\)

• Multiplicative model for handling multiple instruments: \(Y = aX_1^b X_2^c\) where c and c are elasticities. More generally, \(Y = af(X_1)\times bg(X_2)\)

• Multiplicative and additive model: \(Y = af(X_1) + bg(X_2) + cf(X_1) g(X_2)\)

• Dynamic response model: \(Y_t = a_0 + a_1 X_t + \lambda Y_{t-1}\) where \(a_1\) = current effect, \(\lambda\) = carry-over effect

Dynamic Effects

• Carry-over effect: current marketing expenditure influences future sales

  • Advertising adstock/ advertising carry-over is the same thing: lagged effect of advertising on sales

• Delayed-response effect: delays between when marketing investments and their impact

• Customer holdout effects

• Hysteresis effect

• New trier and wear-out effect

• Stocking effect

Simple Decay-effect model:

\[ A_t = T_t + \lambda T_{t-1}, t = 1,..., \]

where

• \(A_t\) = Adstock at time t
• \(T_t\) = value of advertising spending at time t
• \(\lambda\) = decay/ lag weight parameter

Response Models can be characterized by:

1. The number of marketing variables

2. whether they include competition or not

3. the nature of the relationship between the input variables

   1. Linear vs. S-shape

4. whether the situation is static vs. dynamic

5. whether the models reflect individual or aggregate response

6. the level of demand analyzed

   1. sales vs. market share

Market Share Model and Competitive Effects: \(Y = M \times V\) where

• Y = Brand sales models

• V = product class sales models

• M = market-share models

Market share (attraction) models

\[ M_i = \frac{A_i}{A_1 + ..+ A_n} \]

where \(A_i\) attractiveness of brand i

Individual Response Model:

Multinomial logit model representing the probability of individual i choosing brand l is

\[ P_{il} = \frac{e^{A_{il}}}{\sum_j e^{A_{ij}}} \]

where

• \(A_{ij}\) = attractiveness of product j for individual i \(A_{ij} = \sum_k w_k b_{ijk}\)
• \(b_{ijk}\) = individual i’s evaluation of product j on product attribute k, where the summation is over all the products that individual i is considering to purchase
• \(w_k\) = importance weight associated with attribute k in forming product preferences.

21.7 Technology and Marketing Structure and Economics of Compatibility and Standards

Amaldoss and Jain (2005)

Balachander and Stock (2009)

Sajeesh, Hada, and Raju (2020)

21.8 Conjoint Analysis and Augmented Conjoint Analysis

More technical on 27.1

Jedidi and Zhang (2002)

• Augmenting Conjoint Analysis to Estimate Consumer Reservation Price

• Using conjoint analysis (coefficients) to derive at consumers’ reservation prices for a product in a category.

• Can be applied in the context of

  • product introduction

  • calculating customer switching effect

  • the cannibalization effect

  • the market expansion effect

\[ Utility(Rating) = \alpha + \beta_i Attribute_i \]

where \(\alpha\)

Netzer and Srinivasan (2011)

• Break conjoint analysis down to a sequence of constant-sum paired comparison questions.

• Can also calculate the standard errors for each attribute importance.

21.9 Distribution Channels

McGuire and Staelin (1983)

Assumptions:

1. Two manufacturing (wholesaling) firms differentiated and competing products: Upstream firms (manufacturers) and downstream channel members (retailers)

3 types of structure:

1. Both manufacturers with privately owned retailers (4 players: 2 manufacturers, 2 retailers)
2. Both vertically integrated (2 manufacturers)
3. Mix: one manufacturer with a private retailer, and one manufacturer with vertically integrated company store (3 players)

Each retail outlet has a downward sloping demand curve:

\[ q_i = f_i(p_1,p_2) \]

Under decentralized system (4 players), the Nash equilibrium demand curve is a function of wholesale prices:

\[ q_i^* = g_i (w_1, w_2) \]

More rules:

1. Assume 2 retailers respond, but not the competing manufacturer

And unobserved wholesale prices and market is not restrictive, and Nash equilibrium whole prices is still possible.

Under mixed structure, the two retailers compete, and non-integrated firm account for all responses in the market

Under integrated structure, this is a two-person game, where each chooses the retail price

Decision variables are prices (not quantities)

Under what conditions a manufacturer want to have intermediaries

Retail demand functions are assumed to be linear in prices

Demand functions are

\[ q_1' = \mu S [ 1 - \frac{\beta}{1 - \theta} p_1' + \frac{\beta \theta}{1- \theta}p_2'] \]

\[ q_2' = (1- \mu) S [ 1+ \frac{\beta \theta}{1- \theta} p_1' - \frac{\beta}{1- \theta} p_2'] \]

where

• \(0 \le \mu , \theta \le 1; \beta, S >0\)

• S is a scale factor, which equals industry demand (\(q' \equiv q_1' + q_2'\)) when prices are 0.

• \(\mu\) = absolute difference in demand

• \(\theta\) = substutability of products (reflected by the cross elasticities), or the ratio of the rate of change of quantity with respect to the competitor’s price to the rate of change of quantity with respect to own price.

  • \(\theta = 0\) means independent demands (firms are monopolists)

  • \(\theta \to 1\) means maximally substitutable

3 more conditions:

\[ P = \{ p_1', p_2' | p_i' -m' - s' \ge 0, i = 1,2; (1-\theta) - \beta p_1' \beta \theta p_2' \ge 0, (1- \theta) + \beta \theta p_1' - \beta p_2' \ge 0 \} \]

where \(m', s'\) are fixed manufacturing and selling costs per unit

To have a set of \(P\), then

\[ \beta \le \frac{1}{m' + s'} \]

and to have industry demand no increase with increases in either price then

\[ \frac{\theta}{1 + \theta} \le \mu \le \frac{1}{1 + \theta} \]

After rescaling, the industry demand is

\[ q = 2 (1- \theta) (p_1+ p_2) \]

Results:

• When each manufacturer is a monopolist (\(\theta = 0\)), it’s twice as profitable for each to sell through its own channel

• When demand is maximally affected by the actions of the competing retailers (\(\theta \to 1\)), it’s 3 times as profitable to have private dealers.

• The breakeven point happens at \(\theta = .708\)

• In conclusion, the optimal distribution system depends of the degree of substitubability at the retail level.

Jeuland and Shugan (2008)

• Quantity discounts is offered because

  1. Cost-based economies of scale

  2. Demand based - large purchases tend to be more price sensitive

  3. Strategic reason- single sourcing

  4. Channel Coordination (this is where this paper contributes to the literature

K. S. Moorthy (1987)

• Price discrimination - second degree

Geylani, Dukes, and Srinivasan (2007)

Jerath and Zhang (2010)

21.10 Advertising Models

Three types of advertising:

1. Informative Advertising: increase overall demand of your brand
2. Persuasive Advertising: demand shifting to your brand
3. Comparison: demand shifting away from your competitor (include complementary)

n customers distributed uniformly along the Hotelling’s line (more likely for mature market where demand doesn’t change).

\[ U_A = V - p_A - tx \\ U_B = V - p_B - t(1-x) \]

For Persuasive advertising (highlight the value of the product to the consumer):

\[ U_A = A_A V - p_A - tx \]

or increase value (i.e., reservation price).

\[ U_A = \sqrt{Ad_A} V - p_A - tx \]

or more and more customers want the product (i.e., more customers think firm A product closer to what they want)

\[ U_A = V - p_A - \frac{tx}{\sqrt{Ad_A}} \]

Comparison Advertising:

\[ U_A = V - p_A - t\sqrt{Ad_{B}}x \\ U_B = V - p_B - t \sqrt{Ad_A}(1 - x) \]

Find marginal consumers

\[ V - p_A - t\sqrt{Ad_{B}}x = V - p_B - t \sqrt{Ad_A}(1 - x) \]

\[ x = \frac{1}{t \sqrt{Ad_A} + t \sqrt{Ad_B}} (-p_A + p_B + t \sqrt{Ad_A}) \]

then profit functions are (make sure the profit function is concave)

\[ \pi_A = p_A x n - \phi Ad_A \\ \pi_B = p_B (1-x) n - \phi Ad_B \]

where

• \(\phi\) = per unit cost of advertising (e.g., TV advertising vs. online advertising in this case, TV advertising per unit cost is likely to be higher than online advertising per unit cost)

• t can also be thought of as return on advertising (traditional Hotelling’s model considers t as transportation cost)

Equilibrium prices conditioned on advertising

\[ \frac{d \pi_A}{p_A} = - \frac{d}{p_A} () \\ \frac{d \pi_B}{p_B} = \frac{d}{p_B} \]

Then optimal pricing solutions are

\[ p_A = \frac{2}{3} t \sqrt{Ad_A} + \frac{1}{3} t \sqrt{Ad_B} \\ p_B = \frac{1}{3} t \sqrt{Ad_A} + \frac{2}{3} t \sqrt{Ad_B} \]

Prices increase with the intensities of advertising (if you invest more in advertising, then you charge higher prices). Each firm price is directly proportional to their advertising, and you will charger higher price when your competitor advertise as well.

Then, optimal advertising (with the optimal prices) is

\[ \frac{d \pi_A}{d Ad_A} \\ \frac{d \pi_B}{d Ad_B} \]

Hence, Competitive equilibrium is

\[ Ad_A = \frac{25 t^2 n^2}{576 \phi^2} \\ Ad_B = \frac{25t^2 n^2}{576 \phi^2} \\ p_A = p_B = \frac{5 t^2 n }{24 \phi} \]

As cost of advertising (\(\phi\)), firms spend less on advertising

Higher level of return on advertising (\(t\)), firms benefit more from advertising

With advertising in the market, the equilibrium prices are higher than if there were no advertising.

Since colluding on prices are forbidden, and colluding on advertising is hard to notice, firms could potential collude on advertising (e.g., pulsing).

Assumption:

1. Advertising decision before pricing decision (reasonable because pricing is earlier to change, while advertising investment is determined at the beginning of each period).

Collusive equilibrium (instead of using \(Ad_A, Ad_B\), use \(Ad\) - set both advertising investment equal):

\[ Ad_A = Ad_B = \frac{t^2 n^2}{16 \phi^2} > \frac{25t^2 n^2}{576 \phi^2} \]

Hence, collusion can be make advertising investment equilibrium higher, which makes firms charge higher prices, and customers will be worse off. (more reference Aluf and Shy - check Modeling Seminar Folder - Advertising).

Combine both Comparison and Persuasive Advertising

\[ U_A = V - p_A - tx \frac{\sqrt{Ad_B}}{\sqrt{Ad_A}} \\ U_B = V - p_B - t(1-x) \frac{\sqrt{Ad_A}}{\sqrt{Ad_B}} \]

Informative Advertising

1. Increase number of n customers (more likely for new products where the number of potential customers can change)

How do we think about customers, how much to consume. People consume more when they have more availability, and less when they have less in stock (Ailawadi and Neslin 1998)

Villas-Boas (1993)

• Under monopoly, firms would be better off to pulse (i.e., alternate advertising between a minimum level and efficient amount of advertising) because of the S-shaped of the advertising response function.

Model assumptions:

1. The curve of the advertising response function is S-shaped
2. Markov strategies: what firms do in this period depends on what might affect profits today or in the future (independent of the history)

Propositions:

1. “If the loss from lowering the consideration level is larger than the efficient advertising expenditures, the unique Markov perfect equilibrium is for firms to advertise, whatever the consideration levels of both firms are.”

Nelson (1974)

• Quality of a brand is determined before a purchase of a brand is “search qualities”

• Quality that is not determined before a purchase is “experience qualities”

• Brand risks credibility if it advertises misleading information, and pays the costs of processing nonbuying customers

• There is a reverse association between quality produced and utility adjusted price

• Firms that want to sell more advertise more

• Firms advertise to their appropriate audience, i.e., “those whose tastes are best served by a given brand are those most likely to see an advertisement for that brand” (p. 734).

• Advertising for experience qualities is indirect information while advertising for search qualities is direct information . (p. 734).

• Goods are classified based on quality variation (i.e., whether the quality variation was based on searhc of experience).

• 3 types of goods

  • experience durable

  • experience nondurable

  • search goods

• Experience goods are advertised more than search goods because advertisers increase sales via increasing the reputability of the sellers.

• The marginal revenue of advertisement is greater for search goods than for experience goods (p. 745). Moreover, search goods will concentrate in newspapers and magazines while experience goods are seen on other media.

• For experience goods, WOM is better source of info than advertising (p. 747).

• Frequency of purchase moderates the differential effect of WOM and advertising (e.g., for low frequency purchases, we prefer WOM) (p. 747).

• When laws are moderately enforced, deceptive advertising will happen (too little law, people would not trust, too much enforcement, advertisers aren’t incentivized to deceive, but moderate amount can cause consumers to believe, and advertisers to cheat) (p. 749). And usually experience goods have more deceptive advertising (because laws are concentrated here).

Iyer, Soberman, and Villas-Boas (2005)

• Firms advertise to their targeted market (those who have a strong preference for their products) than competitor loyalists, which endogenously increase differentiation in the market, and increases equilibrium profits

• Targeted advertising is more valuable than target pricing. Target advertising leads to higher profits regardless whether firms have target pricing. Target pricing increased competition for comparison shoppers (no improvement in equilibrium profits). (p. 462 - 463).

Comparison shoppers size:

\[ s = 1 - 2h \]

where \(h\) is the market size of each firm’s consumers (those who prefer to buy product from that firm). Hence, \(h\) also represents the differentiation between the two firms

See table 1 (p. 469).

\(A\) is the cost for advertising the entire market

\(r\) is the reservation price

Yuxin Chen et al. (2009)

• Combative vs. constructive advertising

• Informative complementary and persuasive advertising

  • Informative: increase awareness, reduce search costs, increase product differentiation

  • Complementary (under comparison): increase utility by signaling social prestige

  • Persuasive: decrease price sensitivity (include combative)

• Consumer response moderates the effect of combative adverting on price competition:

  • It decreases price competition

  • It increases price competition when (1) consumers preferences are biased (firms that advertise have their products favored by the consumers), (2) disfavor firms can’t advertise and only respond with price. because advertising war leads to a price war (when firms want to increase their own profitability while collective outcome is worse off).

21.11 Product Differentiation

• Horizontal differentiation: different consumers prefer different products

• Vertical differentiation: where you can say one good is “better” than the other.

Characteristics approach: products are the aggregate of their characteristics.

21.12 Product Quality, Durability, Warranties

Horizontal Differentiation

\[ U = V -p - t (\theta - a)^2 \]

Vertical Differentiation

\[ U_B = \theta s_B - p_B \\ U_A = \theta s_A - p_A \]

Assume that product B has a higher quality

\(\theta\) is the position of any consumer on the vertical differentiation line.

When \(U_A < 0\) then customers would not buy

Point of indifference along the vertical quality line

\[ \theta s_B - p_B = \theta s_A - p_A \\ \theta(s_B - s_A) = p_B - p_A \\ \bar{\theta} = \frac{p_B - p_A}{s_B - s_A} \]

If \(p_B = p_A\) for every \(\theta\), \(s_B\) is preferred to \(s_A\)

1. K. S. Moorthy (1988)

\[ \pi_A = (p_A - c s_A^2) (Mktshare_A) \\ \pi_B = (p_B - cs_B^2) (Mktshare_B) \\ U_A = \theta s_A - p_A = 0 \\ \bar{\theta}_2 = \frac{p_A}{s_A} \]

2. Wauthy (1996)

\(\frac{b}{a}\) = such that market is covered, then

\[ 2 \le \frac{b}{a} \le \frac{2s_2 + s_1}{s_2 - s_1} \]

for the market to be covered

In vertical differentiation model, you can’t have both \(\theta \in [0,1]\) and full market coverage.

Alternatively, you can also specify \(\theta \in [1,2]; [1,4]\)

\[ \theta \in \begin{cases} [1,4] & \frac{b}{a} = 4 \\ [1,2] & \frac{b}{a} = 2 \end{cases} \]

Under Asymmetric Information

• Adverse Selection: Before contract: Information is uncertain

• Moral Hazard: After contract, intentions are unknown to at least one of the parties.

Alternative setup of Akerlof’s (1970) paper

Used cars quality \(\theta \in [0,1]\)

Seller - car of type \(\theta\)

Buyer = WTP = \(\frac{3}{2} \theta\)

Both of them can be better if the transaction occurs because buyer’s WTP for the car is greater than utility received by seller.

1. Assume quality is observable (both sellers and buyers do know the quality of the cars):

Price as a function of quality \(p(\theta)\) where \(p(\theta) \in [\theta, 3/2 \theta]\) both parties can be better off

2. Assume quality is unobservable (since \(\theta\) is uniformly distributed) (sellers and buyers do not know the quality of the used cars):

\[ E(\theta) = \frac{1}{2} \]

then \(E(\theta)\) for sellers is \(1/2\)

\(E(\theta)\) for buyer = \(3/2 \times 1/2\) = 3/4

then market happens when \(p \in [1/2,3/4]\)

3. Asymmetric info (if only the sellers know the quality)

Seller knows \(\theta\)

Buyer knows \(\theta \sim [0,1]\)

From seller perspective, he must sell at price \(p \ge \theta\) and

From buyer perspective, quality of cars on sale is between \([0, p]\). Then, you will have a smaller distribution than \([0,1]\)

If \(E[(\theta) | \theta \le p] = 0.5 p\)

Buyers’ utility is \(3/4 p\) but the price he has to pay is \(p\) (then market would not happen)

21.12.1 Akerlof (1970)

• This paper is on adverse selection
• The relationship between quality and uncertainty (in automobiles market)
• 2 x 2 (used vs. new, good vs. bad)

\(q\) = probability of getting a good car = probability of good cars produced

and \((1-q)\) is the probability of getting a lemon

• Used car sellers have knowledge about the probability of the car being bad, but buyers don’t. And buyers pay the same price for a lemon as for a good car (info asymmetry).

• Gresham’s law for good and bad money is not transferable (because the reason why bad money drives out goo d money because of even exchange rate, while buyers of a car cannot tell if it is good or bad).

21.12.1.1 Asymmetrical Info

Demand for used automobiles depends on price quality:

\[ Q^d = D(p, \mu) \]

Supply for used cars depends on price

\[ S = S(p) \]

and average quality depends on price

\[ \mu = \mu(p) \]

In equilibrium

\[ S(p) = D(p, \mu(p)) \]

At no price will any trade happen

Example:

Assume 2 groups of graders:

1. First group: \(U_1 = M = \sum_{i=1}^n x_i\) where

   • \(M\) is the consumption of goods other than cars

   • \(x_i\) is the quality of the i-th car

   • n is the number of cars

2. Second group: \(U_2 = M + \sum_{i=1}^n \frac{3}{2} x_i\)

Group 1’s income is \(Y_1\)

Group 2’s income is \(Y_2\)

Demand for first group is

\[ \begin{cases} D_1 = \frac{Y_1}{p} & \frac{\mu}{p}>1 \\ D_1 = 0 & \frac{\mu}{p}<1 \end{cases} \]

Assume we have uniform distribution of automobile quality.

Supply offered by first group is

\[ S_2 = \frac{pN}{2} ; p \le 2 \]

with average quality \(\mu = p/2\)

Demand for second group is

\[ \begin{cases} D_2 = \frac{Y_2}{p} & \frac{3 \mu}{2} >p \\ D_2 = 0 & \frac{3 \mu}{2} < p \end{cases} \]

and supply by second group is \(S_2 = 0\)

Thus, total demand \(D(p, \mu)\) is

\[ \begin{cases} D(p, \mu) = (Y_2 + Y_1) / p & \text{ if } p < \mu \\ D(p, \mu) = (Y_2)/p & \text{ if } \mu < p < 3\mu /2 \\ D(p, \mu) = 0 & \text{ if } p > 3 \mu/2 \end{cases} \]

With price \(p\), average quality is \(p/2\), and thus at no price will any trade happen

21.12.1.2 Symmetric Info

Car quality is uniformly distributed \(0 \le x \le 2\)

Supply

\[ \begin{cases} S(p) = N & p >1 \\ S(p) = 0 \end{cases} \]

Demand

\[ \begin{cases} D(p) = (Y_2 + Y_1) / p & p < 1 \\ D(p) = Y_2/p & 1 < p < 3/2 \\ D(p) = 0 & p > 3/2 \end{cases} \]

In equilibrium

\[ \begin{cases} p = 1 & \text{ if } Y_2< N \\ p = Y_2/N & \text{ if } 2Y_2/3 < N < Y_2 \\ p = 3/2 & \text{ if } N < 2 Y_2 <3 \end{cases} \]

This model also applies to (1) insurance case for elders (over 65), (2) the employment of minorities, (3) the costs of dishonesty, (4) credit markets in underdeveloped countries

To counteract the effects of quality uncertainty, we can have

1. Guarantees
2. Brand-name good
3. Chains
4. Licensing practices

21.12.2 Spence (1973)

Built on (Akerlof 1970) model

Consider 2 employees:

• Employee 1: produces 1 unit of production

• Employee 2: produces 2 units of production

We have \(\alpha\) people of type 1, and \(1-\alpha\) people of type 2

Average productivity

\[ E(P) = \alpha + 2( 1- \alpha) = 2- \alpha \]

You can signal via education.

To model cost of education,

Let E to be the cost of education for type 1

E/2 to be the cost education for type 2

If type 1 signals they are high-quality worker, then they have to go through the education and cost is E, and net utility of type 1 worker

\[ 2 - E < 1 \\ E >1 \]

If type 2 signals they are high-quality worker, then they also have to go through the education and cost is E/2 and net utility of type 2 worker is

\[ 2 - E/2 > 1 \\ E< 2 \]

If we keep \(1 < E < 2\), then we have separating equilibrium (to have signal credible enough of education )

21.12.3 S. Moorthy and Srinivasan (1995)

• Money-back guarantee signals quality

• Transaction cost are those the seller or buyer has to pay when redeeming a money-back guarantee

• Money-back guarantee does not include product return (buyers have to incur expense), but guarantee a full refund of the purchase price.

• If signals are costless, there is no difference between money-back guarantees and price

• But signal are costly,

  • Under homogeneous buyers, low-quality sellers cannot mimic high-quality sellers’ strategy (i.e., money-back guarantee)

  • Under heterogeneous buyers,

    • when transaction costs are too high, the seller chooses either not to use money-back guarantee strategy or signal through price.

    • When transaction costs are moderate, there is a critical value of seller transaction costs where

      • below this point, the high-quality sellers’ profits increase with transaction costs

      • above this point, the high-quality sellers’ profits decrease with transaction costs

• Uninformative advertising (“money-burning”) is defined as expenditures that do not affect demand directly. is never needed

• Moral hazard:

  • Consumers might exhaust consumption within the money-back guarantee period

Model setup

	High-quality sellers (\(h\))	Low-quality sellers (\(l\))
Cost \(c_h > c_l\)	\(c_h\)	\(c_l\)

21.13 Bargaining

Books:

• Abhinay Muthoo - Bargaining Theory with Applications (1999) (check books folder)

• Josh Nash - Nash Bargaining (1950)

Allocation of scare resources

Buyers & Sellers	Type
Many buyers & many sellers	Traditional markets
Many buyers & one seller	Auctions
One buyer & one seller	Bargaining

Allocations of

• Determining the share before game-theoretic bargaining

  • Use a judge/arbitrator

  • Meet-in-the-middle

  • Forced Final: If an agreement is not reached, one party will use take it or leave it

• Art: Negotiation

• Science: Bargaining

• Game theory’s contribution: to the rules for the encounter

• Area that is still fertile for research

21.13.1 Non-cooperative

Outline for non-cooperative bargaining

• The rules

Take-it-or-leave-it Offers

• Bargain over a cake

• If you accept, we trade

• If you reject, no one eats

• Under perfect info, there is a simple rollback equilibrium

• In general, bargaining takes on a “take-it-or-counteroffer” procedure

• If time has value, both parties prefer to trade earlier to trade later

  • E.g., labor negotiations - later agreements come at a price of strikes, work stoppages

• Delays imply less surplus left to be shared among the parties

Two-stage bargaining

• I offer a proportion, \(p\) , of the cake to you

• If rejected, you may counteroffer (and \(\delta\) of the cake melts)

• Payoffs:

  • In the first period: 1-p, p

  • In second period: \((1-\delta) (1-p),(1-\delta)p\)

• Since period 2 is the final period, this is just like a take-it-or-leave-it offer

  • You will offer me the smallest piece that I will accept, leaving you with all of \(1-\delta\) and leaving me with almost 0

• Rollback: then in the first period: I am better off by giving player B more than what he would have in period 2 (i.e., give you at least as much surplus)

• You surplus if you accept in the first period is \(p\)

• Accept if: your surplus in first period greater than your surplus in second period \(p \ge 1 - \delta\)

• IF there is a second stage, you get \(1 - \delta\) and I get 0

• You will reject any offer in the first stage that does not offer you at least \(1 - \delta\)

• In the first period, I offer you \(1 - \delta\)

• Note: the more patient you are (the slower the cake melts) the more you receive now

• Whether first or second mover has the advantage depends on \(\delta\).

  • If \(\delta\) is high (melting fast), then first mover is better.

  • If \(\delta\) is low (melting slower), then second mover is better.

• Either way - if both players think, agreement would be reached in the first period

• In any bargaining setting, strike a deal as early as possible.

Why doesn’t this happen in reality?

• reputation building

• lack of information

Why bargaining doesn’t happen quickly? Information asymmetry

• Likelihood of success (e.g., uncertainty in civil lawsuits)

Lessons:

• Rules of the bargaining game uniquely determine the bargain outcome

• which rules are better for you depends on patience, info

• What is the smallest acceptable piece? Trust your intuition

• delays are always less profitable: Someone must be wrong

Non-monetary Utility

• each side has a reservation price

  • LIke in civil suit: expectation of wining

• The reservation price is unknown

• One must:

  • probabilistically determine best offer

  • but - probability implies a chance that non bargain will take place

Example:

• Company negotiates with a union

• Two types of bargaining:

  • Union makes a take-it-or-leave-it offer

  • Union makes a n offer today. If it’s rejected, the Union strikes, then makes another offer

    • A strike costs the company 10% of annual profits.

• Probability that the company is “highly profitable”, ie., 200k is \(p\)

• If offer wage of $150k

  • Definitely accepted

  • Expected wage = $150K

• If offer wage of $200K

  • Accepted with probability \(p\)

  • Expected wage = $200k(p)

• \(p = .9\) (90% chance company is highly profitable

  • best offer: ask for $200K wage

  • Expected value of offer: \(.9 *200= 180\)

• \(p = .1\) (10% chance company is highly profitable

  • best offer: ask for $200K wage

  • Expected value of offer: \(.1 *200= 20\)

  • If ask for $10k, get $150k

  • not worth the risk to ask for more

• If first-period offer is rejected: A strike costs the company 10% of annual profits

• Strike costs a high-value company more than a low value company

• Use this fact to screen

• What if the union asks for $170k in the first period?

  • Low profit firms ($150k) rejects - as can’t afford to take

  • HIgh profit firm must guess what will happen if it rejects

    • Best case: union strikes and then asks for only $140k (willing to pay for some cost of strike), but not all)

    • In the mean time: strike cost the company $20K

• High-profit firm accepts

Separating equilibrium

• only high-profit firms accept the first period

• If offer is rejected, Union knows that it is facing a low-profit firm

• Ask for $140k

What’s happening

• Union lowers price after a rejection

  • Looks like giving in

  • looks like bargaining

• Actually, the union is screening its bargaining partner

  • Different “types” of firms have different values for the future

  • Use these different values to screen

  • Time is used as a screening device

21.13.2 Cooperative

two people diving cash

• If they do not agree, they each get nothing

• They cant divide up more than the whole thing

21.13.3 Nash (1950)

• Bargaining, bilateral monopoly (nonzero-sum two -person game).

• Non action taken by one individual (without the consent of the other) can affect the other’s gain.

• Assumptions:

  • Rational individuals (maximize gain)

  • Full knowledge: tastes and preferences are known

  • Transitive Ordering: \(A>C\) when \(A>B\), \(B>C\). Also related to substitutability if two events are of equal probability

  • Continuity assumption

• Properties:

  • \(u(A) > u(B)\) means A is more desirable than B where \(u\) is a utility function

  • Linearity property: If \(0 \le p \le 1\), then \(u(pA + (1-p)B) = pu(A) + (1-p)u(B)\)

    • For two person: \(p[A,B] + (1-p)[C,D] = [pA - (1-p)C, pB + (1-p)D]\)

• Anticipation = \(p A - (1-p) B\) where

  • \(p\) is the prob of getting A

  • A and B are two events.

\(u_1, u_2\) are utility function

\(c(s)\) is the solution point in a set S (compact, convex, with 0)

Assumptions:

• If \(\alpha \in S\) s.t there is \(\beta \in S\) where \(u_1(\beta) > u_2(\alpha)\) and \(u_2(\beta) > u_2(\alpha)\) then \(\alpha \neq c(S)\)

  • People try to maximize utility

• If \(S \in T\) , c(T) is in S then \(c(T) = c(S)\)

• If S is symmetric with respect to the line \(u_1 = u_2\), then \(c(S)\) is on the line \(u_1 = u_2\)

  • Equality of bargaining

21.13.4 Iyer and Villas-Boas (2003)

• Presence of a powerful retailer (e.g., Walmart) might be beneficial to all channel members.

21.13.5 Desai and Purohit (2004)

• 2 customers segment: hagglers, nonhagglers.

• When the proportion of nonhagglers is sufficient high, a haggling policy can be more profitable than a fixed-price policy

21.14 Pricing and Search Theory

21.14.1 Varian and Purohit (1980)

• From Stigler’s seminar paper (Stiglitz and Salop 1982; Salop and Stiglitz 1977), model of equilibrium price dispersion is born

  • Spatial price dispersion: assume uninformed and informed consumers

    • Since consumers can learn from experience, the result does not hold over time

  • Temporal price dispersion: sales

• This paper is based on

  • Stiglitz: assume informed (choose lowest price store) and uninformed consumers (choose stores at random)

  • Shilony (Shilony 1977): randomized pricing strategies

\(I >0\) is the number of informed consumers

\(M >0\) is the number of uninformed consumers

\(n\) is the number of stores

\(U = M/n\) is the number of uninformed consumers per store

Each store has a density function \(f(p)\) indicating the prob it charges price \(p\)

Stores choose a price based on \(f(p)\)

• Succeeds if it has the lowest price among n prices, then it has \(I + U\) customers

• Fails then only has \(U\) customers

• Stores charge the same lowest price will share equal size of informed customers

\(c(q)\) is the cost curve

\(p^* = \frac{c(I+U)}{(I+U}\) is the average cost with the maximum number of customers a store can get

Prop 1: \(f(p) = 0\) for \(p >r\) or \(p < p^*\)

Prop 2: No symmetric equilibrium when stores charge the same price

Prop 3: No point masses in the equilibrium pricing strategies

Prop 4: If \(f(p) >0\), then

\[ \pi_s(p) (1-F(p))^{n-1} + \pi_f (p) [1-(1-F(p))^{n-1}] =0 \]

Prop 5: \(\pi_f (p) (\pi_f(p) - \pi_s (p))\) is strictly decreasing in \(p\)

Prop 6: \(F(p^* _ \epsilon) >0\) for any \(\epsilon> 0\)

Prop 7: \(F(r- \epsilon) <1\) for any \(\epsilon > 0\)

Prop 8: No gap \((p_1, p_2)\) where \(f(p) \equiv 0\)

Decision to be informed can be endogenous, and depends on the “full price” (search costs + fixed cost)

21.14.2 Lazear (1984)

Retail pricing and clearance sales

• Goods’ characteristics affect pricing behaviors

• Market’s thinness can affect price volatility

• Relationship between uniqueness of a goods and its price

• Price reduction policies as a function of shelf time

Set up

Single period model

\(V\) = the price of the only buyer who is willing to purchase the product

\(f(V)\) is the density of V (firm’s prior)

\(F(V)^2\) is its distribution function

Firms try to

\[ \underset{R}{\operatorname{max}} R[1 - F(R)] \]

where \(R\) is the price

\(1 - F(R)\) is the prob that \(V > R\)

Assume \(V\) is uniform \([0,1]\) then

\(F(R) = R\) so that the optimum is \(R = 0.5\) with expected profits of \(0.25\)

Two-period model

Failures in period 1 implies \(V<R_1\).

Hence, based on Bayes’ theorem, the posterior distribution in period 2 is \([0, R_1]\)

\(F_2(V) = V/R_1\) (posterior distribution)

\(R_1\) affect (1) sales in period 1, (2) info in period 2

Then, firms want to choose \(R_1, R_2\) .Firms try to

\[ \underset{R_1, R_2}{\operatorname{max}} R_1[1 - F(R_1)] + R_2 [1-F_2(R_2)]F(R_1) \]

Then, in period 2, the firms try to

\[ \underset{R_2}{\operatorname{max}} R_2[1 - F_2(R_2)] \]

Based on Bayes’ Theorem

\[ F_2(R_2) = \begin{cases} F(R_2)/ F(R_1) & \text{for } R_2 < R_1 \\ 1 & \text{otherwise} \end{cases} \]

Due to FOC, second period price is always lower than first price price

Expected profits are higher than that of one-period due to higher expected probability of a sale in the two-period problem.

But this model assume

• no brand recognition

• no contagion or network effects

In thin markets and heterogeneous consumers

we have \(N\) customers examine the good with the prior probability \(P\) of being shoppers, and \(1-P\) being buyers who are willing to buy at \(V\)

There are 3 types of people

1. customers = all those who inspect the good
2. buyers = those whose value equal \(V\)
3. shoppers = those who value equal \(0\)

An individual does not know if he or she is a buyer or shopper until he or she is a customer (i.e., inspect the goods)

Then, firms try to

\[ \begin{aligned} \underset{R_1, R_2}{\operatorname{max}} & R_1(\text{prob sale in 1}) + R_2 (\text{Posterior prob sale in 2})\times (\text{Prob no sale in 1}) \\ & R_1 \times (- F(R_1))(1-P^N) + R_2 \{ (1-F_2(R_2))(1- P^N) \} \times \{ 1 - [(1 - F(R_1))(1-P^N)] \} \end{aligned} \]

Based on Bayes’ Theorem, the density for period 2 is

\[ f_2(V) = \begin{cases} \frac{1}{R_1 (1- P^N) + P^N} \text{ for } V \le R_1 \\ \frac{P^N}{R_1 (1- P^N) + P^N} \text{ for } V > R_1 \end{cases} \]

Conclusion:

As \(P^N \to 1\) (almost all customers are shoppers), there is not much info to be gained. Hence, 2-period is no different than 2 independent one-period problems. Hence, the solution in this case is identical to that of one-period problem.

When \(P^N\) is small, prices start higher and fall more rapid as time unsold increases

When \(P^N \to 1\), prices tend to be constant.

\(P^N\) can also be thought of as search cost and info.

Observable Time patterns of price and quantity

Pricing is a function of

• The number of customers \(N\)

• The proportion of shoppers \(P\)

• The firm’s beliefs about the market (parameterized through the prior on \(V\))

Markets where prices fall rapidly as time passes, the probability that the good will go unsold is low.

Goods with high initial price are likely to sell because high initial price reflects low \(P^N\) - low shoppers

Heterogeneity among goods

The more disperse prior leads to a higher expected price for a given mean. And because of longer time on shelf, expected revenues for such a product can be lower.

Fashion, Obsolescence, and discounting the future

The more obsolete, the more anxious is the seller

Goods that are “classic”, have a higher initial price, and its price is less sensitive to inventory (compared to fashion goods)

Discounting is irrelevant to the pricing condition due to constant discount rate (not like increasing obsolescence rate)

For non-unique good, the solution is identical to that of the one-period problem.

Simple model

Customer’s Valuation \(\in [0,1]\)

Firm’s decision is to choose a price \(p\) (label - \(R_1\))

One-period model

Buy if \(V >R_1\) prob = \(1-R_1\)

Not buy if \(V<R_1\) probability = \(R_1\)

\(\underset{R_1}{\operatorname{max}} [R_1][1-R_1]\) hence, FOC \(R_1 = 1/2\), then total \(\pi = 1/2-(1/2)^2 = 1/4\)

Two-period model

Two prices \(R_1, R_2\)

\(R_1 \in [0,1]\)

\(R_2 \in [0, R_1]\)

\[ \underset{R_1}{\operatorname{max}} [R_1][1-R_1] + R_2 (1 - R_2)(R_1) \]

\[ \underset{R_1}{\operatorname{max}} [R_2][\frac{R_1 - R_2}{R_1}] \]

FOC \(R_2 = R_1/2\)

\[ \underset{R_1}{\operatorname{max}} R_1(1-R_1) + \frac{R_1}{2}(1 - \frac{R_1}{2}) (R_1) \]

FOC: \(R_1 = 2/3\) then \(R_2 = 1/3\)

\(N\) customers

Each customer could be a

• shopper with probability p with \(V <0\)

• buyer with probability \(1-p\) with \(V > \text{price}\)

Modify equation 1 to incorporate types of consumers

\[ R_1(1 - R_1)(1- p^N) + R_2 (1- R_2) R_1 (1-p^N) [ 1 - (1-R_1)(1-p^N)] \]

Reduce costs by

• Economy of scale \(c(\text{number of units})\)

• Economy of scope \(c(\text{number of types of products})\) (typically, due to the transfer of knowledge)

• Experience effect \(c(\text{time})\) (is a superset of economy of scale)

Lal and Sarvary (1999)

• Conventional idea: lower search cost (e.g., Internet) will increase price competition.

• Assumptions:

  • Demand side: info about product attributes:

    • digital attributes (those can be communicated via the Internet)

    • nondigital attributes (those can’t)

  • Supply side: firms have both traditional and Internet stores.

• Monopoly pricing can happen when

  • high proportion of Internet users

  • Not overwhelming nondigital attributes

  • Favor familiar brands

  • destination shopping

• Monopoly pricing can lead to higher prices and discourage consumer from searching

• Stores serve as acquiring tools, while Internet maintain loyal customers.

Kuksov (2004)

• For products that cannot be changed easily (design),lower search costs lead to higher price competition

• For those that can be easily changed, lower search costs lead to higher product differentiation, which in turn decreases price competition, lower social welfare, higher industry profits.

(Salop and Stiglitz 1977)

21.15 Pricing and Promotions

• Extensively studied

• Issue of Everyday Low price vs Hi/Lo pricing

• Short-term price discounts

  • offering trade-deals

  • consumer promotions

    • shelf-price discounts (used by everybody)

    • cents-off coupons (some consumers whose value of time is relatively low)

Loyalty is similar to inform under analytic modeling:

• Uninformed = loyal

• Informed = non-loyal

30 years back, few companies use price promotions

Effects of Short-term price discounts

• measured effects (84%) (Gupta 1988)

  • Brand switching (14%)

  • purchase acceleration (2%)

  • quantity purchased

  • elasticity of ST price changes is an order of magnitude higher

• Other effects:

  • general trial (traditional reason)

  • encourages consumers to carry inventory hence increase consumption

  • higher sales of complementary products

  • small effect on store switching

  • Asymmetric effect (based on brand strength) (bigger firms always benefit more)

    • expect of store brands

Negative Effects

• Expectations of future promotions

• Lowering of Reference Price

• Increase in price sensitivity

• Post-promotional dip

Trade Discounts

Short-term discounts offered to the trade:

• Advantages

  • Incentivize the trade to push our product

  • gets attention of sales force

• Disadvantages

  • might not be passed onto the consumer

  • trade forward buys (hurts production plans)

  • hard to forecast demand

  • trade expects discounts in the future (cost of doing business)

Scanback can help increase retail pass through (i.e., encourage retailers to have consumer discounts)

Determinants of pass through

• Higher when

  • Consumer elasticity is higher

  • promoting brand is stronger

  • shape of the demand function

  • lower frequency of promotions

(Online) Shelf-price discounts (Raju, Srinivasan, and Lal 1990)

• If you are a stronger brand you can discount infrequently because the weaker brands cannot predict when the stronger brands will promote. Hence, it has to promote more frequently

Coupons

• Little over 1% get redeemed each year

• The ability of cents-off coupons to price distribution has reduced considerably because of their very wide availability

• Sales increases required to make free-standing-insert coupons profitable are not attainable

Coupon Design

• Expiration dates

  • Long vs short expiration dates: Stronger brands should have shorter windows (because a lot more of your loyalty customer base will utilize the coupons).

• Method of distribution

  • In-store (is better)

  • Through the package

  • Targeted promotions

Package Coupons acquisition and retention trade-offs

3 types of package coupons:

• Peel-off (lots more use the coupons) lowest profits for the firm

• in-packs (fewer customers will buy the products in the first period)

• on-packs (customers buy the products and they redeem in the next period) best approach

Summary

• Trade and consumer promotion are necessary

• Consumer promotion (avoid shelf price discount/news paper coupons, use package coupons

• strong interaction between advertising and promotion (area for more research)

3 degrees price discrimination

1. First-degree: based on willingness to pay
2. Second-degree: based on quantity
3. Third-degree: based on memberships
4. Fourth-degree: based on cost to serve

21.15.1 Narasimhan (1988)

• Marketing tools to promote products:

  • Advertising

  • Trade promotions

  • Consumer promotions

• Pricing promotions:

  • Price deals

  • Cents-off labels

  • coupons

  • Rebates

• Brand loyalty can help explain the variation in prices (in competitive markets)

• Firms try to make optimal trade-off between

  • attracting brand switchers

  • loss of profits from loyal customers.

• Deviation from the maximum price = promotion

Assumptions:

1. Firms with identical products, and cost structures (constant or declining). Non-cooperative game.

2. Same reservation price

3. Three consumer segments:

   1. Loyal to firm 1 with size \(\alpha_1 (0<\alpha_1<1)\)

   2. Loyal to firm 2 with size \(\alpha_2(0 < \alpha_2 < \alpha_1)\) (asymmetric firm)

   3. Switchers with size \(\beta (0 < \beta = 1 - \alpha_1 - \alpha_2)\)

4. Costless price change, no intertemporal effects (in quantity or loyalty)

To model \(\beta\) either

1. \(d \in (-b, a)\) is switch cost (individual parameter)

\[ \begin{cases} \text{buy brand 1} & \text{if } P_1 \le P_2 - d \\ \text{buy brand 2} & \text{if } P_1 > P_2 - d \end{cases} \]

2. Identical switchers (same d)
3. \(d = 0\) (extremely price sensitive)

For case 1, there is a pure strategy, while case 2 and 3 have no pure strategies, only mixed strategies

Details for case 3:

Profit function

\[ \Pi_i (P_i, P_j) = \alpha_i P_i + \delta_{ij} \beta P_i \]

where

\[ \delta_{ij} = \begin{cases} 1 & \text{ if } P_i < P_j \\ 1/2 & \text{ if } P_i = P_j \\ 0 & \text{ if } P_i > P_j \end{cases} \]

and \(i = 1,2, i \neq j\)

Prop 1: no pure Nash equilibrium

Mixed Strategy profit function

\[ \Pi_i (P_i) = \alpha_i P_i + Prob(P_j > P_i) \beta P_i + Prob (P_j = P_i) \frac{\beta}{2} P_i \]

where \(P_i \in S_i^*, i \neq j; i , j = 1, 2\)

Then the expected profit functions of the two-player game is

\[ \underset{F_i}{\operatorname{max}} E(\Pi_i) = \int \Pi_i (P_i) d F_i (P_i) \]

\(P_i \in S_i^*\)

such that

\[ \Pi_i \ge \alpha_i r \\ \int dF_i (P_i) = 1 \\ P_i \in S_i^* \]

21.15.2 Balachander, Ghosh, and Stock (2010)

• Bundle discounts can be more profitable than price promotions (in a competitive market) due to increased loyalty (which will reduce promotional competition intensity).

21.15.3 Goić, Jerath, and Srinivasan (2011)

• Cross-market discounts, purchases in a source market can get you a price discounts redeemable in a target market.

  • Increase prices and sales in the source market.

21.16 Market Entry Decisions and Diffusion

Peter N. Golder and Tellis (1993)

Peter N. Golder and Tellis (2004)

Boulding and Christen (2003)

Van den Bulte and Joshi (2007)

21.17 Principal-agent Models and Salesforce Compensation

21.17.1 Gerstner and Hess (1987)

21.17.2 Basu et al. (1985)

21.17.3 Raju and Srinivasan (1996)

Compare to (Basu et al. 1985), basic quota plan is superior in terms of implementation

Different from (Basu et al. 1985), basic quota plan has

1. Shape-induced nonoptimality: not a general curvilinear form
2. Heterogeneity-induced nonoptimality: common rate across salesforce

However, only 1% of cases in simulation shows up with nonoptimality. Hence, minimal loss in optimality

Basic quota plan is a also robust against changes in

• salesperson switching territory

• territorial changes (e.g., business condition)

Heterogeneity stems from

• Salesperson: effectiveness, risk level, disutility for effort, and alternative opportunity

• Territory: Sales potential and volatility

Adjusting quotas can accommodate the heterogeneity

To assess nonoptimality, following Basu and Kalyanaram (1990)

Moral hazard: cannot assess salesperson’s true effort.

Assumptions:

• The salesperson reacts to the compensation scheme by deciding on an effort level that maximizes his overall utility, i.e., the expected utility from the (stochastic) compensation minus the effort distuility.

• Firm wants to maximize its profit

• compensation is greater than saleperson’s alternative.

• Dollar sales \(x_i \sim Gamma\) (because sales are non-negative and standard deviation getting proportionately larger as the mean increases) with density \(f_i(x_i|t_i)\)

Expected sales per period

\[ E[x_i |t_i] = h_i + k_i t_i , (h_i > 0, k_i >0) \]

where

• \(h_i\) = base sales level
• \(k_i\) = effectiveness of effort

and \(1/\sqrt{c}\) = uncertainty in sales (coefficient of variation) = standard deviation / mean where \(c \to \infty\) means perfect certainty

salesperson’s overall utility

\[ U_i[s_i(x_i)] - V_i(t_i) = \frac{1}{\delta_i}[s_i (x_i)]^{\delta_i} - d_i t_i^{\gamma_i} \] where

• \(0 < \delta_i <1\) (greater \(\delta\) means less risk-averse salesperson)
• \(\gamma_i >1\) (greater \(\gamma\) means more effort)
• \(V_i(t_i) = d_i t_i^{\gamma_i}\) is the increasing disutility function (convex)

21.17.4 Lal and Staelin (1986)

• A menu of compensation plans (salesperson can select, which depends on their own perspective)

• Proposes conditions when it’s optimal to offer a menu

• Under (Basu et al. 1985), they assume

  • Salespeople have identical risk characteristics

  • identical reservation utility

  • identical information about the environment

• When this paper relaxes these assumptions, menu of contract makes sense

• If you cannot distinguish (or have a selection mechanisms) between high performer and low performer, a menu is recommended. but if you can, you only need 1 contract like (Basu et al. 1985)

21.17.5 Simester and Zhang (2010)

21.18 Branding

Wernerfelt (1988)

• Umbrella branding

W. Chu and Chu (1994)

• retailer reputation

21.19 Marketing Resource Allocation Models

This section is based on (Mantrala, Sinha, and Zoltners 1992)

21.19.1 Case study 1

Concave sales response function

• Optimal vs. proportional at different investment levels
• Profit maximization perspective of aggregate function

\[ s_i = k_i (1- e^{-b_i x_i}) \]

where

• \(s_i\) = current-period sales response (dollars / period)
• \(x_i\) = amount of resource allocated to submarket i
• \(b_i\) = rate at which sales approach saturation
• \(k_i\) = sales potential

Allocation functions

• Fixed proportion

  • \(R_i\) = Investment level (dollars/period)

  • \(w_i\) = fixed proportion or weights

\[ \hat{x}_i = w_i R; \\ \sum_{t=1}^2 w_t = 1; 0 < w_t < 1 \]

• Informed allocator

  • optimal allocations via marginal analysis (maximize profits)

\[ max C = m \sum_{i = 1}^2 k_i (1- e^{-b_i x_i}) \\ x_1 + x_2 \le R; x_i \ge 0 \text{ for } i = 1,2 \\ x_1 = \frac{1}{(b_1 + b_2)(b_2 R + \ln(\frac{k_1b_1}{k_2b_2})} \\ x_2 = \frac{1}{(b_1 + b_2)(b_2 R + \ln(\frac{k_2b_2}{k_1b_1})} \]

21.19.2 Case study 2

S-shaped sales response function:

• Optimal vs. proportional at different investment levels
• Profit maximization perspective of aggregate function

21.19.3 Case study 3

Quadratic-form stochastic response function

• Optimal allocation only with risk averse and risk neutral investors.

21.20 Mixed Strategies

Games with finite number, and finite strategy for each player, there will always be a Nash equilibrium (might not be pure Nash, but always mixed)

Extended game

• Suppose we allow each player to choose randomizing strategies

• For example, the server might serve left half of the time, and right half of the time

• In general, suppose the server serves left a fraction \(p\) of the time

• What is the receiver’s best response?

Best Responses

If \(p = 1\), the receiver should defend to the left

\(p = 0\), the receiver should defend to the right

The expected payoff to the receiver is

\(p \times 3/4 + (1-p) \times 1/4\) if defending left

\(p \times 1/4 + (1-p) \times 3/4\) if defending right

Hence, she should defend left if

\(p \times 3/4 - (1-p)\times 1/4 > p \times 1/4 + (1-p) \times 3/4\)

We said to defend left whenever

\[ p \times 3/4 - (1-p)\times 1/4 > p \times 1/4 + (1-p) \times 3/4 \]

Server’s Best response

• Suppose that the receiver goes left with probability \(q\)

• if \(q = 1\), the server should serve right

• If \(q = 0\), the server should server left

• Hence, serve left if \(1/4 \times q + 3/4 \times (1-q) > 3/4\times q + 1/4 \times (1-q)\)

• Simplifying, he should serve left if \(q < 1/2\)

Mixed strategy equilibrium:

• A mixed strategy equilibrium is a pair of mixed strategies that are mutual best responses

• In the tennis example, this occurred when each play chose a 50-50 mixture of left and right

• Your best strategy is when you make the option given to your opponent is obsolete.

• A player chooses his strategy to make his rival indifferent

• A player earns the same expected payoff for each pure strategy chosen with positive probability

• Important property: When player’s own payoff form a pure strategy goes up (or down), his mixture does not change.

21.21 Bundling

	Equipment	Installation
Customer Type 1	$8,000	$2,000
Customer Type 2	$5,000	$3,000

Say we have equal numbers of type 1 and type 2, then you would like to charge $5,000 for the equipment and $2,000 for installation when considering equipment and installment equally . If you price it separately, then your total profit is 14,000.

But you bundle, you get $16,000.

If we know that bundles work. But we don’t see every company does ti?

Because it depends on the number of type 1 and 2 customers, and negative correlation in willingness to pay.

For example:

• Information Products

  • margin cost is close to 0.

  • Bundling of info products is very easy

  • hence always bundle

21.22 Market Entry and Diffusion

Product Life Cycle model

Bass (1969)

• Discussion of sales has 2 types

  • Innovators

  • Imitators

\(p\) = coefficient of innovation (fraction of innovators of the untapped market who buy in that period)

\(q\) = coefficient of imitation (fraction of the interaction which lead to sales in that period)

\(M\) = market potential

\(N(t)\) = cumulative sales till time \(t\)

\(M - N(t)\) = the untapped market

Sales in any time is People buying because of the pure benefits of the product, plus people buy the product after interacting with people who owned the product.

\[ S(t) = p(M- N(t)) + q \frac{N(t)}{M} [M-N(t)] \\ = pM + (q-p) N(t) - \frac{q}{M} [N(t)]^2 \]

one can estimate \(p,q,M\) from data

\(q > p\) (coefficient of imitation > coefficient of innovation) means that you have life cycle (bell-shaped curve)

Peter N. Golder and Tellis (1993)

Previous use

• limited databases (PIM and ASSESOR) (Urban et al. 1986)

• exclusion of nonsurvivors

• single-informant self-report

New dataset overcomes these limitations and show 50% of the market pioneers fail, and their mean share is much lower

Early market leaders have greater long-term success and enter on average 13 years after pioneers.

Definitions (p. 159)

1. Inventor: firms that develop patent or important technologies in a new product category
2. Product pioneer: the first firm to develop a working model or sample in a new product category
3. Market pioneer is the first firm to sell in a new product category
4. Product category: a group of close substitutes

Boulding and Christen (2003)

At the business level, being the leader can give you long-term profit disadvantage from the samples of consumer and industrial goods.

First-to-market leads to an initial profit advantage, which last about 12 to 14 years before becoming long-term disadvantage.

Consumer learning (education), market position (strong vs. weak) and patent protection can moderate the effect of first-mover on profit.

Peter N. Golder and Tellis (2004)

• Research on product life cycle (PLC)

• Consumer durables typically grow 45 per year over 8 years, then slowdown when sales decline by 15%, and stay below those of the previous peak for 5 years.

• Slowdown typically happens when the product penetrates 35-50% of the market

• large sales increases (at first) will have larger sales declines (at slowdown).

• Leisure-enhancing products tend to have higher growth rate and shorter growth stages than non leisure-enhancing products

• Time-saving products have lower growth rates and longer growth stages than non time-saving products

• Lower likelihood of slowdown correlates with steeper price reduction, lower penetration, and higher economic growth

• A hazard model gives reasonable prediction of the slowdown and takeoff.

Van den Bulte and Joshi (2007)

• Innovations market have two segments:

  • Influentials: aware of new developments an affect imitators

  • Imitators: model after influentials.

• This market structure is reasonable because it exhibits consistent evidence with the prior research and market (e.g., dip between the early and later parts fo the diffusion curve).

• ” Erroneously specifying a mixed-influence model to a mixture process where influentials act independently from each other can generate systematic changes in the parameter values reported in earlier research.”

• Two-segments model performs better than the standard mixed-influence, the Gamma/Shifted Gompertz, the Weibull-Gamma models, and similar to the Karmeshu-Goswami mixed influence model.

21.23 Principal-Agent Models and Salesforce Compensation

Key Question:

1. Ensuring agents exert effort
2. Design compensation plans such that workers exert high effort?

Designing contracts:

• Effort can be monitored

• Monitoring costs are too high

Timing

1. Manger designs the construct
2. manager offers the construct and worker chooses to accept
3. Worker decides the extent of effort
4. Outcome is observed and wage is given to the worker

Scenario 1: Certainty

e = effort put in by worker

2 levels of e

• 2 if he works hard
• 0 if he shirks

Reservation utility = 10 (other alternative: can work somewhere else, or private money allows them not to work)

Agent’s Utility

\[ U = \begin{cases} w - e & \text{if he exerts effort e} \\ 10 & \text{if he works somewhere else} \end{cases} \]

Revenue is a function of effort

\[ R(e) = \begin{cases} H & \text{if } e = 2 \\ L & \text{if } e = 0 \end{cases} \]

Contract

\(w^H\) = wage if \(R(e) = H\)

\(w^L\) = wage if \(R(e) = L\)

Constraints:

• Worker has to participate in this labor market - participation constraint \(w^H - 2 \ge 10\)

• Incentive compatibility constraint (ensure that the works always put in the effort and the manager always pay for the higher wage): \(w^H - 2 \ge w^L -0\)

Hence,

\[ w^H = 12 \\ w^L = 10 \]

Thus, contract is simple because of monitoring

Scenario 2: Under uncertainty

\[ R(2) = \begin{cases} H & \text{w/ prob 0.8} \\ L & \text{w/ prob 0.2} \end{cases} \\ R(0) = \begin{cases} H & \text{w/ prob 0.4} \\ L & \text{w/ prob 0.6} \end{cases} \]

Agent Utility

\[ U = \begin{cases} E(w) - e & \text{if effort e is put} \\ 10 & \text{if they choose outside option} \end{cases} \]

Constraints:

• Participation Constraint: \(0.8w^H + 0.2w^L -2 \ge 10\)

• Incentive compatibility constraint: \(0.8w^H + 0.2w^L - 2 \ge 0.4 w^H + 0.6w^L - 0\)

Thus,

\[ w^H = 13 \\ w^L = 8 \]

Expected wage bill that the manager has to pay:

\[ 13\times 0.8 + 8 \times 0.2 = 12 \]

Hence, the expected money the manager has to pay is the same for both cases (certainty vs. uncertainty)

Scenario 3: Asymmetric Information

Degrees of risk aversion

Manger perspective

\[ R(2) = \begin{cases} H & \text{w/ prob 0.8} \\ L & \text{w/ prob 0.2} \end{cases} \]

Worker perspective (the number for worker is always lower, because they are more risk averse, managers are more risk neural) (the manager also knows this).

\[ R(2) = \begin{cases} H & \text{w/ prob 0.7} \\ L & \text{w/ prob 0.3} \end{cases} \]

Participation Constraint

\[ 0.7w^H + 0.3w^L - 2 \ge 10 \]

Incentive Compatibility Constraint

\[ 0.6 w^H + 0.3 w^L - 2 \ge 0.4 w^H + 0.6 w^L - 0 \]

(take R(0) from scenario 2)

\[ 0.7 w^H + 0.3 w^L = 12 \\ 0.3w^H - 0.3w^L = 2 \]

Hence,

\[ w^H = 14 \\ w^L = 22/3 \]

Expected wage bill for the manager is

\[ 14 * 0.8 + 22/3*0.2 = 12.66 \]

Hence, expected wage bill is higher than scenario 2

Risk aversion from the worker forces the manager to pay higher wage

		Salesperson
		Risk neutral	Risk averse
Effort	Observable	Any mix desired effort	All salary Desired effort
	Not observable	All commission Desired effort	Specific mix (S+C) Salesperson shirks

Grossman and Hart (1986)

• landmark paper for principal agent model

21.23.1 Basu et al. (1985)

Types of compensation plan:

• Independent of salesperson’s performance (e.g., salary only)

• Partly dependent on output (e.g., salary with commissions)

• In comparison to others (e.g., sales contests)

• Options for salesperson to choose the compensation plan

In the first 2 categories, the 3 major schemes:

1. Straight salary
2. Straight commissions
3. Combination of base salary and commission

Compensation Type	Best when	Limitation
Straight salary	Long-term objective Hard to measure performance	Less effort
Straight commission	Easy-to-measure performance	Effort-reward ratio is emphasized High risk (uncertainty) to the salesperson
Combination

Dimensions that affect the proportion of salary tot total pay (p. 270, table 1)

Previous research assumes deterministic relationship between sales and effort, but this study says otherwise (stochastic relationship between sales and effort).

Assumptions:

• Firm: Risk neutral: maximize expected profits

• Salesperson: Risk averse . Hence, diminishing marginal utility for income \(U(s) \ge 0; U'(s) >0, U''(s) <0\)

• Expected utility of the salesperson for this job > alternative

• Utility function of the salesperson: additively separable: \(U(s) - V(t)\) where \(s\) = salary, and \(t\) = effort (time)

• Marginal disutility for effort increases with effort \(V(t) \ge 0, V'(t)>0, V''(t) >0\)

• Constant marginal cost of production and distribution \(c\)

• Known utility function and sales-effort response function (both principal and agent)

• dollar sales \(x \sim Gamma, Binom\)

Expected profit for the firm

\[ \pi = \int[(1-c)x - s(x)]f(x|t)dx \]

Objective of the firm is to

\[ \underset{s(x)}{\operatorname{max}} \int[(1-c)x - s(x)]f(x|t)dx \]

subject to (agent’s best alternative e.g., other job offer - \(m\))

\[ \int [U(s(x))]f(x|t) dx - V(t) \ge m \]

and the agent wants to maximize the the utility

\[ \underset{t}{\operatorname{max}} \int [U(s(x))]f(x|t)dx - V(t) \]

21.23.2 Lal and Staelin (1986)

21.23.3 Raju and Srinivasan (1996)

Compare quota-based compensation with (Basu et al. 1985) curvilinear compensation, the basic quota plan is simpler, and only in specical cases (about 1% in simulation) that differs from (Basu et al. 1985). And it’s easier to adapt to changes in moving salesperson and changing territory, unlike (Basu et al. 1985)’s plan where the whole commission rate structure needs to be changed.

Heterogeneity stems from:

• Salesperson: disutility effort level, risk level, effectiveness, alternative opportunity

• Territory: Sales potential an volatility

Adjusting the quota (per territory) can accommodate the heterogeneity

Quota-based < BLSS (in terms of profits)

Constraints:

1. quota-based from curve (between total compensation and sales) (i.e., shape-induced nonoptimality)
2. common salary and commission rate across salesforce (i.e., heterogeneity-induced nonoptimality)

To assess the shape-induced nonoptimality following

21.23.4 Joseph and Thevaranjan (1998)

21.23.5 Simester and Zhang (2010)

• Tradeoff: Motivating manager effort and info sharing.

21.24 Meta-analyses of Econometric Marketing Models

21.25 Dynamic Advertising Effects and Spending Models

21.26 Marketing Mix Optimization Models

Check this post for implementation in Python

21.27 New Product Diffusion Models

21.28 Two-sided Platform Marketing Models

Example of Marketing Mix Model in practice: link