29 Surveys

Chandon, Morwitz, and Reinartz (2005) posits that “self-generated validity” can obscure the link between purchase intentions and purchase behavior. On average, the link between latent intentions and purchase behavior is 58% stronger among survey consumers that that of nonsurveyed consumers.

Sheppard, Hartwick, and Warshaw (1988) found that the link between intentions and behavior is about 0.53

A little more improvement can be achieved in predictive power if we use segmentation before forecasting sales based on historical purchases and purchase intention Morwitz and Schmittlein (1992)

SICSS Summer 2020 -Survey Research in the Digital Age by professor Matthew Salganik

	Sampling	Interviews	Data environment
1st era	area probability	face-to-face	stand-alone
2nd ear	random digital dial probability	telephone	stand-alone
3rd era	non-probability	computer-administered	linked

Total survey error framework (Groves and Lyberg 2010)

Insight:

1. Errors can come from bias or variance
2. Total survey error = Measurement error + representation error

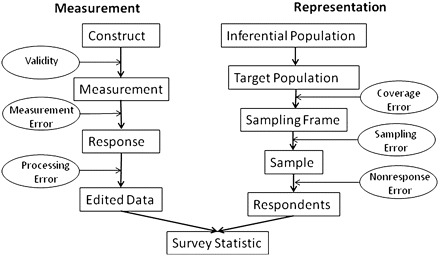
\[@Groves_2010, Fig. 3\]

Probability and Non-probability Sampling

• Probability sample: every unit from a frame population has a known and non-zero probability of inclusion
• With weighting, we can recover bias in your sampling.

• Non-response problem

Horvitz-Thompson estimator (or bias estimator):

\[ \hat{\bar{y}} = \frac{\sum_{i \in s}y_i / \pi_i}{N} \]

where \(\pi_i\) = person i’s probability of inclusion (we have to estimate)

Wiki Survey

• Create a survey that leverages the power of people

Mass Collaboration

• Human Computation: Train People -> Train Lots of People -> Train Machine

  • Cleaning

  • De-biasing

  • Combining

• Open Call:

  • solutions are easier to check than generate

  • required specialized skills

• Distributed Data Collection:

  • People go out and collect data

  • quality check

Fragile family challenges

29.1 Anchoring Vignettes

• Problem of interpersonal incomparability

• Resources:

  • (KING et al. 2004)

  • (G. King and Wand 2007)

  • (Hopkins and King 2010)

  • Examples

• Help with 2 questions:

  • Different respondents understand the same question differently: Incomparaability in Survey Responses (“DIF”). Agreement on theoretical concept is almost nearly impossible.

  • How can we measure concepts that can only be defined by examples

• Measure like usually, then subtract the incomparable portion. (i.e., using the assessment from the same respondents for a particular example/case to correct/adjust for the self-assessment).

• Varying vignette assessments give us DIF (i.e., differential item functioning)

• Since we created the anchors (i.e., examples), we know the true vignette assessments are fixed over respondents

29.1.1 Nonparametric method

Code the relative ranking of self-assessment in accordance to vignettes.

Inconsistencies would be considered ties.

Measurement Assumptions:

• Response consistency: Each responder approaches the self-assessment and vignette categories in a same manner across questions.

• Vignette Equivalence: For every vignette, the real level is the same for all respondents.

Used Ordered Probit to estimate.

29.1.2 Parametric method

The more vignettes that we have better identification. But it will introduce measurement errors.

• Also use an ordinal probit model

• with varying thresholds and a random effect.

# install.packages("anchors")
library(anchors)

# Example from the package's authors
data("freedom")
head(freedom)
a1 <-
    anchors(self ~ vign2 + vign3 + vign4 + vign5 + vign6, freedom, method = "C")
summary(a1)