6 Air Pressure

6.1 Motivation

Air pressure is constantly regulating the characteristics of the atmosphere and impacting the ecosystems. Winds and cloud formation all depends on the differences in air pressure.

The air pressure depends on the weight of the air column above and on the air temperature. In fact the air molecules move faster when air is hot and this increases the pressure (Bonan 2019).

6.2 Background

There are different processes that affects air pressure. The main one is the reduction of air pressure with the increase of elevation. The pressure depends on the weight of the air column above, at a high elevation there is less air above and thus, the pressure is lower.

This dependency of pressure with elevation is commonly used in altimeters to estimate the elevation. However, in case of weather measurements the height effects needs to be removed.

The air pressure has an exponential decay with height. The following formula can be used to estimate the pressure using the measured pressure at a know elevation.

\[p(0) = p(z) exp({\frac{g \Delta z} {R_d T}})\]

The air temperature is an important component of the formula, as warm air is less dense and therefore the air column weights less. However, air temperature also depends on altitude, hence, the mean temperature over the column is used considering an estimate decrease in temperature of \(-0.65 K /100m\). The following equation can be used

\[T=T_{station}+0.00325*z\]

Another correction can be made for air humidity, as wet air is less dense than dry air. This is done by estimating the virtual temperature, which corresponds to the temperature where dry air would have the same density of the wet air. The virtual temperature is always higher than the real one. The following equation can be used for the correction

\[T_v = T (1 + 0.608q)\]

where \(q\) is the specific humidity in (\(Kg/Kg\))

The inverse of the previous formula can be used to calculate the difference of height between 2 points with known pressures.

\[\Delta z = -\frac{R_d}{g T} log(\frac{p_z} {p_0})\]

One peculiarity of air pressure is the wide range of units used around the globe to measure it. The SI defines the Pa (\(N/m^2\)) as the unit for pressure. However, this is a small value so hPa (100 Pa) is commonly used as a reference amount of this unit. Another unit that commonly used in barometers is the torr or mmHg, that originates from the millimeters of mercury used in the first barometers. Those are the values to change between units: \(760 mmHg = 760 torr = 1013.25 hPa\).

Pressure influences the boiling point temperature of water. The following equation can be used to estimate the relationship:

\[T_{boil} = 100 + 2.804 \times 10^{-2} (p-1013.25hPa) - 1.384 \times 10^{-5} (p-1013.25hPa)^2\]

6.3 Sensors and measuring principle

There are several sensors to measure the air pressure and each of these use different measurement principles.

• Mercury barometer. This is the oldest barometer and works by having a column of mercury in a tube with vacuum on one side and air in the other. On the mercury there is the gravitational force that make it going down, while the air pressure pushes the column up. This two forces reaches and equilibrium and therefore it is possible to read the pressure using the height of the mercury column. This sensor is not commonly used nowadays anymore. First of all, because mercury is dangerous and then, it also requires error corrections for both: temperature (mercury expands with higher temperatures) and gravity acceleration constant, which changes depending on altitude and latitude.

• Aneroid barometer. They have an aneroid capsule with vacuum (or low pressure) inside, air pressure tends to reduce the collapse the capsule while a spring keeps in open. By measuring the width of the capsule is possible to estimate the air pressure. The width of the capsule can be measured both in analog instruments or digital one, using a capacitor. Those are the most widely used pressure sensors as they are compact, reliable and require no error correction.

• Boiling barometer. First, it measures the boiling temperature of water, and then, uses this information to estimate the air pressure. There is a heater to make water boil and then an accurate thermometer measure the temperature of the water vapour. The main disadvantage is their reduced convenience due to the procedure to boil water at each sample, but they can have a high accuracy, up to 0.5 hPa (Richner, Joss, and Ruppert 1996).

6.4 Analysis

pres <- read_csv(here("Data_lectures/6_Air_pressure/TA_RH_PA_Leinefelde.csv"))

#utility funcs from air humidity notebook

# temp is in degrees celcius
get_es <-  function(ta)  6.1078 * exp((17.08085 * ta) / (234.175 + ta))

rh2ea <- function(rh, e_s) rh/100 * e_s
get_spec_hum <- function(e_a, p) 0.622 * e_a / (p - 0.378 * e_a) # note Kg Kg-1

c2k <- function(c) c + 273.15
k2c <- function(k) k - 273.15

# get virtual temperature. Ta is the air temp and q the specific humidity
get_tv <- function(ta, q) ta * (1 + 0.608 * q)

Rd <- 287.05 # J Kg-1 K-1 gas constant of dry air
get_press_sea_level <- function(pz, tv, Dz, g = 9.81) {
  pz * exp((g * Dz)/(Rd * c2k(tv)))
}

6.4.1 Air pressure sea level

The air pressure at sea level is always higher than at Leinefelde (Figure 6.1) The difference is around 53 hPa, and it is quite constant during the year. In the plot it is also possible to see that there are no clear seasonal patterns during the year as the pressure oscillate roughly +/- 25 hPa around the mean. Moreover, it is also interesting to notice the stability of the air pressure in a short time frame, as the data plotted has a 30 min frequency but no high frequency patterns can be observed.

heigth_diff <- 451 + 44 # elevation + tower height

pres <- pres %>%
  mutate(
    es = get_es(TA_degC),
    ea = rh2ea(RH_Perc, TA_degC),
    q = get_spec_hum(ea, PA_hPa),
    tv = get_tv(TA_degC, q),
    p0 = get_press_sea_level(PA_hPa, tv, heigth_diff)
  )

pres %>%
        gather("location", "pressure", p0, PA_hPa, factor_key = T) %>%
ggplot(aes(Date, pressure, color=location)) +
  geom_line() +
labs(y="Pressure (hPa)") +
scale_colour_colorblind(name="Location", labels = c("Sea level", "Leinefelde"))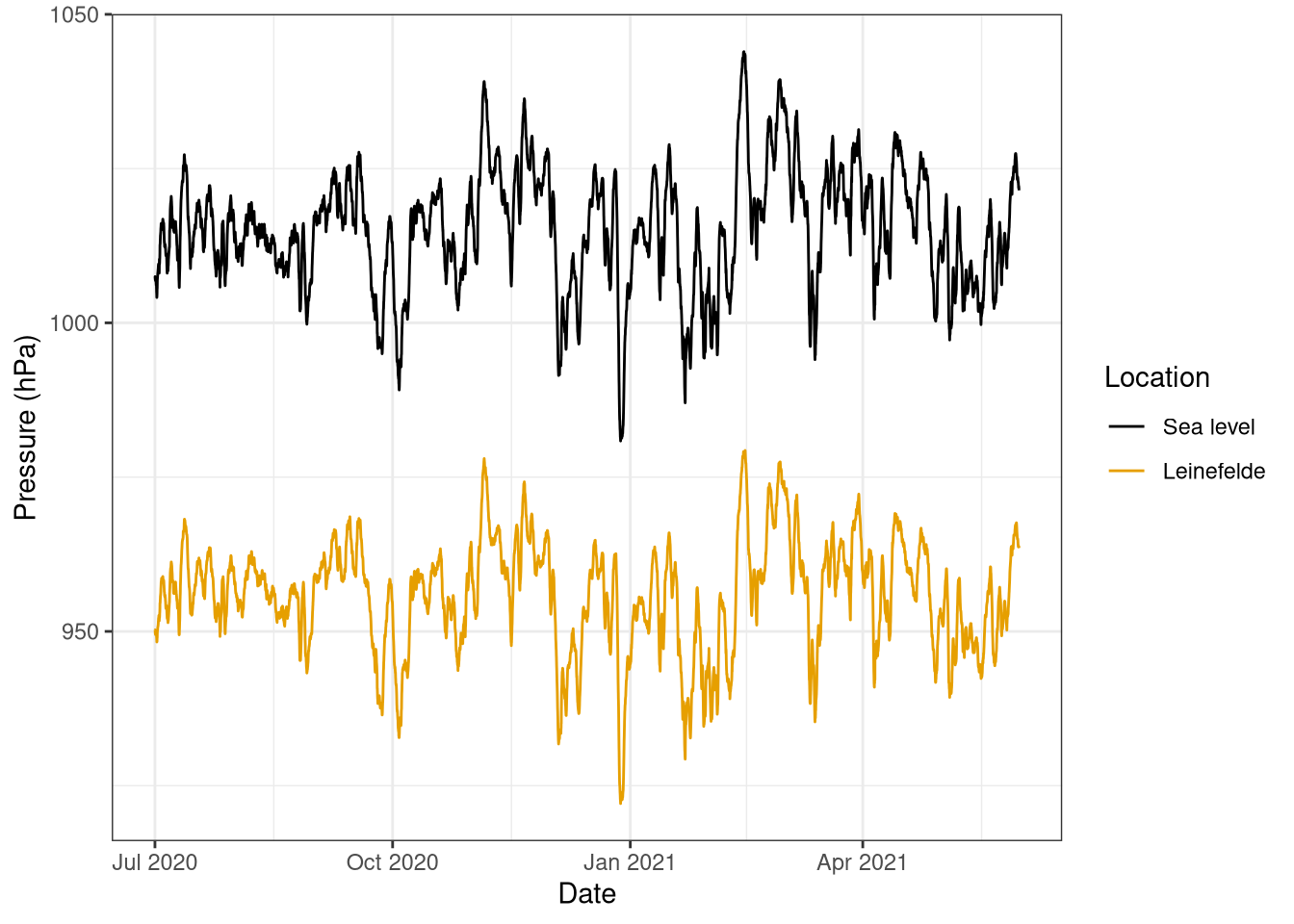

Figure 6.1: Air pressure at Leinefelde and estimated air pressure at sea level. Pressure has been corrected for air humidity. Data from Leinefelde flux tower (451 m + 41m tower) July 2020 - May 2021, 30 min frequency.

6.4.2 Air pressure Brocken and water boling temperature

Calculate the air pressure at top of the Brocken mountain (1141 m) for a pressure of 991.3 hPa and an air temperature of 15°C at the North campus (185 m). Assume a mean air temperature decrease of 0.5 K/100 m. At which temperature would water boil at the North Campus and on the Brocken?

pa_nc <- 991.3  # Air pressure north campus
Rd <- 287.05 # J Kg-1 K-1 gas constant of dry air
g <- 9.81# m/s^2
z1 <- 1141 #m Brocken mountain Height
z0 <- 185 #m North campus Height
Z <- z0-z1
ta <- 15 # C measuered at the north campus
t_column <- ta + 0.00325 * Z #correction of temperature for elevation
#hPa would be the pressure at the Brocken mountain
pa_brocken<-  (991.3 * exp((g * Z)/(Rd * c2k(t_column)))) %>% round(2)

On the top of the Brocken the air pressure would be 883.95 hPa

t_boil_nc <- (100 + 2.804e-2 * (pa_nc-1013.25) - 1.384e-5 *(pa_nc-1013.25)^2 ) %>%
                round(2)
t_boil_brocken <- (100 + 2.804e-2 * (pa_brocken-1013.25) - 1.384e-5 *
                     (pa_brocken-1013.25)^2 ) %>% round(2)

The water would boil at 99.38 °C at the North Campus and 96.14 °C on the Brocken. As expected, the boiling temperature is lower at a higher elevation.

The pressure value of the Brocken mountain was calculated using the formula mentioned in the theory background, adding correction for temperature decrease. \[p(0) = p(z) exp({\frac{g \Delta z} {R_d T}})\]