S
s_agrupada() {resumiR}¡Atención!
Instalar el paquete resumiR para hacer uso de la función s_agrupada.
Para ello utilizar el siguiente código:
install.packages("resumiR")| Descripción | Argumentos |
|---|---|
| Devuelve la tabla de frecuencias de una serie univariada de datos numéricos enteros o continuos. En el caso de datos de tipo continuo, es posible especificar los límites y la amplitud de los intervalos de clase. Por defecto, construye los intervalos de clase cerrados por derecha, con la regla de Sturges | x = vector numérico de tipo decimales = el número de posiciones decimales de los resultados. Por defecto es 1. li = límite inferior del primer intervalo de clase, para datos de tipo ls = límite superior del intervalo de clase superior, para datos de tipo a = amplitud del intervalo de clase, para datos de tipo derecha = si los intervalos de clase son cerrados por derecha, para datos de tipo grafico = texto indicando el tipo de gráfico a realizar: frecuencias simples, acumuladas o ambas. Los valores posibles son “ninguno”, “fs” y “fa”. Por defecto es “ninguno” frec = texto indicando tipo de frecuencia a utilizar en caso de realizar un gráfico. Los valores posibles son “absoluta” y “relativa”. Por efecto es “absoluta” pf = Sí es |
library(resumiR)
# Vector numérico
AT = c(6.05,2.32,2.18,3.08,4.83,6.52,1.06,0.96,5.61,2.12,3.31,7.53,6.28,6.52,2.99,0.87,4.71)
# Tipo de clase
class(AT)## [1] "numeric"## [1] 0.87## [1] 7.53## # A tibble: 6 × 6
## Clase mc fi fri Fi Fri
## <chr> <dbl> <int> <dbl> <int> <dbl>
## 1 [0,9 - 2] 1.4 3 0.2 3 0.2
## 2 (2 - 3] 2.5 5 0.3 8 0.5
## 3 (3 - 4] 3.6 1 0.1 9 0.5
## 4 (4 - 5] 4.8 2 0.1 11 0.6
## 5 (5 - 6] 5.9 3 0.2 14 0.8
## 6 (6 - 8] 7 3 0.2 17 1# Se define li, ls y a
tabla_con = s_agrupada(x = AT,
li = 0.80, ls = 8, a = 1.2)
tabla_con$`Tabla de frecuencias`## # A tibble: 6 × 6
## Clase mc fi fri Fi Fri
## <chr> <dbl> <int> <dbl> <int> <dbl>
## 1 [0,8 - 2] 1.4 3 0.2 3 0.2
## 2 (2 - 3] 2.6 5 0.3 8 0.5
## 3 (3 - 4] 3.8 1 0.1 9 0.5
## 4 (4 - 6] 5 2 0.1 11 0.6
## 5 (6 - 7] 6.2 5 0.3 16 0.9
## 6 (7 - 8] 7.4 1 0.1 17 1tabla_con_graf = s_agrupada(x = AT,
li = 0.80, ls = 8, a = 1.2,
grafico = "fs")
tabla_con_graf$Grafico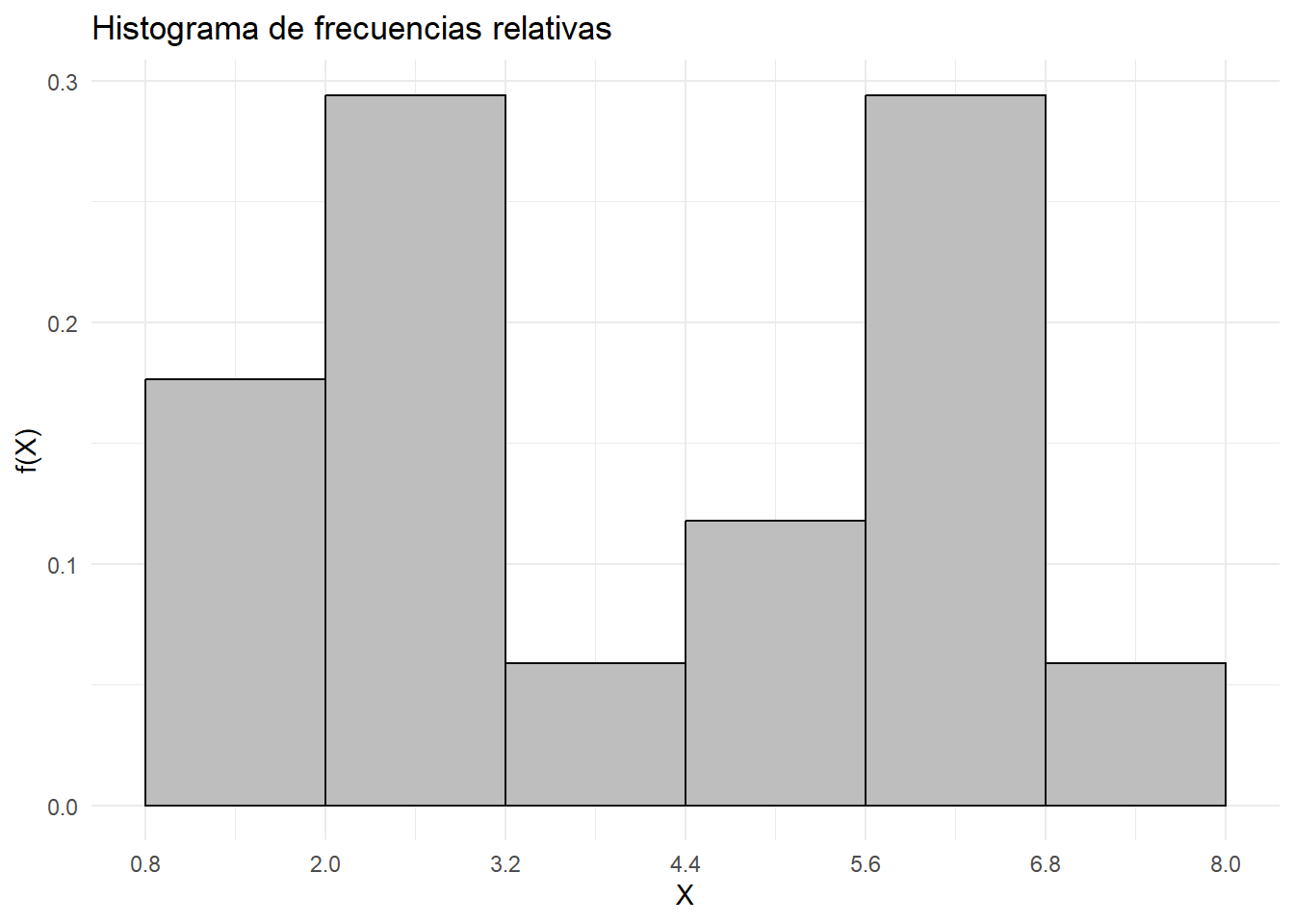
s_simple() {resumiR}¡Atención!
Instalar el paquete resumiR para hacer uso de la función s_simple.
Para ello utilizar el siguiente código:
install.packages("resumiR")| Descripción | Argumentos |
|---|---|
| Devuelve medidas de resumen univariadas de los datos numéricos ingresados, discretos o continuos, como series simples. Permite graficar la serie por medio de un gráfico de cajas y bigotes | x = vector numérico de tipo decimales = el número de posiciones decimales de los resultados. Por defecto es 1 recorte = proporción de recorte unilateral de la serie ordenada para la estimación de la media recortada; el máximo valor admitido es 0.25. Por defecto es 0.1 percenteiles = vector numérico de probabilidades acumuladas para el cálculo de percentiles. Por defecto 0.25, 0.5, 0.75 boxplot = Sí es |
library(resumiR)
AT = c(6.05,2.32,2.18,3.08,4.83,6.52,1.06,0.96,5.61,2.12,3.31,7.53,6.28,6.52,2.99,0.87,4.71)
resultados = s_simple(x = AT, recorte = 0.05, boxplot = TRUE)
medidas = resultados$MedidasView(medidas)
| Medida | Valor |
|---|---|
| n0 | 17.0 |
| n | 17.0 |
| Omitidos | 0.0 |
| Infinitos | 0.0 |
| Media | 3.9 |
| Media recortada al 5% | 3.9 |
| Min. | 0.9 |
| Max. | 7.5 |
| 25% | 2.2 |
| 50% | 3.3 |
| 75% | 6.0 |
| Varianza muestral | 4.9 |
| Desviación típica muestral | 2.2 |
| CV | 56.1 |
| ee | 0.5 |
| Rango | 6.7 |
| RI | 3.9 |
| Asimetría (momentos) | 0.1 |
| Curtosis (momentos) | 1.6 |
| Atipicos | 0.0 |
| Extremos | 0.0 |
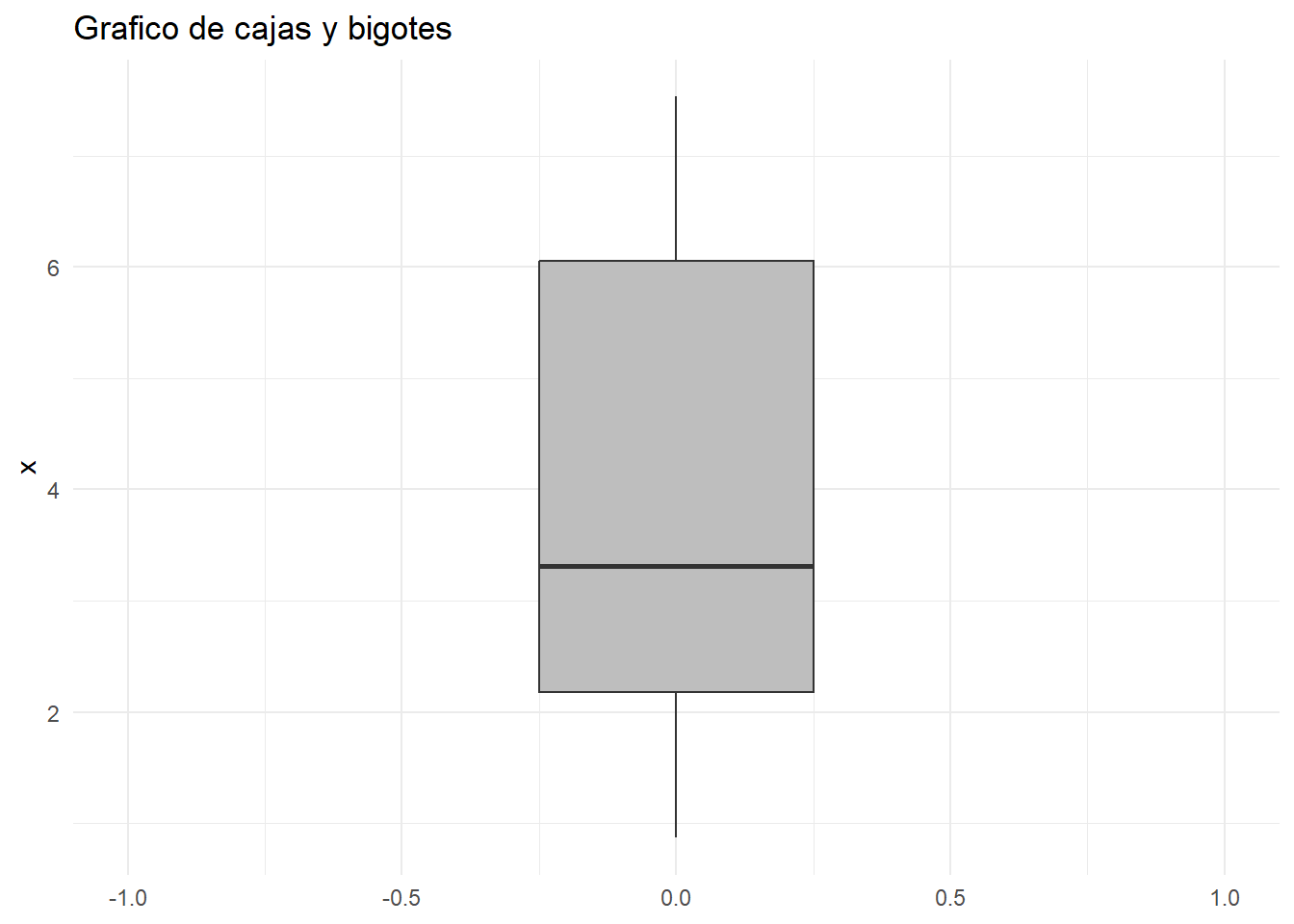
sample() {base}| Descripción | Argumentos |
|---|---|
| Permite realizar muestreos aleatorios | x = un vector de uno o más elementos entre los que elegir, o un número entero postivo size = un n° entero no negativo que indica el número de elementos a elegir replace = ¿el muestreo debe ser con reemplazo? |
## [1] "c" "c" "a" "d"scheffe.test() {agricolae}¡Atención!
Instalar el paquete agricolae para hacer uso de la función scheffe.test.
Para ello utilizar el siguiente código:
install.packages("agricolae")| Descripción | Argumentos |
|---|---|
| Realiza la prueba Scheffe |
|
#El modelo corresponde al planteado en la función duncan.test()
library(agricolae)
scheffe = scheffe.test(
y = modelo.d,
trt = "Tratamiento",
alpha = 0.05,
group = TRUE,
console = TRUE)##
## Study: modelo.d ~ "Tratamiento"
##
## Scheffe Test for Duración
##
## Mean Square Error : 0.08227
##
## Tratamiento, means
##
## Duración std r se Min Max Q25 Q50 Q75
## defilippii 0.916 0.2859371 10 0.09070281 0.56 1.45 0.7525 0.825 0.9750
## loyca 1.323 0.3469246 10 0.09070281 0.86 1.86 1.0350 1.370 1.4450
## superciliaris 1.194 0.2114080 10 0.09070281 0.82 1.46 1.0600 1.210 1.3725
##
## Alpha: 0.05 ; DF Error: 27
## Critical Value of F: 3.354131
##
## Minimum Significant Difference: 0.3322315
##
## Means with the same letter are not significantly different.
##
## Duración groups
## loyca 1.323 a
## superciliaris 1.194 ab
## defilippii 0.916 bsd() {stats}| Descripción |
|---|
| Calcula el desvío estándar de un conjunto de datos |
## [1] 0.60377select() {dplyr}¡Atención!
Instalar el paquete dplyr para hacer uso de la función select.
Para ello utilizar el siguiente código:
install.packages("dplyr")| Descripción |
|---|
| Selecciona variables en un marco de datos, utilizando un minilenguaje conciso que facilita la referencia a las variables según su clasificación (categóricas o numéricas) |
## [1] "Departamento" "Variedad" "Brix" "pH"
## [5] "AT" "PT" "Caracterización"## Brix
## 1 10.5
## 2 10.0
## 3 11.0
## 4 8.0
## 5 17.0
## 6 10.0
## 7 12.0
## 8 15.0
## 9 9.0
## 10 16.0
## 11 10.0
## 12 12.0
## 13 9.0
## 14 12.0
## 15 14.5
## 16 12.0
## 17 16.0Seleccione varias variables separándolas con comas. Observe cómo el orden de las columnas está determinado por el orden de las entradas:
## pH Departamento
## 1 2.97 Tumbaya
## 2 3.72 Tumbaya
## 3 3.70 Tumbaya
## 4 3.59 Tumbaya
## 5 3.38 Humahuaca
## 6 3.40 Humahuaca
## 7 4.71 Humahuaca
## 8 4.86 Humahuaca
## 9 3.17 Humahuaca
## 10 4.79 Humahuaca
## 11 3.94 Humahuaca
## 12 3.42 Humahuaca
## 13 3.28 Humahuaca
## 14 3.49 Humahuaca
## 15 3.74 Humahuaca
## 16 4.73 Humahuaca
## 17 3.95 Humahuacaseq() {base}| Descripción | Argumentos |
|---|---|
| Generar secuencias regulares | from = valor inicial de la secuencia to = valor final de la secuencia by = ¿cada cuánto se incrementa la secuencia? |
## [1] 24 30 36 42 48set.seed() {base}| Descripción | Argumentos |
|---|---|
| Genera números aleatorios |
|
## [1] 0.5923025 0.2886310 -0.9557791 0.7484320 -0.4597529 0.0983391
## [7] 0.7095290 -1.1960426 -2.3115612 -0.7886402## [1] 0.04360146 -0.82151149 -0.10486316 0.22540480 0.12635188 0.27743014
## [7] 0.56331893 -0.26021739 0.31437626 -1.78086737#Creación de 10 valores aleatorios con set.seed()
set.seed(seed = 3)
numeros = rnorm(n = 10)
numeros## [1] 0.5923025 0.2886310 -0.9557791 0.7484320 -0.4597529 0.0983391
## [7] 0.7095290 -1.1960426 -2.3115612 -0.7886402shapiro.test() {stats}| Descripción | Argumentos |
|---|---|
| Realiza la prueba de normalidad de Shapiro-Wilk. La hipótesis nula es que los datos se distribuyen normalmente | x = vector numérico de valores de datos |
##
## Shapiro-Wilk normality test
##
## data: resid(modelo)
## W = 0.89194, p-value = 0.04988skewness() {moments}¡Atención!
Instalar el paquete moments para hacer uso de la función skewness.
Para ello utilizar el siguiente código:
install.packages("moments")| Descripción |
|---|
| Calcula la asimetría de un conjunto de datos |
## [1] 0.6679828sort() {base}| Descripción | Argumentos |
|---|---|
| Ordena una secuencia de vector tipo numérico | decreasing =
Sí no se especifica este argumento por defecto ordena la serie en forma ascendente ( |
## [1] 6 5 4 2 1## [1] 1 2 4 5 6## [1] 1 2 4 5 6sqrt() {base}| Descripción |
|---|
| Calcula la raíz cuadrada de x |
## [1] 5stat_pvalue_manual() {ggpubr}¡Atención!
Instalar el paquete ggpubr para hacer uso de la función stat_pvalue_manual.
Para ello utilizar el siguiente código:
install.packages("ggpubr")| Descripción | Argumentos |
|---|---|
| Añade manualmente valores p a un ggplot |
|
Ejemplo práctico disponible en letra G, función ggboxplot() {ggpubr}stepfun() {stats}| Descripción | Argumentos |
|---|---|
| Permite crear funciones escalonadas. Una función escalonada es una función matemática que toma un valor constante dentro de intervalos específicos y cambia instantáneamente su valor en los límites de estos intervalos |
|
## Step function
## Call: stepfun(x, y)
## x[1:4] = 1, 2, 3, 4
## 5 plateau levels = 7, 5, 3, 4, 1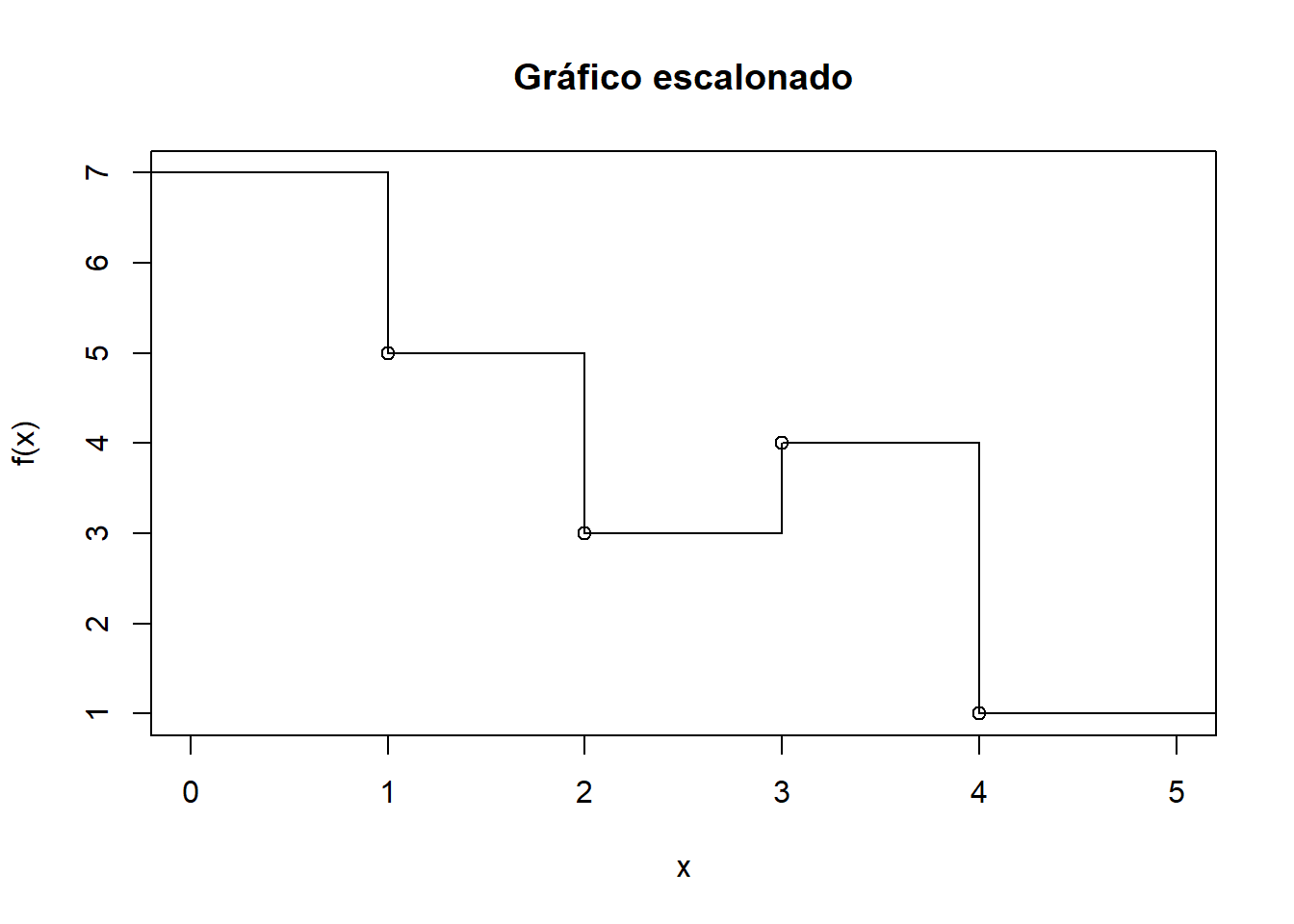
str() {utils}| Descripción |
|---|
| Muestra la estructura de una base de datos. Indica el número de filas, columnas y el nombre de las variables |
## 'data.frame': 17 obs. of 7 variables:
## $ Departamento : Factor w/ 2 levels "Humahuaca","Tumbaya": 2 2 2 2 1 1 1 1 1 1 ...
## $ Variedad : chr "Granny Smith" "Red Delicius" "Red Delicius" "Red Delicius" ...
## $ Brix : num 10.5 10 11 8 17 10 12 15 9 16 ...
## $ pH : num 2.97 3.72 3.7 3.59 3.38 3.4 4.71 4.86 3.17 4.79 ...
## $ AT : num 6.05 2.32 2.18 3.08 4.83 6.52 1.06 0.96 5.61 2.12 ...
## $ PT : num 1.02 1.03 1.3 0.77 0.9 1.27 0.95 0.33 1.01 1.79 ...
## $ Caracterización: chr "Acidulado" "Dulce" "Dulce" "Dulce" ...sum() {base}| Descripción |
|---|
| Realiza la operación suma. Su equivalente es el +. Los dos procedimientos son equivalentes |
## [1] 15## [1] 15summarise() {dplyr}¡Atención!
Instalar el paquete dplyr para hacer uso de la función summarise.
Para ello utilizar el siguiente código:
install.packages("dplyr")| Descripción |
|---|
| Crea un nuevo marco de datos. Devuelve una fila por cada combinación de variables de agrupación. Si no hay variables de agrupación, la salida tendrá una sola fila que resumirá todas las observaciones en la entrada. Contendrá una columna para cada variable de agrupación y una columna para cada una de las estadísticas de resumen que haya especificado |
library(dplyr)
datos %>%
group_by(Departamento) %>%
summarise(Media.AT = mean(AT),
Media.pH = mean(pH),
Media.PT = mean(PT))## # A tibble: 2 × 4
## Departamento Media.AT Media.pH Media.PT
## <fct> <dbl> <dbl> <dbl>
## 1 Humahuaca 4.10 3.91 1.09
## 2 Tumbaya 3.41 3.50 1.03summary() {base}| Descripción |
|---|
| Permite obtener un agregado de medidas de tendencia central |
## Departamento Variedad Brix pH
## Humahuaca:13 Length:17 Min. : 8.0 Min. :2.970
## Tumbaya : 4 Class :character 1st Qu.:10.0 1st Qu.:3.400
## Mode :character Median :12.0 Median :3.700
## Mean :12.0 Mean :3.814
## 3rd Qu.:14.5 3rd Qu.:3.950
## Max. :17.0 Max. :4.860
## AT PT Caracterización
## Min. :0.870 Min. :0.330 Length:17
## 1st Qu.:2.180 1st Qu.:0.860 Class :character
## Median :3.310 Median :1.010 Mode :character
## Mean :3.938 Mean :1.078
## 3rd Qu.:6.050 3rd Qu.:1.270
## Max. :7.530 Max. :2.050