P
pairwise.wilcox.test() {stats}
| Calcula comparaciones por pares entre niveles de grupo con correcciones para pruebas múltiples |
x = vector respuesta g = vector o factor de grupo p.ajust.method = método para ajustar p valores paired = TRUE sí es una prueba pareada (muestras dependientes) y FALSE para prueba apareada (muestras independientes) |
p.adjust.methods
c("holm", "hochberg", "hommel", "bonferroni", "BH", "BY", "fdr", "none")
afluentes = factor(rep(c("Archibarca","Cerro Overo","Rosario"), each = 12))
MOT = c(1.40,2.16,0.74,0.86,1.13,1.75,1.86,1.16,2.36,1.46,0.98,1.14,
4.14,2.25,2.16,2.45,2.56,2.36,2.78,2.69,3.16,2.48,2.63,2.59,
1.10,1.05,1.15,0.60,1.11,0.63,0.89,0.75,1.03,1.06,1.09,0.55)
data.kruskal = data.frame(afluentes, MOT)
pairwise.wilcox.test(x = data.kruskal$MOT,
g = data.kruskal$afluentes,
p.adjust.method = "bonferroni",
paired = FALSE)
##
## Pairwise comparisons using Wilcoxon rank sum test with continuity correction
##
## data: data.kruskal$MOT and data.kruskal$afluentes
##
## Archibarca Cerro Overo
## Cerro Overo 0.00023 -
## Rosario 0.02044 2.2e-06
##
## P value adjustment method: bonferroni
paste() {base}
| Concatena vectores después de convertirlos en caracteres |
… = dos o más objetos R luego de convertir los objetos en caracter sep = indica de qué manera se separan los elementos de los objetos collapse = indica de qué manera se separan los resultados obtenidos de la concatenación |
paste(... = c("MA","RI","A"), c("RIA","TA","NA"))
## [1] "MA RIA" "RI TA" "A NA"
En este ejemplo hay dos objetos R y se obtiene una salida con tres nombres. Los nombres (resultados obtenidos) están separados por comillas (““) y los elementos de los objetos por un espacio en blanco ( )
paste(... = c("MA","RI","A"),c("RIA","TA","NA"),
sep = "")
## [1] "MARIA" "RITA" "ANA"
Los elementos de los objetos no están separados por un espacio en blanco
paste(... = c("MA","RI","A"),c("RIA","TA","NA"),
sep = "",
collapse = ",")
## [1] "MARIA,RITA,ANA"
Los resultados están separados por coma (,)
paste0() {base}: Funciona de manera similar a paste()
paste0(... = c("MA","RI","A"),c("RIA","TA","NA"))
## [1] "MARIA" "RITA" "ANA"
Los elementos de los objetos no aparecen separados por un espacio en blanco. No es necesario indicar el argumento sep=
paste0(... = c("MA","RI","A"),c("RIA","TA","NA"),
collapse = ",")
## [1] "MARIA,RITA,ANA"
paste(... = rep("Bromatologia",2),rep("Comision",2), seq(1,2,1),
collapse = "-")
## [1] "Bromatologia Comision 1-Bromatologia Comision 2"
En este ejemplo se utilizaron 3 objetos y los resultados están separados por un guión
pbinom() {stats}
| Calcula la función de probabilidad acumulada |
q = el valor de x para el cual se desea estimar la probabilidad acumulada size = el tamaño de la muestra prob = la probabilidad de “éxito” lower.tail = TRUE o FALSE. Por defecto, devuelve la probabilidad acumulada por izquierda (TRUE) |
x = 3
n = 6
p = 0.13
pbinom(q = x,size = n, prob = p, lower.tail = T)
## [1] 0.9965587
#Probabilidad acumulada por izquierda
pbinom(q = x,size = n, prob = p, lower.tail = F)
## [1] 0.003441315
#Probabilidad acumulada por derecha
pchisq() {stats}
| Calcula la función de probabilidad acumulada |
|
## [1] 0.198748
pchisq(1, 3, lower.tail = F)
## [1] 0.801252
plot() {graphics}
| Permite realizar gráficos en R |
x = las coordenadas x de los puntos del gráfico y = las coordenadas y de los puntos del gráfico type = indicar el tipo de gráfico main = título del gráfico xlab = título para el el eje x ylab = título para el eje y cex.main = tamaño de texto del título cex.lab = tamaño de etiquetas en ejes |
Cuando type = ...
"p" para puntos,
"l" para líneas,
"b" para ambos,
"c" para la parte de líneas solo de "b",
"o" para ambos 'sobretrazados',
"h" para líneas verticales tipo "histograma" (o "alta densidad"),
"s" para escalones,
"n" para no trazar.
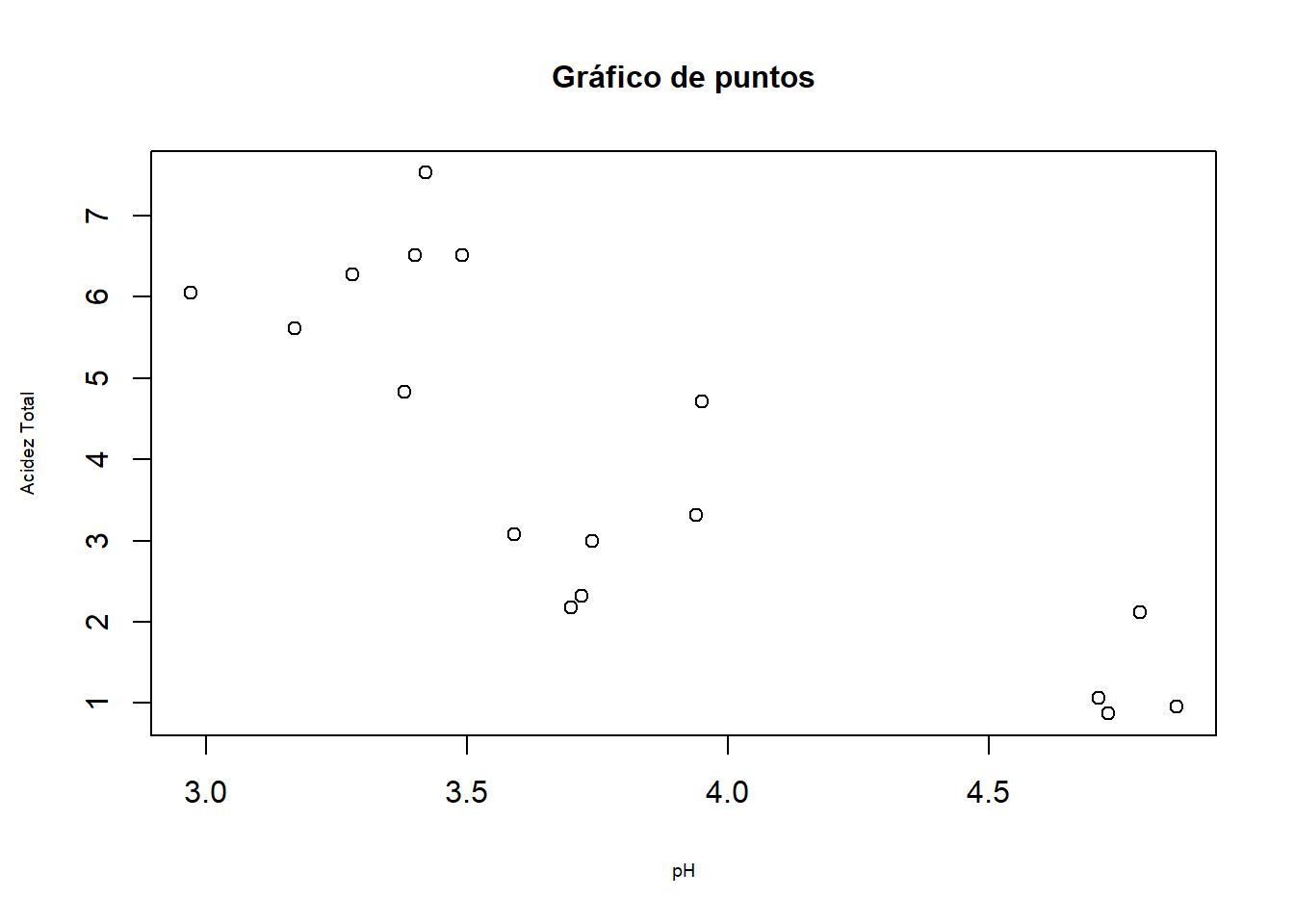
plot(datos$pH, datos$AT,
type = "p",
main = "Gráfico de puntos",
ylab = "Acidez Total",
xlab = "pH",
cex.main = 1,
cex.lab = 0.6)
pnorm() {stats}
| Devuelve la probabilidad acumulada hasta un determinado valor de q |
q = cuantil o valor de la variable cuya probabilidad acumulada se desea conocer lower.tail = TRUE o FALSE. Por defecto, devuelve la probabilidad acumulada por izquierda (TRUE) mean = es el valor de la media. Por defecto mean=0 sd = es el valor del desvío estándar. Por defecto, sd=1 |
media = 27210
sigma = 3000
x = 28000
pnorm(q = x,
mean = media,
sd = sigma,
lower.tail = FALSE) # Probabilidad acumulada por derecha
## [1] 0.3961468
pnorm(q = x,
mean = media,
sd = sigma,
lower.tail = TRUE) # Probabilidad acumulada por izquierda
## [1] 0.6038532
points() {graphics}
| Permite agregar puntos a un gráfico existente |
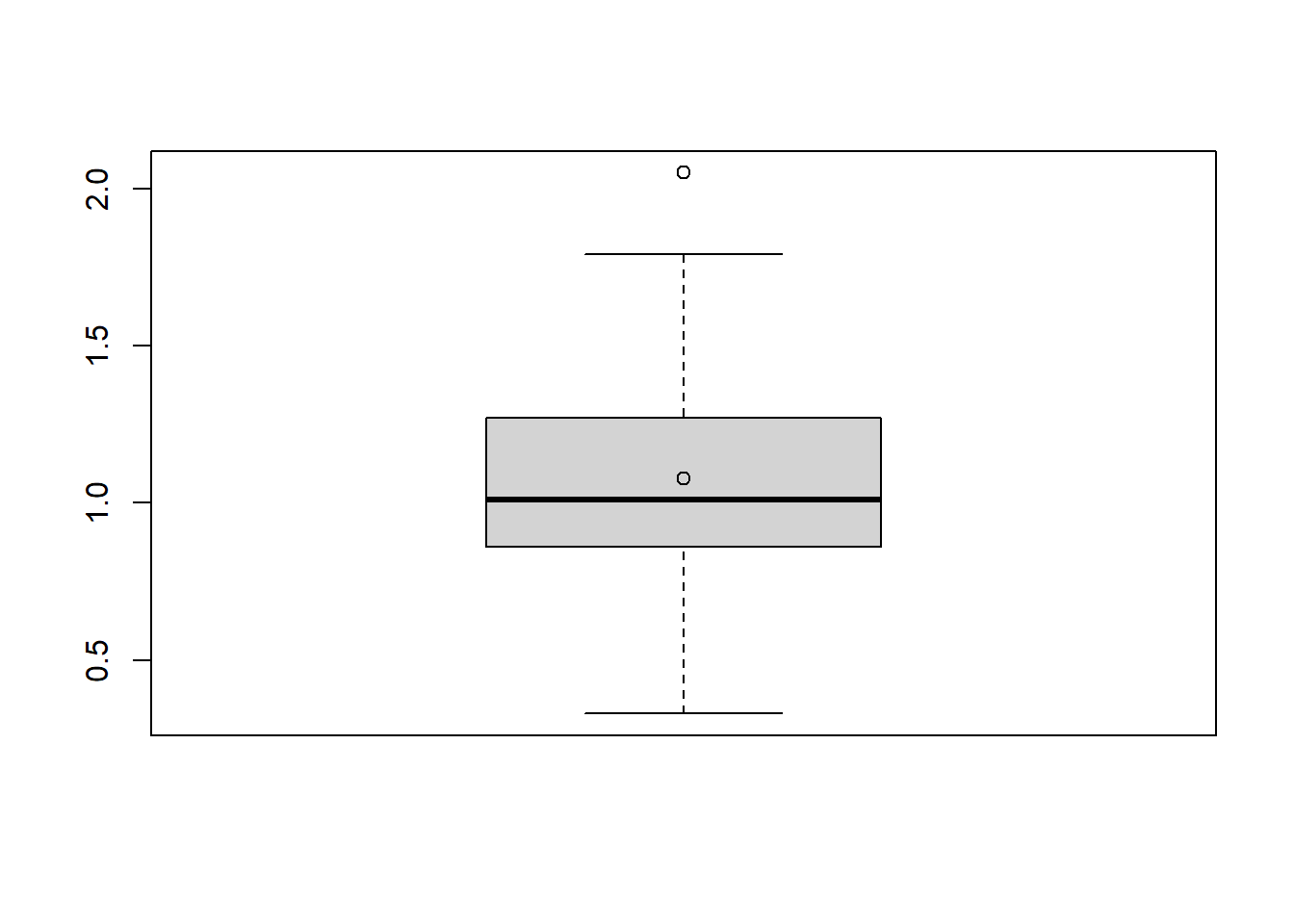
boxplot(datos$PT) # Boxplot para polifenoles totales (PT)
points(mean(datos$PT)) # En este caso se agrega la media como punto en el boxplot anterior
ppois() {stats}
| Calcula la función de distribución acumulativa |
q = el valor de x para el cual se desea estimar la probabilidad acumulada lambda = el valor del parámetro lower.tail = TRUE o FALSE. Por defecto, devuelve la probabilidad acumulada por izquierda (TRUE) |
x = 5
l = 4
ppois(q = x,lambda = l)
## [1] 0.7851304
predict() {stats}
| Permite ajustar los valores observados a la recta de regresión o bien para estimar los valores de la variable respuesta cuando la variable predictora asume determinados valores. En el segundo caso, es necesario especificar los valores de la variable predictora en formato de tabla o data.frame por medio del argumento newdata |
x = c(1038,1039,958,962,1067,960,1099,1033,975,1002,1228,1076)
y = c(391,300,352,317,221,337,521,154,483,269,549,356)
modelo = lm(y ~ x)
predict(modelo)
## 1 2 3 4 5 6 7 8
## 355.2194 355.8844 302.0264 304.6861 374.5019 303.3563 395.7791 351.8949
## 9 10 11 12
## 313.3299 331.2826 481.5528 380.4861
predict(modelo,newdata = data.frame(x=1000))
## 1
## 329.9528
print() {base}
| Permite mostrar información en la consola |
media.PT = mean(datos$PT)
media.PT = mean(datos$PT)
print(media.PT)
## [1] 1.077647
pt() {stats}
| Calcula la función de distribución acumulativa |
q = el valor de x para el cual se desea estimar la probabilidad acumulada df = grados de libertad lower.tail = TRUE o FALSE. Por defecto, devuelve la probabilidad acumulada por izquierda (TRUE) |
q = 3.15
df = 5
pt(q = q,
df = df,
lower.tail = T)
## [1] 0.9873105
pwr.anova.test() {pwr}
¡Atención!
Instalar el paquete pwr para hacer uso de la función pwr.anova.test.
Para ello utilizar el siguiente código:
install.packages("pwr")
| Calcula la potencia de la prueba o determine los parámetros para obtener la potencia objetivo |
|
library(pwr)
pwr.anova.test(
k = 3,
f = 0.25,
sig.level = 0.05,
power = 0.8
)
##
## Balanced one-way analysis of variance power calculation
##
## k = 3
## n = 52.3966
## f = 0.25
## sig.level = 0.05
## power = 0.8
##
## NOTE: n is number in each group
pwr.anova.test(
k = 3,
n = 10,
f = 0.25,
sig.level = 0.05
)
##
## Balanced one-way analysis of variance power calculation
##
## k = 3
## n = 10
## f = 0.25
## sig.level = 0.05
## power = 0.1951401
##
## NOTE: n is number in each group

