4  Interpretations of Probability and Statistics

• There are two main interpretations of probability: relative frequency and “subjective” probability.
• These two interpretations provide the philosophical foundation for two schools of statistics: frequentist and Bayesian

Example 4.1 The following situations involve probability. How are the situations above similar, and how are they different? What is one feature that all of the situations have in common? Is the interpretation of “probability” the same in all situations? The goal here is to just think about these questions, and not to compute any probabilities (or to even think about how you would).

1. The probability that you roll doubles in a turn of a board game.
2. The probability that a “randomly selected” Cal Poly student is a California resident.
3. The probability that the high temperature in San Luis Obispo tomorrow is above 70 degrees F.
4. The probability that President Biden wins the 2024 U.S. Presidential Election.
5. The probability that extraterrestrial life currently exists somewhere in the universe.
6. The probability that you ate an apple on April 17, 2009.
   
   
   
   
   

• A phenomenon is random if there are multiple potential outcomes, and there is uncertainty about which outcome will occur. Uncertainty is understood in broad terms, and in particular does not only concern future occurrences.
• The probability of an event associated with a random phenomenon is a number in the interval \([0, 1]\) measuring the event’s likelihood or degree of uncertainty.
• The probability of an event associated with a random phenomenon can be interpreted as a long run proportion or long run relative frequency: the probability of the event is the proportion of times that the event would occur in a very large number of hypothetical repetitions of the random phenomenon, e.g., in a simulation.
• A subjective (a.k.a. personal) probability describes the degree of likelihood a given individual assigns to a certain event. As the name suggests, different individuals (or probabilistic models) might have different subjective probabilities for the same event.
• Think of subjective probabilities as measuring relative degrees of likelihood or uncertainty rather than long run relative frequencies.
• We will use these interpretations interchangeably.
  • With subjective probabilities it is often helpful to consider what might happen in a simulation.
  • It is also useful to consider long run relative frequencies in terms of relative degrees of likelihood.
• Fortunately, the mathematics of probability work the same way regardless of the interpretation.

Example 4.2 What is your subjective probability that Professor Ross has a TikTok account? Consider the following two bets, and suppose you must choose only one.

1. You win $100 if Professor Ross has a TikTok account, and you win nothing otherwise.
2. A box contains 40 green and 60 gold marbles that are otherwise identical. The marbles are thoroughly mixed and one marble is selected at random. You win $100 if the selected marble is green, and you win nothing otherwise.

1. Which of the above bets would you prefer? Or are you completely indifferent? What does this say about your subjective probability that Professor Ross has a Tik Tok account?
   
   
   

2. If you preferred bet B to bet A, consider bet C which has a similar setup to B but now there are 20 green and 80 gold marbles. Do you prefer bet A or bet C? What does this say about your subjective probability that Professor Ross has a Tik Tok account?
   
   
   

3. If you preferred bet A to bet B, consider bet D which has a similar setup to B but now there are 60 green and 40 gold marbles. Do you prefer bet A or bet D? What does this say about your subjective probability that Professor Ross has a Tik Tok account?
   
   
   

4. Continue to consider different numbers of green and gold marbles. Can you zero in on your subjective probability?
   
   
   

Example 4.3 Suppose your subjective probabilities for the 2023 NBA champion satisfy the following conditions.

• The Nuggets and 76ers are equally likely to win
• The Grizzlies are 1.5 times more likely than the Nuggets to win
• The Celtics are 2 times more likely than the Grizzlies to win
• The winner is as likely to be among these four teams — Celtics, Grizzlies, 76ers, Nuggets — as not.

1. Construct a table of your subjective probabilities.
   
   
   
   
   

2. How could you construct a circular spinner (like from a kids game) to simulate the NBA champion according to these subjective probabilities? According to this model, what would you expect the results of 10000 repetitions of a simulation of the champion to look like?
   
   
   
   
   

Example 4.4 How old do you think Professor Ross currently is? Consider age on a continuous scale, e.g., you might be 20.73 or 21.36 or 19.50.

In this example, you will use probability to quantify your uncertainty about your instructor’s age. You only need to give ballpark estimates of your subjective probabilities, but you might consider what kinds of bets you would be willing to accept.

1. What is your subjective probability that your instructor is at most 30 years old? More than 30 years old? (What must be true about these two probabilities?)
   
   
   

2. What is your subjective probability that your instructor is at most 60 years old? More than 60 years old?
   
   
   

3. What is your subjective probability that your instructor is at most 40 years old? More than 40 years old?
   
   
   

4. What is your subjective probability that your instructor is at most 50 years old? More than 50 years old?
   
   
   

5. Fill in the blank: your subjective probability that your instructor is at most [blank] years old is equal to 50%.
   
   
   

6. Fill in the blanks: your subjective probability that your instructor is between [blank] and [blank] years old is equal to 95%.
   
   
   

7. Let \(\theta\) represent your instructor’s age at 8:00am on Jan 12, 2023. Use your answers to the previous parts to sketch a continuous probability density function to represent your subjective probability distribution for \(\theta\).
   
   
   
   
   

8. If you ascribe a probability distribution to \(\theta\), then are you treating \(\theta\) as a constant or a random variable?
   
   
   

• A random variable is a numerical quantity whose value is determined by the outcome of a random or uncertain phenomenon.
• The (probability) distribution of a random variable specifies the possible values of the random variable and a way of determining corresponding probabilities. Like probabilities themselves, probability distributions of random variables can also be interpreted as:
  • relative frequency distributions, e.g., what pattern would emerge if I simulated many values of the random variable? or as
  • subjective probability distributions, e.g., which potential values of this uncertain quantity are relatively more plausible than others?

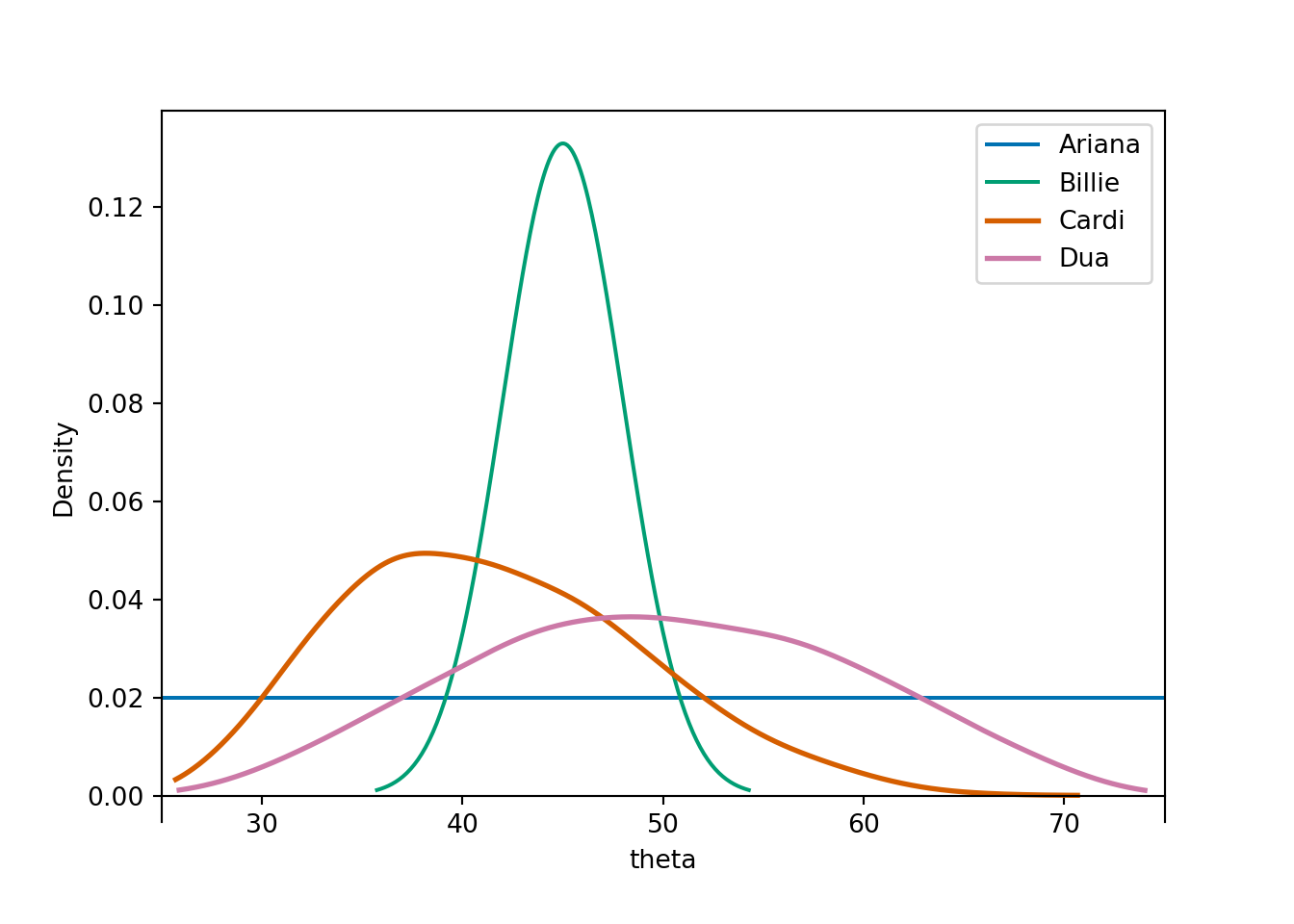
Example 4.5 Continuing the previous example, the figure displays the subjective probability distribution of the instructor’s age for four students.

1. Since age is treated as a continuous random variable, each of the above plots is a probability “density”. Explain briefly what this means. How is probability represented in density plots like these?
   
   
   
   
   

2. Rank the students in terms of their subjective probability that the instructor is at most 40 years old.
   
   
   
   
   

3. Rank the students in terms of their answers to the question: your subjective probability that your instructor is at most [blank] years old is equal to 50%.
   
   
   
   
   

4. Rank the students in terms of their uncertainty about the instructor’s age. Who is the most uncertain? The least?
   
   
   
   
   

• One key aspect of Bayesian analyses is applying a subjective probability distribution to a parameter in a statistical model.

Example 4.6 Let \(\theta_b\) represent the proportion of current Cal Poly students who have ever read any of the books in the Harry Potter series. Let \(\theta_m\) represent the proportion of current Cal Poly students who have ever seen any of the movies in the Harry Potter series.

1. Are \(\theta_b\) and \(\theta_m\) parameters or statistics? Why?
   
   
   
   

2. Are the values of \(\theta_b\) and \(\theta_m\) known or unknown, certain or uncertain?
   
   
   
   

3. What are the possible values of \(\theta_b\) and \(\theta_m\)?
   
   
   
   

4. Sketch a probability distribution representing what you think are more/less credible values of \(\theta_b\). Repeat for \(\theta_m\).
   
   
   
   

5. Are you more certain about the value of \(\theta_b\) or \(\theta_m\)? How is this reflected in your distributions?
   
   
   
   

6. Suppose that in a class of 35 Cal Poly students, 21 have read a Harry Potter book, and 30 have seen a Harry Potter movie. Now that we have observed some data, sketch a probability distribution representing what you think are more/less credible values of \(\theta_b\). Repeat for \(\theta_m\). How do your distributions after observing data compare to the distributions you sketched before?
   
   
   
   

• Observational units (a.k.a., cases, individuals, subjects) are the people, places, things, etc we collect information on.
• A variable is any characteristic of an observational unit that we can measure.
• Statistical inference involves using data collected on a sample to make conclusions about a population.
• Inference often concerns specific numerical summaries, using values of statistics to make conclusions about parameters.
• A statistic is a number that describes the sample, e.g., sample mean, sample proportion.
• A parameter is a number that describes the population or model, e.g., population mean, population proportion. The actual value of a parameter is almost always unknown.
  • Parameters are often denoted with Greek letters. We’ll often use the Greek letter \(\theta\) (“theta”) to denote a generic parameter.
• In “traditional”, frequentist statistical analysis, parameters are treated as fixed — that is, not random — constants.
  • Any randomness in a frequentist analysis arises from how the data were collected, e.g., via random sampling or random assignment.
  • In a frequentist analysis, statistics are random variables; parameters are fixed numbers.
• On the other hand, in a Bayesian statistical analysis, since a parameter \(\theta\) is unknown — that is, it’s value is uncertain to the observer — \(\theta\) is treated as a random variable.
  • That is, in Bayesian statistical analyses unknown parameters are random variables that have probability distributions.
  • The (subjective) probability distribution of a parameter quantifies the degree of uncertainty about the value of the parameter.
  • Therefore, the Bayesian perspective allows for probability statements about parameters.
  • We start with “prior” distributions that represent our uncertainty based on our “beliefs”, then we revise to obtain “posterior” distributions after observing some data.
  • We will see (among other things) (1) how to quantify uncertainty about parameters using probability distributions, and (2) how to update those distributions to reflect new data.