21 Topic Modeling

Topic Modeling ist das aktuell wohl am häufigsten eingesetzte Verfahren (bzw. genauer: Gruppe von Verfahren) der automatisierten Inhaltsanalyse in der kommunikationswissenschaftlichen Forschung. Im Gegensatz zur vorab beschriebenen Textklassifikation (siehe Kapitel 20) handelt es sich um Verfahren des unüberwachten maschinellen Lernens – also Verfahren, die ohne Vorabwissen in Form annotierter Klassen und mit oft nur minimalem (aber bedeutsamen) Input des Forschenden selbstständig Muster in Dokumenten erkennen. Topic Modeling eignet sich daher insbesondere zur Exploration und Deskription großer Textmengen.

In diesem Kapitel setzen wir uns zunächst mit den Grundlagen dieser Verfahrensgruppe auseinander und setzen dann ein eigenes Topic Model in R um. Im Vergleich zu den bisher besprochenen Verfahren sind Topic-Modeling-Verfahren sowohl mathematisch als auch interpretatorisch deutlich komplexer; wir müssen zudem auf einige Konzepte und Techniken zurückgreifen, die im Kurs schon einige Wochen zurückliegen. Es ist daher sehr sinnvoll, alle beschriebenen Schritte selbst am eigenen Rechner nachzuvollziehen und längere Pipes nach und nach auszuführen.

21.1 Grundlagen

Wer schon einmal in einer (manuellen) Inhaltsanalyse Themen in einem Textkorpus untersucht hat, weiß, wie schwierig es sein kann, den Begriff Thema zu definieren und operationalisieren und eine trennscharfe und eindeutige Codierung vorzunehmen. Handelt es sich bei einem Artikel zu den Corona-Maßnahmen bei Bundesligaspielen um einen Artikel aus dem Themenbereich Gesundheit, Innenpolitik oder Sport? Entsprechend finden sich in Codebüchern zum Thema oft lange Codieranweisungen mit vielen (Negativ-)Beispielen und es steht in der Regel eine lange Schulung der Codierer*innen an, bevor die Codierung auch nur annähernd reliabel verläuft.

Topic Modeling bietet hier eine reizvolle Alternative: Themen werden strikt auf Basis von Worthäufigkeiten in den einzelnen Dokumenten vermeintlich objektiv berechnet, ganz ohne subjektive Einschätzungen und damit einhergehenden etwaigen Verzerrungen. Wie wir aber sehen werden, ist die Sache bei weitem nicht so straightforward – und menschlicher Input und Intepretation letztlich ebenso relevant wie bei der manuellen Themencodierung.

Wie oben bereits angeprochen, handelt es sich bei Topic Modeling um eine Gruppe von Verfahren, die ähnlichen Grundprinzipien folgen, sich aber in der genauen mathematischen Ausführung unterscheiden. Die bekanntesten dieser Verfahren sind LDA (Latent Dirichlet Allocation) sowie die darauf aufbauenden CTM (Correlated Topic Models) und STM (Structural Topic Models). All diesen Verfahren sind wesentliche Annahmen und Schritte gemein:

Ein Textkorpus besteht aus \(D\) Dokumenten (z. B. Artikel oder Posts, wobei die einzelnen Dokumente als \(d_1, d_2, ...\) bezeichnet werden) und \(V\) Wörtern bzw. Terms (d.h. alle Wörter, die im gesamten Korpus vorkommen, wobei die einzelnen Wörter als \(w_1, w_2, ...\) bezeichnet werden). Dabei wird dem Bag-of-Words-Modell (siehe Kapitel 17.2) gefolgt, das heißt es zählt lediglich die Worthäufigkeit je Dokument, die syntaktischen und grammatikalischen Zusammenhänge zwischen einzelnen Wörtern werden ignoriert.
Es wird nun angenommen, dass latente Themen \(K\) zu unterschiedlichen Anteilen in den Dokumenten \(D\) vorkommen und alle Wörter \(V\) mit unterschiedlicher Wahrscheinlichkeit zu den \(K\) Themen gehören. \(K\) muss dabei vorab vom Forschenden festgelegt werden.
Ziel der Verfahren ist die Berechnung zweier Matrizen \(D \times K\) und \(V \times K\). Die erste Matrix \(D \times K\) enthält für jedes einzelne Dokument \(d\) und jedes einzelne Thema \(k\) die Wahrscheinlichkeit, dass das Thema in diesem Dokument vorkommt. Analog enthält \(V \times K\) für jedes einzelne Wort \(w\) und jedes einzelne Thema \(k\) die Wahrscheinlichkeit, dass das jeweilige Wort in diesem Thema vorkommt.
Mit Hilfe dieser Matrizen können die Themen dann beschrieben und interpretiert werden. So können aus \(V \times K\) die wichtigsten Wörter je Thema (d.h., die Wörter mit der höchsten konditionalen Wahrscheinlichkeit, zu einem bestimmten Thema \(k\) zu gehören) abgelesen werden; mittels \(D \times K\) können Themen Dokumenten und umgekehrt zugeordnet werden, z. B. in dem für jedes Dokument \(d\) das Thema \(k\) mit der höchsten konditionalen Wahrscheinlichkeit identifiziert wird.
Zur Berechnung dieser Matrizen wird sozusagen der umgekehrte Weg gegangen und die Erzeugung der Dokumente als statistischer Prozess beschrieben: ein Dokument wird demnach erzeugt, in dem zufällig Themen aus der zum Dokument zugehörigen Themenverteilung und Wörter aus der den Themen zugehörigen Wortverteilungen gezogen werden. Hierzu wird das Topic Model zunächst mit zufälligen Themen- und Wortverteilungen initialisiert und dann in einem iterativen, algorithmischen Verfahren nach und nach adaptiert, bis es möglichst gut zu den Daten (dem Textkorpus) passt (d.h. die gemeinsame Likelihood der Themen- und Wortverteilungen maximiert wird).⁵³

Daraus ergeben sich einige Konsequenzen für die Interpretation und Unterschiede zum gewöhnlichen Vorgehen bei einer manuellen Themenanalyse:

Der im Topic Modeling verwendete algorithmische Themenbegriff unterscheidet sich von dem, was wir im intuitiven, alltäglichen Begriffsverständnis meinen, wenn wir von “Themen” besprechen (wobei wir dieses alltägliche Begriffsverständnis auch nur sehr schwer operational definieren können) und beschreibt letztlich semantische Wortgruppierungen. Das können je nach Textkorpus und verwendetem Verfahren Themen sein, die wir klassisch als Themen der Berichterstattung beschreiben würden, also z. B. Wortgruppierungen, die auf Berichterstattung zu Sport, zu Politik oder zu bestimmten Nachrichtenereignissen verweisen, aber eben auch andere Arten von Wortgruppierungen, die der Algorithmus im Textkorpus identifziert und die z. B. auf Handlungsstränge, wiederkehrende sprachliche Stilmittel etc. verweisen.
Wo es bei der manuellen Themencodierung in der Regel darum geht, Artikel Themen eindeutig und trennscharf zuzuweisen, gehen Topic-Modeling-Verfahren von sogenannter Mixed Membership aus, d.h. Dokumente können in wechselnden Anteilen zu verschiedenen Themen gehören. Um Dokumenten Themen und umgekehrt zuzuordnen, müssen also manuell Entscheidungen getroffen werden, z. B. indem jedes Dokument das Thema bzw. die Themen zugeordnet bekommt, das für das jeweilige Dokument die höchste Wahrscheinlichkeit aufweist bzw. die über einem bestimmten Cutoff-Wert (z. B. 30%, 50%) liegen.
Topic Modeling führt immer zu der vorgegebenen Anzahl an Themen. Ob es sich dabei auch um sinnvoll interpretierbare Themen handelt, muss manuell erörtert werden.

Wenn dies bis hierher sehr abstrakt klang, keine Sorge: Wir werden uns all diese Schritte nun an einem konkreten Beispiel genauer ansehen.

21.2 Topic Modeling mit `stm`

Für das Beispiel berechnen wir ein Structural Topic Model mit dem Package stm. Falls noch nicht geschehen, muss dieses wie gewohnt installiert werden:

install.packages("stm")

Neben diesem Package benötigen wir außerdem einige bereits bekannte Packages: das tidyverse zum allgemeinen Datenhandling und für Grafiken sowie tidytext und quanteda für die Arbeit mit Textdaten:

library(tidyverse)
library(tidytext)
library(quanteda)
library(stm)

Im Folgenden replizieren wir Teile der Analyse des Papers Whose ideas are worth spreading? The representation of women and ethnic groups in TED talks von Carsten Schwemmer und Sebastian Jungkunz, in dem Zusammenhänge von Ethnie und Geschlecht der Sprecher*innen aller TED Talks zwischen 2006 und 2017 mit den Themen der Talks untersucht werden. Der Datensatz für die Analyse wurde dankenswerterweise im Harvard Dataverse öffentlich zugänglich gemacht – wir benötigen lediglich die Datei ted_main_dataset.tab, die die Transkripte aller Talks enthält.⁵⁴

21.2.1 Vorbereitung: Daten laden und Preprocessing

Die Dateiendung .tsv dürfte vielen noch unbekannt sein, es handelt sich jedoch um ein Dateiformat, das dem bereits bekannten CSV-Format sehr ähnlich ist – nur werden die Werte nicht durch Kommas, sondern durch Tabstopps voneinander getrennt. Auch für dieses Dateiformat gibt es eine passende read_-Funktion:

ted_talks <- read_tsv("data/ted_main_dataset.tsv")

Wir nehmen zudem einige kurze Modifikationen an dem Originaldatensatz vor:

Wir entfernen alle Talks, zu denen keine Speaker-Daten vorliegen, um dieselbe Datenbasis wie das Paper zu haben.
Wir erzeugen eine numerische id für jeden Talk.
Wir wandeln die Variable date von einem Character- zu einem Datumsobjekt um. Hierzu nutzen wir die Funktion ymd() aus dem lubridate-Package; da im Originaldatensatz lediglich Jahr und Monat, nicht aber Tag, des jeweiligen Talks festgehalten ist (z. B. 2006-06), geben wir mit dem Argument truncated = 1 an, dass auf ein Datumsbestandteil (hier also der Tag) verzichtet werden kann. Das Datum wird dann automatisch auf den Monatsersten gesetzt.
Schließlich entfernen wir der Übersicht halber alle Variablen außer dem Datum des Talks (date), dem title des Talks und dem Transkript des Talks text.

ted_talks <- ted_talks %>% 
  filter(!is.na(speaker_image_nr_faces)) %>% 
  mutate(id = 1:n(),
         date = lubridate::ymd(date, truncated = 1)) %>% 
  select(id, date, title, text)

ted_talks

## # A tibble: 2,333 x 4
##       id date       title                              text                                                                                                     
##    <int> <date>     <chr>                              <chr>                                                                                                    
##  1     1 2006-06-01 Do schools kill creativity?        Good morning. How are you? It's been great, hasn't it? I've been blown away by the whole thing. In fact,~
##  2     2 2006-06-01 Averting the climate crisis        Thank you so much, Chris. And it's truly a great honor to have the opportunity to come to this stage twi~
##  3     3 2006-06-01 The best stats you've ever seen    About 10 years ago, I took on the task to teach global development to Swedish undergraduate students. Th~
##  4     4 2006-06-01 Why we do what we do               Thank you. I have to tell you I'm both challenged and excited. My excitement is: I get a chance to give ~
##  5     5 2006-06-01 Simplicity sells                   Hello voice mail, my old friend. I've called for tech support again. I ignored my boss's warning. I call~
##  6     6 2006-06-01 Greening the ghetto                If you're here today — and I'm very happy that you are — you've all heard about how sustainable developm~
##  7     7 2006-07-01 My wish: A global day of film      I can't help but this wish: to think about when you're a little kid, and all your friends ask you, If a ~
##  8     8 2006-07-01 Behind the design of Seattle's li~ I'm going to present three projects in rapid fire. I don't have much time to do it. And I want to reinfo~
##  9     9 2006-07-01 My wish: Help me stop pandemics    I'm the luckiest guy in the world. I got to see the last case of killer smallpox in the world. I was in ~
## 10    10 2006-07-01 Let's teach religion — all religi~ It's wonderful to be back. I love this wonderful gathering. And you must be wondering, What on earth? Ha~
## # ... with 2,323 more rows

Insgesamt haben wir also 2333 Talks vorliegen. Als nächstes folgen die schon bekannten Schritte zur Textvorbereitung. Zunächst überführen wir unseren Datensatz in ein Quanteda-Corpus-Objekt:

ted_corpus <- corpus(ted_talks, text_field = "text")

Als nächstes erzeugen wir eine Document-Feature-Matrix und führen dabei auch einige Preprocessing-Schritte wie Konvertierung in Kleinschreibung, das Entfernen von Stopwords, Ziffern, Satzzeichen, Symbolen und URLs sowie Stemming durch – das Argument verbose = TRUE sorgt dafür, dass wir etwas zusätzlichen Output für die einzelnen Preprocessing-Schritte erhalten:

ted_dfm <- dfm(ted_corpus,
               stem = TRUE,
               tolower = TRUE,
               remove_punct = TRUE,
               remove_url = FALSE,
               remove_numbers = TRUE,
               remove_symbols = TRUE,
               remove = stopwords('english'),
               verbose = TRUE)

## Creating a dfm from a corpus input...

##  ...lowercasing

##  ...found 2,333 documents, 68,271 features

##  ...removed 175 features
##  ...stemming types (English)
##  ...complete, elapsed time: 5.72 seconds.
## Finished constructing a 2,333 x 44,692 sparse dfm.

Das Ergebnis ist eine sehr große DFM mit über Einhundertmillionen Zellen (2333 Dokumente mal 44692 Features). Da Topic Modeling an sich schon sehr rechenaufwändig ist, kann eine solche DFM so manchen Heimrechner in die Knie zwingen. Um die Berechnung zu vereinfachen und zu beschleunigen, lohnt es sich daher die DFM zu reduzieren. Hierzu können wir die Funktion dfm_trim() verwenden, mit der wir Features ausschließen können, die besonders häufig oder selten vorkommen und somit entweder zu generisch oder zu spezifisch für eine sinnvolle Interpretation sein könnten.

Zu beachten ist, dass diese Reduktion der DFM einen großen Einfluss auf das Ergebnis des Topic Modelings haben kann. Die verwendeten Werte sollten also wohlüberlegt sein und im Idealfall mit einigen alternative Berechnungen mit anderen Werten verglichen werden. Für unser Beispiel folgen wir der Analyse aus dem Paper und schließen alle Wörter bzw. Features aus, die in mehr als der Hälfte oder in weniger als einem Prozent aller Talks vorkommen:

ted_dfm <- dfm_trim(ted_dfm, 
                    max_docfreq = 0.50,
                    min_docfreq = 0.01,
                    docfreq_type = 'prop')

ted_dfm

## Document-feature matrix of: 2,333 documents, 4,803 features (93.4% sparse) and 3 docvars.
##        features
## docs    morn blown away whole leav theme run confer relev extraordinari
##   text1    1     1    2     7    2     1   4      2     1             4
##   text2    0     1    1     0    0     0   2      1     0             0
##   text3    0     0    2     1    0     0   1      0     1             0
##   text4    0     0    0     1    2     0   1      0     0             0
##   text5    1     0    1     2    2     0   1      0     0             0
##   text6    1     0    0     0    1     0   1      1     0             0
## [ reached max_ndoc ... 2,327 more documents, reached max_nfeat ... 4,793 more features ]

Die resultierende DFM umfasst “nur” noch rund 11 Millionen Zellen, da wir die Feature-Zahl auf rund 4800 reduziert haben. Zu sehen ist außerdem, dass das Stemming erfolgreich war.

Das stm-Package arbeitet mit einem etwas anderen Dateiformat als Quanteda. Praktischerweise gibt es aber in Quanteda die Funktion convert, mit der Quanteda-Objekte für andere gängige Textanalyse-Packages umgewandelt werden können:

stm_dfm <- convert(ted_dfm, to = "stm")

str(stm_dfm, max.level = 1)

## List of 3
##  $ documents:List of 2333
##  $ vocab    : chr [1:4803] "10th" "15-year-old" "15th" "17th" ...
##  $ meta     :'data.frame':   2333 obs. of  3 variables:

21.2.2 Ein erstes Topic Model

Wir können nun unser erstes Modell berechnen. Der zentrale Input-Parameter ist wie oben beschrieben \(K\), die Anzahl der Themen. Zu Demonstrationszwecken wählen wir – vollkommen willkürlich – 20, möchten also 20 Themen berechnen lassen; wir setzen uns gleich damit auseinander, wie man \(K\) sinnvoller bestimmt, aber dafür lohnt es sich, schon etwas Erfahrung mit der Modellierung und Modell-Kennwerten zu haben.

Die Modellierung erfolgt über die Funktion stm(). Zentrale Input-Paramter sind documents und vocab, die jeweils unter diesem Namen in unserem neu erzeugten stm_dfm-Objekt enhalten sind, sowie K, mit der wir die Anzahl der Themen bestimmen. Mit verbose = FALSE lasse ich für die Darstellung im Kurs den Zusatzoutput während der Berechnung ausblenden. Lassen Sie sich diesen aber gerne anzeigen, wenn Sie das Modell an Ihrem eigenen Rechner berechnen (also verbose = TRUE, was auch die Default-Einstellung ist), um so die Berechnungsschritte verfolgen zu – nicht zuletzt, da die Berechnung durchaus ein paar Minuten dauern kann:⁵⁵

first_model <- stm(documents = stm_dfm$documents,
                   vocab = stm_dfm$vocab,
                   K = 20,
                   verbose = FALSE)

Das erzeugte Objekt enthält alle relevanten Modellparameter, die wir uns in Kürze noch genauer ansehen. Wir können uns Themenverteilung und wichtigste Begriffe direkt plotten lassen:

plot(first_model)

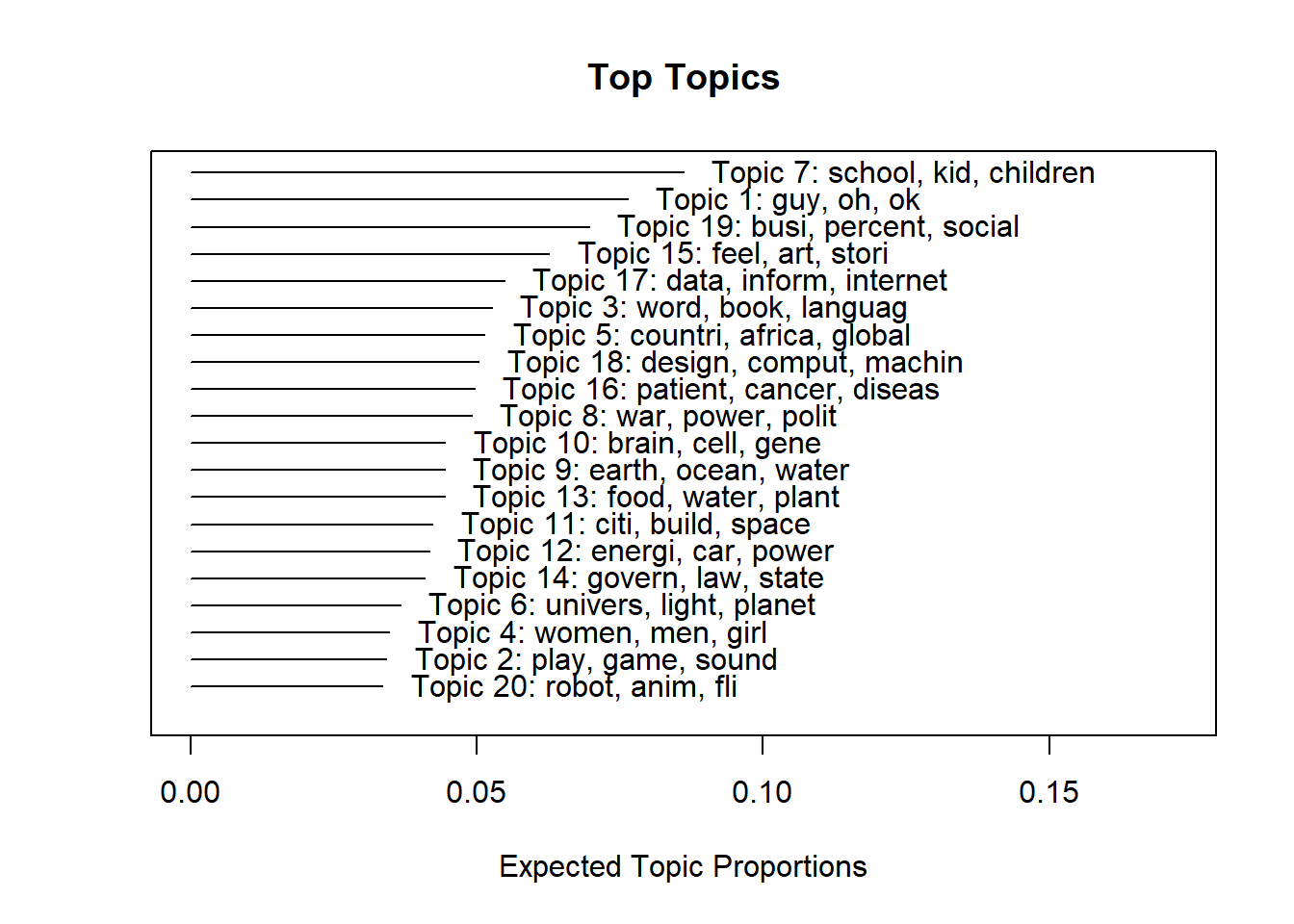
Auch verfügt das Objekt über eine eigene summary()-Funktion mit den wichtigsten Wörtern je Thema, die Sie gerne am eigenen Rechner ausprobieren können (summary(first_model)), deren umfassender Output hier aber das Format sprengen würde.

Stattdessen wenden wir uns zunächst der Frage zu, anhand welcher Metriken wir ein Topic Model beurteilen können. Eine der zentralen Metriken nennt sich hierbei Semantic Coherence, die, vereinfacht gesagt, angibt, wie häufig Wörter, die eine hohe Wahrscheinlichkeit für ein bestimmtes Thema aufweisen, auch gemeinsam in einem Dokument (Kookkurrenz, siehe Kapitel 18.4) auftreten – je höher der Wert, desto häufiger ist dies der Fall. Es hat sich gezeigt, dass es menschlichen Codierer*innen mit steigender Semantic Coherence einfacher fällt, die generierten Themen auch sinnvoll zu interpretieren. Mit der Funktion semanticCoherence() erhalten wir diesen Wert für jedes einzelne Thema:

semanticCoherence(first_model, stm_dfm$documents)

##  [1] -40.06270 -71.19646 -55.47152 -65.88169 -44.53030 -73.06287 -40.03670 -77.25560 -64.96361 -56.37941 -62.32368 -69.20786 -53.72040 -68.14111 -54.66015
## [16] -45.03171 -51.56690 -49.63193 -49.74282 -81.62830

Der absolute Wert lässt sich hierbei kaum interpretieren, stattdessen bietet sich der Vergleich zwischen unterschiedlichen Themen (und vor allem: unterschiedlichen Themenmodellen an). Wir würden hier also erwarten, dass sich z. B. Thema 7 (mit dem Maximalwert von -40.03670) leichter interpretieren lässt als Thema 20 (mit dem Minimalwert von -81.62830).

Zugleich ist es vergleichsweise simpel, die Semantic Coherence zu steigern, indem eine relativ geringe Themenanzahl spezifiziert wird. Daher ist es sinnvoll, Semantic Coherence gemeinsam mit einer zweiten Messgröße zu betrachten, der Exclusivity. Diese gibt an, wie exklusiv die Wörter, die eine hohe Wahrscheinlichkeit für ein bestimmtes Thema aufweisen, für dieses Thema sind, zugleich also bei allen anderen Themen eine möglichst geringe Wahrscheinlichkeit aufweisen. Diese können wir mit der Funktion exclusivity() anfordern, wobei es sinnvoll ist, Semantic Coherence und Exclusivity gegeneinander zu plotten, um einen schnellen Vergleich zu ermöglichen:

tibble(
  topic = 1:20,
  exclusivity = exclusivity(first_model),
  semantic_coherence = semanticCoherence(first_model, stm_dfm$documents)
  ) %>% 
  ggplot(aes(semantic_coherence, exclusivity, label = topic)) +
  geom_point() +
  geom_text(nudge_y = .01) +
  theme_bw()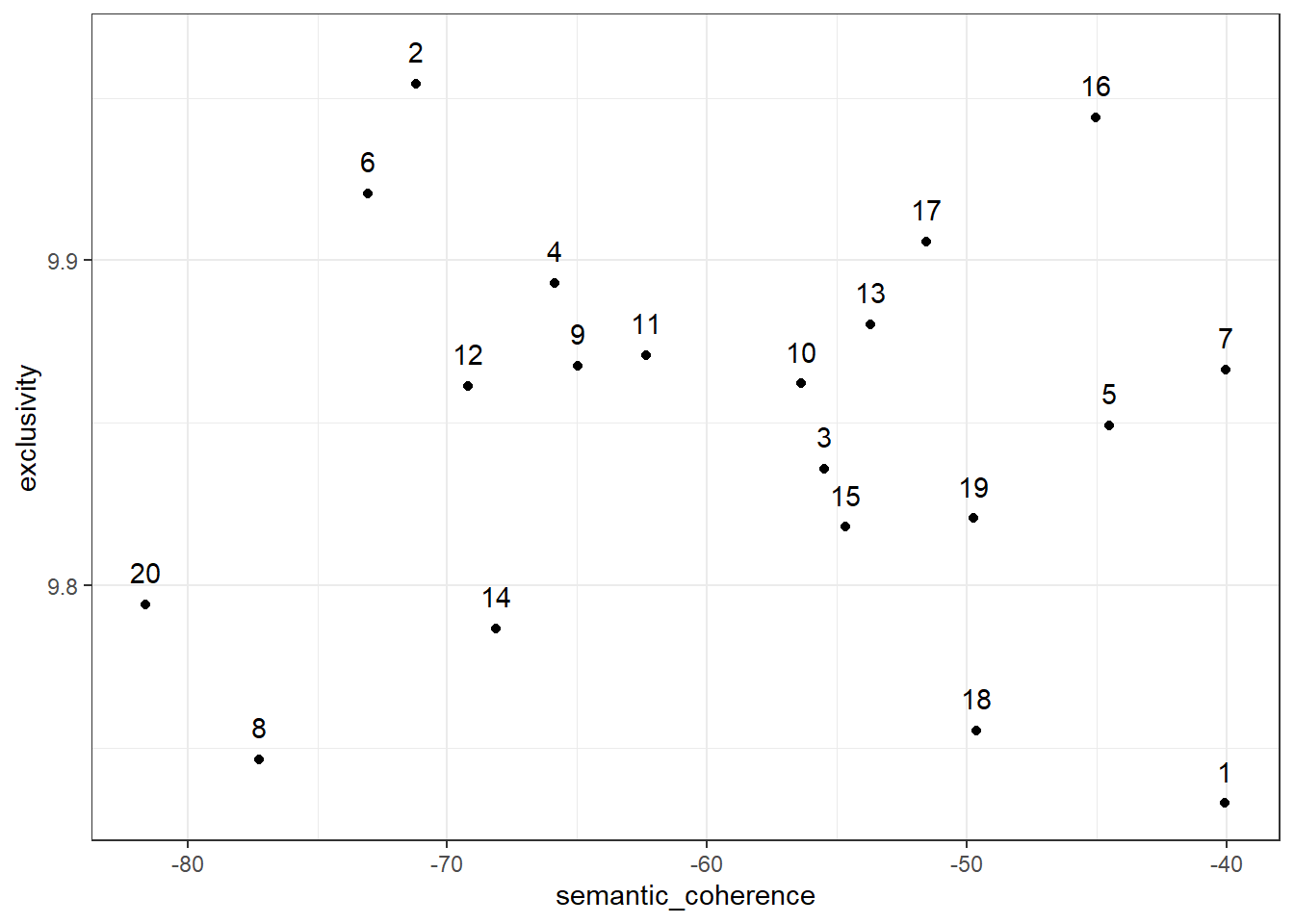

“Gute” Themen finden wir rechts oben in der Grafik (z. B. Thema 16), diese weisen - im Vergleich zu den anderen Themen - sowohl eine hohe Semantic Coherence als auch eine hohe Exklusivität auf. Thema 1 weist zwar eine hohe Semantic Coherence auf (Wörter, die eine hohe Wahrscheinlichkeit für das Thema aufweisen, treten also auch vergleichsweise häufig gemeinsam in einem Dokument auf), hat aber zugleich eine geringe Exclusivity (Wörter, die eine hohe Wahrscheinlichkeit für das Thema aufweisen, weisen tendeziell also auch bei anderen Themen eine hohe Wahrscheinlichkeit auf). Problematisch zu interpretieren könnten entsprechend vor allem die Themen 8, 14 und 20 werden.

21.2.3 Modellvergleiche und Bestimmung von \(K\)

Nachdem wir nun einige Metriken zur Modellbeurteilung kennengelernt haben, wenden wir uns der vielleicht gewichtigsten Entscheidung bei der Berechnung von Topic Models zu: der Bestimmung einer geeigneten Themenanzahl \(K\). Anstatt wie oben eine willkürliche Themenanzahl zu verwenden, ist es sinnvoll, bereits für das erste berechnete Modell eine begründete Wahl zu treffen:

Ist der Untersuchungsgegenstand bzw. der Textkorpus schon bekannt (wurde z. B. an einem Teilkorpus bereits eine manuelle Inhaltsanalyse durchgeführt), kann man sich daran orientieren. Auch vergleichbare Studien bieten Anhaltspunkte – untersucht man z. B. die Berichterstattung zu einer bestimmten Wahl, hat vielleicht schon einmal jemand eine Inhaltsanalyse zu einer der vorherigen Wahlen durchgeführt und dort ebenfalls Themen ausgewertet.
Ss existieren einige Faustregeln, die aber allenfalls grobe Anhaltspunkte darstellen. So empfehlen beispielsweise die Package-Autoren von stm 3-10 Themen für kleine Korpora mit sehr spezifischen Untersuchungsgegenständen (z. B. offene Antworten in einer Befragung von wenigen Hundert Personen), 5-50 Themen für Korpora mit einigen Hundert bis einigen Tausend Dokumenten, und 60-100 Themen für Korpora mit einigen Zehn- bis Hundertausend Dokumenten sowie 100 Themen für noch größere Korpora.
Ist man völlig blank, kann man die stm() mit dem Argument K = 0 ausführen; es wird dann ein Algorithmus genutzt, der eine “geeignete” Themenzahl bestimmt. Diese ist aber keinesfalls mit der “wahren” oder “besten” Themenanzahl gleichzusetzen, sondern versucht lediglich, einige Modellanpassungswerte zu maximieren.

In jedem Fall muss das Themenmodell auch manuell interpretiert werden und auf seine Sinnhaftigkeit geprüft werden. Ist eine genaue Themenanzahl vorab nicht festgelegt – was in den allermeisten Anwendungsfällen zutreffen dürfte –, sollten mehrere Modelle mit unterschiedlicher Themenanzahl gerechnet und verglichen werden (sowohl auf Basis von Kennwerten als auch manuell über die Intepretation von Themen).

R macht es uns zum Glück einfach, mehrere Modelle auf einen Schlag zu berechnen. Hierzu nutzen wir Funktionen zur Iteration und die Fähigkeit von Tibbles, so gut wie jedes Objekt – also auch Topic-Modelle – in Listen verpackt als Werte speichern zu können. Das mag auf den ersten Blick nun etwas unüblich wirken, aber erklärt sich schnell:

Wir erzeugen zunächst ein Tibble, das in einer Variablen K alle unterschiedlichen Werte von \(K\) enthält, die wir nutzen möchten. In unserem Fall berechen wir insgesamt vier Modelle mit 20, 30, 40 und 50 Themen.
Nun erzeugen wir mittels mutate() eine neue Variable model, in der die zugehörigen Modelle berechnet und gespeichert werden sollen. Hierzu nutzen wir die Funktion map() (siehe Kapitel 13), mit der wir über einen Vektor iterieren und die einzelnen Vektorwerte als Argument in einer Funktion verwenden können. Wir iterieren also über K und setzen den jeweiligen Wert von K an der entsprechend Stelle der stm()-Funktion, symbolisiert durch den ., ein.

Das Resultat ist ein Tibble, das all unsere Modelle enthält. Achtung: die folgende Berechnung kann, je nach vorhandener Hardware, eine ganze Zeit dauern⁵⁶ – machen Sie also ruhig einen Spaziergang o.ä., während der Rechner arbeitet.⁵⁷

many_models <- tibble(K = c(20, 30, 40, 50)) %>% 
  mutate(model = map(K, ~ stm(stm_dfm$documents, 
                              stm_dfm$vocab, 
                              K = .,
                              verbose = FALSE)))

many_models

## # A tibble: 4 x 2
##       K model 
##   <dbl> <list>
## 1    20 <STM> 
## 2    30 <STM> 
## 3    40 <STM> 
## 4    50 <STM>

Das praktische ist nun, dass wir ähnlich auch über die Modelle iterieren können, um beispielsweise schnell für alle Modelle Semantic Coherence und Exclusivity zu berechnen:

model_scores <- many_models %>% 
  mutate(exclusivity = map(model, exclusivity),
         semantic_coherence = map(model, semanticCoherence, stm_dfm$documents)) %>% 
  select(K, exclusivity, semantic_coherence)

model_scores

## # A tibble: 4 x 3
##       K exclusivity semantic_coherence
##   <dbl> <list>      <list>            
## 1    20 <dbl [20]>  <dbl [20]>        
## 2    30 <dbl [30]>  <dbl [30]>        
## 3    40 <dbl [40]>  <dbl [40]>        
## 4    50 <dbl [50]>  <dbl [50]>

Die jeweiligen Modell-Kennwerte stehen nun jeweils als Listen verpackt in den Zellen - für das Modell mit K = 20 entsprechend 20 Werte für Semantic Coherence und Exclusivity, für das Modell mit K = 30 30 Werte etc.

Zum Modellvergleich müssen wir diese Werte nun mit der Funktion unnest() aus den Listen “entpacken” und können diese anschließend plotten:

model_scores %>% 
  unnest(c(exclusivity, semantic_coherence)) %>% 
  ggplot(aes(x = semantic_coherence, y = exclusivity, color = as.factor(K))) +
  geom_point() +
  theme_bw()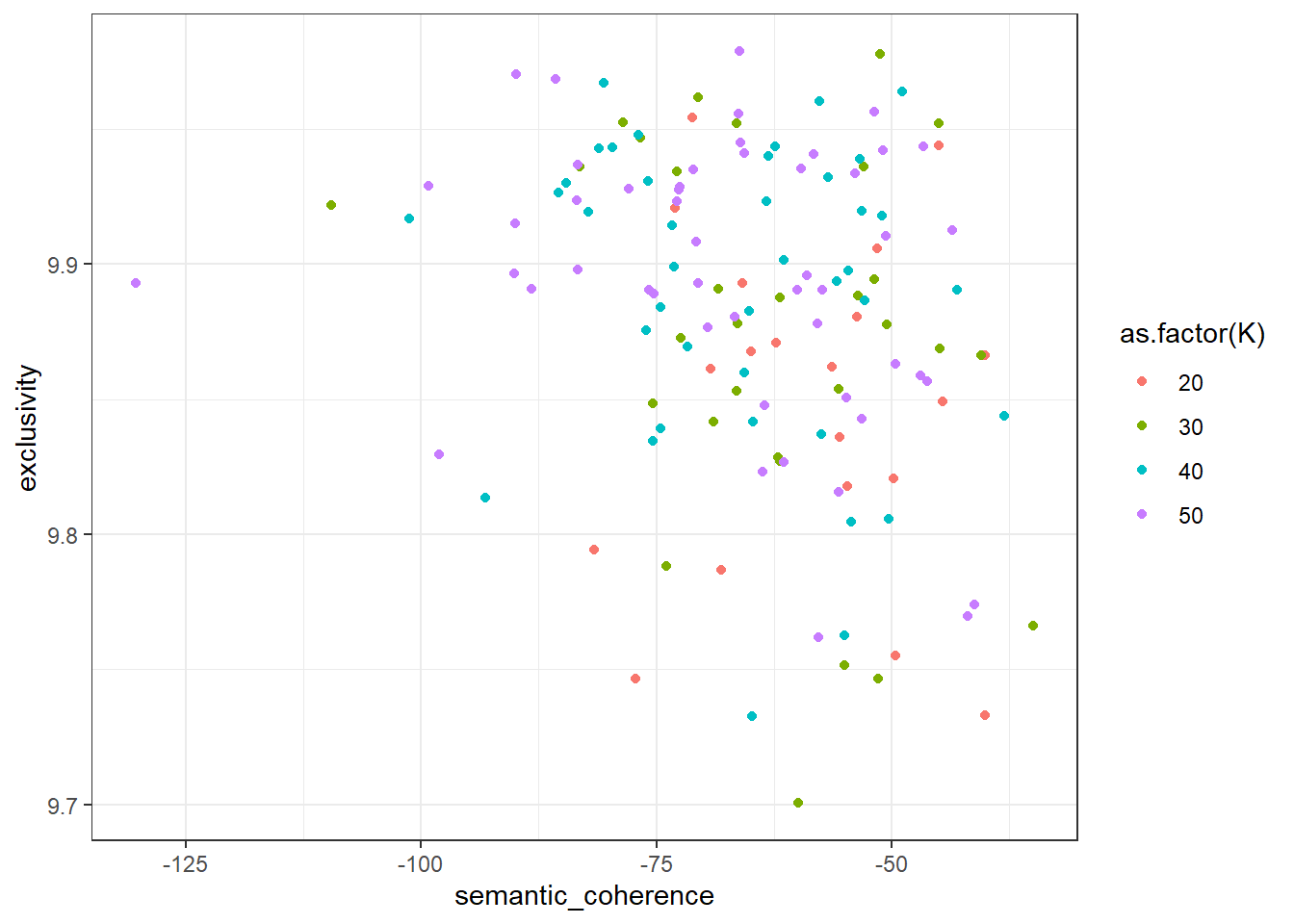

Auf den ersten Blick unterscheiden sich die Modelle nicht sonderlich – lediglich für das Modell mit K = 50 können wir ein klares Ausreißer-Thema mit deutlich geringerer Semantic Coherence erkennen; auch scheint es bei allen Modellen einige Themen mit verhältnismäßig geringerer Exclusivity zu geben.

Um die Modelle schneller miteinander vergleichen zu können, berechnen wir den Mittelwert der jeweiligen Kennwerte:

model_scores %>% 
  unnest(c(exclusivity, semantic_coherence)) %>% 
  group_by(K) %>% 
  summarize(exclusivity = mean(exclusivity),
            semantic_coherence = mean(semantic_coherence)) %>% 
  ggplot(aes(x = semantic_coherence, y = exclusivity, color = as.factor(K))) +
  geom_point() +
  theme_bw()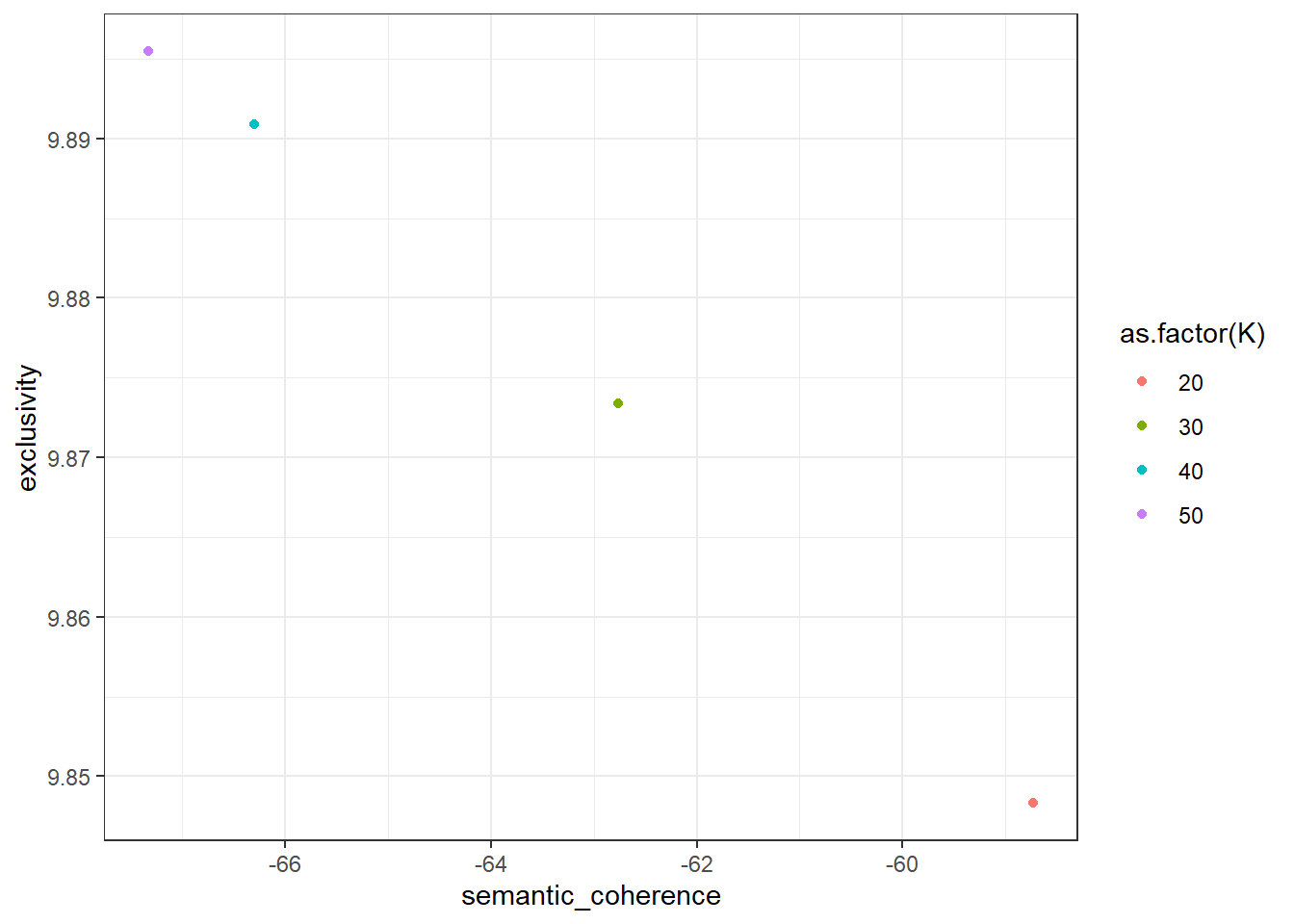

Hier zeigt sich nun recht deutlich der typische Tradeoff von Semantic Coherence und Exclusivity – das Modell mit der höchsten Semantic Coherence hat die geringste Exclusivity (K = 20), umgekehrt weisen sowohl K = 40 und K = 50 die höchste Exclusivity und geringste Semantic Coherence auf, unterscheiden sich von einander aber kaum auf den beiden Dimensionen. Als Mittelweg empfiehlt sich das Modell mit K = 30, das wir nun – ebenso wie die Autoren der Originalstudie – auswählen werden.

Hierzu “ziehen” wir das Modell aus dem Tibble heraus – wir filtern zunächst die entsprechende Zeile an und extrahieren den Zelleninhalt der Spalte model dann mittels pull(). Da das Modell noch in einer Liste verpackt ist, extrahieren wir danach noch das (erste und einzige) Listenelement mit [[1]] (der vorangestellte Punkt . bedeutet in etwa so viel wie “setze hier das aktuelle Objekt in der Pipe ein” – das wirkt zunächst auch etwas unüblich, ist aber die einzige Möglichkeit, Listenelemente direkt in Pipes zu anzusteuern).

final_model <- many_models %>% 
  filter(K == 30) %>% 
  pull(model) %>% 
  .[[1]]

final_model

## A topic model with 30 topics, 2333 documents and a 4803 word dictionary.

21.2.4 Modellinterpretation

Wenden wir uns nun der Modellinterpretation zu. Wie bereits oben geschildert, sind zur Beschreibung und Interpretation eines Topic Models die Wortwahrscheinlichkeiten je Thema und die Themenwahrscheinlichkeiten je Dokument zentral. Aus ersteren können wir die gefundenen Themen inhaltlich interpretieren, zweitere geben uns Auskunft über die Prävalenz von Themen.

Einen ersten Überblick gibt uns die Funktion labelTopics() aus dem stm-Package, das uns die wichtigsten Wörter je Thema (Default-Wert: 7) anhand von vier Metriken angibt. Um die Übersichtlichkeit zu wahren, werden in der Kursansicht nur die ersten fünf Themen angezeigt; führen Sie den Code zu Hause aus, sollten Sie eine lange Ausgabe mit allen 30 Themen erhalten:

terms <- labelTopics(final_model)
terms

## Topic 1 Top Words:
##       Highest Prob: guy, stuff, oh, ok, sort, yeah, mayb 
##       FREX: guy, oh, ok, stuff, hey, card, everybodi 
##       Lift: da, dude, gotta, comedi, ass, fuck, hey 
##       Score: da, guy, ok, stuff, oh, card, yeah 
## Topic 2 Top Words:
##       Highest Prob: play, game, music, sound, hear, video, listen 
##       FREX: music, game, song, play, musician, player, sound 
##       Lift: jersey, orchestra, music, musician, piano, violin, vocal 
##       Score: music, jersey, game, song, play, player, piano 
## Topic 3 Top Words:
##       Highest Prob: ca, ted, yeah, chris, poem, la, mr 
##       FREX: ca, la, poem, chris, ted, anderson, mr 
##       Lift: ca, la, anderson, poem, chris, poetri, mr 
##       Score: la, ca, poem, poetri, anderson, chris, ted 
## Topic 4 Top Words:
##       Highest Prob: women, men, girl, woman, black, sex, boy 
##       FREX: women, men, sexual, gender, gay, sex, girl 
##       Lift: ski, gay, women, lesbian, feminist, gender, men 
##       Score: women, ski, men, girl, gay, gender, sex 
## Topic 5 Top Words:
##       Highest Prob: countri, africa, global, china, india, develop, percent 
##       FREX: china, africa, india, aid, african, countri, incom 
##       Lift: curtain, ghana, sub-saharan, china, capita, gdp, poorest 
##       Score: curtain, africa, countri, india, china, african, economi

Zunächst zu den Metriken: Highest Prob bezieht sich auf die oben angesprochene Wortwahrscheinlichkeit je Thema (bezeichnet als \(\beta\)), angegeben sind also die sieben Wörter, die das höchste \(\beta\) je Thema erhalten haben. Bei den anderen drei Metriken handelt es sich um alternative Berechnungen der bedeutsamsten Wörter je Thema; so ist FREX (für Frequency-Exclusivity) die Worthäufigkeit und -exklusivität ins Verhältnis, versucht also diejenigen Wörter zu identifzieren, die für ein bestimmtes Thema besonders distinkt sind, da sie sowohl häufig im betrachteten Thema als auch in anderen Themen selten vorkommen (ein Wort kann nämlich auch bei verschiedenen Themen ein hohes \(\beta\) aufweisen). Auch Score und Lift nehmen zusätzliche Gewichtungen vor. Im Idealfall stützt sich die Interpretation daher auf mehrere bzw. alle vier Metriken.

Inhaltlich sehen wir sowohl Themen, die sich relativ eindeutig einem thematischen Überbegriff zuordnen lassen – Talks, die Thema 2 enthalten, beschäftigen sich augenscheinlich mit Musik, bei Thema 4 mit Gender- und Sexualitätsfragen, bei Thema 5 mit Armut, vorrangig in Entwicklungsländern im globalen Süden – wie auch Themen, die offenbar gängige Sprachmuster aufgreifen (Thema 1 und 3, die in der Originalpublikation als “Miscellaneous” und “Stopwords” bezeichnet werden). Zu beachten ist außerdem, dass wir die gestemmten Wörter sehen – das erschwert die Interpretation bei bestimmten Wörtern wie "ca" und "la" etwas, sodass wir hier in den ungestemmten Originaldaten nachsehen könnten, auf was sich diese Wortfragmente beziehen.

Zwar können wir die gesamten Wahrscheinlichkeitsmatrizen auch direkt aus dem Modellobjekt erhalten, der Output wird jedoch besser weiterverarbeitbar, wenn wir wieder die bereits bekannte tidy()-Funktion aus dem tidytext-Package nutzen. Standardmäßig gibt uns diese die Wortwahrscheinlichkeiten je Thema \(\beta\) aus:

terms_probs <- tidy(final_model)
terms_probs

## # A tibble: 144,090 x 3
##    topic term      beta
##    <int> <chr>    <dbl>
##  1     1 10th  7.67e-15
##  2     2 10th  3.81e- 5
##  3     3 10th  4.56e-58
##  4     4 10th  2.45e-47
##  5     5 10th  4.70e-43
##  6     6 10th  1.53e- 7
##  7     7 10th  1.75e- 4
##  8     8 10th  5.03e-42
##  9     9 10th  6.31e- 5
## 10    10 10th  3.38e-25
## # ... with 144,080 more rows

Das Resultat ist eine lange Tabelle, in der für jedes der 4803 Wörter in unserer DFM und jedes Thema ein Wahrscheinlichkeitswert zwischen 0 und 1 angegeben wird. Alle \(\beta\)-Werte je Thema summieren sich zu 1 auf:

terms_probs %>% 
  group_by(topic) %>% 
  summarise(sum_beta = sum(beta))

## # A tibble: 30 x 2
##    topic sum_beta
##    <int>    <dbl>
##  1     1     1   
##  2     2     1.00
##  3     3     1   
##  4     4     1.00
##  5     5     1   
##  6     6     1   
##  7     7     1   
##  8     8     1   
##  9     9     1.00
## 10    10     1   
## # ... with 20 more rows

Ebenfalls mit der tidy()-Funktion können wir die Themenwahrscheinlichkeiten je Dokument (bezeichnet als \(\gamma\)) abrufen. Hierfür müssen wir lediglich mit dem Argument matrix = "gamma" angeben, dass wir nun eben die \(\gamma\)-Werte abrufen möchten. Mit dem Argument document_names können wir zudem einen Vektor angeben, der die Namen der Dokumente enthält – hier bietet sich beispielsweise der Titel der Vorträge an.

doc_probs <- tidy(final_model, matrix = "gamma", document_names = stm_dfm$meta$title)
doc_probs

## # A tibble: 69,990 x 3
##    document                                         topic   gamma
##    <chr>                                            <int>   <dbl>
##  1 Do schools kill creativity?                          1 0.0810 
##  2 Averting the climate crisis                          1 0.0964 
##  3 The best stats you've ever seen                      1 0.00131
##  4 Why we do what we do                                 1 0.167  
##  5 Simplicity sells                                     1 0.237  
##  6 Greening the ghetto                                  1 0.0196 
##  7 My wish: A global day of film                        1 0.0558 
##  8 Behind the design of Seattle's library               1 0.0287 
##  9 My wish: Help me stop pandemics                      1 0.0433 
## 10 Let's teach religion — all religion — in schools     1 0.0112 
## # ... with 69,980 more rows

Auch hier erhalten wir nun eine lange Tabelle, in der für jedes Dokument (in unserem Fall für jeden Vortrag) für alle identifizierten Themen eine Themenwahrscheinlichkeit angegeben ist. Auch die \(\gamma\)-Werte summieren sich je Dokument zu 1:

doc_probs %>% 
  group_by(document) %>% 
  summarise(sum_gamma = sum(gamma))

## # A tibble: 2,333 x 2
##    document                                        sum_gamma
##    <chr>                                               <dbl>
##  1 "\"(Nothing But) Flowers\" with string quartet"      1.00
##  2 "\"Black Men Ski\""                                  1   
##  3 "\"Clonie\""                                         1   
##  4 "\"High School Training Ground\""                    1.00
##  5 "\"Kiteflyer's Hill\""                               1.00
##  6 "\"La Vie en Rose\""                                 1   
##  7 "\"Love Is a Loaded Pistol\""                        1.  
##  8 "\"Mother of Pearl,\" \"If I Had You\""              1.00
##  9 "\"Peace on Earth\""                                 1.  
## 10 "\"Redemption Song\""                                1.  
## # ... with 2,323 more rows

Natürlich können wir die Daten nun auch miteinander verbinden und beispielsweise Topic-Prävalenz und bedeutsamste Wörter gemeinsam plotten:

top_terms <- tibble(topic = terms$topicnums,
                    prob = apply(terms$prob, 1, paste, collapse = ", "),
                    frex = apply(terms$frex, 1, paste, collapse = ", "))

gamma_by_topic <- doc_probs %>% 
  group_by(topic) %>%
  summarise(gamma = mean(gamma)) %>%
  arrange(desc(gamma)) %>%
  left_join(top_terms, by = "topic") %>%
  mutate(topic = paste0("Topic ", topic),
         topic = reorder(topic, gamma))

gamma_by_topic %>% 
  ggplot(aes(topic, gamma, label = frex, fill = topic)) +
  geom_col(show.legend = FALSE) +
  geom_text(hjust = 0, nudge_y = 0.0005, size = 3) +
  coord_flip() +
  scale_y_continuous(expand = c(0, 0), limits = c(0, 0.11), labels = scales::percent) +
  theme_bw() +
  theme(panel.grid.minor = element_blank(),
        panel.grid.major = element_blank()) +
  labs(x = NULL, y = expression(gamma))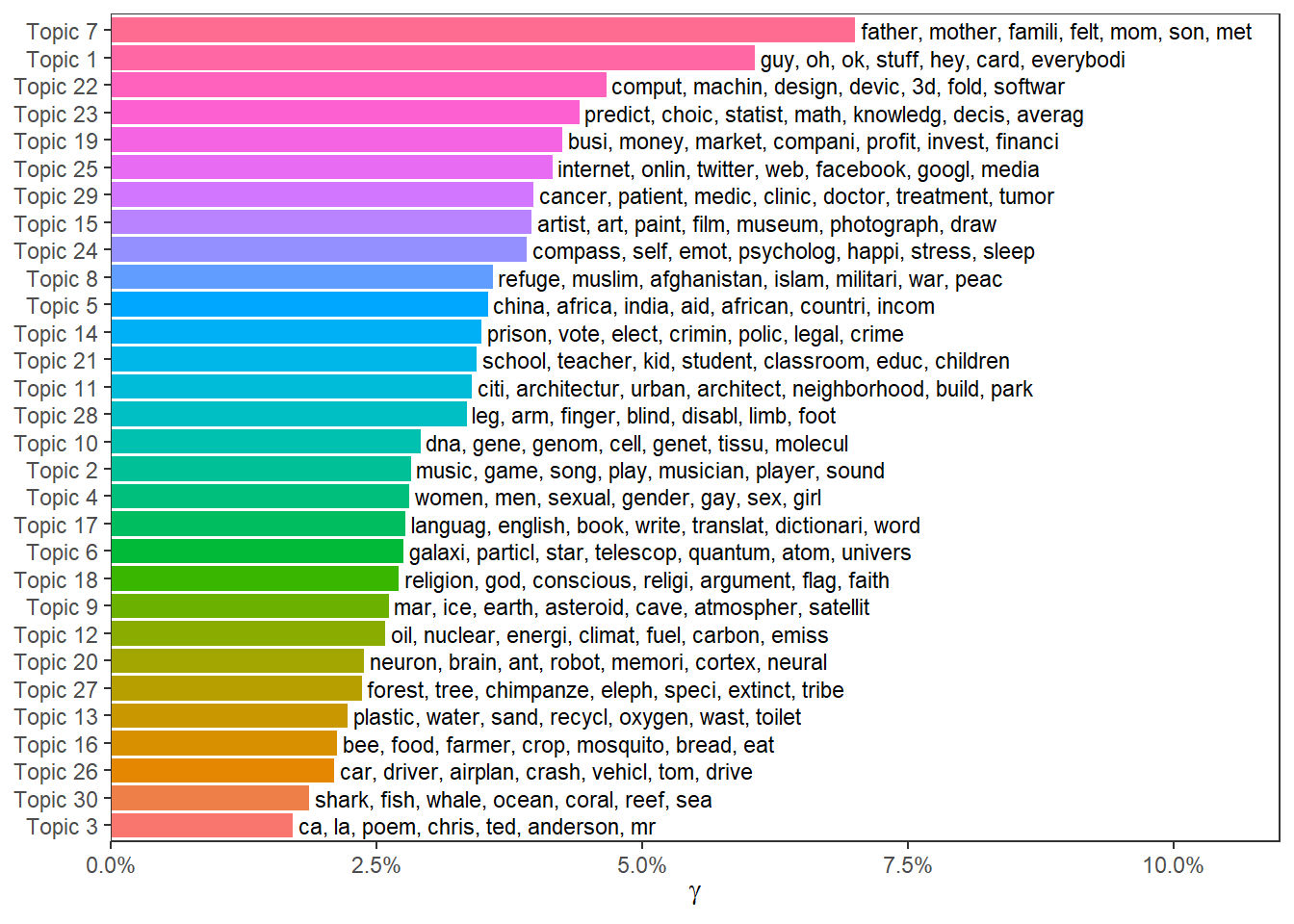

Auch können wir andere Informationen, die wie über unsere Dokumente haben, nun hinzuziehen und beispielsweise uns die Prävalenz einzelner Topics im Zeitverlauf ansehen:

doc_probs %>% 
  left_join(ted_talks, by = c("document" = "title")) %>% 
  group_by(topic, date) %>% 
  summarise(n = n(),
            gamma = mean(gamma), 
            .groups = "drop") %>% 
  mutate(ci_ll = gamma - qnorm(0.975) * gamma/sqrt(n),
         ci_ul = gamma + qnorm(0.975) * gamma/sqrt(n),
         ci_ll = if_else(ci_ll < 0, 0, ci_ll),
         topic = as_factor(topic)) %>% 
  filter(topic %in% c(7, 4)) %>% 
  ggplot(aes(x = date, y = gamma, ymin = ci_ll, ymax = ci_ul, color = topic, fill = topic)) +
  geom_line(size = 1) +
  geom_ribbon(alpha = .2, linetype = 0) +
  theme_bw() +
  theme(panel.grid.minor = element_blank(),
        panel.grid.major.x = element_blank(),
        legend.position = "bottom") +
  scale_y_continuous(expand = c(0, 0), limits = c(0, 0.35), labels = scales::percent) +
  labs(x = "Date", y = expression(gamma), color = "Topic", fill = "Topic")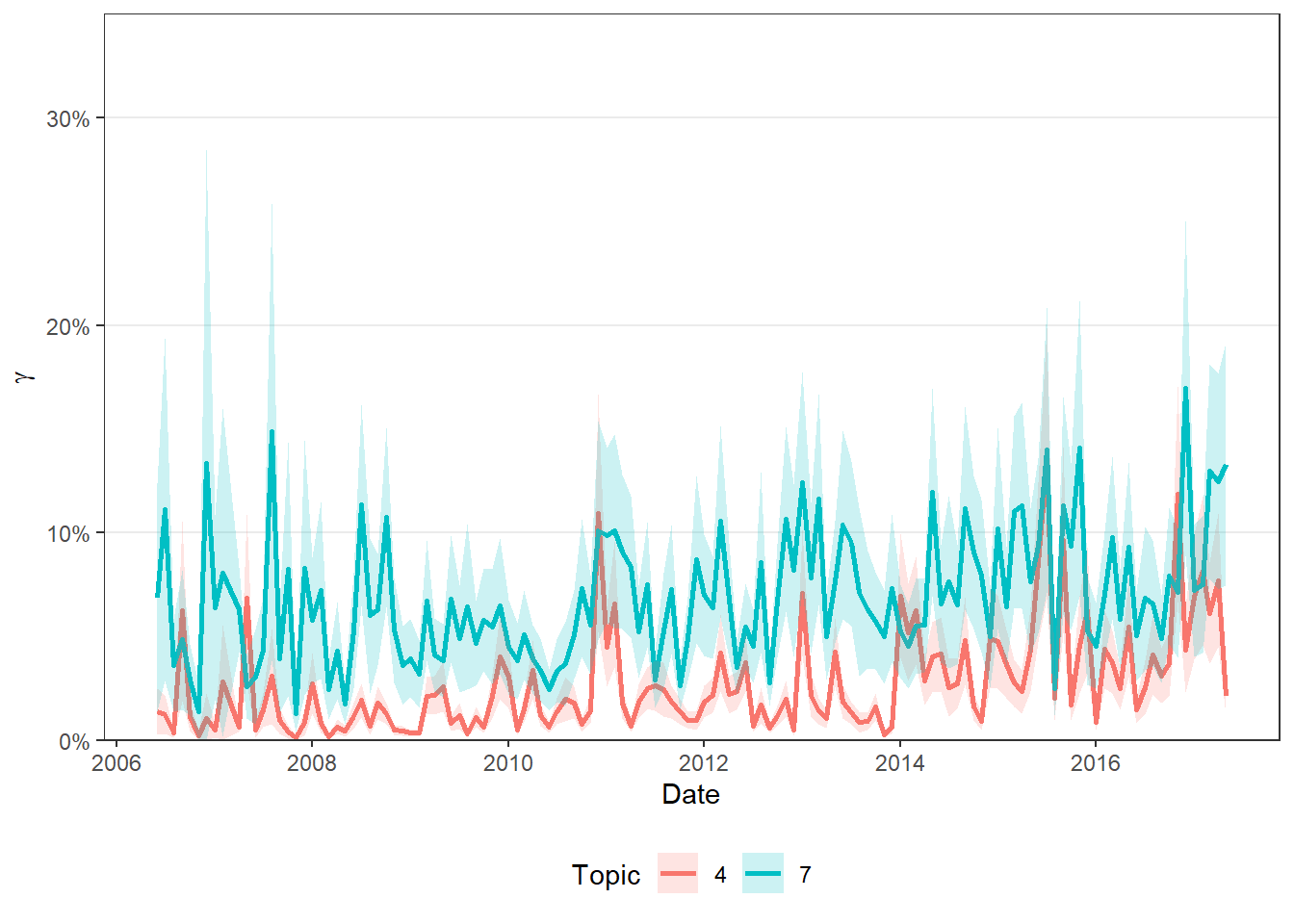

21.3 Übungsaufgaben

Erstellen Sie für die folgende Übungsaufgabe eine eigene Skriptdatei oder eine R-Markdown-Datei und speichern diese als ue21_nachname.R bzw. ue21_nachname.Rmd ab.

Für die Übungsaufgabe verwenden wir einen Korpus aus Artikeln des Guardian. Dieser ist in einem Zusatzpaket zu Quanteda enthalten, das einige Beispielkorpora enthält: quanteda.corpora. Wir können dieses Package mit folgendem Befehl installieren:

remotes::install_github("quanteda/quanteda.corpora")

Anschließend lässt sich der gewünschte Korpus über den download()-Befehl des Pakets herunterladen:

guardian_corpus <- quanteda.corpora::download("data_corpus_guardian")

guardian_corpus

## Corpus consisting of 6,000 documents and 9 docvars.
## text136751 :
## "London masterclass on climate change | Do you want to unders..."
## 
## text118588 :
## "As colourful fish were swimming past him off the Greek coast..."
## 
## text45146 :
## "FTSE 100 | -101.35 | 6708.35 | FTSE All Share | -58.11 | 360..."
## 
## text93623 :
## "Australia's education minister, Christopher Pyne, has vowed ..."
## 
## text136585 :
## "block-time published-time 3.05pm GMT | The former leader of ..."
## 
## text65682 :
## "Darren Wilson will be unable to return to work as a police o..."
## 
## [ reached max_ndoc ... 5,994 more documents ]

Wie wir sehen, handelt es sich bereits um ein Korpus-Objekt, dieser erste Konvertierungsschritt entfällt also. Enthalten sind 6,000 Artikel als Volltext.

Übungsaufgabe 21.1 Topic Modeling:

Rechnen Sie ein Topic Model mit 20 Themen. Führen Sie daher zunächst die notwendigen Preprocessing-Schritte durch.

Interpretieren Sie das vorgeschlagene Themenmodell anhand der Funktion labelTopics(). Können Sie die einzelnen Themen sinnvoll benennen? Gibt es Problemfälle?

Bonus: Wie verteilen sich die Themen über den Korpus? Besteht die Möglichkeit, sich die Themenprävalenz auch im Zeitverlauf anzusehen?

Die einzelnen Topic-Modeling-Verfahren unterscheiden sich u.a. in den verwendeten Wahrscheinlichkeitsverteilungen. So wird bei der LDA die namensgebende Dirichlet-Verteilung verwendet, die mit einer Unabhängigkeitsannahme einhergeht; entsprechend sind die Themen in der LDA unabhängig voneinander, die Wahrscheinlichkeit eines Themas beeinflusst also nicht die Wahrscheinlichkeit der anderen Themen. Beim CTM hingegen wird die Logit-Normalverteilung verwendet, die korrelierte Themenverteilungen erlaubt. Entsprechend können sich hier Themenwahrscheinlichkeiten gegenseitig beeinflussen, z. B. indem das Thema “Sport” mit einer höheren Wahrscheinlichkeit für das Thema “Gesundheit” einhergeht als das Thema “Außenhandel”.↩︎
Beim Download als “Original File Format” sollte die Datei mit der Endung .tsv heruntergeladen werden.↩︎
Die Modellspezifikation bietet noch deutlich mehr Einstellungsmöglichkeiten. Insbesondere lassen wir hier einen großen Vorteil von STMs gegenüber anderen Topic-Modeling-Verfahren außer Acht: wir könnten auch Kovariaten modellieren, um z. B. den Einfluss anderer Variablen im Datensatz – in der Originalstudie werden hier Ethnie und Geschlecht des Speakers sowie das Datum verwendet – auf die Prävalenz von einzelnen Themen zu untersuchen. Aus Gründen der Einfachkeit belassen wir es aber vorerst bei einem simplen Topic Model ohne Kovariaten.↩︎
auf meinem relativ modernen Heimrechner in etwa eine Viertelstunde.↩︎
Eine Möglichkeit, die Berechnungszeit zu verkürzen, ist – entsprechend leistungsfähige Hardware, d.h. vor allem schnelle Mehrkernprozessoren und viel Arbeitsspeicher, vorausgesetzt – die Modelle nicht nacheinander, sondern parallel über mehrere Prozessorkerne verteilt berechnen zu lassen. Das wird natürlich umso relevanter, je größer die Textkorpora werden und je mehr unterschiedliche Modelle berechnet werden sollen. Eine genaue Erklärung würde hier zu weit führen, aber wer mag, darf sich gerne mit dem Package furrr auseinandersetzen.↩︎