3 Funktionen
Wir haben bereits im vorherigen Kapitel einige Funktionen eingesetzt. Tatsächlich ist alles, was in R ausgeführt wird, eine Funktion. Zeit also, dass wir uns etwas detaillierter mit Funktionen auseinandersetzen.
3.1 Funktionen aufrufen
In den allermeisten Fällen rufen wir Funktionen nach dem folgenden Schema auf:
Der Funktionsname wird gefolgt von Klammern (), in die in aller Regel mindestens ein Argument übergeben wird.9 Die Funktion gibt daraufhin ein Resultat oder eine Fehlermeldung zurück, wobei das Resultat jede Datenstruktur in R annehmen kann – also sowohl einzelne Werte als auch komplexe Listen oder Dataframes.
Da Funktionen im Erfolgsfall immer exakt ein Resultat ausgeben, können wir dieses problemlos wiederum einem Objekt zuweisen und weiterverwenden:
3.1.1 Funktionsargumente
Funktionen benötigen mindestens ein Argument, oft auch mehrere Argumente, um korrekt ausgeführt zu werden. Oftmals umfassen Funktionsargumente zum einen (Daten-)Objekte, die von der Funktion verwendet werden sollen, zum anderen “Optionen”, die die Funktion berücksichtigen soll.
Die Funktion round(), die numerische Werte rundet, beispielsweise hat zwei Argumente:
x: ein numerischer Vektor, der gerundet werden soll.digits: ein Integer, der angibt, auf wie viele Dezimalstellen gerundet werden soll.
Der vollständige Funktionsaufruf läuft dementsprechend in der Form round(x, digits) ab:
## [1] 3.1
## [1] 3.1423.1.1.1 Funktionsargumente übergeben
Funktionsargumente können auf zwei Arten übergeben werden: zum einen implizit, wie im obigen Beispiel, durch die Reihenfolge der Funktionsargumente; zum anderen explizit über den Namen des Funktionsarguments in der Form argument = wert:
## [1] 3.14
## [1] 3.14In diesem Fall macht es keinen Unterschied, ob wir explizit digits = angeben oder nicht. In der Praxis ist es jedoch üblich, maximal die ersten ein oder zwei Funktionsargumente unbenannt zu übergeben, alle anderen Argumente jedoch benannt zu übergeben. Gerade bei Funktionen mit vielen Argumenten müssen Sie so zum einen nicht die exakte Reihenfolge der Argumente einhalten, zum anderen wird ihr Code auch für andere nachvollziehbarer und lesbarer.
Schauen wir uns hierzu als zweites Beispiel die schon bekannte mean()-Funktion an und nutzen sie mit einigen zusätzlichen, uns noch nicht bekannten Argumenten. Was passiert wohl hier?
## [1] 3.76Ohne Kenntnis der Funktionsargumente ist dieser Aufruf schwer nachzuvollziehen – wir berechnen wohl den Mittelwert der Variablen Petal.Length im Datensatz iris, aber was bedeutet der Rest? Durchschaubarer wird es, wenn wir die beiden hinteren Argumente mit ihrem Namen übergeben:
## [1] 3.76Hier können wir anhand der Argumentnamen Vermutungen anstellen, auch ohne die genaue Funktion zu kennen. trim wird wohl bedeuten, dass ein bestimmter Anteil der Werte getrimmt, also abgeschnitten wird. Tatsächlich gibt trim den Anteil der niedrigsten und höchsten Werte an, der nicht bei der Berechnung berücksichtigt wird – nützlich, um den Einfluss von Ausreißern auf den Mittelwert abzuschwächen. In unserem Fall, trim = 0.1, schließen wir also die untersten und obersten 10% der Werte aus. Mit na.rm = TRUE geben wir an, dass etwaige fehlende Werte NA vor der Berechnung aus dem Vektor entfernt werden sollen (rm steht hier also für “remove”).
Die Benennung erlaubt es uns nun auch, die Reihenfolge der Argumente im Funktionsaufruf zu tauschen:
## [1] 3.76Natürlich könnten wir auch das erste Argument benennen, aber das verspricht – auch ob des generischen Namens x – keinen zusätzlichen Erkenntnisgewinn und wäre wohl eher Overkill:
## [1] 3.76Die mittlere Variante – implizite Übergabe des ersten Funktionsarguments, explizite Nennung der weiteren Funktionsargumente – stellt also das gesunde Mittelmaß aus Kürze und Lesbarkeit dar.
3.1.1.2 Default-Werte von Argumenten
Wenn die mean()-Funktion drei Argumente besitzt, wie war es uns dann bisher möglich, sie mit nur einem Argument zu übergeben? Funktionsargumente, die eher Optionen als zwingende Voraussetzung für eine Funktion darstellen, haben in R oftmals Default-Werte – Standardwerte, auf die die Funktion zurückgreift, wenn diese nicht im Funktionsaufruf angegeben wurden. So ist es auch bei der mean()-Funktion, die wie folgt definiert ist: mean(x, trim = 0, na.rm = FALSE):
xhat keinen Default-Wert und muss daher zwingend angegeben werden. Ohne Angabe vonxwird eine Fehlermeldung zurückgegeben.trimhat einen Default-Wert von0, ohne Angabe vontrimwerden also keine Werte abgeschnitten.na.rmhat einen Default-Wert vonFALSE, standardmäßig werden fehlende Werte also nicht ausgeschlossen.
## Error in mean.default(): argument "x" is missing, with no default## [1] NA## [1] 2In der Regel haben insbesondere Argumente, die eher eine Option denn zwingende Voraussetzung für die Ausführung einer Funktion darstellen, Default-Werte, sodass diese bei der gebräuchlichsten Verwendung weggelassen werden können.
3.1.2 Hilfestellungen zu Funktionen
R und RStudio bieten verschiedene Möglichkeiten, Hilfestellungen zu Funktionen anzuzeigen – also z. B. zur Verwendung der Funktion, ihren Argumenten, den zugehörigen Default-Werten usw.
Tippen Sie einen Funktionsnamen ein, so macht Ihnen R Vorschläge, welche Funktion Sie meinen könnten. Daneben wird ein Tooltip angezeigt, der die Funktion beschreibt. Geben Sie beispielsweise die Buchstaben rou in ein R-Skript oder die Konsole ein, sollten Sie nach kurzer Zeit eine Auswahl von Funktionen sehen, die mit eben diesen Buchstaben beginnen, darunter an erster Stelle die round()-Funktion. Die anderen vorgeschlagenen Funktionen können Sie mit den Cursortasten ↑ und ↓ wählen. Neben der ausgewählten Funktion wird die Funktionsbeschreibung angezeigt.
Drücken Sie nun die tab-Taste, wird nicht nur die Funktion inklusive Klammern () eingefügt; ein Tooltip zeigt Ihnen zudem noch die Argumente am. Im Falle der round()-Funktion sollte round(x, digits = 0) angezeigt werden. Daran sehen Sie, dass round() zwei Argumente annimmt – ein Argument x ohne Default-Wert und ein Argument digits mit dem Default-Wert 0 – ohne Angabe des digits-Arguments rundet round() also standardmäßig auf ganze Zahlen ohne Nachkommastellen.
Oftmals benötigen Sie jedoch noch mehr Informationen zu einer Funktion. In diesem Fall können Sie vor einen beliebigen Funktionsnamen ein ? stellen und ausführen – dieser Befehl öffnet die Dokumentationsseite der jeweiligen Funktion im Bereich rechts unten in RStudio:
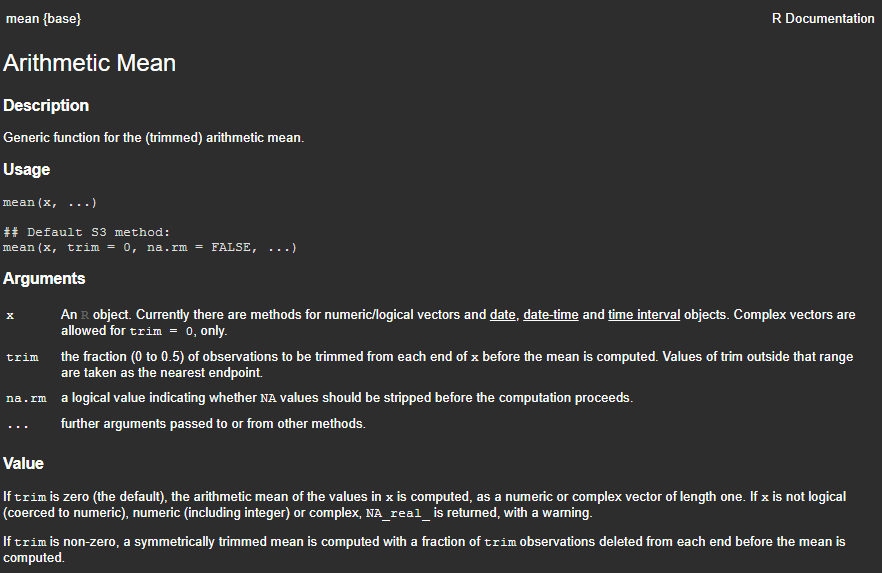
Dokumentation der mean()-Funktion
Dokumentationsseiten in R sind zumeist nach demselben Schema aufgebaut:
- Beschriftung der Funktion. In Falle von
mean()also “Arithmetic Mean”. - Description: Kurze Beschreibung der Funktion.
- Usage: Verwendung der Funktion. Anhand von
mean(x, trim = 0, na.rm = FALSE, ...)können wir die Argumente und deren Default-Werte ablesen. Die...weisen hier auf einen Spezialfall hin, dass bestimmte Objekttypen und Datenstrukturen noch zusätzliche Argumente für die Funktion bereitstellen können – dies braucht uns an dieser Stelle aber nicht weiter zu kümmern. - Arguments: Hier werden alle Argumente der Funktion aufgelistet und ausführlicher beschrieben. Wir erfahren im Falle von
mean()beispielsweise, welche Objekttypen fürxunterstützt werden, wastrimbedeutet etc. - Value: Hier wird das Resultat, das die Funktion ausgibt, beschrieben.
Außerdem können Funktionsdokumentationen noch weitere Abschnitte, beispielsweise Verwendungsbeispiele oder Literaturverweise, enthalten. Es ist daher immer sinnvoll, vor der ersten Verwendung einer Funktion die zugehörige Dokumentation zu konsultieren.
3.2 Eigene Funktionen erstellen
Wir wissen nun einiges über Funktionen; tatsächlich reicht unser Wissen sogar schon aus, um eigene Funktionen zu programmieren. Wir beschäftigen uns daher abschließend in diesem Kapitel mit der Frage, warum und wann wir eigene Funktionen schreiben sollten, und schauen uns an, wie wir unseren Code in Funktionen übersetzen und so weiterverwertbar machen.
3.2.1 Funktionen erstellen: wann und warum?
Viele Schritte in der Datenaufbereitung und -analye wiederholen sich: oft müssen wir mehrere Variablen transformieren, meistens führen wir zur Deskription die gleichen oder zumindest ähnliche Schritte durch, interessieren uns bei Auswertungsverfahren immer wieder für die gleichen Kennwerte.
Funktionen sind das zentrale Element des Programmierens. Im Prinzip handelt es sich bei Funktionen um Code-Fragmente oder Skripte, die durch die Verwendung von “Platzhaltern” (= Variablen, Argumente) so angepasst werden, dass sie immer wieder auf vergleichbare Problemstellungen angewendet werden können.
Nehmen wir das Beispiel der Variablendeskription. Wenn wir Daten erhoben haben, sind wir bei metrischen Variablen in der Regel zunächst an den selben Kennwerten interessiert: der Anzahl der Werte, dem arithmetischen Mittel, der Standardabweichung, dem Minimum und Maximum, eventuell noch dem Median oder anderen Perzentilen. Mit unserem bisherigen Wissen (und drei neuer, aber ebenso einfacher Funktionen) können wir diese Kennwerte einzeln anfordern, zum Beispiel für die Variable Sepal.Length im Beispiel-Datensatz iris:
length(iris$Sepal.Length) # Anzahl Werte
mean(iris$Sepal.Length) # Arithmetisches Mittel
sd(iris$Sepal.Length) # Standardabweichung
min(iris$Sepal.Length) # Minimum
max(iris$Sepal.Length) # Maximum
median(iris$Sepal.Length) # Median## [1] 150
## [1] 5.843333
## [1] 0.8280661
## [1] 4.3
## [1] 7.9
## [1] 5.8Die Ausgabe ist jedoch etwas unübersichtlich. Schöner wird es, wenn wir alle Werte in einem benannten Vektor ablegen:
sepal_length_descriptives <- c(
n = length(iris$Sepal.Length),
M = mean(iris$Sepal.Length),
SD = sd(iris$Sepal.Length),
Minimum = min(iris$Sepal.Length),
Maximum = max(iris$Sepal.Length),
Median = median(iris$Sepal.Length)
)
sepal_length_descriptives## n M SD Minimum Maximum Median
## 150.0000000 5.8433333 0.8280661 4.3000000 7.9000000 5.8000000Das sieht doch gleich übersichtlicher aus – in einem Vektor haben wir alle relevanten Werte gespeichert und können diese auf einen Schlag anzeigen.
Nun haben wir im iris-Datensatz aber noch weitere Variablen, die wir ebenfalls auf diese Art beschreiben möchten (ganz zu schweigen von zukünftigen Datensätzen, für deren Variablen diese Beschreibung ebenfalls relevant ist). Wir könnten natürlich den obigen Code für jede weitere Variablen kopieren und den Variablennamen austauschen; das würde aber unser Skript unnötig aufblähen und unübersichtlicher machen.
Sobald Sie Code(-Fragmente) mehrfach verwenden möchten, ist daher der Zeitpunkt gekommen, darübernachzudenken, ob es nicht sinnvoll ist, ihn in eine Funktion umzuwandeln. Dies hat einige entscheidende Vorteile:
- Code ist einfacher wiederzuverwenden. Anstatt mehrerer Codezeilen ist in Zukunft für dasselbe Ergebnis dann nur noch eine Codezeile – der Funktionsaufruf – erforderlich.
- Skripte werden weniger redundant und dadurch übersichtlicher.
- Fehlerkorrekturen und Anpassungen werden vereinfacht – möchten wir im obigen Beispiel etwa noch einen weiteren Kennwert (z. B. die Spannweite) ergänzen, müssten wir den Code für jede einzelne Variable erneut anpassen; hätten wir eine entsprechende Funktion, wäre die Anpassung nur einmal im Funktionscode nötig.
Schauen wir uns also an, wie wir aus obigen Code eine Funktion erstellen können.
3.2.2 Aufbau und Erstellung von Funktionen
Funktionen in R sind ebenfalls Objekte und werden dementsprechend erstellt: indem einem Objektnamen durch den Zuweisungs-Operator <- die Funktion zugewiesen wird. Neben dem Namen haben Funktionen zwei zentrale Komponenten:
- die Funktionsargumente, wie wir sie auch schon vom Aufruf von eingebauten Funktionen kennen
- den Body der Funktion, der den Code enthält, den die Funktion ausführt
Die Erstellung von Funktionen läuft dabei nach folgendem Schema ab:
Wir weisen also einem Objektnamen ein Funktionsobjekt zu; dies geschieht mit der Funktion function(), wobei wir innerhalb der Klammern die Argumente definieren, die wir im Code der Funktion verwenden möchten. Zwischen zwei geschweiften Klammern {} steht dann der Code, den wir ausführen wollen.
Sehen wir uns nochmals unser obiges Beispiel an:
sepal_length_descriptives <- c(
n = length(iris$Sepal.Length),
M = mean(iris$Sepal.Length),
SD = sd(iris$Sepal.Length),
Minimum = min(iris$Sepal.Length),
Maximum = max(iris$Sepal.Length),
Median = median(iris$Sepal.Length)
)Um den Code auf eine andere Variable anzuwenden, müssten wir jeweils iris$Sepal.Length ersetzen – z. B. durch iris$Sepal.Width, iris$Petal.Length oder eine Variable aus einem anderen Datensatz. Wir möchten diesen Teil also durch einen Platzhalter ersetzen, den wir dann als Funktionsargument übergeben können. Mit einem generischen Platzhalter, den wir der Einfachheit halber (und vollkommen willkürlich!) als x bezeichnen, sähe der Code also wie folgt aus:
descriptives_vector <- c(
n = length(x),
M = mean(x),
SD = sd(x),
Minimum = min(x),
Maximum = max(x),
Median = median(x)
)Zuletzt müssen wir diesen Code nun nur noch als Funktion einem Objekt zuweisen – und dabei unserer Funktionen einen treffenden Namen geben, z. B. descriptives, und dabei x als Funktionsargument definieren:
descriptives <- function(x) { # Wir definieren 'x' als Argument
descriptives_vector <- c(
n = length(x),
M = mean(x),
SD = sd(x),
Minimum = min(x),
Maximum = max(x),
Median = median(x)
)
}Einmal ausgeführt, taucht unsere neue Funktion nun in unserer Arbeitsumgebung auf (siehe den Bereich Environment rechts oben in RStudio, in dem descriptives nun unter Functions erscheinen sollte) und wir können Sie auf beliebige Vektoren anwenden:
Nur warum sehen wir keine Ausgabe? Das liegt daran, dass wir noch nicht definiert haben, was die Funktion zurückgeben soll. Wir erstellen derzeit lediglich den Vektor descriptives_vector, machen aber noch nichts mit ihm – ähnlich, wie uns die Konsole noch keine Ausgabe anzeigt wenn wir ein Objekt lediglich zuweisen.
3.2.2.1 Rückgabe-Werte
Es gibt zwei Möglichkeiten, die Ausgabe einer Funktion zu definieren:
- generell wird das zuletzt im Funktionscode ausgegebene Objekt zurückgegeben. Wir könnten also im Funktionscode ganz am Ende noch eine Zeile hinzufügen, in der unser neu erstellter Vektor ausgeben wird, in dem wir einfach den Objektnamen tippen
descriptives_vector. - mit der speziellen Funktion
return()können wir im Funktionscode explizit ein im Funktionscode erstelltes Objekt angeben, das zurückgegeben werden soll.
Wir müssen also noch eine kleine Anpassung vornehmen:
descriptives <- function(x) {
descriptives_vector <- c(
n = length(x),
M = mean(x),
SD = sd(x),
Minimum = min(x),
Maximum = max(x),
Median = median(x)
)
return(descriptives_vector) # Oder alternativ: lediglich 'descriptives_vector'
}Unsere Funktion ist nun flexibel für numerische Vektoren einsetzbar:
## n M SD Minimum Maximum Median
## 150.0000000 5.8433333 0.8280661 4.3000000 7.9000000 5.8000000## n M SD Minimum Maximum Median
## 150.000000 3.758000 1.765298 1.000000 6.900000 4.350000## n M SD Minimum Maximum Median
## 6.000000 3.500000 1.870829 1.000000 6.000000 3.5000003.2.2.2 Funktionsargumente und Default-Werte
Unsere Funktion funktioniert also schon ganz gut; im nächsten Schritt möchten wir sie aber noch verbessern, um auch Problemfälle abzudecken. Schauen wir uns einmal an, was passiert, wenn wir einen numerischen Vektor mit fehlenden Werten übergeben:
## n M SD Minimum Maximum Median
## 5 NA NA NA NA NAWir sehen, dass alle Kennwerte (außer der Anzahl der Werte) ebenfalls NA sind. Wir erinnern uns, dass Funktionen wie mean() oder sd() bei vorhandenen fehlenden Werten auch einen fehlenden Wert zurückgeben – es sei denn, wir übergeben zusätzlich das Argument na.rm = TRUE, sodass fehlende Werte vor der Berechnung gelöscht werden. Wir möchten dieses Argument nun auch in unserer Funktion nutzen.
Hierzu benötigen wir ein weiteres Funktionsargument, das wir dann als Platzhalter für das na.rm-Argument der jeweiligen Kennwert-Funktionen verwenden können. Aus Konsistenzgründen nennen wir es ebenfalls na.rm:
descriptives <- function(x, na.rm) { # Wir fügen ein weiteres Argument 'na.rm' hinzu...
descriptives_vector <- c(
n = length(x),
M = mean(x, na.rm = na.rm), # ... und übergeben dessen Wert an
SD = sd(x, na.rm = na.rm), # das jeweilige 'na.rm'-Argument der
Minimum = min(x, na.rm = na.rm), # Kennwert-Funktionen
Maximum = max(x, na.rm = na.rm),
Median = median(x, na.rm = na.rm)
)
return(descriptives_vector)
}Wir können unsere Funktion nun auch für Vektoren mit fehlenden Werten verwenden, indem wir analog zu mean(), sd() usw. das Argument na.rm = TRUE übergeben.
## n M SD Minimum Maximum Median
## 5.000000 2.500000 1.290994 1.000000 4.000000 2.500000Allerdings ist unsere Funktion nun weniger komfortabel einzusetzen, wenn wir dieses Argument weglassen möchten:
## Error in mean.default(x, na.rm = na.rm): argument "na.rm" is missing, with no defaultWie wir unter 3.1.1.2 gesehen haben, haben viele Funktionsargumente, die eher optionalen Charakter aufweisen, Default-Werte. Wir können diese ganz einfach bei der Erstellung definieren, indem wir den Default-Wert per = dem jeweiligen Funktionsargument zuweisen:
descriptives <- function(x, na.rm = FALSE) { # Default-Wert für 'na.rm' = FALSE
descriptives_vector <- c(
n = length(x),
M = mean(x, na.rm = na.rm),
SD = sd(x, na.rm = na.rm),
Minimum = min(x, na.rm = na.rm),
Maximum = max(x, na.rm = na.rm),
Median = median(x, na.rm = na.rm)
)
return(descriptives_vector)
}Dieser Default-Wert wird nun also immer verwendet, wenn wir das Argument nicht angegeben haben. Unsere Funktion ist somit noch flexibler geworden:
## n M SD Minimum Maximum Median
## 150.0000000 1.1993333 0.7622377 0.1000000 2.5000000 1.3000000## n M SD Minimum Maximum Median
## 5 NA NA NA NA NA## n M SD Minimum Maximum Median
## 5.000000 2.500000 1.290994 1.000000 4.000000 2.5000003.3 Übungsaufgaben
Erstellen Sie für die folgenden Übungsaufgaben eine eigene Skriptdatei und speichern diese als ue3_nachname.R ab. Antworten auf Fragen können Sie direkt als Kommentare in das Skript einfügen.
Die Funktion seq() kann verwendet werden, um Zahlenfolgen zu erstellen. Lesen Sie sich die Dokumentationsseite der Funktion durch. Wie müssen Sie die Funktion aufrufen (und welche Argumente benötigen Sie dafür), um eine Zahlenfolge von 0 bis 100 in 5er-Schritten zu erzeugen?
Erstellen Sie eine Funktion fahrenheit_to_celsius, die eine Temperaturangabe in Grad Fahrenheit (als numerischen Wert, also z. B. 80) in Grad Celsius umrechnet und diesen Wert zurückgibt.
Die Formel zur Umrechnung von Fahrenheit in Celsius lautet \(°C = (°F - 32) × 5/9\).
Käpseles-Aufgabe (optional)
Erweitern Sie die in Kapitel 3.2.2.2 erstellte Funktion descriptives um folgende Features:
- Die Kennwerte sollen um die Anzahl der fehlenden Werte ergänzt werden (dieses Element soll den Namen
missingtragen). Hierfür benötigen Sie die Funktionis.na(), die für jeden Wert eines Vektors prüft, ob es sich dabei umNAhandelt oder nicht und entsprechendTRUEoderFALSEzurückgibt. - Die Funktion soll alle Kennwerte einheitlich auf eine gewünschte Anzahl an Nachkommastellen, standardmäßig auf 2 Nachkommastellen runden.
Hier nochmals der bisherige Funktionscode:
Da der Funktionsname vor den Argumenten steht, wird hierbei auch von Prefix-Funktionen gesprochen. Wir haben im vorherigen Kapitel auch schon zwei andere Arten von Funktionen kennengelernt: Infix-Funktionen, bei dir der Funktionsname zwischen zwei Argumenten steht (dazu zählen beispielsweise alle arithmetischen Operatoren, z. B.
+,-,*und/), und Replacement-Funktionen, die Teile eines bestehenden Objekts direkt verändern (z. B.names(x) <-). Das sind aber Spezialfälle – im Alltag werden wir vorrangig Prefix-Funktionen verwenden.↩︎