Capítulo 13 Variaveis Instrumentais

Motivação para usar Variáveis Instrumentais: \(\mathbb{E}(xe) \neq 0\)

Vamos ver duas formas de estuturar um modelo onde exista uma variável endógena e um ou mais instrumentos:

set.seed(1)
n= 1000

z1 = rnorm(n)
z2 = runif(n,0,1)
u = rnorm(n)

x1 = rnorm(n)
x2 = u + 1.5*z2 + 0.7*z1 + rnorm(n)
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1)
beta = c(2,5,2)
y = X%*%beta + u

cor(x2,u)

## [1] 0.6290406

cor(z1,u)

## [1] 0.01866414

cor(z1,x2)

## [1] 0.4387025

cor(z2,u)

## [1] 0.02076497

cor(z2,x2)

## [1] 0.2871934

Matriz de Variância e Covariância

#install.packages("mvtnorm")
library(mvtnorm)

  sigma = matrix(c(4,3,3,30), ncol=2)
  colnames(sigma) = c("x1","x2")
  rownames(sigma) = c("x1","x2")
  sigma

##    x1 x2
## x1  4  3
## x2  3 30

Normal Bivariada

n = 1000
mv = rmvnorm(n, mean=c(10,0), sigma=sigma)
dim(mv)

## [1] 1000    2

x1 = mv[,1]
x2 = mv[,2]
var(x1)

## [1] 4.019209

mean(x1)

## [1] 9.918847

var(x2)

## [1] 31.36548

mean(x2)

## [1] 0.075497

cov(x1,x2)

## [1] 3.458533

Endogeneidade

\(E(x_2u) \neq 0\)

Lembre que: \(E(x_2u) = E(x_2)E(u) + Cov(X_2,u)\), e, como \(E(u) = 0\), então \(E(x_2u) = Cov(x_2,u)\)

  n = 1000
  x1 = rnorm(n)
  sigma = matrix(c(4,3,3,30), ncol=2)
  colnames(sigma) = c("x2","u")
  rownames(sigma) = c("x2","u")
  sigma

##    x2  u
## x2  4  3
## u   3 30

  mv = rmvnorm(n, mean=c(10,0), sigma=sigma)
  x2 = mv[,1]
  u = mv[,2]
  cov(x2,u)

## [1] 2.905598

Endogeneidade gera inconsistência no estimador de OLS

Se $Cov(x_2,u) > 0 $, então o estimador é enviesado para cima:

iv = function(n){
  x1 = rnorm(n)
  sigma = matrix(c(4,3,3,30), ncol=2)
  colnames(sigma) = c("x2","u")
  rownames(sigma) = c("x2","u")
  mv = rmvnorm(n, mean=c(10,0), sigma=sigma)
  x2 = mv[,1]
  u = mv[,2]
  X = cbind(1,x1,x2)
  beta = c(2,5,0.5)
  y = X%*%beta  + u
  B = solve(t(X)%*%X)%*%t(X)%*%y
  B
}
z = replicate(10000, expr = iv(1000))
plot(density(z[3, 1, ]), xlim = c(0,2))
abline(v = 0.5)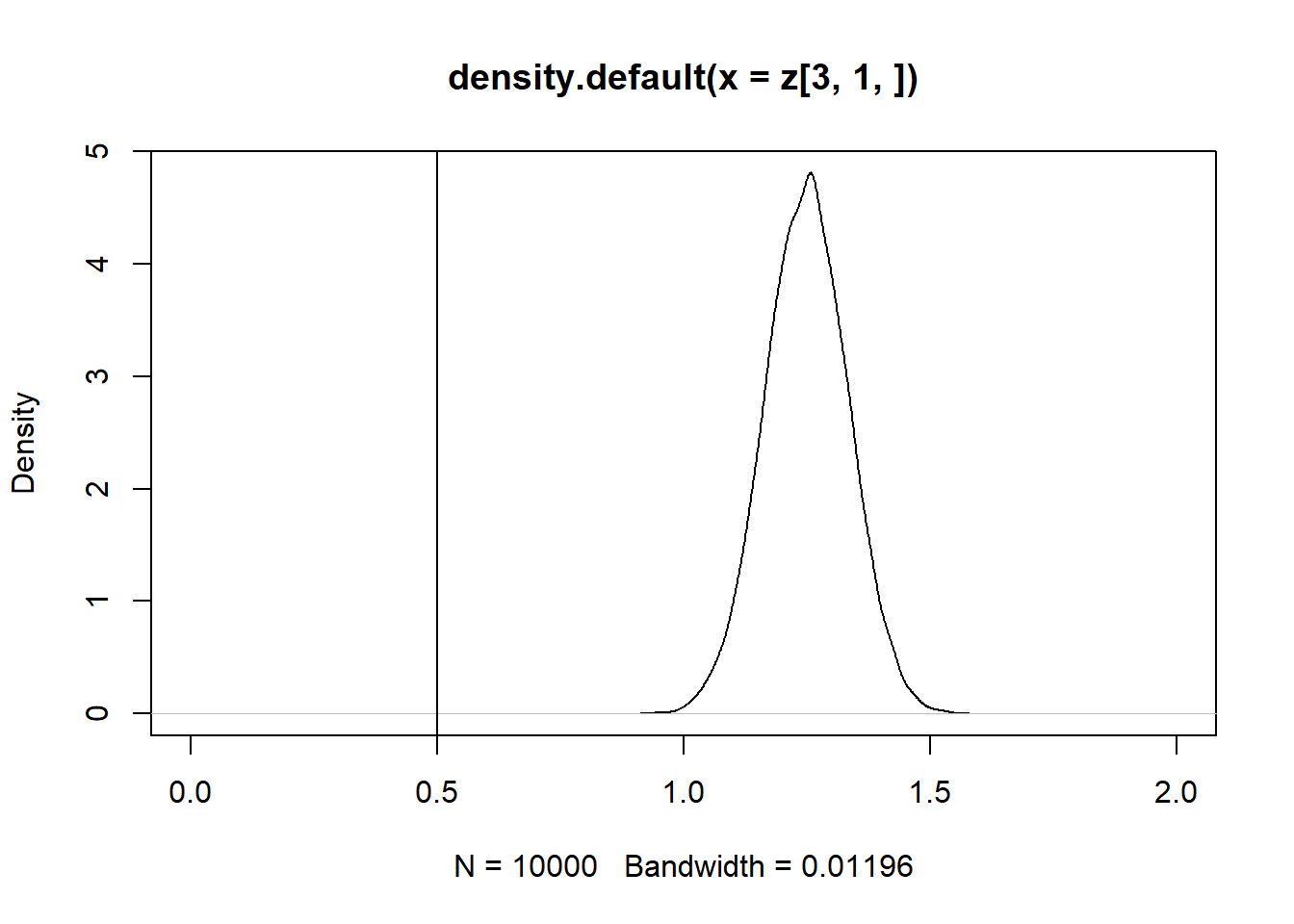

Se $Cov(x_2,u) < 0 $, então o estimador é enviesado para baixo:

iv = function(n){
  x1 = rnorm(n)
  sigma = matrix(c(4,-3,-3,30), ncol=2)
  colnames(sigma) = c("x2","u")
  rownames(sigma) = c("x2","u")
  mv = rmvnorm(n, mean=c(10,0), sigma=sigma)
  x2 = mv[,1]
  u = mv[,2]
  X = cbind(1,x1,x2)
  beta = c(2,5,0.5)
  y = X%*%beta  + u
  B = solve(t(X)%*%X)%*%t(X)%*%y
  B
}
z = replicate(10000, expr = iv(1000))
plot(density(z[3, 1, ]), xlim = c(-1,1))
abline(v = 0.5)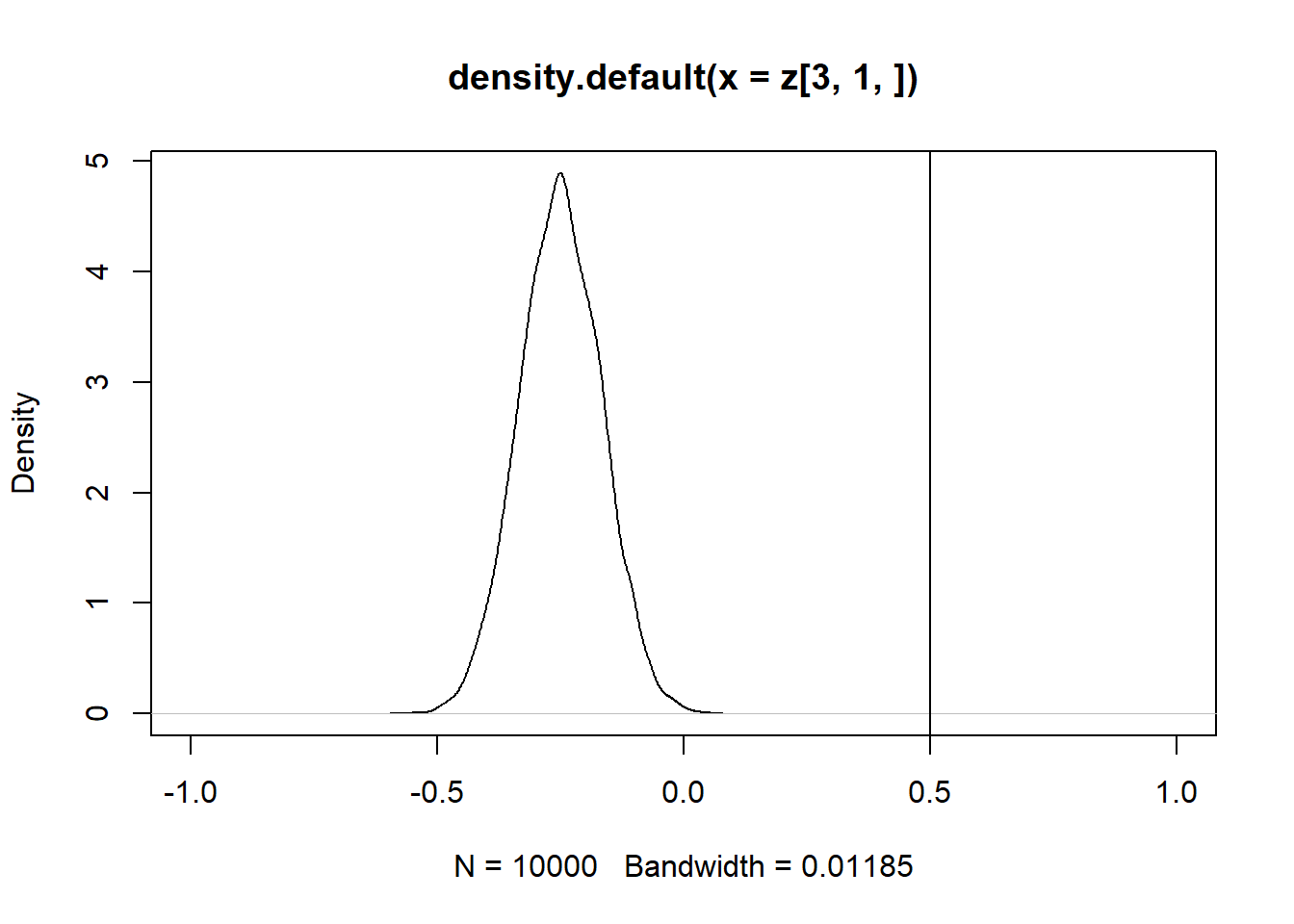

Se \(Cor(x_1,x_2) = 0\), então apenas a estimativa de \(\beta_2\) é enviesada.

iv = function(n){
  x1 = rnorm(n)
  sigma = matrix(c(4,-3,-3,30), ncol=2)
  mv = rmvnorm(n, mean=c(10,0), sigma=sigma)
  x2 = mv[,1]
  u = mv[,2]
  X = cbind(1,x1,x2)
  beta = c(2,5,0.5)
  y = X%*%beta  + u
  B = solve(t(X)%*%X)%*%t(X)%*%y
  B
}
z = replicate(10000, expr = iv(1000))
par(mfrow = c(1, 2))

plot(density(z[2, 1, ]), xlim = c(4.5,5.5))
abline(v = 5)

plot(density(z[3, 1, ]), xlim = c(-0.5,1))
abline(v = 0.5)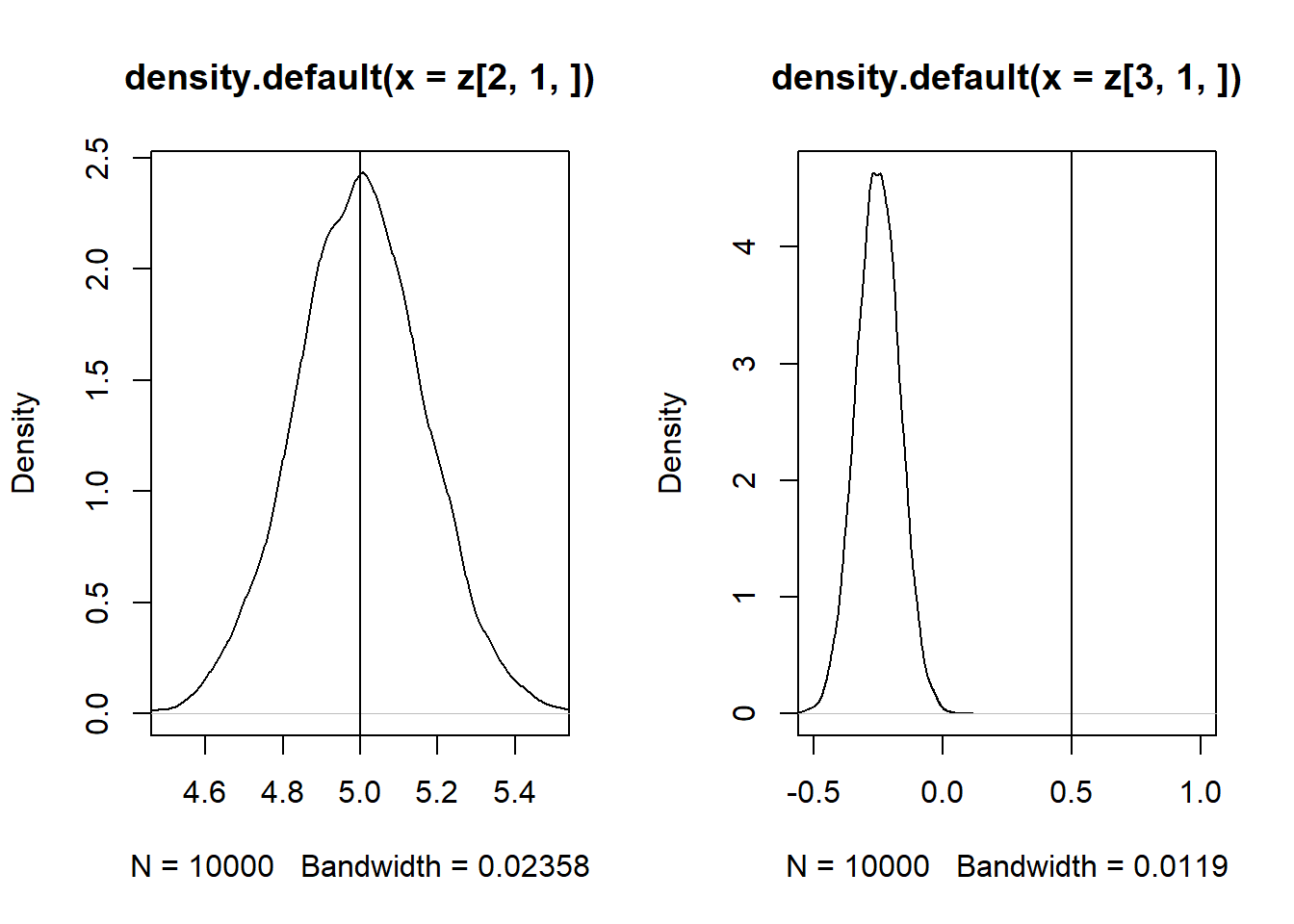

Se \(Cor(x_1,x_2) \neq 0\), então as estimativas de \(\beta_1\) e \(\beta_2\) são enviesadas.

iv = function(n){
  
sigma = matrix(c(4,-3,2,-3,5,0,2,0,7), ncol=3)
mv = rmvnorm(n, mean=c(10,0,3), sigma=sigma)
x2 = mv[,1]
u = mv[,2]
x1 = mv[,3]
X = cbind(1,x1,x2)

beta = c(2,5,0.5)
y = X%*%beta  + u


B = solve(t(X)%*%X)%*%t(X)%*%y
B
}
z = replicate(10000, expr = iv(1000))
par(mfrow = c(1, 2))

plot(density(z[2, 1, ]), xlim = c(4.5,6))
abline(v = 5)

plot(density(z[3, 1, ]), xlim = c(-0.5,1))
abline(v = 0.5)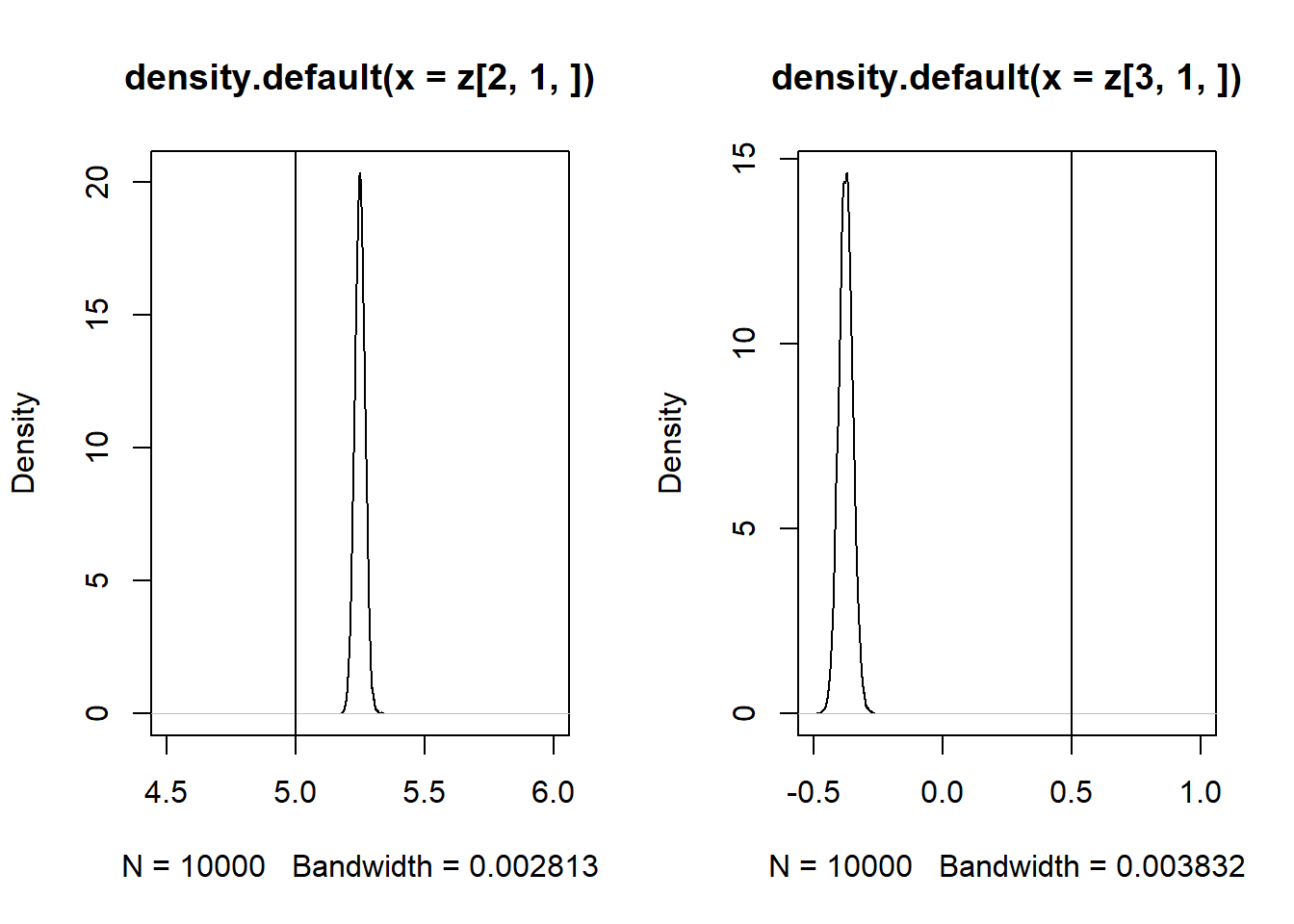

13.1 Estimador de Variáveis Instrumentais

\(\hat\beta{iv} = (Z'X)^{-1}Z'y\)

sigma = matrix(c(4,-3,2,-3,5,0,2,0,7), ncol=3)
colnames(sigma) = c("x2","u","z1")
rownames(sigma) = c("x2","u","z1")
sigma

##    x2  u z1
## x2  4 -3  2
## u  -3  5  0
## z1  2  0  7

iv = function(n){
x1 = rnorm(n)
sigma = matrix(c(4,-3,2,-3,5,0,2,0,7), ncol=3)
mv = rmvnorm(n, mean=c(10,0,3), sigma=sigma)
x2 = mv[,1]
u = mv[,2]
z1 = mv[,3]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1)
beta = c(2,5,0.5)
y = X%*%beta  + u
Biv = solve(t(Z)%*%X)%*%t(Z)%*%y 
Biv
}
z = replicate(10000, expr = iv(1000))

plot(density(z[3, 1, ]), xlim = c(0,1))
abline(v = 0.5)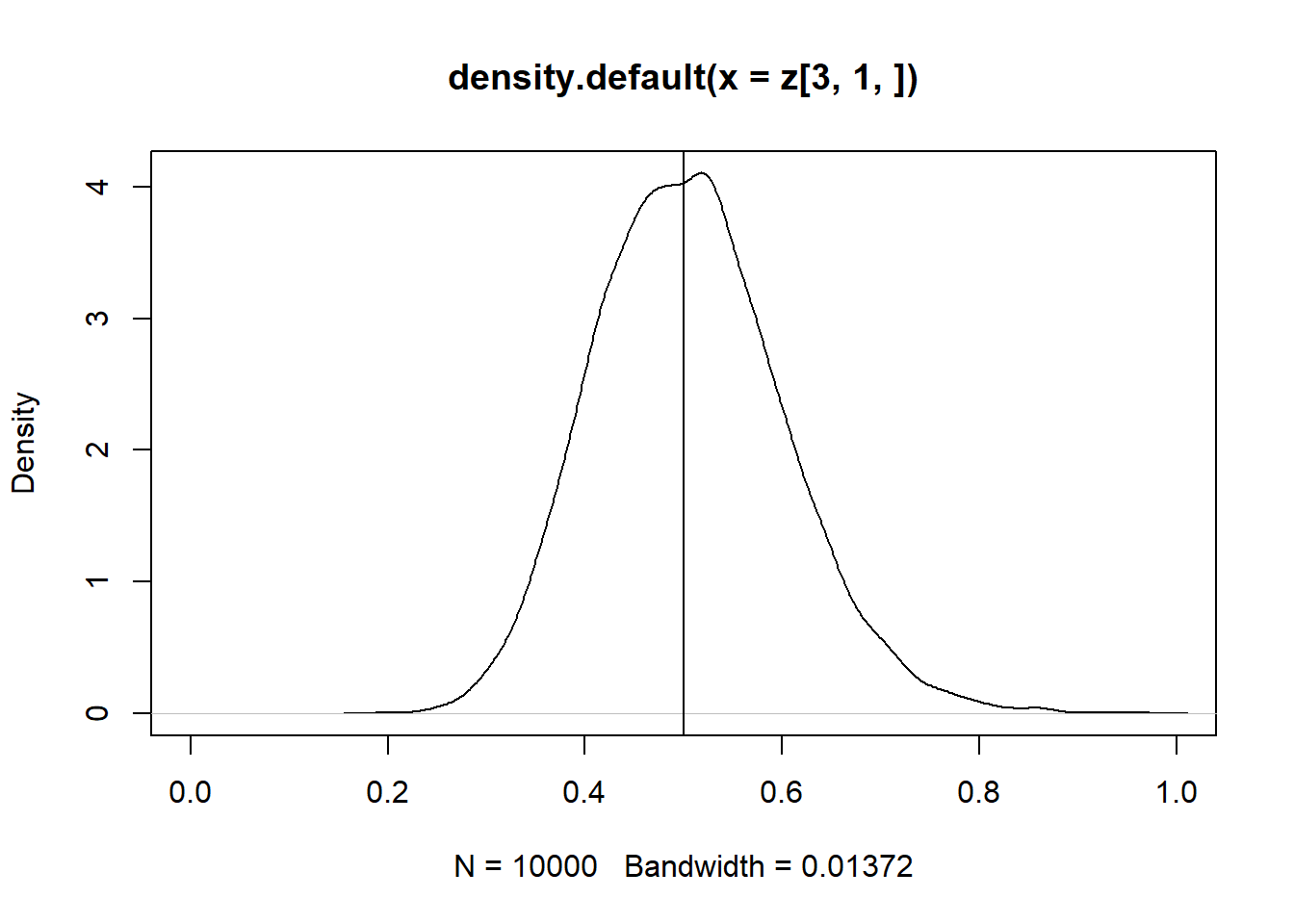

\(Cov(x_1,x_2) \ne 0\)

iv = function(n){
sigma = matrix(c(5,-3,0,0,-3,10,2,-5,0,2,4,0,0,-5,0,10), ncol=4)
mv = rmvnorm(n, mean=c(10,2,3,0), sigma=sigma)
x1 = mv[,1]
x2 = mv[,2]
u = mv[,4]
z1 = mv[,3]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1)
beta = c(2,5,0.5)
y = X%*%beta  + u
Biv = solve(t(Z)%*%X)%*%t(Z)%*%y 
Biv
}
z = replicate(10000, expr = iv(1000))
par(mfrow = c(1, 2))

plot(density(z[2, 1, ]), xlim = c(4.5,5.5))
abline(v = 5)

plot(density(z[3, 1, ]), xlim = c(-0.5,1))
abline(v = 0.5)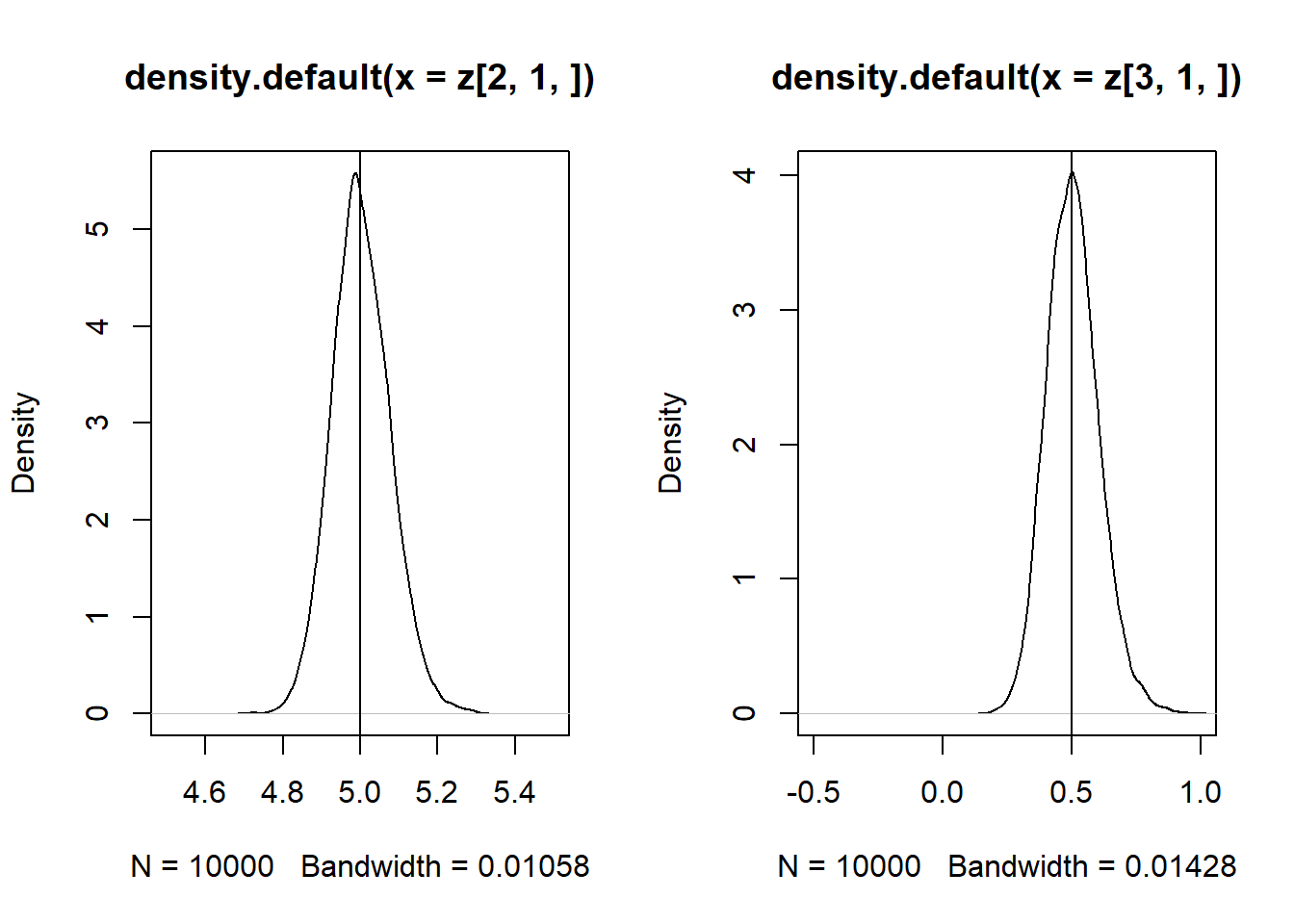

13.2 Estimador de Mínimos Quadrados em Dois Estágios - 2SLS

Utilizando apenas um instrumento: as estimativas de IV e 2SLS

\(\hat \beta_{2sls} = (X'Z(Z'Z)^{-1}Z'X)^{-1}X'Z(Z'Z)^{-1}Z'y\)

  set.seed(1)
x1 = rnorm(n)
sigma = matrix(c(4,-3,2,-3,5,0,2,0,7), ncol=3)
mv = rmvnorm(n, mean=c(10,0,3), sigma=sigma)
x2 = mv[,1]
u = mv[,2]
z1 = mv[,3]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1)
beta = c(2,5,0.5)
y = X%*%beta  + u
Biv = solve(t(Z)%*%X)%*%t(Z)%*%y 
Biv

##         [,1]
##    1.1023513
## x1 4.9974349
## x2 0.5842413

B2sls = solve(t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%X)%*%t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%y
B2sls

##         [,1]
##    1.1023513
## x1 4.9974349
## x2 0.5842413

Por que o nome de dois estágios? Pois é possível obter as mesmas estimativas realizando um procedimento em dois estágios conforme pode ser observado abaixo.

Estimar: \(x_2 = \hat\beta_0 + \hat\beta_1 X_1 + \gamma Z_1 + e\)

set.seed(1)
n = 1000
x1 = rnorm(n)
sigma = matrix(c(4,-3,2,-3,5,0,2,0,7), ncol=3)
mv = rmvnorm(n, mean=c(10,0,3), sigma=sigma)
x2 = mv[,1]
u = mv[,2]
z1 = mv[,3]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1)
beta = c(2,5,0.5)
y = X%*%beta  + u


B1 = solve(t(Z)%*%Z)%*%t(Z)%*%x2
x_hat = Z%*%B1

Antes de estimar o 2º estágio, repare que o 1º estágio “limpou” a endogeneidade que existia em \(x2\).

cor(x_hat,u)

##           [,1]
## [1,] 0.0286093

res =x2 - x_hat
cor(res,u)

##            [,1]
## [1,] -0.7148447

2º estágio: \(y = \beta_0 + \beta_1 X_1 + \beta_2 \hat{X_2} + u\)

X_hat = cbind(1,x1,x_hat)
B2sls = solve(t(X_hat)%*%X_hat)%*%t(X_hat)%*%y
B2sls

##         [,1]
##    1.1023513
## x1 4.9974349
##    0.5842413

Comparar os resultados obtidos pelo estimador 2SLS com o procedimento em 2 estágios:

B2sls = solve(t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%X)%*%t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%y
B2sls

##         [,1]
##    1.1023513
## x1 4.9974349
## x2 0.5842413

Dois Instrumentos

sigma = matrix(c(5,-2,5,3,-2,10,0,0,5,0,8,0,3,0,0,10), ncol=4)
colnames(sigma) = c("x2","z1","z2","u")
rownames(sigma) = c("x2","z1","z2","u")
sigma

##    x2 z1 z2  u
## x2  5 -2  5  3
## z1 -2 10  0  0
## z2  5  0  8  0
## u   3  0  0 10

set.seed(1)
x1 = rnorm(n)
sigma = matrix(c(5,-2,5,3,-2,10,0,0,5,0,8,0,3,0,0,10), ncol=4)
mv = rmvnorm(n, mean=c(10,5,3,0), sigma=sigma)
x2 = mv[,1]
z1 = mv[,2]
z2 = mv[,3]
u = mv[,4]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1,z2)
beta = c(2,5,0.5)
y = X%*%beta  + u
B2sls = solve(t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%X)%*%t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%y
B2sls

##         [,1]
##    2.0407802
## x1 5.0159400
## x2 0.4980277

Usar dois instrumentos aumenta a eficiência, conforme veremos abaixo. Mas usando um ou dois instrumentos o estimador é consistente:

sls2 = function(n){
x1 = rnorm(n)
sigma = matrix(c(5,-2,5,3,-2,10,0,0,5,0,8,0,3,0,0,10), ncol=4)
mv = rmvnorm(n, mean=c(10,5,3,0), sigma=sigma)
x2 = mv[,1]
z1 = mv[,2]
z2 = mv[,3]
u = mv[,4]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1,z2)
beta = c(2,5,0.5)
y = X%*%beta  + u
B2sls2 = solve(t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%X)%*%t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%y
B2sls2
}

sls = function(n){
x1 = rnorm(n)
sigma = matrix(c(5,-2,5,3,-2,10,0,0,5,0,8,0,3,0,0,10), ncol=4)
mv = rmvnorm(n, mean=c(10,5,3,0), sigma=sigma)
x2 = mv[,1]
z1 = mv[,2]
z2 = mv[,3]
u = mv[,4]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1)
beta = c(2,5,0.5)
y = X%*%beta  + u
B2sls2 = solve(t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%X)%*%t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%y
B2sls2
}

set.seed(10)
z = replicate(10000, expr = sls2(1000))
set.seed(10)
z1 = replicate(10000, expr = sls(1000))

par(mfrow = c(1, 2))

plot(density(z[3, 1, ]), xlim = c(0,1))
abline(v = 0.5)

plot(density(z1[3, 1, ]), xlim = c(0,1))
abline(v = 0.5)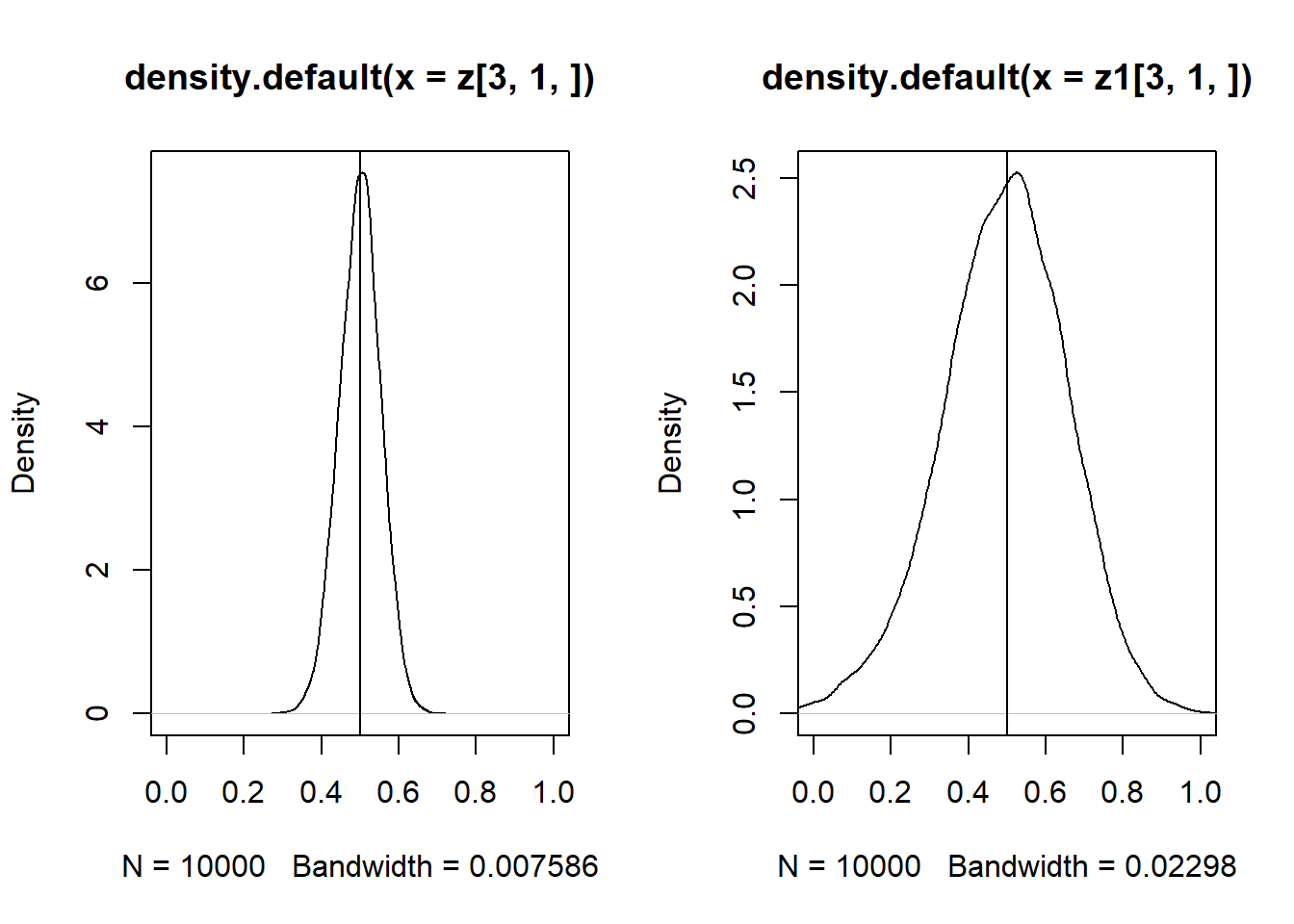

13.3 Matriz de Variânicia-Covariância de Variáveis Instrumentais

Estimador de Varáveis Instrumentais

set.seed(1)
n = 1000
x1 = rnorm(n)
sigma = matrix(c(4,-3,2,-3,5,0,2,0,7), ncol=3)
mv = rmvnorm(n, mean=c(10,0,3), sigma=sigma)
x2 = mv[,1]
u = mv[,2]
z1 = mv[,3]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1)
beta = c(2,5,0.5)
y = X%*%beta  + u
Biv = solve(t(Z)%*%X)%*%t(Z)%*%y 
Biv

##         [,1]
##    1.1023513
## x1 4.9974349
## x2 0.5842413

\(Var(\hat\beta_{iv}) = \sigma_{iv}^2 (X'P_zX)^{-1}\), onde \(P_z = Z(Z'Z)^{-1}Z1\)

Portanto: \(Var(\hat\beta_{iv}) = \sigma_{iv}^2 (X'Z(Z'Z)^{-1}Z'X)^{-1}\)

e_hat_iv = y - X%*%Biv
k = ncol(X)
sigma_hat_iv = (1/(n-k)) * t(e_hat_iv)%*%e_hat_iv  ## O R faz a correção do viés dividindo por (n-k) o Stata só divide por n
sigma_hat_iv

##          [,1]
## [1,] 5.943146

V_iv = sigma_hat_iv[1,1] * solve((t(X)%*%Z)%*%solve(t(Z)%*%Z)%*%t(Z)%*%X)
ep_iv = sqrt(diag(V_iv))
ep_iv

##                    x1         x2 
## 0.98725579 0.07471610 0.09789995

Estimador de Mínimos Quadrados de Dois Estágios

  set.seed(1)
x1 = rnorm(n)
sigma = matrix(c(4,-3,2,-3,5,0,2,0,7), ncol=3)
mv = rmvnorm(n, mean=c(10,0,3), sigma=sigma)
x2 = mv[,1]
u = mv[,2]
z1 = mv[,3]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1)
beta = c(2,5,0.5)
y = X%*%beta  + u
B2sls = solve(t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%X)%*%t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%y
B2sls

##         [,1]
##    1.1023513
## x1 4.9974349
## x2 0.5842413

e_hat_2sls = y - X%*%B2sls
k = ncol(X)
sigma_hat_2sls = (1/(n-k)) * t(e_hat_2sls)%*%e_hat_2sls  ## O R faz a correção do viés dividindo por (n-k) o Stata só divide por n
sigma_hat_2sls

##          [,1]
## [1,] 5.943146

V_2sls = sigma_hat_2sls[1,1] * solve((t(X)%*%Z)%*%solve(t(Z)%*%Z)%*%t(Z)%*%X)
ep_2sls = sqrt(diag(V_2sls))
ep_2sls

##                    x1         x2 
## 0.98725579 0.07471610 0.09789995

Estimador de Mínimos Quadrados em Dois Estágios

set.seed(1)
n = 1000
x1 = rnorm(n)
sigma = matrix(c(4,-3,2,-3,5,0,2,0,7), ncol=3)
mv = rmvnorm(n, mean=c(10,0,3), sigma=sigma)
x2 = mv[,1]
u = mv[,2]
z1 = mv[,3]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1)
beta = c(2,5,0.5)
y = X%*%beta  + u

B1 = solve(t(Z)%*%Z)%*%t(Z)%*%x2
x_hat = Z%*%B1

X_hat = cbind(1,x1,x_hat)

B2sls = solve(t(X_hat)%*%X_hat)%*%t(X_hat)%*%y
B2sls

##         [,1]
##    1.1023513
## x1 4.9974349
##    0.5842413

e_hat_2sls = y - X%*%B2sls  # usar o vetor original de X, e não o vetor do segundo estágio
k = ncol(X)
sigma_hat_2sls = (1/(n-k)) * t(e_hat_2sls)%*%e_hat_2sls   # n-k correção de viés
sigma_hat_2sls

##          [,1]
## [1,] 5.943146

V_2sls = sigma_hat_2sls[1,1] * solve((t(X_hat)%*%X_hat))
ep_2sls = sqrt(diag(V_2sls))
ep_2sls

##                    x1            
## 0.98725579 0.07471610 0.09789995

13.4 Teste de Hausman

#install.packages("ivreg")
library(ivreg)

## Warning: package 'ivreg' was built under R version 4.1.3

## Registered S3 methods overwritten by 'ivreg':
##   method              from
##   anova.ivreg         AER 
##   hatvalues.ivreg     AER 
##   model.matrix.ivreg  AER 
##   predict.ivreg       AER 
##   print.ivreg         AER 
##   print.summary.ivreg AER 
##   summary.ivreg       AER 
##   terms.ivreg         AER 
##   update.ivreg        AER 
##   vcov.ivreg          AER

## 
## Attaching package: 'ivreg'

## The following objects are masked from 'package:AER':
## 
##     ivreg, ivreg.fit

Modelo com Endogeneidade

set.seed(1)
n =1000
x1 = rnorm(n)
sigma = matrix(c(4,-3,2,-3,5,0,2,0,7), ncol=3)
mv = rmvnorm(n, mean=c(10,0,3), sigma=sigma)
x2 = mv[,1]
u = mv[,2]
z1 = mv[,3]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1)
beta = c(2,5,0.5)
y = X%*%beta  + u

df = data.frame(y,x1,x2,z1)
iv = ivreg(y ~ x1 + x2 | x1 + z1, data = df)
summary(iv)

## 
## Call:
## ivreg(formula = y ~ x1 + x2 | x1 + z1, data = df)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -7.71597 -1.63461 -0.02373  1.63873  7.22710 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.10235    0.98726   1.117    0.264    
## x1           4.99743    0.07472  66.886  < 2e-16 ***
## x2           0.58424    0.09790   5.968 3.34e-09 ***
## 
## Diagnostic tests:
##                  df1 df2 statistic p-value    
## Weak instruments   1 997     170.8  <2e-16 ***
## Wu-Hausman         1 996     183.4  <2e-16 ***
## Sargan             0  NA        NA      NA    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.438 on 997 degrees of freedom
## Multiple R-Squared: 0.805,   Adjusted R-squared: 0.8047 
## Wald test:  2294 on 2 and 997 DF,  p-value: < 2.2e-16

Modelo sem Endogeneidade

set.seed(1)
n =1000
x1 = rnorm(n)
sigma = matrix(c(4,0,2,0,5,0,2,0,7), ncol=3)
mv = rmvnorm(n, mean=c(10,0,3), sigma=sigma)
x2 = mv[,1]
u = mv[,2]
z1 = mv[,3]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1)
beta = c(2,5,0.5)
y = X%*%beta  + u

df = data.frame(y,x1,x2,z1)
iv = ivreg(y ~ x1 + x2 | x1 + z1, data = df)
summary(iv)

## 
## Call:
## ivreg(formula = y ~ x1 + x2 | x1 + z1, data = df)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -7.96475 -1.55691 -0.01991  1.63352  7.36388 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.86049    0.90828   0.947    0.344    
## x1           5.01820    0.07201  69.691  < 2e-16 ***
## x2           0.60938    0.09015   6.760 2.35e-11 ***
## 
## Diagnostic tests:
##                  df1 df2 statistic p-value    
## Weak instruments   1 997   184.298  <2e-16 ***
## Wu-Hausman         1 996     0.711   0.399    
## Sargan             0  NA        NA      NA    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.347 on 997 degrees of freedom
## Multiple R-Squared: 0.8391,  Adjusted R-squared: 0.8388 
## Wald test:  2509 on 2 and 997 DF,  p-value: < 2.2e-16

13.5 Eficiência dos Estimadores

Modelo sem Endogeneidade: OLS vs IV

IV

set.seed(1)
n =1000
x1 = rnorm(n)
sigma = matrix(c(4,0,2,0,5,0,2,0,7), ncol=3)
mv = rmvnorm(n, mean=c(10,0,3), sigma=sigma)
x2 = mv[,1]
u = mv[,2]
z1 = mv[,3]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1)
beta = c(2,5,0.5)
y = X%*%beta  + u

Biv = solve(t(Z)%*%X)%*%t(Z)%*%y 
Biv

##         [,1]
##    0.8604895
## x1 5.0181987
## x2 0.6093826

e_hat_iv = y - X%*%Biv
k = ncol(X)
sigma_hat_iv = (1/(n-k)) * t(e_hat_iv)%*%e_hat_iv  ## O R faz a correção do viés dividindo por (n-k) o Stata só divide por n
sigma_hat_iv

##          [,1]
## [1,] 5.507993

V_iv = sigma_hat_iv[1,1] * solve((t(X)%*%Z)%*%solve(t(Z)%*%Z)%*%t(Z)%*%X)
V_iv

##                            x1            x2
##     0.824970876  0.0055776590 -0.0816072406
## x1  0.005577659  0.0051849073 -0.0005494873
## x2 -0.081607241 -0.0005494873  0.0081269665

ep_iv = sqrt(diag(V_iv))
ep_iv

##                    x1         x2 
## 0.90827907 0.07200630 0.09014969

OLS

Bols = solve(t(X)%*%X)%*%t(X)%*%y 
Bols

##         [,1]
##    1.5605990
## x1 5.0229128
## x2 0.5396613

e_hat = y - X%*%Bols
k = ncol(X)
sigma_hat = (1/(n-k)) * t(e_hat)%*%e_hat   # n-k correção de viés
V = sigma_hat[1,1] * solve(t(X)%*%X)

ep = sqrt(diag(V))
ep

##                    x1         x2 
## 0.36447618 0.07165008 0.03553926

iv = function(n){
  x1 = rnorm(n)
sigma = matrix(c(4,0,2,0,5,0,2,0,7), ncol=3)
mv = rmvnorm(n, mean=c(10,0,3), sigma=sigma)
x2 = mv[,1]
u = mv[,2]
z1 = mv[,3]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1)
beta = c(2,5,0.5)
y = X%*%beta  + u
Biv = solve(t(Z)%*%X)%*%t(Z)%*%y 
Biv 
}

ols = function(n){
  x1 = rnorm(n)
#  x3 = rnorm(n,5,5)
sigma = matrix(c(4,0,2,0,5,0,2,0,7), ncol=3)
mv = rmvnorm(n, mean=c(10,0,3), sigma=sigma)
x2 = mv[,1]
u = mv[,2]
z1 = mv[,3]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1)
beta = c(2,5,0.5)
y = X%*%beta  + u
Bols = solve(t(X)%*%X)%*%t(X)%*%y 
Bols
 
}

set.seed(10)
z = replicate(1000, expr = iv(1000))
set.seed(10)
z1 = replicate(1000, expr = ols(1000))

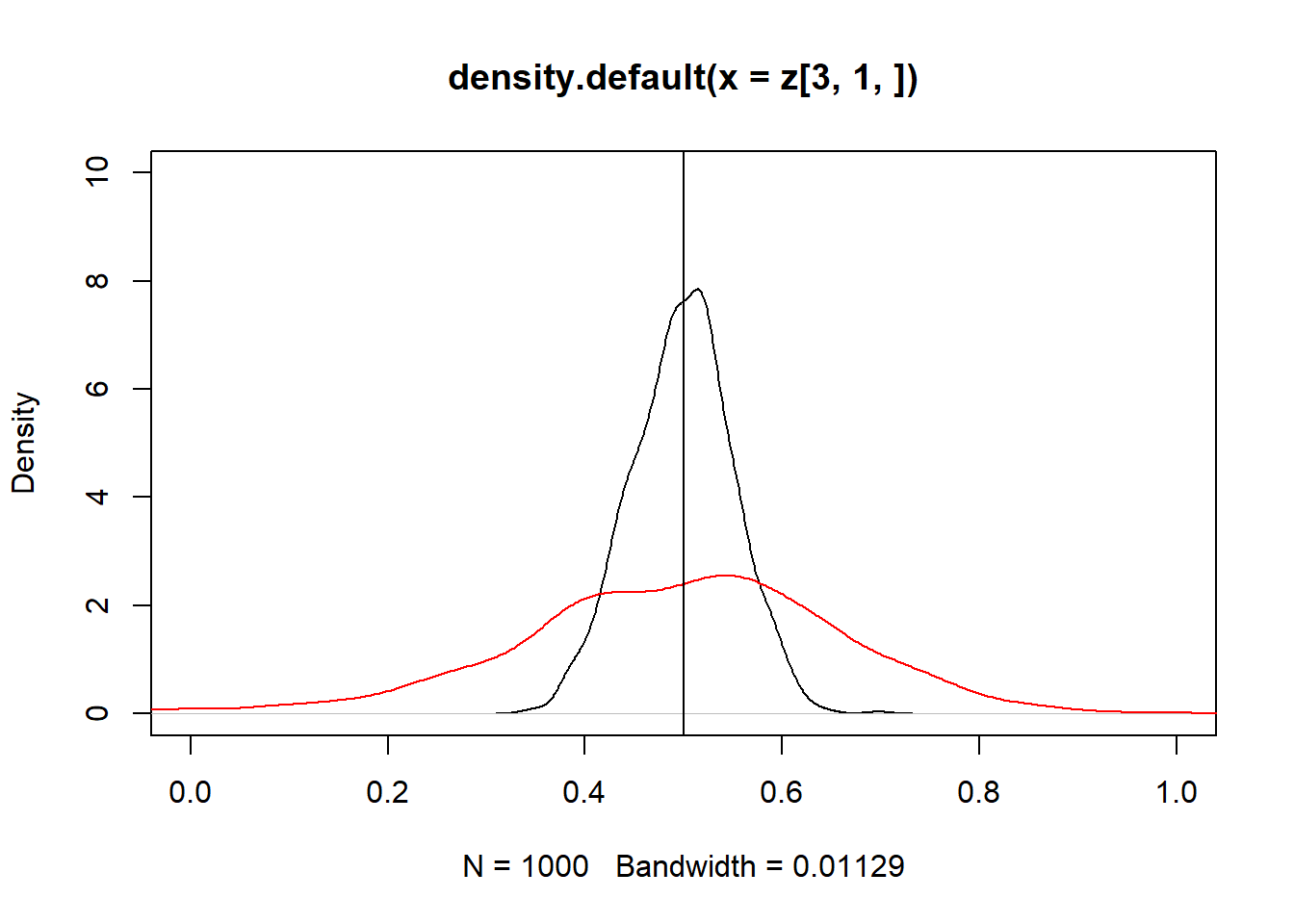
plot(density(z[3, 1, ]), xlim = c(-0,1), ylim = c(0,12))
lines(density(z1[3, 1, ]), add = TRUE, col = "red")

## Warning in plot.xy(xy.coords(x, y), type = type, ...): "add" não é um parâmetro
## gráfico

abline(v = 0.5)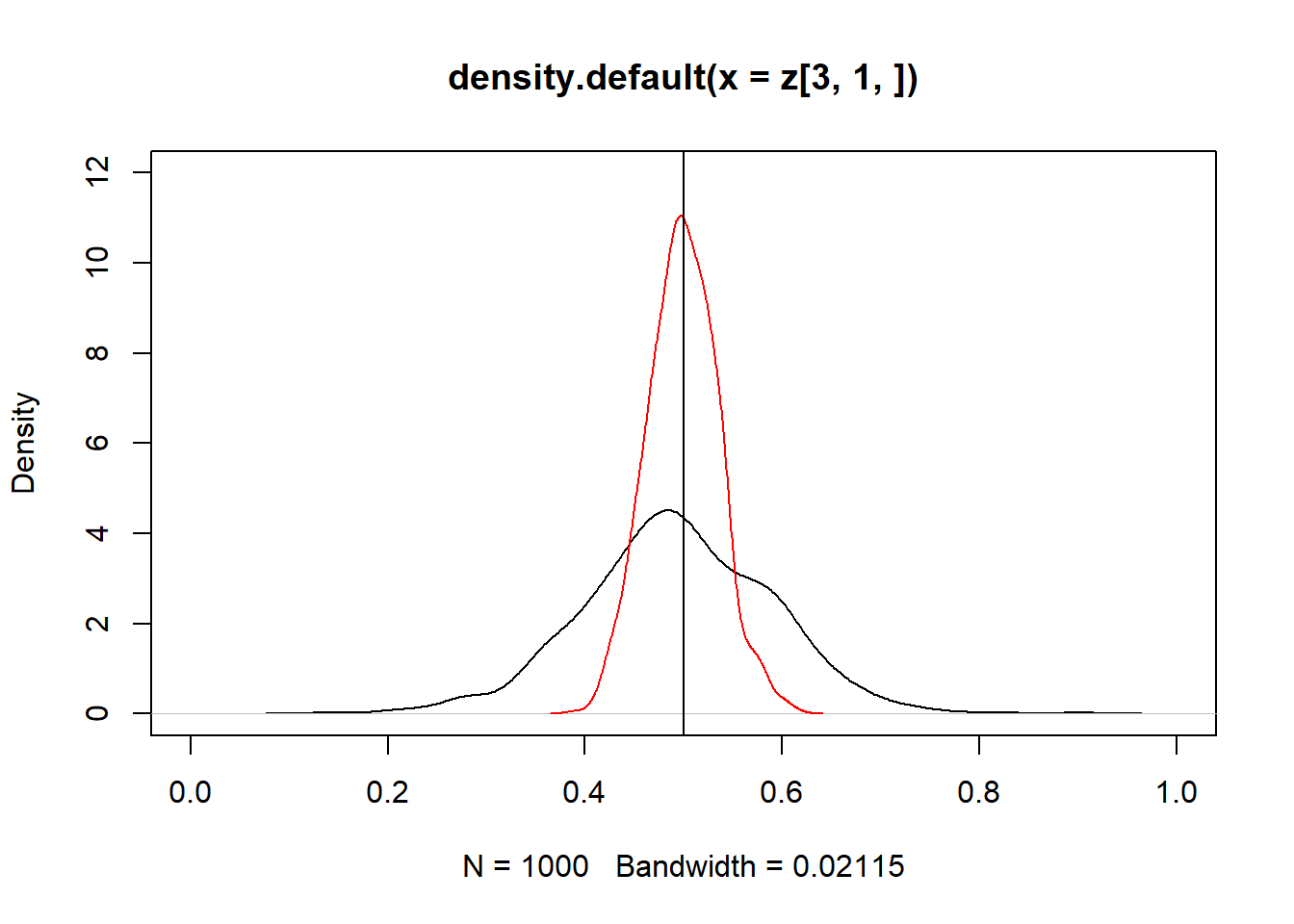

Modelo com endogeneidade: 1 instrumento vs 2 instrumentos

2 instrumentos

set.seed(1)
x1 = rnorm(n)
sigma = matrix(c(5,-2,5,3,-2,10,0,0,5,0,8,0,3,0,0,10), ncol=4)
mv = rmvnorm(n, mean=c(10,5,3,0), sigma=sigma)
x2 = mv[,1]
z1 = mv[,2]
z2 = mv[,3]
u = mv[,4]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1,z2)
beta = c(2,5,0.5)
y = X%*%beta  + u
B2sls = solve(t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%X)%*%t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%y
B2sls

##         [,1]
##    2.0407802
## x1 5.0159400
## x2 0.4980277

e_hat_2sls = y - X%*%B2sls
k = ncol(X)
sigma_hat_2sls = (1/(n-k)) * t(e_hat_2sls)%*%e_hat_2sls  ## O R faz a correção do viés dividindo por (n-k) o Stata só divide por n
sigma_hat_2sls

##          [,1]
## [1,] 10.42011

V_2sls = sigma_hat_2sls[1,1] * solve((t(X)%*%Z)%*%solve(t(Z)%*%Z)%*%t(Z)%*%X)
ep_2sls = sqrt(diag(V_2sls))
ep_2sls

##                    x1         x2 
## 0.53649921 0.09868849 0.05283104

1 instrumento

set.seed(1)
x1 = rnorm(n)
sigma = matrix(c(5,-2,5,3,-2,10,0,0,5,0,8,0,3,0,0,10), ncol=4)
mv = rmvnorm(n, mean=c(10,5,3,0), sigma=sigma)
x2 = mv[,1]
z1 = mv[,2]
z2 = mv[,3]
u = mv[,4]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1)
beta = c(2,5,0.5)
y = X%*%beta  + u
B2sls = solve(t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%X)%*%t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%y
B2sls

##         [,1]
##    2.4567813
## x1 5.0166521
## x2 0.4563002

e_hat_2sls = y - X%*%B2sls
k = ncol(X)
sigma_hat_2sls = (1/(n-k)) * t(e_hat_2sls)%*%e_hat_2sls  ## O R faz a correção do viés dividindo por (n-k) o Stata só divide por n
sigma_hat_2sls

##          [,1]
## [1,] 10.69194

V_2sls = sigma_hat_2sls[1,1] * solve((t(X)%*%Z)%*%solve(t(Z)%*%Z)%*%t(Z)%*%X)
ep_2sls = sqrt(diag(V_2sls))
ep_2sls

##                    x1         x2 
## 1.57171541 0.09999934 0.15731133

iv2 = function(n){
  
  x1 = rnorm(n)
sigma = matrix(c(5,-2,5,3,-2,10,0,0,5,0,8,0,3,0,0,10), ncol=4)
mv = rmvnorm(n, mean=c(10,5,3,0), sigma=sigma)
x2 = mv[,1]
z1 = mv[,2]
z2 = mv[,3]
u = mv[,4]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1,z2)
beta = c(2,5,0.5)
y = X%*%beta  + u
B2sls = solve(t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%X)%*%t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%y
B2sls
}

iv = function(n){
x1 = rnorm(n)
sigma = matrix(c(5,-2,5,3,-2,10,0,0,5,0,8,0,3,0,0,10), ncol=4)
mv = rmvnorm(n, mean=c(10,5,3,0), sigma=sigma)
x2 = mv[,1]
z1 = mv[,2]
z2 = mv[,3]
u = mv[,4]
X = cbind(1,x1,x2)
Z = cbind(1,x1,z1)
beta = c(2,5,0.5)
y = X%*%beta  + u
B2sls = solve(t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%X)%*%t(X)%*%Z%*%solve(t(Z)%*%Z)%*%t(Z)%*%y
B2sls
}

set.seed(10)
z = replicate(1000, expr = iv2(1000))
set.seed(10)
z1 = replicate(1000, expr = iv(1000))

plot(density(z[3, 1, ]), xlim = c(-0,1), ylim = c(0,10))
lines(density(z1[3, 1, ]), add = TRUE, col = "red")

## Warning in plot.xy(xy.coords(x, y), type = type, ...): "add" não é um parâmetro
## gráfico

abline(v = 0.5)