Capítulo 9 Teoria Assintotica

9.1 Convergência de séries não aleatórias

Exemplo de uma série não convergente $$f(N)=N^2$$

f = function(x) x^2
N = 1:30
plot(N, f(N), type="l", col="lightblue", lwd=4)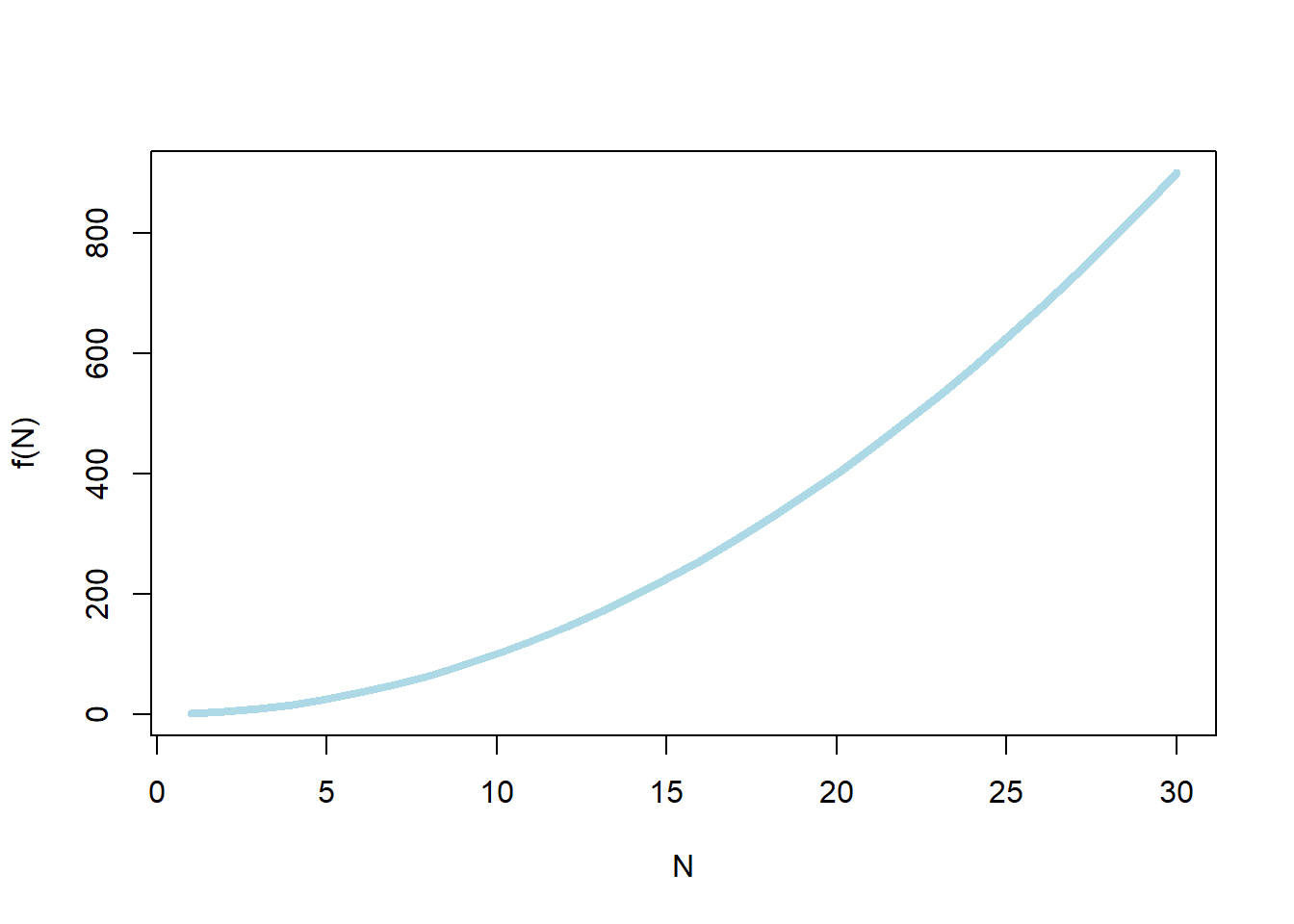

Série convergente

$$g(N)=10x^{-99/100}sin(x)+pi$$

g = function(x) 10*x^(-99/100) * sin(x) + pi
N = 1:100
plot(N, g(N), type="l", lwd=2)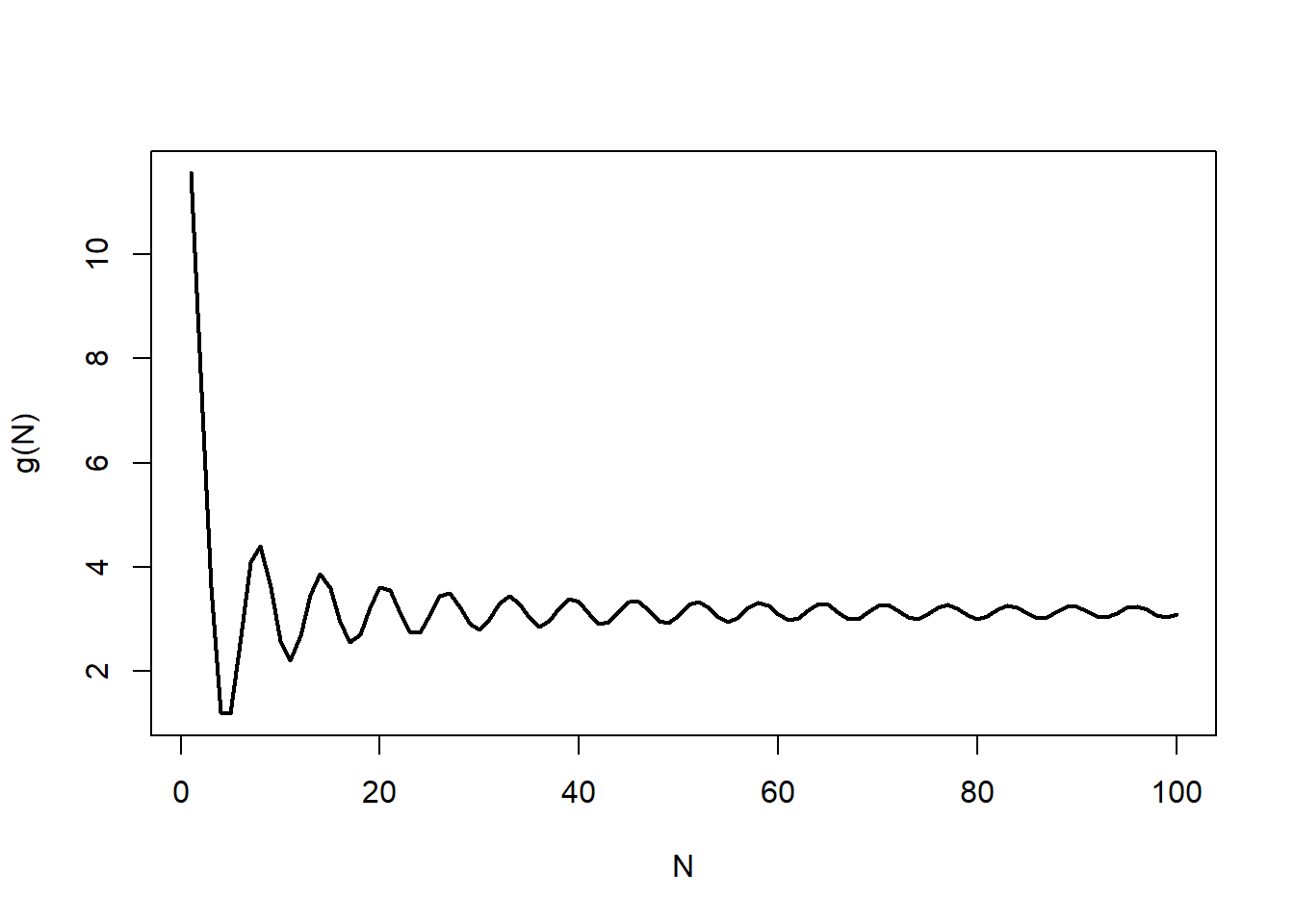

e1 = 2
plot(N, g(N), type="l", lwd=2)
abline(h=pi+e1, lwd=2, col="darkred")
abline(h=pi-e1, lwd=2, col="darkred")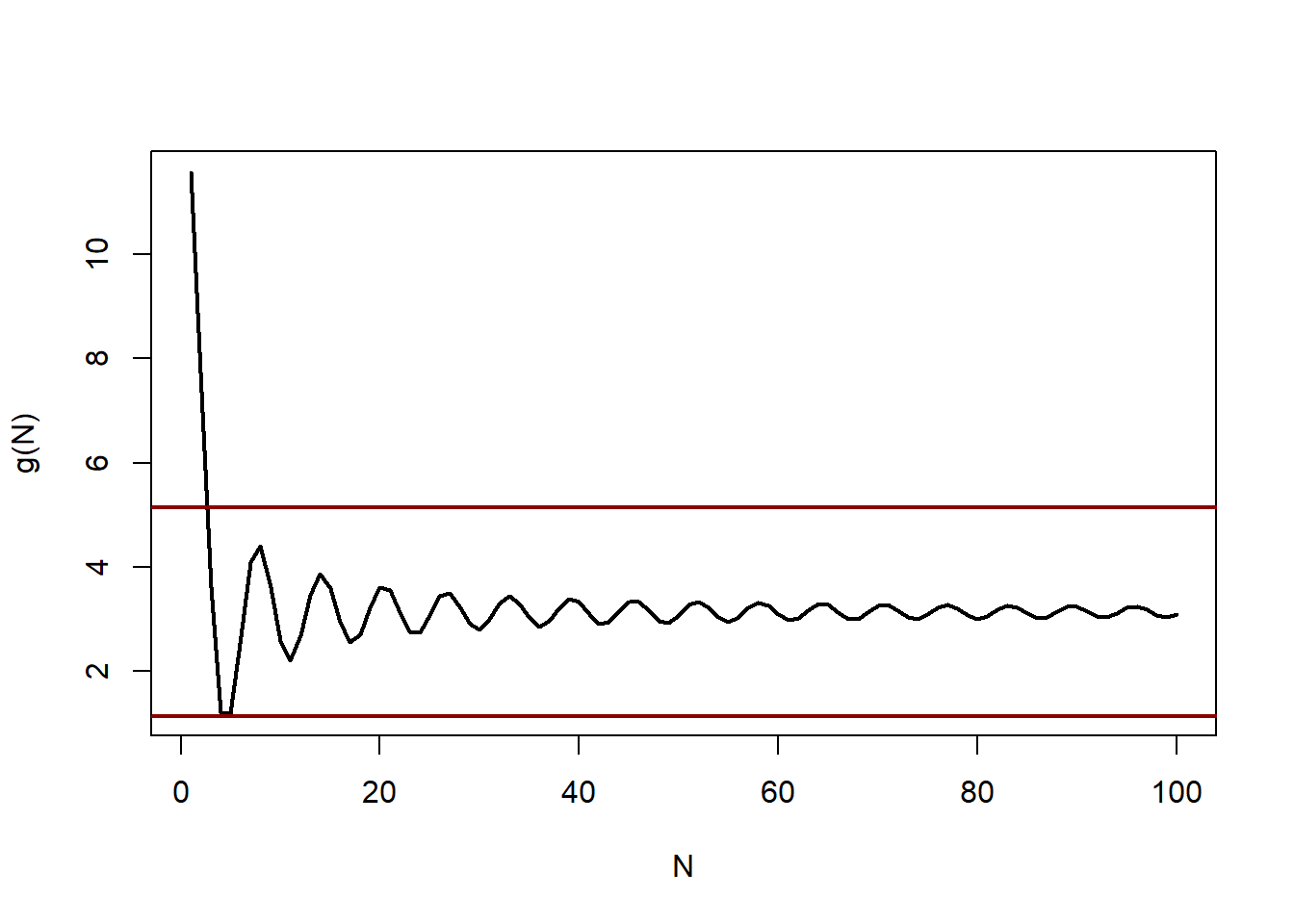

e2 = .5
plot(N, g(N), type="l", lwd=2)
abline(h=pi+e2, lwd=2, col="darkblue")
abline(h=pi-e2, lwd=2, col="darkblue")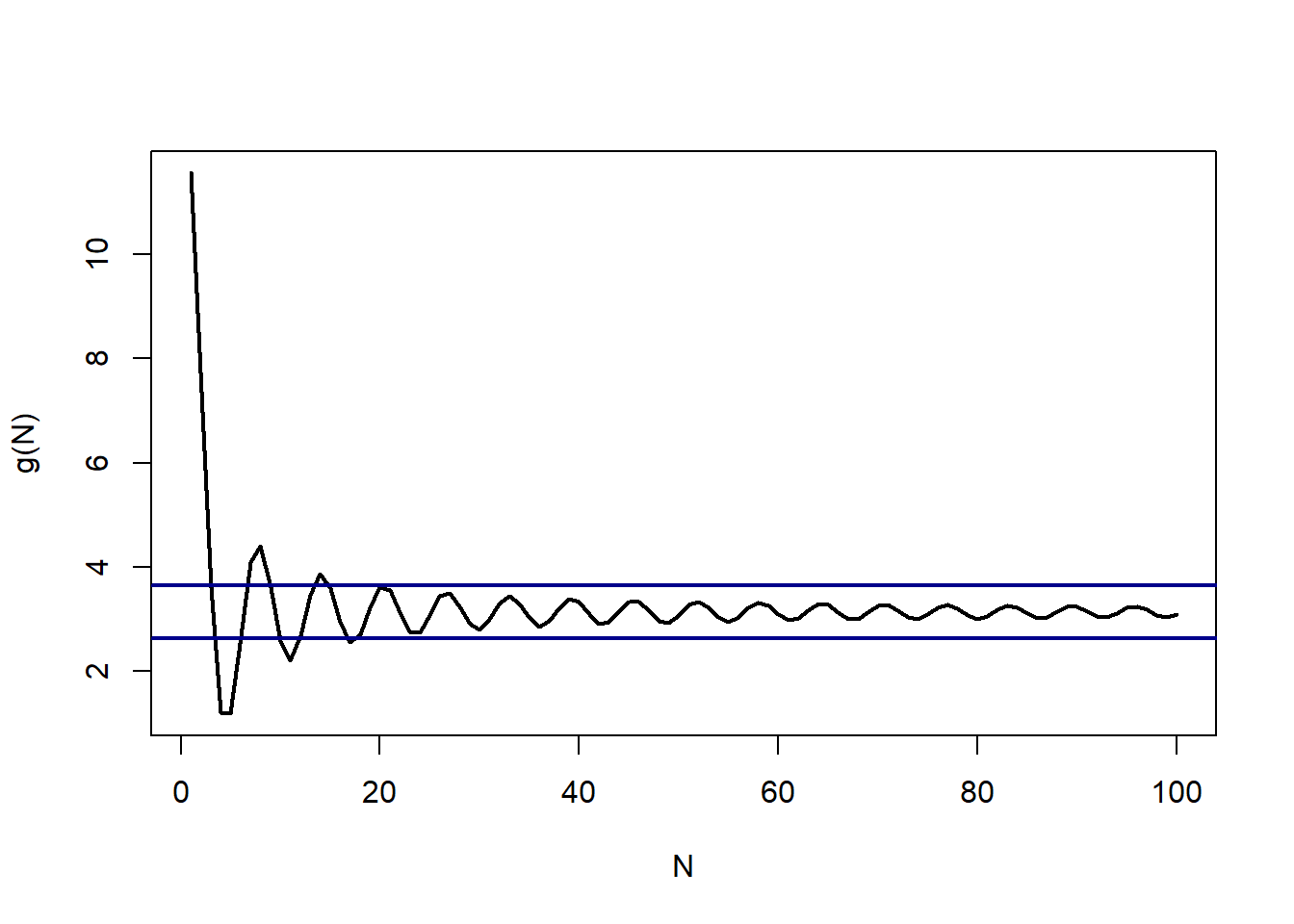

e3 = .1
plot(N, g(N), type="l", lwd=2)
abline(h=pi+e3, lwd=2, col=rgb(.3,.6,1,.5))
abline(h=pi-e3, lwd=2, col=rgb(.3,.6,1,.5))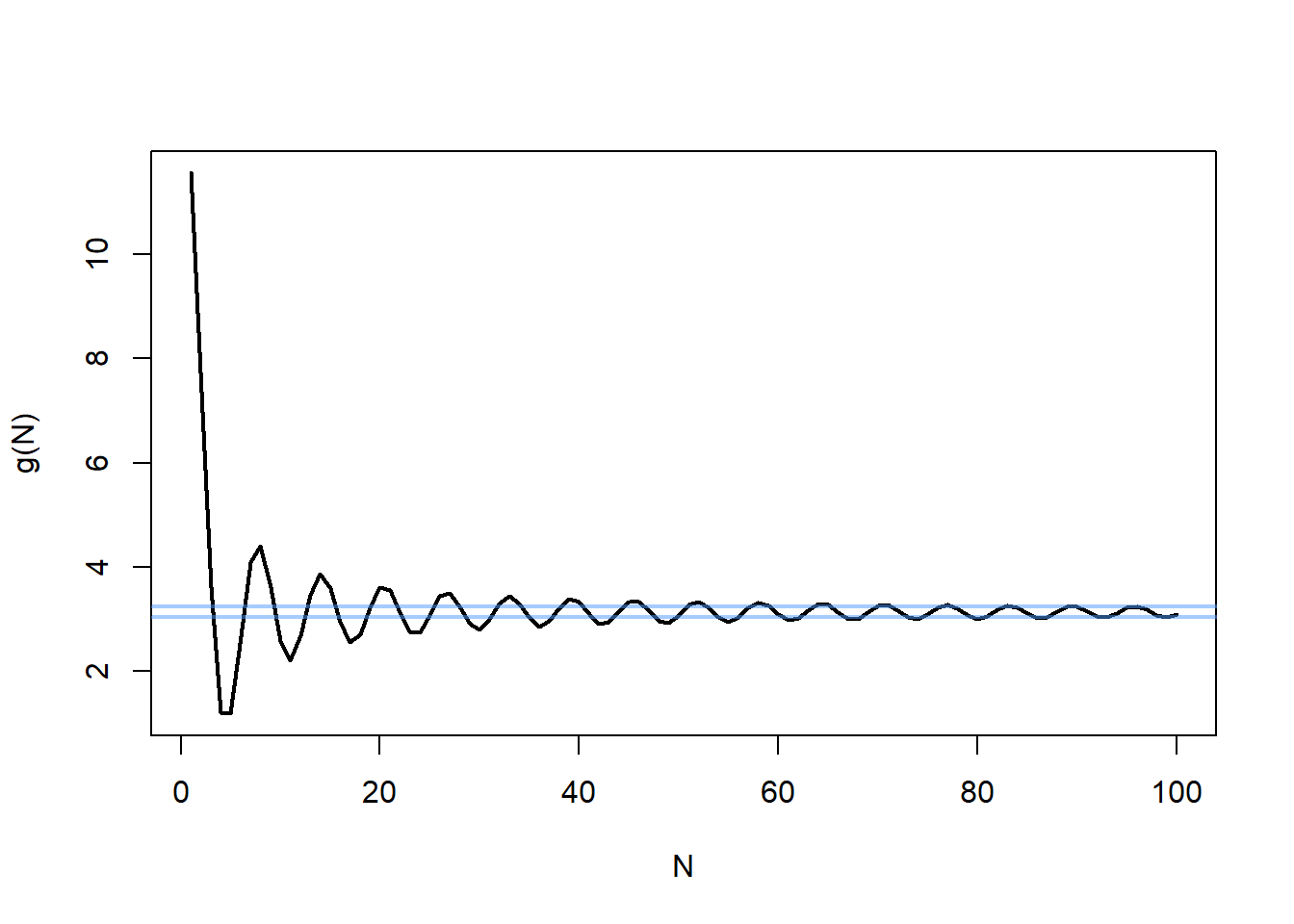

N = 100:200
plot(N, g(N), type="l", lwd=2)
e3 = .1
abline(h=pi+e3, lwd=2, col=rgb(.3,.6,1,.5))
abline(h=pi-e3, lwd=2, col=rgb(.3,.6,1,.5))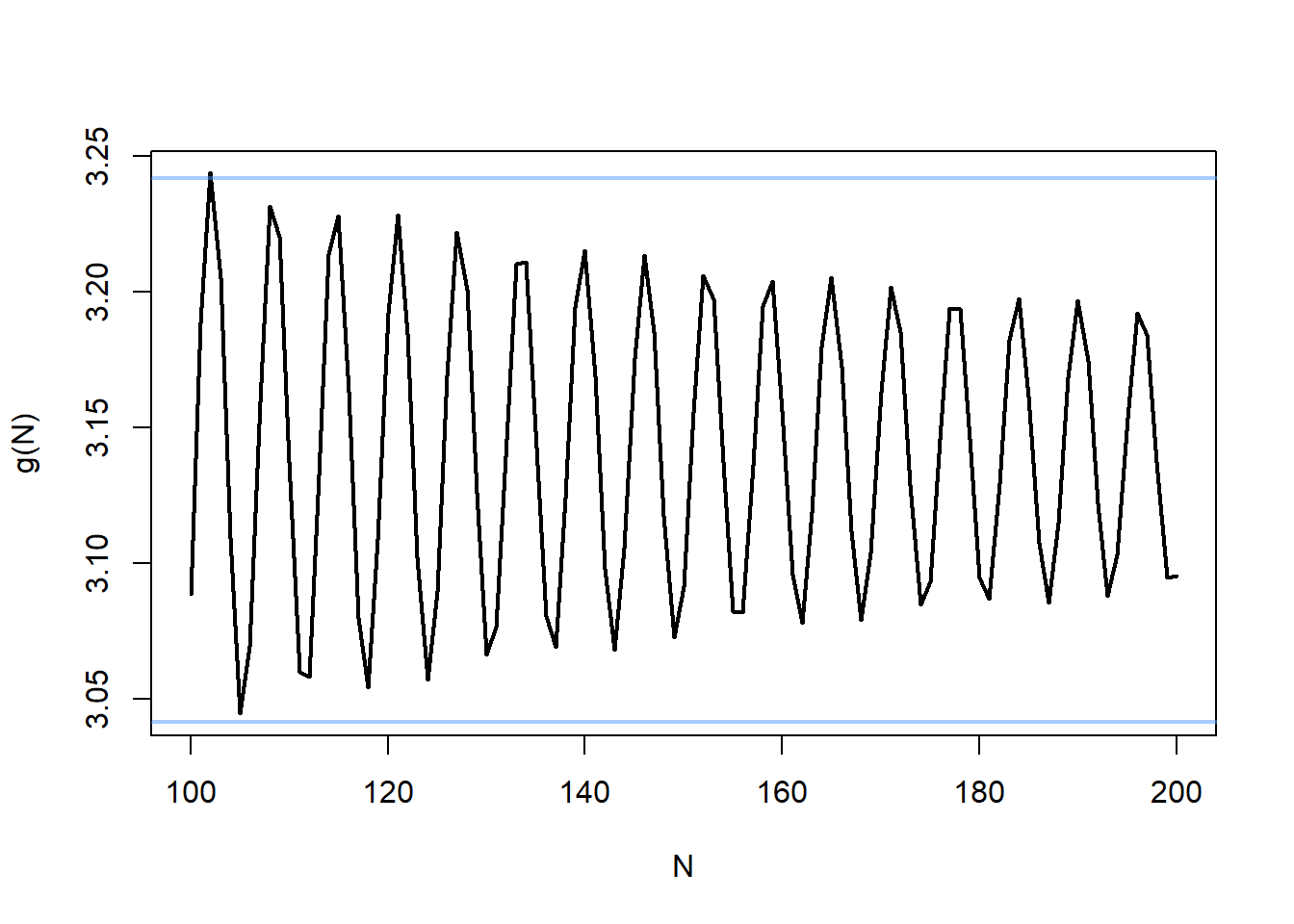

9.2 Convergência em Probabilidade e Lei Fraca dos Grandes Números

Definição Uma variável aleatória converge em probabilidade para $c$ quando $n \to \infty$, denotado por $Z_n \xrightarrow[p]{} c$ ou $plim_{n \to \infty} Z_n = c$ se para todo $\delta > 0$,

$$lim_{n \to \infty} P{|Z_n - c| \leq \delta]} = 1$$

De forma mais simples, o conceito de convergência em probabilidade se refere a uma sequência de variáveis aleatórias concentrando ao redor de um ponto na medida em que o tamanho amostral cresce.

A=matrix(NA,100,30)

for(i in 1:30){
  A[,i]=replicate(100,expr = mean(rnorm(i*10)) )
}
boxplot(A)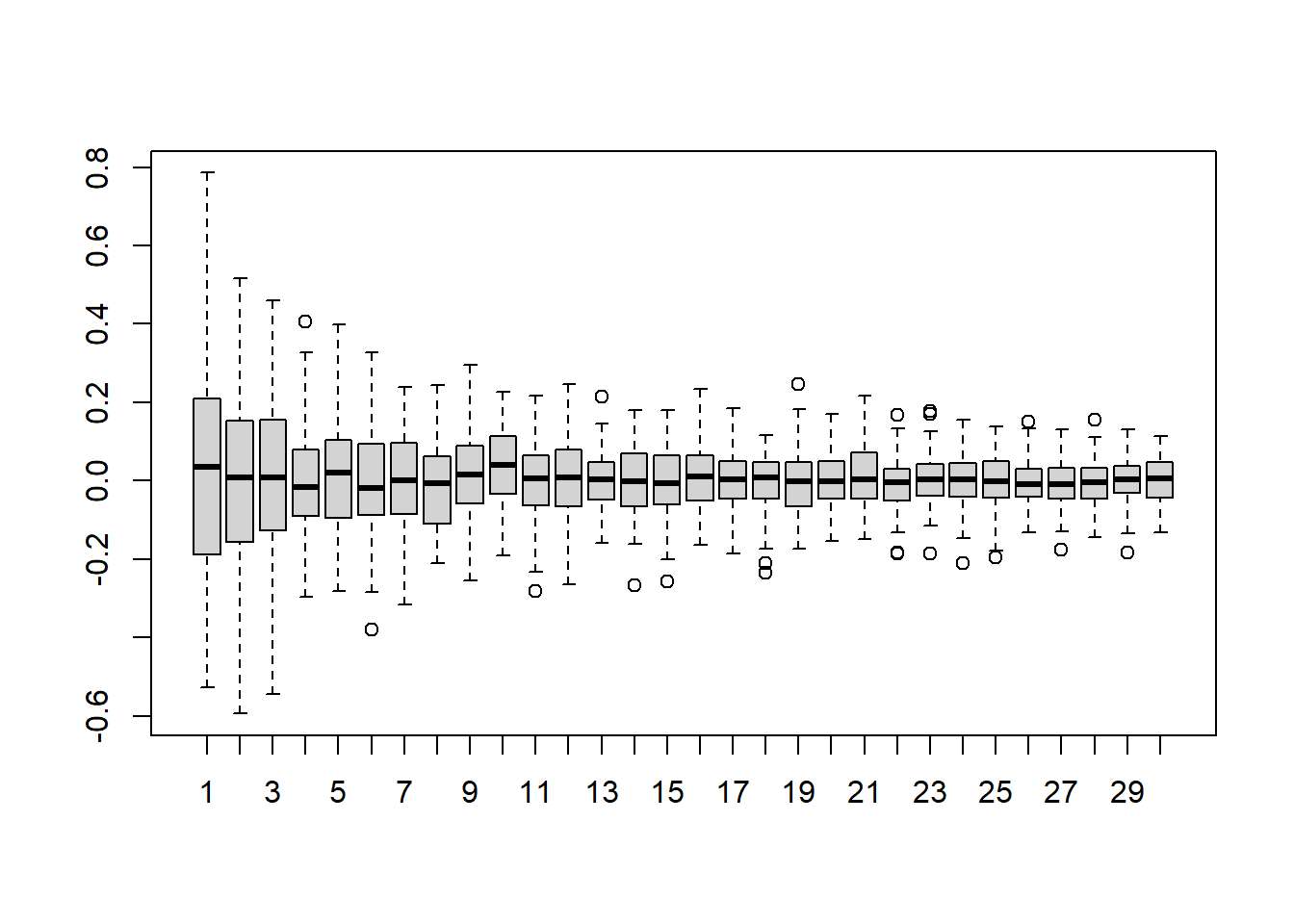

A=matrix(NA,100,30)

for(i in 1:30){
  A[,i]=replicate(100,expr = mean(rnorm(i*10,10)) )
}
boxplot(A)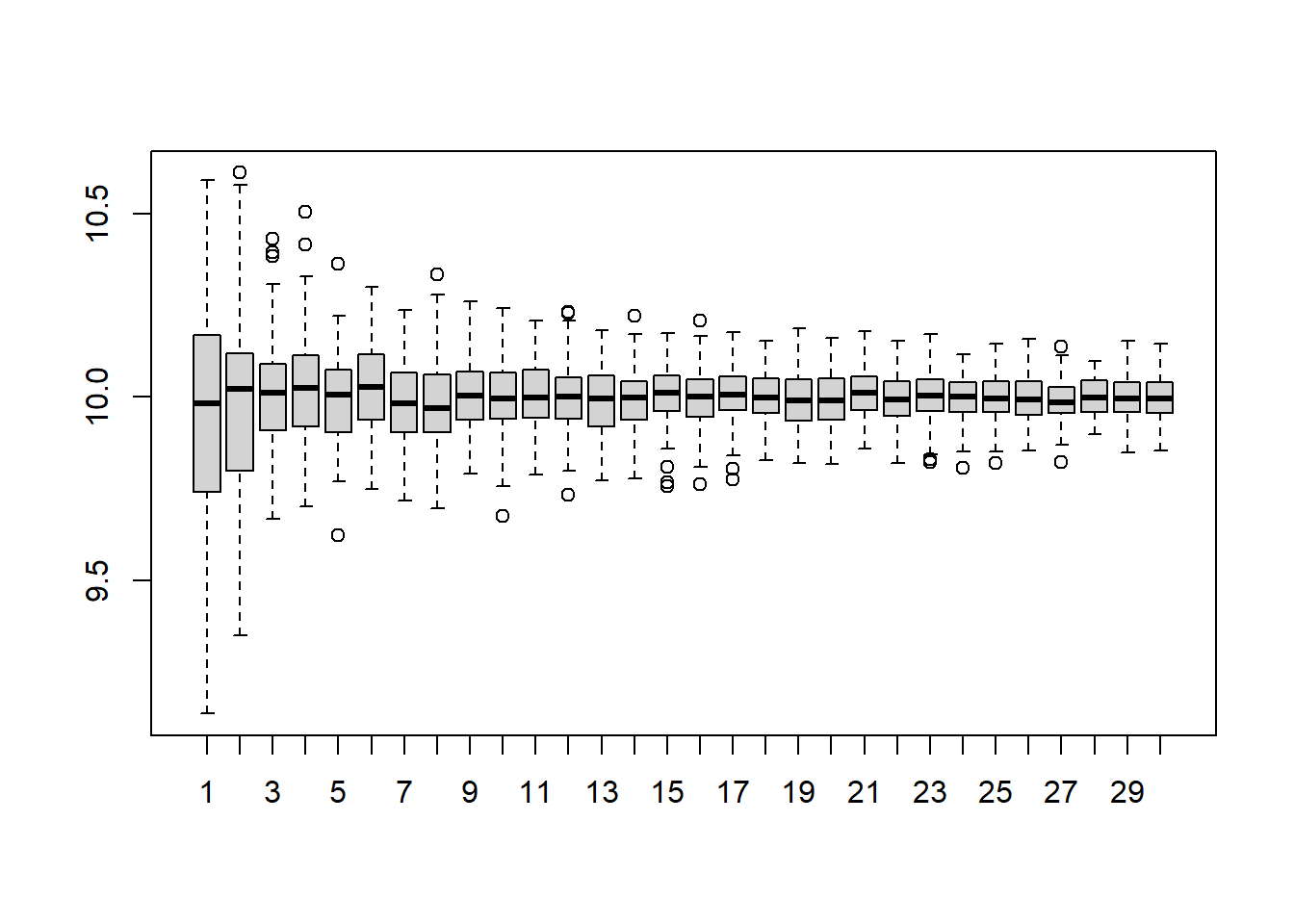

Definição A Lei Fraca dos Grandes Números: se $X_i$ é independente e identicamente distribuído e $E|X| < \infty$, então, quando $n \to \infty$

$$\bar{X_n} = \frac{1}{n} \sum_{i = 1}^n \xrightarrow[p]{} E[X]$$

Portanto, a Lei Fraca dos Grandes Números diz que a média amostral converge em probabilidade para a média populacional. Um estimador que converge em probabilidade para o verdadeiro parâmetro populacional é um estimador consistente.

par(mfrow = c(2, 2))
#loop em n
for (nn in c(5, 10, 50, 100)) {

  xbarra = replicate(n = 1000, expr = mean(runif(nn, 0, 5)))
  hist(xbarra, col="blue", breaks = 20, xlim = c(0,5), main = paste("n=",nn))
}

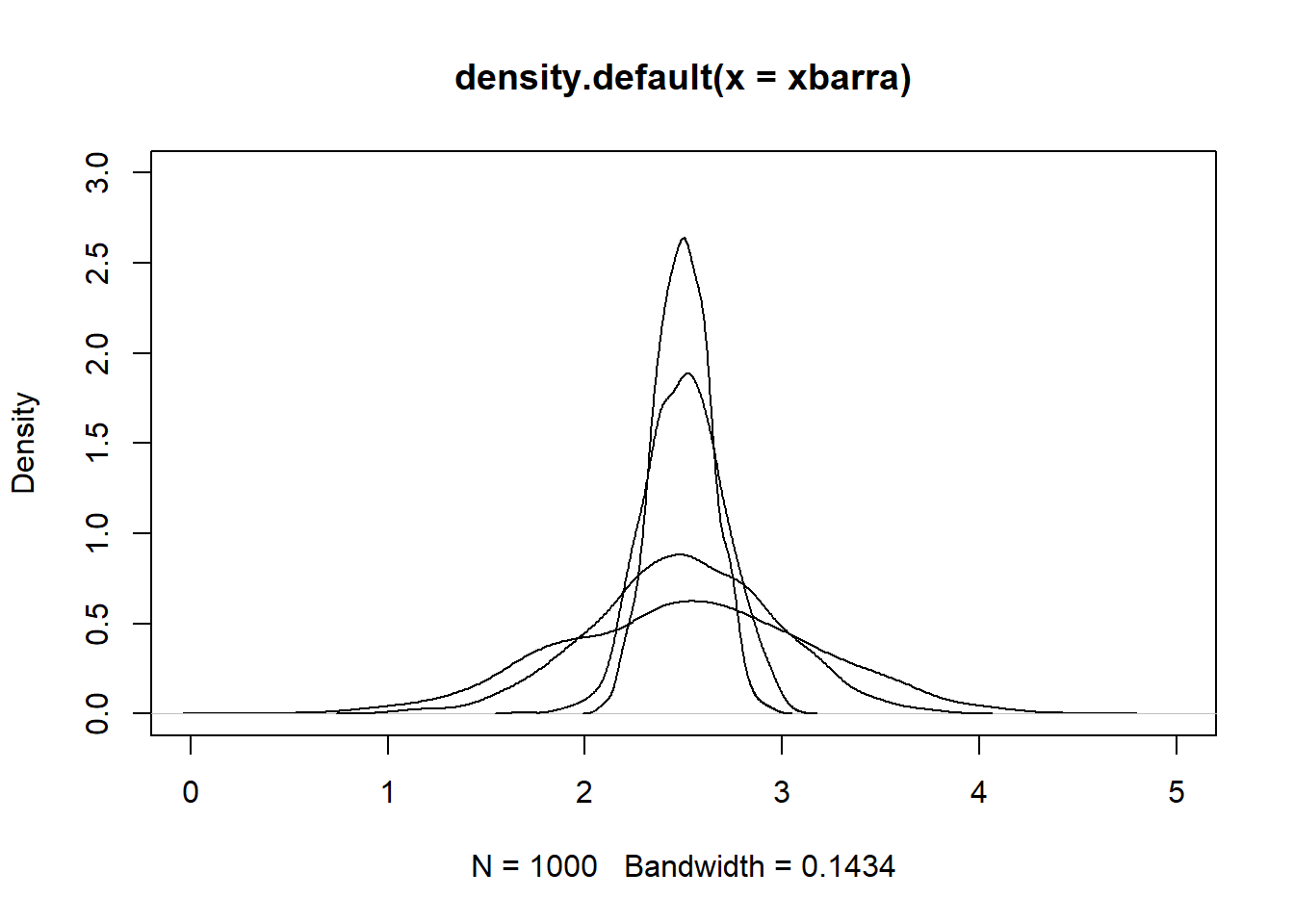
xbarra = replicate(n = 1000, expr = mean(runif(5, 0, 5)))
plot(density(xbarra), ylim=c(0,3), xlim = c(0,5))



#loop em n
for (n in c(10, 50, 100)) {
  
  xbarra = replicate(n = 1000, expr = mean(runif(n, 0, 5)))
  lines(density(xbarra))        # Draws a plot of the empirical CDF (see below)
  
}

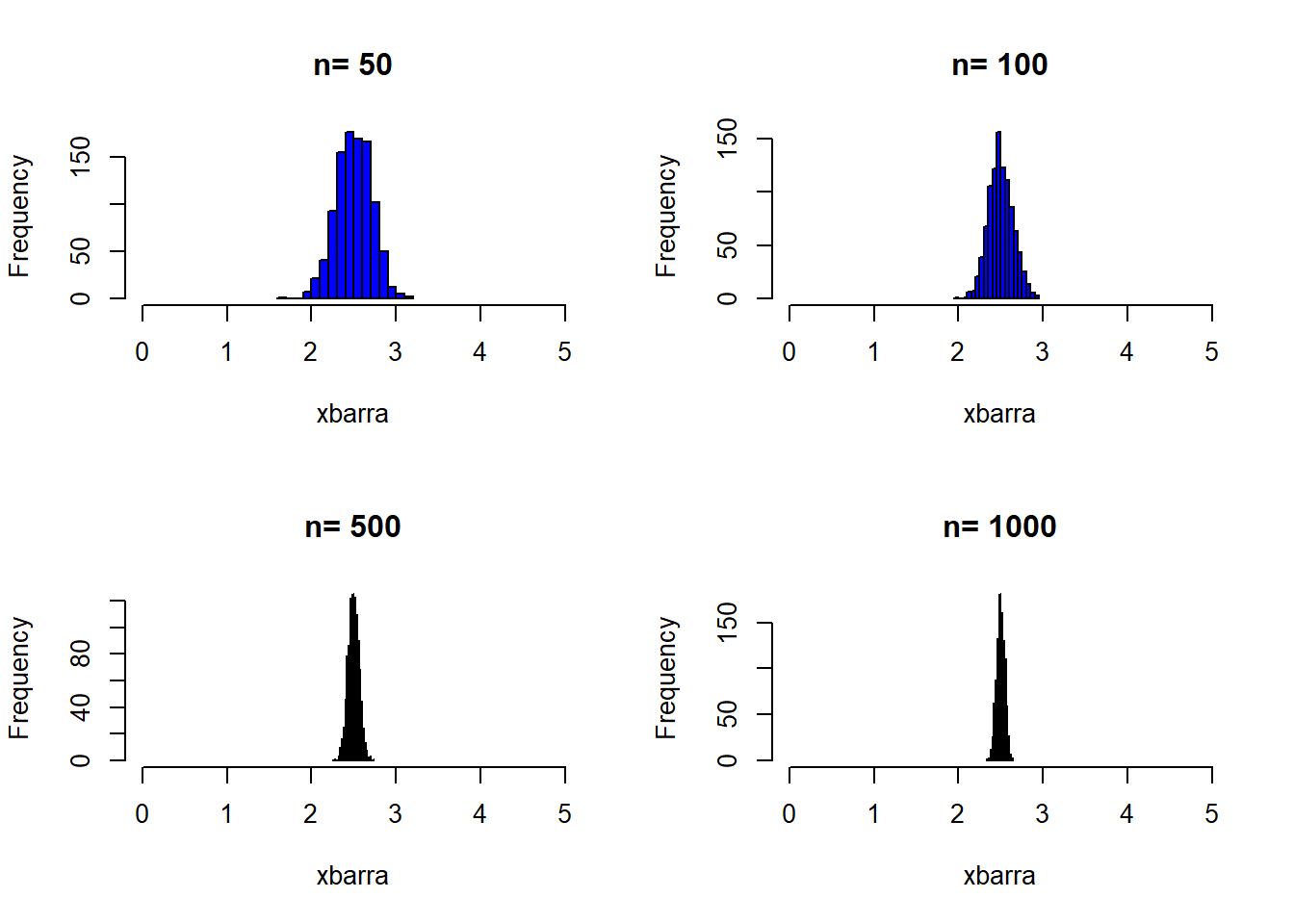
par(mfrow = c(2, 2))
#loop em n
for (nn in c(50, 100, 500, 1000)) {

  xbarra = replicate(n = 1000, expr = mean(runif(nn, 0, 5)))
  hist(xbarra, col="blue", breaks = 20, xlim = c(0,5), main = paste("n=",nn))
}

9.2.1 Viés x consistência

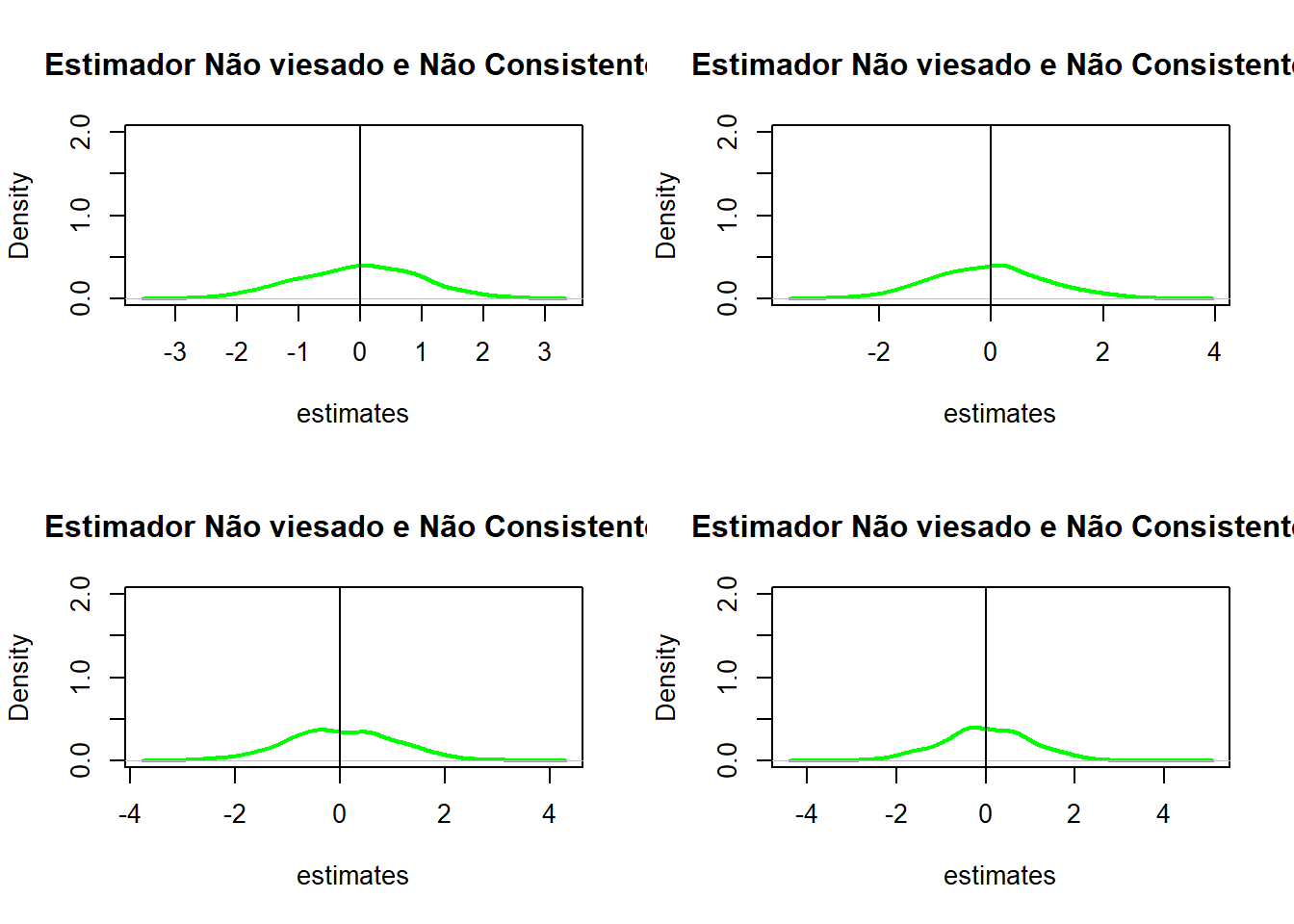
set.seed(16)


par(mfrow = c(2, 2))

pop = 1000
for (i in c(20,100,1000,10000)){
  
  fo = replicate(n = pop, expr = rnorm(i)[1])

  plot(density(fo),
       col = 'green',
       lwd = 2,
       ylim = c(0, 2),
       xlab = 'estimates',
       main = 'Estimador Não viesado e Não Consistente')
  abline(v=0)
}

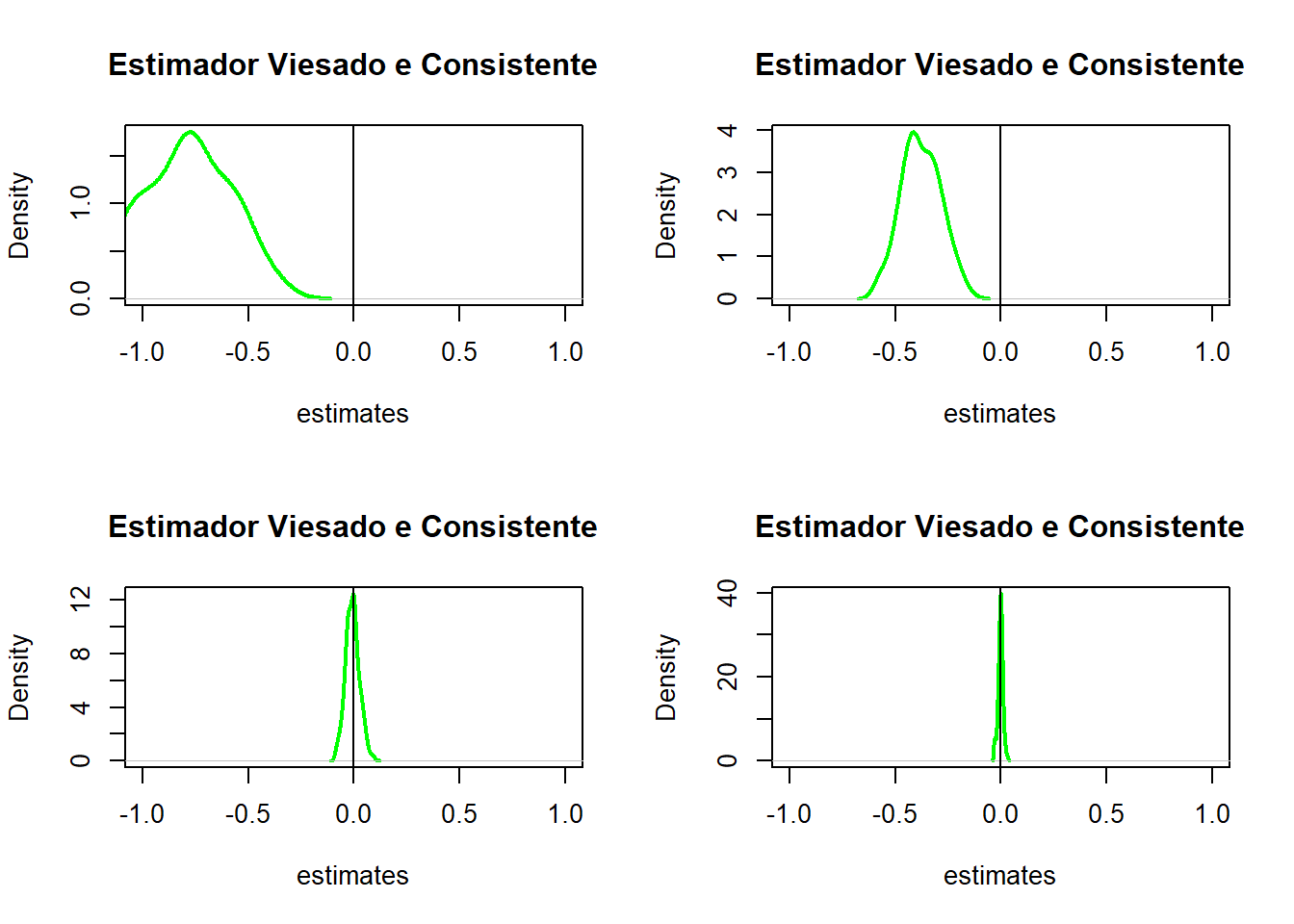
set.seed(16)
par(mfrow = c(2, 2))

pop = 100
for (i in c(20,100,1000,10000)){

  fo = replicate(n = pop, expr = mean(rnorm(i)) - 0.99^i )
  plot(density(fo),
       col = 'green',
       lwd = 2,
       xlab = 'estimates',
       xlim = c(-1,1),
       main = 'Estimador Viesado e Consistente')
  abline(v=0)
}

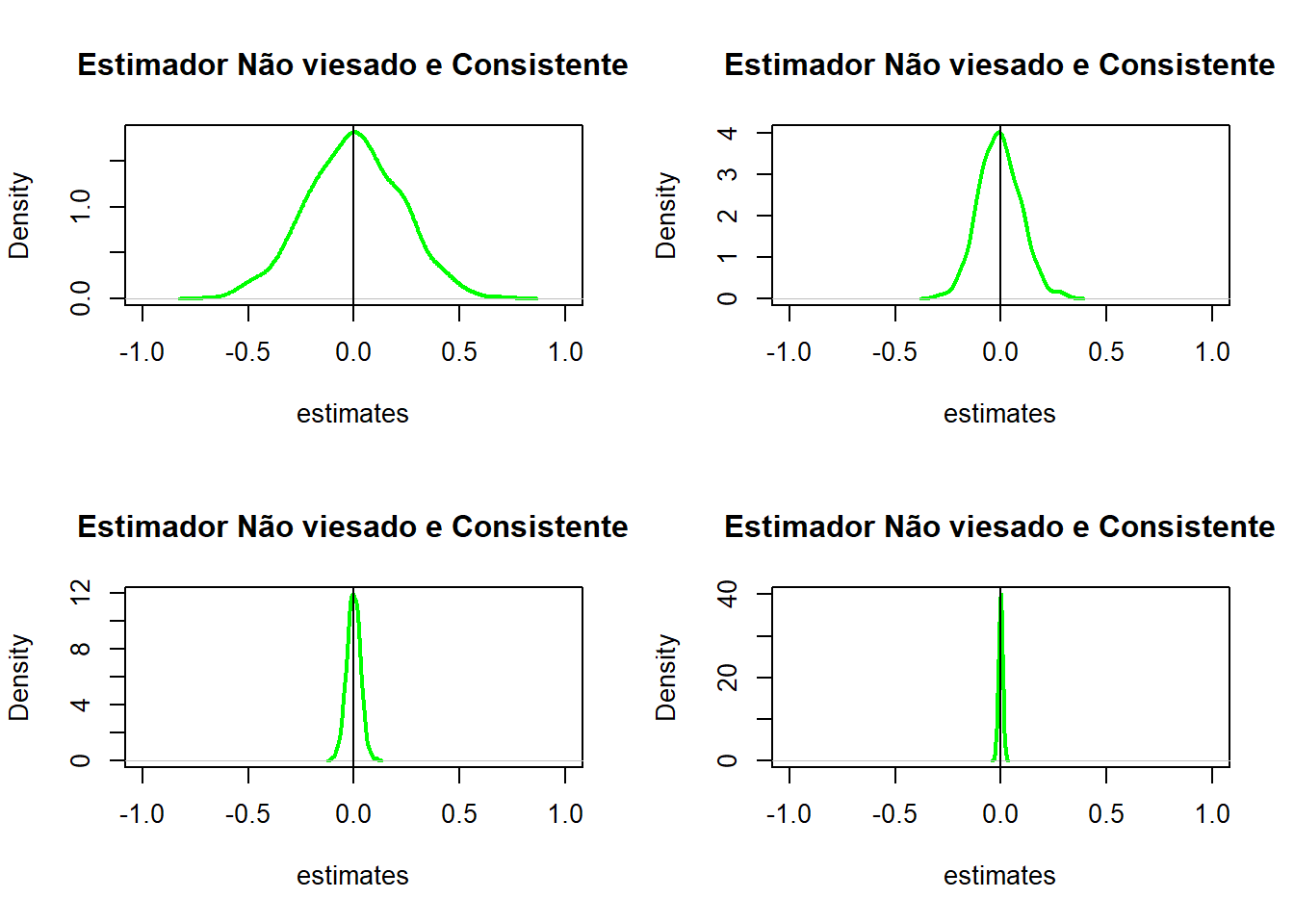
set.seed(16)
par(mfrow = c(2, 2))

pop = 1000
for (i in c(20,100,1000,10000)){
  
  fo = replicate(n = pop, expr = mean(rnorm(i)))
  
  plot(density(fo),
       col = 'green',
       lwd = 2,
       xlab = 'estimates',
       xlim = c(-1,1),
       main = 'Estimador Não viesado e Consistente')
  abline(v=0)
}

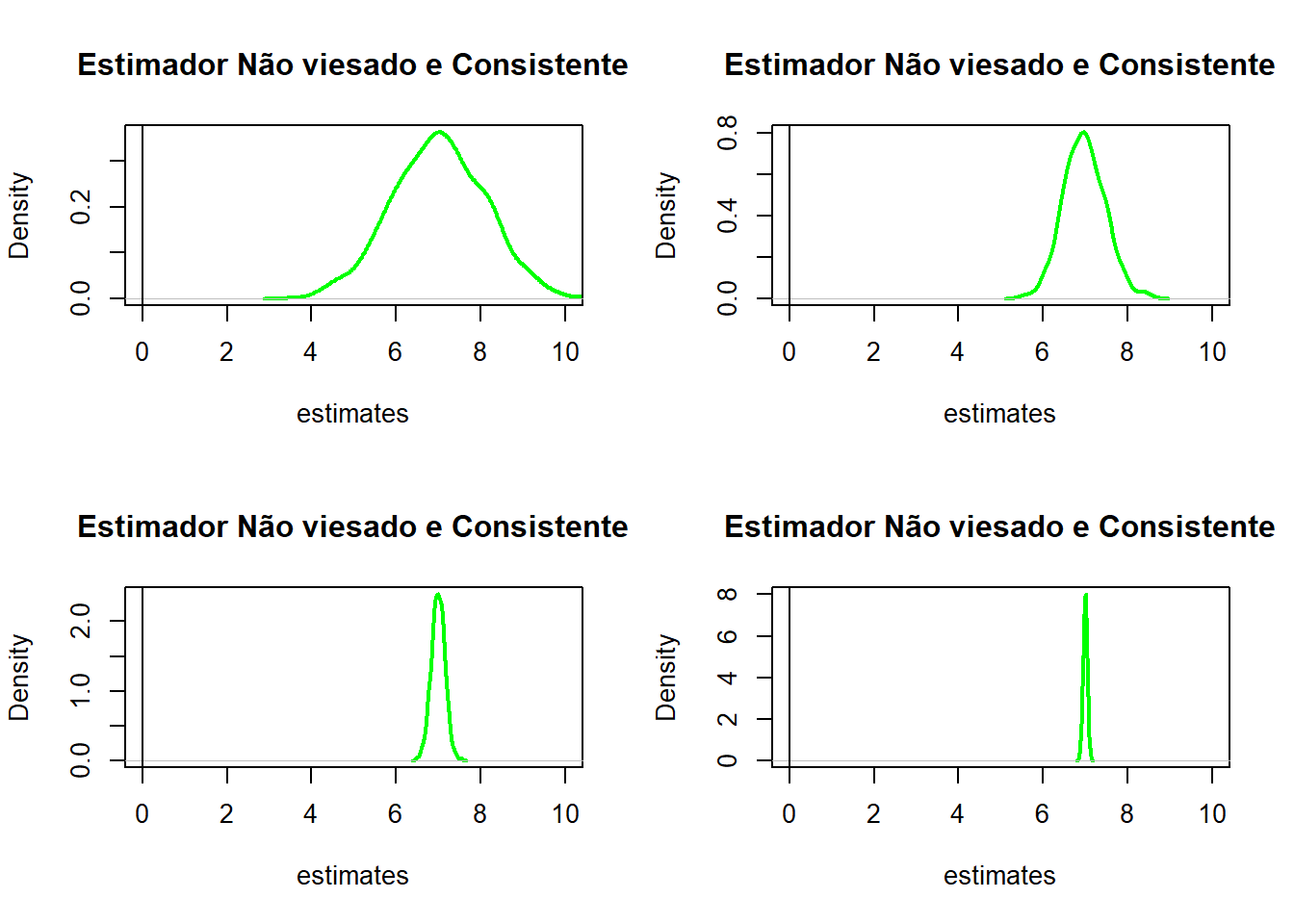
Definição: Teorema do Mapeamento Contínuo - Se $Z_n \xrightarrow[p]{} c$ quando $n \to \infty$ e $h(.)$ é contínua em $c$, então $h(Z_n) \xrightarrow[p]{} h(c)$ quando $n \to \infty$

set.seed(16)
par(mfrow = c(2, 2))

pop = 1000
for (i in c(20,100,1000,10000)){
  
x = replicate(n = pop, expr = mean(2 + 5*(rnorm(i,1))))
  
  plot(density(x),
       col = 'green',
       lwd = 2,
       xlab = 'estimates',
       xlim = c(0,10),
       main = 'Estimador Não viesado e Consistente')
  abline(v=0)
}

9.3 Convergência em Distribuição e Teorema Central do Limite

Um outro tipo de convergência importante no estudo das propriedades de um estimador é a convergência em distribuição. Vimos que a média amostral converge em probabilidade para a média populacional, mas para realizar inferência estatística é necessário conhecer o comportamento assintótico da distribuição da média amostral.

Definição Seja $Z_n$ uma variável aleatória com distribuição $G_(u) = P[Z_n \leq u]$. $Z_n$ converge em distribuição para Z quando $n \to \infty$, denotado por $Z_n \xrightarrow[d]{} Z$, se para todo $u$ em que $G(u) = P[Z \leq u]$ é contínua, $G_n(u) \to G(u)$ quando $n \to \infty$.

Média Amostral: A média amostral $\bar{X}_n$ é uma função da distribuição $F$ das observações e do tamanho amostral $n$. O objetivo é encontrar a distribuição assintótica de $\bar{X}_n$, ou seja, queremos mostrar que $\bar{X}_n \xrightarrow[d]{} Z$. Pela li dos Grandes Números sabemos que $\bar{X}_n \xrightarrow[p]{} \mu$. Desde que convergência em probabilidade para uma constante é o mesmo que convergência em distribuição, isso implica que $\bar{X}_n \xrightarrow[d]{} \mu$. No entanto, esta não é uma distribuição útil pois o limite da distribuição é degenerado. Para obter uma distribuição não degenerada precisamos reescalonar $\bar{X}_n$. Lembre que $var(\bar{X}_n - \mu) = \frac{\sigma^2}{n}$. Isso implica que $var(\sqrt{n}(\bar{X}_n - \mu)) = \sigma^2$. Portanto, esse resultado sugere uma normalização da estatística:

$$Z_N = \sqrt{n}(\bar{X}_n - \mu)$$

Feito isso, temos que $E[Z_n] = 0$ e $var(Z_n) = \sigma^2$. Portanto a média e a variância da distribuição amostral do estimador da média estão estabelecidos. Portanto, o próximo passo é encontrar a distribuição assintótica de $Z_n$.

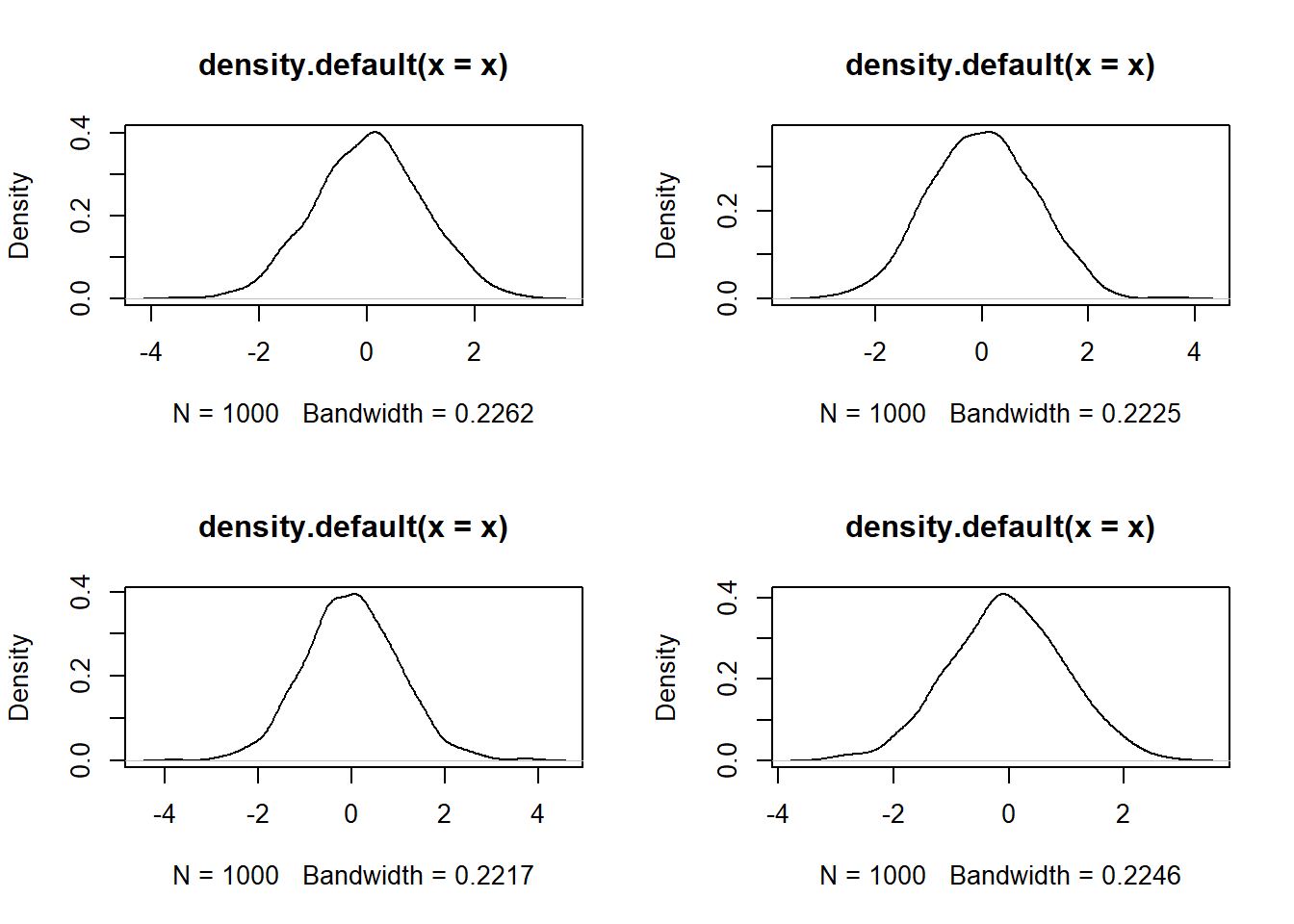
Definição Teorema Central do Limite: se $X_i$ representa uma amostra i.i.d e $E[X^2] < \infty$, então, quando $n \to \infty$

$$\sqrt{n}(\bar{X}_n - \mu) \xrightarrow[d]{} N(0,\sigma^2)$$

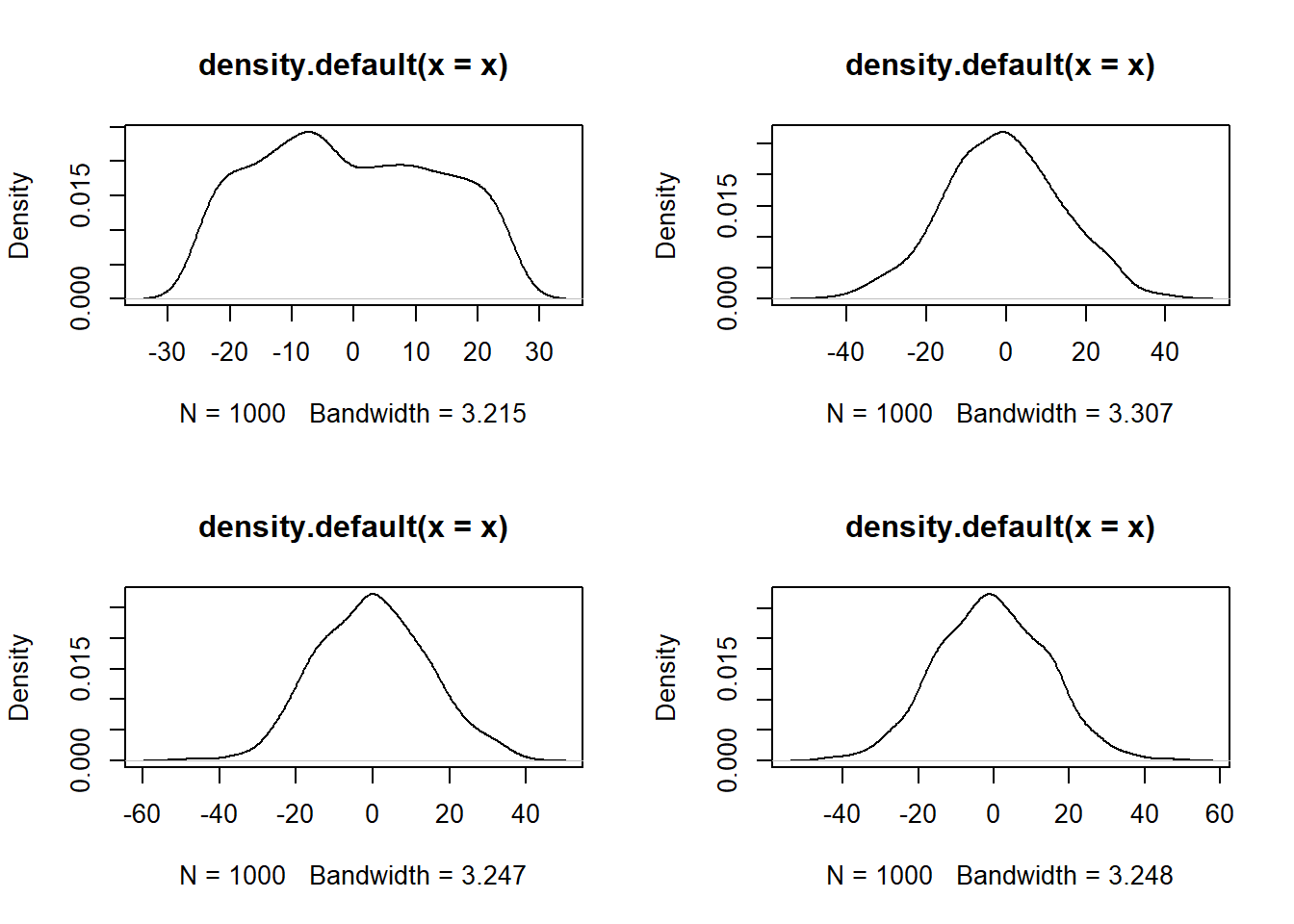
reps <- 10000
sample.sizes <- c(5, 20, 75, 100)

Distribuição Normal

par(mfrow = c(2, 2))
for (n in sample.sizes) {
  x=replicate(1000,expr = sqrt(i)*mean(rnorm(i)))
  plot(density(x))                
}

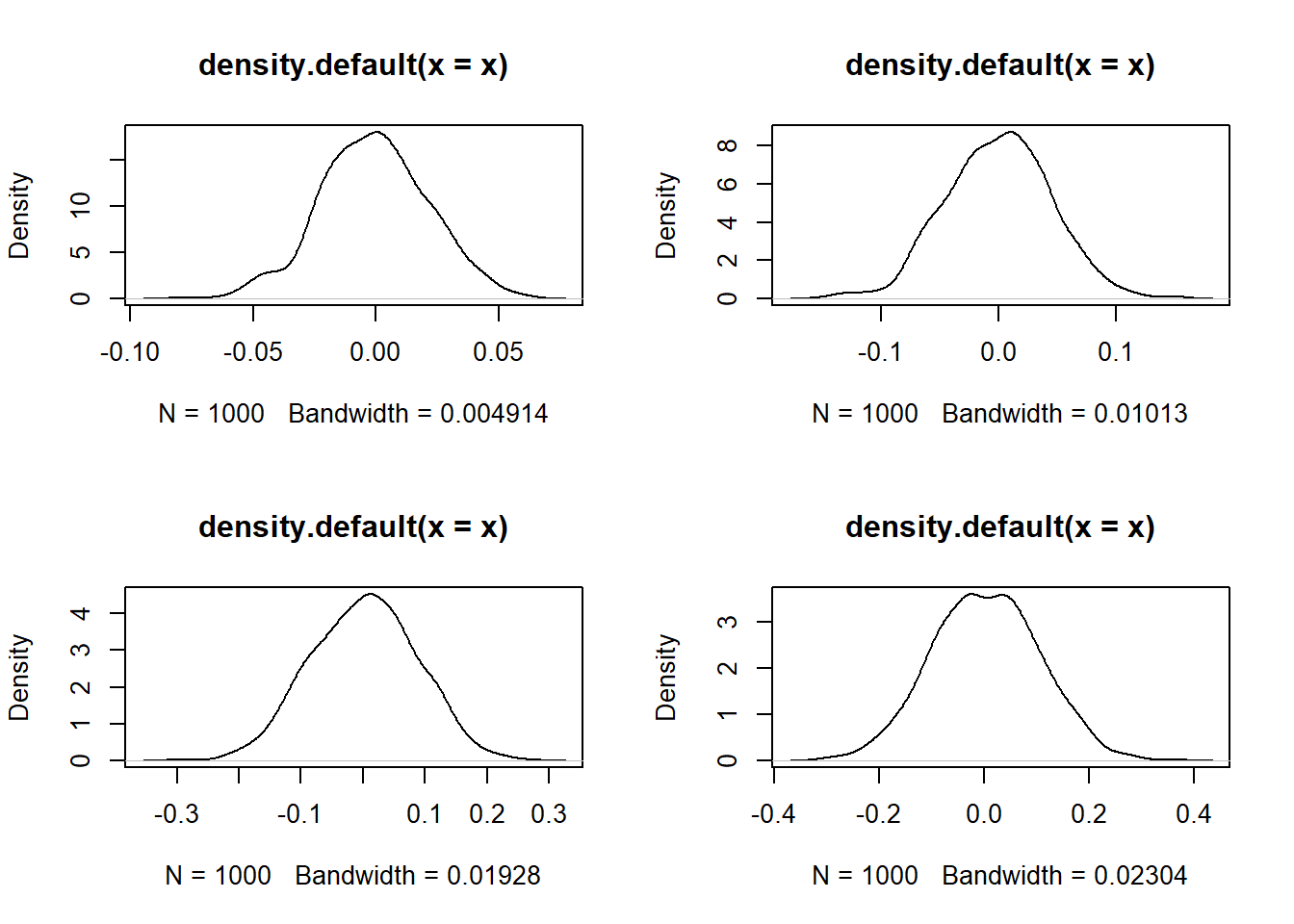
Distribuição Poison

par(mfrow = c(2, 2))
set.seed(123)
lambda = 1
for (n in sample.sizes) {
    x=replicate(1000,expr = sqrt(n)*(mean(rpois(i,lambda)-lambda)))
  plot(density(x))                

}

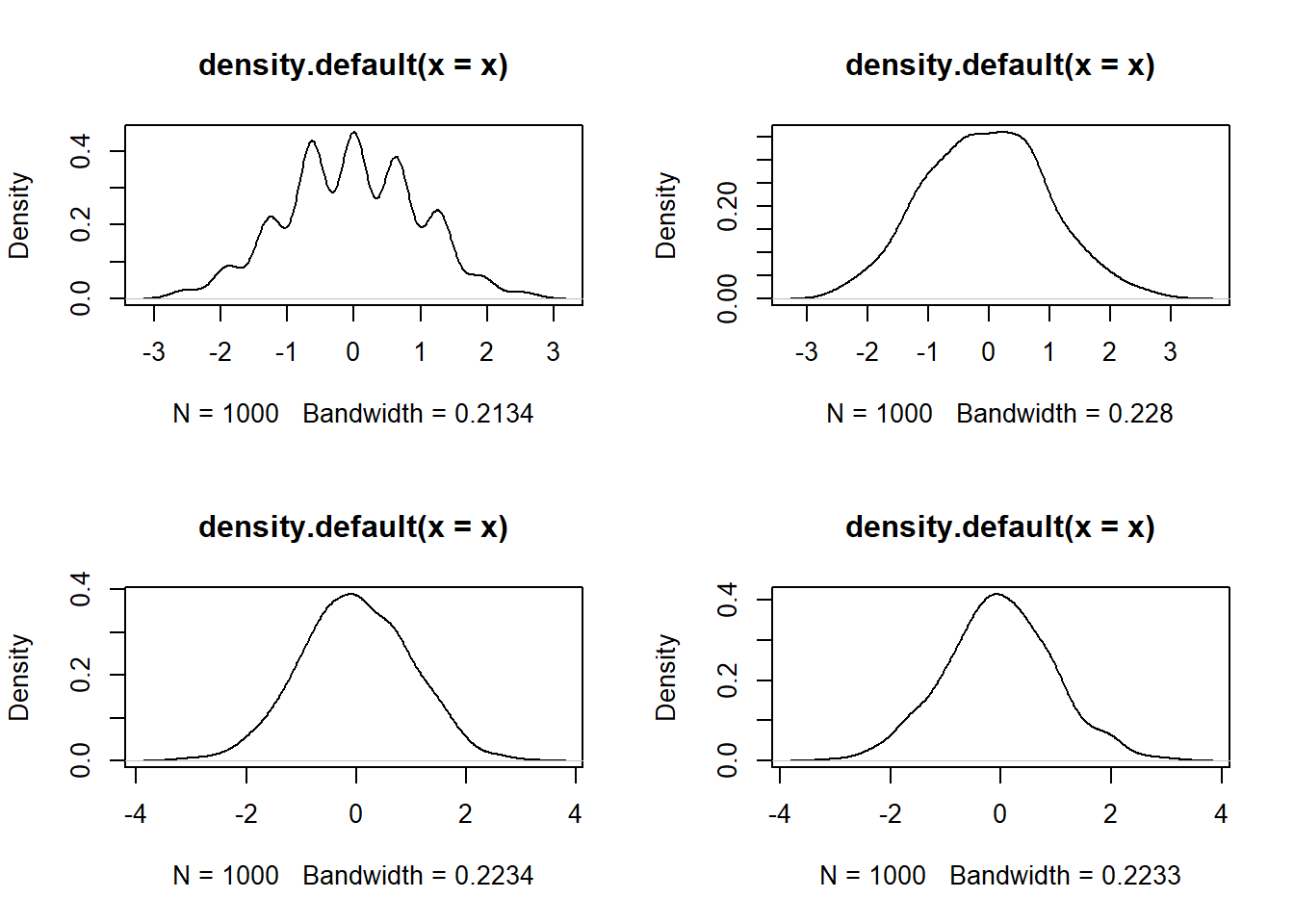
Distribuição Binomial

par(mfrow = c(2, 2))
set.seed(123)

for(i in c(10,100,500,1000)){
  x=replicate(1000,expr = sqrt(i)*(mean(rbinom(i,1,0.5)-0.5)/0.5))
  plot(density(x))                
}  

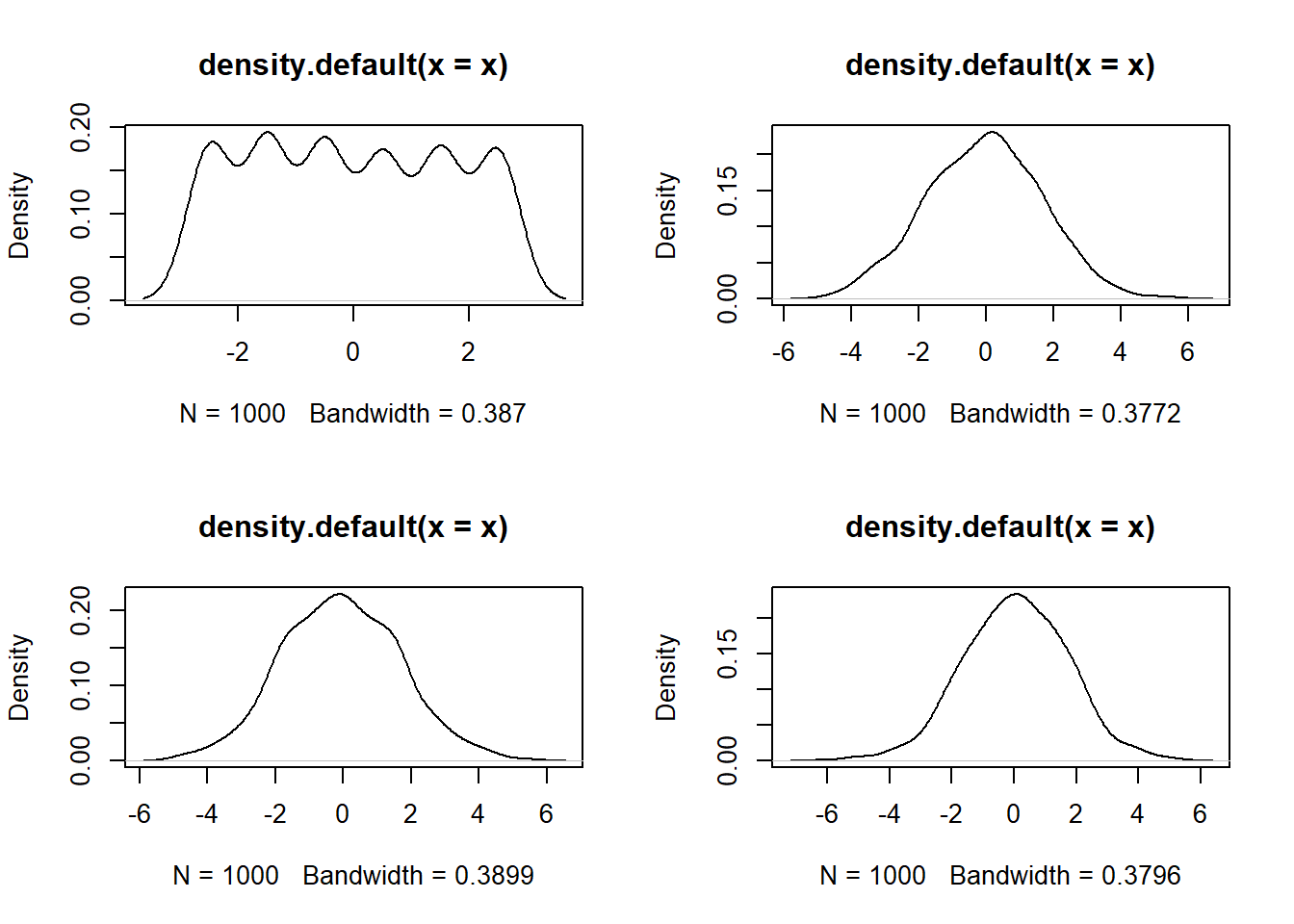
Distribuição Uniforme

par(mfrow = c(2, 2))

set.seed(123)

par(mfrow = c(2, 2))
for(i in c(1,5,10,50)){
  x=replicate(1000,expr = sqrt(i)*(mean(sample(1:6,i,replace = TRUE)-3.5)))
  plot(density(x))                
}

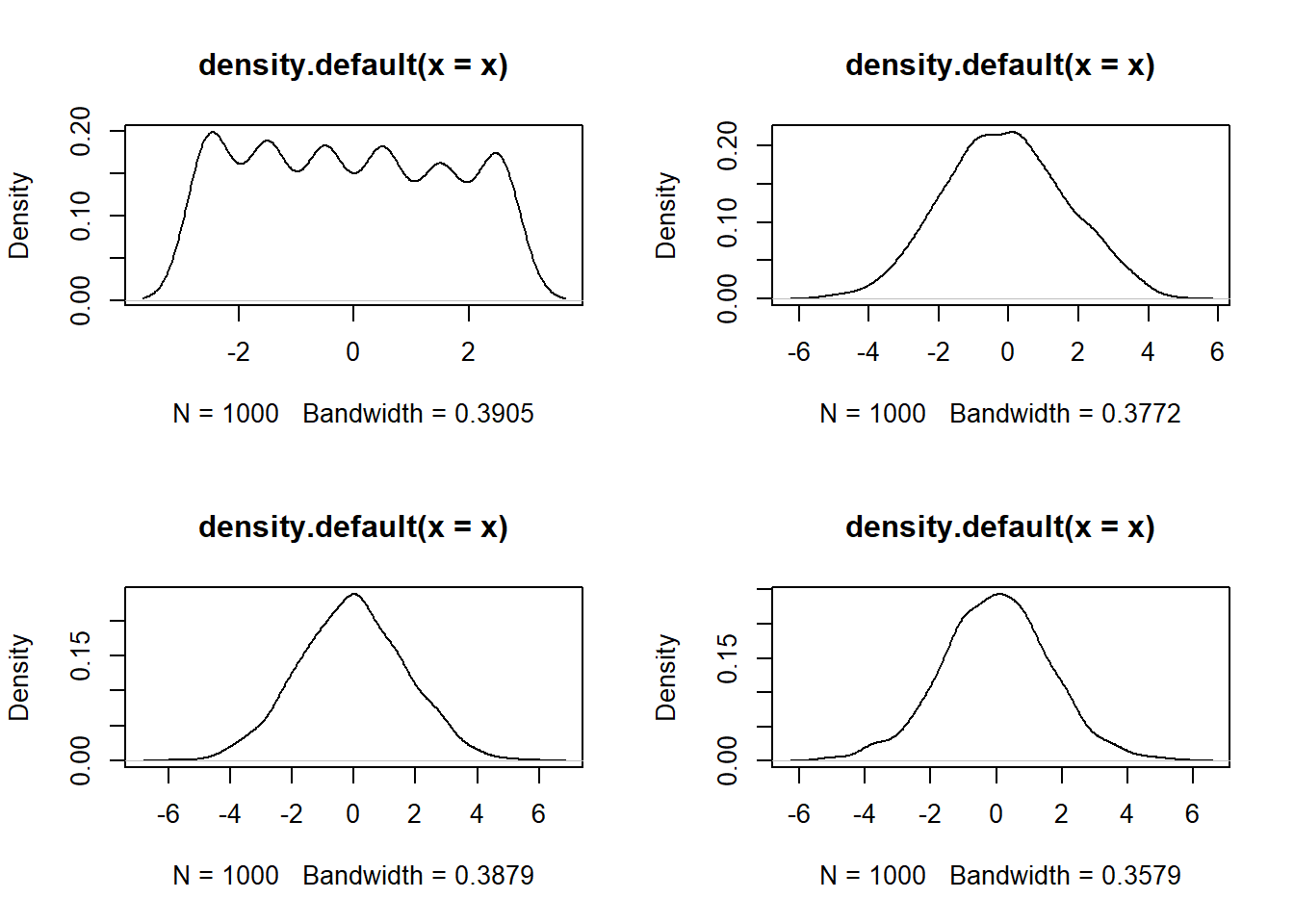
Jogar um dado

par(mfrow = c(2, 2))
for(i in c(1,5,10,50)){
  x=replicate(1000,expr = sqrt(i)*(mean(sample(1:6,i,replace = TRUE)-3.5)))
  plot(density(x))                
}

Distribuição Uniforme discreta

par(mfrow = c(2, 2))
for(i in c(1,5,10,50)){
  x=replicate(1000,expr = sqrt(i)*(mean(sample(1:50,i,replace = TRUE)-25.5)))
  plot(density(x))                
}