Capítulo 11 Teoria Assintotica dos Estimadores de MQO

11.1 Consistência de MQO

f = function(n){
  x1 = rnorm(n,10,15)
  e = rnorm(n,0,50)
  y = 10 + 5*x1 + e
  X = cbind(1,x1)
  beta = solve(t(X)%*%X)%*%t(X)%*%y
  beta
}

f(10)

##        [,1]
##    3.562267
## x1 4.865959

for (i in c(5,50,100,1000)){
  x = replicate(n = 100, expr = f(i))
  print(mean(x[2, 1, ]))
}

## [1] 4.927486
## [1] 4.943381
## [1] 5.021904
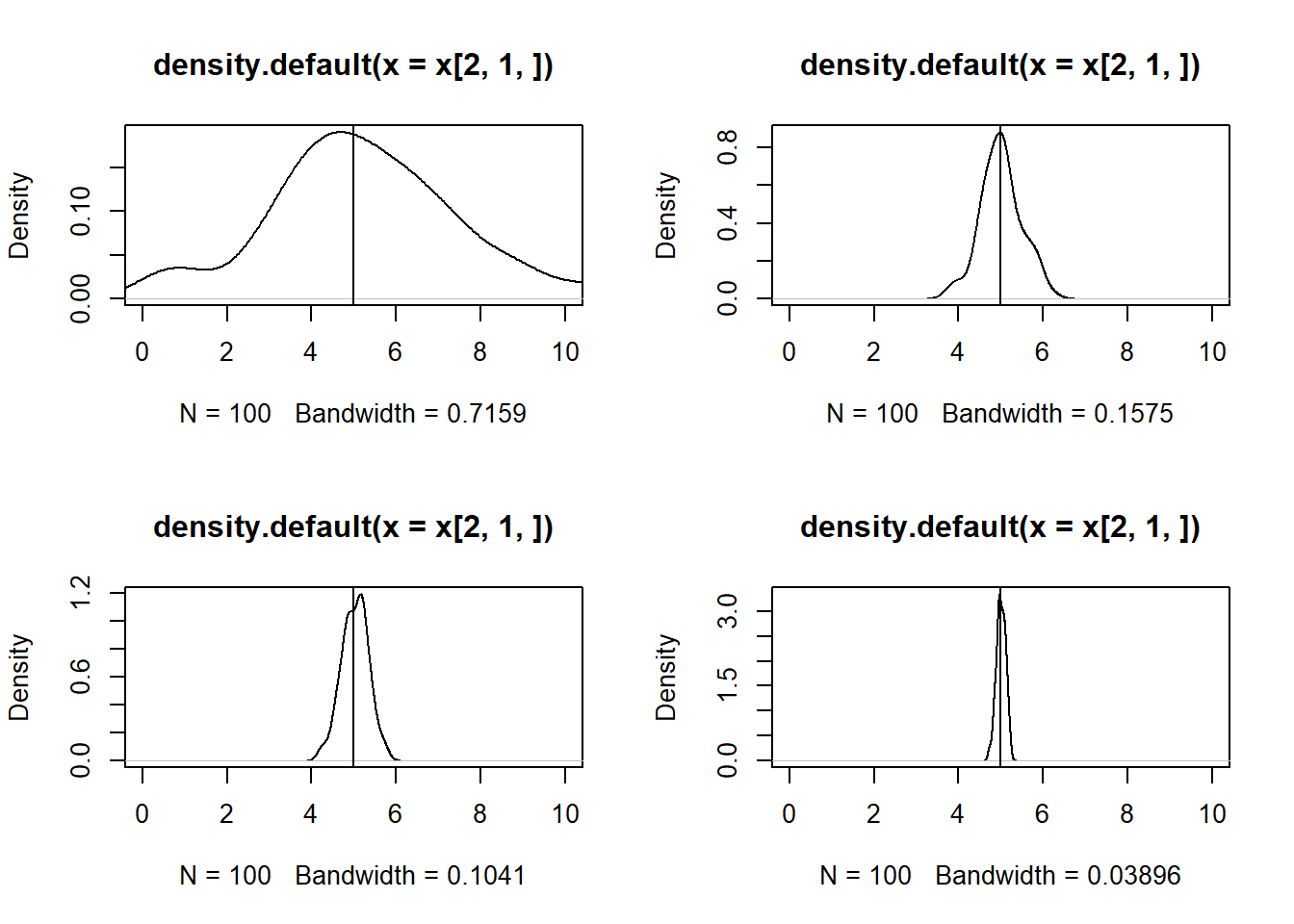
## [1] 4.993664

par(mfrow = c(2, 2))
for (i in c(5,50,100,1000)){
  x = replicate(n = 100, expr = f(i))
  plot(density( x[2, 1, ]), xlim = c(0,10))
  abline(v=5)
 }

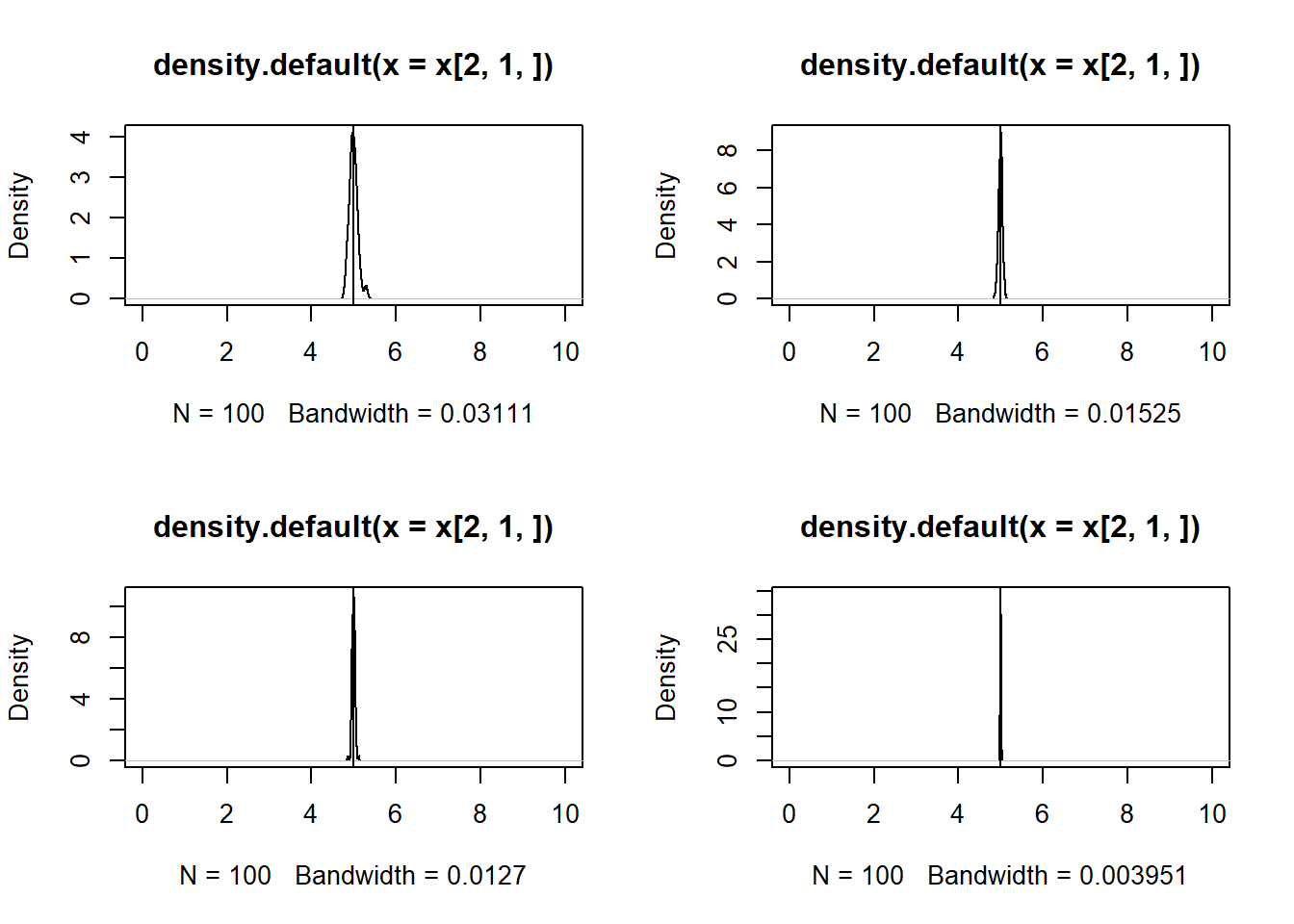
par(mfrow = c(2, 2))
for (i in c(1000,5000,10000,100000)){
  x = replicate(n = 100, expr = f(i))
  plot(density( x[2, 1, ]), xlim = c(0,10))
  abline(v=5)
 }

11.2 Normalidade Assintótica

Distribuição Uniforme

Mostrar a distribuição do termo de erro

N = 10000
beta = 5

n = 1000
x = runif(n, min = 0, max = 100)
e = runif(n = n, min = -10, max = 10)
X = cbind(1,x)
y = 10 + beta * x + e
B = solve(t(X)%*%X)%*%t(X)%*%y
e_hat = y - X%*%B

hist(e_hat)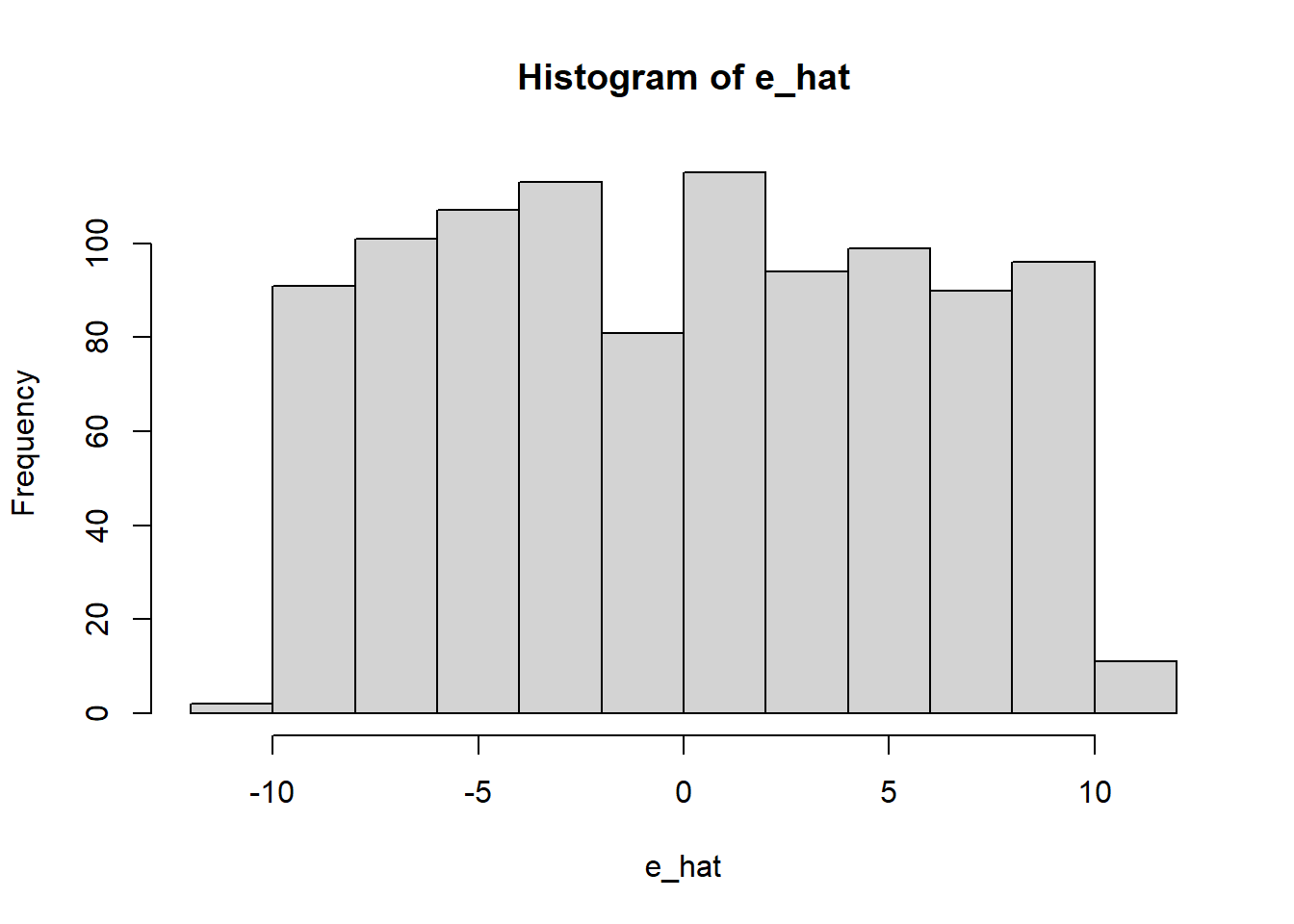

f = function(n){
  x = runif(n, min = 0, max = 100)
  e = runif(n = n, min = -10, max = 10)
  X = cbind(1,x)
  y = 10 + beta * x + e
  B = solve(t(X)%*%X)%*%t(X)%*%y
  B
}

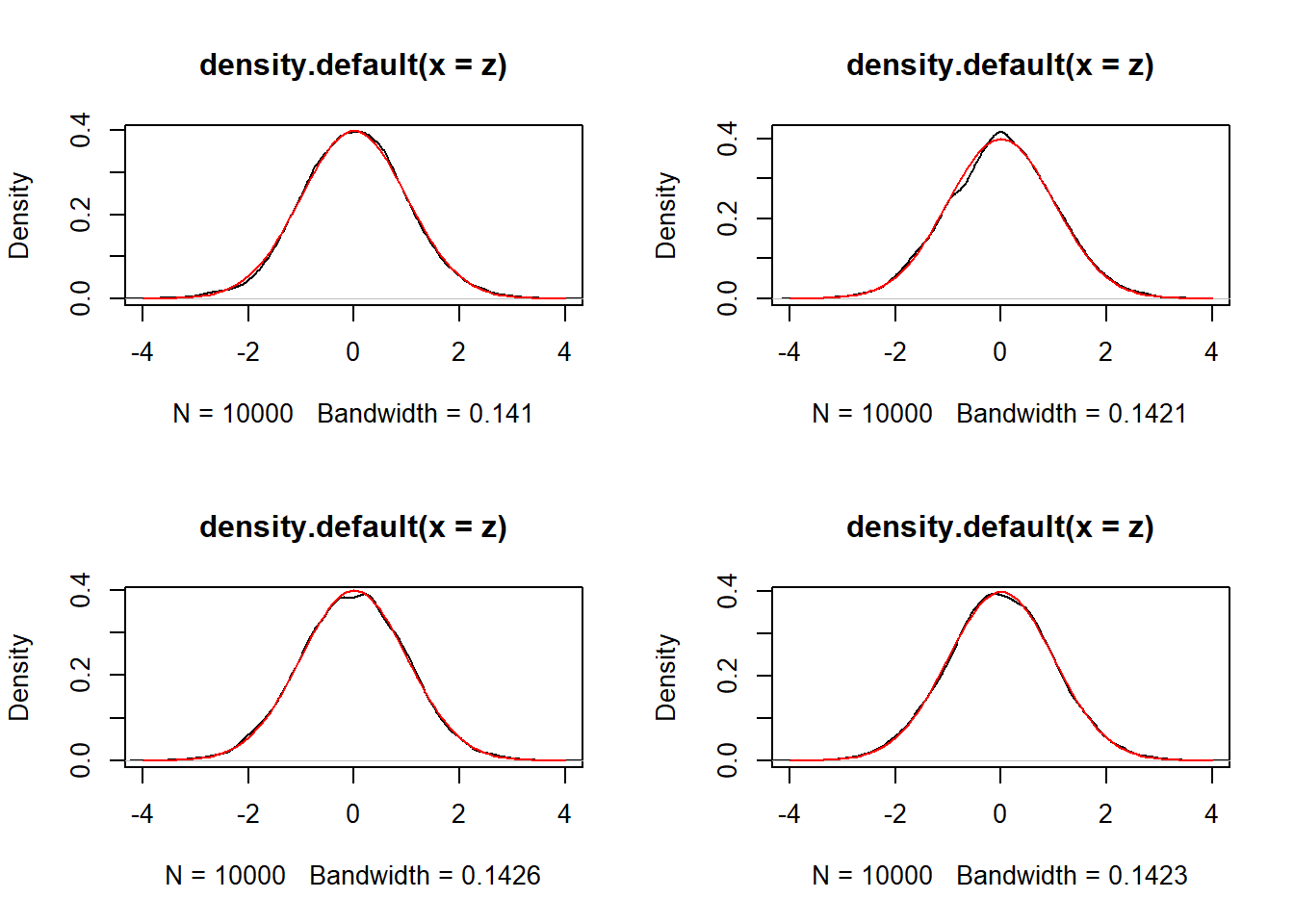
par(mfrow = c(2, 2))
for (i in c(10,50,100,1000)){
  x = replicate(n = N, expr = f(i))
  var = (var(x[2,1,]) * i)
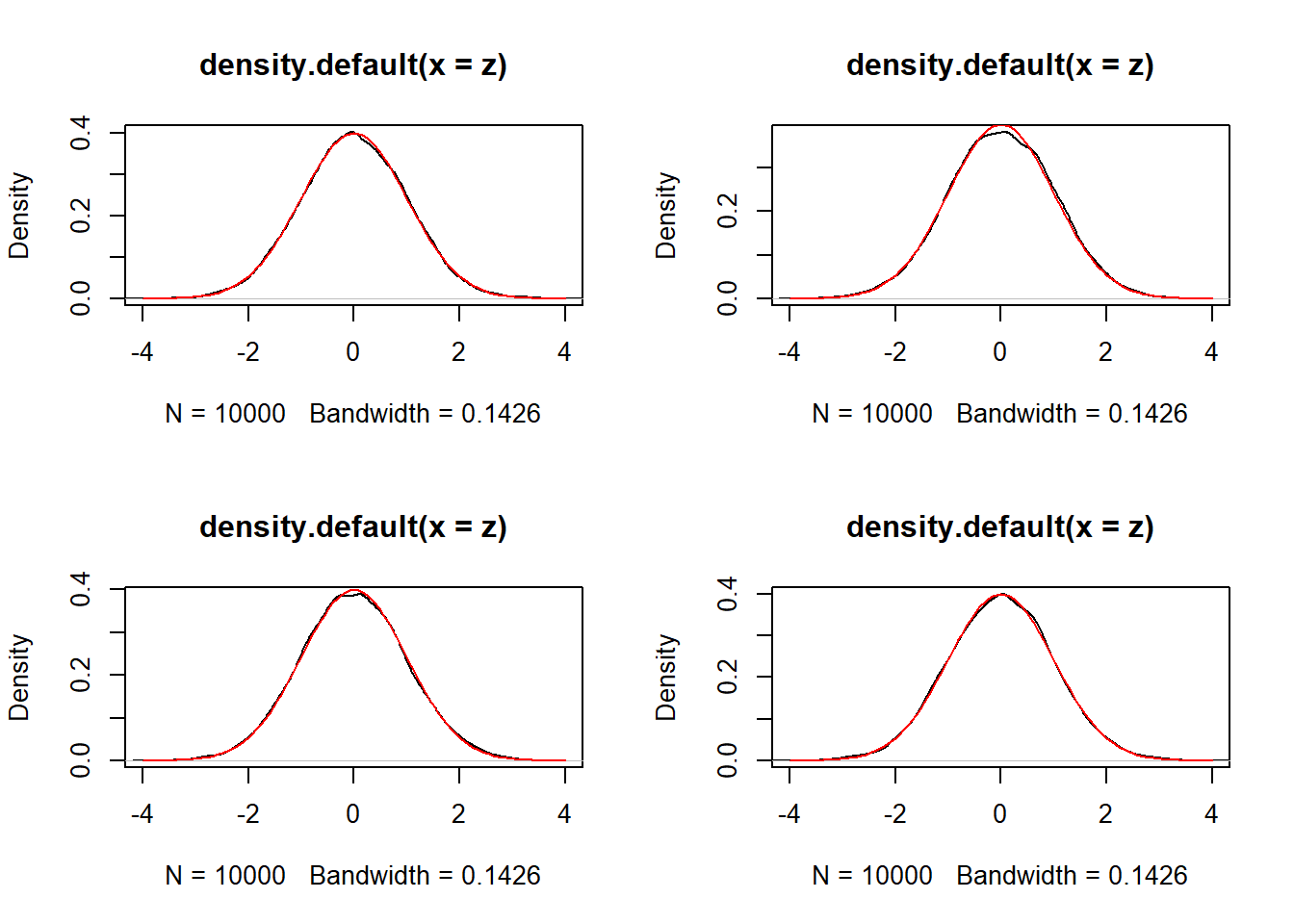
  z = sqrt(i) *( (x[2, 1, ] - beta)) / sqrt(var)
  plot(density(z), xlim = c(-4,4))
  curve(dnorm(x,0,1), col = "red", xlim = c(-4,4), add = TRUE)
}

Distribuição Poison

Mostrar a distribuição do termo de erro

N = 10000
beta = 5

n = 1000
x = runif(n, min = 0, max = 100)
e = rpois(n = n, lambda = 1 ) - 1
X = cbind(1,x)
y = 10 + beta * x + e
B = solve(t(X)%*%X)%*%t(X)%*%y
e_hat = y - X%*%B

hist(e_hat)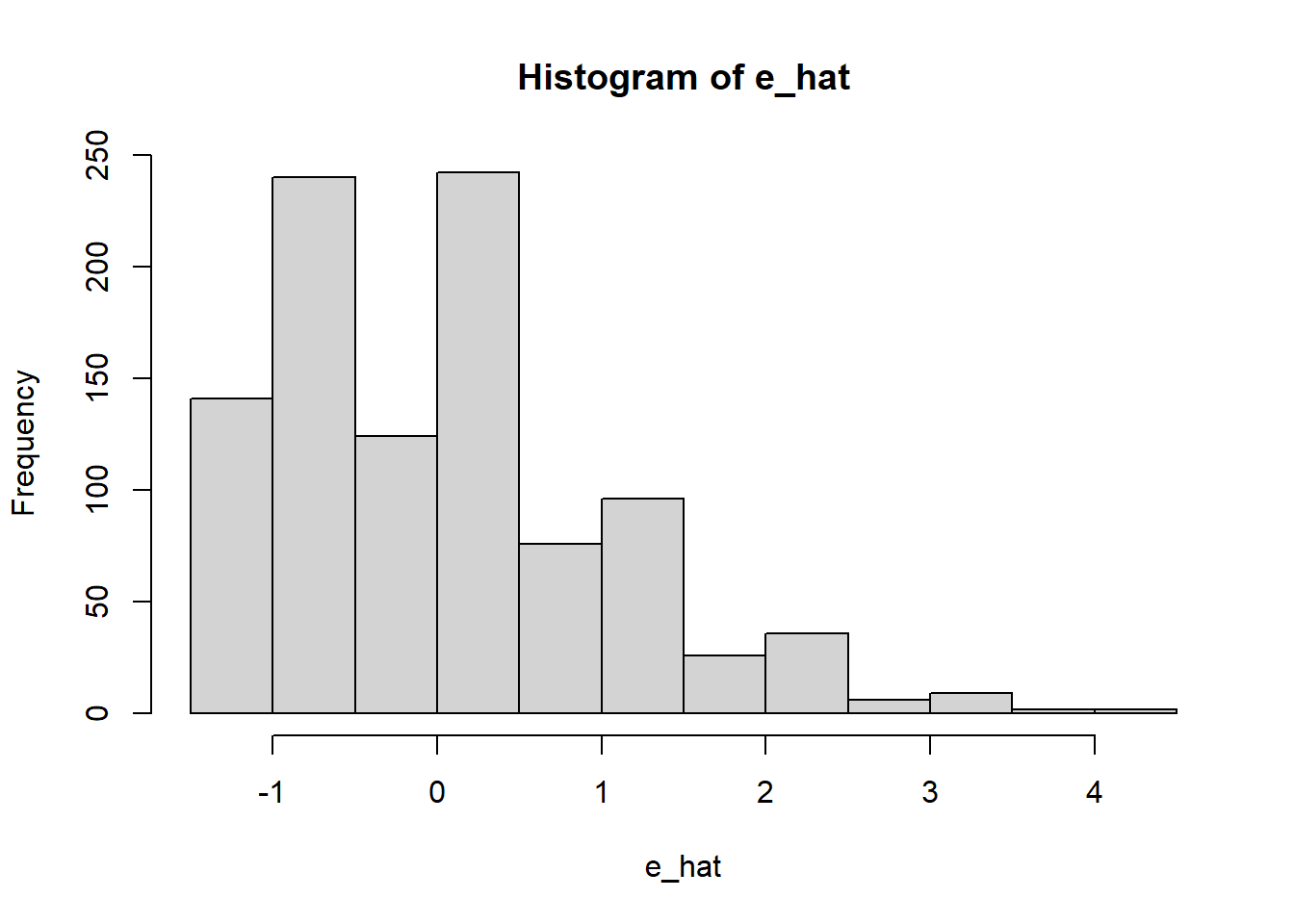

f = function(n){
  x = runif(n, min = 0, max = 100)
e = rpois(n = n, lambda = 1 ) - 1
  X = cbind(1,x)
  y = 10 + beta * x + e
  B = solve(t(X)%*%X)%*%t(X)%*%y
  B
}

par(mfrow = c(2, 2))
for (i in c(10,50,100,1000)){
  x = replicate(n = N, expr = f(i))
  var = (var(x[2,1,]) * i)
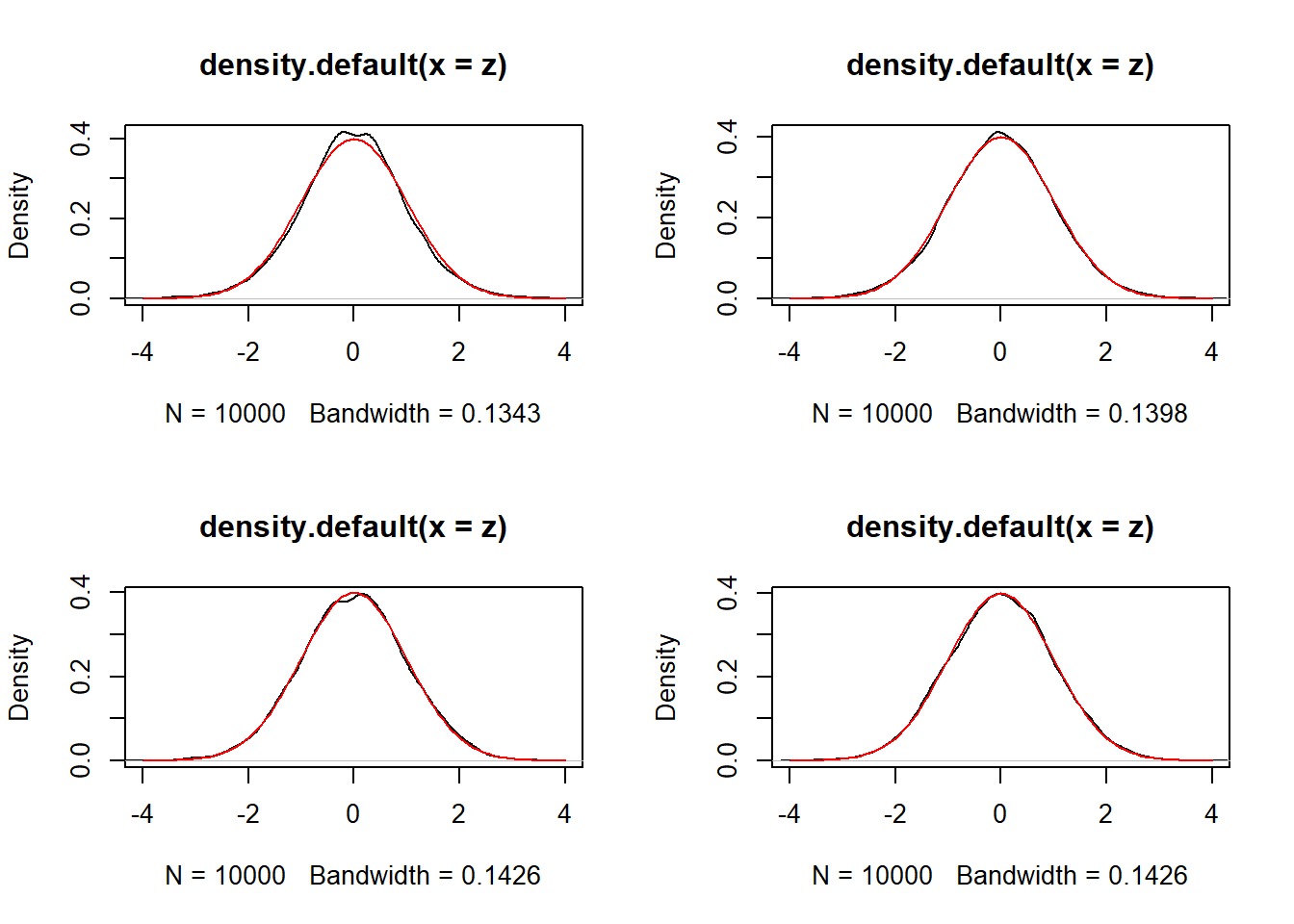
  z = sqrt(i) *( (x[2, 1, ] - beta)) / sqrt(var)
  plot(density(z), xlim = c(-4,4))
  curve(dnorm(x,0,1), col = "red", xlim = c(-4,4), add = TRUE)
}

Distribuição Binomial

Mostrar a distribuição do termo de erro

N = 10000
beta = 5

n = 1000
x = runif(n, min = 0, max = 100)
e = rbinom(n = n, size = 5, prob = 0.5 ) - ((5*0.5)/1-0.5)
X = cbind(1,x)
y = 10 + beta * x + e
B = solve(t(X)%*%X)%*%t(X)%*%y
e_hat = y - X%*%B

hist(e_hat)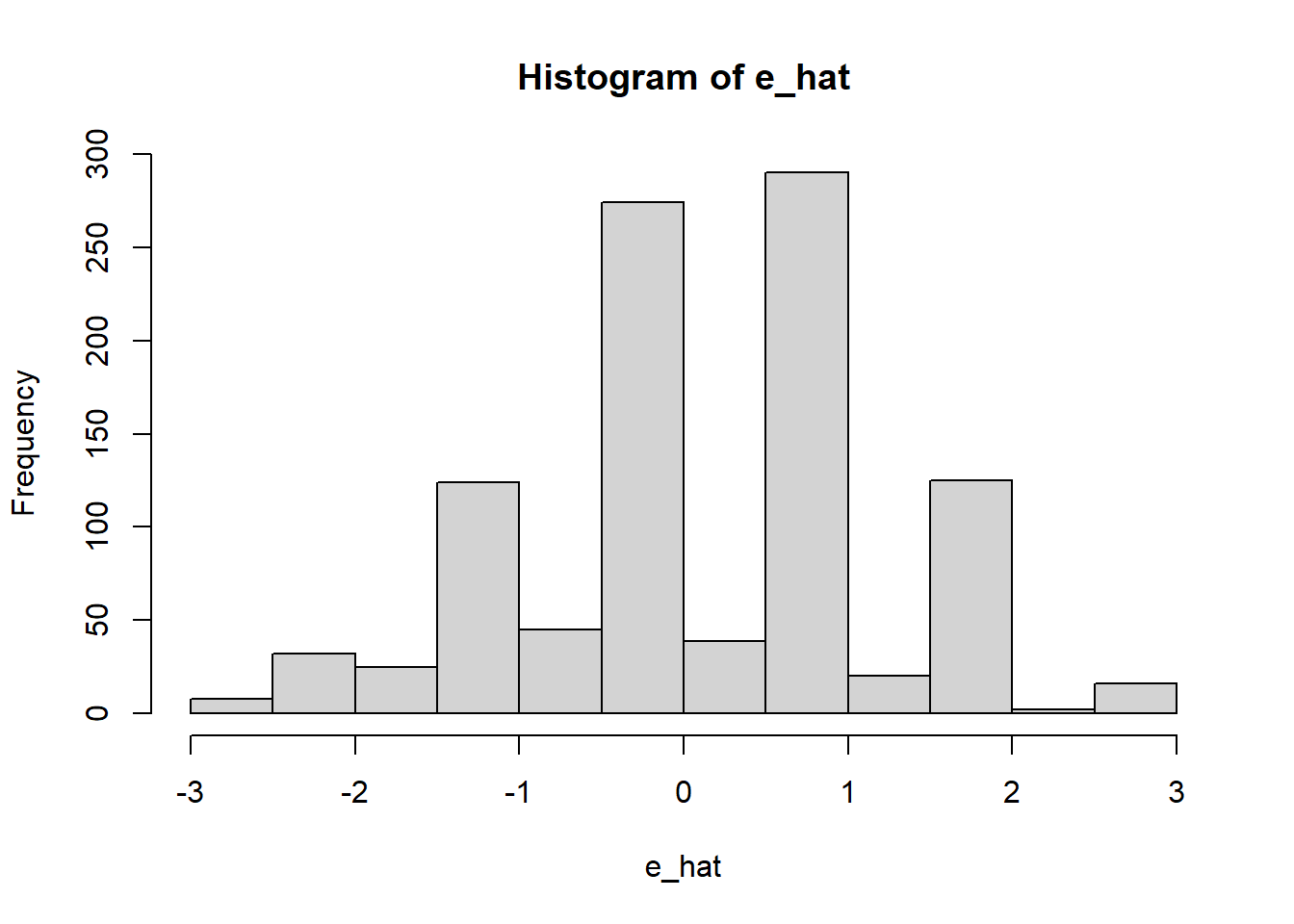

f = function(n){
  x = runif(n, min = 0, max = 100)
  e = rbinom(n = n, size = 5, prob = 0.5 ) - ((5*0.5)/1-0.5)
  X = cbind(1,x)
  y = 10 + beta * x + e
  B = solve(t(X)%*%X)%*%t(X)%*%y
  B
}

par(mfrow = c(2, 2))
for (i in c(10,50,100,1000)){
  x = replicate(n = N, expr = f(i))
  var = (var(x[2,1,]) * i)
  z = sqrt(i) *( (x[2, 1, ] - beta)) / sqrt(var)
  plot(density(z), xlim = c(-4,4))
  curve(dnorm(x,0,1), col = "red", xlim = c(-4,4), add = TRUE)
}