Capítulo 6 Distribuicoes Continuas

As Variáveis Aleatórias Contínuas são caracterizadas por possuírem um suporte contínuo, sendo toda a reta Real ou um intervalo.

Vamos supor uma variável aleatória \(X\) com a seguinte função de densidade de probabilidade : \[f_X(x) = 3x^2 \], com \(0 \le x \le1\)

f <- function(x) 3 * x^2

Vamos verificar se a integral de \(f_X\) no suporte da distribuição é igual a 1:

integrate(f, lower = 0, upper = 1)

## 1 with absolute error < 1.1e-14

Vamos calcular \(P(0.14 \le X \le 0.71)\)

integrate(f, lower = 0.14, upper = 0.71)

## 0.355167 with absolute error < 3.9e-15

g = function(x) x * 3 * x^2

integrate(g, lower = 0, upper = 1)

## 0.75 with absolute error < 8.3e-15

O pacote distr possui algumas funcionalidades para analisar funções de distribuição.

#install.packages("distr")
library(distr)

f <- function(x) 3 * x^2
X <- AbscontDistribution(d = f, low1 = 0, up1 = 1)

p(X)(0.71) - p(X)(0.14)

## [1] 0.355167

E(X)

## [1] 0.7496337

6.1 Variável Aleatória Normal

curve(dnorm(x), xlim = c(-5,5))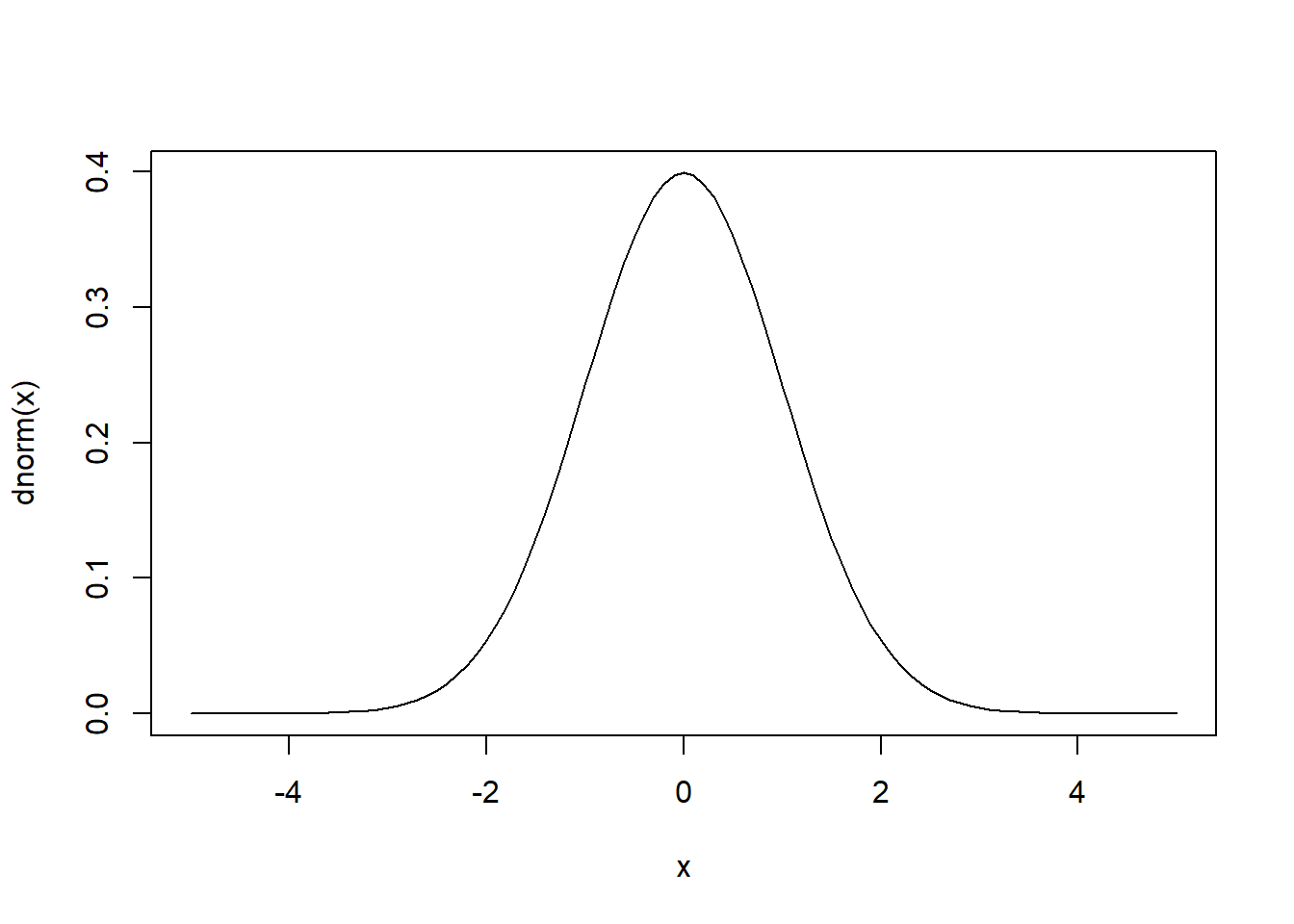

curve(pnorm(x), xlim = c(-5,5))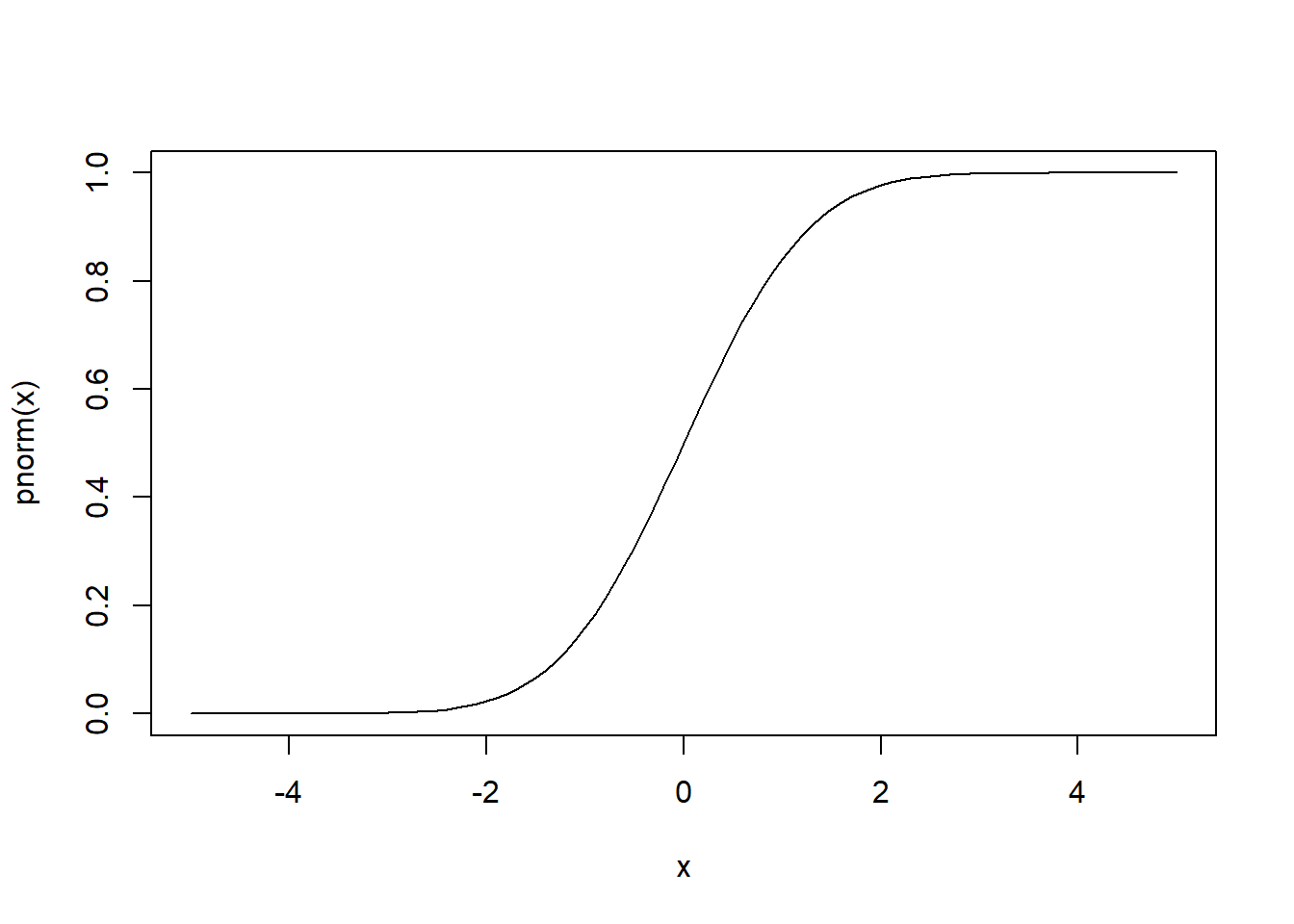

par(mfrow = c(2,1))
    
plot(function(x) dnorm(x), xlim = c(-5,5))
curve(dnorm(x,2), xlim = c(-5,5), add = TRUE, col="red")

plot(function(x) pnorm(x), xlim = c(-5,5))
curve(pnorm(x,2), xlim = c(-5,5), add = TRUE, col = "red")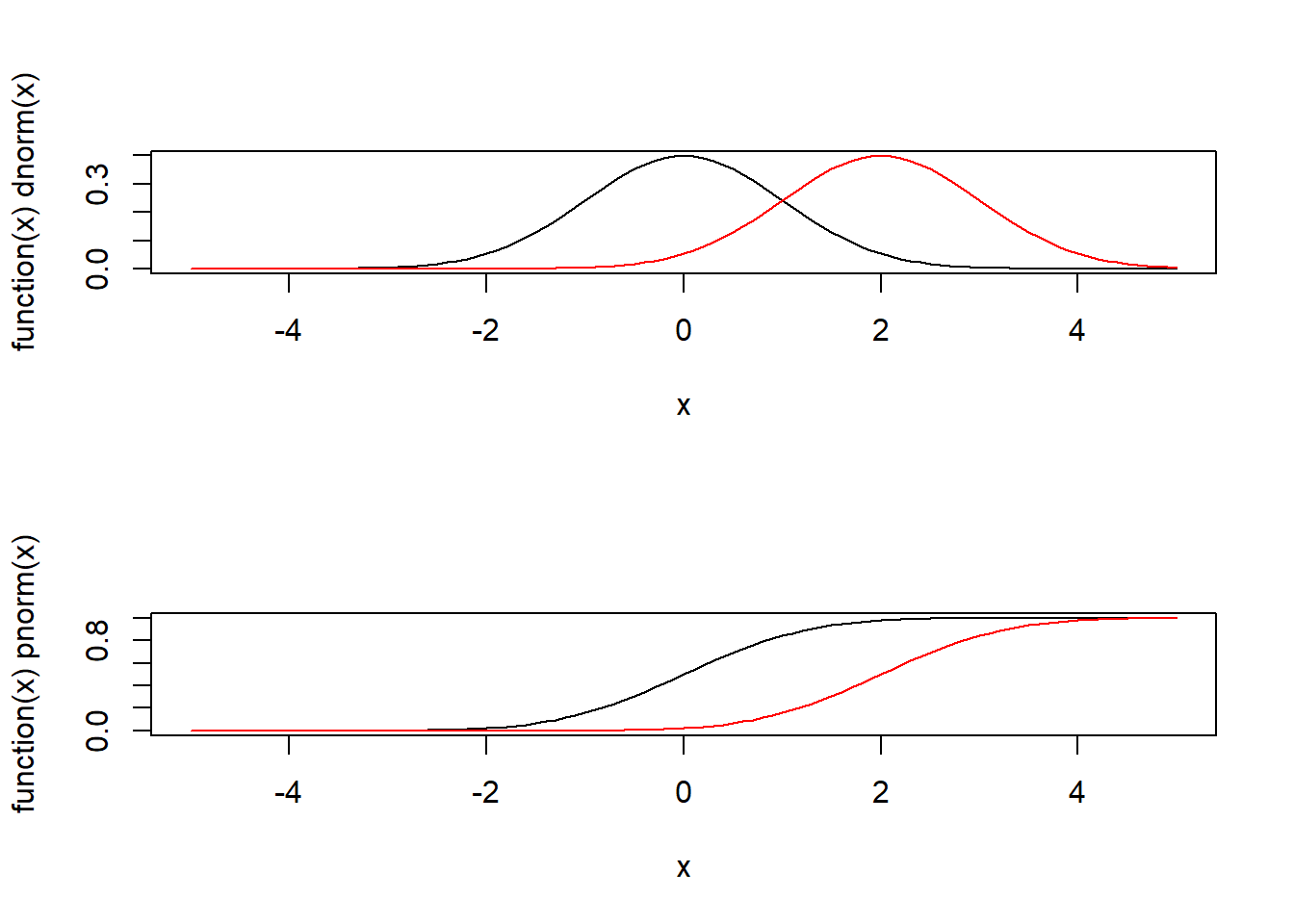

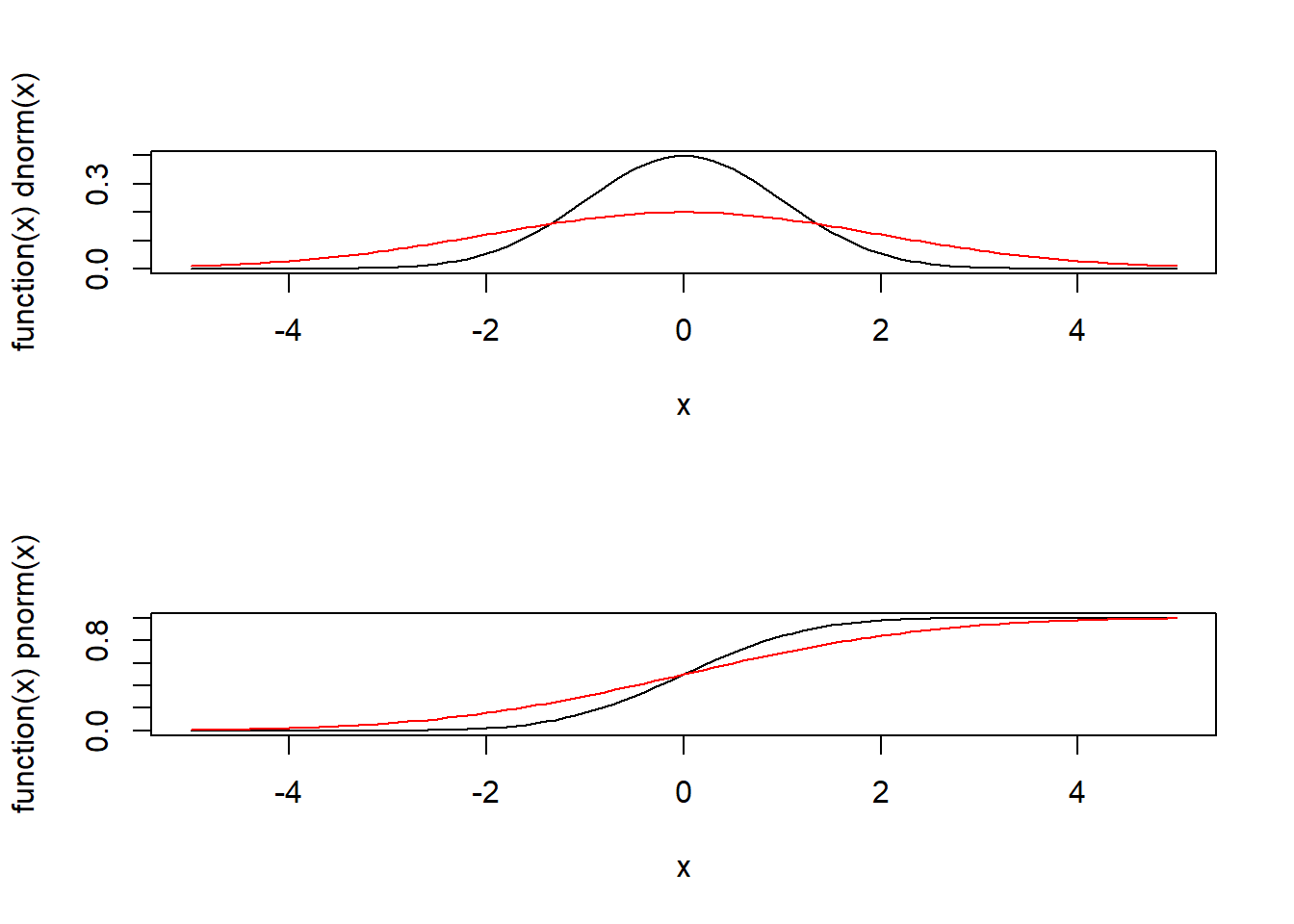
par(mfrow = c(2,1))
    
plot(function(x) dnorm(x), xlim = c(-5,5))
curve(dnorm(x,0,2), xlim = c(-5,5), add = TRUE, col="red")

plot(function(x) pnorm(x), xlim = c(-5,5))
curve(pnorm(x,0,2), xlim = c(-5,5), add = TRUE, col = "red")