Capítulo 4 Probabilidade
A Teoria da Probabilidade é a base para a econometria. Probabilidade é a linguagem matemática usada para lidar com a incerteza, que é central na moderna Teoria Econométrica. A Teoria da Probabilidade é também a base da estatística matemática, que por sua vez é a base da Econometria.
4.1 Espaço Amostral
Espaço amostral é o conjunto de todos os possíveis resultados de um experimento.
O pacote prob é uma ferramenta interessante do R para o estudo de probabilidades. No pacote probo espaço amostral é representado por um dataframe. Cada linha do dataframe corresponde a um resultado do experimento.
#install.packages("prob")
library(prob)4.1.1 Alguns exemplos de espaços amostrais
Jogar uma moeda.
tosscoin(1)## toss1
## 1 H
## 2 TJogar duas moedas
tosscoin(2)## toss1 toss2
## 1 H H
## 2 T H
## 3 H T
## 4 T TJogar um dado de seis faces.
rolldie(1)## X1
## 1 1
## 2 2
## 3 3
## 4 4
## 5 5
## 6 6Jogar dois dados de seis faces.
rolldie(2)## X1 X2
## 1 1 1
## 2 2 1
## 3 3 1
## 4 4 1
## 5 5 1
## 6 6 1
## 7 1 2
## 8 2 2
## 9 3 2
## 10 4 2
## 11 5 2
## 12 6 2
## 13 1 3
## 14 2 3
## 15 3 3
## 16 4 3
## 17 5 3
## 18 6 3
## 19 1 4
## 20 2 4
## 21 3 4
## 22 4 4
## 23 5 4
## 24 6 4
## 25 1 5
## 26 2 5
## 27 3 5
## 28 4 5
## 29 5 5
## 30 6 5
## 31 1 6
## 32 2 6
## 33 3 6
## 34 4 6
## 35 5 6
## 36 6 6Jogar cartas
cards()## rank suit
## 1 2 Club
## 2 3 Club
## 3 4 Club
## 4 5 Club
## 5 6 Club
## 6 7 Club
## 7 8 Club
## 8 9 Club
## 9 10 Club
## 10 J Club
## 11 Q Club
## 12 K Club
## 13 A Club
## 14 2 Diamond
## 15 3 Diamond
## 16 4 Diamond
## 17 5 Diamond
## 18 6 Diamond
## 19 7 Diamond
## 20 8 Diamond
## 21 9 Diamond
## 22 10 Diamond
## 23 J Diamond
## 24 Q Diamond
## 25 K Diamond
## 26 A Diamond
## 27 2 Heart
## 28 3 Heart
## 29 4 Heart
## 30 5 Heart
## 31 6 Heart
## 32 7 Heart
## 33 8 Heart
## 34 9 Heart
## 35 10 Heart
## 36 J Heart
## 37 Q Heart
## 38 K Heart
## 39 A Heart
## 40 2 Spade
## 41 3 Spade
## 42 4 Spade
## 43 5 Spade
## 44 6 Spade
## 45 7 Spade
## 46 8 Spade
## 47 9 Spade
## 48 10 Spade
## 49 J Spade
## 50 Q Spade
## 51 K Spade
## 52 A Spade4.1.2 Subespaços (Eventos)
S = tosscoin(2)
subset(S, toss2 == "H")## toss1 toss2
## 1 H H
## 2 T HS <- cards()
subset(S, suit == "Heart")## rank suit
## 27 2 Heart
## 28 3 Heart
## 29 4 Heart
## 30 5 Heart
## 31 6 Heart
## 32 7 Heart
## 33 8 Heart
## 34 9 Heart
## 35 10 Heart
## 36 J Heart
## 37 Q Heart
## 38 K Heart
## 39 A Heartsubset(rolldie(2), X1+X2 > 8)## X1 X2
## 18 6 3
## 23 5 4
## 24 6 4
## 28 4 5
## 29 5 5
## 30 6 5
## 33 3 6
## 34 4 6
## 35 5 6
## 36 6 6nrow(subset(rolldie(2), X1+X2 > 8))## [1] 104.2 Álgebra de conjuntos
União
S = cards()
A = subset(S, suit == "Heart")
B = subset(S, suit == "Club" )
union(A,B)## rank suit
## 1 2 Club
## 2 3 Club
## 3 4 Club
## 4 5 Club
## 5 6 Club
## 6 7 Club
## 7 8 Club
## 8 9 Club
## 9 10 Club
## 10 J Club
## 11 Q Club
## 12 K Club
## 13 A Club
## 27 2 Heart
## 28 3 Heart
## 29 4 Heart
## 30 5 Heart
## 31 6 Heart
## 32 7 Heart
## 33 8 Heart
## 34 9 Heart
## 35 10 Heart
## 36 J Heart
## 37 Q Heart
## 38 K Heart
## 39 A HeartInterseção
intersect(A,B)## [1] rank suit
## <0 linhas> (ou row.names de comprimento 0)S = rolldie(2)
A = subset(S, X1 == 5)
B = subset(S, X1 + X2 >= 10)A## X1 X2
## 5 5 1
## 11 5 2
## 17 5 3
## 23 5 4
## 29 5 5
## 35 5 6B## X1 X2
## 24 6 4
## 29 5 5
## 30 6 5
## 34 4 6
## 35 5 6
## 36 6 6intersect(A,B)## X1 X2
## 29 5 5
## 35 5 6Diferença
A operação de diferença entre conjuntos, \(A-B\), forma um novo conjunto, contendo os elementos de \(A\) que não pertencem ao conjunto \(B\).
setdiff(A,B)## X1 X2
## 5 5 1
## 11 5 2
## 17 5 3
## 23 5 4Note que a operação diferença não é simétrica.
setdiff(B,A)## X1 X2
## 24 6 4
## 30 6 5
## 34 4 6
## 36 6 6Com a função setdiff é possivel calcular o complemento de um conjunto. Por exemplo, o complemento de A, denotado por Ac, é definido pelos elementos de S que não estão em A.
setdiff(S,A)## X1 X2
## 1 1 1
## 2 2 1
## 3 3 1
## 4 4 1
## 6 6 1
## 7 1 2
## 8 2 2
## 9 3 2
## 10 4 2
## 12 6 2
## 13 1 3
## 14 2 3
## 15 3 3
## 16 4 3
## 18 6 3
## 19 1 4
## 20 2 4
## 21 3 4
## 22 4 4
## 24 6 4
## 25 1 5
## 26 2 5
## 27 3 5
## 28 4 5
## 30 6 5
## 31 1 6
## 32 2 6
## 33 3 6
## 34 4 6
## 36 6 64.3 Espaço de Probabilidades
Até aqui os elementos dos conjuntos não possuiam uma probabilidade associada. A partir de agora, acrescenta-se probabilidade a cada elemento do espaço amostral, transformando-o em um espaço de probabilidades.
O comando probspace atribui probabilidades a um espaço amostral. É possível definir manualmente um vetor de probabilidades ou permitir que o próprio comando atribua as probabilidades.
outcomes = rolldie(1)
probability = rep(1/6, 6)
S = probspace(outcomes, probs = probability)
S## X1 probs
## 1 1 0.1666667
## 2 2 0.1666667
## 3 3 0.1666667
## 4 4 0.1666667
## 5 5 0.1666667
## 6 6 0.1666667probspace(1:6, probs = probability)## x probs
## 1 1 0.1666667
## 2 2 0.1666667
## 3 3 0.1666667
## 4 4 0.1666667
## 5 5 0.1666667
## 6 6 0.1666667probspace(1:6)## x probs
## 1 1 0.1666667
## 2 2 0.1666667
## 3 3 0.1666667
## 4 4 0.1666667
## 5 5 0.1666667
## 6 6 0.1666667Uma outra forma é utilizar o atributo makespace no momento em que se cria o espaço amostral.
rolldie(1, makespace = TRUE)## X1 probs
## 1 1 0.1666667
## 2 2 0.1666667
## 3 3 0.1666667
## 4 4 0.1666667
## 5 5 0.1666667
## 6 6 0.1666667Probabilidades desiguais
As funções acima criaram espaços de probabilidade com probabilidades iguais para cada possível resultado. Em muitos casos os possíveis resultados possuem probabilidades difentes.
Moeda não balanceada
probspace(tosscoin(1), probs = c(0.70, 0.30))## toss1 probs
## 1 H 0.7
## 2 T 0.3Experimentos idênticos e independentes repetidos
Situação em que certo experimento é repetido múltiplas vezes sob condições idênticas e de maneira independente.
iidspace(c("H","T"), ntrials = 3, probs = c(0.7, 0.3))## X1 X2 X3 probs
## 1 H H H 0.343
## 2 T H H 0.147
## 3 H T H 0.147
## 4 T T H 0.063
## 5 H H T 0.147
## 6 T H T 0.063
## 7 H T T 0.063
## 8 T T T 0.0274.4 Função de probabilidades
S = cards(makespace = TRUE)
A = subset(S, suit == "Heart")
B <- subset(S, rank %in% 7:9)Prob(A)## [1] 0.25Prob(S, suit == "Heart")## [1] 0.25Prob(B)## [1] 0.2307692Axiomas da Probabilidade
1 - \(P(A) \ge 0\)
2 - \(P(S) = 1\)
3 - Se \(A_1,A_2~,...\) forem disjunto, então \(P[ \cup_{j=1}^{\infty} A_j] = \sum_{j=1}^{\infty} P(A_j)\)
Definir Espaço de Probabilidades
S = rolldie(1, makespace = TRUE)
S## X1 probs
## 1 1 0.1666667
## 2 2 0.1666667
## 3 3 0.1666667
## 4 4 0.1666667
## 5 5 0.1666667
## 6 6 0.1666667Criar partição de \(S\).
A1 = subset(S, X1 == 1)
A2 = subset(S, X1 == 2 | X1 == 3)
A3 = subset(S, X1 == 4 | X1 == 5)
A4 = subset(S, X1 == 6)1 - \(P(A) \ge 0\)
Prob(A1)## [1] 0.16666672 - \(P(S) = 1\)
Prob(S)## [1] 13 - Se \(A_1,A_2~,...\) forem disjunto, então \(P[ \cup_{j=1}^{\infty} A_j] = \sum_{j=1}^{\infty} P(A_j)\)
Prob(union(A1,union(A2,A3)))## [1] 0.8333333Prob(A1) + Prob(A2) + Prob(A3)## [1] 0.8333333Propriedades da Função de Probabilidade
Para verificar algumas propriedades da Função de Probabilidade vamos criar três subconjuntos do espaço amostral \(S\).
A = subset(S, X1 >3)
A## X1 probs
## 4 4 0.1666667
## 5 5 0.1666667
## 6 6 0.1666667B = subset(S, X1 == 3 | X1 == 4)
B## X1 probs
## 3 3 0.1666667
## 4 4 0.1666667C = subset(S,X1 == 4 | X1 == 5)
C## X1 probs
## 4 4 0.1666667
## 5 5 0.16666671 - \(P(A^c) = 1 - P(A)\)
Prob(setdiff(S,A))## [1] 0.51 - Prob(A)## [1] 0.52 - \(P(\emptyset) = 0\)
empty = subset(S, X1 == 7)
Prob(empty)## [1] NA3 - \(P(A) \le 1\)
Prob(A)## [1] 0.54 - Se \(C \subset A\), então \(P(C) \le P(A)\)
isin(A[,1],C[,1])## [1] TRUEProb(C)## [1] 0.3333333Prob(A)## [1] 0.55 - \(P(A \cup B) = P(A) + P(B) - P(A \cap B)\)
Prob(union(A,B))## [1] 0.6666667Prob(A) + Prob(B) - Prob(intersect(A,B))## [1] 0.66666676 - \(P(A \cup B) \le P(A) + P(B)\)
Prob(union(A,B))## [1] 0.6666667Prob(A) + Prob(B)## [1] 0.8333333Probabilidade Condicional
\(P(A \mid B) = \frac{P(A \cap B)}{P(B)}, se P(B) >0\)
S = cards(makespace = TRUE)
A = subset(S, suit == "Heart")
B <- subset(S, rank %in% 7:9)\(P(A \mid B)\)
Prob(A, given = B)## [1] 0.25\(\frac{P(A \cap B)}{P(B)}\)
Prob(intersect(A,B) ) / Prob(B)## [1] 0.25Prob(S, suit=="Heart", given = rank %in% 7:9)## [1] 0.25Prob(B, given = A) ## [1] 0.2307692Regra da Adição
\(P(A \cup B) = P(A) + P(B) - P(A \cap B)\)
Prob(union(A,B))## [1] 0.4230769Prob(A) + Prob(B) - Prob(intersect(A,B))## [1] 0.4230769Regra da Multiplicação
\(P(A \cap B)=P(A)*P(B \mid A)\)
\(P(A \cap B)=P(B)*P(A \mid B)\)
Prob(intersect(A,B))## [1] 0.05769231Prob(A) * Prob(B, given = A)## [1] 0.05769231Prob(B) * Prob(A, given = B)## [1] 0.05769231Eventos Independentes
Três formas de mostrar que dois eventos são independentes.
\(P(A \cap B) = P(A) * P(B)\)
\(P(A \mid B) = P(A)\)
\(P(B \mid A) = P(B)\)
S <- tosscoin(2, makespace = TRUE)
S## toss1 toss2 probs
## 1 H H 0.25
## 2 T H 0.25
## 3 H T 0.25
## 4 T T 0.25A = subset(S, toss1 == "H")
B = subset(S, toss2 == "H")Prob(intersect(A,B))## [1] 0.25Prob(A)*Prob(B)## [1] 0.25Prob(A)## [1] 0.5Prob(A, given = B)## [1] 0.5Prob(B)## [1] 0.5Prob(B, given = A)## [1] 0.5Lei da Probabilidade Total
Teorema da Partição
\(A = \cup_{i=1}^{\infty} (A \cap B_i)\) , sendo \(B_i\) uma partição do Espaço Amostral S.
Como os eventos \((A \cap B_i)\) são disjuntos:
\(P(A) = \sum_{i=1}^{\infty} p(A \cap B_ì) = \sum_{i=1}^{\infty} P(A \mid B_i)*P(B_i)\)
S = rolldie(1, makespace = T)
B1 = subset(S, X1 == 1)
B2 = subset(S, X1 == 2 | X1 == 3)
B3 = subset(S, X1 == 4 | X1 == 5)
B4 = subset(S, X1 == 6)
A = subset(S, X1 >1 & X1 <=4)
A## X1 probs
## 2 2 0.1666667
## 3 3 0.1666667
## 4 4 0.1666667\(A = \cup_{i=1}^{\infty} (A \cap B_i)\)
union(intersect(A,B1),union(intersect(A,B2),union(intersect(A,B3),intersect(A,B4))))## X1 probs
## 2 2 0.1666667
## 3 3 0.1666667
## 4 4 0.1666667Prob(A)## [1] 0.5#Prob(union(intersect(A,B1),union(intersect(A,B2),union(intersect(A,B3),intersect(A,B4)))))
sum(Prob(intersect(A,B1)),Prob(intersect(A,B2)),Prob(intersect(A,B3)),Prob(intersect(A,B4)),na.rm=T)## [1] 0.5sum(Prob(A, given = B1)*Prob(B1),Prob(A, given = B2)* Prob(B2),Prob(A,given = B3) * Prob(B3),Prob(A,given = B4)*Prob(B4),na.rm=T)## [1] 0.54.5 Funções de distribuições
Para cada Distribuição Teórica existem quatro funções associadas:
Exemplo para Variável Normal:
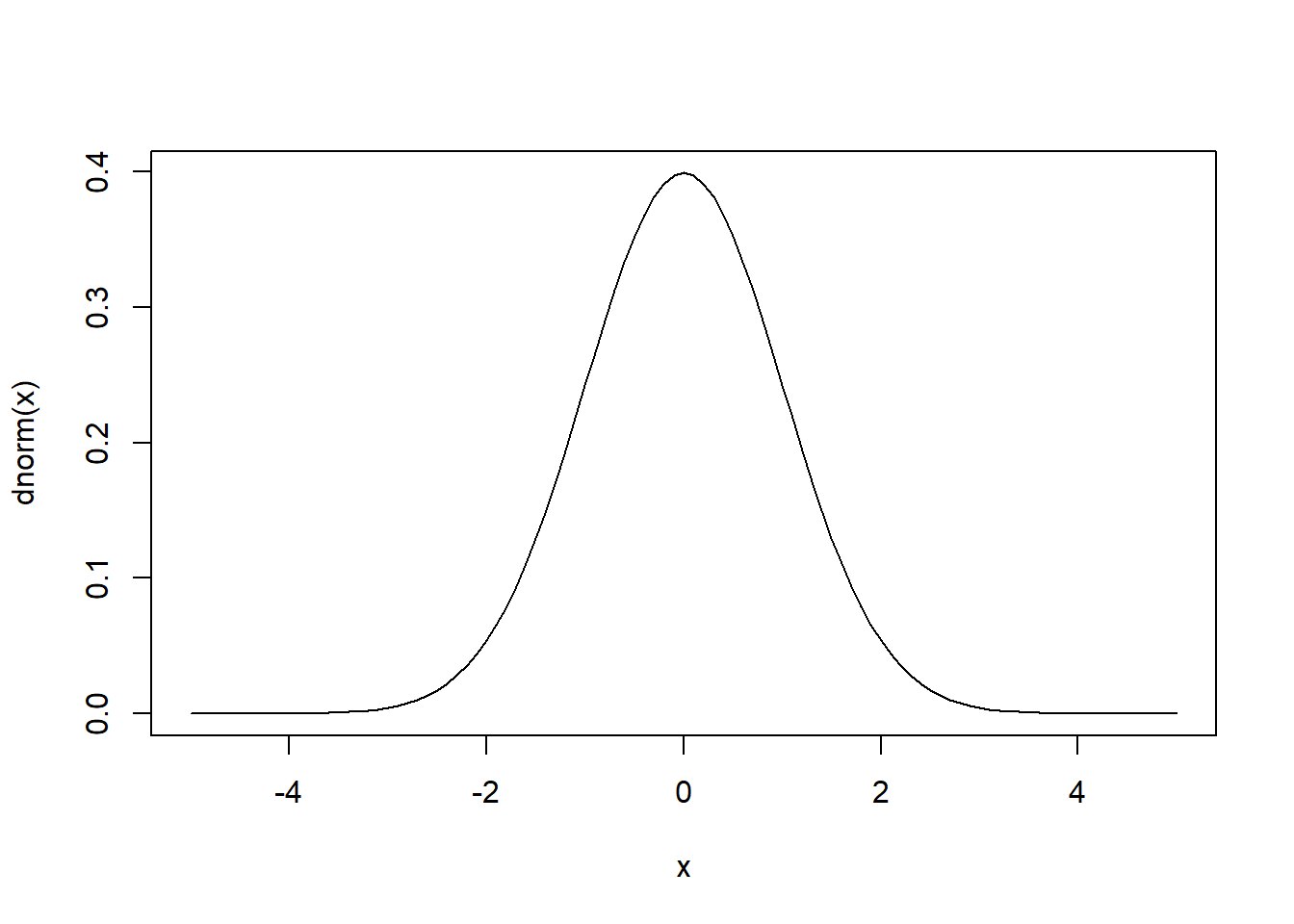
dnorm(x, mean, sd) –> função de densidade
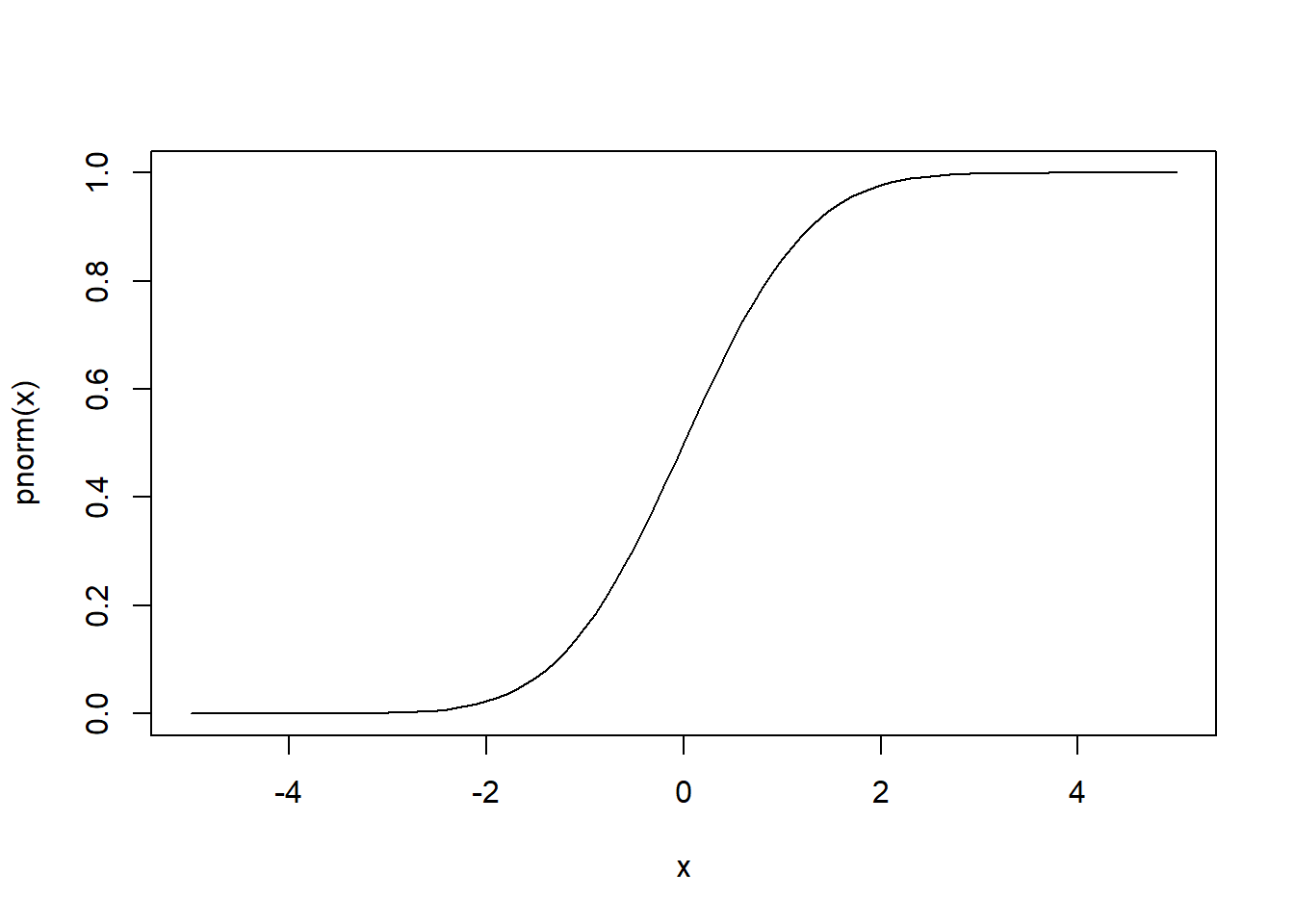
pnorm(x, mean, sd) –> função de distribuição - distribuição cumulativa
qnorm(p, mean, sd) –> função quantílica (em um primeiro momento não vamos trabalhar com esta função)
rnorm(n ,mean, sd) –> gerador de amostras aleatórias
onde,
x é um vetorde números, p é um vetor de probabilidades e n é o numero de observações - tamanho amostral.
É possivel também criar uma função no R com a expressão desejada. Para ilustrar segue a função de densidade de propabilidade normal:
\[f(x) = \frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2} \]
normal = function(x){
r = (1/sqrt(2*pi))*exp(-x^2/2)
return(r)
}set.seed(1)
normal(4)## [1] 0.0001338302dnorm(4)## [1] 0.0001338302x = rnorm(5,0,1)
mean(x)## [1] 0.1292699x = rnorm(500,0,1)
mean(x)## [1] 0.02055156x = rnorm(5000,0,1)
mean(x)## [1] -0.006913248x = rnorm(5000,0,0.1)
mean(x)## [1] -0.0008409202n = 1
mean(rnorm(n,0,0))## [1] 0pnorm(0)## [1] 0.5qnorm(0.5)## [1] 0