Capítulo 10 Estimador de MQO e sua Algebra Matricial
População e Amostra Aleatória
O objetivo dessa seção é estimar \(\beta = E(xx')^{-1}E(xy)\)
A verdadeira relação entre a variável dependente \(Y\) e as variáveis explicativas \(X\) nunca é conhecida. No entanto, podemos nos valer de um ambiente computacional e realizar simulações de dados tanto para exemplificar os conceitos de população e amostras quanto para destacar as propriedades do estimador de Mínimos Quadrados.
Vamos trabalhar com um mundo hipotético em que temos controle e conhecimento sobre as distribuições marginais do vetor de variáveis \(X\) e da relação entre \(X\) e \(Y\).
\(Y = X\beta + e\)
onde \(X = (1,X1,X2)\), sendo \(X1 \sim N(12,3)\), \(X2 \sim U(1,20)\) e \(e \sim N(0,1)\). O vetor \(\beta = (10,3,9)\) é o vetor de parâmetros do modelo a ser estimado. Estas informações definem a População de interesse.
Obtendo 1000 amostras aleatórias \({x_i}\), sendo que \(x1\) possui uma distribuição normal com média 12 e desvio padrão 3 e \(x2\) possui uma distribuição uniforme com parâmetros mínimo igual a 1 e máximo igual a 20. O termo de erro provém de uma distribuição normal padrão (média 0 e desvio padrão 1).
set.seed(16)
n = 1000x1 = rnorm(1000, mean = 12, sd = 3) # Variável X1
x2 = runif(1000, min = 1, max = 20) # Variável X2
X = cbind(1,x1,x2)
e = rnorm(1000)Vamos criar um vetor de parâmetros \(\beta\) pré determinados. Lembre-se que na vida real nunca conheceremos os verdadeiros parâmetros.
beta = matrix(c(10,3,9),nrow = 3)Calcular \(y\) a partir dos valores pré estabelecidos.
y = X%*%beta + ePortanto, o modelo é:
\(y_i = 10 + 3x1_i + 9x2_i + e_i\)
Estimar \(\hat\beta = (X'X)^{-1}(X'y)\) utilizando a notação matricial:
B = solve(t(X)%*%X)%*%(t(X)%*%y)
B## [,1]
## 9.995817
## x1 2.997791
## x2 9.003035Valores ajustados e resíduos de Mínimos Quadrados \(\hat e = y - X\hat\beta\)
y_hat = X%*%B
e_hat = y - y_hate_hat = y - X%*%BEstimação da Variância do erro: \(\sigma^2 = \mathbb{E}(e_i^2)\). O estimador natural para \(\sigma^2\) é o estimador de momentos \(\tilde\sigma = \frac{1}{n} \sum_{i=1}^n e_i^2\). No entanto, este estimador não é factível, pois não se conhece \(e_i\). A solução é adotar um estimador em dois estágios, substituindo \(e_i\) por \(\hat e_i\). Portanto, o estimador de \(\sigma^2\) é: \(\hat\sigma ^2 = \frac{1}{n} \sum_{i=1}^n \hat e_i^2\)
Em notação matricial \(\hat\sigma^2 = n^{-1}\hat e' \hat e\) ou \(\hat\sigma^2 = \frac{1}{n-k}\hat e' \hat e\).
k = ncol(X)
sigma_hat = (1/(n-k)) * t(e_hat)%*%e_hat # n-k correção de viés
sigma_hat## [,1]
## [1,] 1.014736\(R^2 = 1 - \frac{\sum_{i=1}^n \hat e_i^2}{\sum_{i=1}^n(y_i - \bar{y})}\)
y_barra = mean(y)
desvio = y - y_barra
R2 = 1 - (( t(e_hat)%*%e_hat)/(t(desvio)%*%desvio))
R2## [,1]
## [1,] 0.9995928Matriz de Variância Covariância
\[V_{\hat\beta} = (X'X)^{-1}X'DX(X'X)^{-1}\] onde \(D = diag(\sigma^2_1,...,\sigma^2_n)\)
\[D = \begin{bmatrix}\sigma^2_1 & ... & ...\\ 0 & \sigma^2_2 & 0 \\ & & \\ 0 & & \sigma^2_n \end{bmatrix}\]
e \(\sigma^2_i = E[e_i^2 | X_i]\)
O problema é que \(D\) não é observado e precisa ser estimada.
Matriz de Variância Covariância Homocedástica: se o modelo for homocedástico \(D = I_n\sigma^2\) e a matriz \(V_{\hat\beta}\) passa a ser escrita como
\(\hat{V}_{\hat\beta}=\hat\sigma ^2 (X'X)^{-1}\), onde \(\hat\sigma^2 = \frac{1}{n-k}\hat e' \hat e\).
V = sigma_hat[1,1] * solve(t(X)%*%X)
V ## x1 x2
## 0.0229722105 -1.465321e-03 -3.932383e-04
## x1 -0.0014653210 1.183668e-04 2.816107e-06
## x2 -0.0003932383 2.816107e-06 3.371004e-05Os erros padrão são a raiz quadrada dos elementos da diagonal principal.
ep = sqrt(diag(V))
ep## x1 x2
## 0.151565862 0.010879649 0.005806035Matriz de Variância Covariância Heterocedástica
É preciso estimar \(D\). O estimador mais utilizado é:
\(\hat D = diag(\hat e^2_1, ... ,\hat e^2_n)\)
e = c(e_hat)
e = e * e
D = diag(e)
V_h = solve(t(X)%*%X)%*%(t(X)%*%D%*%X)%*%solve(t(X)%*%X)
V_h = (n/(n-k)) * V_h
V_h## x1 x2
## 0.0209004837 -1.352671e-03 -3.364705e-04
## x1 -0.0013526709 1.123094e-04 -5.335789e-07
## x2 -0.0003364705 -5.335789e-07 3.270841e-05Erros padrão.
ep_h = sqrt(diag(V_h))
ep_h## x1 x2
## 0.144569996 0.010597615 0.005719127Para verificar as estimações da matriz de Variância e Covariância bem como os próprios estimadores de \(\beta\), vamos utilizar as funções já programadas do \(R\).
df = data.frame(y,x1,x2)
ols = lm(y~x1 + x2)
summary(ols)##
## Call:
## lm(formula = y ~ x1 + x2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.3423 -0.6863 -0.0020 0.6477 3.4863
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 9.995817 0.151566 65.95 <2e-16 ***
## x1 2.997791 0.010880 275.54 <2e-16 ***
## x2 9.003035 0.005806 1550.63 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.007 on 997 degrees of freedom
## Multiple R-squared: 0.9996, Adjusted R-squared: 0.9996
## F-statistic: 1.224e+06 on 2 and 997 DF, p-value: < 2.2e-16Modelo Heterocedástico
n = 1000
x = trunc(runif(n,1,10))
X = cbind(1,x)
e = rnorm(n,mean=0,sd= 2*x )
beta = c(10,3)
y = X%*%beta + e
beta_hat = solve(t(X)%*%X)%*%t(X)%*%y
beta_hat## [,1]
## 9.989843
## x 2.959186plot(x,y)
abline(beta_hat[1],beta_hat[2], col = "red")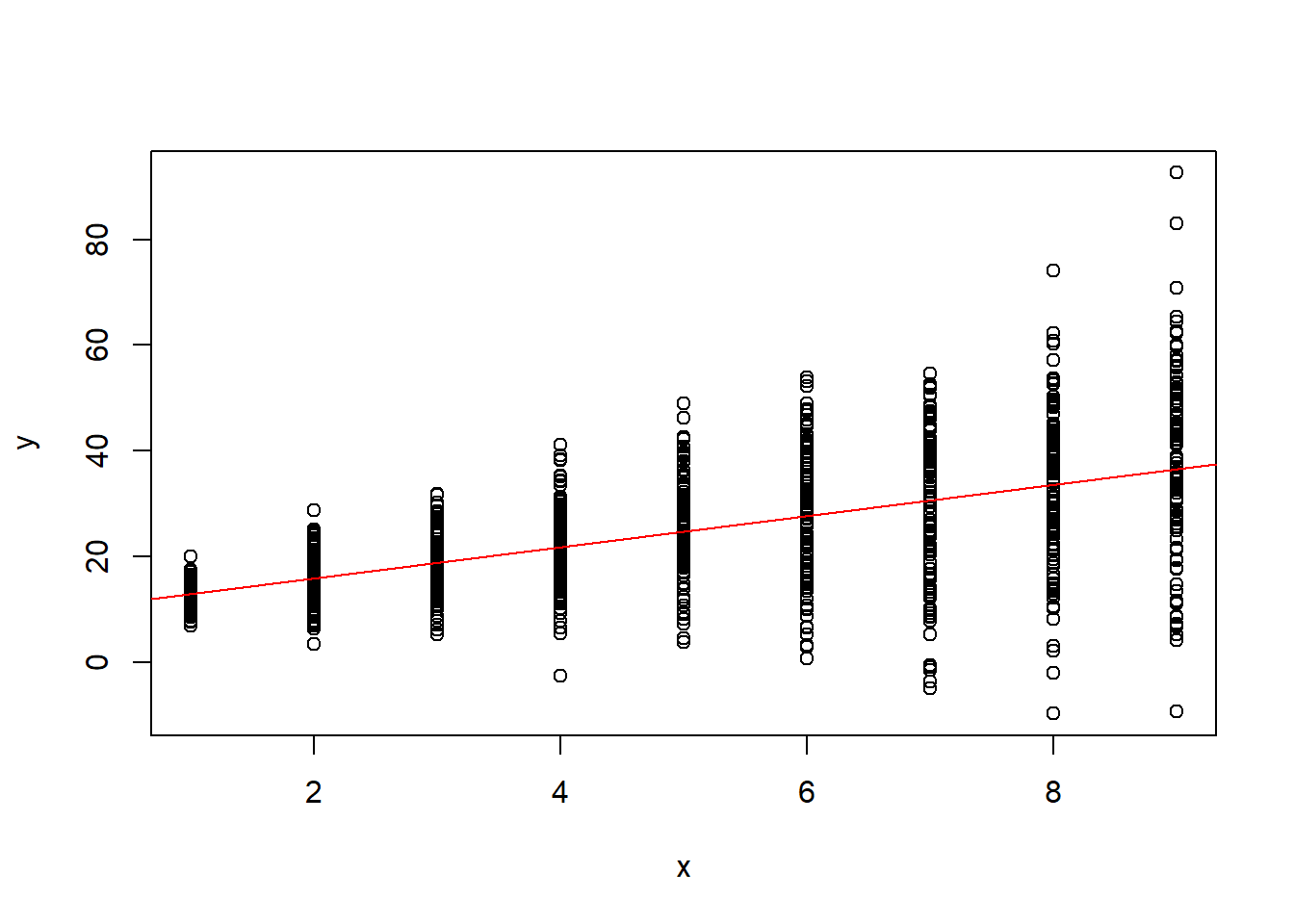
k = ncol(X)
e_hat = y - X%*%beta_hat
e = c(e_hat)
e = e * e
D = diag(e)
V_h = solve(t(X)%*%X)%*%(t(X)%*%D%*%X)%*%solve(t(X)%*%X)
V_h = (n/(n-k)) * V_h
V_h## x
## 0.24547305 -0.06132685
## x -0.06132685 0.01958208Erros padrão.
ep_h = sqrt(diag(V_h))
ep_h## x
## 0.4954524 0.1399360df = data.frame(y,x)
ols = lm(y~x)
summary(ols)##
## Call:
## lm(formula = y ~ x)
##
## Residuals:
## Min 1Q Median 3Q Max
## -45.918 -5.244 0.032 5.760 55.960
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 9.9898 0.7466 13.38 <2e-16 ***
## x 2.9592 0.1327 22.31 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 10.98 on 998 degrees of freedom
## Multiple R-squared: 0.3327, Adjusted R-squared: 0.3321
## F-statistic: 497.6 on 1 and 998 DF, p-value: < 2.2e-16#install.packages("AER")
library(AER)vcov <- vcovHC(ols, type = "HC1")
vcov## (Intercept) x
## (Intercept) 0.24547305 -0.06132685
## x -0.06132685 0.01958208sqrt(diag(vcov))## (Intercept) x
## 0.4954524 0.1399360Outro exemplo de heterocedasticidade:
n = 1000
x = rnorm(n,5,10)
X = cbind(1,x)
e = rnorm(n,mean=0,sd= 0.2*x^2 )
beta = c(10,3)
y = X%*%beta + e
beta_hat = solve(t(X)%*%X)%*%t(X)%*%y
beta_hat## [,1]
## 8.113169
## x 3.123120plot(x,y)
abline(beta_hat[1],beta_hat[2], col = "red")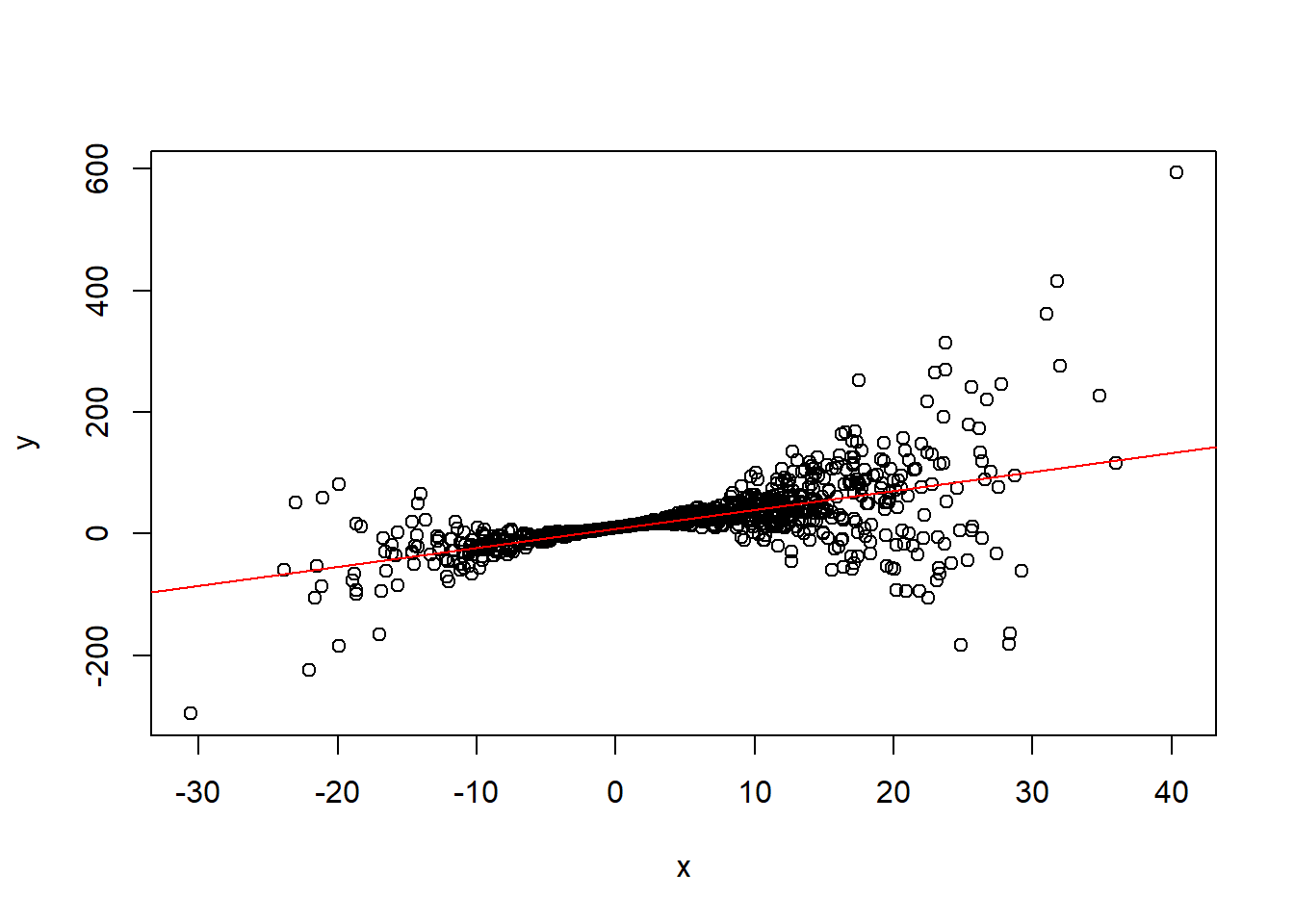
k = ncol(X)
e_hat = y - X%*%beta_hat
e = c(e_hat)
e = e * e
D = diag(e)
V_h = solve(t(X)%*%X)%*%(t(X)%*%D%*%X)%*%solve(t(X)%*%X)
V_h = (n/(n-k)) * V_h
V_h## x
## 1.322280 -0.14083699
## x -0.140837 0.08947298Erros padrão.
ep_h = sqrt(diag(V_h))
ep_h## x
## 1.1499044 0.2991203