Capítulo 8 Distribuicao Amostral

Este capítulo faz a ligação entre a Teoria da Probabilidade estudada nos capítulos anteriores e os próximos capítulos, onde será estudada a inferência nos modelos econométricos bem como o comportamento dos estimadores em diferentes amostras.

Em inferência estatística, utiliza-se características da amostra (estatística ou estimador) para estimar os parâmetros populacionais de interesse. Todo estimador é uma variável aleatória, e portanto, é possível entender o comportamento de um estimador com uso de funções de probabilidades, médias e desvios padrão.

A distribuição amostral de um estimador (ou de uma estatística) é a distribuição de probabilidade de um grande número de amostras de tamanho \(n\) de uma dada população. Portanto, a distribuição amostral não é a distribuição de uma única amostra. Vamos chamar a distribuição da amostra realizada de distribuição empírica.

Na prática, quando estamos analisando determinada relação entre dois ou mais eventos, observamos apenas uma realização da amostra, e portanto, tanto a distribuição populacional quanto a distribuição amostral são desconhecidas. No entanto, é possível utilizar um ambiente computacional com simulação de dados para ganhar intuição e entender melhor a distribuição amostral dos estimadores.

Antes de estudar a distribuição amostral, é importante aprendermos como extrair amostras aleatórias, comparar o comportamento da distribuição populacional com a distribuição empírica e como utilizar as ferramentas do R para realizar as simulações necessárias para construir a distribuição amostral.

8.1 Extração de Amostras Aleatórias

library(prob)
library(distr)
library(distrEx)

O comando `sample’ extrai uma amostra aleatória de um objeto. Essa amostra pode ser com ou sem repetição.

sample(x, size, replace = FALSE, prob = NULL)

Extrair uma observação de uma população finita composta por seis elementos enumerados de 1 a 6 com probabilidades iguais.

sample(1:6, 1)

## [1] 6

sample(1:6, 1)

## [1] 2

sample(1:6, 1)

## [1] 5

Extrair três elementos dessa mesma população sem repetição.

sample(1:6,3)

## [1] 3 6 4

Extrair quatro elementes dessa mesma população mas agora com repetição.

sample(1:6, 4, replace = T)

## [1] 2 3 2 2

Definir o espaço amostral de um lançamento de duas moedas:

coins = tosscoin(2)
coins

##   toss1 toss2
## 1     H     H
## 2     T     H
## 3     H     T
## 4     T     T

Extrair duas amostras aleatórias do espaço amostral definido acima:

coins[sample(nrow(coins),2),]

##   toss1 toss2
## 3     H     T
## 2     T     H

Repetir o procedimento.

coins[sample(nrow(coins),2),]

##   toss1 toss2
## 2     T     H
## 1     H     H

Criar um espaço amostral do lançamento de 3 dados com 4 faces.

S = rolldie(3, nsides = 4, makespace = TRUE)
S

##    X1 X2 X3    probs
## 1   1  1  1 0.015625
## 2   2  1  1 0.015625
## 3   3  1  1 0.015625
## 4   4  1  1 0.015625
## 5   1  2  1 0.015625
## 6   2  2  1 0.015625
## 7   3  2  1 0.015625
## 8   4  2  1 0.015625
## 9   1  3  1 0.015625
## 10  2  3  1 0.015625
## 11  3  3  1 0.015625
## 12  4  3  1 0.015625
## 13  1  4  1 0.015625
## 14  2  4  1 0.015625
## 15  3  4  1 0.015625
## 16  4  4  1 0.015625
## 17  1  1  2 0.015625
## 18  2  1  2 0.015625
## 19  3  1  2 0.015625
## 20  4  1  2 0.015625
## 21  1  2  2 0.015625
## 22  2  2  2 0.015625
## 23  3  2  2 0.015625
## 24  4  2  2 0.015625
## 25  1  3  2 0.015625
## 26  2  3  2 0.015625
## 27  3  3  2 0.015625
## 28  4  3  2 0.015625
## 29  1  4  2 0.015625
## 30  2  4  2 0.015625
## 31  3  4  2 0.015625
## 32  4  4  2 0.015625
## 33  1  1  3 0.015625
## 34  2  1  3 0.015625
## 35  3  1  3 0.015625
## 36  4  1  3 0.015625
## 37  1  2  3 0.015625
## 38  2  2  3 0.015625
## 39  3  2  3 0.015625
## 40  4  2  3 0.015625
## 41  1  3  3 0.015625
## 42  2  3  3 0.015625
## 43  3  3  3 0.015625
## 44  4  3  3 0.015625
## 45  1  4  3 0.015625
## 46  2  4  3 0.015625
## 47  3  4  3 0.015625
## 48  4  4  3 0.015625
## 49  1  1  4 0.015625
## 50  2  1  4 0.015625
## 51  3  1  4 0.015625
## 52  4  1  4 0.015625
## 53  1  2  4 0.015625
## 54  2  2  4 0.015625
## 55  3  2  4 0.015625
## 56  4  2  4 0.015625
## 57  1  3  4 0.015625
## 58  2  3  4 0.015625
## 59  3  3  4 0.015625
## 60  4  3  4 0.015625
## 61  1  4  4 0.015625
## 62  2  4  4 0.015625
## 63  3  4  4 0.015625
## 64  4  4  4 0.015625

S[sample(nrow(S),3),]

##    X1 X2 X3    probs
## 59  3  3  4 0.015625
## 54  2  2  4 0.015625
## 16  4  4  1 0.015625

S[sample(nrow(S),3),]

##    X1 X2 X3    probs
## 32  4  4  2 0.015625
## 16  4  4  1 0.015625
## 55  3  2  4 0.015625

Distribuição Normal

A função rnorm é um gerador de números aleatórios de uma distribuição normal. Possui três parâmetros. O número de realizações a serem extraídas da distribuição teórica, a média e o desvio padrão.

rnorm(1)

## [1] -1.373982

rnorm(5)

## [1] -1.13632832  0.02972808 -1.05083231  0.73908187 -0.86853863

rnorm(5,2,3)

## [1]  0.7101015  3.9166634  1.7442517 -0.8210868  1.4569061

Distribuição Uniforme

runif(1)

## [1] 0.9258298

runif(10)

##  [1] 0.7757844 0.4638127 0.1150527 0.3388508 0.4755708 0.4910929 0.1160265
##  [8] 0.9689752 0.1643502 0.9367687

runif(10,10,20)

##  [1] 19.78291 14.09771 12.98943 16.20636 14.52122 11.69022 11.05784 16.11251
##  [9] 17.11823 16.62783

8.2 Características da Amostra vs Características da População

Para que todos tenhamos os mesmos resultados, vamos fixar a semente do gerador de números aleatórios.

set.seed(1)

A primeira comparação a ser feita é entre a média populacional e a média da amostra de uma distribuição Normal Padrão.

x = rnorm(5,0,1)
mean(x)

## [1] 0.1292699

x = rnorm(500,0,1)
mean(x)

## [1] 0.02055156

Agora vamos comparar o desvio padrão:

x = rnorm(5,0,1)
sd(x)

## [1] 1.329763

x = rnorm(500,0,1)
sd(x)

## [1] 1.060446

Gráfico da densidade da distribuição empírica e da sua distribuição teórica associada.

set.seed(1)
plot(density(rnorm(10)), ylim=c(0,0.5), xlim = c(-5,5))
curve(dnorm(x), add = TRUE, col = "red")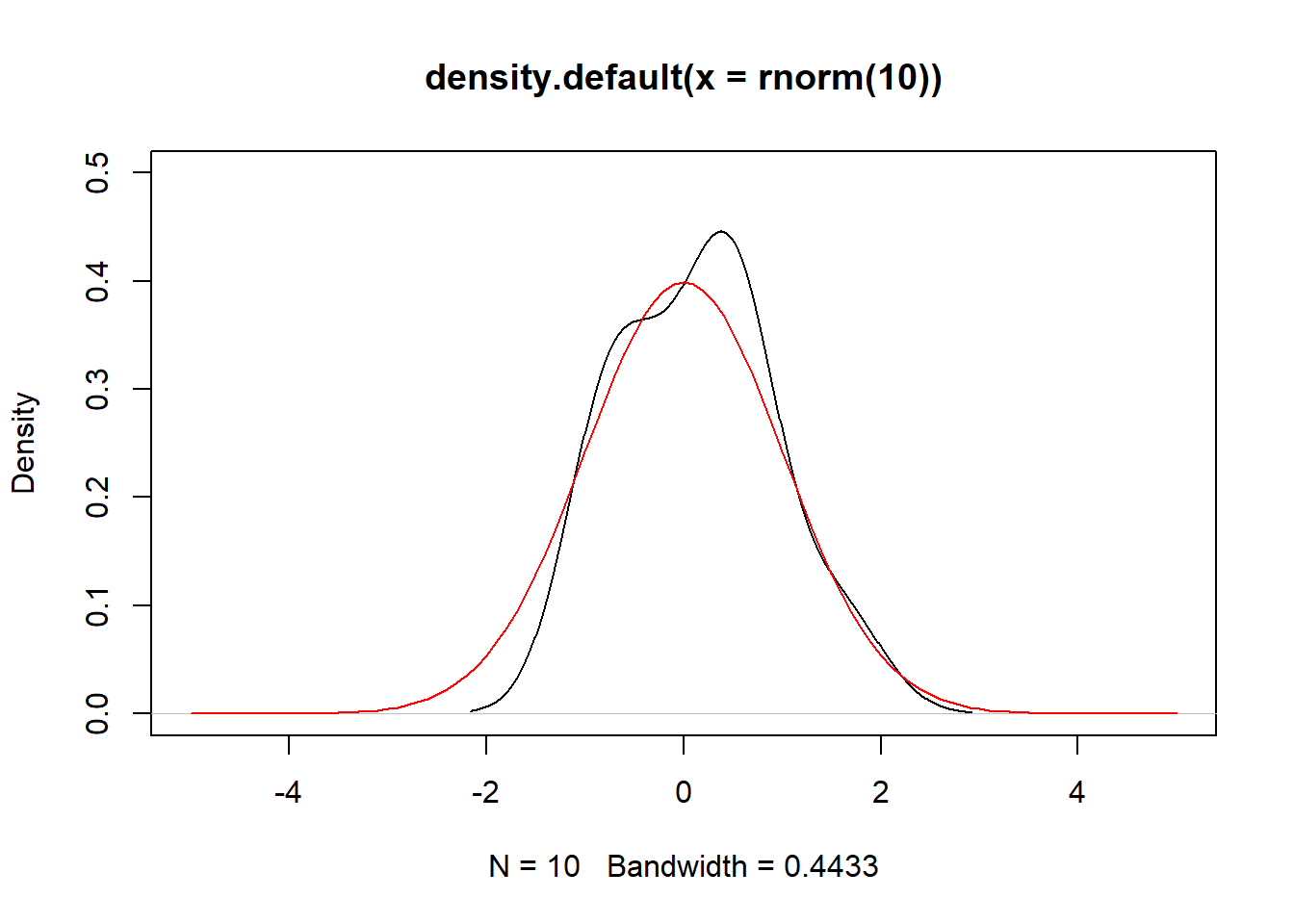

set.seed(1)
plot(density(rnorm(100)), ylim=c(0,0.5), xlim = c(-5,5))
curve(dnorm(x), add = TRUE, col = "red")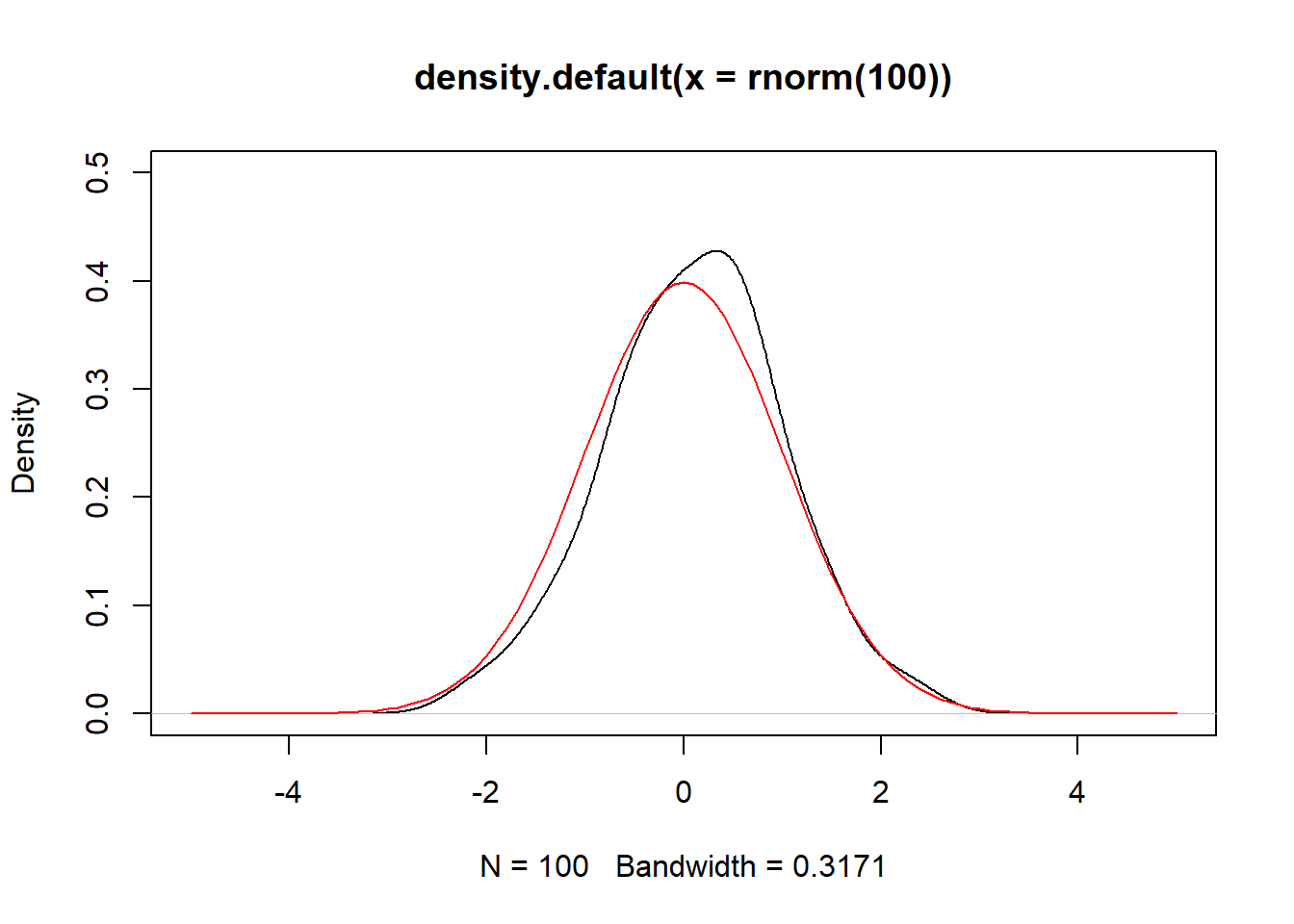

set.seed(1)
plot(density(rnorm(1000)), ylim=c(0,0.5), xlim = c(-5,5))
curve(dnorm(x), add = TRUE, col = "red")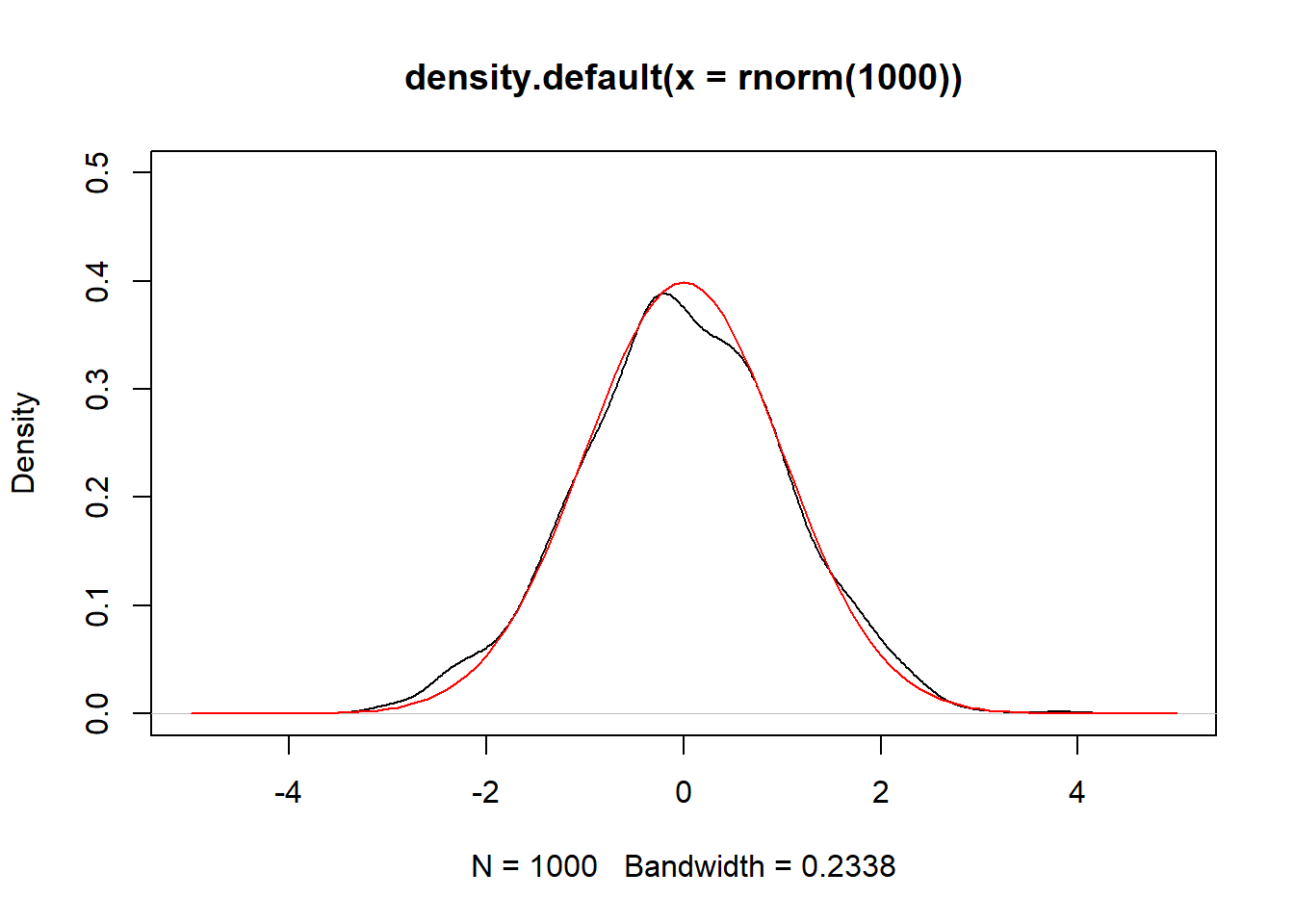

Função Distribuição Cumulativa

Distribuição Teórica

curve(pnorm(x), xlim = c(-5,5))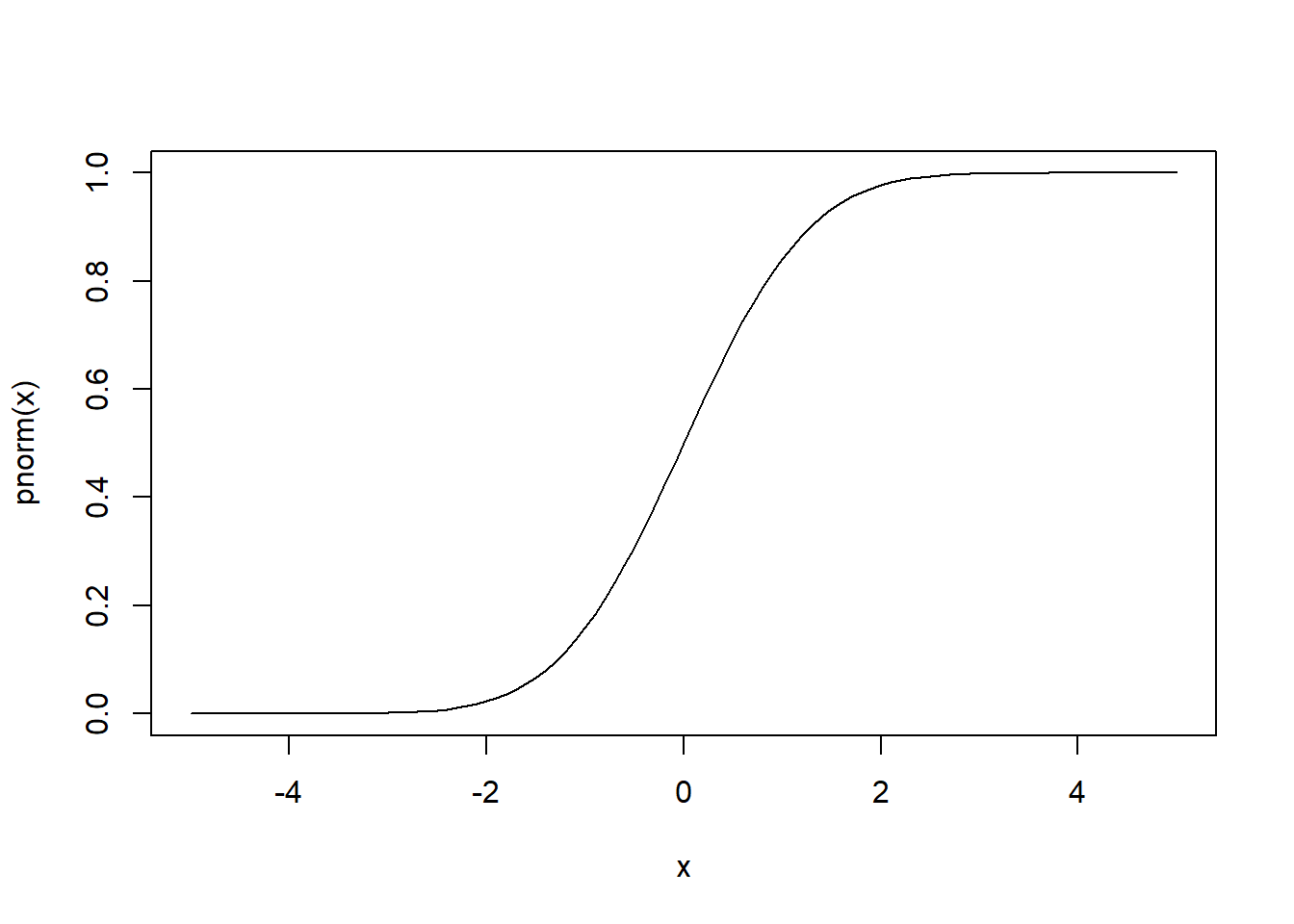

Distribuição Empírica

set.seed(1)
X = rnorm(100) 
P = ecdf(X)

pnorm(0)

## [1] 0.5

P(0)         # This returns the empirical CDF at zero (should be close to 0.5)

## [1] 0.46

plot(P)        # Draws a plot of the empirical CDF (see below)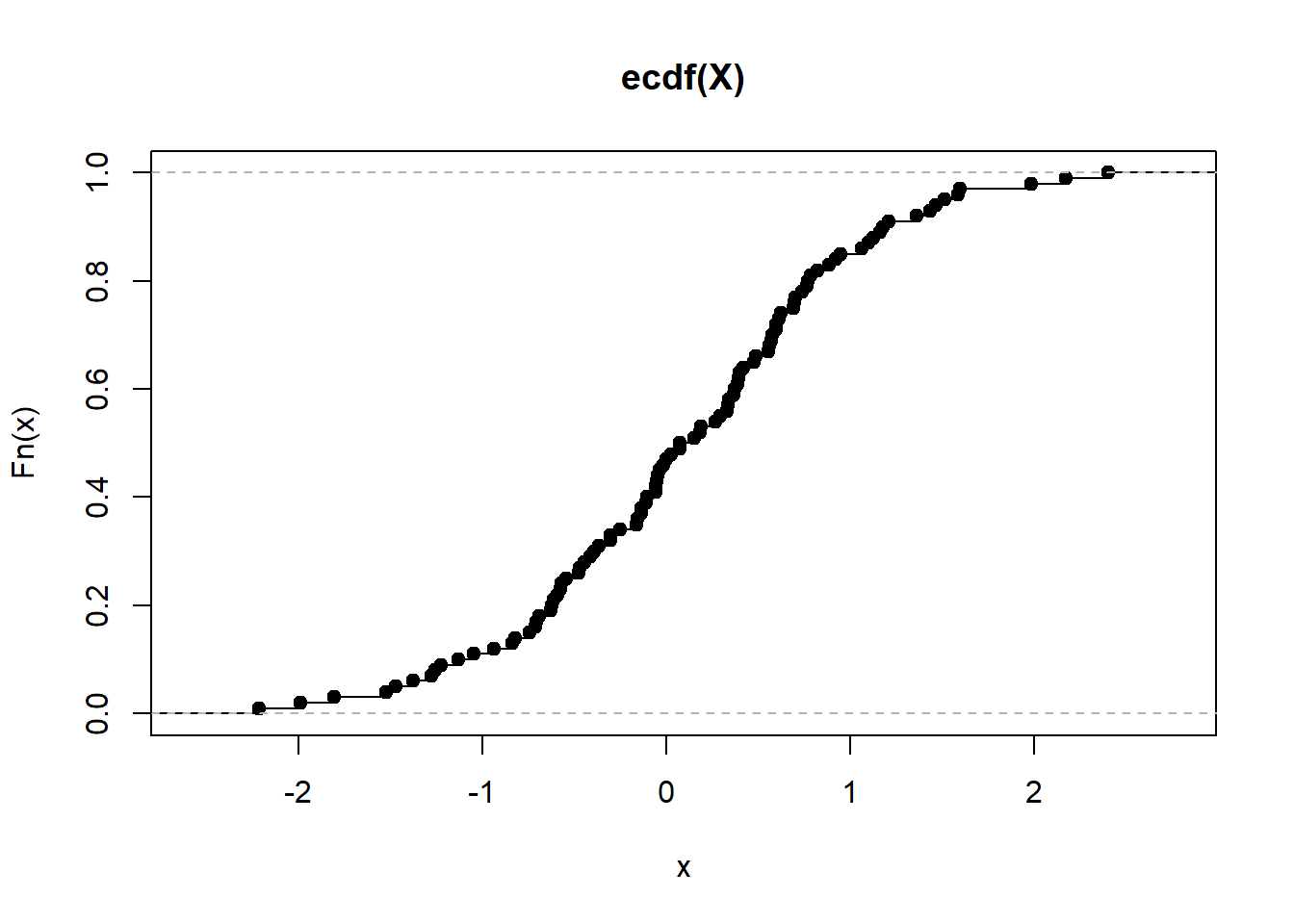

curve(pnorm(x), xlim = c(-5,5))
lines(P, col = "red")        # Draws a plot of the empirical CDF (see below)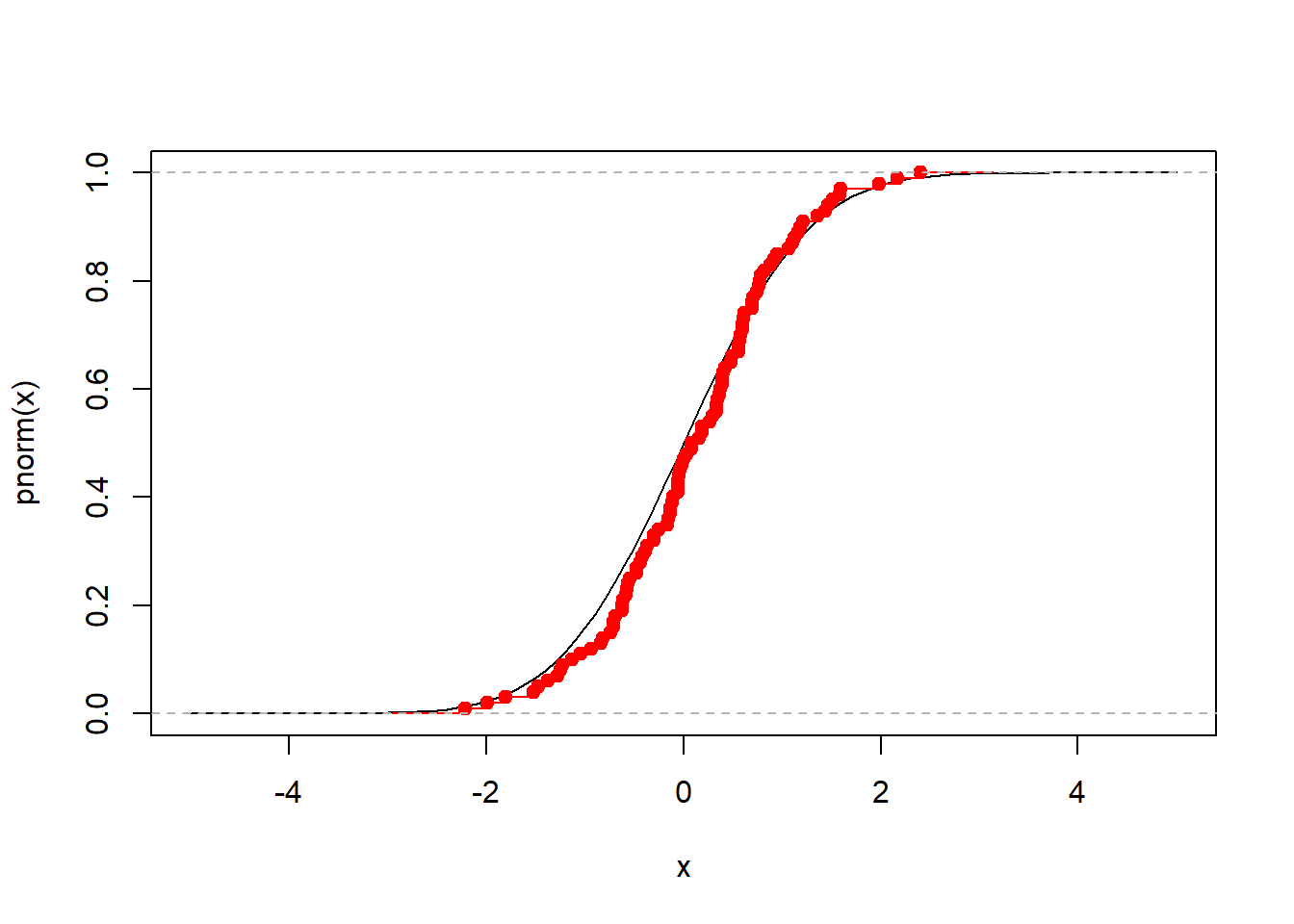

X = rnorm(1000) 
P = ecdf(X)

P(0.0)         # This returns the empirical CDF at zero (should be close to 0.5)

## [1] 0.521

curve(pnorm(x), xlim = c(-5,5))
lines(P, col = "red")        # Draws a plot of the empirical CDF (see below)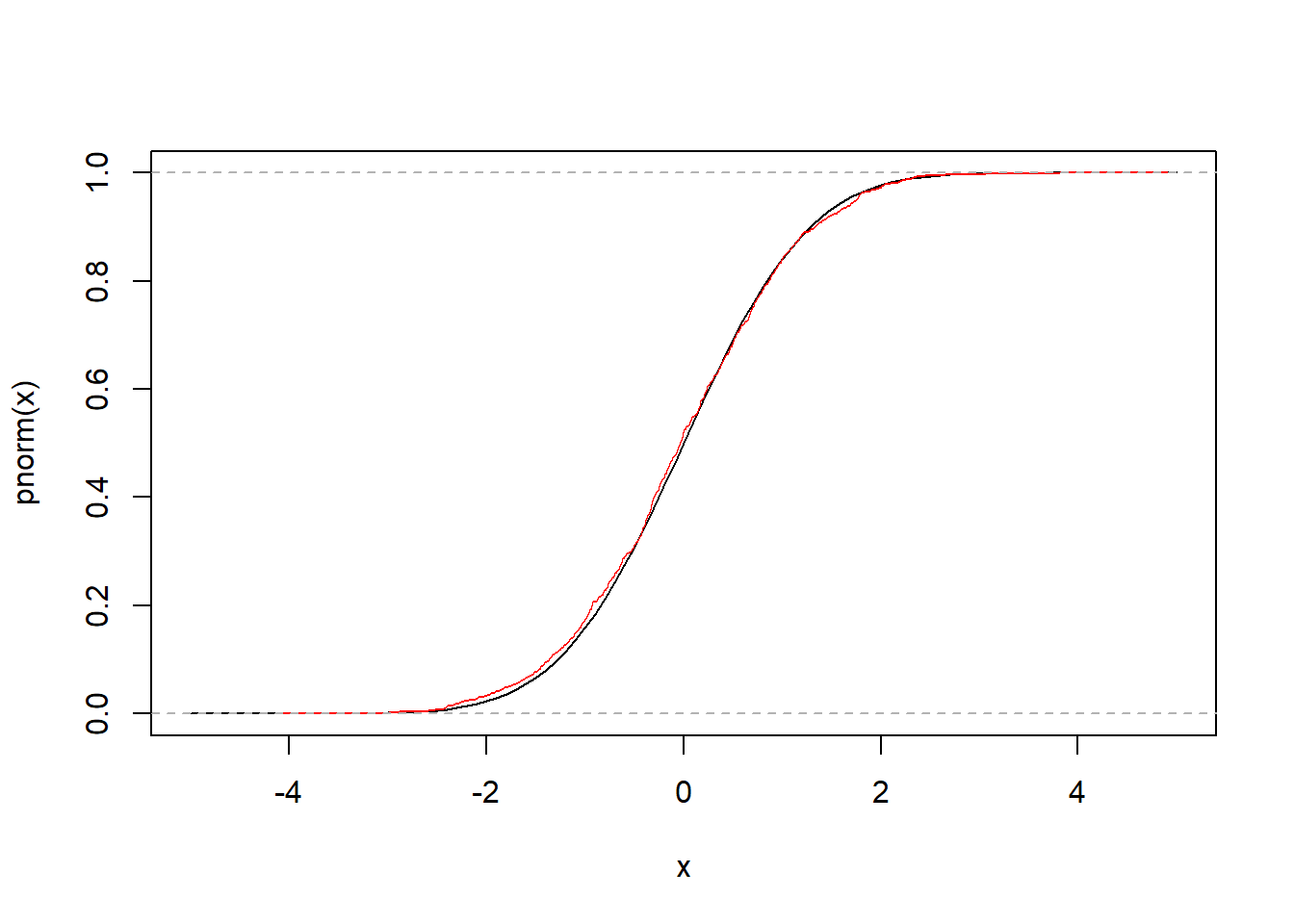

Distribuição Uniforme

X = Unif()
E(X)

## [1] 0.5

mean(runif(10))

## [1] 0.5013657

mean(runif(100))

## [1] 0.4656684

mean(runif(1000))

## [1] 0.5001652

X = Unif(0,10)
E(X)

## [1] 5

mean(runif(10,0,10))

## [1] 5.920047

mean(runif(100,0,10))

## [1] 4.615105

mean(runif(1000,0,10))

## [1] 4.956762

8.3 Introdução à simulação

A simulação de dados é uma ferramenta importante para o aprendizado de características de distribuições de probabilidade e consequentemente para um melhor entendimento do comportamento de um estimador.

Vamos apresentar duas ferramentas do \(R\) que auxiliam na realização de simulações, looping e o comando replicate.

Uma das formas de utilizar looping é com o uso do comando for:

for (i in 1:5){
  print(i)
}

## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5

for (i in c(1,5,3,8)){
  print(i)
}

## [1] 1
## [1] 5
## [1] 3
## [1] 8

v = c(1,4,5,10)
for (n in 1:length(v)){
  print(v[n])
}

## [1] 1
## [1] 4
## [1] 5
## [1] 10

Criar uma matriz:

A = matrix(rep(NA, 25), nrow = 5 )
for (j in 1:dim(A)[2]){
  A[,j] = rnorm(5)
}
A

##             [,1]        [,2]       [,3]        [,4]        [,5]
## [1,] -0.80816189 -1.56379809  1.3697870 -0.41850169  0.78040847
## [2,] -0.60677918 -1.49347152 -0.3783807 -0.03764293 -0.54214238
## [3,]  0.08690882 -1.09713482 -0.7787449  1.18729857 -2.02653215
## [4,] -0.23429703 -0.02910675  1.2640853 -0.10565769 -0.02167199
## [5,]  1.26252690  2.17368492  0.3080131  0.20244165  1.22228261

A = matrix(rep(NA, 25), nrow = 5 )
for (i in 1:dim(A)[1]){
  for (j in 1:dim(A)[2]){
    A[i,j] = rnorm(1)
  }
}
A

##            [,1]       [,2]        [,3]       [,4]       [,5]
## [1,] -0.1736816  0.6640132 -0.54783820 -0.9174420  0.4371058
## [2,] -0.3849686  0.8423753  0.95301631 -0.4106318  0.1008083
## [3,]  0.9207557  1.4595952 -0.39684253 -0.4830838 -0.3162191
## [4,]  1.2100039 -0.7529806 -0.64926724 -0.2542445 -1.2963696
## [5,] -0.4246571 -0.3991557  0.05987491  0.6806779  1.5694218

v = c()
for (i in 1:10){
  v[i] = mean(rnorm(5))
}
v

##  [1]  0.3832562  0.4072287 -1.0581297 -0.2736223  0.2920137  0.3944080
##  [7] -0.3745748  0.1069506 -0.2771388  0.5251626

v = c()
for (n in c(5,10,50,100,1000)){
  for (i in 1:5){
    v[i] = mean(rnorm(n))
  }
}
v

## [1] -0.0166026325 -0.0181839023 -0.0005956172 -0.0375908951  0.0053728775

Comando replicate

set.seed(1)
x = replicate(n = 10, expr = rnorm(1))
x

##  [1] -0.6264538  0.1836433 -0.8356286  1.5952808  0.3295078 -0.8204684
##  [7]  0.4874291  0.7383247  0.5757814 -0.3053884

x1 =c()
set.seed(1)
for (i in 1:10){
  x1[i] = rnorm(1)
}
x1

##  [1] -0.6264538  0.1836433 -0.8356286  1.5952808  0.3295078 -0.8204684
##  [7]  0.4874291  0.7383247  0.5757814 -0.3053884

x == x1

##  [1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE

x = replicate(n = 5, expr = rnorm(10))
x

##              [,1]        [,2]        [,3]       [,4]       [,5]
##  [1,]  1.51178117  0.91897737  1.35867955 -0.1645236  0.3981059
##  [2,]  0.38984324  0.78213630 -0.10278773 -0.2533617 -0.6120264
##  [3,] -0.62124058  0.07456498  0.38767161  0.6969634  0.3411197
##  [4,] -2.21469989 -1.98935170 -0.05380504  0.5566632 -1.1293631
##  [5,]  1.12493092  0.61982575 -1.37705956 -0.6887557  1.4330237
##  [6,] -0.04493361 -0.05612874 -0.41499456 -0.7074952  1.9803999
##  [7,] -0.01619026 -0.15579551 -0.39428995  0.3645820 -0.3672215
##  [8,]  0.94383621 -1.47075238 -0.05931340  0.7685329 -1.0441346
##  [9,]  0.82122120 -0.47815006  1.10002537 -0.1123462  0.5697196
## [10,]  0.59390132  0.41794156  0.76317575  0.8811077 -0.1350546

x = replicate(n = 5, expr = mean(rnorm(10)))
x

## [1]  0.4512100 -0.2477361  0.1273603  0.1123413  0.3474802

x = replicate(n = 5, expr = mean(rnorm(100)))
x

## [1] -0.01984126  0.02244953  0.01877427 -0.05562816 -0.02607009

8.4 Distribuição Amostral

Finalmente, nessa seção, estamos prontos para estudar a distribuição amostral de um estimador.

Estimador da média: \(\bar{x}_n = \frac{1}{n} \sum_{i=1}^nX_i\)

mean(rnorm(100))

## [1] -0.2155784

Vamos estudar algumas características deste estimador analisando aspectos de sua distribuição amostral:

\[E[\bar{X}_n] = \mu \]

mean(replicate(n = 1000, expr = mean(rnorm(10))))

## [1] -0.005145448

\[var[\bar{X}_n] = \frac{\sigma^2}{n}\]

var(replicate(n = 1000, expr = mean(rnorm(10))))

## [1] 0.09110611

var(replicate(n = 1000, expr = mean(rnorm(100))))

## [1] 0.01018165

Distribuição do estimador da média amostral \(\bar{X}_n\):

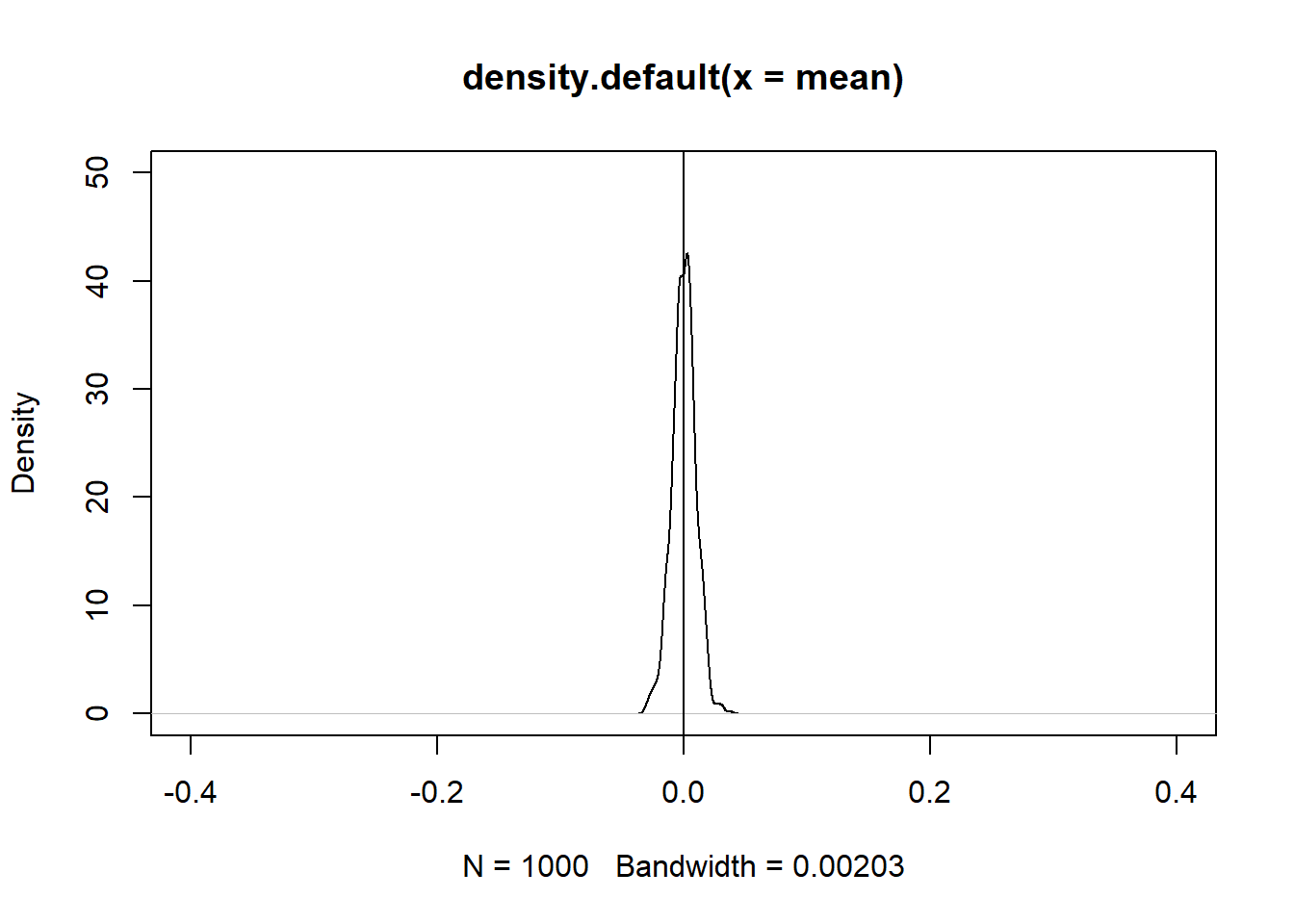
mean = replicate(n = 1000, expr = mean(rnorm(100)))

plot(density(mean),
       ylim = c(0,10),
       xlim = c(-0.4,0.4))
abline(v=0)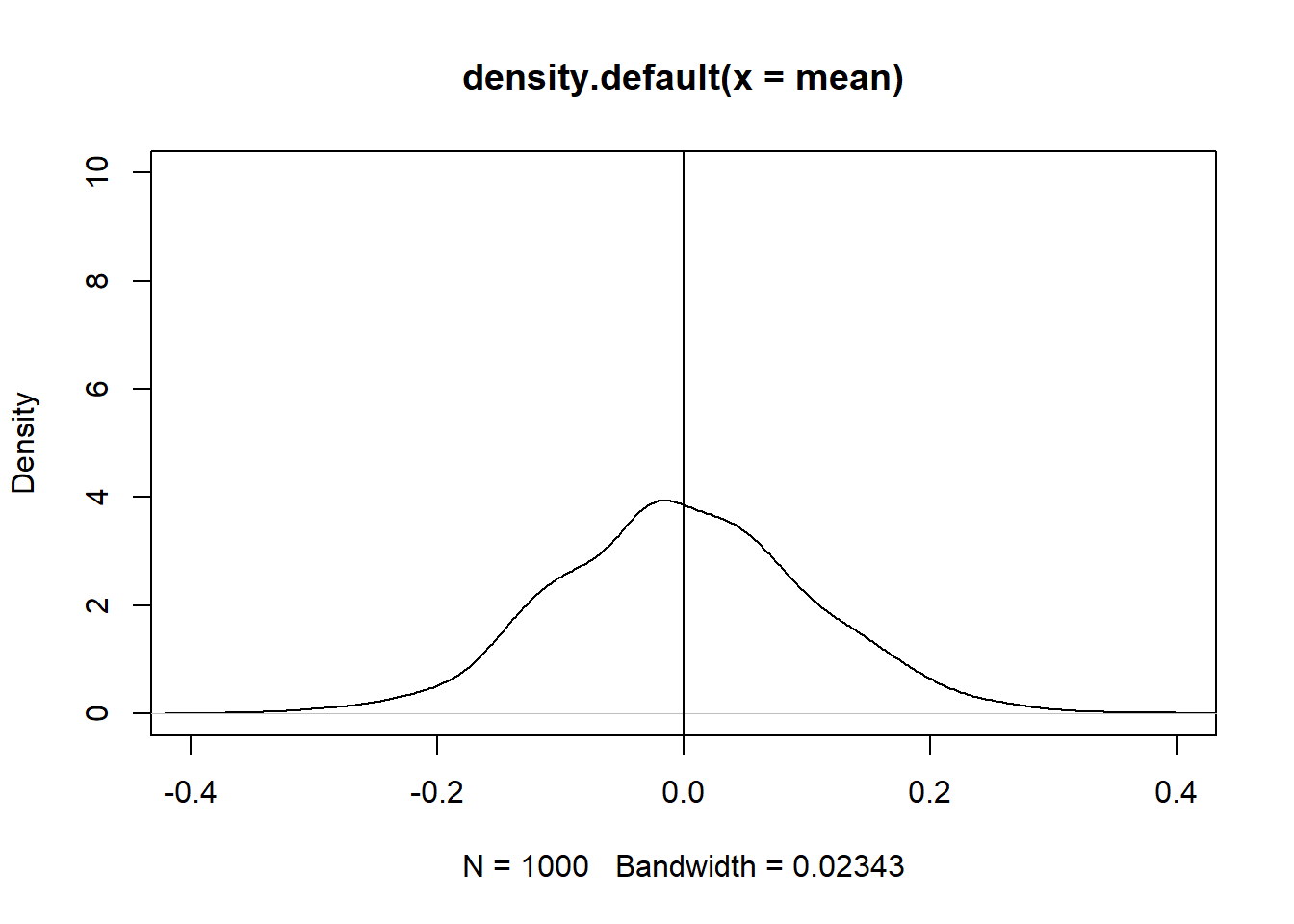

#mean = replicate(n = 1000, expr = mean(rnorm(100)[1])
mean = replicate(n = 1000, expr = mean(rnorm(1000)))
                 
plot(density(mean),
       ylim = c(0,15),
       xlim = c(-0.4,0.4))
abline(v=0)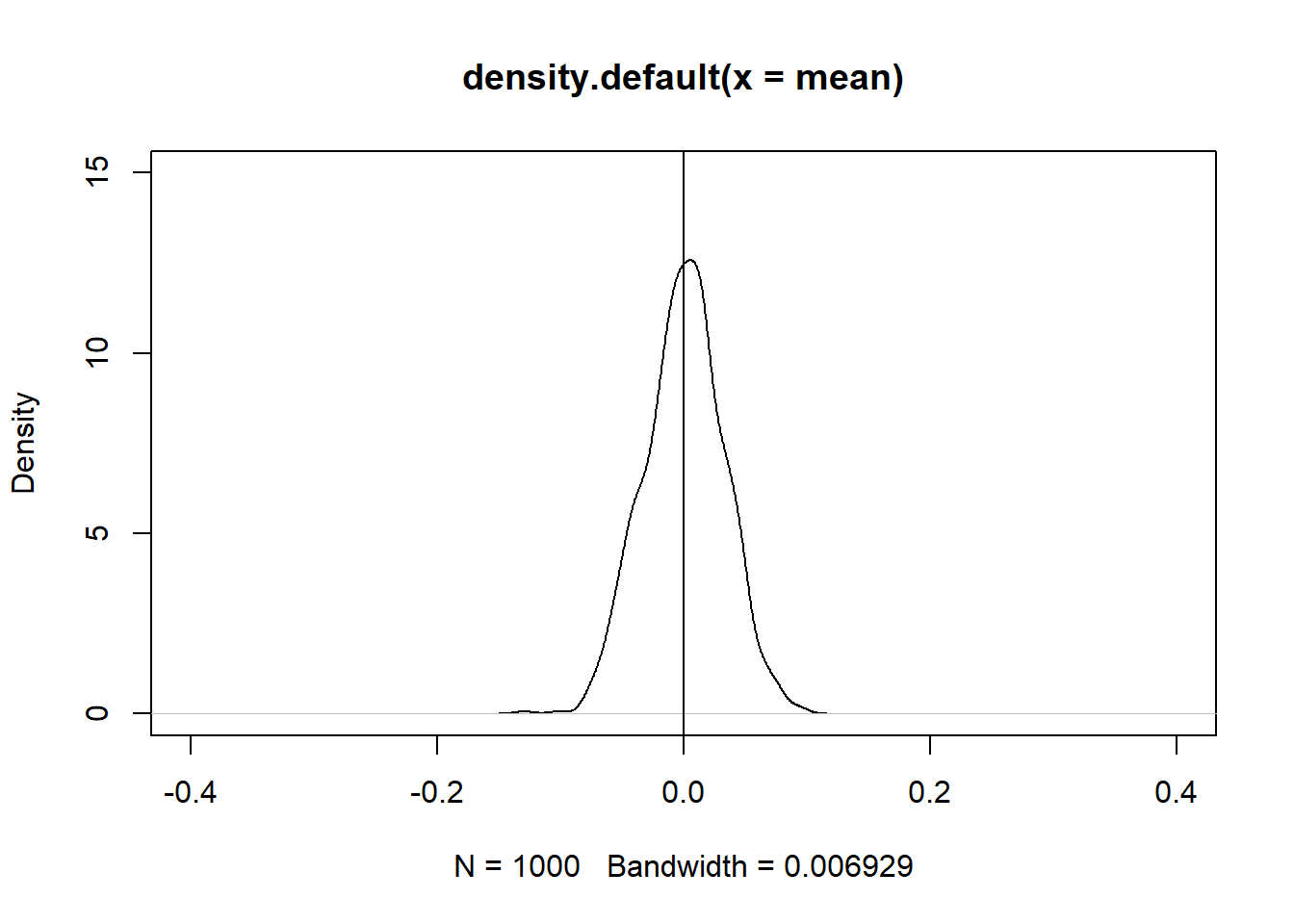

#mean = replicate(n = 1000, expr = mean(rnorm(100)[1])
mean = replicate(n = 1000, expr = mean(rnorm(10000)))
                 
plot(density(mean),
       ylim = c(0,50),
       xlim = c(-0.4,0.4))
abline(v=0)