Capítulo 5 Distribuicoes Discretas

Variáveis aleatórias discretas são caracterizadas pelo seu suporte, que toma valores finitos ou infitos enumeráveis. A cada variável aleatória X é associada uma função de probabilidade ou função de massa de probabilidade.

A Função de probabilidade de uma variável aleatória discreta é \(\pi(x) = P(X=x)\)

  x = c(0,1,2,3)
  f = c(1/8, 3/8 , 2/8, 2/8)

plot(x,f, type = "h")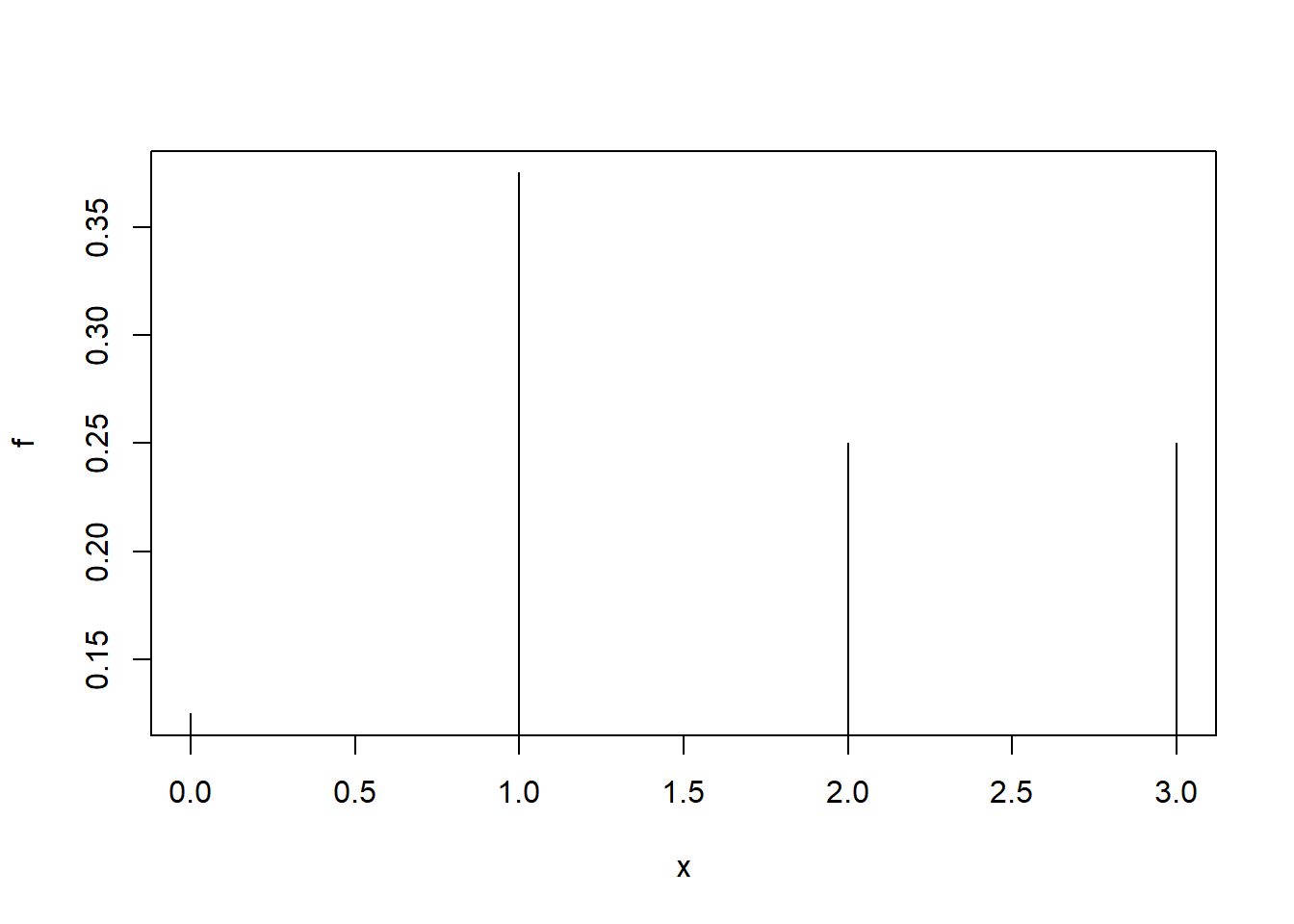

Esperança

Para uma Variável Aleatória Discreta com suporte {x_j}, a esperança de X é:

$ E(X) = _{j=1}^{}x_j _j$

mu = sum(x * f)
mu

## [1] 1.625

Variância

sigma2 <- sum((x-mu)^2 * f)
sigma2

## [1] 0.984375

Desvio Padrão

sigma = sqrt(sigma2)
sigma

## [1] 0.9921567

OBservação: é preciso ter cuidado com variáveis que possuem probabilidades desiguais. As funções mean e var só devem ser usadas nos casos de probabilidades iguais. Para exemplificar esse problema, vamos calcular abaixo a média, a variância e o desvio padrão da variável \(x\).

mean(x)

## [1] 1.5

var(x)

## [1] 1.666667

sqrt(var(x))

## [1] 1.290994

O pacote distrEx fornece funções para calcular alguns momentos de distribuições mesmo com probabilidades desiguais.

#install.packages("distrEx")
library(distrEx)

## Warning: package 'distrEx' was built under R version 4.1.3

## Carregando pacotes exigidos: distr

## Warning: package 'distr' was built under R version 4.1.3

## Carregando pacotes exigidos: startupmsg

## Utilities for Start-Up Messages (version 0.9.6)

## For more information see ?"startupmsg", NEWS("startupmsg")

## Carregando pacotes exigidos: sfsmisc

## Warning: package 'sfsmisc' was built under R version 4.1.3

## Object Oriented Implementation of Distributions (version 2.8.0)

## Attention: Arithmetics on distribution objects are understood as operations on corresponding random variables (r.v.s); see distrARITH().
## Some functions from package 'stats' are intentionally masked ---see distrMASK().
## Note that global options are controlled by distroptions() ---c.f. ?"distroptions".

## For more information see ?"distr", NEWS("distr"), as well as
##   http://distr.r-forge.r-project.org/
## Package "distrDoc" provides a vignette to this package as well as to several extension packages; try vignette("distr").

## 
## Attaching package: 'distr'

## The following object is masked from 'package:prob':
## 
##     prob

## The following object is masked from 'package:fAsianOptions':
## 
##     igamma

## The following objects are masked from 'package:stats':
## 
##     df, qqplot, sd

## Extensions of Package 'distr' (version 2.8.0)

## Note: Packages "e1071", "moments", "fBasics" should be attached /before/ package "distrEx". See distrExMASK().Note: Extreme value distribution functionality has been moved to
##       package "RobExtremes". See distrExMOVED().

## For more information see ?"distrEx", NEWS("distrEx"), as well as
##   http://distr.r-forge.r-project.org/
## Package "distrDoc" provides a vignette to this package as well as to several related packages; try vignette("distr").

## 
## Attaching package: 'distrEx'

## The following object is masked from 'package:timeSeries':
## 
##     median

## The following objects are masked from 'package:timeDate':
## 
##     kurtosis, skewness

## The following objects are masked from 'package:stats':
## 
##     IQR, mad, median, var

Criar uma variável aleatória com a mesma distribuição da variável \(x\) criada anteriormente usando a função DiscreteDistribution:

X <- DiscreteDistribution(supp = 0:3, prob = c(1,3,2,2)/8)

Calcular a esperança, a variância e o desvio padrão.

E(X)

## [1] 1.625

var(X)

## [1] 0.984375

sd(X)

## [1] 0.9921567

Transformação de \(X\)

\(E[g(x)] = \sum_{j=1}^{\infty} g(x_j) \pi_j\)

  g = x*2 + 3
  sum(g * f)

## [1] 6.25

E(X*2+3)

## [1] 6.25

Linearidade da Esperança

\(E(a+bX) = a + bE(X)\)

E(3+2*X) == 3+2*E(X)

## [1] TRUE

  3 + 2*mu

## [1] 6.25

Função de Distribuição (Função de Distribuição Cumulativa)

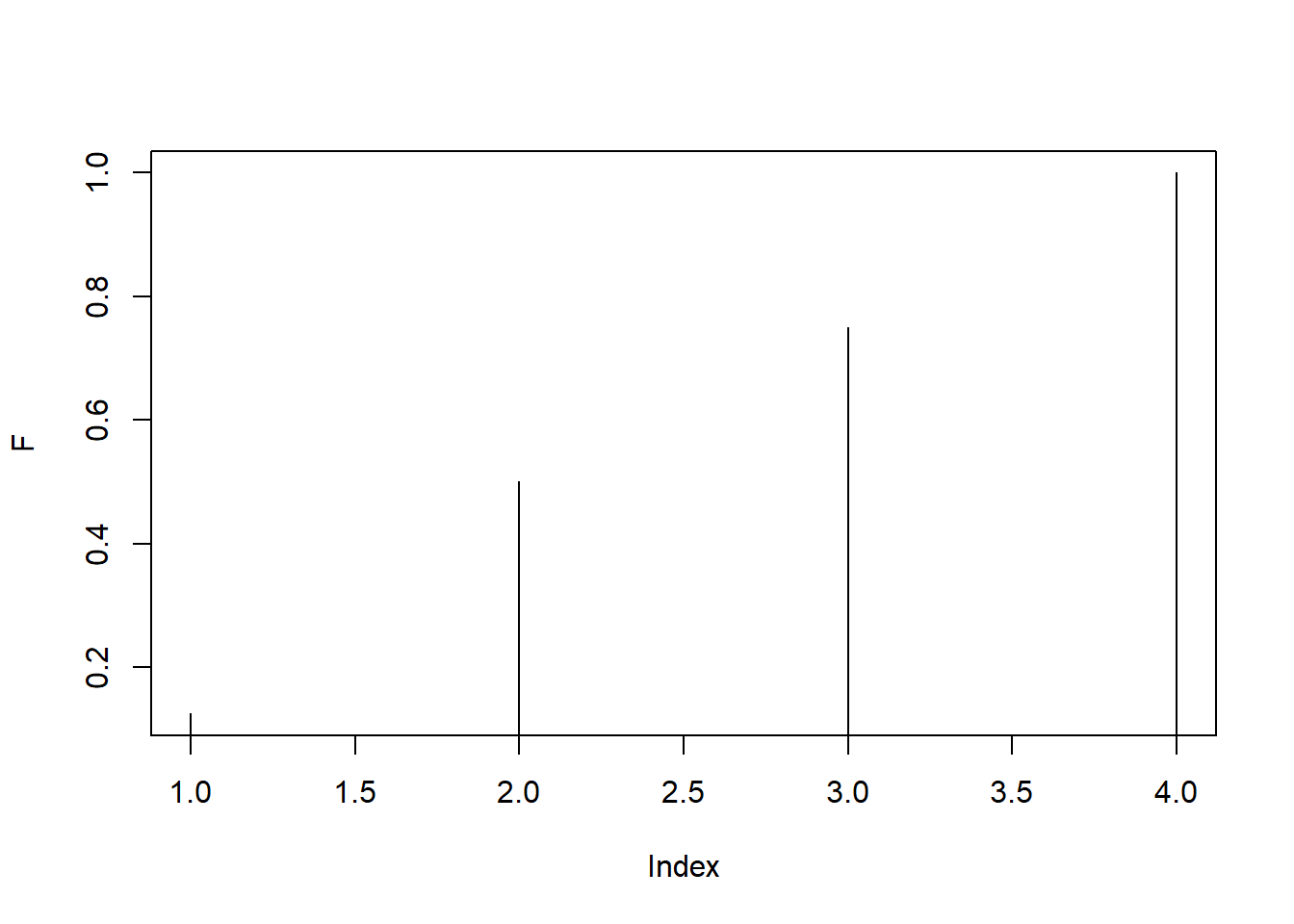
A função de distribuição é \(F(x) = P(X \le x)\), que é a probabilidade do evento \({X \le x}\).

Para uma Variável Aleatória Discreta, com pontos de suporte \({x_j}\), a função de distribuição nos pontos do suporte é igual à soma cumulativa das probabilidades.

\(F(x_j) = \sum_{k=1}^j \pi(x_j)\)

F = cumsum(f)
F

## [1] 0.125 0.500 0.750 1.000

plot(F, type = "h")