Capítulo 16 Dados em Painel com efeitos nao observados
Modelo geral: \(y_{it} = X_{it}\beta + c_i + u_{it}\)
Exemplo de modelo com \(n = 3\) e \(T = 2\).
set.seed(1)
n = 3
T = 2
id = seq(1:n)
period = matrix(seq(1:T),ncol = 1)
UM = matrix(rep(1,n), ncol = 1)
period = kronecker(period,UM)
J = matrix(rep(1,T), ncol = 1) # vetor de 1'sc = rnorm(n,5) # efeito individual
x11 = matrix(rnorm(n,10,10) , ncol = 1)
x12 = rnorm(n)
x21 = matrix(rnorm(n,5,15) + 0.7*c, ncol = 1)
x22 = 1.5*c + rnorm(n)
X1 = cbind(x11,x21)
X2 = cbind(x12,x22)
X = rbind(X1,X2)
u1 = matrix(rnorm(n,0,3),ncol=1)
u2 = matrix(rnorm(n,0,2),ncol = 1)
u = rbind(u1,u2)
beta = c(5,-3)
y1 = X1%*%beta + 10*c + u1
y2 = X2%*%beta + 12*c + u2
y = rbind(y1,y2)modelo = cbind(id,period,X,kronecker(J,c),u)
modelo= modelo[order(modelo[,1],modelo[,2],decreasing=FALSE),]
colnames(modelo) = c("id","período","X1","X2","c","u")
head(modelo)## id período X1 X2 c u
## [1,] 1 1 25.9528080 3.480657 4.373546 -0.13480083
## [2,] 1 2 0.4874291 5.939079 4.373546 1.64244239
## [3,] 2 1 13.2950777 31.305268 5.183643 -0.04857079
## [4,] 2 2 0.7383247 5.560765 5.183643 1.18780264
## [5,] 3 1 1.7953162 13.762709 4.164371 2.83150863
## [6,] 3 2 0.5757814 7.371488 4.164371 1.8379547416.0.1 Efeitos Fixos
Transformmação within
## 1 individuo e 2 períodos de tempo
um = matrix(rep(1,2),ncol = 1) ## t = 2
um## [,1]
## [1,] 1
## [2,] 1solve(t(um)%*%um)%*%t(um)## [,1] [,2]
## [1,] 0.5 0.5y = matrix(c(3,6),ncol = 1) ## t = 2,
y## [,1]
## [1,] 3
## [2,] 6solve(t(um)%*%um)%*%t(um)%*%y## [,1]
## [1,] 4.5M = diag(2) - um%*%solve(t(um)%*%um)%*%t(um)
M## [,1] [,2]
## [1,] 0.5 -0.5
## [2,] -0.5 0.5M%*%y## [,1]
## [1,] -1.5
## [2,] 1.5library(simex)## Warning: package 'simex' was built under R version 4.1.3## 2 individuo e 2 períodos de tempo
N = 2
T = 2
um = matrix(rep(1,N),ncol = 1) ## t = 2
um## [,1]
## [1,] 1
## [2,] 1D = diag.block(um,T)
D## [,1] [,2]
## [1,] 1 0
## [2,] 1 0
## [3,] 0 1
## [4,] 0 1solve(t(D)%*%D)%*%t(D)## [,1] [,2] [,3] [,4]
## [1,] 0.5 0.5 0.0 0.0
## [2,] 0.0 0.0 0.5 0.5y = matrix(c(3,6,8,12),ncol = 1) ## t = 2,
y## [,1]
## [1,] 3
## [2,] 6
## [3,] 8
## [4,] 12solve(t(D)%*%D)%*%t(D)%*%y## [,1]
## [1,] 4.5
## [2,] 10.0M = diag(N*T) - D%*%solve(t(D)%*%D)%*%t(D)
M## [,1] [,2] [,3] [,4]
## [1,] 0.5 -0.5 0.0 0.0
## [2,] -0.5 0.5 0.0 0.0
## [3,] 0.0 0.0 0.5 -0.5
## [4,] 0.0 0.0 -0.5 0.5M%*%y## [,1]
## [1,] -1.5
## [2,] 1.5
## [3,] -2.0
## [4,] 2.0## 2 individuo e 3 períodos de tempo
N = 2
T = 3
um = matrix(rep(1,N),ncol = 1) ## t = 2
um## [,1]
## [1,] 1
## [2,] 1D = diag.block(um,T)
D## [,1] [,2] [,3]
## [1,] 1 0 0
## [2,] 1 0 0
## [3,] 0 1 0
## [4,] 0 1 0
## [5,] 0 0 1
## [6,] 0 0 1solve(t(D)%*%D)%*%t(D)## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 0.5 0.5 0.0 0.0 0.0 0.0
## [2,] 0.0 0.0 0.5 0.5 0.0 0.0
## [3,] 0.0 0.0 0.0 0.0 0.5 0.5y = matrix(c(3,6,8,12,4,4),ncol = 1) ## t = 2,
y## [,1]
## [1,] 3
## [2,] 6
## [3,] 8
## [4,] 12
## [5,] 4
## [6,] 4solve(t(D)%*%D)%*%t(D)%*%y## [,1]
## [1,] 4.5
## [2,] 10.0
## [3,] 4.0M = diag(N*T) - D%*%solve(t(D)%*%D)%*%t(D)
M## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 0.5 -0.5 0.0 0.0 0.0 0.0
## [2,] -0.5 0.5 0.0 0.0 0.0 0.0
## [3,] 0.0 0.0 0.5 -0.5 0.0 0.0
## [4,] 0.0 0.0 -0.5 0.5 0.0 0.0
## [5,] 0.0 0.0 0.0 0.0 0.5 -0.5
## [6,] 0.0 0.0 0.0 0.0 -0.5 0.5M%*%y## [,1]
## [1,] -1.5
## [2,] 1.5
## [3,] -2.0
## [4,] 2.0
## [5,] 0.0
## [6,] 0.0Estimação por Efeitos Fixos
set.seed(1)
n = 500
T = 2
id = seq(1:n)
period = matrix(seq(1:T),ncol = 1)
I = matrix(rep(1,n), ncol = 1)
period = kronecker(period,I)
c = rnorm(n,5,7)
u1 = matrix(rnorm(n,0,8),ncol=1)
u2 = matrix(rnorm(n,0,10),ncol = 1)
u = rbind(u1,u2)
J = matrix(rep(1,T), ncol = 1)
x11 = rnorm(n,10,10)
x12 = rnorm(n)
x21 = rnorm(n,5,15) + 0.7*c
x22 = 1.5*c + rnorm(n)
beta = c(10,5,-3)
X1 = cbind(1,x11,x21)
X2 = cbind(1,x12,x22)
y1 = X1%*%beta + 10*c + u1
y2 = X2%*%beta + 12*c + u2
X = rbind(X1,X2)modelo = cbind(id,period,X,kronecker(J,c),u)
modelo= modelo[order(modelo[,1],modelo[,2],decreasing=FALSE),]
head(modelo)## id x11 x21
## [1,] 1 1 1 18.5004347 -21.65187701 0.6148233 0.618425
## [2,] 1 2 1 -0.8861496 1.66134991 0.6148233 11.349651
## [3,] 2 1 1 0.7468700 -0.77075794 6.2855033 -2.374949
## [4,] 2 2 1 -1.9222549 9.81486363 6.2855033 11.119318
## [5,] 3 1 1 18.9358121 -2.69495097 -0.8494003 -9.465938
## [6,] 3 2 1 1.6197007 0.02229674 -0.8494003 -8.707776X = modelo[,c(3,4,5)]
y = X%*%beta + kronecker(c,J) + upols = solve(t(X)%*%X)%*%t(X)%*%y
pols## [,1]
## 12.410487
## x11 5.064769
## x21 -2.733347X = modelo[,c(4,5)]
I = diag(n*T)
D = diag.block(J,n)
M = I - (D%*%solve(t(D)%*%D)%*%t(D))
x_til = M%*%X
y_til = M%*%y fe = solve(t(x_til)%*%x_til)%*%t(x_til)%*%y_til
fe## [,1]
## x11 5.027163
## x21 -2.981721e_hat = y_til - x_til%*%fe
sigma_hat = (1/(n*(T-1)-2)) * t(e_hat)%*%e_hat # n-k correção de viés
#sigma_hat
V = sigma_hat[1,1] * solve(t(x_til)%*%x_til)
#V
ep = sqrt(diag(V))
ep## x11 x21
## 0.03914274 0.03388399Simulações
fe = function(n){
n = 100
id = seq(1:n)
T = 2
period = matrix(seq(1:T),ncol = 1)
I = matrix(rep(1,n), ncol = 1)
period = kronecker(period,I)
c = rnorm(n,10,10)
u1 = matrix(rnorm(n,0,8),ncol=1)
u2 = matrix(rnorm(n,0,9),ncol = 1)
u = rbind(u1,u2)
J = matrix(rep(1,T), ncol = 1)
x11 = matrix(rnorm(n,10,10) , ncol = 1)
x12 = rnorm(n)
x21 = matrix(rnorm(n,5,15) + 0.7*c, ncol = 1)
x22 = 1.5*c + rnorm(n)
beta = c(10,5,-3)
X1 = cbind(1,x11,x21)
X2 = cbind(1,x12,x22)
X = rbind(X1,X2)
modelo = cbind(id,X,kronecker(J,c),u,period)
modelo= modelo[order(modelo[,1],modelo[,7],decreasing=FALSE),]
#head(modelo)
X = modelo[,c(2,3,4)]
y = X%*%beta + kronecker(c,J) + u
bpols = solve(t(X)%*%X)%*%t(X)%*%y
bpols
X = modelo[,c(3,4)]
I = diag(n*T)
D = diag.block(J,n)
M = I - (D%*%solve(t(D)%*%D)%*%t(D))
x_til = M%*%X
y_til = M%*%y
bfe = solve(t(x_til)%*%x_til)%*%t(x_til)%*%y_til
bfe
return(c(bpols,bfe))
}z = replicate(1000, expr = fe(100))
par(mfrow = c(2, 2))
plot(density(z[2, ]), xlim = c(4,6), main = "Beta1 POLS")
abline(v = 5)
plot(density(z[3, ]), xlim = c(-4,-2), main = "Beta2 POLS")
abline(v = -3)
plot(density(z[4, ]), xlim = c(4,6), main = "Beta1 FE")
abline(v = 5)
plot(density(z[5, ]), xlim = c(-4,-2), main = "Beta2 FE")
abline(v = -3)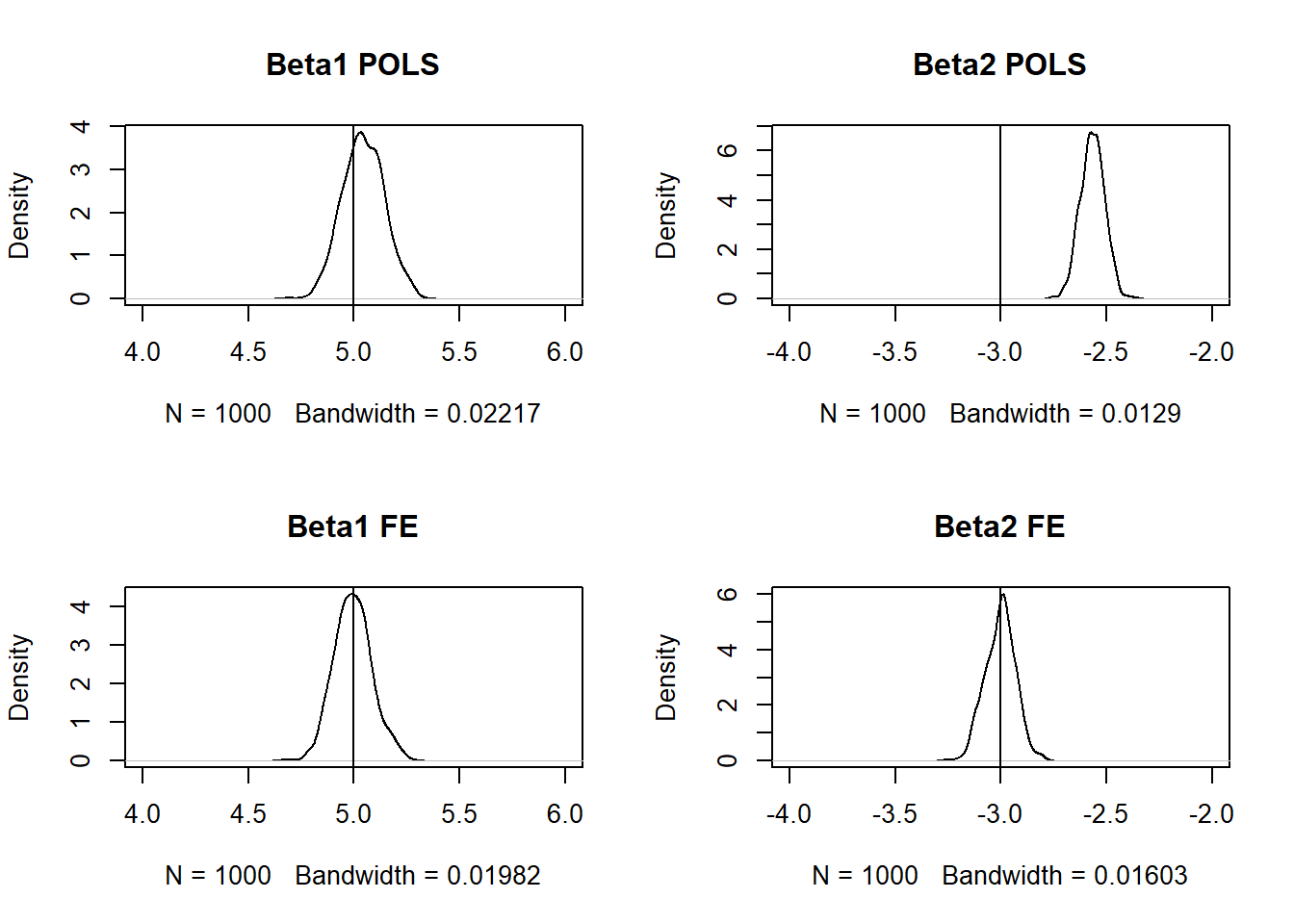
16.1 Efeitos Aleatórios
set.seed(1)
n = 500
id = seq(1:n)
T = 2
period = matrix(seq(1:T),ncol = 1)
I = matrix(rep(1,n), ncol = 1)
period = kronecker(period,I)
sigmac=10
c = rnorm(n,0,sigmac)
sigmau = 5
u1 = matrix(rnorm(n,0,sigmau),ncol=1)
u2 = matrix(rnorm(n,0,sigmau),ncol = 1)
u = rbind(u1,u2)
J = matrix(rep(1,T), ncol = 1)It = diag(T)
omega = sigmau^2*It + sigmac^2*(J%*%t(J))
omega## [,1] [,2]
## [1,] 125 100
## [2,] 100 125v = kronecker(J,c) + ux11 = matrix(rnorm(n,10,10) , ncol = 1)
x12 = 0.8*x11 + rnorm(n)
x21 = matrix(rnorm(n,5,15), ncol = 1)
x22 = 0.5*x21 + rnorm(n)
beta = c(10,5,-3)
X1 = cbind(1,x11,x21)
X2 = cbind(1,x12,x22)
y1 = X1%*%beta + c + u1
y2 = X2%*%beta + c + u2
X = rbind(X1,X2)
y = X%*%beta + kronecker(J,c) + umodelo = cbind(y,X,id,kronecker(J,c),v,u,period)
modelo= modelo[order(modelo[,5],modelo[,9],decreasing=FALSE),]
head(modelo)## id
## [1,] 162.87091 1 18.500435 -22.0822533 1 -6.264538 -5.8780225 0.3865156 1
## [2,] 109.88731 1 13.914198 -10.3020117 1 -6.264538 -0.5897127 5.6748254 2
## [3,] 29.59827 1 0.746870 -5.1706102 2 1.836433 0.3520900 -1.4843432 1
## [4,] 17.36839 1 -1.324759 -2.1986964 2 1.836433 7.3960925 5.5596592 2
## [5,] 96.70768 1 18.935812 -2.1003708 3 -8.356286 -14.2724973 -5.9162112 1
## [6,] 80.39294 1 16.768350 0.2462118 3 -8.356286 -12.7101743 -4.3538882 2bpols = solve(t(X)%*%X)%*%t(X)%*%y
bpols## [,1]
## [1,] 9.583563
## [2,] 5.069931
## [3,] -3.022429e_hat1 = y1 - X1%*%bpols
e_hat2 = y2 - X2%*%bpols
e_hat = cbind(e_hat1,e_hat2)sigma = t(e_hat)%*%e_hat
sigma/n## [,1] [,2]
## [1,] 125.05625 95.94474
## [2,] 95.94474 124.32150I = diag(n)
S = kronecker(solve(sigma),I)Bre = solve(t(X)%*%S%*%X)%*%t(X)%*%S%*%y
Bre## [,1]
## [1,] 9.598763
## [2,] 5.065440
## [3,] -3.015998V_h = solve(t(X)%*%(S)%*%X)
V_h = (1/n) * V_h
ep_h = sqrt(diag(V_h))
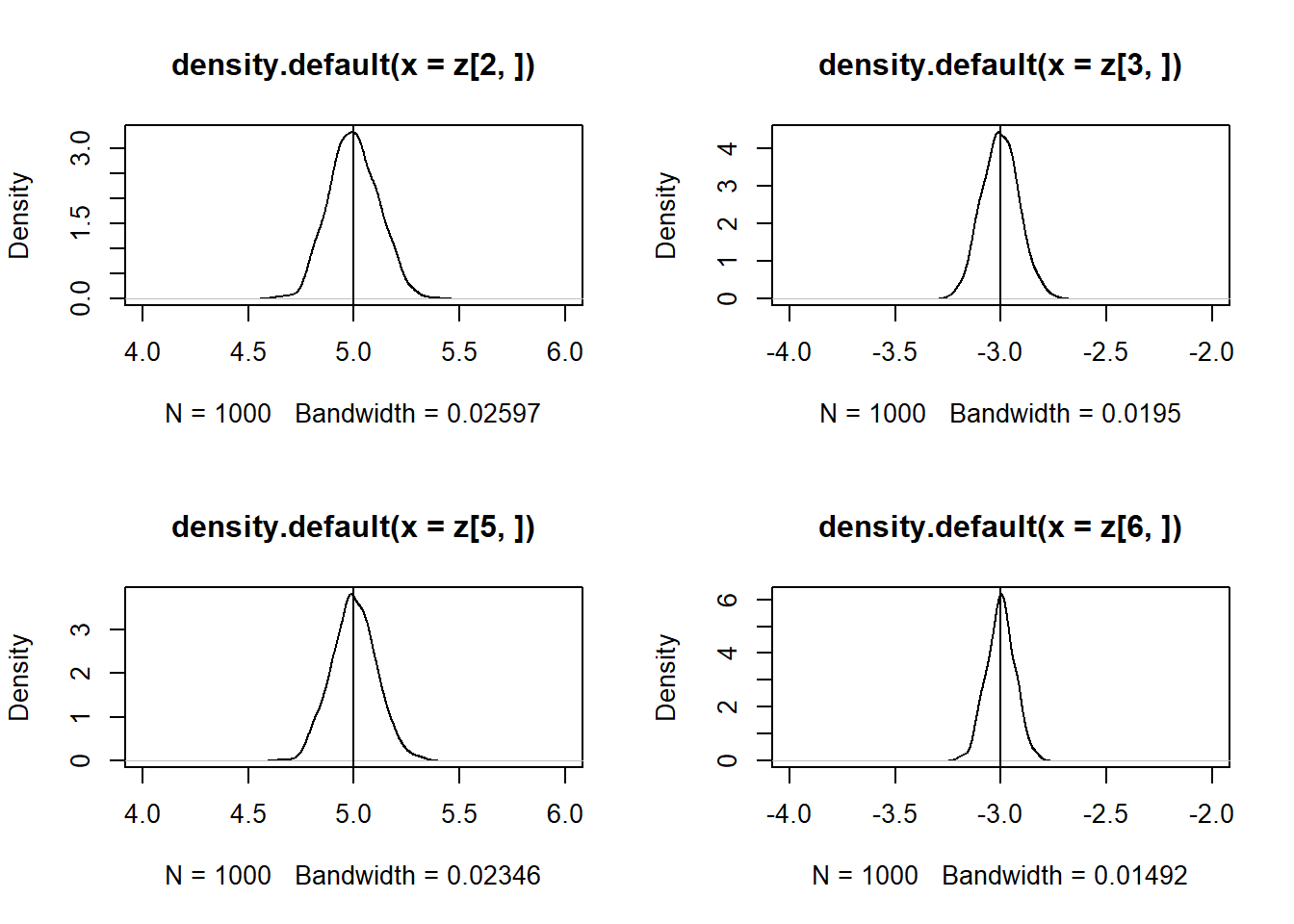
ep_h## [1] 0.61683692 0.04478039 0.02921716Simulações
re = function(n){
id = seq(1:n)
T = 2
period = matrix(seq(1:T),ncol = 1)
I = matrix(rep(1,n), ncol = 1)
period = kronecker(period,I)
sigmac=10
c = rnorm(n,0,sigmac)
sigmau = 5
u1 = matrix(rnorm(n,0,sigmau),ncol=1)
u2 = matrix(rnorm(n,0,sigmau),ncol = 1)
u = rbind(u1,u2)
J = matrix(rep(1,T), ncol = 1)
x11 = matrix(rnorm(n,10,10) , ncol = 1)
x12 = 0.8*x11 + rnorm(n)
x21 = matrix(rnorm(n,5,15), ncol = 1)
x22 = 0.5*x21 + rnorm(n)
beta = c(10,5,-3)
X1 = cbind(1,x11,x21)
X2 = cbind(1,x12,x22)
y1 = X1%*%beta + c + u1
y2 = X2%*%beta + c + u2
X = rbind(X1,X2)
y = X%*%beta + kronecker(J,c) + u
bpols = solve(t(X)%*%X)%*%t(X)%*%y
bpols
e_hat1 = y1 - X1%*%bpols
e_hat2 = y2 - X2%*%bpols
e_hat = cbind(e_hat1,e_hat2)
sigma = t(e_hat)%*%e_hat
I = diag(n)
S = kronecker(solve(sigma),I)
Bre = solve(t(X)%*%S%*%X)%*%t(X)%*%S%*%y
Bre
return(c(bpols,Bre))
}z = replicate(1000, expr = re(100))
par(mfrow = c(2, 2))
plot(density(z[2, ]), xlim = c(4,6))
abline(v = 5)
plot(density(z[3, ]), xlim = c(-4,-2))
abline(v = -3)
plot(density(z[5, ]), xlim = c(4,6))
abline(v = 5)
plot(density(z[6, ]), xlim = c(-4,-2))
abline(v = -3)