Documento 17 Regresion - Fuel Efficiency
Usaremos el dataset FuelEfficiency.csv del CV. El objetivo es ajustar la efciencia de consumo de gasoil (fuel).
Los principales atributos son: GPM (gallons per 100 miles), MPG (miles per gallon), WT (weigth), DIS (distance), HP (horsepower), NC (number of cylinders).
Importar el dataset y gráficamente encontrar relaciones entre las variables.
## Parsed with column specification:
## cols(
## MPG = col_double(),
## GPM = col_double(),
## WT = col_double(),
## DIS = col_double(),
## NC = col_double(),
## HP = col_double(),
## ACC = col_double(),
## ET = col_double()
## )## [1] "MPG" "GPM" "WT" "DIS" "NC" "HP"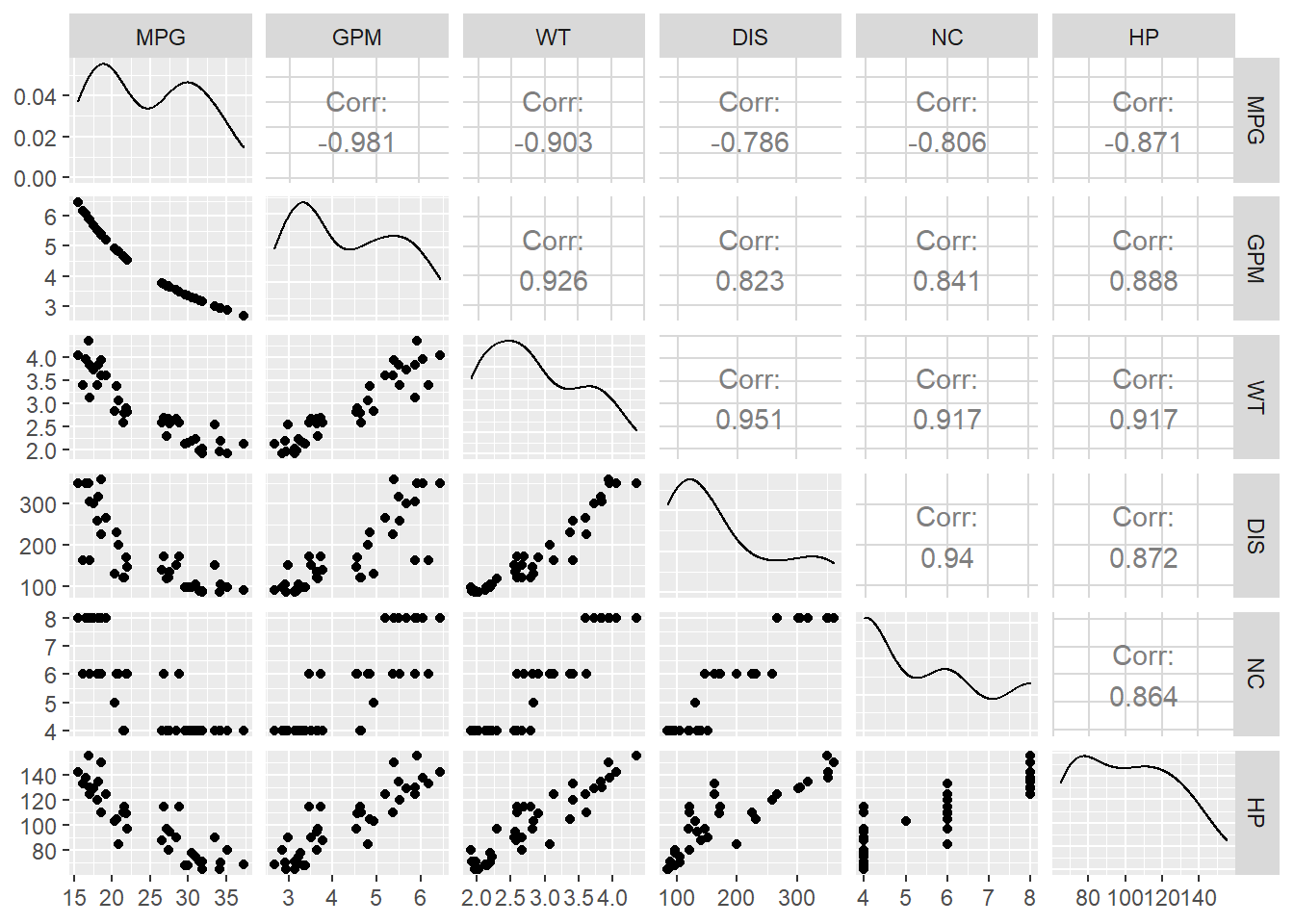
Podemos ver una relación muy clara entre GPM y MPG, siendo una relación lineal negativa, ya que para valores altos de GPM la variable MPG toma valores bajos. Su correlación es de -0.98, esta correlación negativa indica que están asociadas de forma inversa, esto es, valores altos de una de las variables se corresponden con valores bajos de la otra.
## [1] -0.9807972Intentar un modelo de regresión lineal entre GPM y el resto de variables.
##
## Call:
## lm(formula = GPM ~ ., data = FuelEfficiency)
##
## Coefficients:
## (Intercept) MPG WT DIS NC HP
## 6.219794 -0.131807 0.397032 -0.001392 0.070298 0.001035Evaluar el modelo.
Tenemos un F-estadístico grande y un p-value muy pequeño (cercano a 0) por lo que aceptamos H1 y rechazamos H0, declarando que existe un modelo.
Con la función summary() obtenemos los errores estándar de los coeficientes, los p-values así como el estadístico F y R2.
##
## Call:
## lm(formula = GPM ~ ., data = FuelEfficiency)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.32836 -0.15706 -0.01305 0.12006 0.44487
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.219794 0.962248 6.464 2.85e-07 ***
## MPG -0.131807 0.015531 -8.487 1.07e-09 ***
## WT 0.397032 0.273554 1.451 0.156
## DIS -0.001392 0.001826 -0.762 0.451
## NC 0.070298 0.066613 1.055 0.299
## HP 0.001035 0.003420 0.303 0.764
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2079 on 32 degrees of freedom
## Multiple R-squared: 0.972, Adjusted R-squared: 0.9676
## F-statistic: 222.3 on 5 and 32 DF, p-value: < 2.2e-16- ¿Con qué variables hay mayor relación?.
Tenemos una mayor relación con la variable MPG, debido a que su p-value es muy cercano a 0 por lo que es muy significativo (***).
Por detrás, tenemos también dos variables algo significativas, que son….
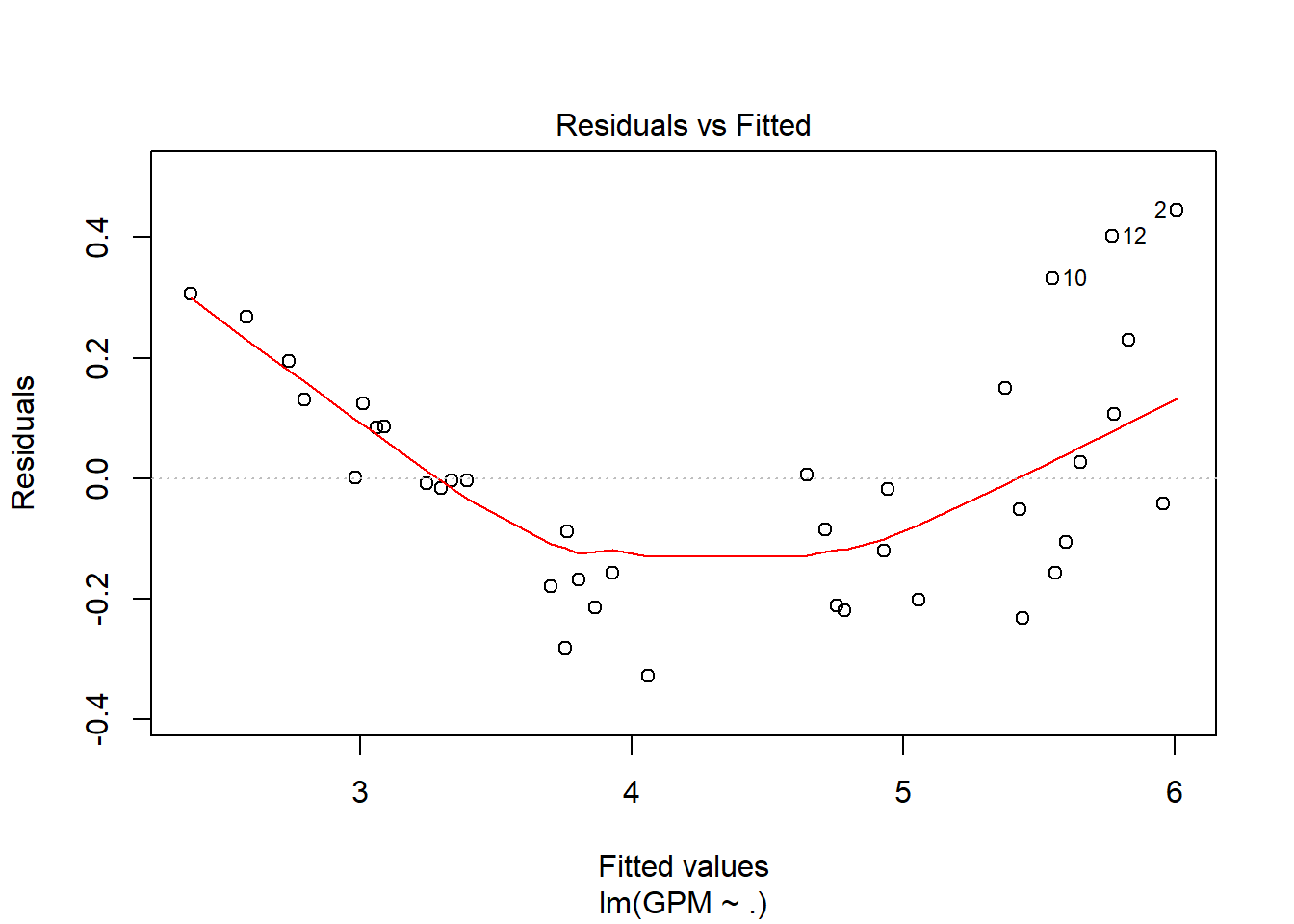
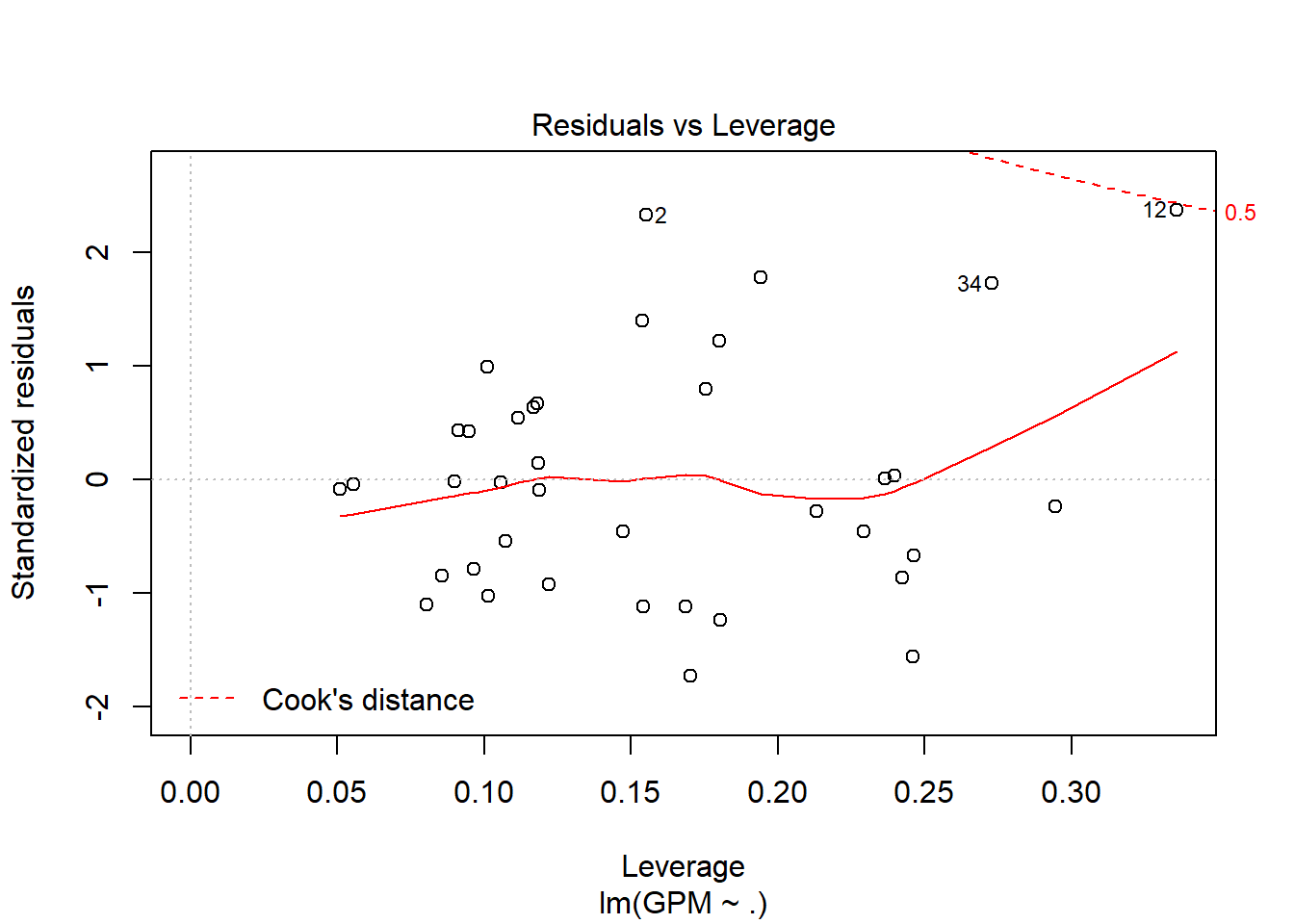
Explicando las gráficas resultantes para decir cuánto de bueno es el modelo:
Residuals vs Fitted values: Los residuos están linealmente distribuidos, debido a que la línea de la gráfica se aproxima a y=0 (teniendo en cuenta además la escala del eje y, que va de -0.4 a 0.4).
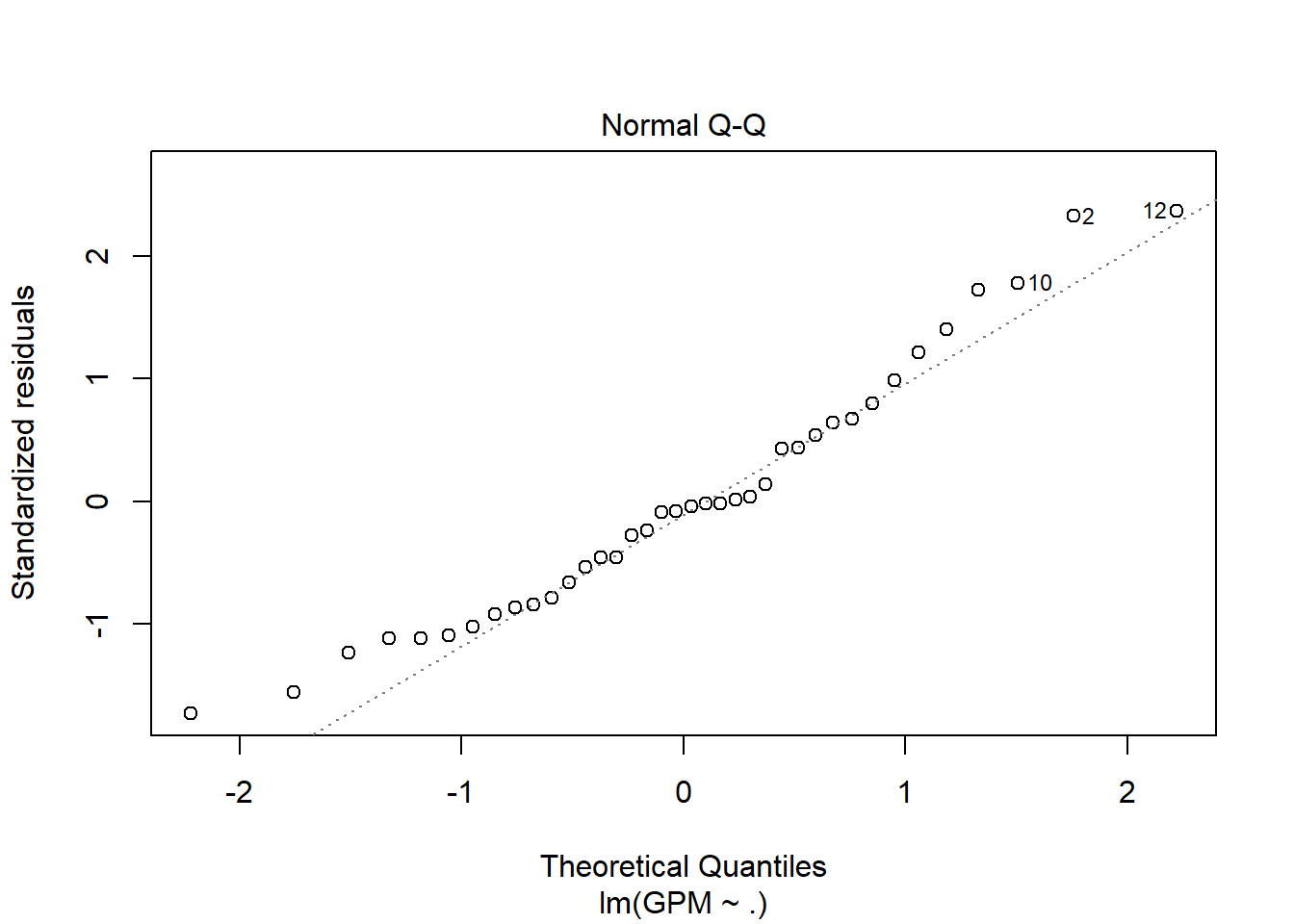
Los residuos están prácticamente distribuidos siguiendo una normal, debido a que los punto representativos de la gráfica se acercan (o simulan) la recta y=x. También detecta outliers y valores importantes.
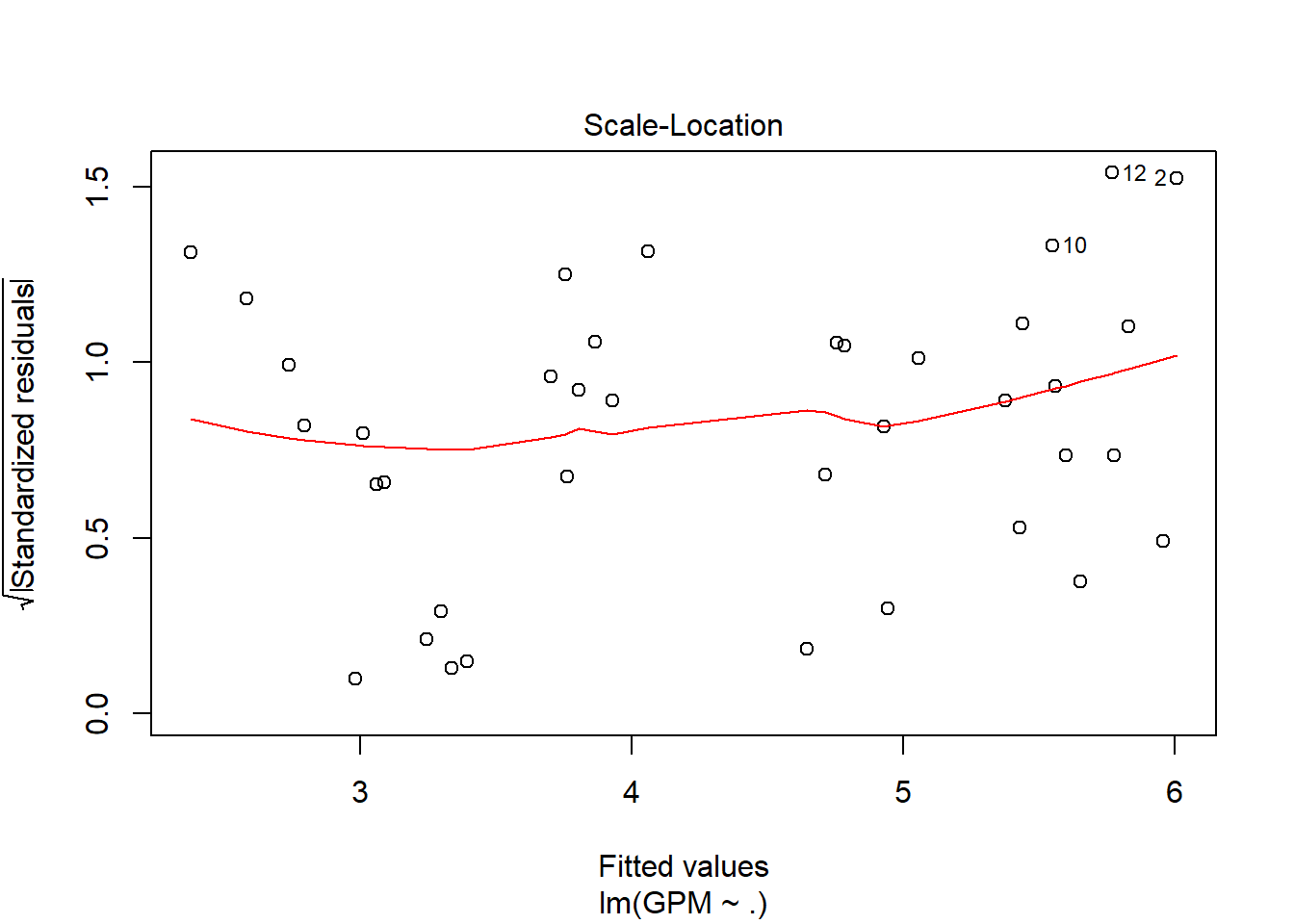
Los puntos se encuentran muy dispersos dentro de la gráfica (sin patrones identificables), por lo que nos sigue garantizando que el modelo es bastante bueno.
Con la distancia de Cook, detectamos outliers y valores importantes. Si en ambas gráficas (3 y 4) se marca el mismo punto podemos decir que tiene todas las papeletas para ser un outlier y poder así eliminarlo del conjunto de muestras.
Hacer gráficos de dataset junto con los modelos.
## The following objects are masked from FuelEfficiency (pos = 3):
##
## DIS, GPM, HP, MPG, NC, WT## `geom_smooth()` using formula 'y ~ x'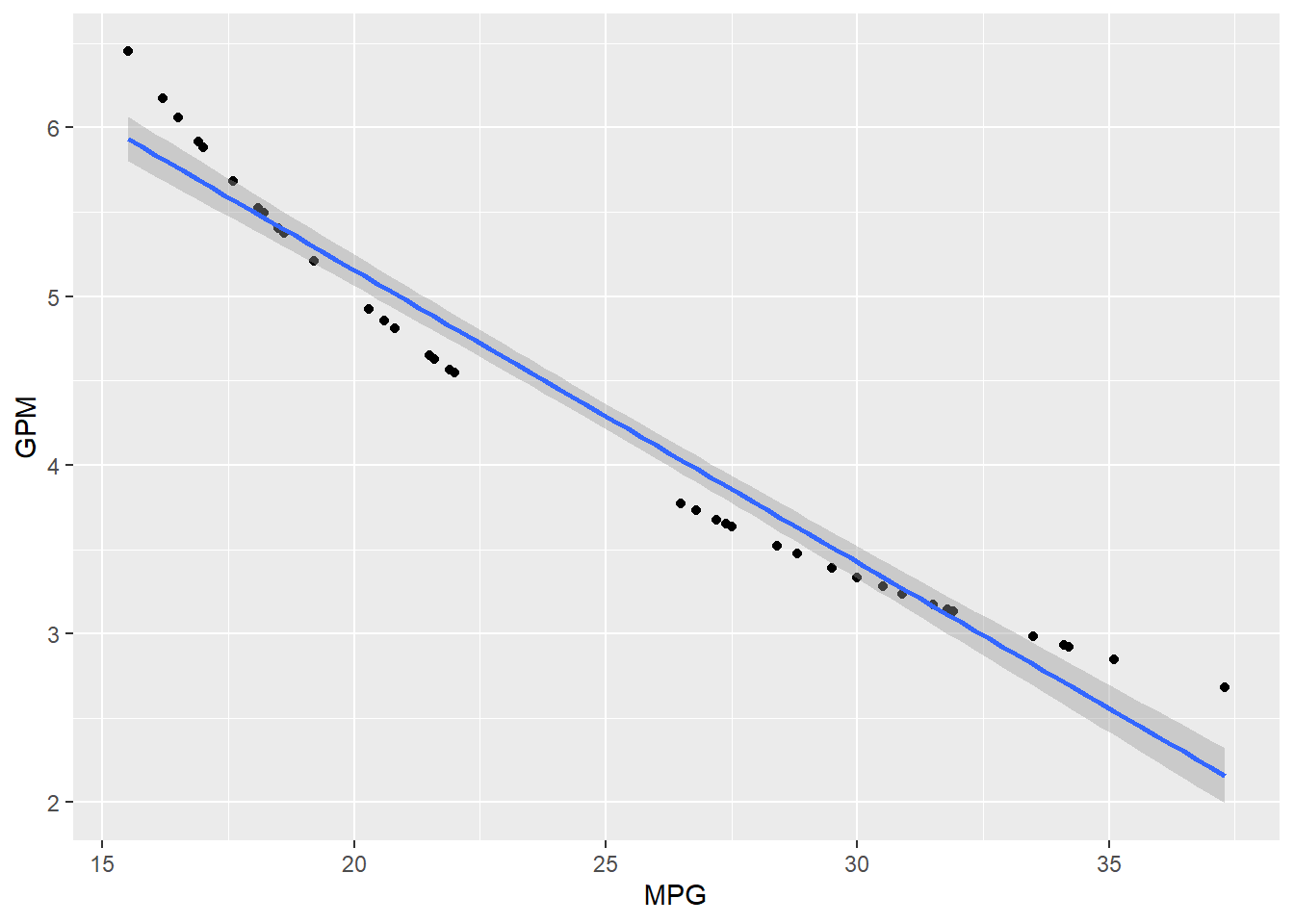
## `geom_smooth()` using formula 'y ~ x'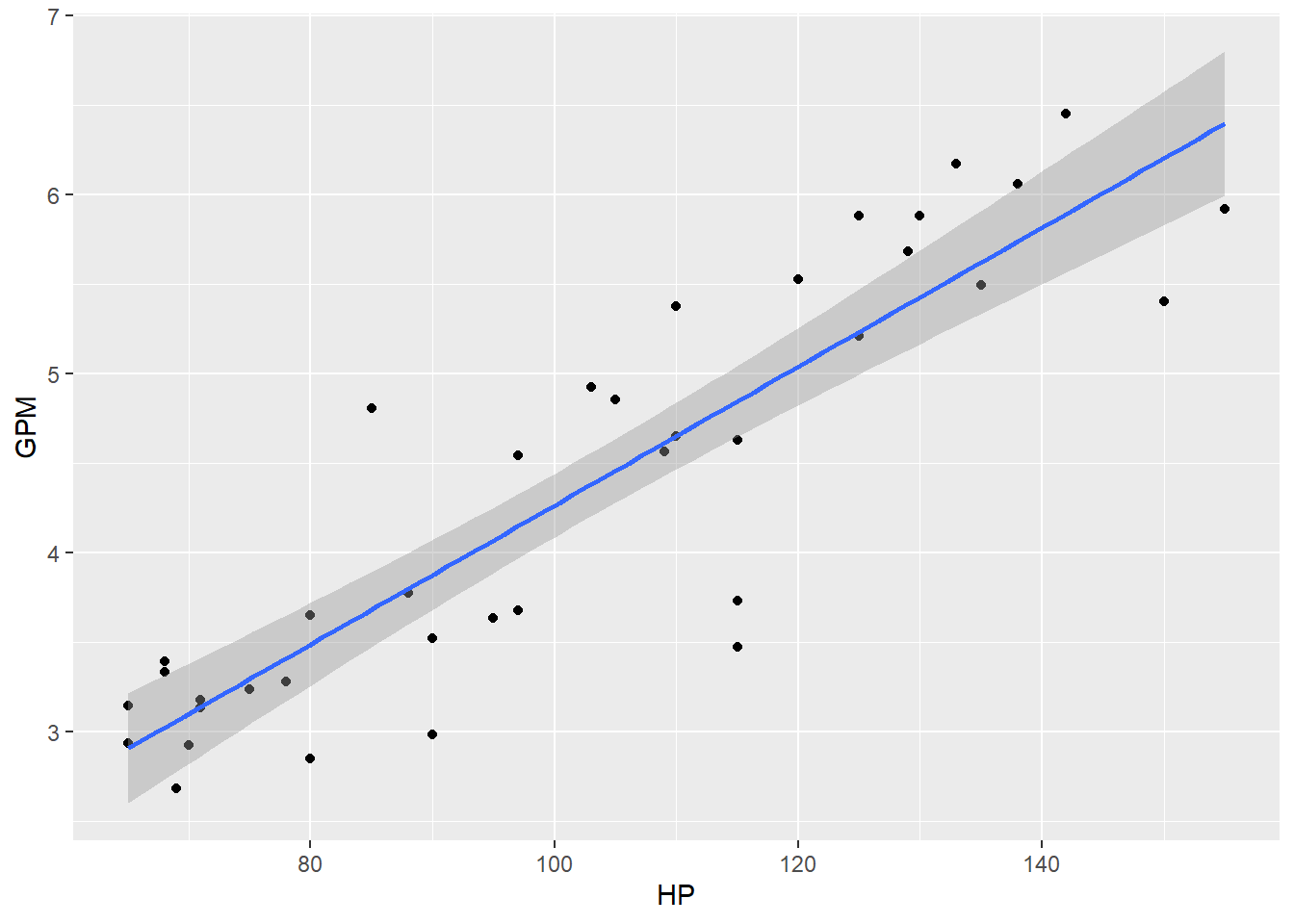
## `geom_smooth()` using formula 'y ~ x'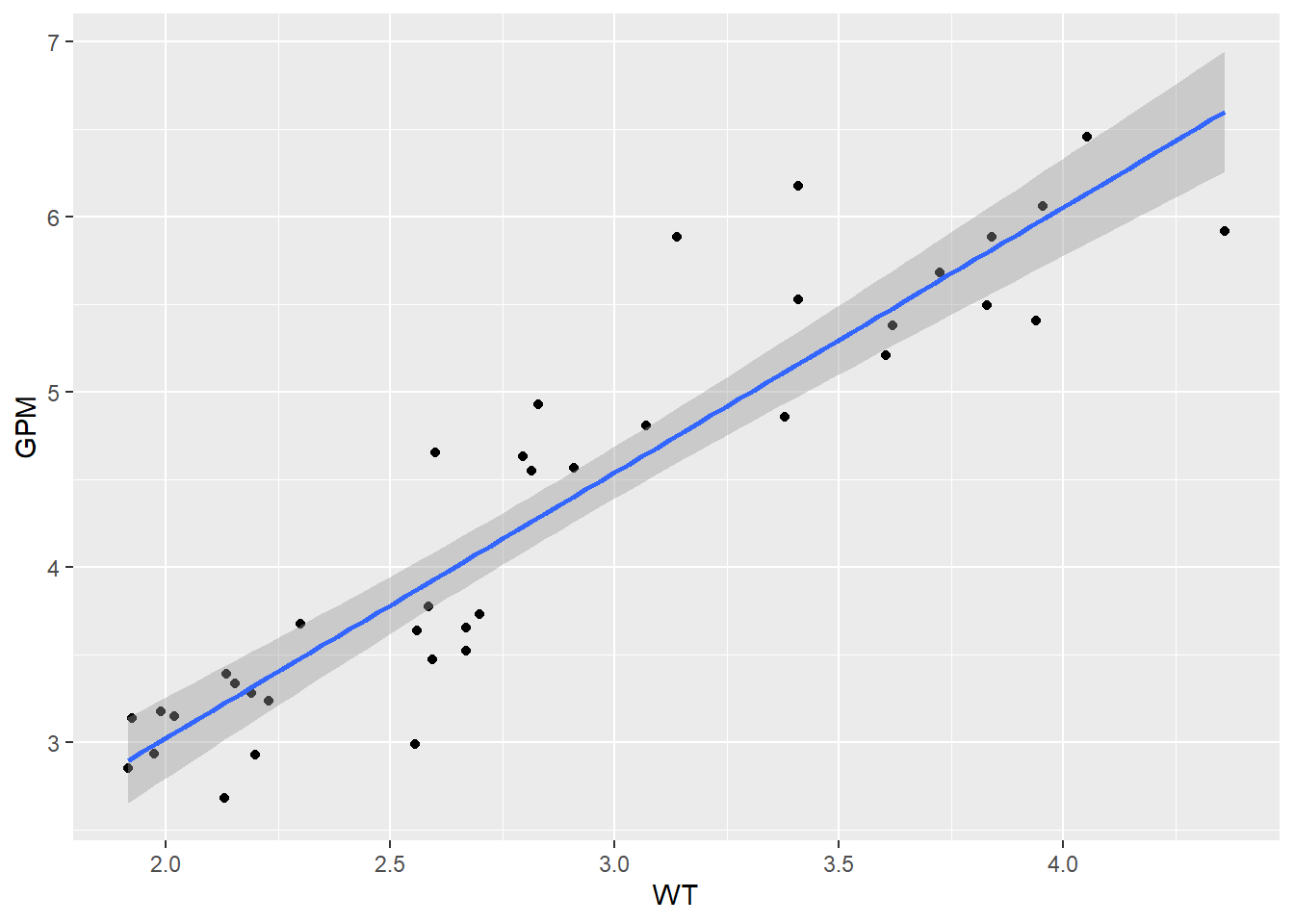
Como hemos visto, GPM es la inversa de MPG, por lo que no es muy representativo comparar la una con la otra, por lo que la quitamos y hacemos otro modelo:
##
## Call:
## lm(formula = GPM ~ WT + DIS + NC + HP, data = FuelEfficiency)
##
## Coefficients:
## (Intercept) WT DIS NC HP
## -1.620785 2.046783 -0.010236 0.187667 0.008787##
## Call:
## lm(formula = GPM ~ WT + DIS + NC + HP, data = FuelEfficiency)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.66694 -0.20075 0.01016 0.23997 0.62668
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.620785 0.477872 -3.392 0.001818 **
## WT 2.046783 0.341733 5.989 9.95e-07 ***
## DIS -0.010236 0.002662 -3.845 0.000522 ***
## NC 0.187667 0.115695 1.622 0.114301
## HP 0.008787 0.005852 1.502 0.142716
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3692 on 33 degrees of freedom
## Multiple R-squared: 0.909, Adjusted R-squared: 0.898
## F-statistic: 82.43 on 4 and 33 DF, p-value: < 2.2e-16En este nuevo caso, vemos que las más signficativas son DIS y WT (***), encontrándose por detrás el término ind (Intercept).
Intentar modelos de regresión de GPM con varias variables o incluso usando modelos no lineales. Evaluar los modelos. Hacer gráficos de dataset junto con los modelos.
##
## Call:
## lm(formula = GPM ~ poly(MPG, 2), data = FuelEfficiency)
##
## Coefficients:
## (Intercept) poly(MPG, 2)1 poly(MPG, 2)2
## 4.331 -6.897 1.329##
## Call:
## lm(formula = GPM ~ poly(MPG, 2), data = FuelEfficiency)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.13914 -0.04538 0.01597 0.03840 0.15278
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.330605 0.009294 466.0 <2e-16 ***
## poly(MPG, 2)1 -6.896655 0.057289 -120.4 <2e-16 ***
## poly(MPG, 2)2 1.328849 0.057289 23.2 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.05729 on 35 degrees of freedom
## Multiple R-squared: 0.9977, Adjusted R-squared: 0.9975
## F-statistic: 7515 on 2 and 35 DF, p-value: < 2.2e-16##
## Call:
## lm(formula = GPM ~ poly(MPG + WT, 2), data = FuelEfficiency)
##
## Coefficients:
## (Intercept) poly(MPG + WT, 2)1 poly(MPG + WT, 2)2
## 4.331 -6.854 1.448##
## Call:
## lm(formula = GPM ~ poly(MPG + WT, 2), data = FuelEfficiency)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.20782 -0.04188 0.02535 0.05236 0.24150
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.33061 0.01683 257.33 < 2e-16 ***
## poly(MPG + WT, 2)1 -6.85352 0.10374 -66.06 < 2e-16 ***
## poly(MPG + WT, 2)2 1.44817 0.10374 13.96 7.17e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1037 on 35 degrees of freedom
## Multiple R-squared: 0.9924, Adjusted R-squared: 0.9919
## F-statistic: 2280 on 2 and 35 DF, p-value: < 2.2e-16##
## Call:
## lm(formula = GPM ~ MPG + WT, data = FuelEfficiency)
##
## Coefficients:
## (Intercept) MPG WT
## 6.7219 -0.1381 0.3594##
## Call:
## lm(formula = GPM ~ MPG + WT, data = FuelEfficiency)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.25935 -0.15547 -0.02623 0.11816 0.46330
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.72191 0.59414 11.314 3.05e-13 ***
## MPG -0.13813 0.01186 -11.647 1.36e-13 ***
## WT 0.35939 0.10985 3.272 0.00241 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2029 on 35 degrees of freedom
## Multiple R-squared: 0.9709, Adjusted R-squared: 0.9692
## F-statistic: 583.3 on 2 and 35 DF, p-value: < 2.2e-16