Documento 19 Examen Regresion (3)

Paquetes necesarios:

library(readr)
library(dplyr)
library(ggplot2)
library(magrittr)
library(GGally)

Usaremos el dataset dataset1697.csv que está en el directorio con posbiles datasets para el control. Importa el dataset. Cuidado no equivocarte al importarla, compruébalo.

El dataset contiene información de empresas. Para cada una de ellas, aparece el número de empleados y los gastos directos por personal en miles de euros.

dataset <- read_csv("datasets/dataset1697.csv")
## Parsed with column specification:
## cols(
##   empleados = col_double(),
##   gastos = col_double()
## )
attach(dataset)
  1. Construir un modelo de regresión lineal para estimar los gastos en empresas según su número de empleados. Introduce el coeficiente del término independiente del modelo lineal encontrado (solo el número con comas si es con decimales).
m <- lm(data=dataset, formula = gastos ~ empleados)
m
## 
## Call:
## lm(formula = gastos ~ empleados, data = dataset)
## 
## Coefficients:
## (Intercept)    empleados  
##    12297.19        14.34
m$coefficients[1]
## (Intercept) 
##    12297.19
  • Intercept: Término ind de la ecuación de la recta. Se define como el resultado esperado cuando empleados es cero (ordenada al origen).
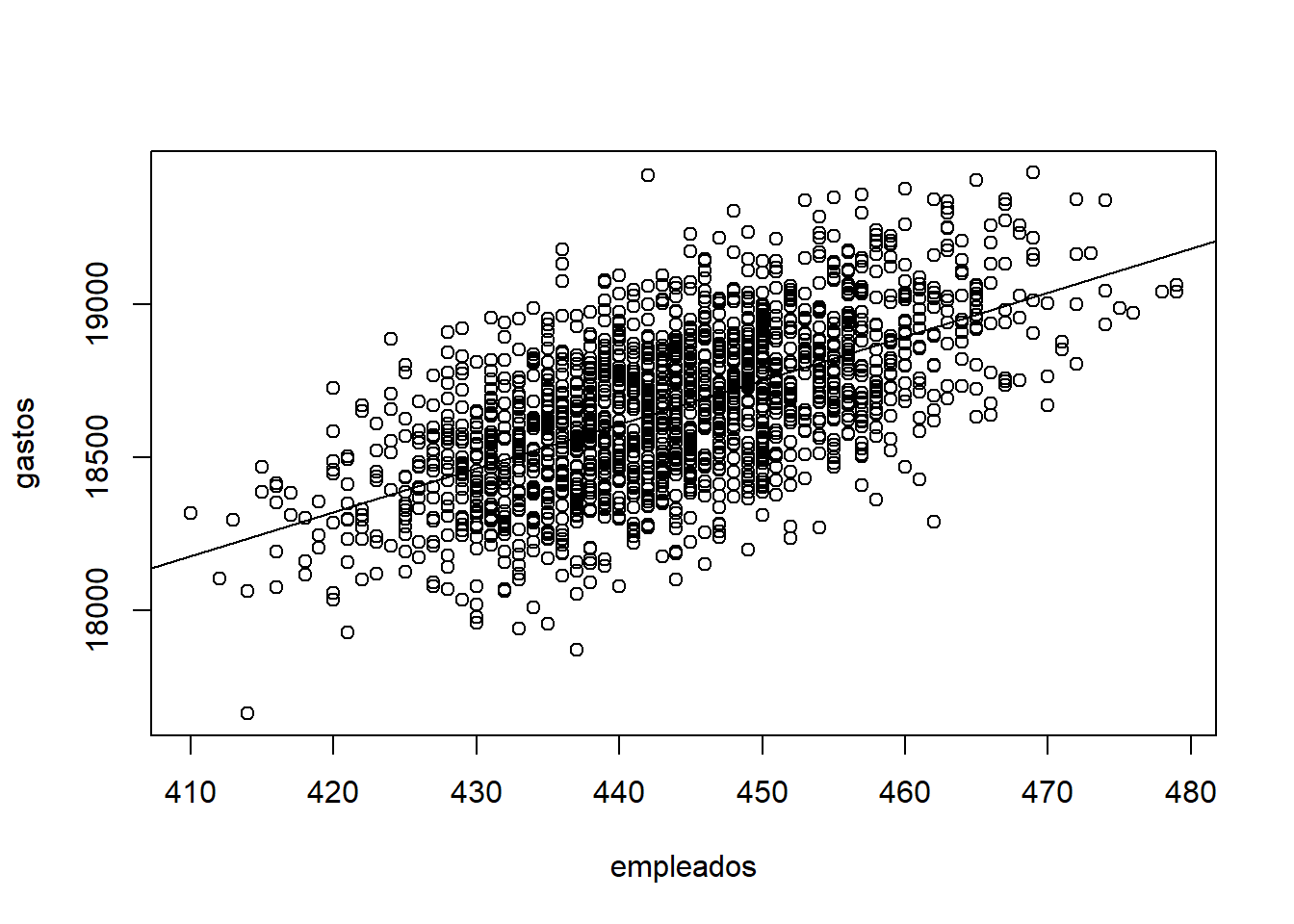
  1. Dibujar el dataset junto con el modelo encontrado. Introduce un 0 en el cuestionario si explicas en el .Rmd. Dar explicación a la vista de la visualización de que te parece el modelo encontrado.
plot(x=empleados, y=gastos)
abline(m)

dataset %>%
  ggplot(aes(x=empleados, y=gastos)) +
  geom_point() +
  stat_smooth(method = lm)
## `geom_smooth()` using formula 'y ~ x'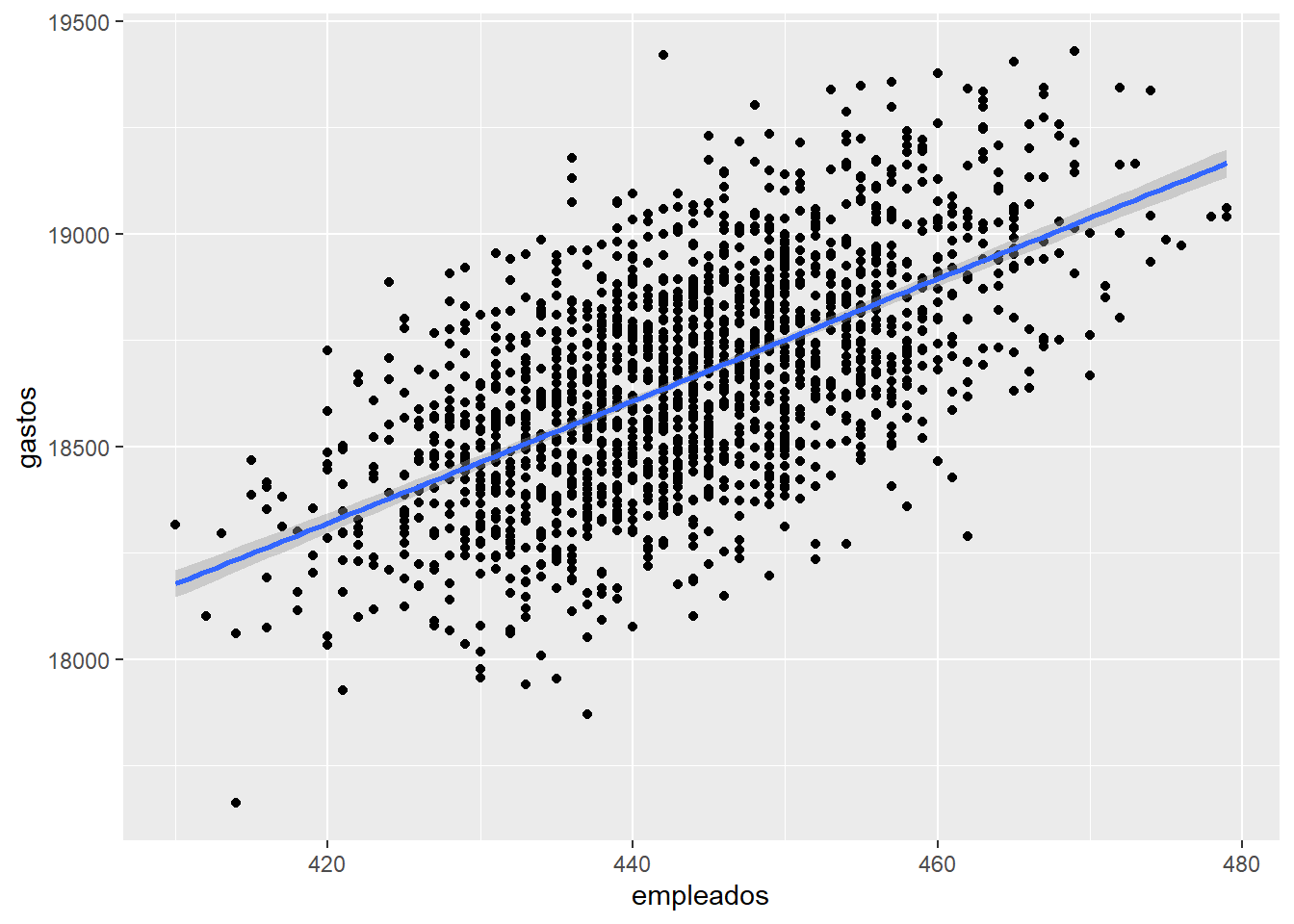

El modelo encontrado a simple vista no parece muy bueno debido a que se producen errores muy grandes entre la recta y muchos puntos del dataset. Podríamos encontrar otro modelo que represente mejor los datos.

  1. Estimar la cantidad esperada de gastos para empresas con 483, 485, 487 empleados usando el modelo encontrado anteriormente. Introduce en el cuestionario la media de los gastos para estas empresas.

El modelo es el siguiente:

gastos = 12297.19 + empleados * 14.34

Siendo la fórmula general:

gastos = intercept + empleados * slope

Esto nos dice que: por cada unidad los gastos se incrementan en un 14.34, siendo con 0 empleados un gasto de 12297.19.

interc <- 12297.19
slope <- 14.24

g1 <- interc + c(483, 485, 487) * slope
g1
## [1] 19175.11 19203.59 19232.07
mean(g1)
## [1] 19203.59
# El vector g1 nos muestra los gastos de 483, 485, 487, en ese orden.
  1. Analisis descriptivo del modelo encontrado. Con varias frases, muy brevemente dime cómo es el modelo que has encontrado. Señala características importantes. Introduce un 0 en el cuestionario en este apartado si lo explicas en el .Rmd. Se revisa el .Rmd

Con la función summary() obtenemos los errores estándar de los coeficientes, los p-values así como el estadístico F y R2. En modelos lineales simples (como este caso), dado que solo hay un predictor, el p-value del test F es igual al p-value del t-test del predictor.

summary(m)
## 
## Call:
## lm(formula = gastos ~ empleados, data = dataset)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -694.45 -150.72    1.46  140.87  783.80 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 12297.191    202.396   60.76   <2e-16 ***
## empleados      14.341      0.456   31.45   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 210.1 on 1695 degrees of freedom
## Multiple R-squared:  0.3685, Adjusted R-squared:  0.3682 
## F-statistic: 989.3 on 1 and 1695 DF,  p-value: < 2.2e-16

Para empezar, vemos que los residuos tienen una gran dispersión (como comentamos en el análisis visual), siendo el mínimo de -694.45 y el máximo de 783.80.

Tanto el término independiente como la variable empleados son muy significativos debido a que su p-value es entorno a 0 (***).

El R-squared nos indica cuánto representa el modelo a los datos, siendo este de 0.3685. El rango en las regresiones lineales positivas va de 0 a 1 (siendo 0 que no representa nada el conjunto de datos), por lo que 0.3685 es una dato bastante malo, por lo que no representa bien el malo.

Además, el F-stadistic es 989.3 y el p-value es en torno a 0 (<2e-16), por lo que podemos rechazar H0 y aceptar H1 (hay modelo).

  1. Introduce en el cuestionario el coeficiente de determinación R2. Explicar en Rmd lo que significa el resultado que te ofrece en el modelo encontrado.

El coeficiente, como hemos dicho antes, es 0.3685. Siendo el coeficiente ajustado de 0.3682. Ya hemos explicado el coeficiente en el apartado anterior.

  1. Calcula e introduce en el cuestionario la media de los residuos obtenidos en todos los puntos. Explica en Rmd que información te dan los residuos obtenidos.
mean(abs(m$residuals))
## [1] 169.2169
# Para obtener la media de todos ellos, primero los convertimos a valor absoluto para poder compararlos y luego hacemos la media.

Vemos que la media es 169.2169, que de forma más coloquial lo podemos definir como cuánto de alejo están la media de los puntos de la recta (ya sea por arriba o por abajo).

Residuals: Nos da 5 estadísticos sobre la distribución de los residuos del modelo: 1er, 2do y 3er cuartil y valor máximo y mínimo.

  1. Visualiza el modelo (plot modelo) y explica el segundo gráfico que el plot te devuelve. Introduce un 0 en el cuestionario si explicas en el .Rmd.
plot(m,2)

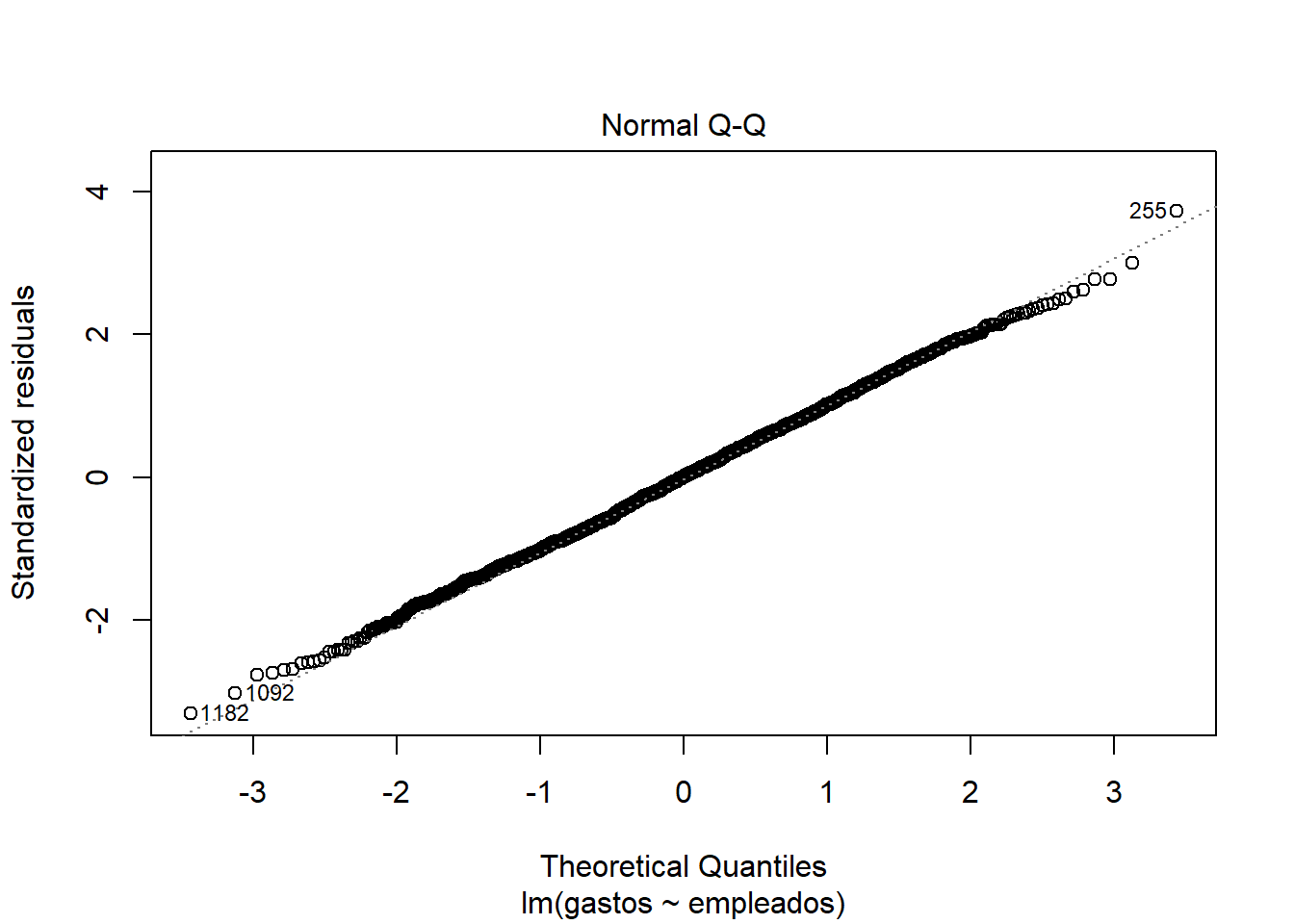
Como vemos, los residuos están prácticamente distribuidos siguiendo una normal, debido a que los puntos representativos de la gráfica se acercan (o simulan) la recta y=x. También detecta outliers y valores importantes (como 1182, 1092 y 255).

  1. Cual es el valor del F estadístico? Introduce el valor en el cuestionario. Explica significado en el Rmd.

Lo podemos ver en el summary anterior, su valor es: F-statistic: 989.3

Es la base de una prueba de hipótesis en la que contrasta a nuestro modelo con uno hipotético en el que las variables no tienen efectos, es decir, con todos los coeficientes iguales a 0. Nos sirve para determinar si rechazamos o aceptamos H0.

  1. Introduce el comando para obtener los valores ajustados del modelo1.
# Mostramos solo los 20 primeros ya que son demasiados.

m$fitted.values[1:20]
##        1        2        3        4        5        6        7        8 
## 18679.10 18808.18 18822.52 18707.79 18435.30 18707.79 18478.32 19023.30 
##        9       10       11       12       13       14       15       16 
## 18564.37 18980.27 18636.08 18621.74 18664.76 18507.01 18679.10 18865.54 
##       17       18       19       20 
## 18535.69 18550.03 18521.35 18679.10
  1. Intentar mejorar el modelo. Buscar función polinomial de grado cinco.
m2 <- lm(data = dataset, gastos ~ poly(empleados, 5))
m2
## 
## Call:
## lm(formula = gastos ~ poly(empleados, 5), data = dataset)
## 
## Coefficients:
##         (Intercept)  poly(empleados, 5)1  poly(empleados, 5)2  
##            18661.14              6608.31                56.71  
## poly(empleados, 5)3  poly(empleados, 5)4  poly(empleados, 5)5  
##             -191.31              -260.16                23.05
#Realizamos un summary para compararlo con el anterior

summary(m)
## 
## Call:
## lm(formula = gastos ~ empleados, data = dataset)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -694.45 -150.72    1.46  140.87  783.80 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 12297.191    202.396   60.76   <2e-16 ***
## empleados      14.341      0.456   31.45   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 210.1 on 1695 degrees of freedom
## Multiple R-squared:  0.3685, Adjusted R-squared:  0.3682 
## F-statistic: 989.3 on 1 and 1695 DF,  p-value: < 2.2e-16
summary(m2)
## 
## Call:
## lm(formula = gastos ~ poly(empleados, 5), data = dataset)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -689.60 -151.15    1.49  141.41  790.14 
## 
## Coefficients:
##                      Estimate Std. Error  t value Pr(>|t|)    
## (Intercept)         18661.145      5.103 3657.233   <2e-16 ***
## poly(empleados, 5)1  6608.309    210.197   31.439   <2e-16 ***
## poly(empleados, 5)2    56.713    210.197    0.270    0.787    
## poly(empleados, 5)3  -191.310    210.197   -0.910    0.363    
## poly(empleados, 5)4  -260.156    210.197   -1.238    0.216    
## poly(empleados, 5)5    23.053    210.197    0.110    0.913    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 210.2 on 1691 degrees of freedom
## Multiple R-squared:  0.3695, Adjusted R-squared:  0.3676 
## F-statistic: 198.2 on 5 and 1691 DF,  p-value: < 2.2e-16
  • Explicar las diferencias entre los modelos. Analizar si se ha mejorado explicando en que te basas. Explicar que coeficientes del modelo son significativos.

Ahora el R-squared es 0.3695, siendo una milésimas mejor que el anterior. Los coeficientes más signficativos son el término independiente y poly(empleados, 5)1, que es la variable de menos grado.

¿Con cuál nos quedaríamos?

Nos seguiríamos quedando con el lineal, debido a que además de que los residuos no mejoran, se produce el denominado efecto Overfitting, que consiste en buscar una fórmula más complicada pero no mejora demasiado el modelo, por lo que nos quedamos con el primero.

Probamos a mejorar el modelo con una función cuadrática.

m_cuad <- lm(data = dataset, gastos ~ poly(empleados, 2))
m_cuad
## 
## Call:
## lm(formula = gastos ~ poly(empleados, 2), data = dataset)
## 
## Coefficients:
##         (Intercept)  poly(empleados, 2)1  poly(empleados, 2)2  
##            18661.14              6608.31                56.71
summary(m_cuad)
## 
## Call:
## lm(formula = gastos ~ poly(empleados, 2), data = dataset)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -693.86 -150.92    1.22  140.21  784.77 
## 
## Coefficients:
##                      Estimate Std. Error t value Pr(>|t|)    
## (Intercept)         18661.145      5.102 3657.91   <2e-16 ***
## poly(empleados, 2)1  6608.309    210.158   31.44   <2e-16 ***
## poly(empleados, 2)2    56.713    210.158    0.27    0.787    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 210.2 on 1694 degrees of freedom
## Multiple R-squared:  0.3686, Adjusted R-squared:  0.3678 
## F-statistic: 494.4 on 2 and 1694 DF,  p-value: < 2.2e-16

Como vemos, tampoco mejora el modelo por lo explicado anteriormente, el nuevo coeficiente no es significativo y no mejora el r-squared en exceso.

  • Visualizar modelo, dataset, resumenes del modelo, etc. Introduce un 0 en el cuestionario si haces este apartado en el Rmd.
plot(m2)

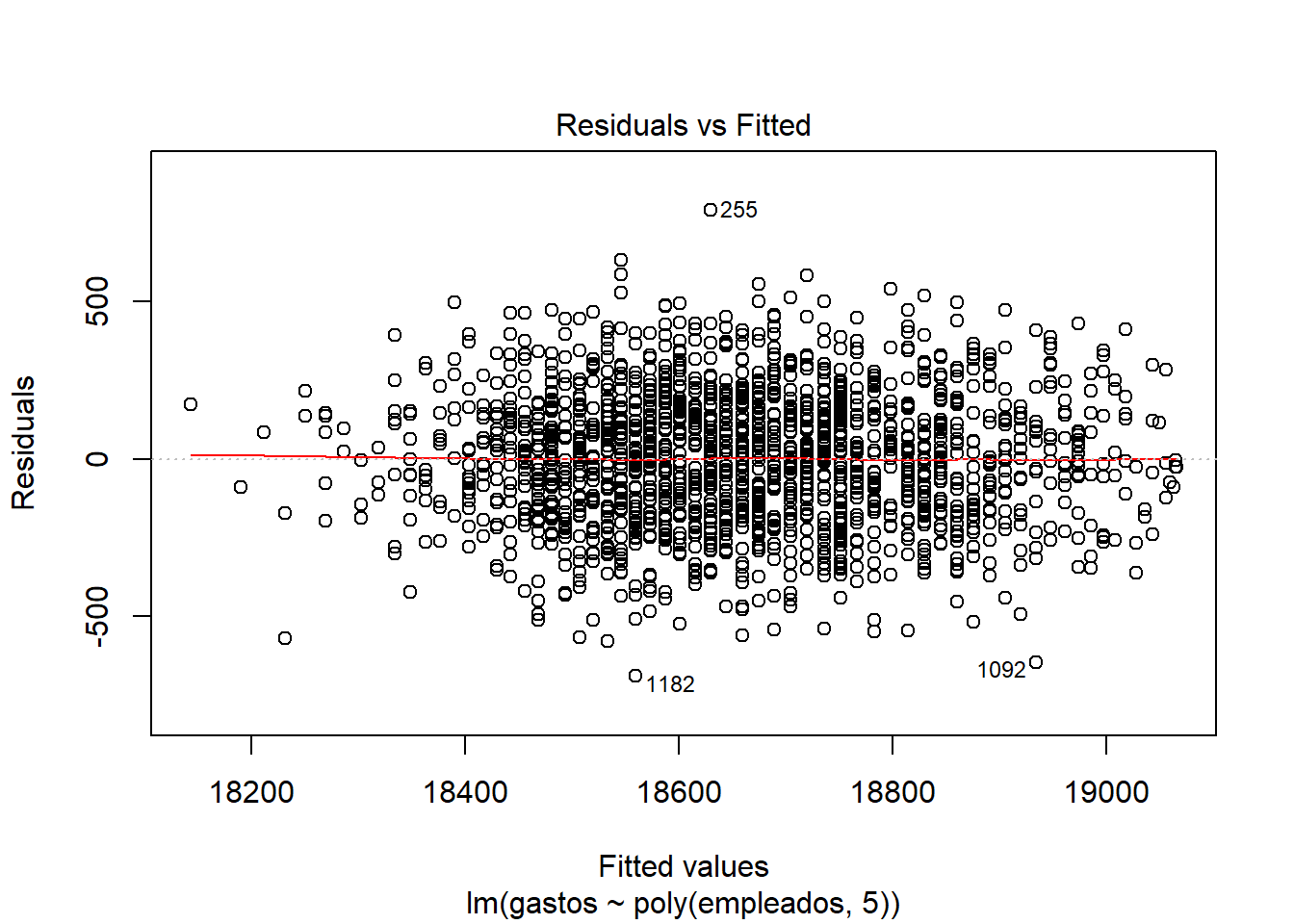
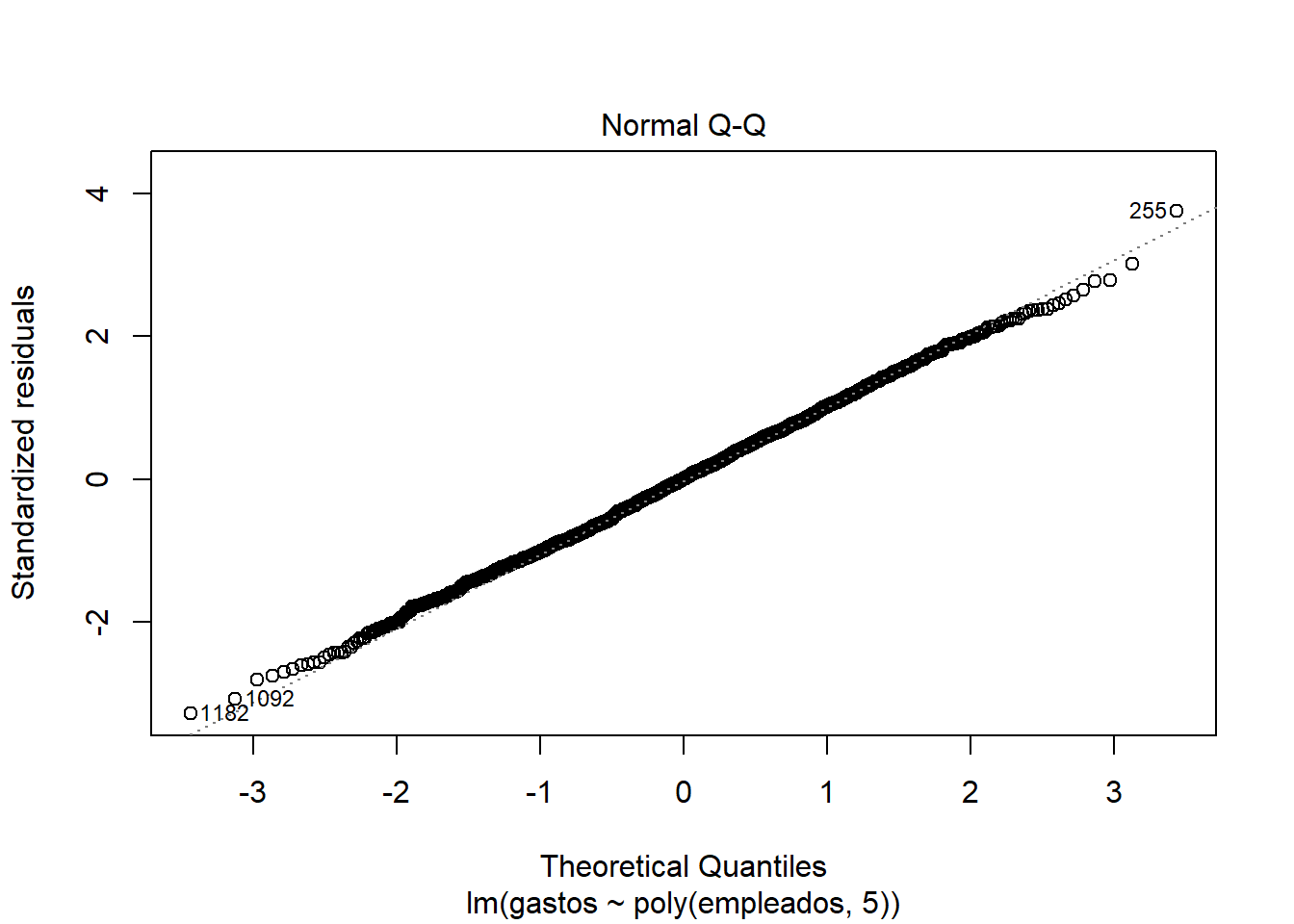
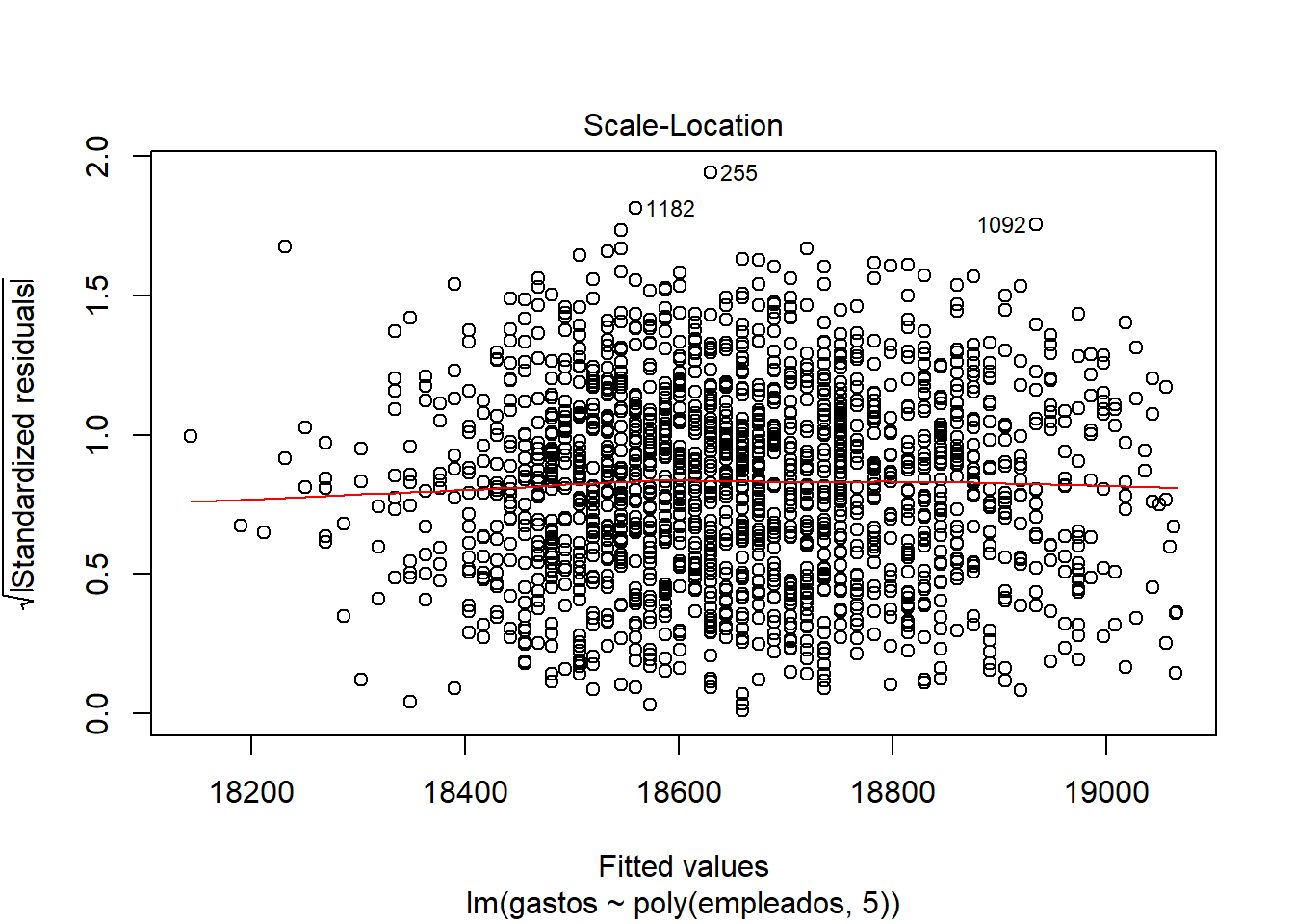
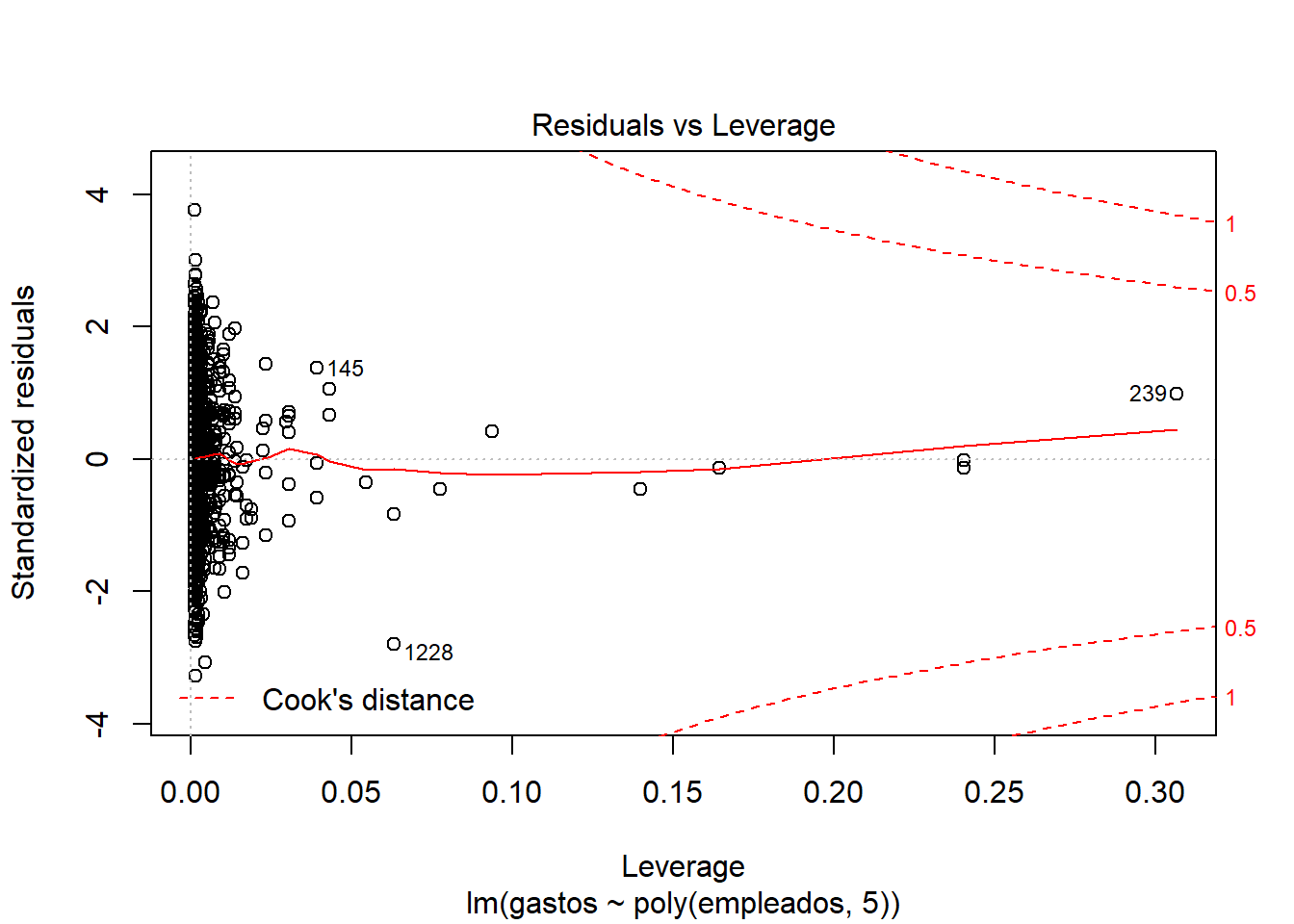
Explicando las gráficas:

  1. Enfrenta los residuos y los valores ajustados, cuanto más cerca esté la línea a y=0, mejor será la regresión. Al visualizar las gráfica 1 del modelo, parece que los residuos están linealmente distribuidos (cerca del y=0), pero si nos fijamos en las dimensiones del eje y (de 500 a -500) y de los errores en el summary, vemos que no es un buen modelo.

  2. Los residuos están prácticamente distribuidos siguiendo una normal, ya que siguen la recta x=y. También detecta outliers y valores importantes.

  3. Los puntos se acumulan por el centro en vez de estar distribuidos por toda la gráfica, lo que nos indica que la regresión no es muy buena.

  4. Distancia Cook –> Outliers, valores importantes: Como el 1228 o el 239.

# Modelo

m2$model[1:10, ]
##      gastos poly(empleados, 5).1 poly(empleados, 5).2 poly(empleados, 5).3
## 1  18687.08          0.002717550         -0.017843614         -0.002577869
## 2  18850.11          0.022249379         -0.004440397         -0.021455788
## 3  18779.41          0.024419582         -0.001522538         -0.021882256
## 4  18619.30          0.007057956         -0.016865180         -0.008206691
## 5  18840.36         -0.034175905          0.019983898          0.010427792
## 6  18737.30          0.007057956         -0.016865180         -0.008206691
## 7  18640.52         -0.027665295          0.007308279          0.018097559
## 8  19145.36          0.054802427          0.069328371          0.048000055
## 9  18682.32         -0.014644076         -0.010328447          0.017131368
## 10 19069.01          0.048291817          0.049431610          0.017902952
##    poly(empleados, 5).4 poly(empleados, 5).5
## 1           0.017218716          0.002013652
## 2          -0.005829941          0.019227944
## 3          -0.010030150          0.017151735
## 4           0.015492307          0.009557557
## 5          -0.029085935          0.017928358
## 6           0.015492307          0.009557557
## 7          -0.021182990         -0.001222404
## 8          -0.004888134         -0.055439912
## 9           0.002140971         -0.018549036
## 10         -0.027430749         -0.049399281

EJERCICIO EXTRA

Implementar en R vosotros una función que calcule el F-statistic:

TSS = sum((m$residuals)^2)
TSS
## [1] 74821135