Documento 16 Ejemplo Regresion

Paquetes necesarios:

# Instalamos devtools y el dataset con el que vamos a trabajar si no lo tenemos aún:
# install.packages("devtools")
# install.packages("GGally")
# devtools::install_github("kassambara/datarium")

library(datarium)
library(dplyr)
library(ggplot2)
library(magrittr)
library(GGally)
  • Data marketing: inversión en youtube, facebook y periódicos –> ventas
data("marketing")

16.1 Análisis exploratorio

dim(marketing)
## [1] 200   4
str(marketing)
## 'data.frame':    200 obs. of  4 variables:
##  $ youtube  : num  276.1 53.4 20.6 181.8 217 ...
##  $ facebook : num  45.4 47.2 55.1 49.6 13 ...
##  $ newspaper: num  83 54.1 83.2 70.2 70.1 ...
##  $ sales    : num  26.5 12.5 11.2 22.2 15.5 ...

La función summary() muestra la media, mediana, cuartiles, valor mínimo y valor máximo, para variables cuantitativas y la frecuencia absoluta para variables cualitativas.

Los cuartiles son valores que dividen una muestra de datos en cuatro partes iguales. Utilizando cuartiles puede evaluar rápidamente la dispersión y la tendencia central de un conjunto de datos, que son los pasos iniciales importantes para comprender sus datos.

La manera más simple de medir la dispersión es identificar los valores mayor y menor de un conjunto de datos. La diferencia entre los valores mínimo y máximo se denomina el rango (o recorrido) de las observaciones.

summary(marketing)
##     youtube          facebook       newspaper          sales      
##  Min.   :  0.84   Min.   : 0.00   Min.   :  0.36   Min.   : 1.92  
##  1st Qu.: 89.25   1st Qu.:11.97   1st Qu.: 15.30   1st Qu.:12.45  
##  Median :179.70   Median :27.48   Median : 30.90   Median :15.48  
##  Mean   :176.45   Mean   :27.92   Mean   : 36.66   Mean   :16.83  
##  3rd Qu.:262.59   3rd Qu.:43.83   3rd Qu.: 54.12   3rd Qu.:20.88  
##  Max.   :355.68   Max.   :59.52   Max.   :136.80   Max.   :32.40

Por ejemplo, vemos que existe mayor dispersión en Youtube (Min: 0.84, Max: 355,68) que en Facebook (Min: 0, Max: 59.52).

quantile(marketing$youtube)
##     0%    25%    50%    75%   100% 
##   0.84  89.25 179.70 262.59 355.68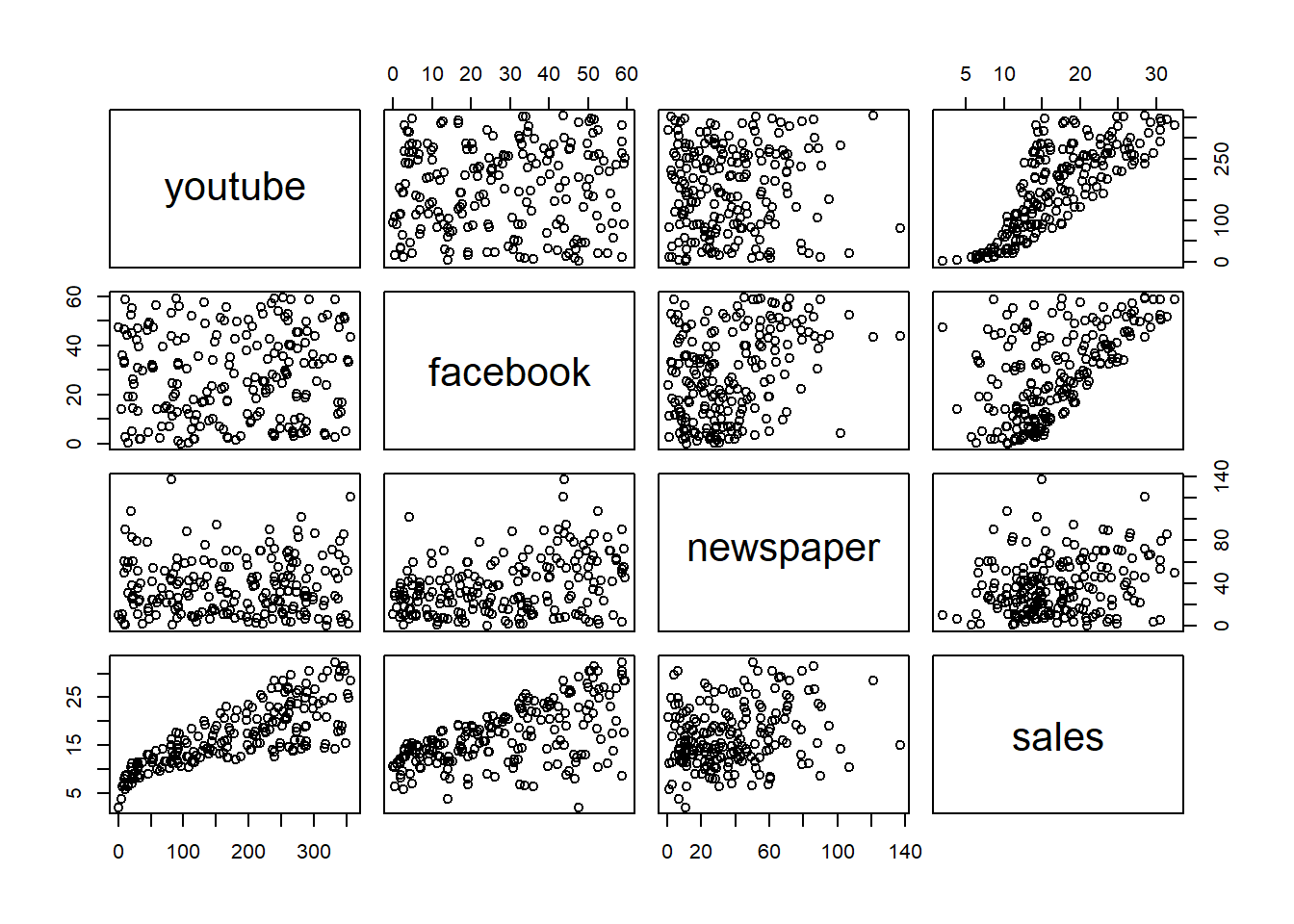
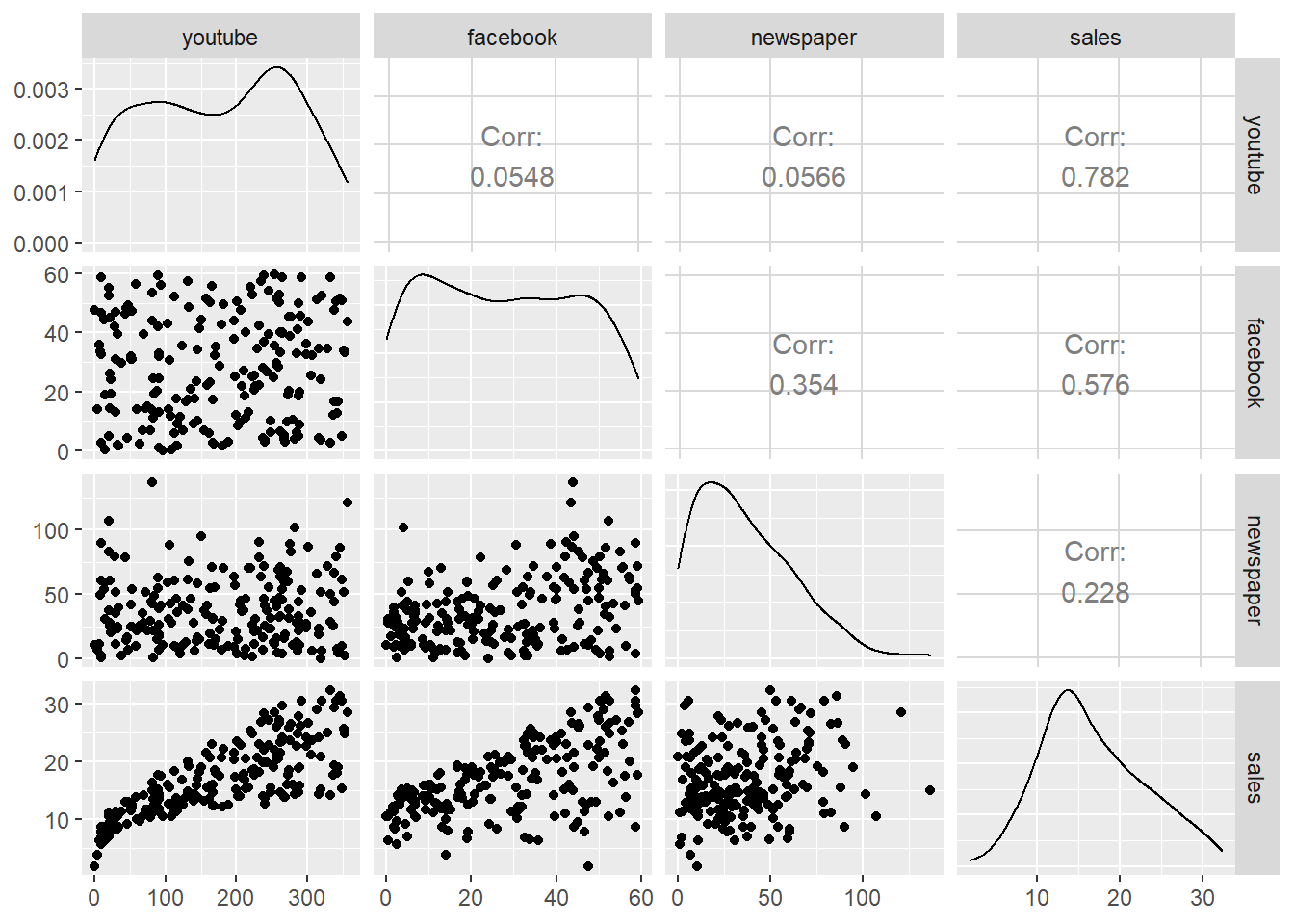
plot(marketing)

ggpairs(marketing)

Podemos apreciar que tanto Youtube como Facebook siguen una relación lineal positiva: esto significa que ambas variables aumentan o disminuyen simultáneamente a un ritmo constante.

  • La correlación negativa indica que están asociadas de forma inversa, esto es, valores altos de una de las variables se corresponden con valores bajos de la otra.
# Relación positiva y parece que es lineal:

# Nuestra variable y será la que queramos predecir.

marketing %>%
  ggplot(aes(x=youtube, y=sales)) +
  geom_point() +
  stat_smooth()
## `geom_smooth()` using method = 'loess' and formula 'y ~ x'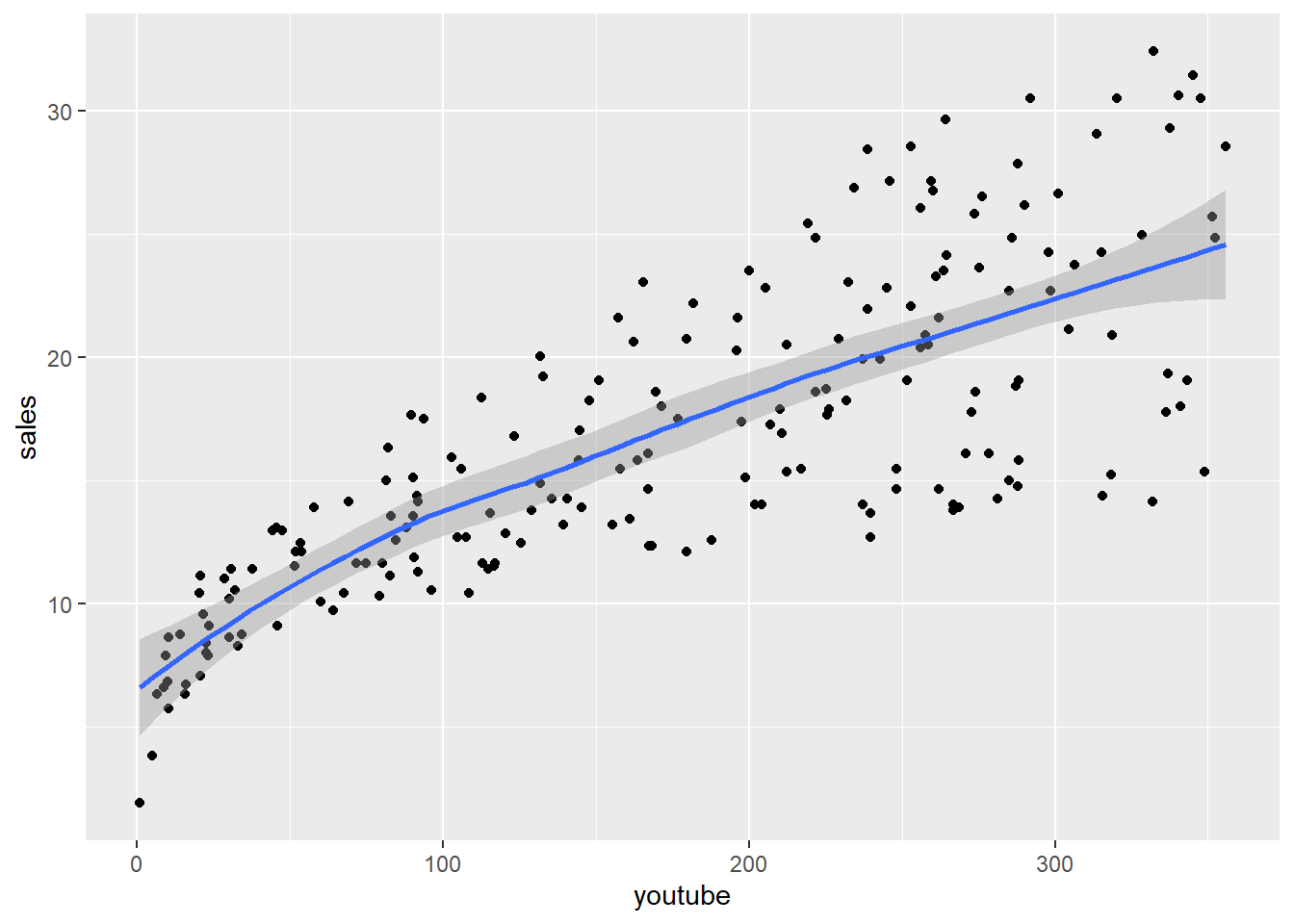

marketing %>%
  ggplot(aes(x=facebook, y=sales)) +
  geom_point() +
  stat_smooth()
## `geom_smooth()` using method = 'loess' and formula 'y ~ x'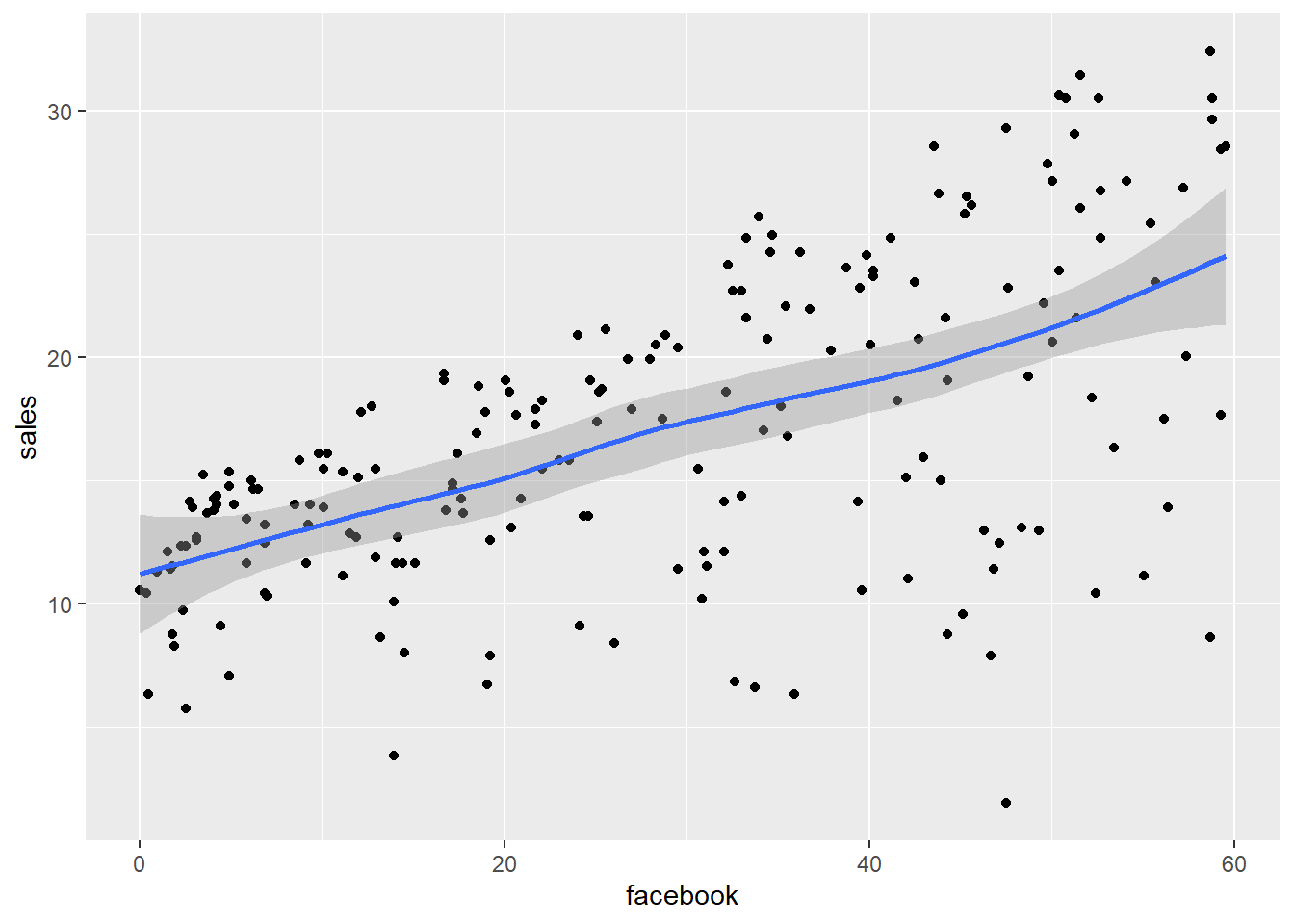

# No es lineal:

marketing %>%
  ggplot(aes(x=newspaper, y=sales)) +
  geom_point() +
  stat_smooth()
## `geom_smooth()` using method = 'loess' and formula 'y ~ x'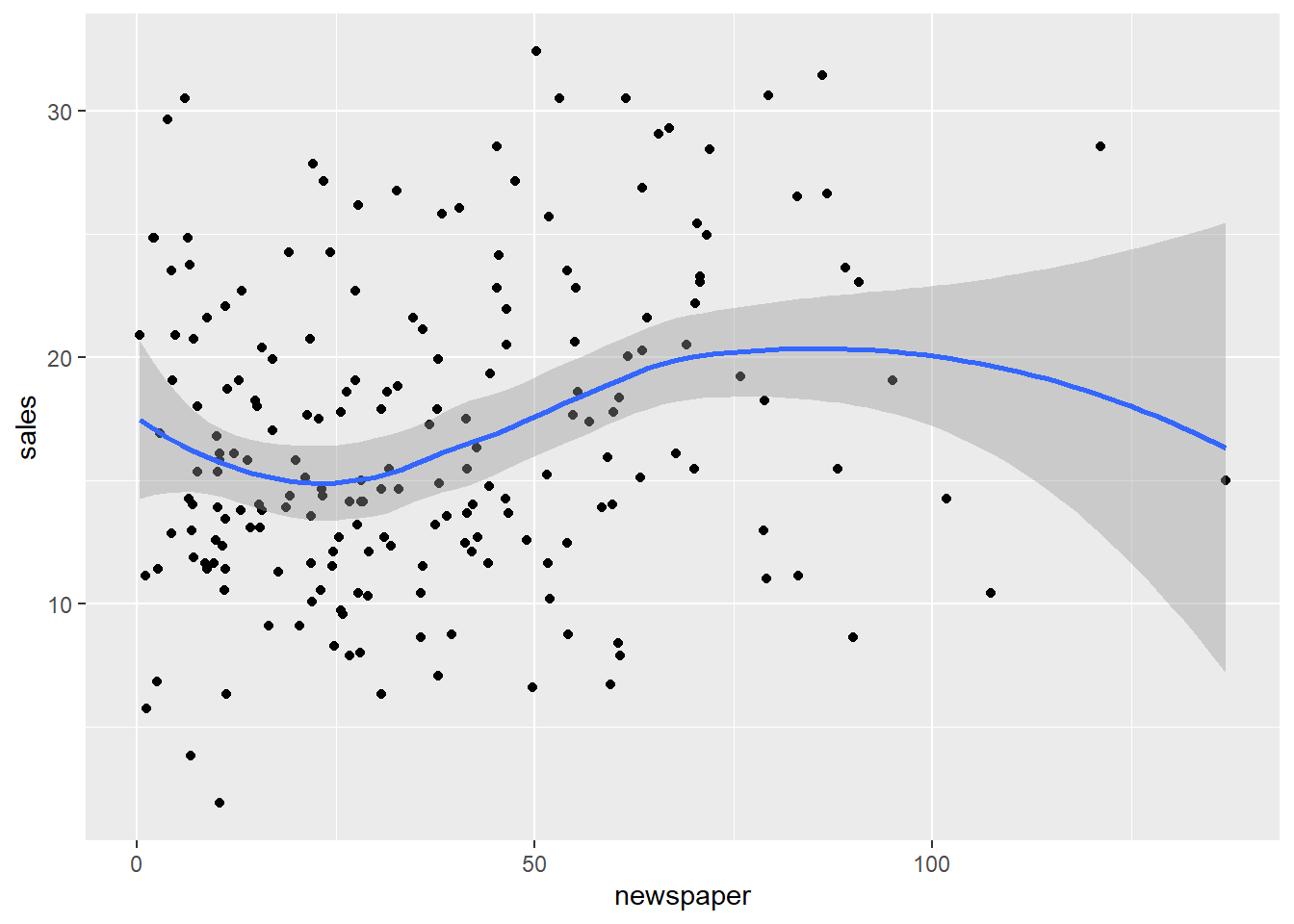

16.2 Correlación:

Segunda forma para sacar la correlación (aparte de verlo visualmente con ggpairs):

# Hay que explicar el significado de cada cosa
cor(marketing$sales, marketing$youtube)
## [1] 0.7822244
# Al ser el coeficiente de correlación de 0.78
# podemos afirmar que la correlación es lineal positiva.

La correlación es usada para determinar la relación entre dos o más variables. El Coeficiente de Correlación es un valor cuantitativo de la relación entre dos o más variables, pudiendo variar desde -1.00 hasta 1.00.

La correlación de proporcionalidad directa o positiva se establece con los valores +1.00 y de proporcionalidad inversa o negativa, con -1.00.

No existe relación entre las variables cuando el coeficiente es de 0.00.

16.3 Modelo:

¿Hay relación entre la inversión y las ventas?

La función lm() la utilizamos cuando queremos predecir –o explicar– una variable dependiente a partir de una o más variables independientes.

# Variable depend: Sales // Variables independ: Youtube
ventas_youtube <- lm(data = marketing, formula = sales ~ youtube)
ventas_youtube
## 
## Call:
## lm(formula = sales ~ youtube, data = marketing)
## 
## Coefficients:
## (Intercept)      youtube  
##     8.43911      0.04754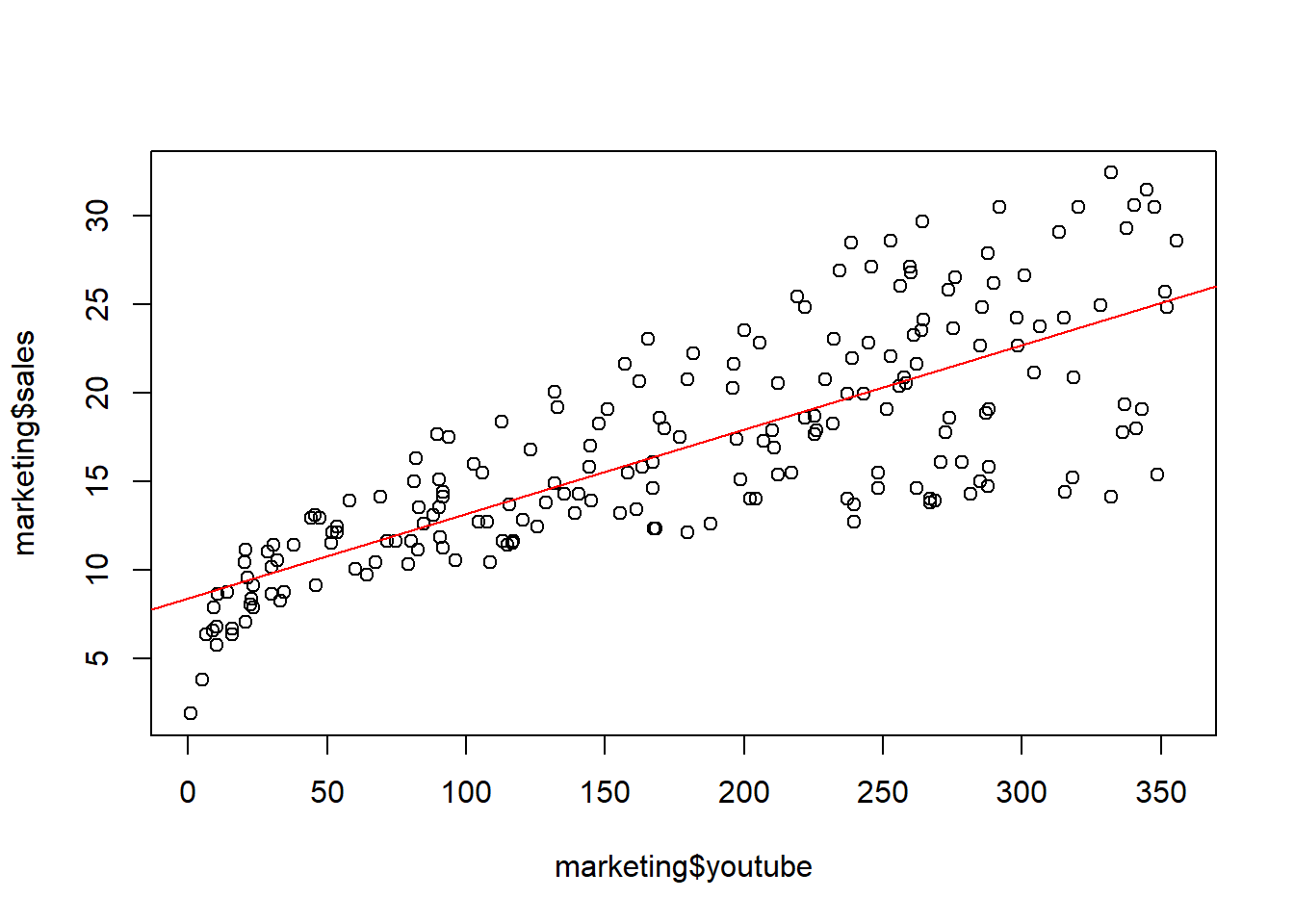
plot(marketing$youtube, marketing$sales)
abline(ventas_youtube, col = "red")

Output de lm():

La ordenada al origen (Intercept) y las pendientes estimadas para cada variable.

  • Intercept: Término ind de la ecuación de la recta. Se define como el resultado esperado cuando Youtube es cero (ordenada al origen).

  • Slope: Pendiente de la recta. Si yo incremento en una unidad la variable Youtube, las ventas van a subir en 0.04754.

  • Modelo lineal encontrado?

Ventas = 8.43911 + 0.04754 * youtube Por cada unidad las ventas se incrementan en un 0.04754

ventas_youtube$coefficients
## (Intercept)     youtube 
##  8.43911226  0.04753664
# coefficients(ventas_youtube)

# ventas_youtube$residuals   # Error en cada punto, hay bastantes (200 observaciones)
ventas_youtube$residuals[1]  # Cogemos el primero
##        1 
## 4.955071
#residuals(ventas_youtube)

ventas_youtube$fitted.values[1:10] # y-aproximado
##         1         2         3         4         5         6         7         8 
## 21.564929 10.977569  9.420269 17.081273 18.752662  8.935395 11.719140 15.295797 
##         9        10 
##  8.929690 19.836497
# ventas_youtube$model[1:10]   Para visualizar el modelo

16.4 Dibujar el modelo y el dataset

attach(marketing) 
plot(youtube, sales)
abline(ventas_youtube)

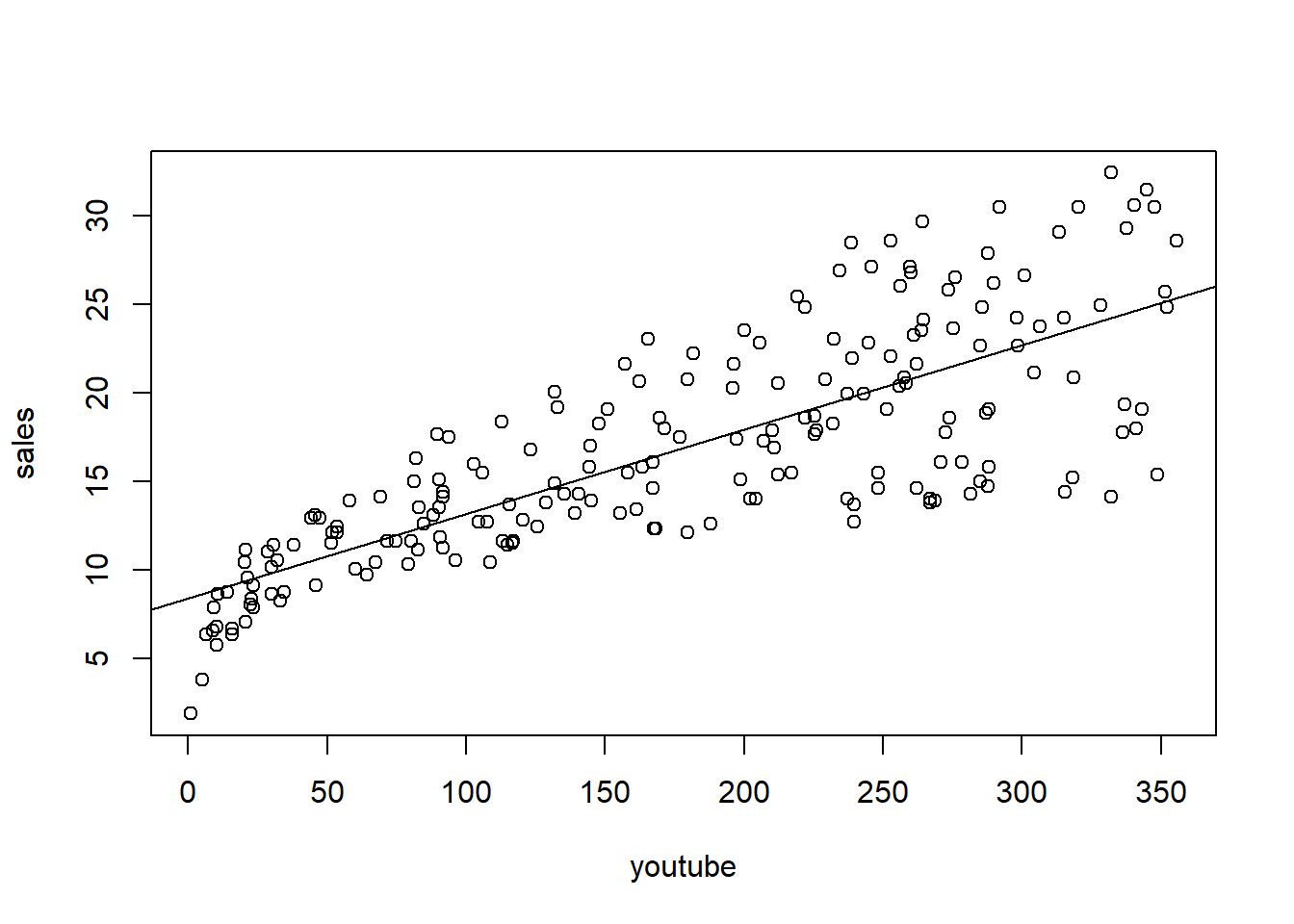
# En la Y va la funcion que tu quieres predecir, es decir la ventas
marketing %>%
  ggplot(aes(x=youtube, y=sales)) +
  geom_point() +
  stat_smooth(method = lm)
## `geom_smooth()` using formula 'y ~ x'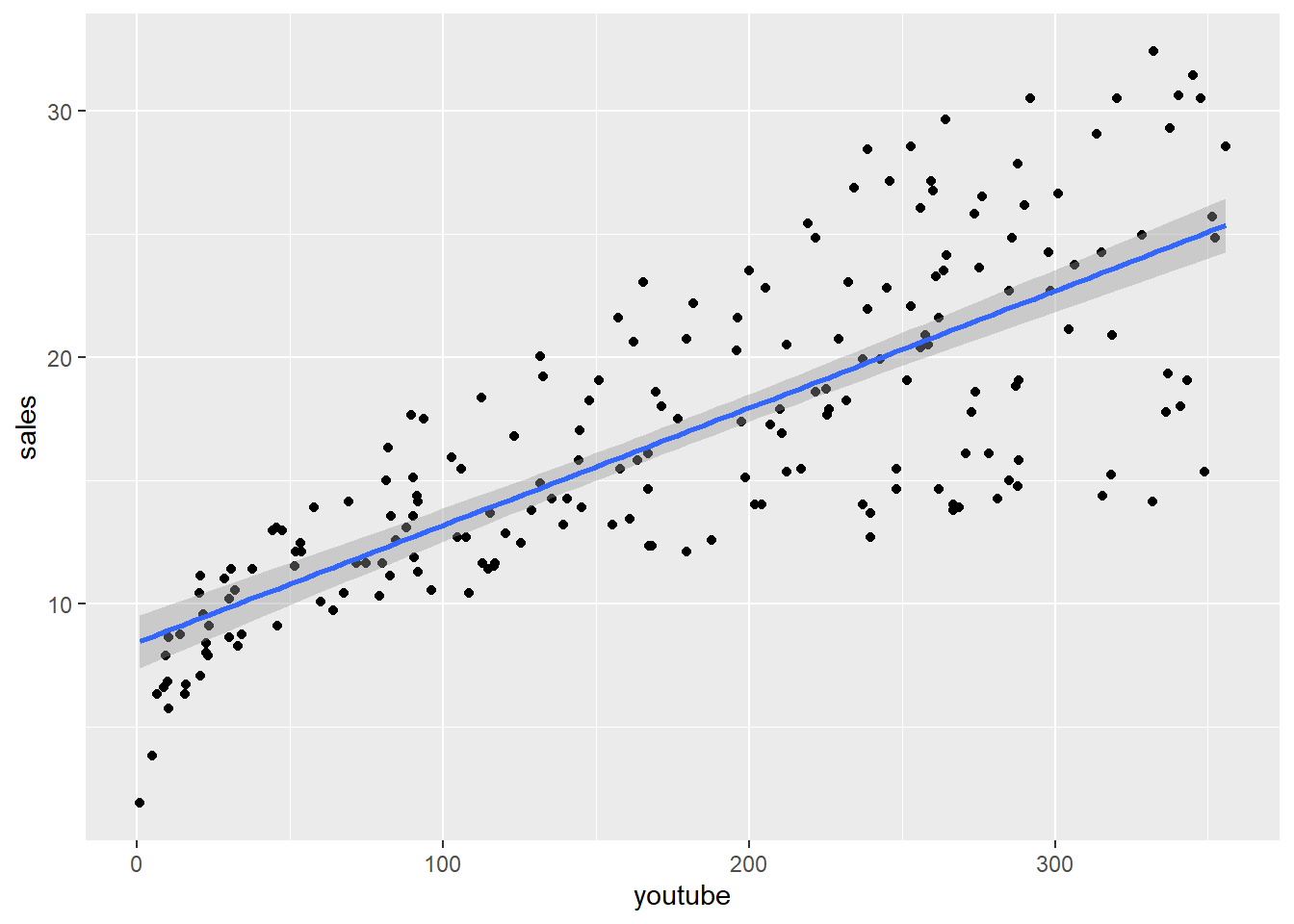

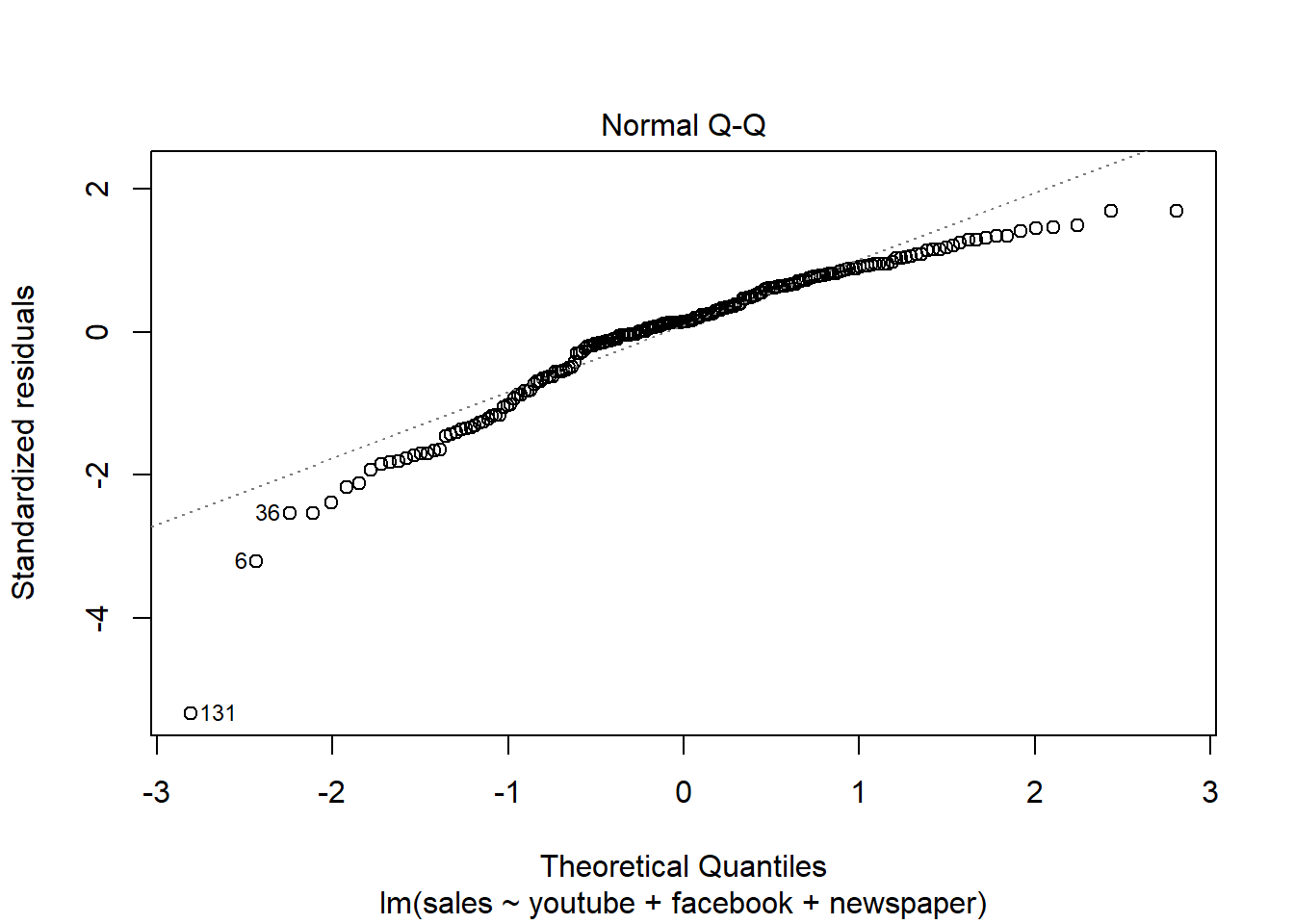
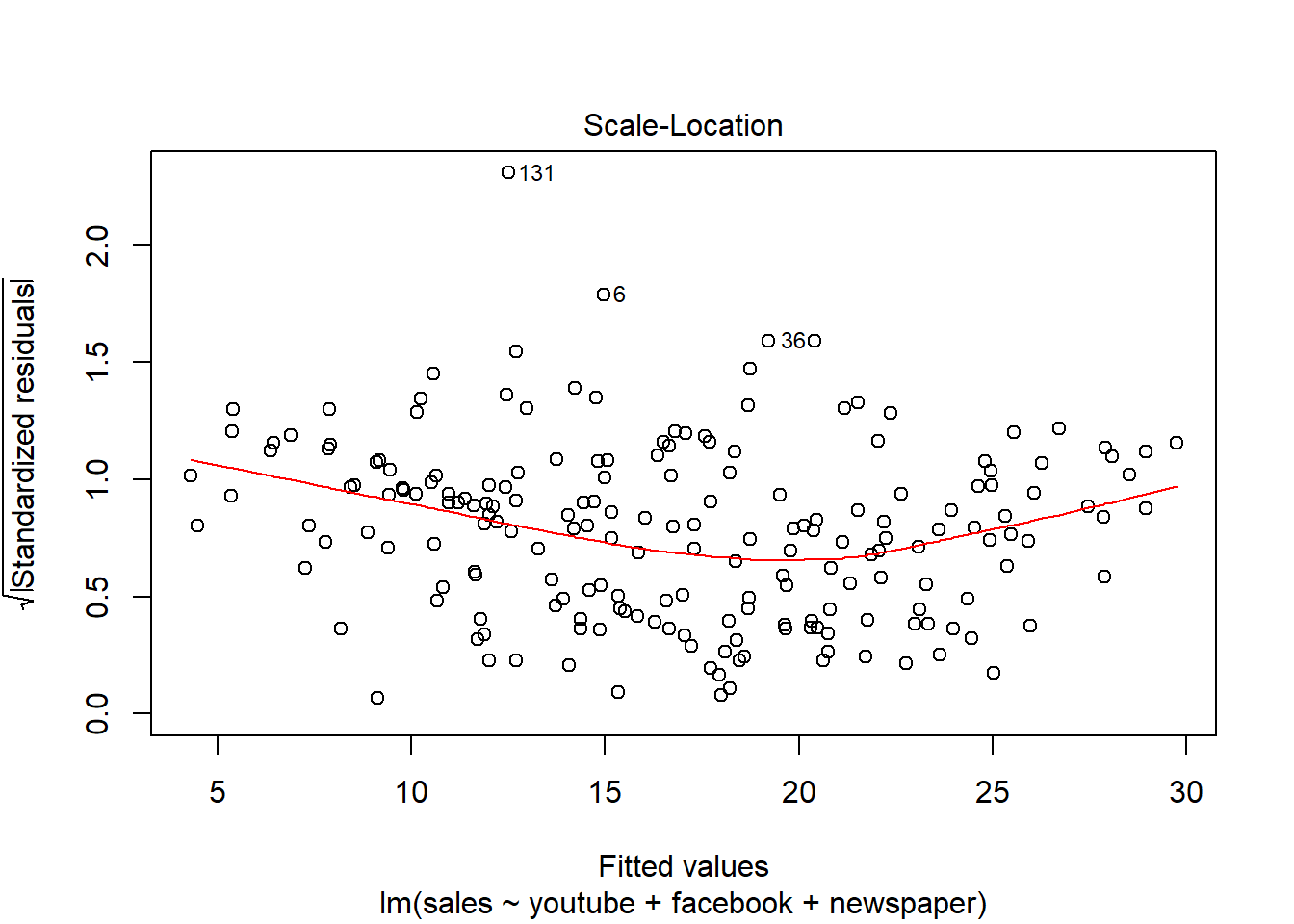
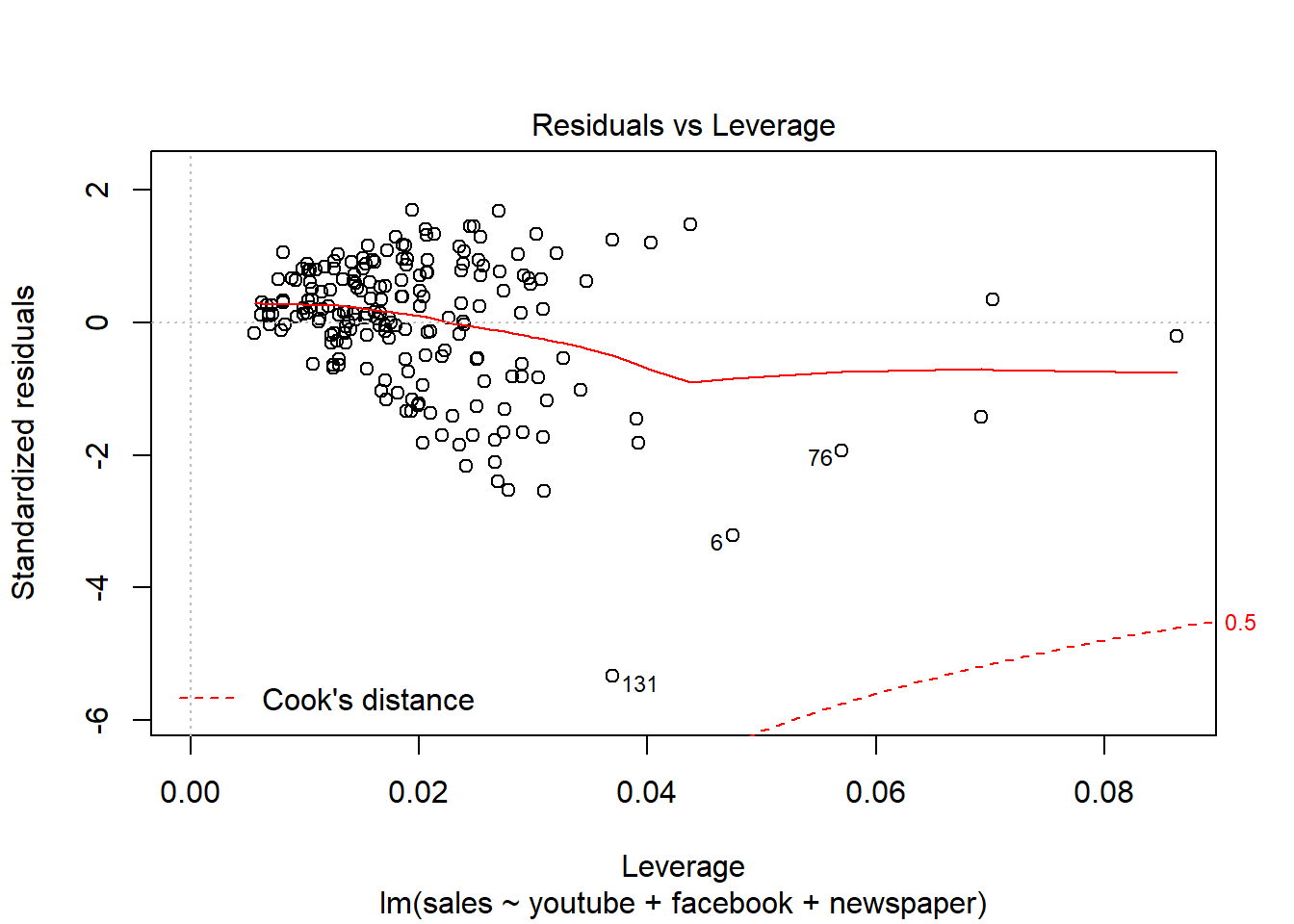
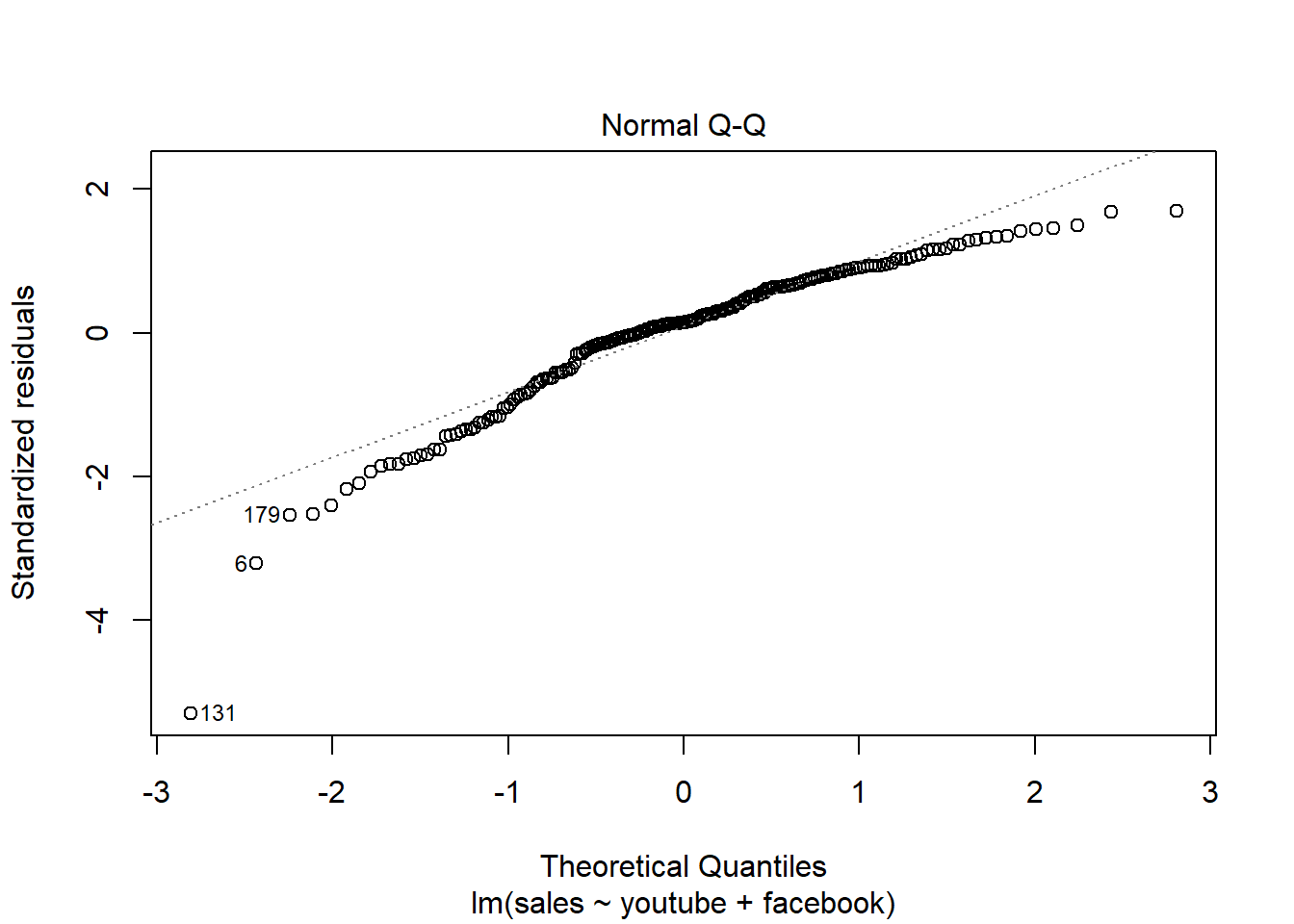
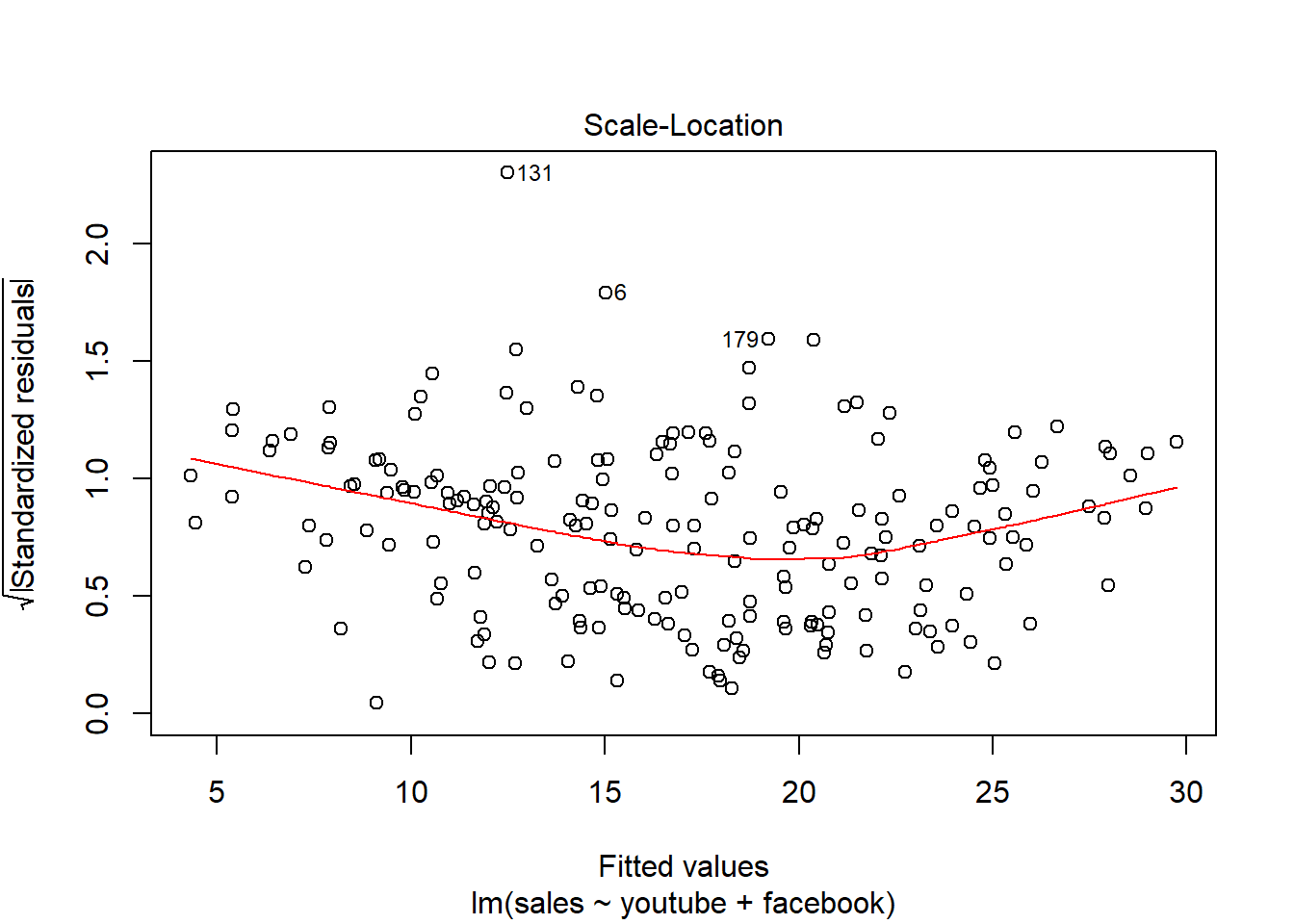
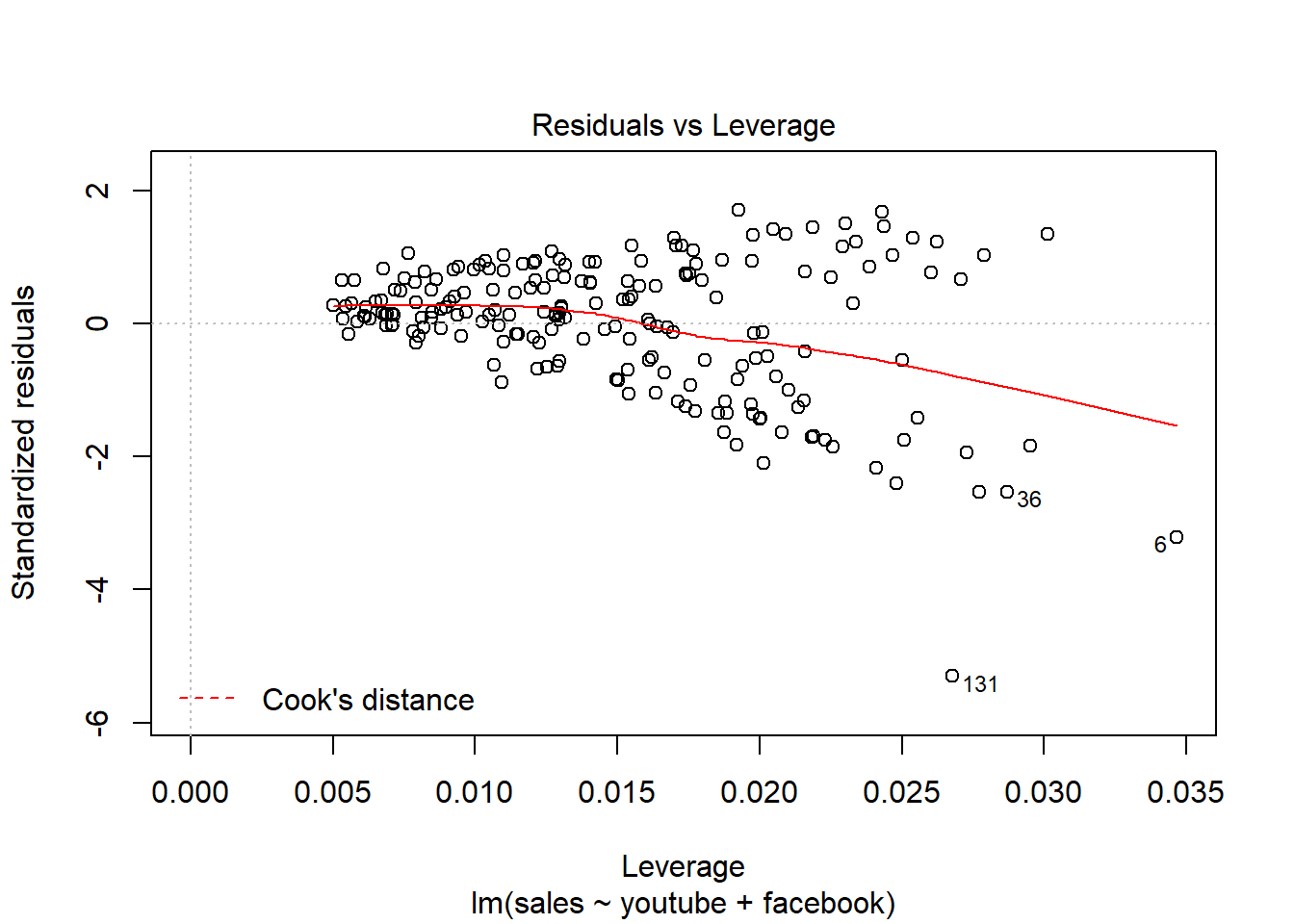
16.5 Plot del modelo:

plot(ventas_youtube)

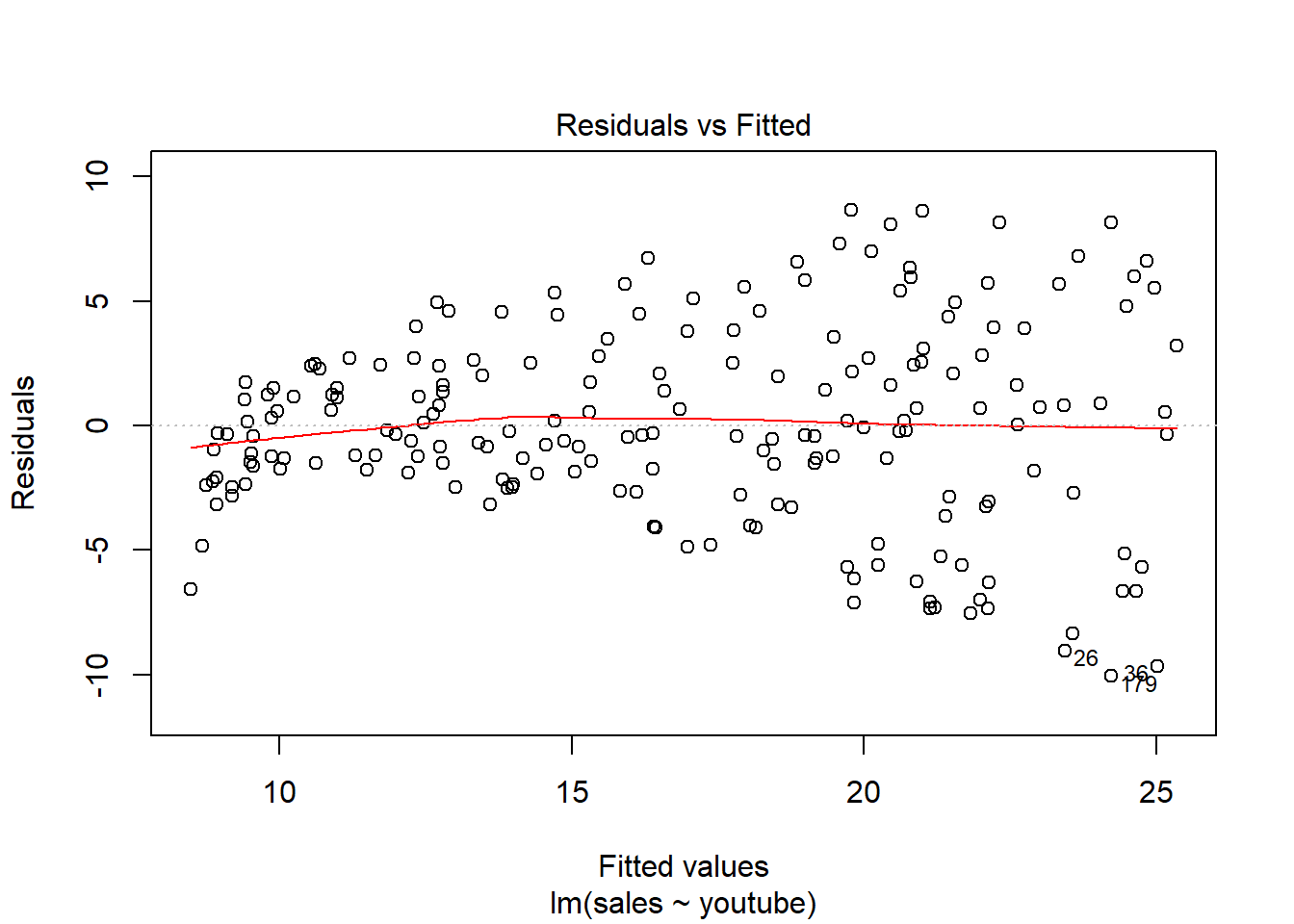
  1. Residuos linealmente distribuidos, cerca del y = 0

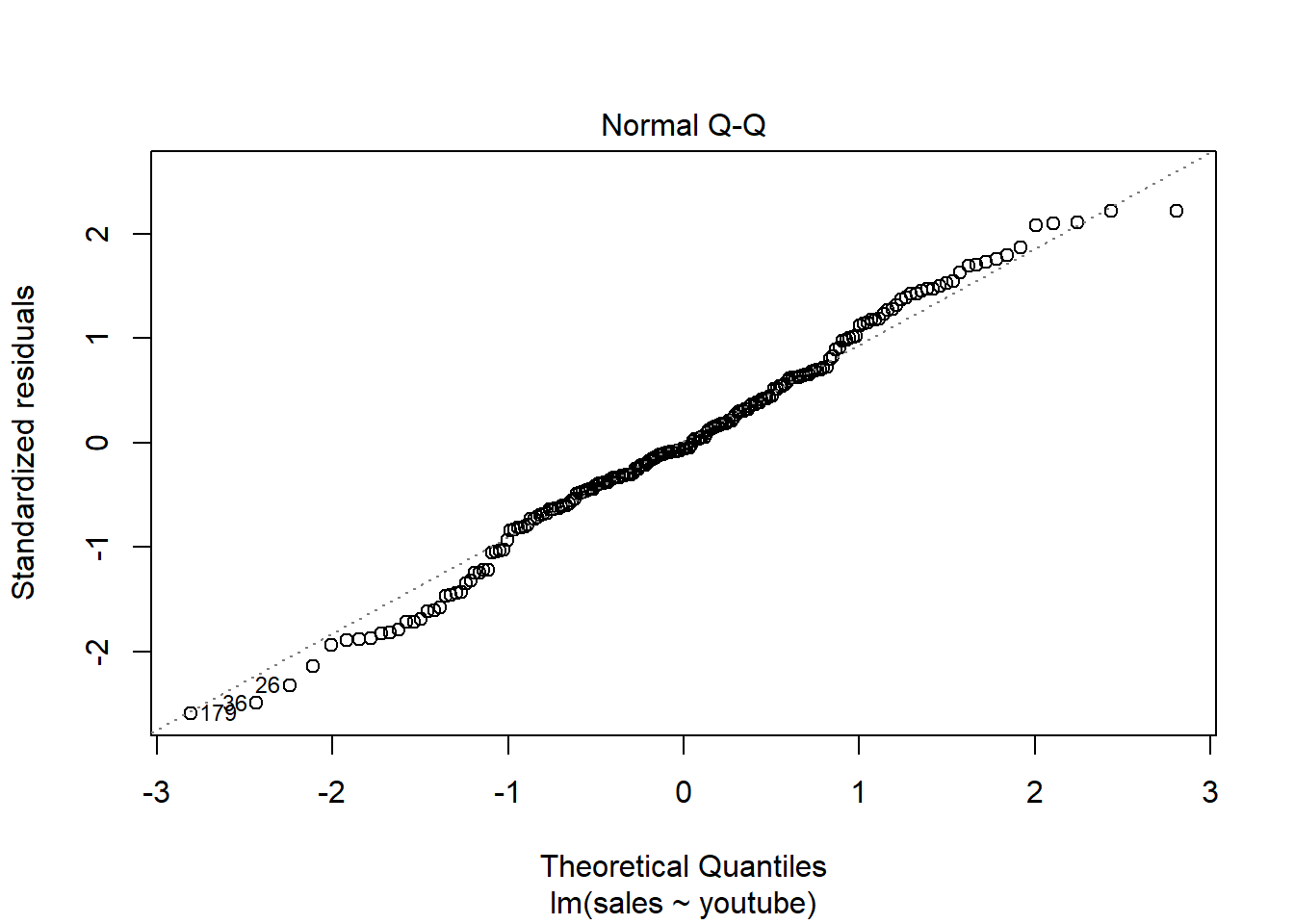
  2. Los residuos están prácticamente distribuidos siguiendo una normal. También detecta outliers y valores importantes.

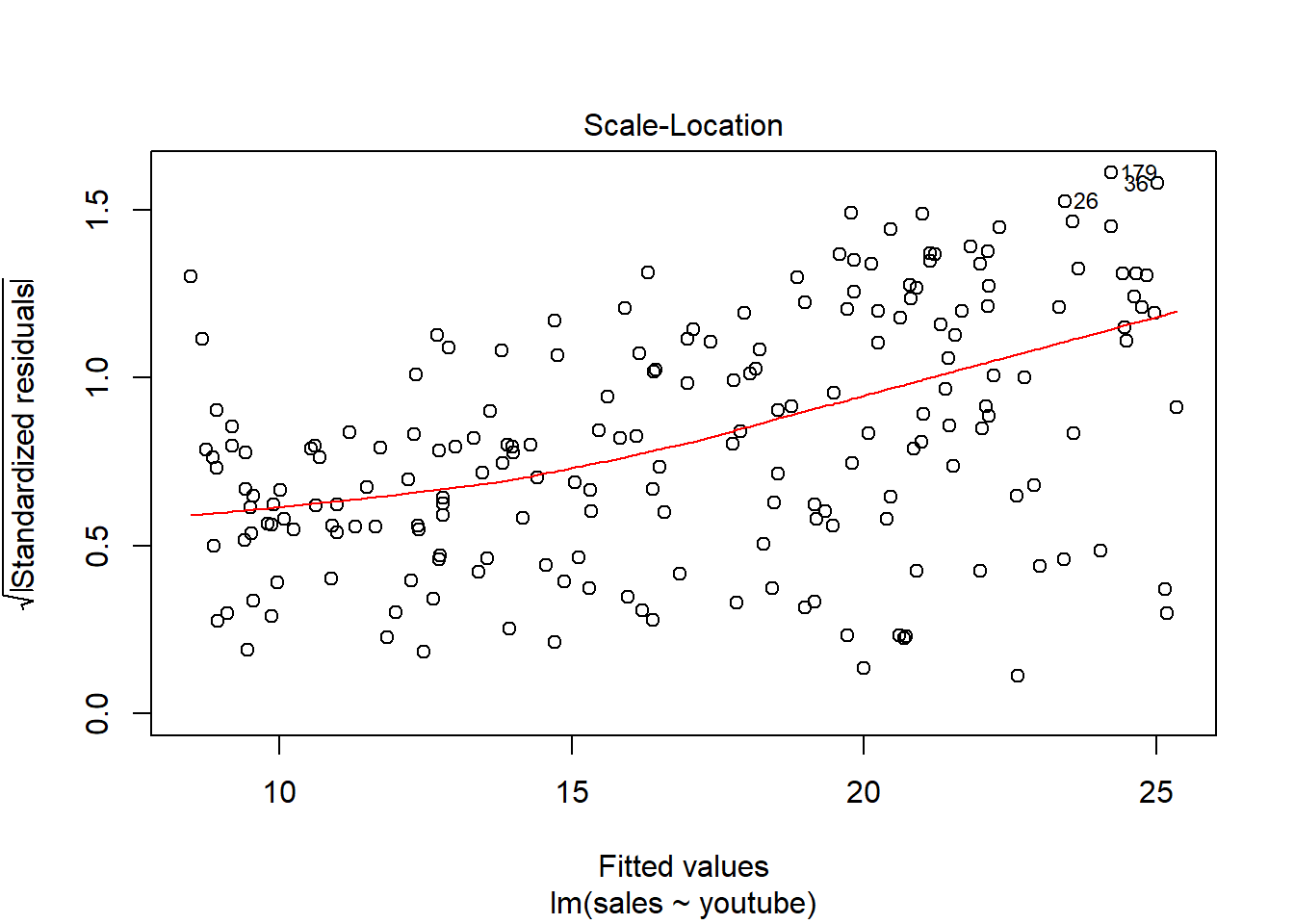
  3. Residuos distribuidos aleatoriamente -> Mucha dispersión de los errores.

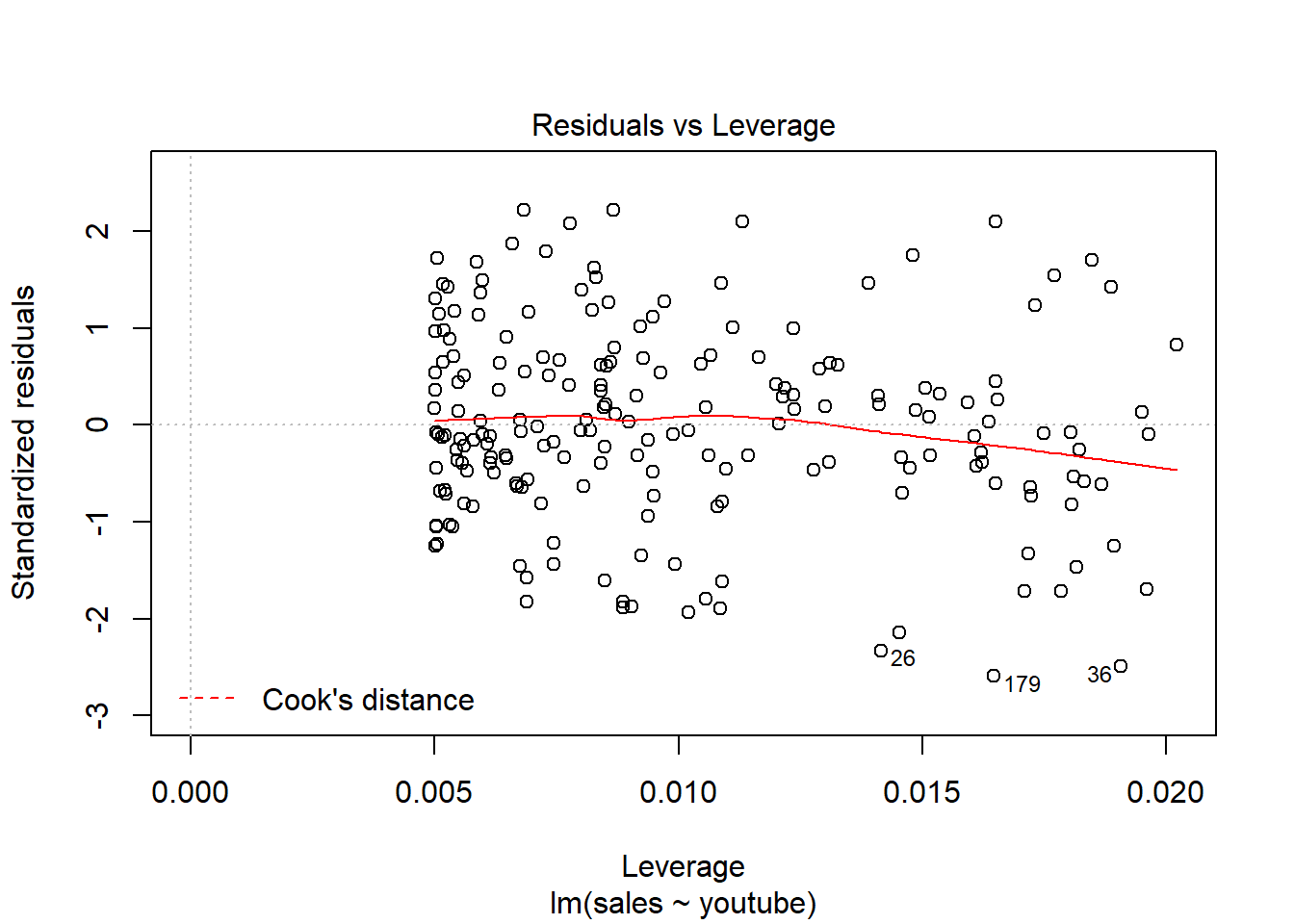
  4. Distancia Cook –> Outliers, valores importantes.

Ahora, cómo de bueno es el modelo:

Con la función summary() obtenemos los errores estándar de los coeficientes, los p-values así como el estadístico F y R2. En modelos lineales simples (como este caso), dado que solo hay un predictor, el p-value del test F es igual al p-value del t-test del predictor.

summary(ventas_youtube)
## 
## Call:
## lm(formula = sales ~ youtube, data = marketing)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -10.0632  -2.3454  -0.2295   2.4805   8.6548 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 8.439112   0.549412   15.36   <2e-16 ***
## youtube     0.047537   0.002691   17.67   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.91 on 198 degrees of freedom
## Multiple R-squared:  0.6119, Adjusted R-squared:  0.6099 
## F-statistic: 312.1 on 1 and 198 DF,  p-value: < 2.2e-16

¿Hay modelo? H0 o H1

  • H0: no hay modelo, ai=0
  • F-estadístico –> 312.1 (muy cerca de 1 - no hay relaciones de dependecia - no hay modelo —> se cumple H0)
  • p-value (probabilidad): 2.2e-16 no se cumple H0, H1 es cierta (si hay modelo)

Residuos - Calidad del ajuste realizado - media, dispersión…

R2 - 0.6119 -> 61.19% de la variabilidad de las ventas viene reflejado por la variante youtube.

R2 ajustado -> 60.99%. No está sobrecargado (overfitting)

  • Probabilidad Pr(>|t|)

  • Pr(>|t|) = <2e-16 *** muy significativo

Si tuviéramos (por ejemplo):

  • Pr(>|t|) = 0.13 nada significativo

Entonces, en este caso:

Ventas = 0.04754 * youtube

16.6 Modelo regresión multivariable:

ventas <- lm(data = marketing, sales ~ youtube+facebook+newspaper)

# ventas <- lm(data = marketing, sales ~ .)

ventas
## 
## Call:
## lm(formula = sales ~ youtube + facebook + newspaper, data = marketing)
## 
## Coefficients:
## (Intercept)      youtube     facebook    newspaper  
##    3.526667     0.045765     0.188530    -0.001037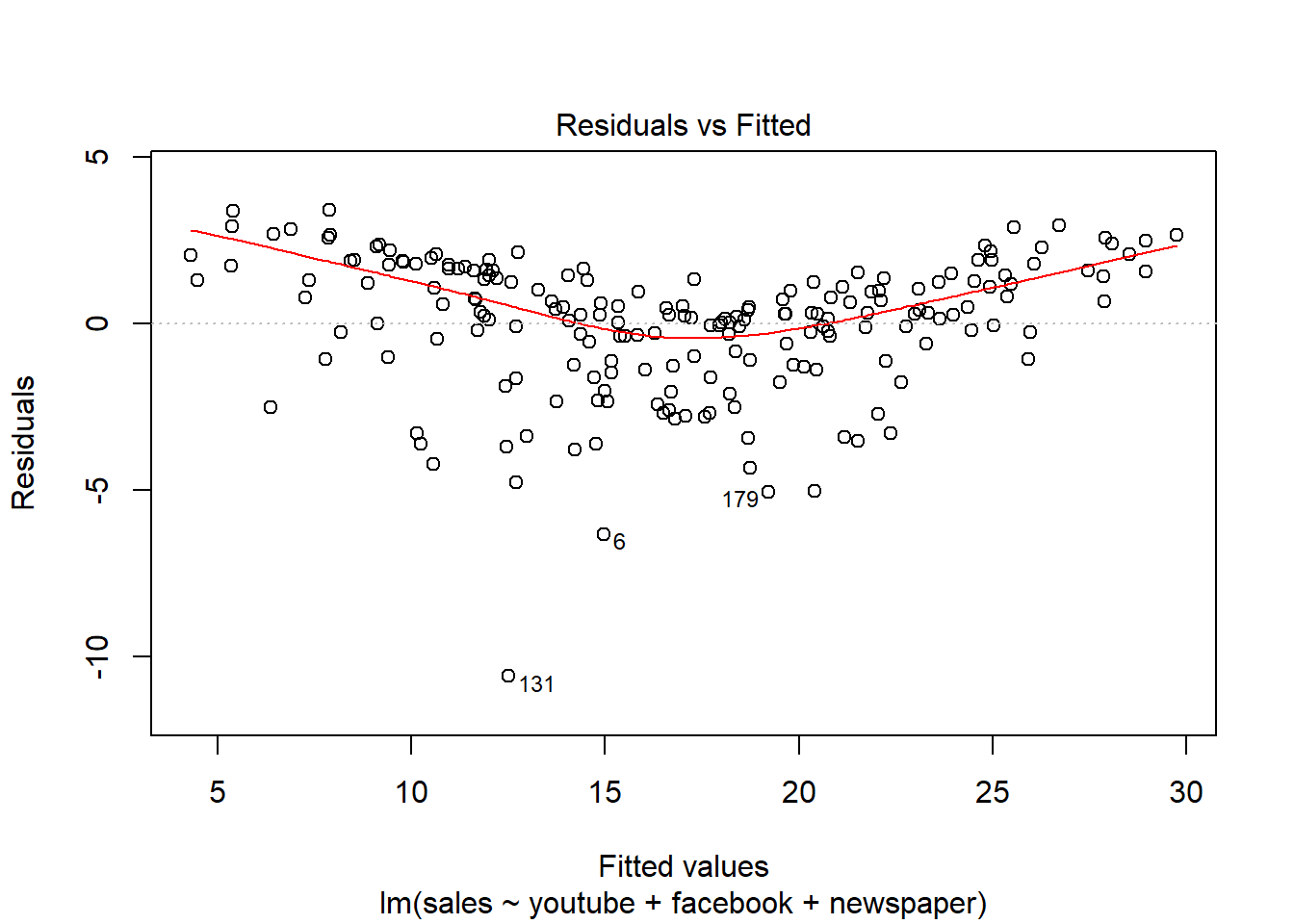
plot(ventas)

summary(ventas)
## 
## Call:
## lm(formula = sales ~ youtube + facebook + newspaper, data = marketing)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -10.5932  -1.0690   0.2902   1.4272   3.3951 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3.526667   0.374290   9.422   <2e-16 ***
## youtube      0.045765   0.001395  32.809   <2e-16 ***
## facebook     0.188530   0.008611  21.893   <2e-16 ***
## newspaper   -0.001037   0.005871  -0.177     0.86    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.023 on 196 degrees of freedom
## Multiple R-squared:  0.8972, Adjusted R-squared:  0.8956 
## F-statistic: 570.3 on 3 and 196 DF,  p-value: < 2.2e-16
# La probabilidad del newspaper es demasiada alta, nos dice que no es significativa en las ventas. No nos interesa invertir en newspaper.

# Quitaríamos del modelo el newspaper


ventas2 <- lm(data = marketing, sales ~ youtube+facebook)
ventas2
## 
## Call:
## lm(formula = sales ~ youtube + facebook, data = marketing)
## 
## Coefficients:
## (Intercept)      youtube     facebook  
##     3.50532      0.04575      0.18799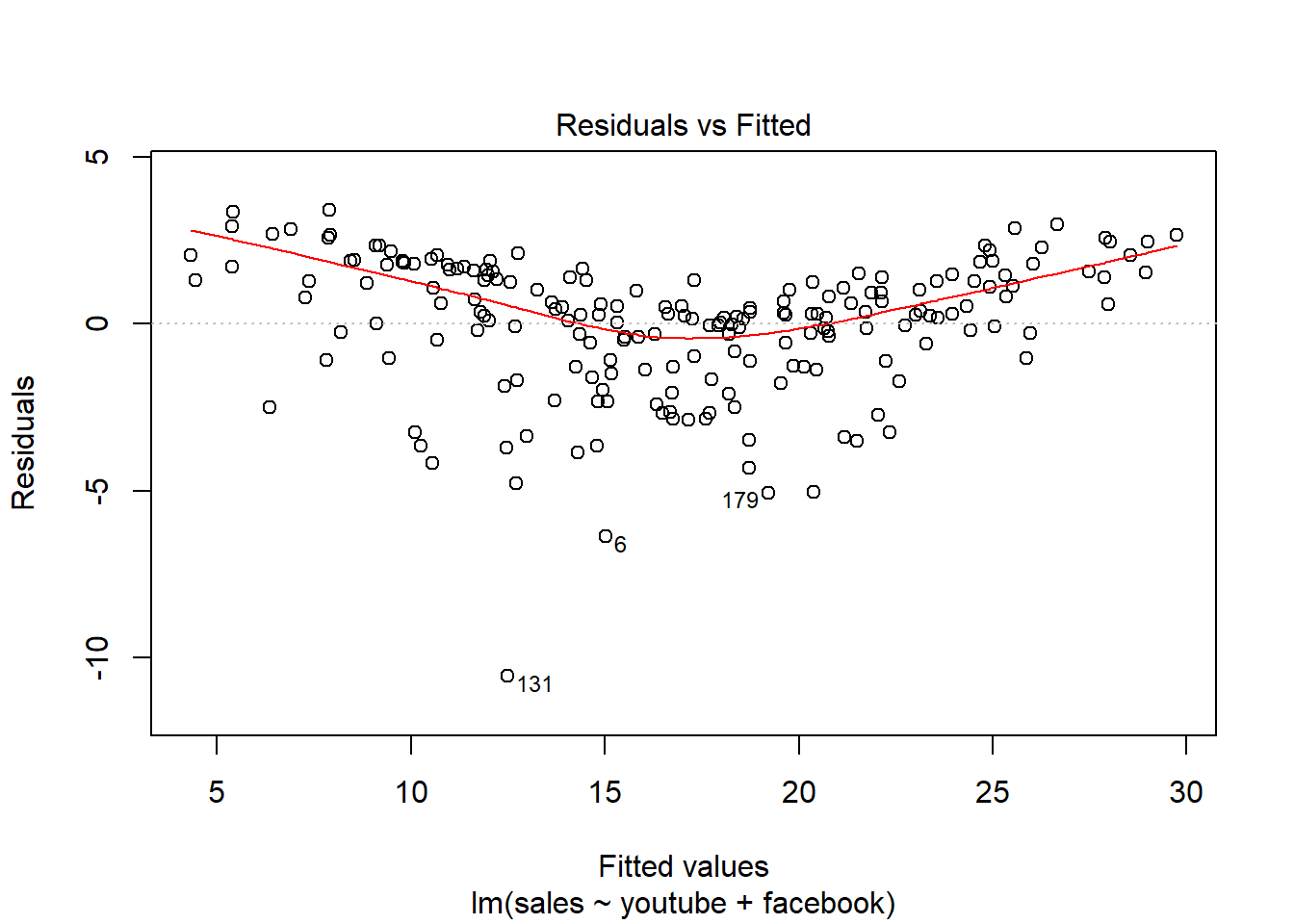
plot(ventas2)

summary(ventas2)
## 
## Call:
## lm(formula = sales ~ youtube + facebook, data = marketing)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -10.5572  -1.0502   0.2906   1.4049   3.3994 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3.50532    0.35339   9.919   <2e-16 ***
## youtube      0.04575    0.00139  32.909   <2e-16 ***
## facebook     0.18799    0.00804  23.382   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.018 on 197 degrees of freedom
## Multiple R-squared:  0.8972, Adjusted R-squared:  0.8962 
## F-statistic: 859.6 on 2 and 197 DF,  p-value: < 2.2e-16

16.7 Modelo polinomial:

¿Hay una parabola sales-youtube?

ventas_pol2 <- lm(data = marketing, sales ~ youtube+I(youtube^2))
ventas_pol2
## 
## Call:
## lm(formula = sales ~ youtube + I(youtube^2), data = marketing)
## 
## Coefficients:
##  (Intercept)       youtube  I(youtube^2)  
##    7.337e+00     6.727e-02    -5.706e-05
summary(ventas_pol2)
## 
## Call:
## lm(formula = sales ~ youtube + I(youtube^2), data = marketing)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -9.2213 -2.1412 -0.1874  2.4106  9.0117 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   7.337e+00  7.911e-01   9.275  < 2e-16 ***
## youtube       6.727e-02  1.059e-02   6.349 1.46e-09 ***
## I(youtube^2) -5.706e-05  2.965e-05  -1.924   0.0557 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.884 on 197 degrees of freedom
## Multiple R-squared:  0.619,  Adjusted R-squared:  0.6152 
## F-statistic: 160.1 on 2 and 197 DF,  p-value: < 2.2e-16
# Vemos que no ha mejorado mucho

16.8 EJEMPLO INTERNET

Para la salida:

## 
## Call:
## lm(formula = ausencias ~ salario, data = df)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -9.516 -3.053  1.428  2.961  5.475 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  47.6002     3.0789  15.460 9.50e-10 ***
## salario      -3.0094     0.4027  -7.474 4.67e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.294 on 13 degrees of freedom
## Multiple R-squared:  0.8112, Adjusted R-squared:  0.7967 
## F-statistic: 55.86 on 1 and 13 DF,  p-value: 4.672e-06

Interpretación:

El modelo ajustado es significativo: Los coeficientes de regresión son 47.6002 y -3.0094, estos parámetros son significativos, con p-valor menor de 0.05 (9.50e-10, 4.67e-06). El error estándar para cada parámetro es 3.0789 y 0.4027 respectivamente. La R2 ajustada es 0.7967, que indica un buen ajuste del modelo (próximo a 1),

El modelo tiene la forma de:

  • ausencias=47.60−3.01×salario

  • Los coeficientes de regresión son 47.60 y -3.01.

  • 47.60 es el valor medio de la variable dependiente (ausencias) cuando la predictora es cero (salario).

  • 3.01 es el efecto medio (negativo) sobre la variable dependiente Y (ausencias) al aumentar en una unidad el valor de la predictora X (salario). Esto es, variación que se produce en Y (-3.01) por cada unidad de incremento en X.

EN CONCLUSIÓN: Existe una relación lineal negativa entre las variables: cuando aumentamos en una unidad el salario, las ausencias disminuyen en 3.01 unidades. De forma que por cada aumento de la categoría del salario, las ausencias de los trabajadores disminuyen en 3.01 días.