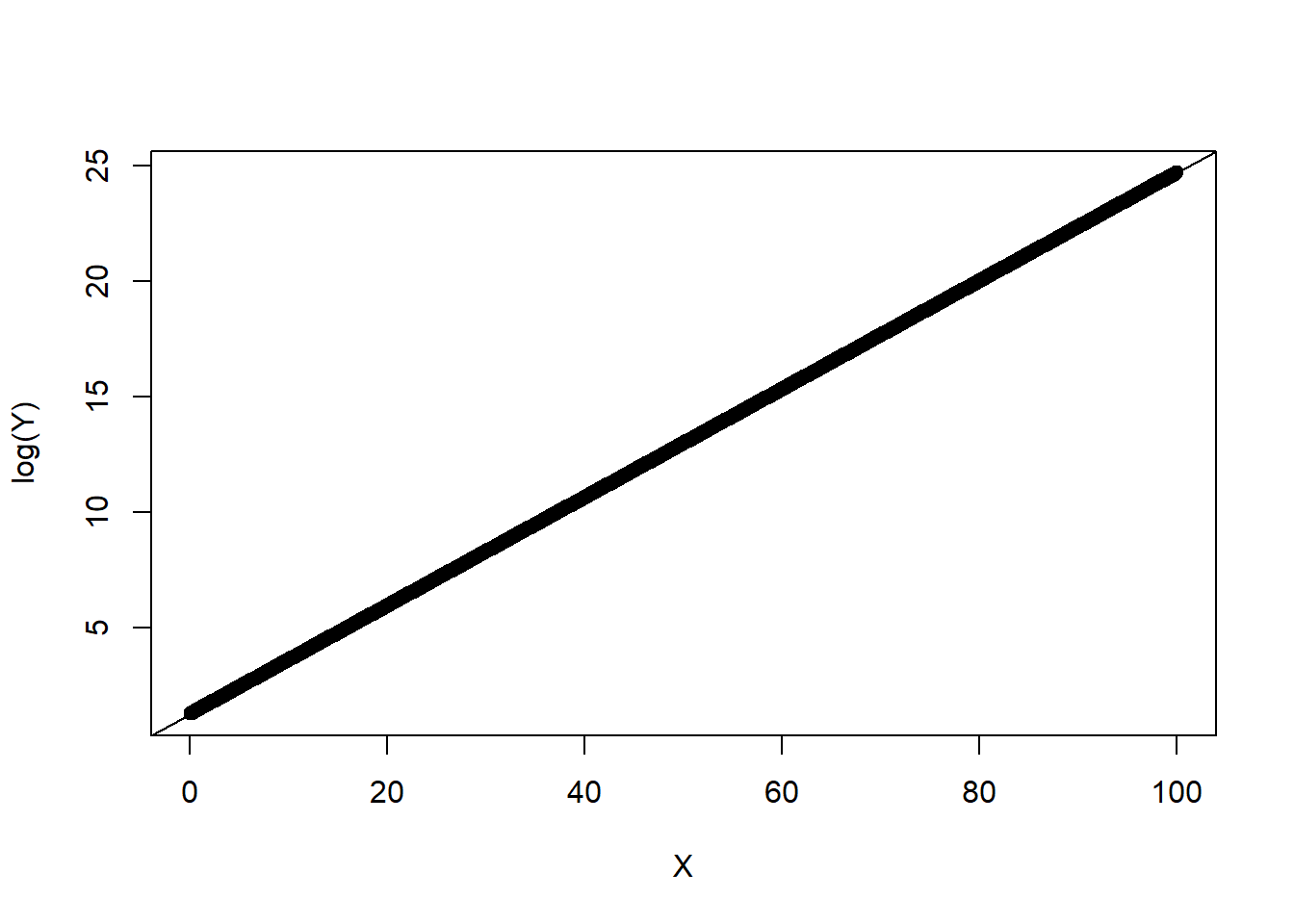Documento 18 Regresion - Fitting Dataset

Usar el dataset que se encuentra en fitting1.xls en el CV. Importarlo en R.

library(readxl)
library(xlsx)

library(dplyr)
library(ggplot2)
library(magrittr)
library(GGally)

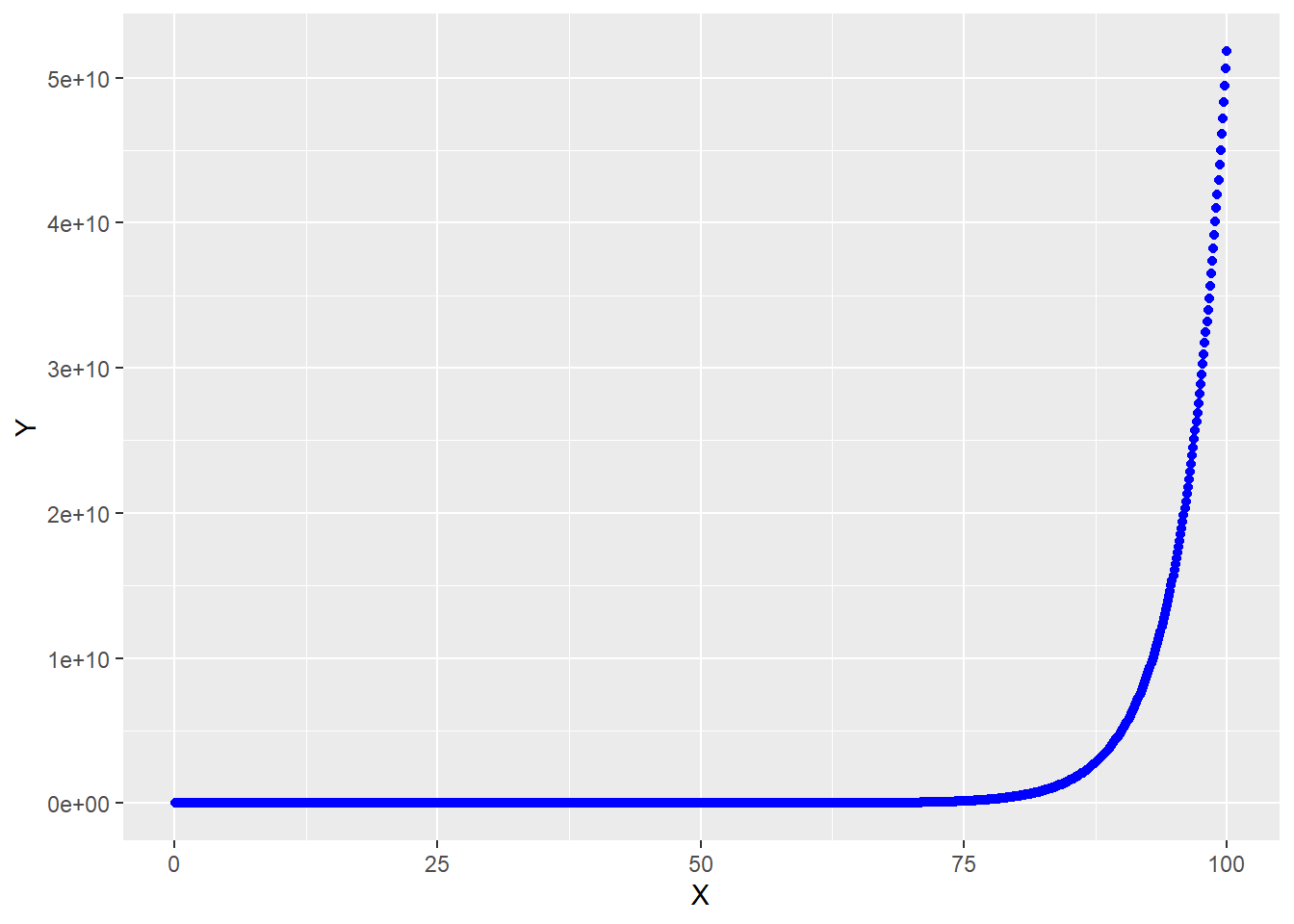
fitting1 <- read_excel("datasets/fitting1.xls")

Realizar un gráfico para explorar qué modelo sería más interesante.

plot(fitting1)

ggpairs(fitting1)

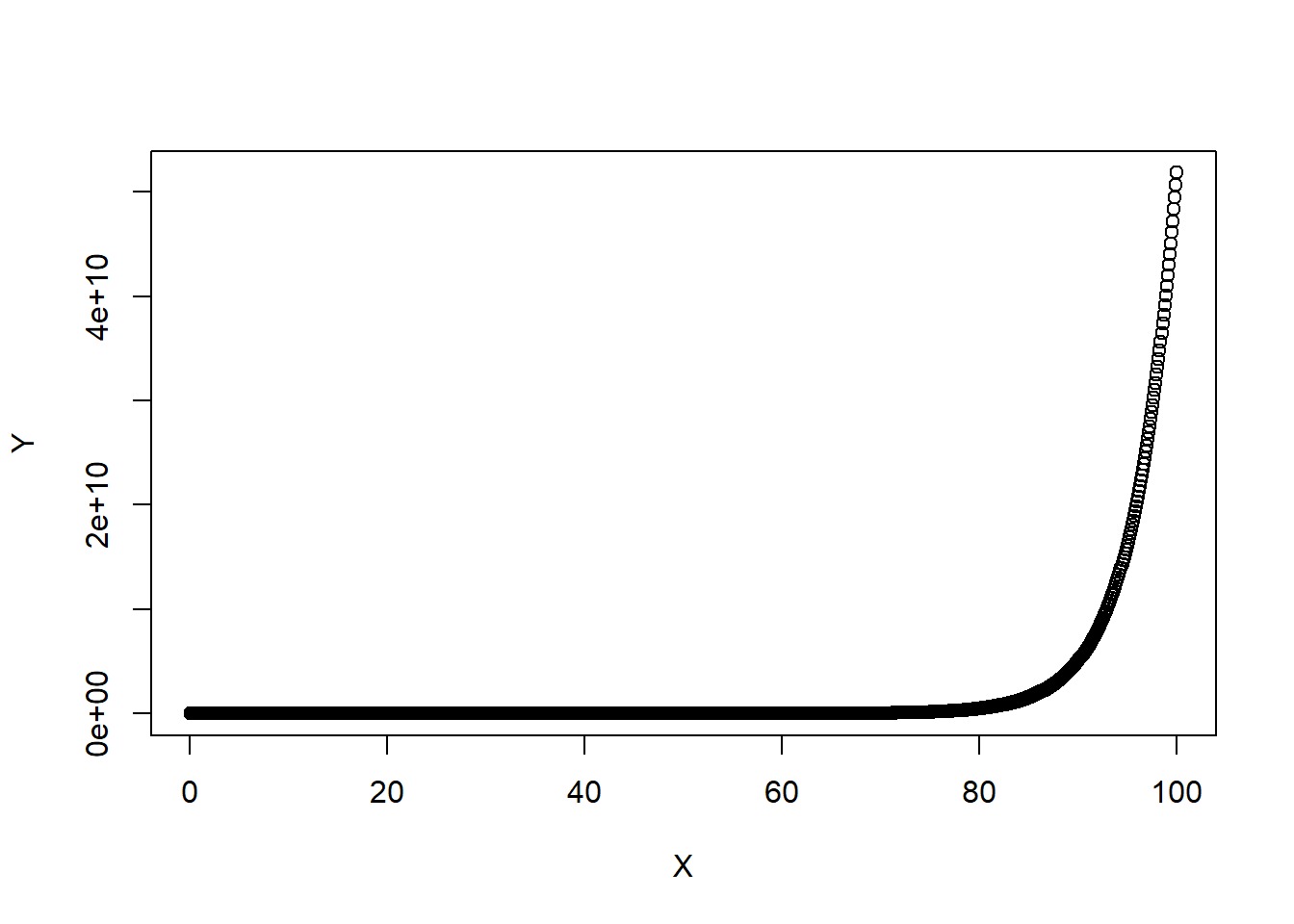
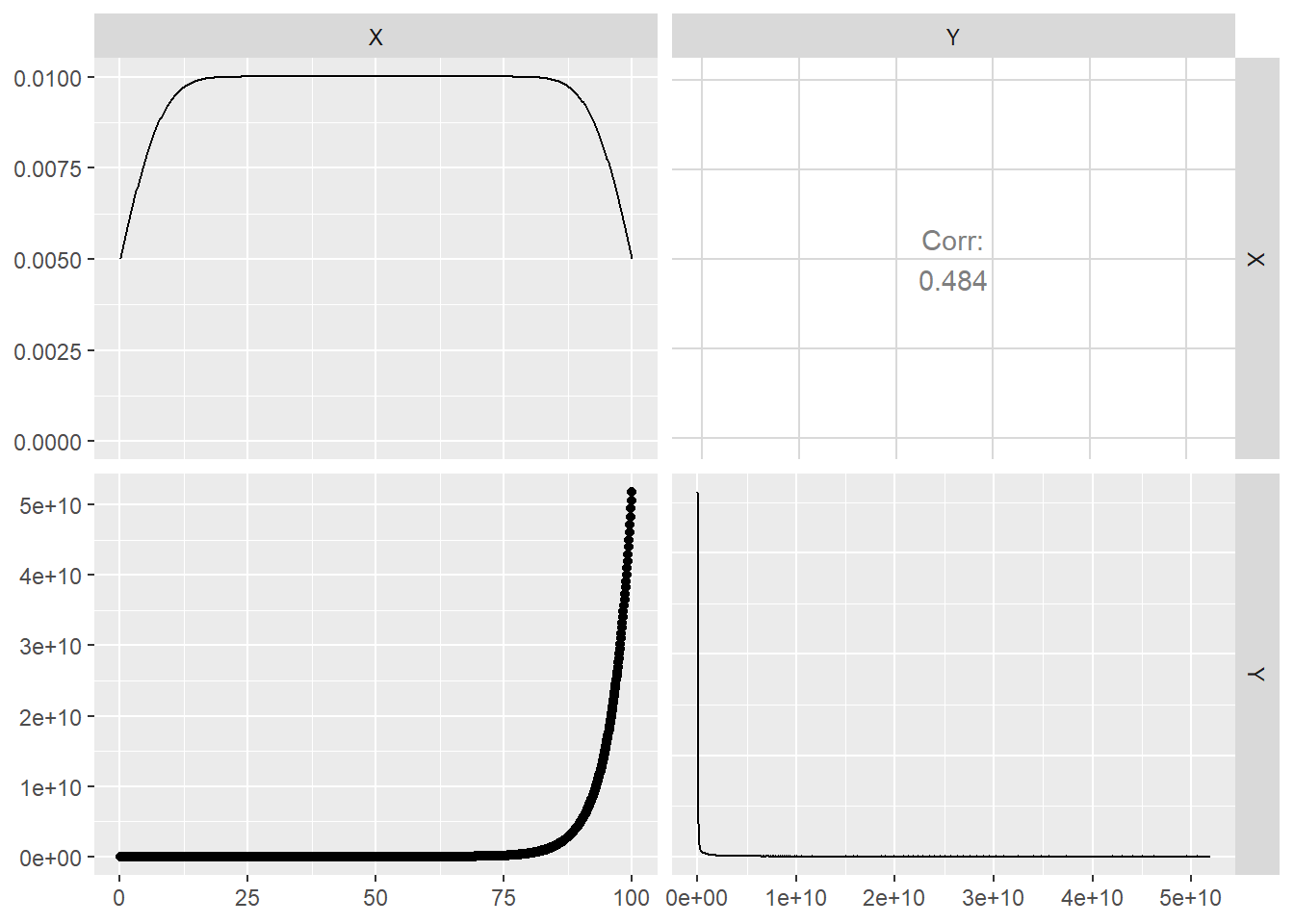
A partir del gráfico mostrado podemos ver que tiene forma exponencial, por lo que suponemos que será el modelo adecuado.

18.1 Calcula en R el modelo que ajuste mejor los datos.

# Let’s attach the entire dataset so that we can refer to all variables directly by name.
attach(fitting1)

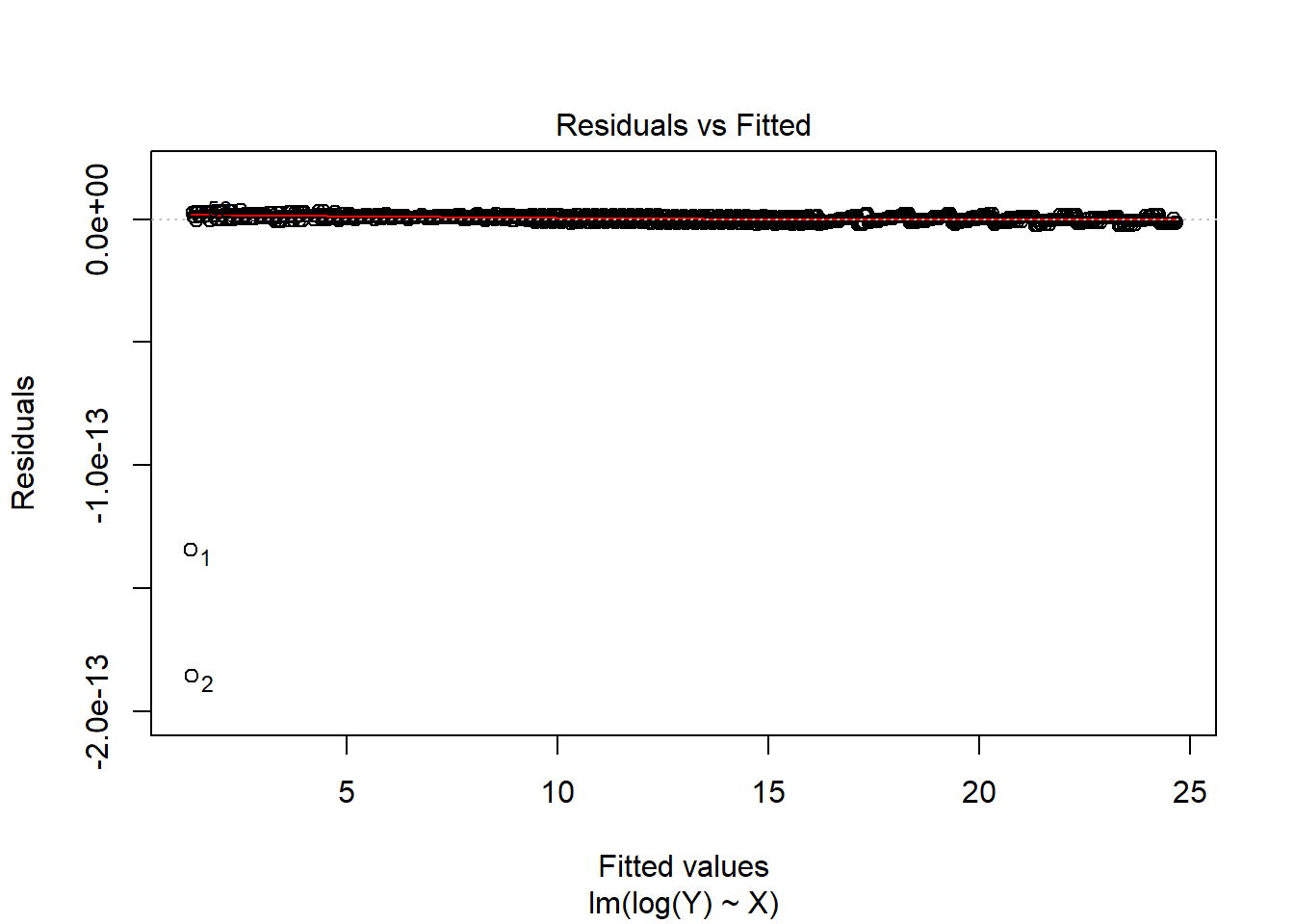
model_exp <- lm(log(Y) ~ X)
model_exp

## 
## Call:
## lm(formula = log(Y) ~ X)
## 
## Coefficients:
## (Intercept)            X  
##       1.271        0.234

summary(model_exp)

## Warning in summary.lm(model_exp): essentially perfect fit: summary may be
## unreliable

## 
## Call:
## lm(formula = log(Y) ~ X)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -1.857e-13 -4.970e-16  4.320e-16  1.168e-15  3.683e-15 
## 
## Coefficients:
##              Estimate Std. Error   t value Pr(>|t|)    
## (Intercept) 1.271e+00  4.660e-16 2.728e+15   <2e-16 ***
## X           2.340e-01  8.065e-18 2.901e+16   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 7.362e-15 on 998 degrees of freedom
## Multiple R-squared:      1,  Adjusted R-squared:      1 
## F-statistic: 8.418e+32 on 1 and 998 DF,  p-value: < 2.2e-16

model_cuadratic <- lm(Y ~ X+I(X^2))
model_cuadratic

## 
## Call:
## lm(formula = Y ~ X + I(X^2))
## 
## Coefficients:
## (Intercept)            X       I(X^2)  
##  4688487086   -392095038      5145175

summary(model_cuadratic)

## 
## Call:
## lm(formula = Y ~ X + I(X^2))
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -7.070e+09 -3.070e+09  2.596e+08  2.267e+09  3.489e+10 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 4688487086  489203580   9.584   <2e-16 ***
## X           -392095038   22571365 -17.371   <2e-16 ***
## I(X^2)         5145175     218342  23.565   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 5.146e+09 on 997 degrees of freedom
## Multiple R-squared:  0.5083, Adjusted R-squared:  0.5074 
## F-statistic: 515.4 on 2 and 997 DF,  p-value: < 2.2e-16

model_linear <- lm(Y ~ X)
model_linear

## 
## Call:
## lm(formula = Y ~ X)
## 
## Coefficients:
## (Intercept)            X  
##  -3.913e+09    1.229e+08

summary(model_linear)

## 
## Call:
## lm(formula = Y ~ X)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -5.444e+09 -3.814e+09 -1.109e+09  1.740e+09  4.344e+10 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -3.913e+09  4.062e+08  -9.631   <2e-16 ***
## X            1.229e+08  7.031e+06  17.485   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 6.418e+09 on 998 degrees of freedom
## Multiple R-squared:  0.2345, Adjusted R-squared:  0.2337 
## F-statistic: 305.7 on 1 and 998 DF,  p-value: < 2.2e-16

Nos quedamos con el modelo exponencial, ya que es el que mejor se ajusta con los datos del dataset.

18.2 Dibujar los valores ajustados en un mismo gráfico junto con los puntos del dataset.

plot(X, log(Y))
abline(model_exp)

a1 <- fitting1 %>%
  ggplot(aes(x=X, y=Y)) +
  geom_point(color = "red")

a2 <- a1 +
  geom_point(data = fitting1, aes(x=X, y=exp(model_exp$fitted.values)), color = "blue")
  

a2

a1 <- fitting1 %>%
  ggplot(aes(x=X, y=Y)) +
  geom_point(color = "red")

a2 <- a1 +
  geom_point(data = fitting1, aes(x=X, y=exp(model_exp$fitted.values)), color = "red")

18.3 Residuos frente a valores ajustados

Dibujar los residuos frente a los valores ajustados. Analiza los errores con las técnicas vistas en clase.

Como ya se analizó y explicó en otros ejemplos, he decidido no profundizar más en este apartado para no repetir lo mismo.

plot(model_exp, 1)