2.6 Practical issues
We discuss in this section several practical issues for kernel density estimation.
2.6.1 Boundary issues and transformations
In Section 2.3 we assumed certain regularity conditions for \(f.\) Assumption A1 stated that \(f\) should be twice continuously differentiable (on \(\mathbb{R}\)). It is simple to think a counterexample for that: take any density with bounded support, for example a \(\mathcal{LN}(0,1)\) in \((0,\infty),\) as seen below. The the kde will run into troubles.
# Sample from a LN(0, 1)
set.seed(123456)
samp <- rlnorm(n = 500)
# kde and density
plot(density(samp), ylim = c(0, 1))
curve(dlnorm(x), from = -2, to = 10, col = 2, add = TRUE)
rug(samp)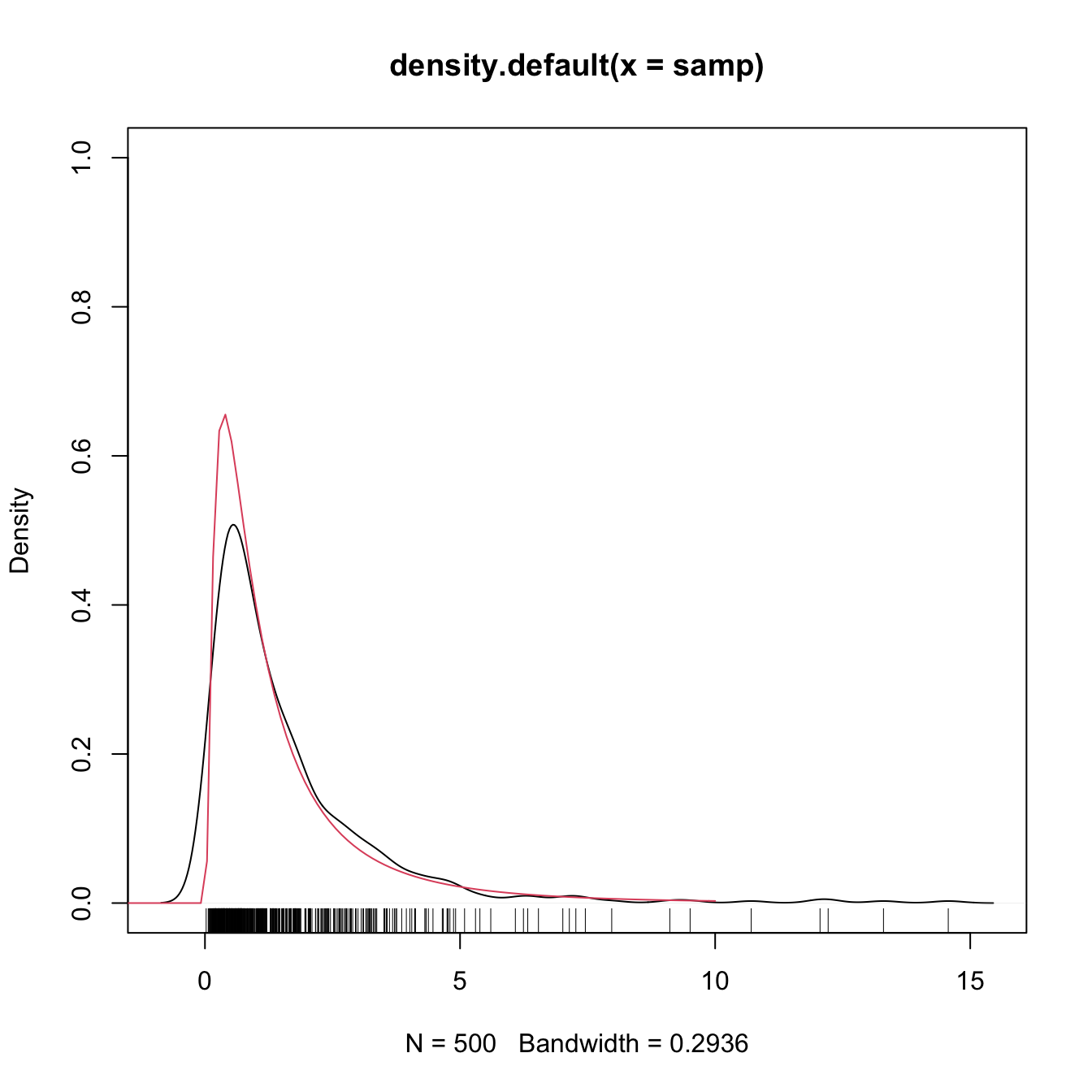
What is happening is clear: the kde is spreading probability mass outside the support of \(\mathcal{LN}(0,1),\) because the kernels are functions defined in \(\mathbb{R}.\) Since the kde places probability mass at negative values, it takes it from the positive side, resulting in a severe negative bias around \(0.\) As a consequence, the kde does not integrate one in the support of the data. No matter what is the sample size considered, the kde will always have a negative bias of \(O(h)\) at the boundary, instead of the standard \(O(h^2).\)
A simple approach to deal with the boundary bias is to map a compactly-supported density \(f\) into a real-supported density \(g,\) that is simpler to estimate, by means of a transformation \(t\):
\[\begin{align*} f(x)=g(t(x))t'(x). \end{align*}\]
The transformation kde is obtained by replacing \(g\) by the usual kde:
\[\begin{align} \hat f_T(x;h,t):=\frac{1}{n}\sum_{i=1}^nK_h(t(x)-t(X_i))t'(x). \tag{2.28} \end{align}\]
Note that \(h\) is in the scale of \(t(X_i),\) not \(X_i.\) Hence another plus of this approach is that bandwidth selection can be done transparently in terms of the previously seen bandwidth selectors applied to \(t(X_1),\ldots,t(X_n).\) A table with some common transformations is:
| Transformation | Useful for | \(t(x)\) | \(t'(x)\) |
|---|---|---|---|
| Log | Data in \((a,\infty),\) \(a\in\mathbb{R}\) | \(\log(x-a)\) | \(\frac{1}{x-a}\) |
| Probit | Data in \((a,b)\) | \(\Phi^{-1}\left(\frac{x-a}{b-a}\right)\) | \((b-a)\phi\left(\frac{\Phi^{-1}(x)-a}{b-a}\right)^{-1}\) |
| Shifted power | Heavily skewed data in \(\mathbb{R}\) and above \(-\lambda_1\) | \((x+\lambda_1)^{\lambda_2}\mathrm{sign}(\lambda_2)\) if \(\lambda_2\neq0\) and \(\log(x+\lambda_1)\) if \(\lambda_2=0\) | \(\lambda_2(x+\lambda_1)^{\lambda_2-1}\mathrm{sign}(\lambda_2)\) if \(\lambda_2\neq0\) and \(\frac{1}{x+\lambda_1}\) if \(\lambda_2=0\) |
Figure 2.5: Construction of the transformation kde for the log and probit transformations. The left panel shows the kde (2.4) applied to the transformed data. The right plot shows the transformed kde (2.28). Application also available here.
The code below illustrates how to compute a transformation kde in practice.
# kde with log-transformed data
kde <- density(log(samp))
plot(kde, main = "kde of transformed data")
rug(log(samp))
# Careful: kde$x is in the reals!
range(kde$x)
## [1] -4.542984 3.456035
# Untransform kde$x so the grid is in (0, infty)
kdeTransf <- kde
kdeTransf$x <- exp(kdeTransf$x)
# Transform the density using the chain rule
kdeTransf$y <- kdeTransf$y * 1 / kdeTransf$x
# Transformed kde
plot(kdeTransf, main = "Transformed kde")
curve(dlnorm(x), col = 2, add = TRUE)
rug(samp)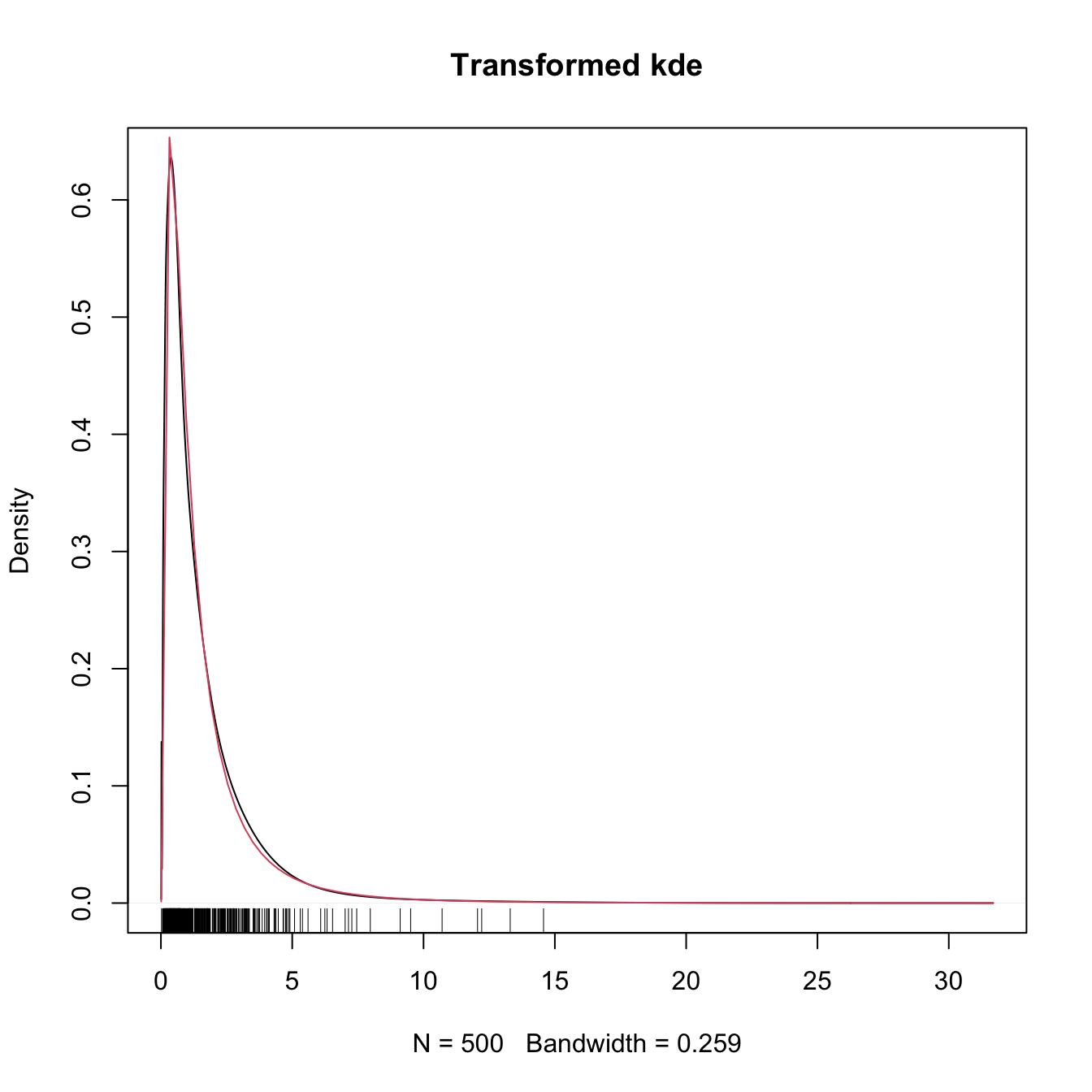
2.6.2 Sampling
Sampling a kde is relatively straightforward. The trick is to recall
\[\begin{align*} \hat f(x;h)=\frac{1}{n}\sum_{i=1}^nK_h(x-X_i) \end{align*}\]
as a mixture density made of \(n\) mixture components in which each of them is sampled independently. The only part that might require special treatment is sampling from the density \(K,\) although for most of the implemented kernels R contains specific sampling functions.
The algorithm for sampling \(N\) points goes as follows:
- Choose \(i\in\{1,\ldots,n\}\) at random.
- Sample from \(K_h(\cdot-X_i)=\frac{1}{h}K\left(\frac{\cdot-X_i}{h}\right).\)
- Repeat the previous steps \(N\) times.
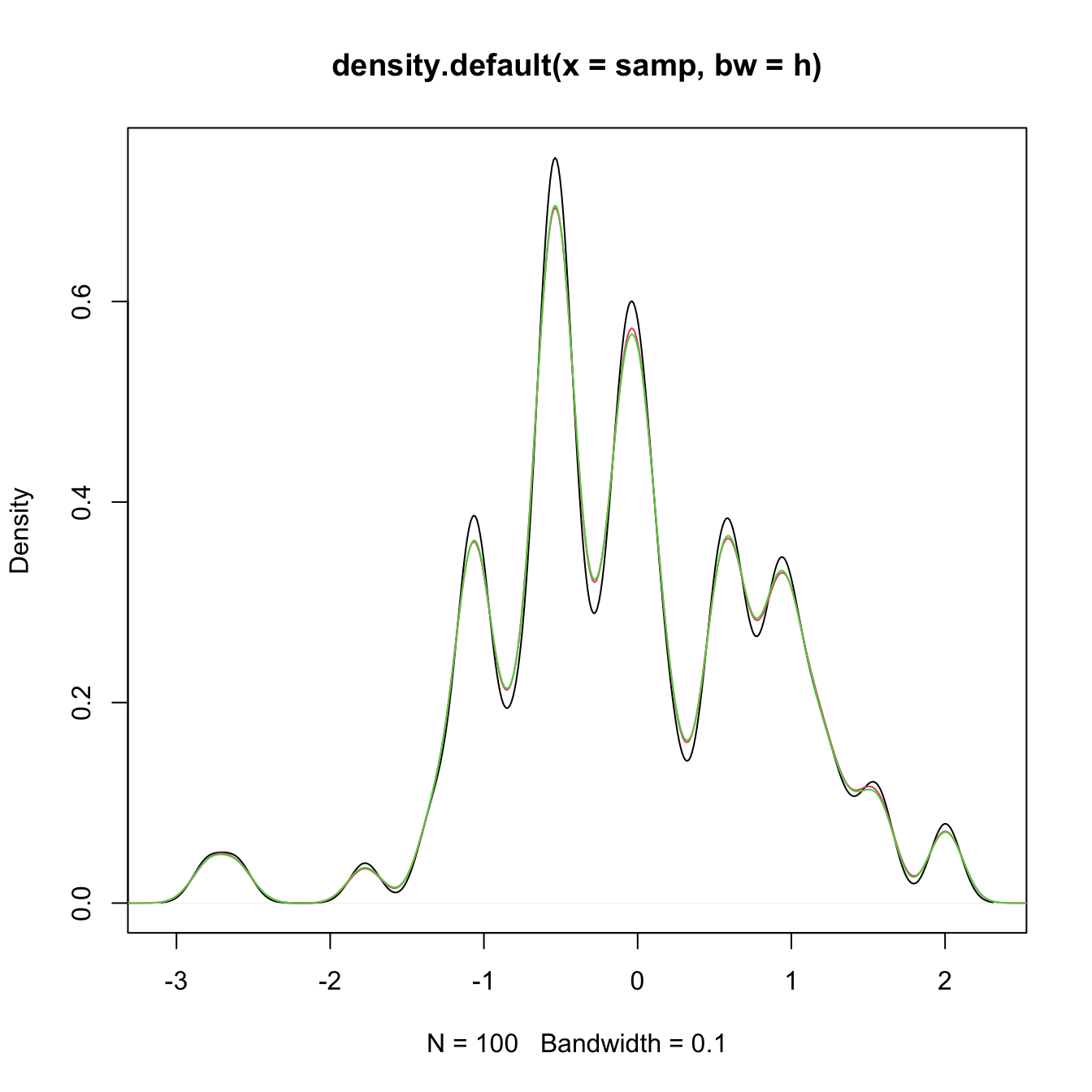
Let’s see a quick application.
# Sample the Claw
n <- 100
set.seed(23456)
samp <- rnorMix(n = n, obj = MW.nm10)
# Kde
h <- 0.1
plot(density(samp, bw = h))
# Naive sampling algorithm
sampKde <- numeric(1e6)
for (k in 1:1e6) {
i <- sample(x = 1:100, size = 1)
sampKde[k] <- rnorm(n = 1, mean = samp[i], sd = h)
}
# Add kde of the sampled kde - almost equal
lines(density(sampKde), col = 2)
# Sample 1e6 points from the kde
i <- sample(x = 100, size = 1e6, replace = TRUE)
sampKde <- rnorm(1e6, mean = samp[i], sd = h)
# Add kde of the sampled kde - almost equal
lines(density(sampKde), col = 3)