C Introduction to R
This section provides a collection of self-explainable snippets of the programming language R (R Core Team 2017) that show the very basics of the language. It is not meant to be an exhaustive introduction to R, but rather a reminder/panoramic of a collection of basic functions and methods.
In the following, # denotes comments to the code and ## outputs of the code.
Simple computations
# The console can act as a simple calculator
1.0 + 1.1
## [1] 2.1
2 * 2
## [1] 4
3/2
## [1] 1.5
2^3
## [1] 8
1/0
## [1] Inf
0/0
## [1] NaN
# Use ";" for performing several operations in the same line
(1 + 3) * 2 - 1; 3 + 2
## [1] 7
## [1] 5
# Elemental mathematical functions
sqrt(2); 2^0.5
## [1] 1.414214
## [1] 1.414214
exp(1)
## [1] 2.718282
log(10) # Neperian logarithm
## [1] 2.302585
log10(10); log2(10) # Logs in base 10 and 2
## [1] 1
## [1] 3.321928
sin(pi); cos(0); asin(0)
## [1] 1.224647e-16
## [1] 1
## [1] 0
tan(pi/3)
## [1] 1.732051
sqrt(-1)
## [1] NaN# Remember to close the parenthesis
1 +
(1 + 3
## Error: <text>:4:0: unexpected end of input
## 2: 1 +
## 3: (1 + 3
## ^Exercise C.1 Compute:
- \(\frac{e^{2}+\sin(2)}{\cos^{-1}\left(\tfrac{1}{2}\right)+2}.\) Answer:
2.723274. - \(\sqrt{3^{2.5}+\log(10)}.\) Answer:
4.22978. - \((2^{0.93}-\log_2(3 + \sqrt{2+\sin(1)}))10^{\tan(1/3))}\sqrt{3^{2.5}+\log(10)}.\) Answer:
-3.032108.
Variables and assignment
# Any operation that you perform in R can be stored in a variable (or object)
# with the assignment operator "<-"
x <- 1
# To see the value of a variable, simply type it
x
## [1] 1
# A variable can be overwritten
x <- 1 + 1
# Now the value of x is 2 and not 1, as before
x
## [1] 2
# Careful with capitalization
X
## Error in eval(expr, envir, enclos): object 'X' not found
# Different
X <- 3
x; X
## [1] 2
## [1] 3
# The variables are stored in your workspace (a .RData file)
# A handy tip to see what variables are in the workspace
ls()
## [1] "x" "X"
# Now you know which variables can be accessed!
# Remove variables
rm(X)
X
## Error in eval(expr, envir, enclos): object 'X' not foundExercise C.2 Do the following:
- Store \(-123\) in the variable
y. - Store the log of the square of
yinz. - Store \(\frac{y-z}{y+z^2}\) in
yand removez. - Output the value of
y. Answer:4.366734.
Vectors
# These are vectors - arrays of numbers
# We combine numbers with the function "c"
c(1, 3)
## [1] 1 3
c(1.5, 0, 5, -3.4)
## [1] 1.5 0.0 5.0 -3.4
# A handy way of creating integer sequences is the operator ":"
# Sequence from 1 to 5
1:5
## [1] 1 2 3 4 5
# Storing some vectors
myData <- c(1, 2)
myData2 <- c(-4.12, 0, 1.1, 1, 3, 4)
myData
## [1] 1 2
myData2
## [1] -4.12 0.00 1.10 1.00 3.00 4.00
# Entrywise operations
myData + 1
## [1] 2 3
myData^2
## [1] 1 4
# If you want to access a position of a vector, use [position]
myData[1]
## [1] 1
myData2[6]
## [1] 4
# You also can change elements
myData[1] <- 0
myData
## [1] 0 2
# Think on what you want to access...
myData2[7]
## [1] NA
myData2[0]
## numeric(0)
# If you want to access all the elements except a position, use [-position]
myData2[-1]
## [1] 0.0 1.1 1.0 3.0 4.0
myData2[-2]
## [1] -4.12 1.10 1.00 3.00 4.00
# Also with vectors as indexes
myData2[1:2]
## [1] -4.12 0.00
myData2[myData]
## [1] 0
# And also
myData2[-c(1, 2)]
## [1] 1.1 1.0 3.0 4.0
# But do not mix positive and negative indexes!
myData2[c(-1, 2)]
## Error in myData2[c(-1, 2)]: only 0's may be mixed with negative subscripts
# Remove the first element
myData2 <- myData2[-1]Exercise C.3 Do the following:
- Create the vector \(x=(1, 7, 3, 4).\)
- Create the vector \(y=(100, 99, 98, ..., 2, 1).\)
- Create the vector \(z=c(4, 8, 16, 32, 96).\)
- Compute \(x_2+y_4\) and \(\cos(x_3) + \sin(x_2) e^{-y_2}.\) Answers:
104and-0.9899925. - Set \(x_{2}=0\) and \(y_{2}=-1.\) Recompute the previous expressions. Answers:
97and2.785875. - Index \(y\) by \(x+1\) and store it as
z. What is the output? Answer:zisc(-1, 100, 97, 96).
Some functions
# Functions take arguments between parenthesis and transform them into an output
sum(myData)
## [1] 2
prod(myData)
## [1] 0
# Summary of an object
summary(myData)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0 0.5 1.0 1.0 1.5 2.0
# Length of the vector
length(myData)
## [1] 2
# Mean, standard deviation, variance, covariance, correlation
mean(myData)
## [1] 1
var(myData)
## [1] 2
cov(myData, myData^2)
## [1] 4
cor(myData, myData * 2)
## [1] 1
quantile(myData)
## 0% 25% 50% 75% 100%
## 0.0 0.5 1.0 1.5 2.0
# Maximum and minimum of vectors
min(myData)
## [1] 0
which.min(myData)
## [1] 1
# Usually the functions have several arguments, which are set by "argument = value"
# In this case, the second argument is a logical flag to indicate the kind of sorting
sort(myData) # If nothing is specified, decreasing = FALSE is assumed
## [1] 0 2
sort(myData, decreasing = TRUE)
## [1] 2 0
# Do not know what are the arguments of a function? Use args and help!
args(mean)
## function (x, ...)
## NULL
?meanExercise C.4 Do the following:
- Compute the mean, median and variance of \(y.\) Answers:
49.5,49.5,843.6869. - Do the same for \(y+1.\) What are the differences?
- What is the maximum of \(y\)? Where is it placed?
- Sort \(y\) increasingly and obtain the 5th and 76th positions. Answer:
c(4,75). - Compute the covariance between \(y\) and \(y.\) Compute the variance of \(y.\) Why do you get the same result?
Matrices, data frames, and lists
# A matrix is an array of vectors
A <- matrix(1:4, nrow = 2, ncol = 2)
A
## [,1] [,2]
## [1,] 1 3
## [2,] 2 4
# Another matrix
B <- matrix(1, nrow = 2, ncol = 2, byrow = TRUE)
B
## [,1] [,2]
## [1,] 1 1
## [2,] 1 1
# Matrix is a vector with dimension attributes
dim(A)
## [1] 2 2
# Binding by rows or columns
rbind(1:3, 4:6)
## [,1] [,2] [,3]
## [1,] 1 2 3
## [2,] 4 5 6
cbind(1:3, 4:6)
## [,1] [,2]
## [1,] 1 4
## [2,] 2 5
## [3,] 3 6
# Entrywise operations
A + 1
## [,1] [,2]
## [1,] 2 4
## [2,] 3 5
A * B
## [,1] [,2]
## [1,] 1 3
## [2,] 2 4
# Accessing elements
A[2, 1] # Element (2, 1)
## [1] 2
A[1, ] # First row - this is a vector
## [1] 1 3
A[, 2] # First column - this is a vector
## [1] 3 4
# Obtain rows and columns as matrices (and not as vectors)
A[1, , drop = FALSE]
## [,1] [,2]
## [1,] 1 3
A[, 2, drop = FALSE]
## [,1]
## [1,] 3
## [2,] 4
# Matrix transpose
t(A)
## [,1] [,2]
## [1,] 1 2
## [2,] 3 4
# Matrix multiplication
A %*% B
## [,1] [,2]
## [1,] 4 4
## [2,] 6 6
A %*% B[, 1]
## [,1]
## [1,] 4
## [2,] 6
A %*% B[1, ]
## [,1]
## [1,] 4
## [2,] 6
# Care is needed
A %*% B[1, , drop = FALSE] # Incompatible product
## Error in A %*% B[1, , drop = FALSE]: non-conformable arguments
# Compute inverses with "solve"
solve(A) %*% A
## [,1] [,2]
## [1,] 1 0
## [2,] 0 1
# A data frame is a matrix with column names
# Useful when you have multiple variables
myDf <- data.frame(var1 = 1:2, var2 = 3:4)
myDf
## var1 var2
## 1 1 3
## 2 2 4
# You can change names
names(myDf) <- c("newname1", "newname2")
myDf
## newname1 newname2
## 1 1 3
## 2 2 4
# The nice thing is that you can access variables by its name with
# the "$" operator
myDf$newname1
## [1] 1 2
# And create new variables also (it has to be of the same
# length as the rest of variables)
myDf$myNewVariable <- c(0, 1)
myDf
## newname1 newname2 myNewVariable
## 1 1 3 0
## 2 2 4 1
# A list is a collection of arbitrary variables
myList <- list(myData = myData, A = A, myDf = myDf)
# Access elements by names
myList$myData
## [1] 0 2
myList$A
## [,1] [,2]
## [1,] 1 3
## [2,] 2 4
myList$myDf
## newname1 newname2 myNewVariable
## 1 1 3 0
## 2 2 4 1
# Reveal the structure of an object
str(myList)
## List of 3
## $ myData: num [1:2] 0 2
## $ A : int [1:2, 1:2] 1 2 3 4
## $ myDf :'data.frame': 2 obs. of 3 variables:
## ..$ newname1 : int [1:2] 1 2
## ..$ newname2 : int [1:2] 3 4
## ..$ myNewVariable: num [1:2] 0 1
str(myDf)
## 'data.frame': 2 obs. of 3 variables:
## $ newname1 : int 1 2
## $ newname2 : int 3 4
## $ myNewVariable: num 0 1
# A less lengthy output
names(myList)
## [1] "myData" "A" "myDf"Exercise C.5 Do the following:
Create a matrix called
Mwith rows given byy[3:5],y[3:5]^2andlog(y[3:5]).Create a data frame called
myDataFramewith column names “y,” “y2” and “logy” containing the vectorsy[3:5],y[3:5]^2andlog(y[3:5]), respectively.Create a list, called
l, with entries forxandM. Access the elements by their names.Compute the squares of
myDataFrameand save the result asmyDataFrame2.Compute the log of the sum of
myDataFrameandmyDataFrame2. Answer:## y y2 logy ## 1 9.180087 18.33997 3.242862 ## 2 9.159678 18.29895 3.238784 ## 3 9.139059 18.25750 3.234656
More on data frames
# Let's begin importing the iris dataset
data(iris, package = "datasets")
# "names" gives you the variables in the data frame
names(iris)
## [1] "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width" "Species"
# The beginning of the data
head(iris)
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1 5.1 3.5 1.4 0.2 setosa
## 2 4.9 3.0 1.4 0.2 setosa
## 3 4.7 3.2 1.3 0.2 setosa
## 4 4.6 3.1 1.5 0.2 setosa
## 5 5.0 3.6 1.4 0.2 setosa
## 6 5.4 3.9 1.7 0.4 setosa
# So we can access variables by "$" or as in a matrix
iris$Sepal.Length[1:10]
## [1] 5.1 4.9 4.7 4.6 5.0 5.4 4.6 5.0 4.4 4.9
iris[1:10, 1]
## [1] 5.1 4.9 4.7 4.6 5.0 5.4 4.6 5.0 4.4 4.9
iris[3, 1]
## [1] 4.7
# Information on the dimension of the data frame
dim(iris)
## [1] 150 5
# "str" gives the structure of any object in R
str(iris)
## 'data.frame': 150 obs. of 5 variables:
## $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
## $ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
## $ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
## $ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
## $ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
# Recall the species variable: it is a categorical variable (or factor),
# not a numeric variable
iris$Species[1:10]
## [1] setosa setosa setosa setosa setosa setosa setosa setosa setosa setosa
## Levels: setosa versicolor virginica
# Factors can only take certain values
levels(iris$Species)
## [1] "setosa" "versicolor" "virginica"
# If a file contains a variable with character strings as observations (either
# encapsulated by quotation marks or not), the variable will become a factor
# when imported into RExercise C.6 Do the following:
- Load the
faithfuldataset into R. - Get the dimensions of
faithfuland show beginning of the data. - Retrieve the fifth observation of
eruptionsin two different ways. - Obtain a summary of
waiting.
Vector-related functions
# The function "seq" creates sequences of numbers equally separated
seq(0, 1, by = 0.1)
## [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
seq(0, 1, length.out = 5)
## [1] 0.00 0.25 0.50 0.75 1.00
# You can short the latter argument
seq(0, 1, l = 5)
## [1] 0.00 0.25 0.50 0.75 1.00
# Repeat number
rep(0, 5)
## [1] 0 0 0 0 0
# Reverse a vector
myVec <- c(1:5, -1:3)
rev(myVec)
## [1] 3 2 1 0 -1 5 4 3 2 1
# Another way
myVec[length(myVec):1]
## [1] 3 2 1 0 -1 5 4 3 2 1
# Count repetitions in your data
table(iris$Sepal.Length)
##
## 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9 6 6.1 6.2 6.3 6.4 6.5 6.6 6.7 6.8 6.9 7 7.1 7.2
## 1 3 1 4 2 5 6 10 9 4 1 6 7 6 8 7 3 6 6 4 9 7 5 2 8 3 4 1 1 3
## 7.3 7.4 7.6 7.7 7.9
## 1 1 1 4 1
table(iris$Species)
##
## setosa versicolor virginica
## 50 50 50Exercise C.7 Do the following:
- Create the vector \(x=(0.3, 0.6, 0.9, 1.2).\)
- Create a vector of length 100 ranging from \(0\) to \(1\) with entries equally separated.
- Compute the amount of zeros and ones in
x <- c(0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0). Check that they are the same as inrev(x). - Compute the vector \((0.1, 1.1, 2.1, ..., 100.1)\) in four different ways using
seqandrev. Do the same but using:instead ofseq. (Hint: add0.1)
Logical conditions and subsetting
# Relational operators: x < y, x > y, x <= y, x >= y, x == y, x!= y
# They return TRUE or FALSE
# Smaller than
0 < 1
## [1] TRUE
# Greater than
1 > 1
## [1] FALSE
# Greater or equal to
1 >= 1 # Remember: ">="" and not "=>"" !
## [1] TRUE
# Smaller or equal to
2 <= 1 # Remember: "<="" and not "=<"" !
## [1] FALSE
# Equal
1 == 1 # Tests equality. Remember: "=="" and not "="" !
## [1] TRUE
# Unequal
1 != 0 # Tests inequality
## [1] TRUE
# TRUE is encoded as 1 and FALSE as 0
TRUE + 1
## [1] 2
FALSE + 1
## [1] 1
# In a vector-like fashion
x <- 1:5
y <- c(0, 3, 1, 5, 2)
x < y
## [1] FALSE TRUE FALSE TRUE FALSE
x == y
## [1] FALSE FALSE FALSE FALSE FALSE
x != y
## [1] TRUE TRUE TRUE TRUE TRUE
# Subsetting of vectors
x
## [1] 1 2 3 4 5
x[x >= 2]
## [1] 2 3 4 5
x[x < 3]
## [1] 1 2
# Easy way of work with parts of the data
data <- data.frame(x = c(0, 1, 3, 3, 0), y = 1:5)
data
## x y
## 1 0 1
## 2 1 2
## 3 3 3
## 4 3 4
## 5 0 5
# Data such that x is zero
data0 <- data[data$x == 0, ]
data0
## x y
## 1 0 1
## 5 0 5
# Data such that x is larger than 2
data2 <- data[data$x > 2, ]
data2
## x y
## 3 3 3
## 4 3 4
# In an example
iris$Sepal.Width[iris$Sepal.Width > 3]
## [1] 3.5 3.2 3.1 3.6 3.9 3.4 3.4 3.1 3.7 3.4 4.0 4.4 3.9 3.5 3.8 3.8 3.4 3.7 3.6 3.3 3.4 3.4 3.5 3.4 3.2 3.1 3.4 4.1 4.2
## [30] 3.1 3.2 3.5 3.6 3.4 3.5 3.2 3.5 3.8 3.8 3.2 3.7 3.3 3.2 3.2 3.1 3.3 3.1 3.2 3.4 3.1 3.3 3.6 3.2 3.2 3.8 3.2 3.3 3.2
## [59] 3.8 3.4 3.1 3.1 3.1 3.1 3.2 3.3 3.4
# Problem - what happened?
data[x > 2, ]
## x y
## 3 3 3
## 4 3 4
## 5 0 5
# In an example
summary(iris)
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100 setosa :50
## 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300 versicolor:50
## Median :5.800 Median :3.000 Median :4.350 Median :1.300 virginica :50
## Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
## 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
## Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
summary(iris[iris$Sepal.Width > 3, ])
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## Min. :4.400 Min. :3.100 Min. :1.000 Min. :0.1000 setosa :42
## 1st Qu.:5.000 1st Qu.:3.200 1st Qu.:1.450 1st Qu.:0.2000 versicolor: 8
## Median :5.400 Median :3.400 Median :1.600 Median :0.4000 virginica :17
## Mean :5.684 Mean :3.434 Mean :2.934 Mean :0.9075
## 3rd Qu.:6.400 3rd Qu.:3.600 3rd Qu.:5.000 3rd Qu.:1.8000
## Max. :7.900 Max. :4.400 Max. :6.700 Max. :2.5000
# On the factor variable only makes sense == and !=
summary(iris[iris$Species == "setosa", ])
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## Min. :4.300 Min. :2.300 Min. :1.000 Min. :0.100 setosa :50
## 1st Qu.:4.800 1st Qu.:3.200 1st Qu.:1.400 1st Qu.:0.200 versicolor: 0
## Median :5.000 Median :3.400 Median :1.500 Median :0.200 virginica : 0
## Mean :5.006 Mean :3.428 Mean :1.462 Mean :0.246
## 3rd Qu.:5.200 3rd Qu.:3.675 3rd Qu.:1.575 3rd Qu.:0.300
## Max. :5.800 Max. :4.400 Max. :1.900 Max. :0.600
# Subset argument in lm
lm(Sepal.Width ~ Petal.Length, data = iris, subset = Sepal.Width > 3)
##
## Call:
## lm(formula = Sepal.Width ~ Petal.Length, data = iris, subset = Sepal.Width >
## 3)
##
## Coefficients:
## (Intercept) Petal.Length
## 3.59439 -0.05455
lm(Sepal.Width ~ Petal.Length, data = iris, subset = iris$Sepal.Width > 3)
##
## Call:
## lm(formula = Sepal.Width ~ Petal.Length, data = iris, subset = iris$Sepal.Width >
## 3)
##
## Coefficients:
## (Intercept) Petal.Length
## 3.59439 -0.05455
# Both iris$Sepal.Width and Sepal.Width in subset are fine: data = iris
# tells R to look for Sepal.Width in the iris dataset
# AND operator "&"
TRUE & TRUE
## [1] TRUE
TRUE & FALSE
## [1] FALSE
FALSE & FALSE
## [1] FALSE
# OR operator "|"
TRUE | TRUE
## [1] TRUE
TRUE | FALSE
## [1] TRUE
FALSE | FALSE
## [1] FALSE
# Both operators are useful for checking for ranges of data
y
## [1] 0 3 1 5 2
index1 <- (y <= 3) & (y > 0)
y[index1]
## [1] 3 1 2
index2 <- (y < 2) | (y > 4)
y[index2]
## [1] 0 1 5
# In an example
summary(iris[iris$Sepal.Width > 3 & iris$Sepal.Width < 3.5, ])
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## Min. :4.400 Min. :3.100 Min. :1.200 Min. :0.100 setosa :20
## 1st Qu.:4.925 1st Qu.:3.125 1st Qu.:1.500 1st Qu.:0.200 versicolor: 8
## Median :5.950 Median :3.200 Median :4.450 Median :1.400 virginica :14
## Mean :5.781 Mean :3.245 Mean :3.460 Mean :1.145
## 3rd Qu.:6.700 3rd Qu.:3.400 3rd Qu.:5.375 3rd Qu.:2.075
## Max. :7.200 Max. :3.400 Max. :6.000 Max. :2.500Exercise C.8 Do the following for the iris dataset:
- Compute the subset corresponding to
Petal.Lengtheither smaller than1.5or larger than2. Save this dataset asirisPetal. - Compute and summarize a linear regression of
Sepal.WidthintoPetal.Width + Petal.Lengthfor the datasetirisPetal. What is the \(R^2\)? Solution:0.101. - Check that the previous model is the same as regressing
Sepal.WidthintoPetal.Width + Petal.Lengthfor the datasetiriswith the appropriatesubsetexpression. - Compute the variance for
Petal.WidthwhenPetal.Widthis smaller or equal that1.5and larger than0.3. Solution:0.1266541.
Plotting functions
# "plot" is the main function for plotting in R
# It has a different behavior depending on the kind of object that it receives
# How to plot some data
plot(iris$Sepal.Length, iris$Sepal.Width, main = "Sepal.Length vs Sepal.Width")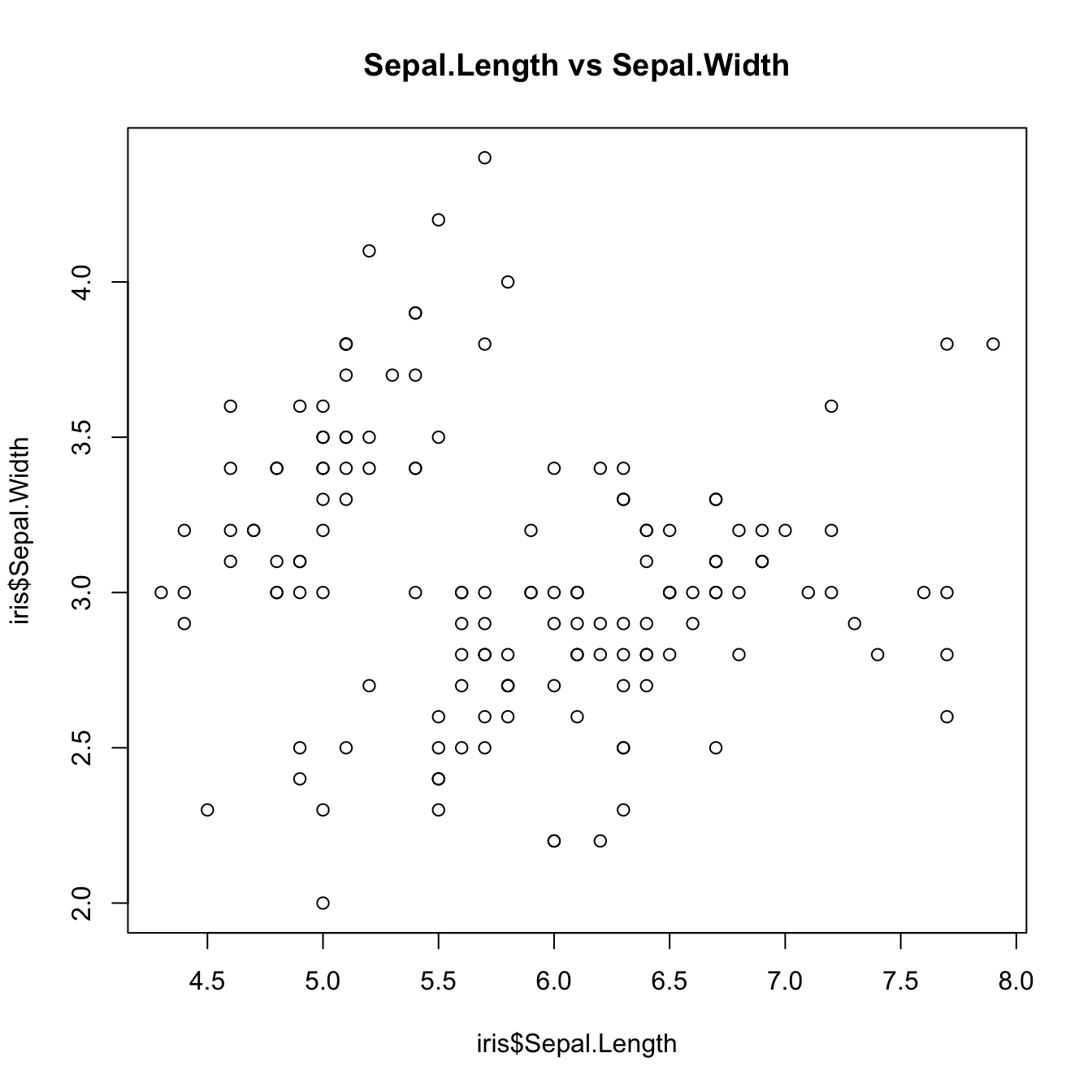
# Alternatively
plot(iris[, 1:2], main = "Sepal.Length vs Sepal.Width")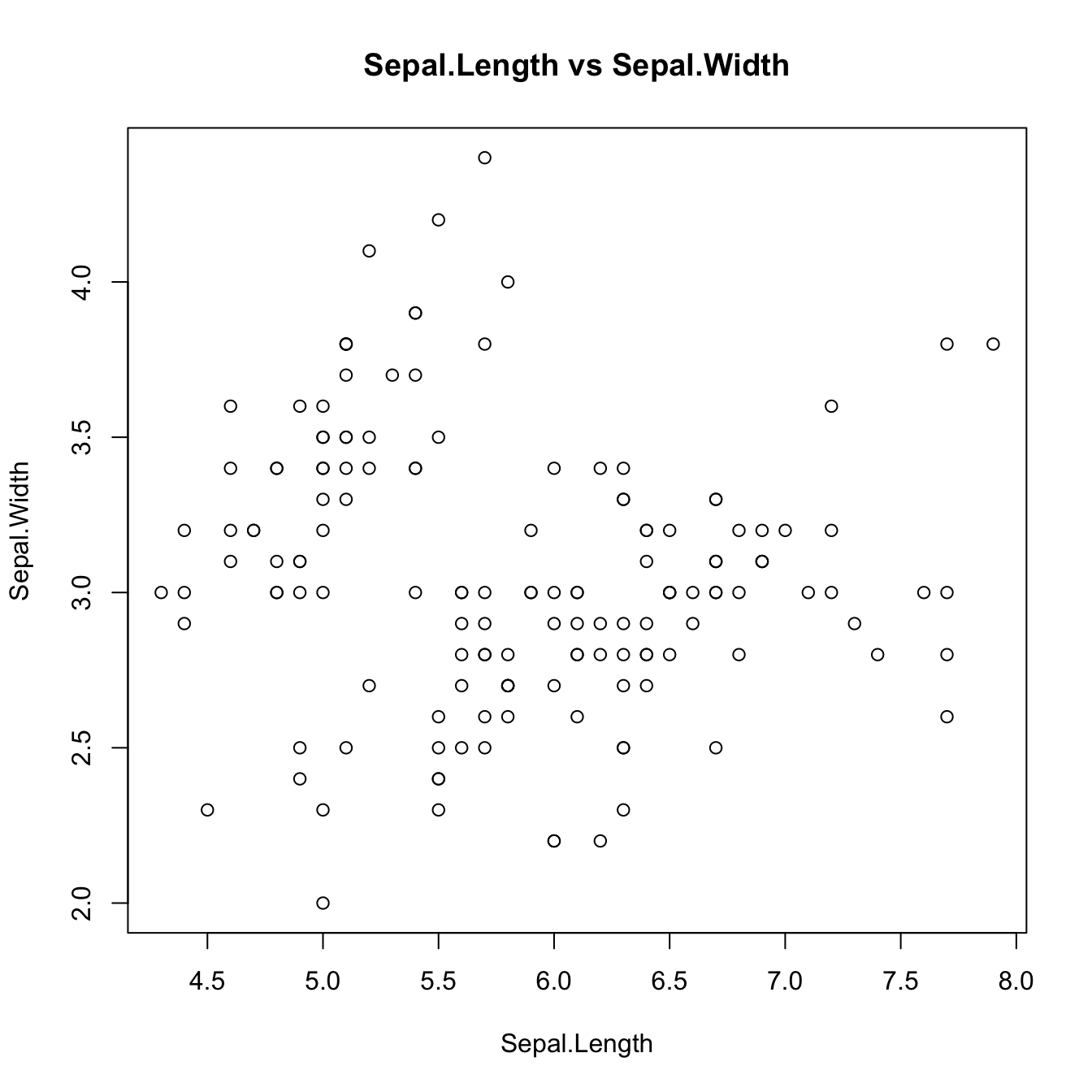
# Change the axis limits
plot(iris$Sepal.Length, iris$Sepal.Width, xlim = c(0, 10), ylim = c(0, 10))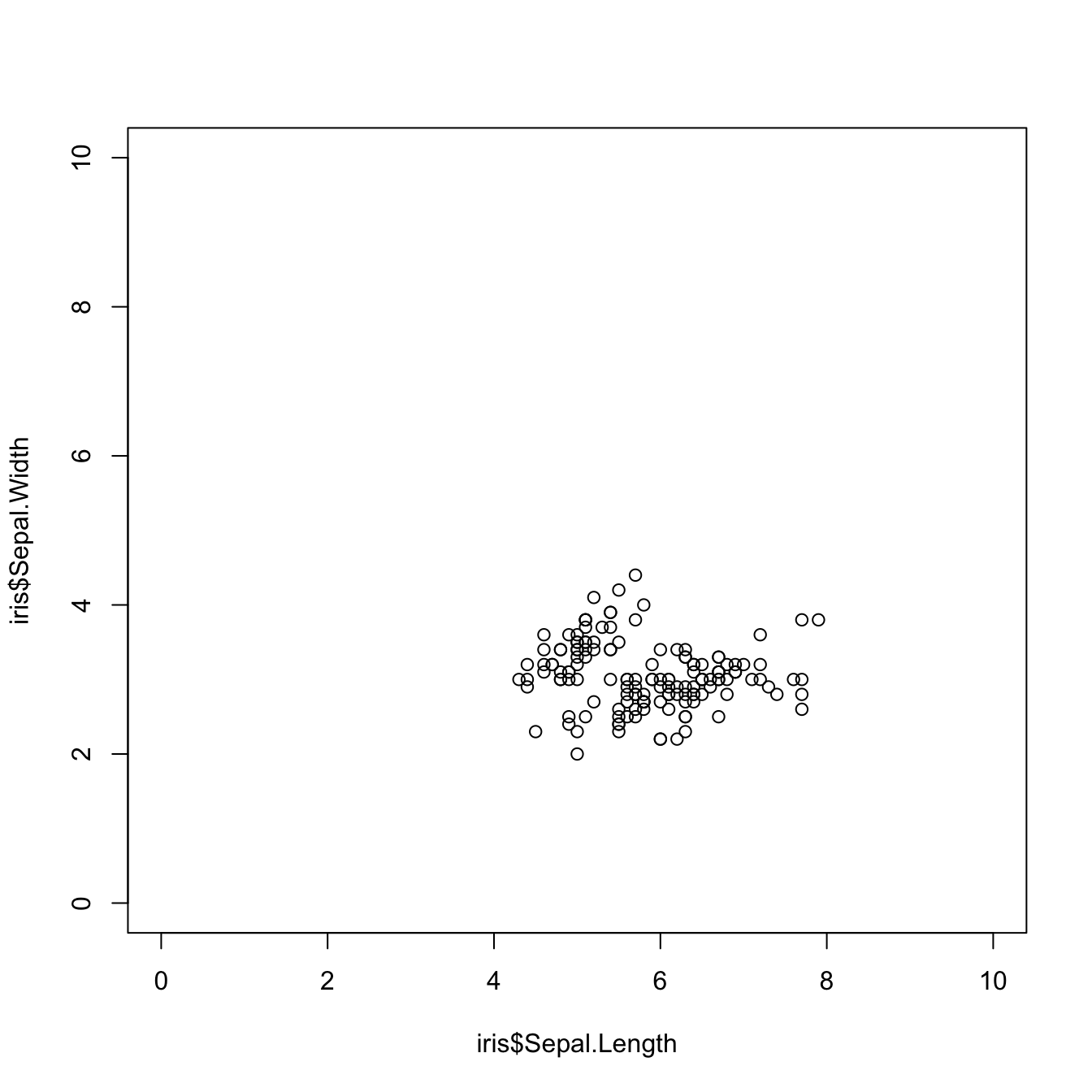
# How to plot a curve (a parabola)
x <- seq(-1, 1, l = 50)
y <- x^2
plot(x, y)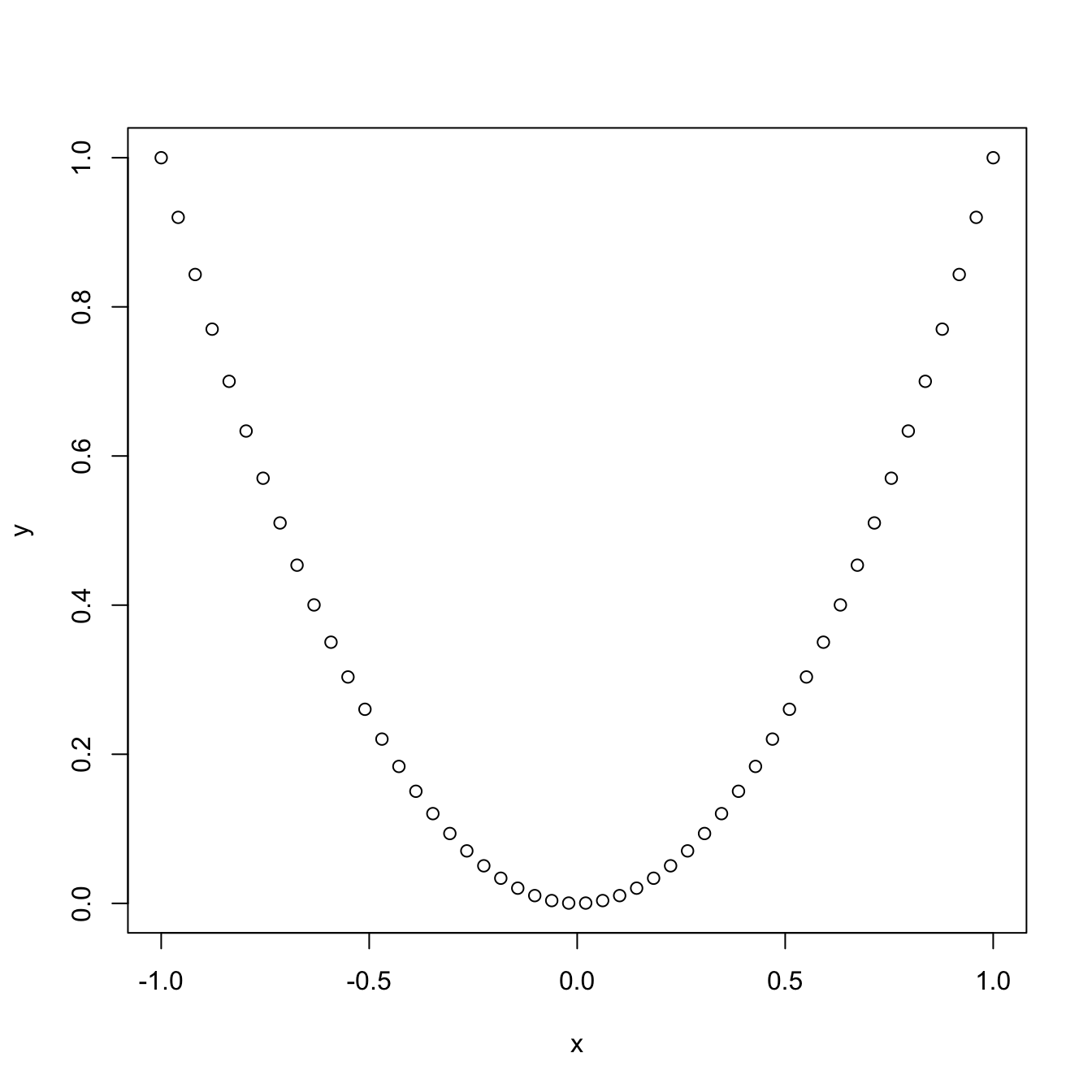
plot(x, y, main = "A dotted parabola")
plot(x, y, main = "A parabola", type = "l")
plot(x, y, main = "A red and thick parabola", type = "l", col = "red", lwd = 3)
# Plotting a more complicated curve between -pi and pi
x <- seq(-pi, pi, l = 50)
y <- (2 + sin(10 * x)) * x^2
plot(x, y, type = "l") # Kind of rough...
# Remember that we are joining points for creating a curve!
# More detailed plot
x <- seq(-pi, pi, l = 500)
y <- (2 + sin(10 * x)) * x^2
plot(x, y, type = "l")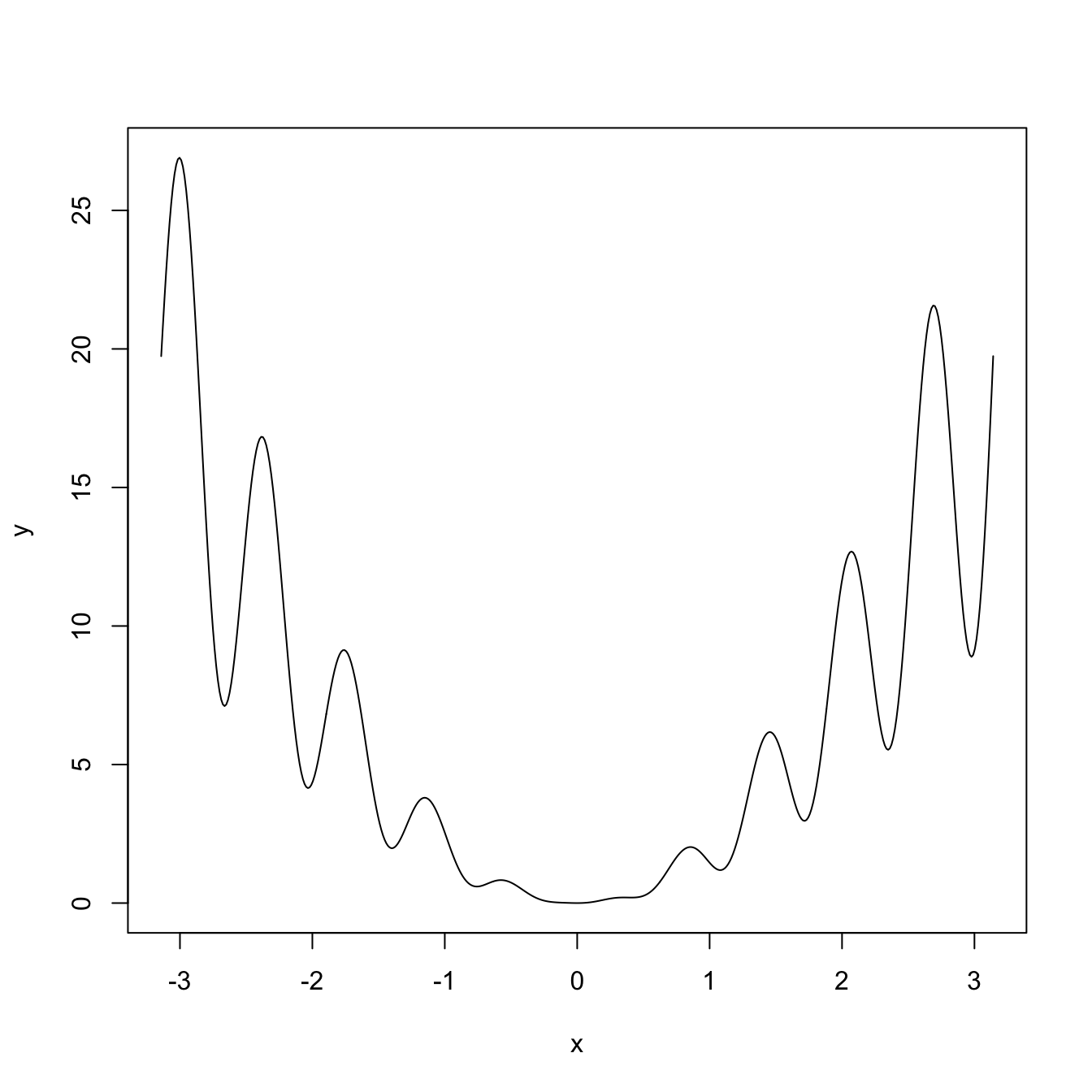
# For more options in the plot customization see
?plot
## Help on topic 'plot' was found in the following packages:
##
## Package Library
## base /Library/Frameworks/R.framework/Resources/library
## graphics /Library/Frameworks/R.framework/Versions/4.1-arm64/Resources/library
##
##
## Using the first match ...
?par
# "plot" is a first level plotting function. That means that whenever is called,
# it creates a new plot. If we want to add information to an existing plot, we
# have to use a second level plotting function such as "points", "lines" or "abline"
plot(x, y) # Create a plot
lines(x, x^2, col = "red") # Add lines
points(x, y + 10, col = "blue") # Add points
abline(a = 5, b = 1, col = "orange", lwd = 2) # Add a straight line y = a + b * x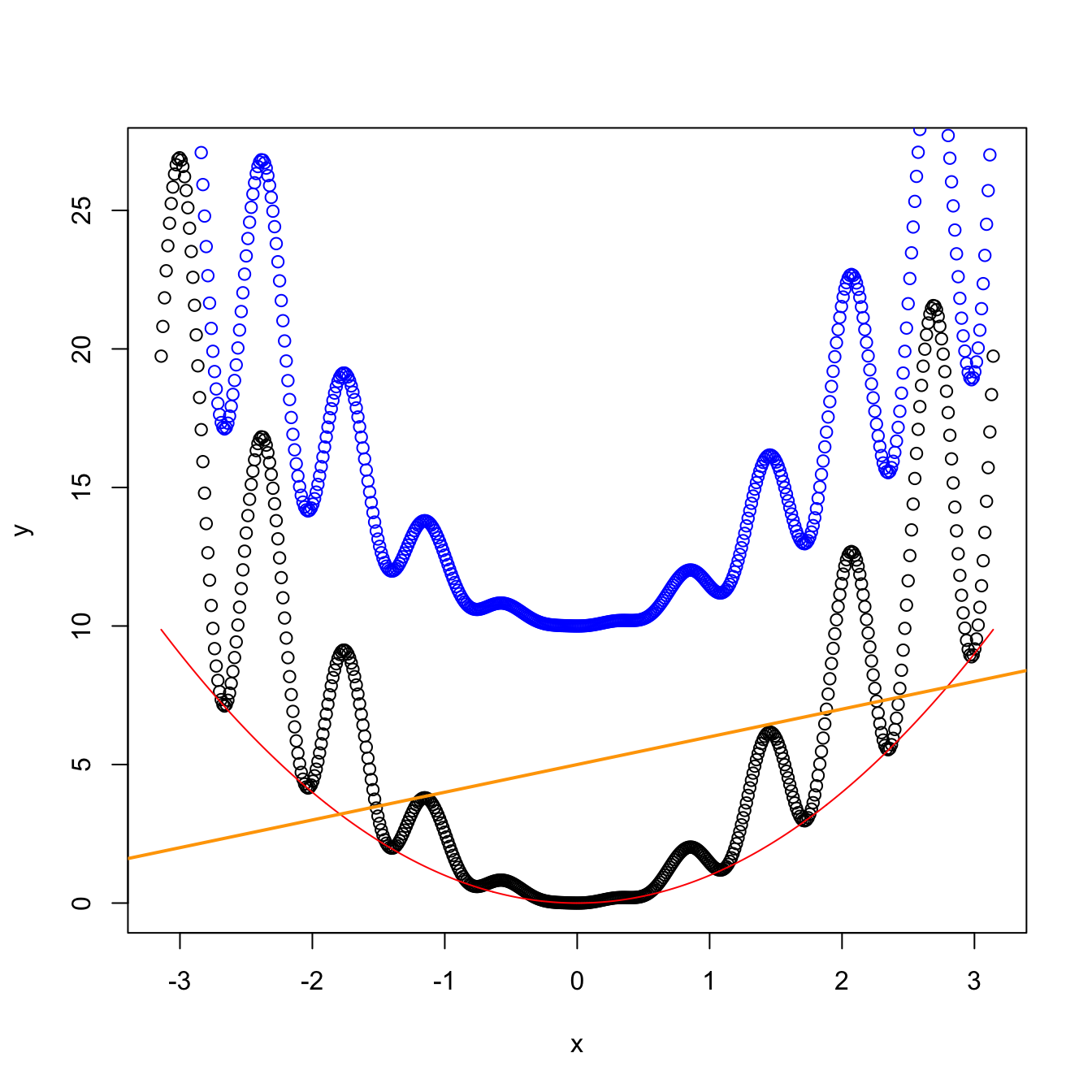
Exercise C.9 Do the following:
- Plot the
faithfuldataset. - Add the straight line \(y=110-15x\) (red).
- Make a new plot for the function \(y=\sin(x)\) (black). Add \(y=\sin(2x)\) (red), \(y=\sin(3x)\) (blue), and \(y=\sin(4x)\) (orange).
Distributions
# R allows to sample [r], compute density/probability mass functions [d],
# compute distribution function [p], and compute quantiles [q] for several
# continuous and discrete distributions. The format employed is [rdpq]name,
# where name stands for:
# - norm -> Normal
# - unif -> Uniform
# - exp -> Exponential
# - t -> Student's t
# - f -> Snedecor's F
# - chisq -> Chi squared
# - pois -> Poisson
# - binom -> Binomial
# More distributions:
?Distributions
# Sampling from a Normal - 5 random points from a N(0, 1)
rnorm(n = 5, mean = 0, sd = 1)
## [1] -1.12055305 -0.06232391 0.71414179 0.77304492 1.98370559
# If you want to have always the same result, set the seed of the random number
# generator
set.seed(45678)
rnorm(n = 5, mean = 0, sd = 1)
## [1] 1.4404800 -0.7195761 0.6709784 -0.4219485 0.3782196
# Plotting the density of a N(0, 1) - the Gauss bell
x <- seq(-4, 4, l = 100)
y <- dnorm(x = x, mean = 0, sd = 1)
plot(x, y, type = "l")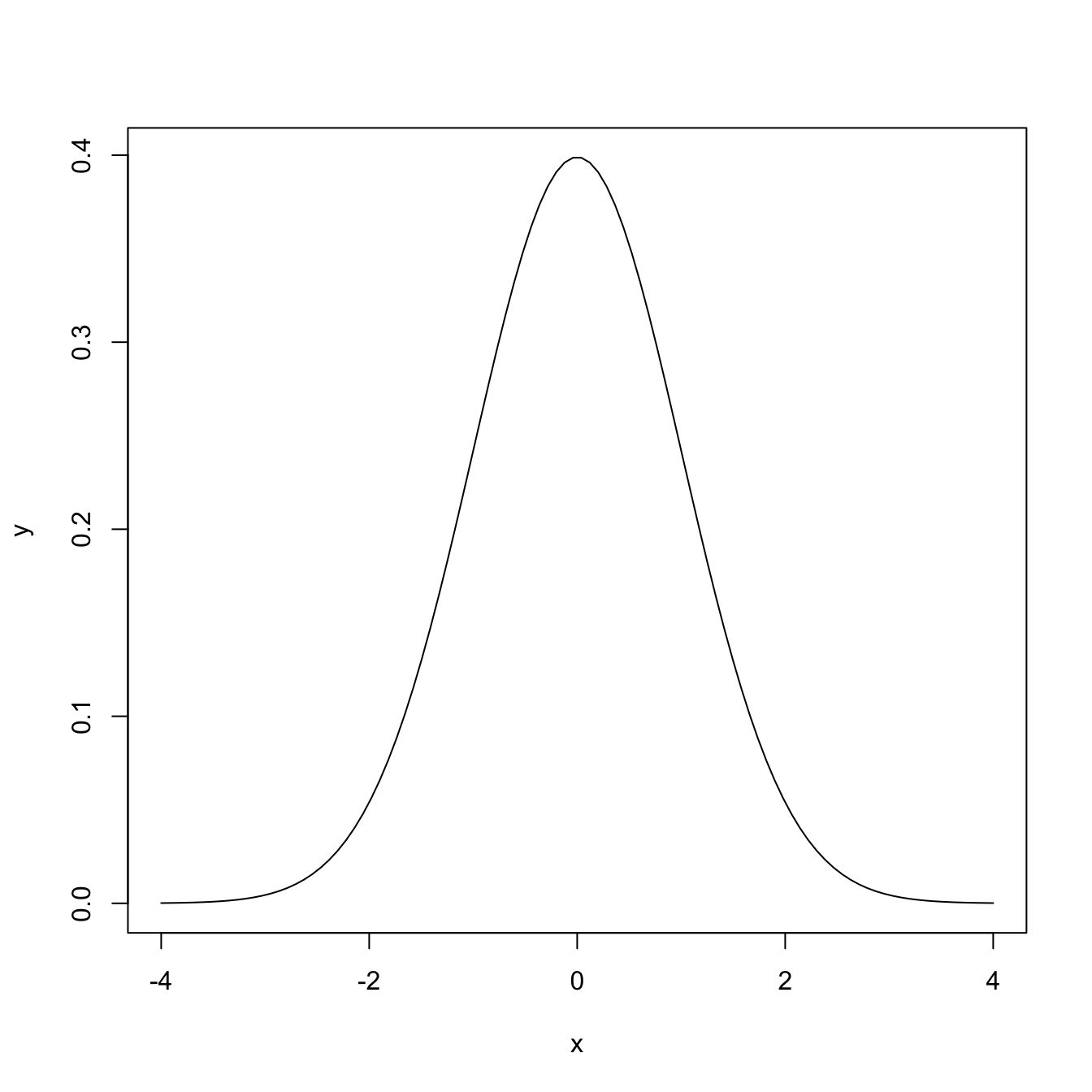
# Plotting the distribution function of a N(0, 1)
x <- seq(-4, 4, l = 100)
y <- pnorm(q = x, mean = 0, sd = 1)
plot(x, y, type = "l")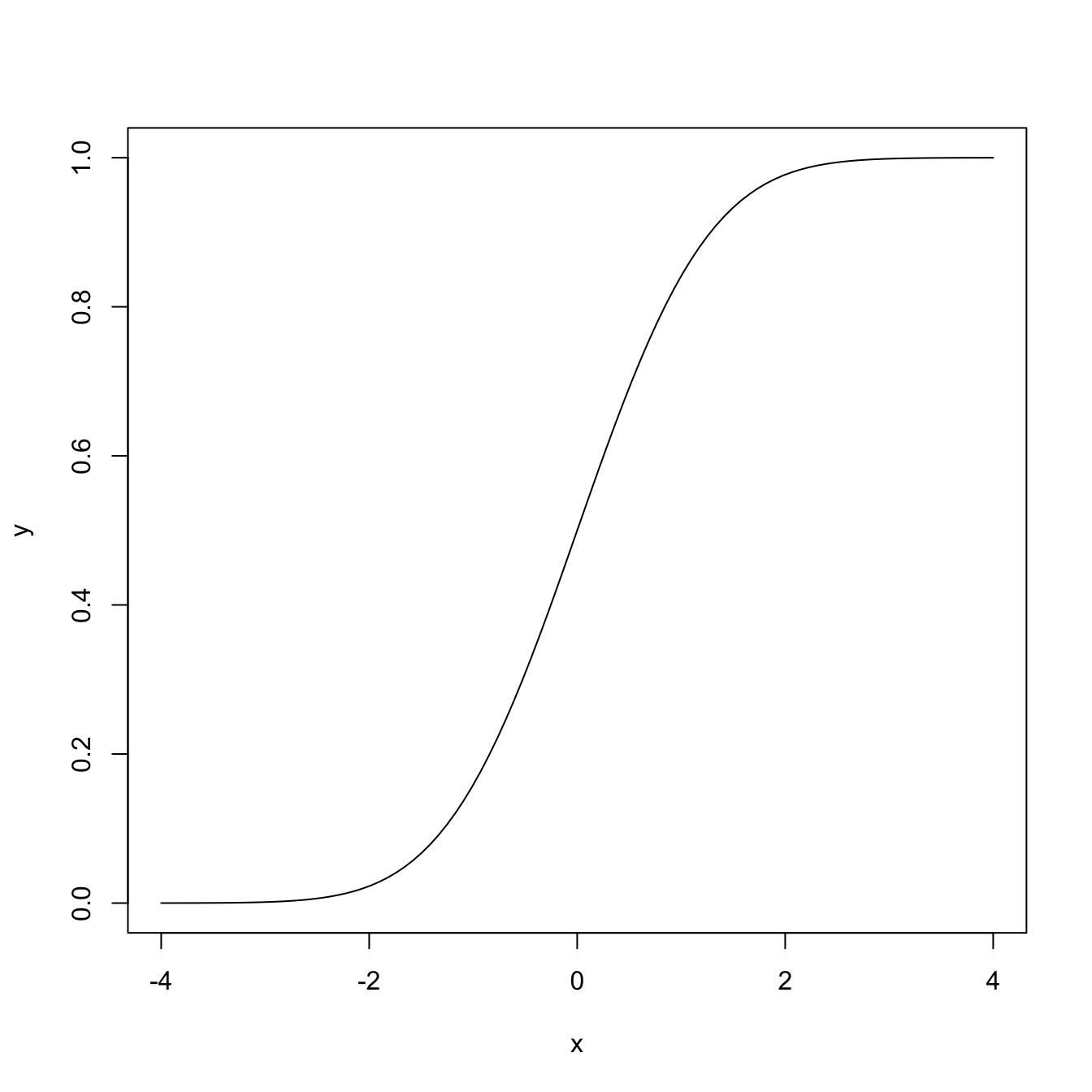
# Computing the 95% quantile for a N(0, 1)
qnorm(p = 0.95, mean = 0, sd = 1)
## [1] 1.644854
# All distributions have the same syntax: rname(n,...), dname(x,...), dname(p,...)
# and qname(p,...), but the parameters in ... change. Look them in ?Distributions
# For example, here is the same for the uniform distribution
# Sampling from a U(0, 1)
set.seed(45678)
runif(n = 5, min = 0, max = 1)
## [1] 0.9251342 0.3339988 0.2358930 0.3366312 0.7488829
# Plotting the density of a U(0, 1)
x <- seq(-2, 2, l = 100)
y <- dunif(x = x, min = 0, max = 1)
plot(x, y, type = "l")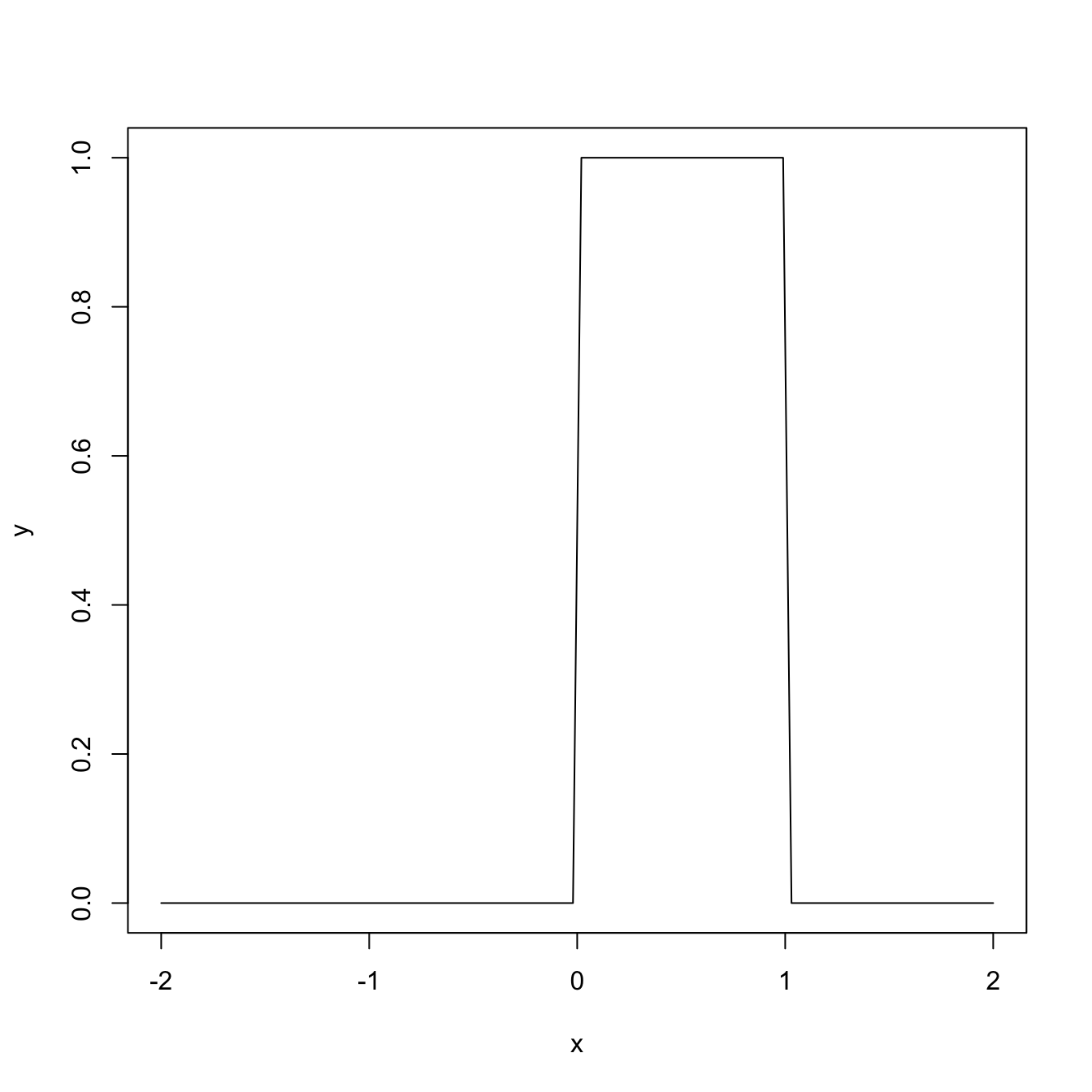
# Computing the 95% quantile for a U(0, 1)
qunif(p = 0.95, min = 0, max = 1)
## [1] 0.95
# Sampling from a Bi(10, 0.5)
set.seed(45678)
samp <- rbinom(n = 200, size = 10, prob = 0.5)
table(samp) / 200
## samp
## 1 2 3 4 5 6 7 8 9
## 0.010 0.060 0.115 0.220 0.210 0.215 0.115 0.045 0.010
# Plotting the probability mass of a Bi(10, 0.5)
x <- 0:10
y <- dbinom(x = x, size = 10, prob = 0.5)
plot(x, y, type = "h") # Vertical bars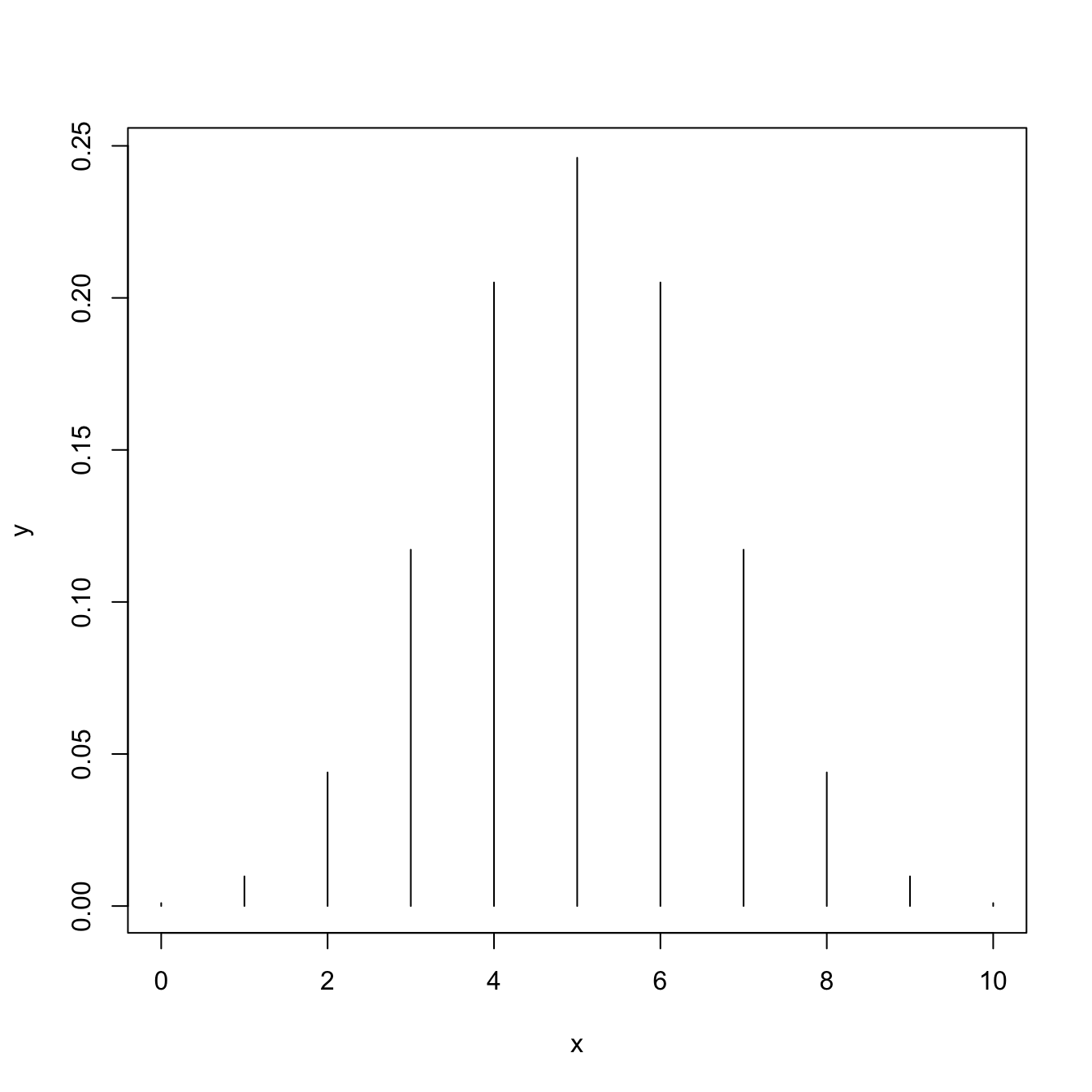
# Plotting the distribution function of a Bi(10, 0.5)
x <- 0:10
y <- pbinom(q = x, size = 10, prob = 0.5)
plot(x, y, type = "h")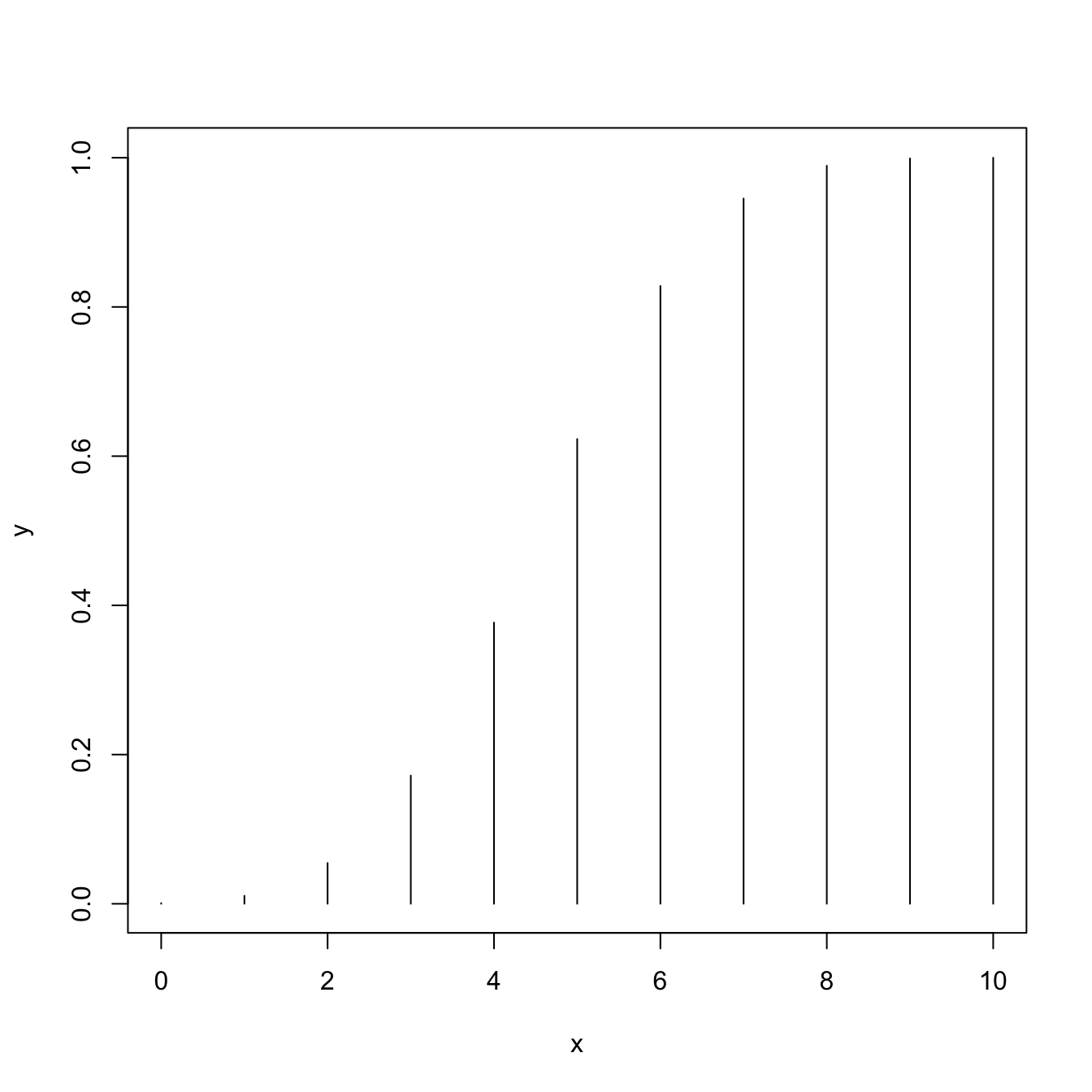
Exercise C.10 Do the following:
- Compute the \(90\%,\) \(95\%\) and \(99\%\) quantiles of a \(F\) distribution with
df1 = 1anddf2 = 5. Answer:c(4.060420, 6.607891, 16.258177). - Plot the distribution function of a \(U(0,1).\) Does it make sense with its density function?
- Sample \(100\) points from a Poisson with
lambda = 5. - Sample \(100\) points from a \(U(-1,1)\) and compute its mean.
- Plot the density of a \(t\) distribution with
df = 1(use a sequence spanning from-4to4). Add lines of different colors with the densities fordf = 5,df = 10,df = 50anddf = 100. Do you see any pattern?
Functions
# A function is a way of encapsulating a block of code so it can be reused easily
# They are useful for simplifying repetitive tasks and organize the analysis
# This is a silly function that takes x and y and returns its sum
# Note the use of "return" to indicate what should be returned
add <- function(x, y) {
z <- x + y
return(z)
}
# Calling add - you need to run the definition of the function first!
add(x = 1, y = 2)
## [1] 3
add(1, 1) # Arguments names can be omitted
## [1] 2
# A more complex function: computes a linear model and its posterior summary.
# Saves us a few keystrokes when computing a lm and a summary
lmSummary <- function(formula, data) {
model <- lm(formula = formula, data = data)
summary(model)
}
# If no return(), the function returns the value of the last expression
# Usage
lmSummary(Sepal.Length ~ Petal.Width, iris)
##
## Call:
## lm(formula = formula, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.38822 -0.29358 -0.04393 0.26429 1.34521
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.77763 0.07293 65.51 <2e-16 ***
## Petal.Width 0.88858 0.05137 17.30 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.478 on 148 degrees of freedom
## Multiple R-squared: 0.669, Adjusted R-squared: 0.6668
## F-statistic: 299.2 on 1 and 148 DF, p-value: < 2.2e-16
# Recall: there is no variable called model in the workspace.
# The function works on its own workspace!
model
## Error in eval(expr, envir, enclos): object 'model' not found
# Add a line to a plot
addLine <- function(x, beta0, beta1) {
lines(x, beta0 + beta1 * x, lwd = 2, col = 2)
}
# Usage
plot(x, y)
addLine(x, beta0 = 0.1, beta1 = 0)
# The function "sapply" allows to sequentially apply a function
sapply(1:5, sqrt)
## [1] 1.000000 1.414214 1.732051 2.000000 2.236068
sqrt(1:5) # The same
## [1] 1.000000 1.414214 1.732051 2.000000 2.236068
# The advantage of "sapply" is that you can use with any function
myFun <- function(x) c(x, x^2)
sapply(1:5, myFun) # Returns a 2 x 5 matrix
## [,1] [,2] [,3] [,4] [,5]
## [1,] 1 2 3 4 5
## [2,] 1 4 9 16 25
# "sapply" is useful for plotting non-vectorized functions
sumSeries <- function(n) sum(1:n)
plot(1:5, sapply(1:10, sumSeries), type = "l")
## Error in xy.coords(x, y, xlabel, ylabel, log): 'x' and 'y' lengths differ
# "apply" applies iteratively a function to rows (1) or columns (2)
# of a matrix or data frame
A <- matrix(1:10, nrow = 5, ncol = 2)
A
## [,1] [,2]
## [1,] 1 6
## [2,] 2 7
## [3,] 3 8
## [4,] 4 9
## [5,] 5 10
apply(A, 1, sum) # Applies the function by rows
## [1] 7 9 11 13 15
apply(A, 2, sum) # By columns
## [1] 15 40
# With other functions
apply(A, 1, sqrt)
## [,1] [,2] [,3] [,4] [,5]
## [1,] 1.00000 1.414214 1.732051 2 2.236068
## [2,] 2.44949 2.645751 2.828427 3 3.162278
apply(A, 2, function(x) x^2)
## [,1] [,2]
## [1,] 1 36
## [2,] 4 49
## [3,] 9 64
## [4,] 16 81
## [5,] 25 100Exercise C.11 Do the following:
- Create a function that takes as argument \(n\) and returns the value of \(\sum_{i=1}^n i^2.\)
- Create a function that takes as input the argument \(N\) and then plots the curve \((n, \sum_{i=1}^n \sqrt{i})\) for \(n=1,\ldots,N.\) Hint: use
sapply.
Control structures
# The "for" statement allows to create loops that run along a given vector
# Prints 5 times a message (i varies in 1:5)
for (i in 1:5) {
print(i)
}
## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5
# Another example
a <- 0
for (i in 1:3) {
a <- i + a
}
a
## [1] 6
# Nested loops are possible
A <- matrix(0, nrow = 2, ncol = 3)
for (i in 1:2) {
for (j in 1:3) {
A[i, j] <- i + j
}
}
# The "if" statement allows to create conditional structures of the forms:
# if (condition) {
# # Something
# } else {
# # Something else
# }
# These structures are thought to be inside functions
# Is the number positive?
isPositive <- function(x) {
if (x > 0) {
print("Positive")
} else {
print("Not positive")
}
}
isPositive(1)
## [1] "Positive"
isPositive(-1)
## [1] "Not positive"
# A loop can be interrupted with the "break" statement
# Stop when x is above 100
x <- 1
for (i in 1:1000) {
x <- (x + 0.01) * x
print(x)
if (x > 100) {
break
}
}
## [1] 1.01
## [1] 1.0302
## [1] 1.071614
## [1] 1.159073
## [1] 1.35504
## [1] 1.849685
## [1] 3.439832
## [1] 11.86684
## [1] 140.9406Exercise C.12 Do the following:
- Compute \(\mathbf{C}_{n\times k}\) in \(\mathbf{C}_{n\times k}=\mathbf{A}_{n\times m} \mathbf{B}_{m\times k}\) from \(\mathbf{A}\) and \(\mathbf{B}.\) Use that \(c_{i,j}=\sum_{l=1}^ma_{i,l}b_{l,j}.\) Test the implementation with simple examples.
- Create a function that samples a \(\mathcal{N}(0,1)\) and returns the first sampled point that is larger than \(4.\)
- Create a function that simulates \(N\) samples from the distribution of \(\max(X_1,\ldots,X_n)\) where \(X_1,\ldots,X_n\) are iid \(\mathcal{U}(0,1).\)