6.1 Modèles liés
Certains des modèles que nous venons de voir dans le cours sont liés. Deux modèles sont liés s’ils sont équivalents pour certaines restrictions paramétriques. Par exemple, nous avons vu que:
- Lorsque le paramètre \(\phi\) d’une Poisson gonflée à zéro est égal à 0, le modèle est équivalent à la Poisson;
- Lorsque le paramètre \(\alpha \rightarrow 0\) pour une NB2, le modèle est équivalent à la Poisson;
- Lorsque le paramètre \(\alpha = 1\) pour une GCD, le modèle est équivalent à la Poisson;
- etc.
Lorsque deux modèles ne peuvent pas être équivalents en utilisant certaines restrictions paramétriques, on parle de modèles non-liés.
Dans les exemples mentionnés plus haut, il est ainsi possible de tester l’hypothèse que les données proviennent d’une Poisson en testant directement le lien qui généralise la Poisson. Il suffit d’utiliser les tests d’hypothèse classiques suivants:
- Le test de Wald;
- Le test du rapport de vraisemblance;
- Le test du multiplicateur de Lagrange.
Même si avec des données réelles, chaque test aura son propre résultat, ces trois tests sont asymptotiquement équivalents.
Généralement, nous noterons l’hypothèse nulle comme:
\[H_0: r(\theta_0) = 0\]
et l’hypothèse alternative comme:
\[H_a: r(\theta_0) \neq 0\]
pour une certaine fonction \(r\) de dimension \(h \times 1\).
Exemple 6.1 Parce qu’une distribution de type NB2 correspond à une distribution géométrique pour \(\alpha = 1\), on dira que la géométrique est la distribution ayant une restriction paramétrique (car \(\alpha = 1\)), et la NB2 sera nommée la distribution sans restriction paramétrique.
Exemple 6.2 On pourrait ainsi tester si l’hypothèse d’une loi géométrique contre un NB2. Dans ce cas, l’hypothèse \(H_0\) pourrait ainsi signifier \(r(\theta_0) = \alpha - 1 = 0\), avec \(\theta_0\) représentant les paramètres à tester (ici \(\alpha\)).
6.1.1 Test du rapport de vraisemblance
Le test du rapport de vraisemblance est basé sur le ratio des deux fonctions de vraisemblance obtenues des modèles avec ou sans les restrictions paramétriques.
Formellement, notons
- \(L_u = \prod_{i=1}^n f_u(y_i)\) la vraisemblance du modèle non-restreint (unrestricted), et
- \(L_r = \prod_{i=1}^n f_r(y_i)\) la vraisemblance du modèle restreint (restricted).
Ainsi, ce rapport des vraisemblance équivaut à \(\frac{L_u}{L_r}\). Nous savons qu’au lieu de travailler avec la fonction de vraisemblance, il est plus pratique de travailler avec les log-vraisemblances. Ainsi, le test du rapport de vraisemblance peut s’exprimer comme:
\[ T_{RV} = 2 \ln \left( \frac{L_u}{L_r} \right) = 2 (\ell_u - \ell_r),\] avec \(\ell_u = \ln(L_u)\), la fonction de logvraisemblance du modèle non-restreint, et \(\ell_r = \ln(L_r)\), la fonction de logvraisemblance du modèle restreint.
Puisque le modèle sans restriction inclut celui avec restrictions, \(\ell_u\) sera toujours plus grand (ou égal) que \(\ell_r\). Ainsi, le test du rapport de vraisemblance sera toujours positif, et aura un distribution suivant une \(\chi^2_q\) où \(q\) est le nombre de restrictions paramétriques.
Une valeur du test \(T_{RV}\) petit signifie que le modèle restreint est presque aussi bon que le modèle non-restreint, ce qui justifie ainsi l’utilisation du modèle le plus simple, i.e. le modèle restreint.
La statistique du rapport de vraisemblance peut être exprimée comme la différence entre les déviances du modèle restreint et du modèle non-restreint, tant que le même estimé de \(\phi\) est utilisé pour la fonction log-vraisemblance des deux modèles.
Le test du rapport de vraisemblance exige l’estimation des deux modèles en compétition. En effet, nous avons besoin du:
- logvraisemblance du modèle sans restriction (\(\ell_u\));
- logvraisemblance du modèle avec restrictions (\(\ell_r\)).
6.1.2 Test de Wald
Nous savons que l’estimation par MLE d’un paramètre suit asymptotiquement une loi normale. Ainsi, on connait la distribution d’un paramètre estimé \(\theta\):
\[\hat{\theta} \sim Normal(\theta_0, \widehat{Var}[\widehat{\theta}])\]
Exercice 6.1 Trouvez l’intervalle de confiance de \(\widehat{\theta}\).
On a donc que:
\[\begin{eqnarray*} \frac{\hat{\theta} - \theta}{\sqrt{\widehat{Var}[\widehat{\theta}] }} &\sim& Normal(0,1) \end{eqnarray*}\]
Ainsi, nous avons l’intervalle de confiance à \(p \%\) suivante:
\[\begin{eqnarray*} -Z_{\frac{1-p}{2}} < &\frac{\hat{\theta} - \theta}{\sqrt{\widehat{Var}[\widehat{\theta}] }} & < Z_{\frac{1-p}{2}} \\ \theta -\sqrt{\widehat{Var}[\widehat{\theta}] } Z_{\frac{1-p}{2}} < & \hat{\theta} & < \theta + \sqrt{\widehat{Var}[\widehat{\theta}] } Z_{\frac{1-p}{2}} \end{eqnarray*}\]
Il s’agit ici de l’usage direct du théorême central limite: en ayant la connaissance \(\theta\), le comportement de l’estimateur \(\widehat{\theta}\) est connu. Cet usage de la loi des grands nombres est intuitif, et ne prête à pratiquement aucune controverse philosophique.
Exercice 6.2 Usage indirect: trouvez l’intervalle de confiance de \(\theta\), i.e. qu’en ayant la connaissance de l’estimateur \(\widehat{\theta}\), le comportement de \(\theta\), la cause a priori pourtant inconnue, peut être estimée.
On a ainsi:
\[\begin{eqnarray*} -Z_{\frac{1-p}{2}} < &\frac{\hat{\theta} - \theta}{\sqrt{\widehat{Var}[\widehat{\theta}] }} & < Z_{\frac{1-p}{2}} \\ \widehat{\theta} -\sqrt{\widehat{Var}[\widehat{\theta}] } Z_{\frac{1-p}{2}} < & \theta & < \widehat{\theta} + \sqrt{\widehat{Var}[\widehat{\theta}] } Z_{\frac{1-p}{2}} \end{eqnarray*}\]
Ainsi, si on veut tester \(R \widehat{\theta} - q = 0\), nous avons:
\[T_W = (R \widehat{\theta} - q)' \left[R \ \widehat{Var}[\widehat{\theta}] \ R'\right]^{-1} (R \widehat{\theta} - q), \]
qui a une distribution \(\chi^2\) de degrés de liberté égal au nombre de restrictions paramétriques.
Exemple 6.3 On veut tester l’hypothèse \(\beta=0\). Indiquez ce que sera la statistique de Wald, \(T_W\).
La forme générale du test est pour \(R \widehat{\beta} - q = 0\). Comme nous cherchons \(\widehat{\beta} = 0\), nous avons \(R=1\) et \(a=0\). Ainsi:
\[\begin{align*} T_W &= (R \widehat{\beta} - q)' \left[R \ \widehat{Var}[\widehat{\beta}] \ R'\right]^{-1} (R \widehat{\beta} - q)\\ &= \widehat{\beta}' \widehat{Var}[\widehat{\beta}]^{-1} \widehat{\beta}. \end{align*}\]
Le test de Wald n’exige que l’estimation d’un seul modèle, soit le modèle sans restriction paramétrique.
Exemple 6.4 Pour tester une géométrique contre une NB2, par exemple, le test du rapport de vraisemblance exige d’obtenir la logvraisemblance de la NB2 et la logvraisemblance de la géométrique.
Pour le test de Wald, seule l’estimation de \(\alpha\) (\(\widehat{\alpha}\)) et de la variance de \(\hat{\alpha}\) est nécessaire. Donc, l’estimation du modèle NB2 suffit et il n’est pas nécessaire d’estimer les paramètres du modèle géométrique.
6.1.3 Test du multiplicateur de Lagrange
Ce test est aussi appelé le test de score.
La statistique du test de Lagrange se base sur le vecteur de score, correspondant à la première dérivée du logvraisemblance du modèle non-restreint, évalué avec les paramètres du modèle avec restrictions paramétriques.
Formellement, notons
- \(\ell_u = \sum_{i=1}^n \ln f_u(y_i)\) la logvraisemblance du modèle non-restreint, et
- \(\ell_r = \sum_{i=1}^n \ln f_r(y_i)\) la logvraisemblance du modèle restreint.
On sait que:
\[\frac{\delta \ell_u}{\delta \theta}\Big|_{\widehat{\theta}_u} = 0 \text{ et } \frac{\delta \ell_r}{\delta \theta}\Big|_{\widehat{\theta}_r} = 0\]
signifiant que \(\theta_u\) et \(\theta_r\) sont les estimateurs par MLE maximisant la fonction de logvraisemblance du modèle non-restreint et du modèle restreint, respectivement.
On sait toutefois que:
\[\frac{\delta \ell_u}{\delta \theta}\Big|_{\widehat{\theta}_r} \ne 0\]
car les MLE du modèle restreint ne sont pas exactement les mêmes que les MLE du modèle non-restreint.
L’idée du test de score est de voir à quel point l’utilisation de \(\theta_r\), i.e. l’estimation par MLE du modèle restreint, dans la log-vraisemblance du modèle non-restreint modifie la valeur de la dérivée de la logvraisemblance pour le modèle non-restreint (ce qu’on appelle le score).
Si l’hypothèse \(H_0\) est vraie, alors on devrait obtenir:
\[\frac{\delta \ell_u}{\delta \theta}\Big|_{\widehat{\theta}_r} \approx 0\]
car cela signifie que la contrainte n’a que très peu d’impact sur l’estimation des paramètres.
Formellement, la statistique du test s’exprime comme:
\[T_{LM} = \left(\frac{\delta \ell_u}{\delta \theta}\Big|_{\widehat{\theta}_r}\right)' [I(\widehat{\theta}_r)]^{-1} \left(\frac{\delta \ell_u}{\delta \theta}\Big|_{\widehat{\theta}_r}\right) \]
où \(I(\widehat{\theta}_r)\) est un estimateur de la matrice Hessienne évalué à \(\hat{\theta}_r\).
Le test est distribué selon une chi-deux avec un degré de liberté égal au nombre de restrictions paramétriques.
6.1.4 Problème des tests d’hypothèse
Un problème avec ces tests classiques survient lorsque l’hypothèses nulle est à la frontière de domaine du paramètre. Lorsque le paramètre est limité par l’hypothèse \(H_0\), la distribution de l’estimateur du paramètre est aussi limitée, ce qui implique que la normalité asymptotique du MLE ne tient plus sous \(H_0\). En conséquence, une correction doit être faite aux tests.
Un exemple classique serait de tester la Poisson contre la NB2. Plus formellement, nous aurions l’hypothèse nulle \(H0: \alpha =0\) contre l’alternative \(\alpha > 0\). Pour mieux comprendre ce problème, simulons une série de variable aléatoire Poisson, et estimons un NB2 pour chaque réalisation.
set.seed(222)
score.nb <- as.formula(nb.sin ~ 1)
all.res <- data.frame()
for(i in 1:500){
simul.db <- data.frame(nb.sin=rpois(10000, 0.15))
model.nb2.MASS <- glm.nb(score.nb, data=simul.db, init.theta = 100)
alpha <- 1/model.nb2.MASS$theta
all.res <- rbind(all.res, cbind(i, alpha))
}On peut ainsi analyser la distribution de l’estimateur de \(\alpha\).
plot(density(all.res$alpha), main = "Kernel density plot")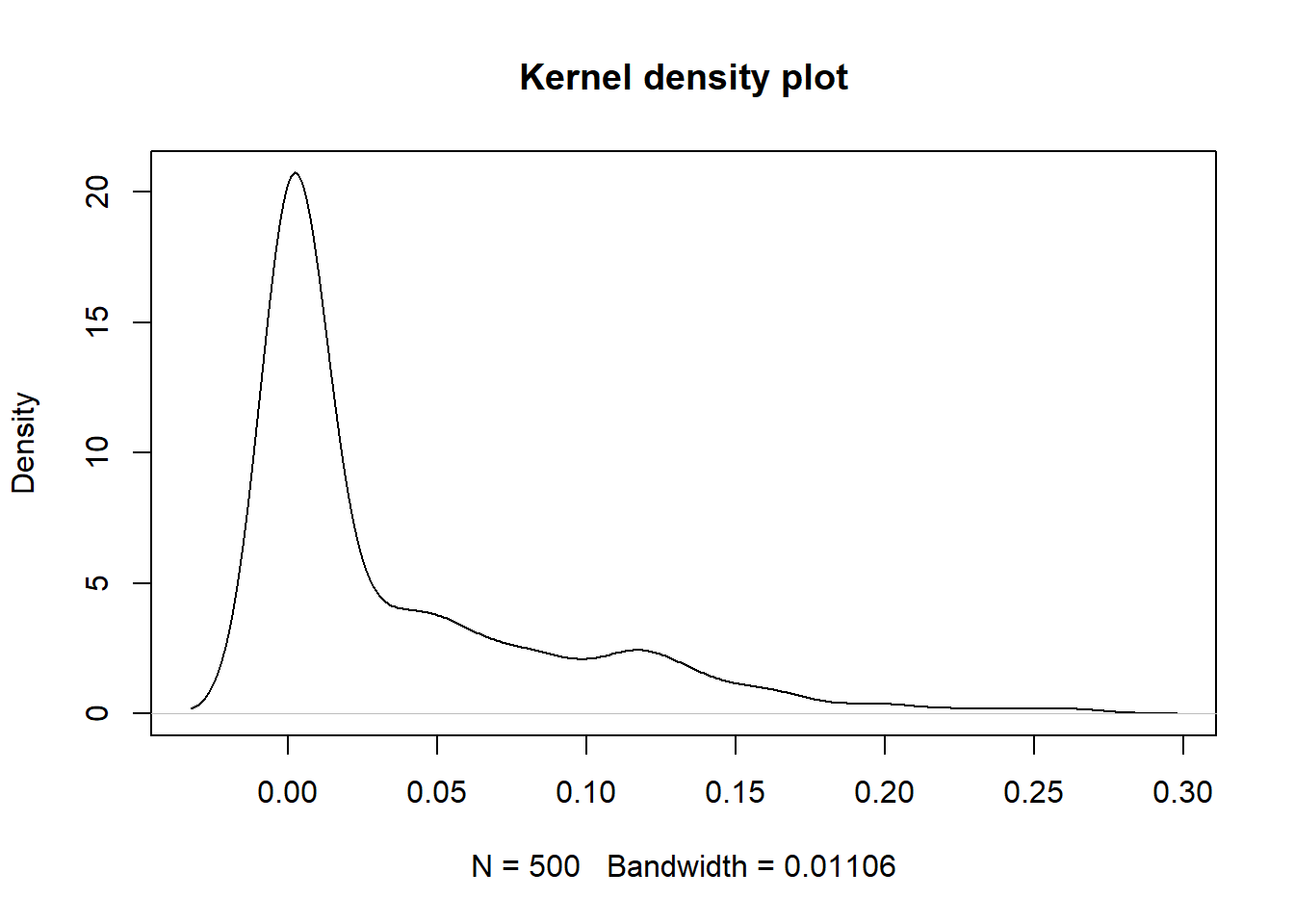
La densité obtenue est étrange car la valeur minimale de \(\alpha\) ne peut être plus petite que 0.
min(all.res$alpha)## [1] 0.0004461635Ainsi, le graph de la densité à noyau est incorrect car il donne du poids aux valeurs inférieures à zéro. Lorsque les données analysées sont strictement positives, et que nous sommes intéressés à voir la forme de la densité, une fonction à noyau gamma est une option à considérer.
library(kdensity)
plot(kdensity(all.res$alpha, start = "gamma", kernel = "gamma", bw='RHE'), main = "Gamma Kernel density plot")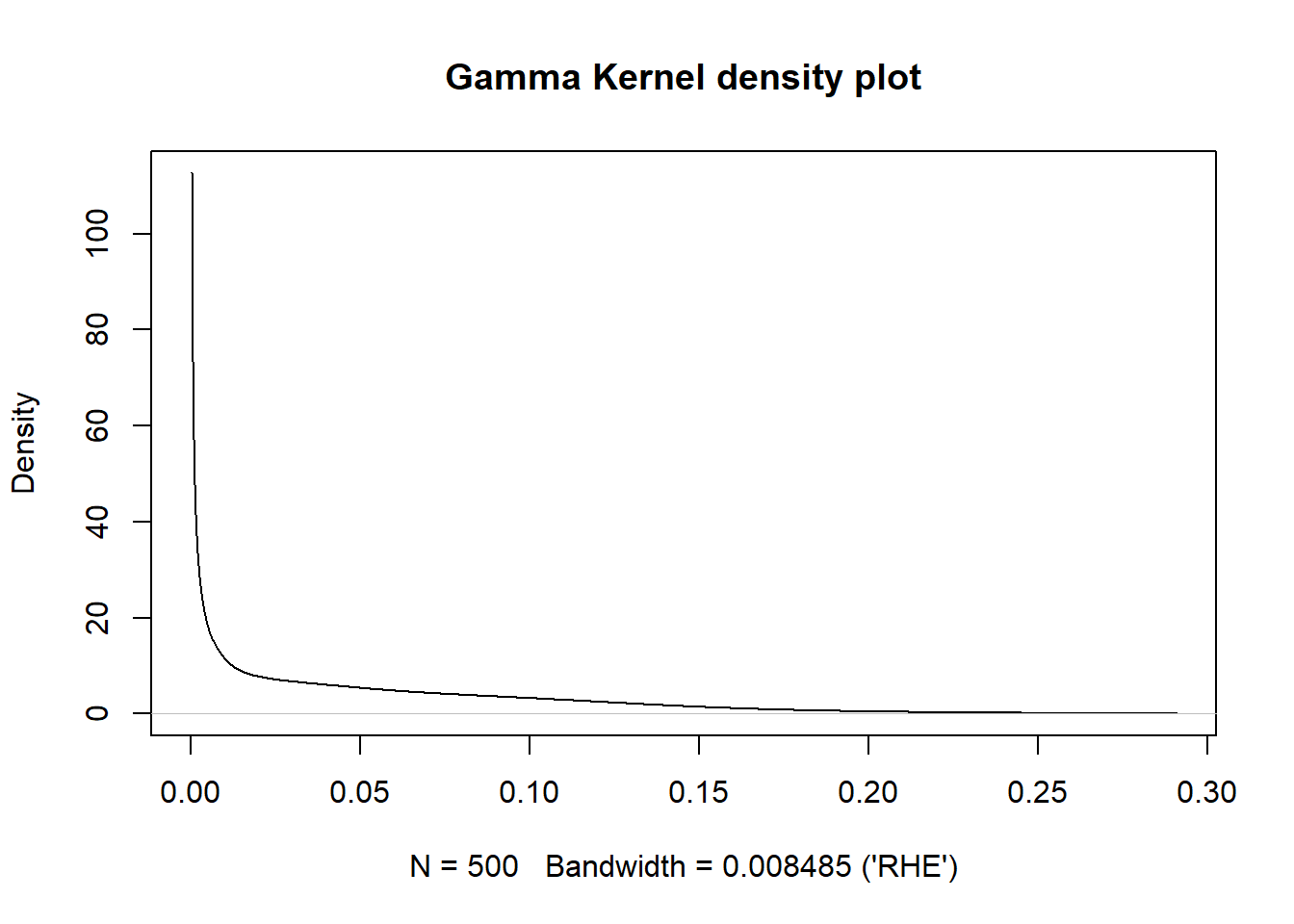
On voit ainsi qu’aucune valeur de \(\hat{\alpha}\) n’est possible. On voit aussi clairement que la distribution de \(\hat{\alpha}\) n’est pas du tout normale. En fait, la moitié de la densité correspond à une masse à 0.
Pour les cas de tests statistiques sur la borne de l’espace paramétrique (ici \(\alpha =0\), car le paramètre de la NB@ ne peut être inférieur à 0), tel qu’abordé dans
Moran, P.A.P. (1971), Maximum Likelihood Estimation in Non-Standard Conditions, Proceedings of the Cambridge Philosophical Society, 70, 441–450.
la distribution asymptotique des tests de \(\chi^2\), tel que le test du rapport de vraisemblance, le test de Wald ou le test de score, a une masse de probabilité d’une demie à 0, et une demie distribution \(\chi^2(1)\).
Cela signifie que pour faire un test à un niveau \(\delta\), pour \(\delta > 0.5\), on rejetera l’hypothèse H0 si le test \(T_{RV}\) est supérieur à une \(\chi^2(1)_{1- 2\delta}\) au lieu de la valeur habituelle \(\chi^2(1)_{1- \delta}\). Ainsi, si nous effectuons un test à un niveau \(5\%\), au lieu de prendre la valeur d’un table \(\chi^2(1)\) au niveau \(95\%\), on prendre le niveau \(90\%\).
6.1.5 Exemple du test du score pour la Poisson
Une application intéressante du test de score se fait pour tester l’équidispersion de la Poisson. Une idée pourrait être de tester la Poisson contre la NB2. Ainsi, selon la définition du test de score, l’idée générale est de définir les équations de premier ordre de la NB2. Nous avions:
\[\begin{eqnarray*} \frac{\delta}{\delta \mathbf{\beta}} \ell &=& \sum_{i=1}^n \Big(\frac{n_i - \lambda_i}{1 + \lambda_i \alpha}\Big) \mathbf{x}_{i} \label{MLEnegbin1} \end{eqnarray*}\]
\[\begin{eqnarray*} \frac{\delta}{\delta \alpha} \ell &=& \sum_{i=1}^n \left[ \frac{1}{\alpha^2} \left( \ln(1+ \alpha \lambda_i) - \sum_{j=1}^{n_i - 1} \frac{1}{j + \alpha^{-1}} \right) + \Big(\frac{n_i - \lambda_i}{\alpha(1 + \lambda_i \alpha)}\Big) \right] \end{eqnarray*}\]
Le principe de base du test de score est d’évaluer les conditions de premier ordre précédentes avec \(\beta = \widehat{\beta}_{\text{Poisson}}\) et \(\alpha = 0\). Alors que c’est assez direct pour :
\[\begin{eqnarray*} \frac{\delta \ell}{\delta \beta} \Bigg|_{\alpha = 0} &=& \sum_{i=1}^n (n_i - \lambda_i) \mathbf{X}_i , \end{eqnarray*}\]
c’est impossible èa effectuer pour la seconde condition de premier ordre, étant la division par \(\alpha\) qui implique donc une division par 0:
\[\begin{eqnarray*} \frac{\delta \ell}{\delta \alpha} \Bigg|_{\alpha = 0} &=& \sum_{i=1}^n \left[ \frac{1}{\alpha^2} \left( \ln(1+ \alpha \lambda_i) - \sum_{j=1}^{n_i - 1} \frac{1}{j + \alpha^{-1}} \right) + \Big(\frac{n_i - \lambda_i}{\alpha(1 + \lambda_i \alpha)}\Big) \right] \Bigg|_{\alpha = 0} \end{eqnarray*}\]
La dérivation du test de score pour les modèles avec hétérogénéité ont plutôt été développés en utilisant la famille de distribution de Katz, qui incluent la NB1 et la NB2. Ce développement est complexe.
Pour les intéressés, on peut référer au chapitre 5, section 5.7, de
Cameron, A. C., & Trivedi, P. K. (2013). Regression analysis of count data. Cambridge university press.
On peut toutefois reprendre certaines conclusions et construire le test de score correspondant.
Une première manière d’analyser le modèle avec hétérogénéité est de commencer avec la forme NB2 et donc:
\[\begin{equation*} Var[Y_i] = \lambda_i + \alpha \lambda_i^2 \label{varformbbb} \end{equation*}\]
En supposant \(\lambda_i = \exp(\mathbf{X}_i' \beta)\) et utilisant la notation du système de Katz avec \(\alpha = 0\), nous avons:
\[\begin{eqnarray*} \frac{\delta \ell}{\delta \beta} \Bigg|_{\alpha = 0} &=& \sum_{i=1}^n \lambda_i^{-1} (y_i - \lambda_i) \frac{\delta \lambda_i}{\delta \beta} = \sum_{i=1}^n (y_i - \lambda_i) \mathbf{X}_i' \\ \frac{\delta \ell}{\delta \alpha} \Bigg|_{\alpha = 0} &=& \sum_{i=1}^n \frac{1}{2} ( (y_i - \lambda_i)^2 - y_i)\\ \end{eqnarray*}\]
Ainsi:
\[\begin{eqnarray*} \frac{\delta \ell}{\delta \theta}\Bigg|_{\beta = \hat{\beta}, \alpha = 0} = \left[ \begin{array}{c} 0 \\ \sum_{i=1}^n \frac{1}{2} ( (y_i - \lambda_i)^2 - y_i) \\ \end{array} \right] \end{eqnarray*}\]
Pour construire le LM test, nous avons aussi besoin d’avoir un estimateur de la matrice de variance. Ainsi, si on suppose:
\[\begin{eqnarray*} M = \left[ \begin{array}{cccc} (y_1 - \lambda_1) X_{1,0} & (y_2 - \lambda_2) X_{2,0} & ... & (y_n - \lambda_n) X_{n,0}\\ (y_1 - \lambda_1) X_{1,1} & (y_2 - \lambda_2) X_{2,1} & ... & (y_n - \lambda_n) X_{n,1}\\ ... & ... & ... & ... \\ (y_1 - \lambda_1) X_{1,p} & (y_2 - \lambda_2) X_{2,p} & ... & (y_n - \lambda_n) X_{n,p}\\ \frac{1}{2} ( (y_1 - \lambda_1)^2 - y_1) & \frac{1}{2} ( (y_2 - \lambda_2)^2 - y_2) & ... & \frac{1}{2} ( (y_p - \lambda_p)^2 - y_p) \\ \end{array} \right], \end{eqnarray*}\]
le produit croisé s’exprime comme \(M'M\):
\[\begin{eqnarray*} M'M = \left[ \begin{array}{cc} \sum_{i=1}^n (y_i - \lambda_i)^2 \mathbf{X}' \mathbf{X} & \sum_{i=1}^n \frac{1}{2} ( (y_i - \lambda_i)^2 - y_i) (y_i - \lambda_i) \mathbf{X}_i\\ \sum_{i=1}^n \frac{1}{2} ( (y_i - \lambda_i)^2 - y_i) (y_i - \lambda_i) \mathbf{X}_i' & \sum_{i=1}^n \frac{1}{4} ( (y_i - \lambda_i)^2 - y_i)^2 \end{array} \right], \end{eqnarray*}\]
Sous \(H_0\), c’est-à-dire lorsque \(Y \sim Poisson(\lambda)\), on peut montrer que les identités suivantes:
\[E[(y-\lambda)^2] = \lambda\] \[E[((y-\lambda)^2 - y)(y-\lambda)] = 0\] \[E[((y-\lambda)^2 - y)^2] = 2\lambda^2\]
Ainsi:
\[\begin{eqnarray*} E[M'M] = \left[ \begin{array}{cc} \sum_{i=1}^n \lambda_i \mathbf{X}' \mathbf{X} & \mathbf{0}\\ \mathbf{0} & \sum_{i=1}^n \frac{1}{2} \lambda_i^2 \end{array} \right] \end{eqnarray*}\]
Finalement, puisque nous cherchons:
\[T_{LM} = \left(\frac{\delta \ell_u}{\delta \theta}\Big|_{\widehat{\theta}_r}\right)' [I(\widehat{\theta}_r)]^{-1} \left(\frac{\delta \ell_u}{\delta \theta}\Big|_{\widehat{\theta}_r}\right),\]
nous avons:
\[\begin{eqnarray*} T_{LM} = && \left[ \begin{array}{c} 0 \\ \sum_{i=1}^n \frac{1}{2} ( (y_i - \lambda_i)^2 - y_i) \\ \end{array} \right]^T \left[ \begin{array}{cc} \sum_{i=1}^n \lambda_i \mathbf{X}' \mathbf{X} & \mathbf{0}\\ \mathbf{0} & \sum_{i=1}^n \frac{1}{2} \lambda_i^2 \end{array} \right]^{-1} \left[ \begin{array}{c} 0 \\ \sum_{i=1}^n \frac{1}{2} ( (y_i - \lambda_i)^2 - y_i) \\ \end{array} \right]\\ &=& [\sum_{i=1}^n \frac{1}{2} \lambda_i^2]^{-1} (\sum_{i=1}^n \frac{1}{2} ( (y_i - \lambda_i)^2 - y_i))^2 \end{eqnarray*}\]
qui suit une \(\chi^2(1)\).
Dans la littérature, on prend souvent la racine de ce test, pour obtenir:
\[\begin{equation*} \sqrt{T_{LM}} = \Big[\sum_{i=1}^n \frac{1}{2} \hat{\lambda}_i^{2} \Big]^{-\frac{1}{2}} \sum_{i=1}^n \frac{1}{2} \big((y_i - \hat{\lambda}_i)^2 - y_i \big) \end{equation*}\]
qui est distribution selon une loi normale de moyenne 0 et variance 1.
6.1.5.1 Remarques importantes
Même si le test semble effectué sur la borne de la NB2, le test a plutôt était fait à partir de la forme des distributions de la famille de Katz, laquelle inclut la NB2 mais aussi des distributions admettant de la sous-dispersion (\(\alpha < 0\)). Ainsi, nous ne testons plus sur la borne, et aucune correction ne doit être apportée au seuil \(\delta\).
Le test de score qu’on vient de développer s’applique à n’importe quelle distribution ayant une forme de variance du type \(Var[Y_i] = \lambda_i + \alpha \lambda_i^2\). Ainsi, on teste la Poisson contre la NB2, mais aussi contre la PIG2 ou la PLN2, par exemple.
La valeur de \(T_{LM}\) ou \(\sqrt{T_{LM}}\) est finalement assez simple à calculer. Mais le développement mathématique pour se rendre à cette forme a été difficile. Sachant que les tests de Wald et du rapport de vraisemblance (avec correction) existent, on peut se demander pourquoi nous avons besoin d’un tel test. La réponse est simple: le test de score ne nécessite pas l’estimation des paramètres du modèle alternatif. On peut ainsi estimer une Poisson et faire directement le test pour la surdispersion sans devoir estimer d’autres modèles.
6.1.5.2 Généralisations
On pourrait généraliser ce résultat de plusieurs façons. Une manière générale d’analyser le modèle avec hétérogénéité est la fonction suivante :
\[\begin{equation*} Var[Y_i] = \lambda_i + \alpha g(\lambda_i) \end{equation*}\]
où la fonction \(g(\lambda_i)\) à être remplacée par la forme souhaitée. Pour une variance de forme NB2, nous avons \(g(\lambda_i) = \lambda_i^2\) (ce qui génèrerait les mêmes résultats que précédemment), alors qu’une variance de forme NB1 serait \(g(\lambda_i) = \lambda_i\) (qui inclut la PIG1 et la PLN1).
Nous aurions ainsi:
\[\begin{equation*} \sqrt{T_{LM}} = \Big[\sum_{i=1}^n \frac{1}{2} \hat{\lambda}_i^{-2} g^2(\hat{\lambda}_i)\Big]^{-\frac{1}{2}} \sum_{i=1}^n \frac{1}{2} \hat{\lambda}_i^{-2} g(\hat{\lambda}_i) \big((n_i - \hat{\lambda}_i)^2 - n_i \big) \end{equation*}\]
qui est normalement distribuée, de moyenne 0 et variance 1.
Exemple 6.5 Nous avons exploré la distribution Poisson gonflée à zéro plus tôt. Nous pouvons ici aussi utiliser un test de score pour ce modèle ayant la fonction de probabilité suivante: \[\begin{eqnarray*} \Pr(N_i =k) &=& \begin{cases} \phi + (1-\phi) \exp(-\lambda_i) & \text{ pour } \ k = 0\\ (1-\phi) \frac{\lambda_i^k \exp(-\lambda_i)}{k!} & \text{ pour } \ k = 1,2,... \end{cases} \end{eqnarray*}\]
Développez un test de score pour tester \(H_0: \phi = 0\).
À faire en exercice. Notez que le développement est beaucoup plus simple que ce que nous venons de voir avec la NB2.
6.1.5.3 Application en R
On peut faire quelques analyses pour les données utilisées pour le cours. Reprenons ainsi les résultats obtenus pour l’estimation des paramètres de la distribution Poisson et de la NB2, vus au chapitre 3.
Pour le test de Wald, nous avons besoin de la valeur de \(\hat{\alpha}\), ainsi que de son écart-type. On peut par la suite calculer facilement \(T_W\). On doit comparer la valeur obtenue avec une \(\chi^2(1)\).
hat.alpha <- parm[ncol(Matrix.X)+1]
var.alpha <- varOP[ncol(Matrix.X)+1]
TW <- hat.alpha^2/var.alpha
cbind(hat.alpha, var.alpha, TW, pchisq(TW, df=1, lower.tail = TRUE))## hat.alpha var.alpha TW
## 0.6366221 0.02000385 20.26049 0.9999932Pour le test du rapport de vraisemblance, on doit simplement calculer la différence des logvraisemblances, et comparer avec une une \(\chi^2(1)\).
ell.r <- logLik(Poisson1)
ell.u <- logLik(model.nb2.MASS)
TRV <- 2*(ell.u - ell.r)
cbind(ell.r, ell.u, TRV, pchisq(TRV, df=1, lower.tail = TRUE))## ell.r ell.u TRV
## [1,] -142286.3 -141503.1 1566.421 1Théoriquement, puisque nous testons sur la borne de l’espace paramétrique, on devrait faire une correction aux p-values obtenues. On peut bien faire cette correction, mais la valeur obtenue pour \(T_W\) et \(T_{RV}\) est tellement élevée qu’on ne verra pas de différence. En effet, la Poisson est clairement rejetée contre la NB2 pour les deux tests.
Finalement, on peut calculer la valeur du test de score \(T_{LM}\). Comme mentionné plus tôt, seuls les paramètres de la Poisson sont utilisés pour calculer le test.
lambda <- predict(Poisson1, newdata=db.train, type="response")
part1 <- sum(0.5*lambda*lambda)
part2 <- sum(0.5*((db.train$nb.sin - lambda)^2 - db.train$nb.sin))
TLM <- part2^2/part1
cbind(TLM, pchisq(TLM, df=1, lower.tail = TRUE))## TLM
## [1,] 1825.268 1Sans surprise, pour le test de score, la Poisson est aussi clairement rejetée.