2.3 Applications avec R

Avec R, c’est la fonction glm() qui est habituellement utilisée pour les GLM. La structure générale de la commande s’exprime comme:

glm(score, family = famille.dist(link = ""), data=,...)

D’autres options sont possibles, mais pour ce petit chapitre de rappels, seuls ces 3 paramètres seront utilisés. Pour d’autres déails, on peut évidemment consulter la documentation en R.

1- score: Ce paramètre est utilisé pour lister les variables qui sont utilisées dans le GLM;

2- famille.dist: On indique ici la distribution que nous voulons utiliser pour ajuster la variable réponse;

3- link est utilisé pour la fonction de lien;

4- data spécifie le jeu de données utilisé.

La fonction glm de R offre 8 possibilités de distributions:

Distribution	Fonction de lien par défault
binomial	(link = “logit”)
gaussian	(link = “identity”)
Gamma	(link = “inverse”)
inverse.gaussian	(link = “1/mu^2”)
poisson	(link = “log”)
quasi	(link = “identity”, variance = “constant”)
quasibinomial	(link = “logit”)
quasipoisson	(link = “log”)

2.3.1 Analyse de la fréquence

On peut reprendre le petit exemple numérique avec 8 observations, pour appliquer la fonction GLM.

x0 <- c(1,1,1,1,1,1,1,1)
x1 <- c(1,1,1,0,1,1,0,1)
x2 <- c(0,0,1,1,0,1,0,0)
x3 <- c(1,0,1,1,0,1,1,1) 
y  <- c(1,0,2,3,1,0,1,2)

db <- data.frame(x0,x1,x2,x3,y)

score.glm <- as.formula(y ~ x1+x2+x3)
modele <- glm(score.glm, family=poisson, data=db)
summary(modele)

## 
## Call:
## glm(formula = score.glm, family = poisson, data = db)
## 
## Deviance Residuals: 
##       1        2        3        4        5        6        7        8  
## -0.1072  -1.0000   0.4862   0.4950   0.6215  -1.6667  -0.6363   0.7572  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)
## (Intercept)  -0.2231     1.2042  -0.185    0.853
## x1           -0.4700     0.6708  -0.701    0.484
## x2            0.2231     0.6708   0.333    0.739
## x3            0.7985     1.1571   0.690    0.490
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 7.6740  on 7  degrees of freedom
## Residual deviance: 5.6352  on 4  degrees of freedom
## AIC: 27.854
## 
## Number of Fisher Scoring iterations: 5

On peut y voir que l’estimé des paramètres, de même que la variance (ici, on montre l’écart-type) des estimateurs et la déviance (\(5.635192\)) sont les mêmes que ceux que nous avions calculés.

On pourrait probablement analyser d’autres éléments de la sortie R, en plus de générer d’autres éléments d’analyse. Nous y reviendrons.

2.3.2 Analyse de la sévérité

Au lieu d’utiliser un petit jeu de données de 8 observations, on pourrait s’attaquer au grand jeu de données introduit dans le chapitre précécent.

Par contre, nous ne modéliserons pas la fréquence de réclamations, mais plutôt la sévérité des réclamations avec la distribution gamma et avec la distribution inverse-gaussienne.

On doit donc prendre le jeu de données dbfictif.Rda, disponible sur Moodle.

load('Data/dbfictif.Rda')

Nous nous intéressons donc à la sévérité des réclamations. Cela signifie que nous ne considérons pas les assurés qui n’ont pas réclamés.

db <- db.fictif %>%
  filter(nb.sin > 0)

nrow(db)

## [1] 63493

sum(db$nb.sin)

## [1] 73703

Le jeu de données db contient \(63,493\) observations, pour un total de \(73,703\) sinistres. En effet, certains assurés ont plus d’une réclamation par contrat. Il nous faut donc modifier le jeu de données db pour qu’il y ait un sinistre par observation (caractéristique de ce qu’on appelait tidy data au premier chapitre).

La fonction gather du package tidyr crée une nouvelle observation pour chacune des colonnes Cost1 à Cost7. Pour ne pas créer d’observation lorsque les colonnes Cost2 à Cost7 sont nulles, un filtre est ajouté.

library(tidyr)
db <- db %>%
  gather(Rang, Cost, Cost1:Cost7) %>%
  filter(Cost > 0)

nrow(db)

## [1] 73703

Le jeu de données db contient maintenant \(73,703\) observations, soit exactement le nombre de sinistres dans la base de données dbfictif.Rda originale.

Avant d’analyser l’impact des diverses caractéristiques du risque sur la sévérité, on peut analyser quelques éléments sommaires.

library(stats)
# moyenne
mean(db$Cost)

## [1] 6623.502

# variance
var(db$Cost)

## [1] 894671899

#variance comme puissance de la moyenne
log(var(db$Cost))/log(mean(db$Cost))

## [1] 2.3427

# quantiles
quantile(db$Cost, probs = seq(0, 1, 0.1),)

##          0%         10%         20%         30%         40%         50%         60%         70%         80% 
##      50.040     123.014     173.220     251.726     367.260     519.640     748.492    1122.904    2155.160 
##         90%        100% 
##   14875.598 1538270.040

# histogramme du log(cost)
hist(log(db$Cost))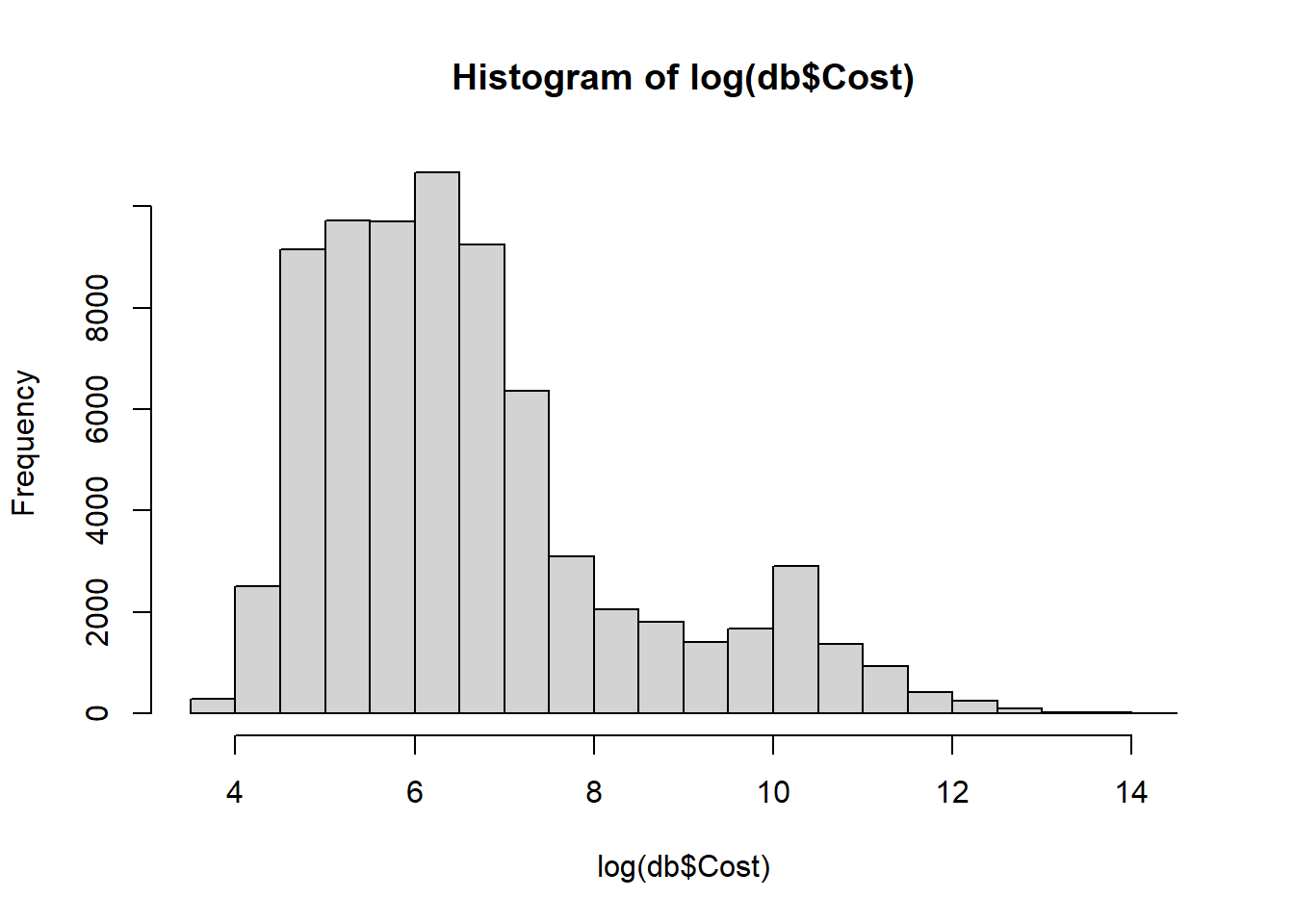

Les variables disponibles pour segmenter la sévérité sont disponibles ici:

colnames(db)

##  [1] "policy_no"       "veh.num"         "renewal_date"    "debut"           "fin"             "expo"           
##  [7] "nb.sin"          "Tot.Cost"        "freq_paiement"   "annee_veh"       "sexe"            "an_naissance"   
## [13] "annee_permis"    "langue"          "type_prof"       "type_voiture"    "type_territoire" "utilisation"    
## [19] "voiture"         "couleur"         "myopie"          "alimentation"    "cheveux"         "ID"             
## [25] "Type"            "Rang"            "Cost"

Même si le jeu de données est fortement plus petit que ce que nous pouvons trouver dans de vraies bases de données de compagnies d’assurance IARD, le nombre de caractéristiques disponibles pour expliquer la sévérité est très grand.

Habituellement, une première analyse sommaire des données, par des analyses individuelles de chacun des variables disponibles, devrait être faite. Cela permet d’avoir rapidement une idée des variables qui semblent les plus importantes.

L’objectif de ce chapitre est de revoir la théorie des GLM, alors nous n’effecutons pas cette analyse et passons directement au modèle proposé.

score.glm <- as.formula(Cost ~ couleur + myopie + type_territoire + cheveux + langue)

modele.gamma <- glm(score.glm, family=Gamma(link= log), data=db)
summary(modele.gamma)

## 
## Call:
## glm(formula = score.glm, family = Gamma(link = log), data = db)
## 
## Deviance Residuals: 
##    Min      1Q  Median      3Q     Max  
## -2.840  -2.236  -1.800  -1.222  21.293  
## 
## Coefficients:
##                            Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                 8.66607    0.14062  61.629  < 2e-16 ***
## couleurRouge               -0.11381    0.07264  -1.567  0.11717    
## myopieOui                   0.01784    0.05104   0.350  0.72667    
## type_territoireSemi-urbain  0.03366    0.04742   0.710  0.47782    
## type_territoireUrbain       0.10858    0.04547   2.388  0.01694 *  
## cheveuxBlonds               0.11586    0.12001   0.965  0.33433    
## cheveuxBruns                0.10108    0.11855   0.853  0.39384    
## cheveuxRoux                 0.10459    0.12188   0.858  0.39082    
## langueF                     0.10751    0.03816   2.818  0.00484 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Gamma family taken to be 20.4016)
## 
##     Null deviance: 320322  on 73702  degrees of freedom
## Residual deviance: 320045  on 73694  degrees of freedom
## AIC: 1336791
## 
## Number of Fisher Scoring iterations: 13

Un lien logarithmique a été supposé, au lieu du lien canonique naturel (link=inverse) de la gamma. La raison principale est pour l’application pratique en assurance. En effet, le système de tarification habituel des assureurs est multiplicatif en fonction des caractéristiques du risque. Nous avons ainsi:

\[\text{Prime} = \text{Prime de base} \times \text{Relativité 1} \times \text{Relativité 2} \times \ldots \times \text{Relativité p},\]
ce qui est similaire à la forme de la prime obtenue par un lien logarithmique:

\[\begin{align*} E[S] = \exp(\mathbf{X}^T \beta) &= \exp(\beta_0 + X_1 \beta_1 + X_2 \beta_2 + \ldots + X_p \beta_p)\\ &= \exp(\beta_0) \times \exp(X_1 \beta_1) \times \exp(X_2 \beta_2) \times \ldots \times \exp(X_p \beta_p) \end{align*}\]

Pour revenir a l’application informatique, nous pouvons constater que plusieurs caractéristiques de l’assuré ne semblent pas être statistiquement significattives. En fait, seule la langue et peut-être le type de territoire semblent être des éléments pouvant expliquer l’hétérogénéité de la sévérité de réclamations.

Classiquement, en statistique, une série de retrait et d’ajout de variables est effectuée pour converger vers un modèle où tous les paramètres étaient statistiquement significatifs. Ces approches sont de type backward, forward ou step-wise. Des packages en R offre des routines intégrées qui font le travail.

2.3.2.1 Approche forward

L’idée de ce que l’approche forward est de débuter avec le modèle le plus simple, c’est-à-dire le modèle n’ayant aucun régresseur, et de tenter d’améliorer le modèle en ajoutant les régresseurs disponibles. On jugera que le modèle est meilleur est se basant sur certains critères statistiques. Pour la fonction step() en R, le critère est l’AIC (Akaike Information Criteria) qui se base sur la logvraisemblance et pénalise le modèle en fonction du nombre de paramètres:

\[AIC = -2 \ell + 2(p+1)\] avec \(\ell\) le logvraisemblance du modèle, et \(p+1\) le nombre de paramètres dans le modèle. D’autres critères de sélection que l’AIC sont possiblement disponibles.

Avec notre jeu de données, nous avons:

### Seulement l'intercept
intercept_only <- glm(Cost ~ 1, family=Gamma(link= log), data=db)
summary(intercept_only)

## 
## Call:
## glm(formula = Cost ~ 1, family = Gamma(link = log), data = db)
## 
## Deviance Residuals: 
##    Min      1Q  Median      3Q     Max  
## -2.790  -2.238  -1.802  -1.223  21.251  
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  8.79838    0.01663   528.9   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Gamma family taken to be 20.39334)
## 
##     Null deviance: 320322  on 73702  degrees of freedom
## Residual deviance: 320322  on 73702  degrees of freedom
## AIC: 1336867
## 
## Number of Fisher Scoring iterations: 12

### Modele avec toutes les variables voulues
all <- glm(Cost ~ couleur + myopie + type_territoire + cheveux + langue, family=Gamma(link= log), data=db)
summary(all)

## 
## Call:
## glm(formula = Cost ~ couleur + myopie + type_territoire + cheveux + 
##     langue, family = Gamma(link = log), data = db)
## 
## Deviance Residuals: 
##    Min      1Q  Median      3Q     Max  
## -2.840  -2.236  -1.800  -1.222  21.293  
## 
## Coefficients:
##                            Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                 8.66607    0.14062  61.629  < 2e-16 ***
## couleurRouge               -0.11381    0.07264  -1.567  0.11717    
## myopieOui                   0.01784    0.05104   0.350  0.72667    
## type_territoireSemi-urbain  0.03366    0.04742   0.710  0.47782    
## type_territoireUrbain       0.10858    0.04547   2.388  0.01694 *  
## cheveuxBlonds               0.11586    0.12001   0.965  0.33433    
## cheveuxBruns                0.10108    0.11855   0.853  0.39384    
## cheveuxRoux                 0.10459    0.12188   0.858  0.39082    
## langueF                     0.10751    0.03816   2.818  0.00484 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Gamma family taken to be 20.4016)
## 
##     Null deviance: 320322  on 73702  degrees of freedom
## Residual deviance: 320045  on 73694  degrees of freedom
## AIC: 1336791
## 
## Number of Fisher Scoring iterations: 13

### Forward stepwise regression
forward <- step(intercept_only, direction='forward', scope=formula(all), trace=0)
#resultats de l'analyse forward
forward$anova

##                Step Df  Deviance Resid. Df Resid. Dev     AIC
## 1                   NA        NA     73702   320322.2 1336867
## 2          + langue -1  68.54741     73701   320253.7 1336846
## 3 + type_territoire -2 134.69494     73699   320119.0 1336805
## 4         + couleur -1  52.21925     73698   320066.7 1336790

#model final
forward$coefficients

##                (Intercept)                    langueF type_territoireSemi-urbain      type_territoireUrbain 
##                 8.77236061                 0.10680115                 0.03497019                 0.11030409 
##               couleurRouge 
##                -0.11441564

On peut voir clairement l’évolution du modèle: i) Débutant avec un intercept seulement, l’AIC du modèle était de \(1336867\);

Parmi toutes les variables disponibles, celle qui améliorait le plus le modèle était la langue. En ajoutant la langue dans le modèle, on passe à un AIC de \(1336846\);
Parmi toutes les variables disponibles, les régresseurs qui amélioraient le plus le modèle étaient le territoire, et ensuite la couleur. En ajoutant successivement ces deux variables dans le modèle, on passe à un AIC de \(1336790\);
Aucune autre variable disponible ne peut améliorer l’AIC, et la procédure s’arrête. On se retrouve donc avec un modèle qui segmente le coût selon la langue, le territoire et la couleur.

On peut faire le même exercice, mais à l’envers: en débutant avec le modèle complet, et enlevant les variables qui améliorent le AIC.

### Backward stepwise regression
backward <- step(all, direction='backward',trace=1)

## Start:  AIC=1336791
## Cost ~ couleur + myopie + type_territoire + cheveux + langue
## 
##                   Df Deviance     AIC
## - cheveux          3   320064 1336786
## - myopie           1   320047 1336789
## <none>                 320045 1336791
## - couleur          1   320096 1336791
## - type_territoire  2   320176 1336793
## - langue           1   320205 1336797
## 
## Step:  AIC=1336791
## Cost ~ couleur + myopie + type_territoire + langue

#resultats de l'analyse backward
backward$anova

##   Step Df Deviance Resid. Df Resid. Dev     AIC
## 1      NA       NA     73694   320044.9 1336791

#model final
backward$coefficients

##                (Intercept)               couleurRouge                  myopieOui type_territoireSemi-urbain 
##                 8.77134355                -0.11409490                 0.01837317                 0.03392360 
##      type_territoireUrbain                    langueF 
##                 0.10831600                 0.10633584

Avec trace=1, il est possible de voir les étapes de sélection de l’algorithme backward. Le meilleur modèle selon cette approche utilise la couleur, la myopie, le territoire et la langue, pour un AIC de 1336791.

Finalement, on peut aussi utiliser une approche step-wise qui combine l’approche forward et l’approche backward. A chaque étape, l’algorithme vérifie si l’ajout ou le retrait d’une variable améliore l’AIC.

#### Forward + bacward stepwise regression
both <- step(intercept_only, direction='both', scope=formula(all), trace=0)

#resultats de l'analyse backward
both$anova

##                Step Df  Deviance Resid. Df Resid. Dev     AIC
## 1                   NA        NA     73702   320322.2 1336867
## 2          + langue -1  68.54741     73701   320253.7 1336846
## 3 + type_territoire -2 134.69494     73699   320119.0 1336805
## 4         + couleur -1  52.21925     73698   320066.7 1336790

#model final
both$coefficients

##                (Intercept)                    langueF type_territoireSemi-urbain      type_territoireUrbain 
##                 8.77236061                 0.10680115                 0.03497019                 0.11030409 
##               couleurRouge 
##                -0.11441564

On se retrouve donc avec un modèle qui segmente le coût selon la langue, le territoire et la couleur.

Depuis une quizaine d’années, d’autres outils de sélection de variables souvent basés sur de la sélection croisée impliquant une division itéerative de la base de données en portion ajustement et validation ont été développés. Des outils techniques de type:

Forêt aléatoire (random forest);
GLM-net, de type régression ridge ou régression LASSO;
Boosting;
Réseaux de neuronnes;
etc.

sont maintenant utilisés couramment dans l’industrie. À l’image de la fonction glm() de R qui ne nécessite finalement aucune connaissance statistique pour l’utiliser, plusieurs packages R sont disponibles et faciles d’utilisation pour la sélection de variables. Bien évidemment, J’aviserai qu’il est toujours un peu plus raisonable, professionnel et même plus moral de bien comprendre la théorie sous-jacente avant d’utiliser un outil technique, surtout dans un contexte réel ayant des vrais impacts.

Pour terminer, on pourrait refaire l’analyse en supposant maintenant une distribution inverse-gaussienne.

modele.ig <- glm(score.glm, family=inverse.gaussian(link="1/mu^2"), data=db)
summary(modele.ig)

## 
## Call:
## glm(formula = score.glm, family = inverse.gaussian(link = "1/mu^2"), 
##     data = db)
## 
## Deviance Residuals: 
##      Min        1Q    Median        3Q       Max  
## -0.14041  -0.06762  -0.04040  -0.02070   0.18792  
## 
## Coefficients:
##                              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                 2.904e-08  6.914e-09   4.200 2.67e-05 ***
## couleurRouge                4.862e-09  2.863e-09   1.698  0.08946 .  
## myopieOui                  -8.418e-10  2.237e-09  -0.376  0.70671    
## type_territoireSemi-urbain -1.467e-09  2.249e-09  -0.652  0.51430    
## type_territoireUrbain      -4.840e-09  2.087e-09  -2.319  0.02042 *  
## cheveuxBlonds              -5.230e-09  6.229e-09  -0.840  0.40113    
## cheveuxBruns               -4.522e-09  6.177e-09  -0.732  0.46419    
## cheveuxRoux                -4.560e-09  6.311e-09  -0.723  0.46993    
## langueF                    -4.762e-09  1.753e-09  -2.716  0.00662 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for inverse.gaussian family taken to be 0.003097986)
## 
##     Null deviance: 228.43  on 73702  degrees of freedom
## Residual deviance: 228.39  on 73694  degrees of freedom
## AIC: 1248335
## 
## Number of Fisher Scoring iterations: 13

Avec une énorme variance de forme \(\mu^3\) (alors que la forme de la variance gamma est \(\mu^2\), la Poisson est \(\mu^1\) et la normale est \(\mu^0\)), dans plusieurs applications en tarification en actuariat, aucune caractéristique ne reste statistiquement significative avec l’inverse-gaussienne.

De plus, comme nous pouvons le voir, (link = “1/mu^2”) a été utilisé au lien du lien logarithmique qu’on préfére habituellement en actuariat. Dans mes analyses rapides, les résultats obtenus avec (link=log) n’avaient pas de sens:

modele.ig <- glm(score.glm, family=inverse.gaussian(link=log), data=db)
summary(modele.ig)

## 
## Call:
## glm(formula = score.glm, family = inverse.gaussian(link = log), 
##     data = db)
## 
## Deviance Residuals: 
##       Min         1Q     Median         3Q        Max  
## -0.141365  -0.069792  -0.043868  -0.026430  -0.000806  
## 
## Coefficients:
##                             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                35.307597   0.108174  326.40   <2e-16 ***
## couleurRouge               -4.291613   0.108046  -39.72   <2e-16 ***
## myopieOui                  -0.385793   0.012259  -31.47   <2e-16 ***
## type_territoireSemi-urbain  2.268817   0.010186  222.75   <2e-16 ***
## type_territoireUrbain       5.678660   0.023569  240.94   <2e-16 ***
## cheveuxBlonds               3.323896   0.013468  246.81   <2e-16 ***
## cheveuxBruns                2.796694   0.010174  274.88   <2e-16 ***
## cheveuxRoux                 1.972171   0.009963  197.94   <2e-16 ***
## langueF                     3.717487   0.010797  344.30   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for inverse.gaussian family taken to be 4.303825e-17)
## 
##     Null deviance: 228.43  on 73702  degrees of freedom
## Residual deviance: 239.56  on 73694  degrees of freedom
## AIC: 1251854
## 
## Number of Fisher Scoring iterations: 3

L’instabilité de la fonction glm() pour l’inverse-gaussienne avec un lien logarithmique serait à analyser plus en détails lorsque nous aurons du temps.

2.3.3 Régression logistique

En plus de la régression Poisson pour le nombre de réclamations, et la régression gamma pour la sévérité, une autre forme de régression est populaire en actuariat: la régression logistique. Celle-ci se base sur la loi Bernoulli(\(p\)) et ne modélise que les situations {0,1}, en cherchant à inclure des régresseurs dans le paramètre \(p\).

On pourra utiliser la régression logistique pour modéliser, par exemple, la probabilité de renouvellement d’un contrat d’assurance. Pour notre base de données du cours, afin de se pratiquer, on pourra créer une nouvelle variable indiquant si l’assuré a réclamé ou non pendant l’année.

db <- db.fictif %>%
  mutate(CLAIM01 = ifelse(nb.sin >0, 1, 0))

mean(db$CLAIM01)

## [1] 0.1641142

On voit ainsi qu’en moyenne, environ \(16.4\%\) des contrats ont réclamé dans l’année.

score.glm <- as.formula(CLAIM01 ~ couleur + myopie + type_territoire + cheveux + langue)
reg.log <- glm(score.glm, family=binomial(link=logit), data=db)
summary(reg.log)

## 
## Call:
## glm(formula = score.glm, family = binomial(link = logit), data = db)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -0.6893  -0.6273  -0.5617  -0.5431   1.9972  
## 
## Coefficients:
##                             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)                -1.628971   0.036931 -44.109  < 2e-16 ***
## couleurRouge                0.007330   0.018957   0.387    0.699    
## myopieOui                   0.060502   0.013320   4.542 5.57e-06 ***
## type_territoireSemi-urbain -0.115929   0.012600  -9.201  < 2e-16 ***
## type_territoireUrbain      -0.185760   0.012117 -15.331  < 2e-16 ***
## cheveuxBlonds              -0.033435   0.031357  -1.066    0.286    
## cheveuxBruns               -0.029218   0.030977  -0.943    0.346    
## cheveuxRoux                -0.024526   0.031846  -0.770    0.441    
## langueF                     0.245066   0.009957  24.612  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 345432  on 386882  degrees of freedom
## Residual deviance: 344020  on 386874  degrees of freedom
## AIC: 344038
## 
## Number of Fisher Scoring iterations: 4

2.3.3.1 Interactions

Des interactions entre les variables explicatives peuvent aussi être ajoutées aux différents modèles.

Par exemple, nous pourrions avoir le score :

score.glm <- as.formula(CLAIM01 ~ couleur*myopie + type_territoire*myopie + cheveux*langue)

2.3.3.2 Regroupement de modalités

Pour plusieurs variables disponibles, le nombre de valeurs possibles, appelées modalités peut être très grand. Dans notre base de données pour le cours, certaines variables ont un très grand nombre de modalités possible.

table(db.fictif$voiture)

## 
##       AUDI     Autres        BMW       FORD      HONDA      MAZDA   MERCEDES     NISSAN     TOYOTA VOLKSWAGEN 
##      12418     201499      13617      34360       7799      11595      14852      18453      24461      47829

Ce n’est qu’un exemple. Dans les données réelles en assurance, il est commun de voir des centaines de modalités possibles pour une même variable de segmentation. Par exemple, si on avait utilisé non seulement la marque de la voiture, mais aussi le modèle et l’année, le nombre de valeurs différentes aurait fortement augmenté.

Il n’est pas très stratégique de supposer que chaque modalité pourrait avoir son propre paramètre \(\beta\) dans un modèle GLM. Dans un tel cas, le nombre de paramètres dans le modèle exploserait, et il serait surprenant que les paramètres soient statistiquement significatif.

Il est certain que les approches de type step-wise qu’on a vus plus tôt pourraient nous aider. D’autres approches statistiques récentes pourraient aussi être testés. Dans tous les cas, au départ, si trop de modalités sont disponibles, il est plutôt suggérer de regrouper les modalités selon leur signification.

Par exemple, le code postal de l’assuré est souvent une variable de segmentation importante. On ne regroupera pas n’importe quels codes postaux: on choisira un regroupement logique basé sur la proximité géographique. Initialement, on devrait toujours agir ainsi, pour ensuite utiliser des modèles statistiques plus avancés qui pourraient probablement permettre une meilleure granularité.

2.3.3.3 Régresseurs continus

Une autre possibilité est la présence de variables continues dans le modèle. On peut penser à l’âge de l’assuré, le nombre de kilomètres parcourus ou encore l’âge du véhicule. Si on utilise directement une variable continue comme régresseur, un modèle GLM de base supposera un lien linéaire, comme on peut le voir ici.

\[\lambda = \exp(\beta_0 + \beta_1 Age) \]

On pourrait probablement ajouter d’autres transformations de l’âge, comme \(Age^2\), \(Age^3\), \(log(Age)\) ou n’importe quelle transformation. Mais ce genre de solutions risque de mener à un surajustement. Pour de telles situations, la communauté statistique a plutôt réussi à développer des approches avec splines qui sont très efficaces.

Les modèles GLM qui utilisent des splines sont appelés Generalized Additive Models (noté GAM). Ces modèles ne seront pas couverts directement dans le séminaire.

Exercice 2.1 Ajustez divers modèles de régression logistique, de régression Poisson et de régression gamma en utilisant la base de données du cours, et la fonction glm() et tous les régresseurs disponibles.

Utilisez les algorithmes de type forward, backward ou both pour trouver les meilleurs modèles;
Utilisez d’autres critères que l’AIC pour sélectionner les meilleurs modèles;
Ajoutez des interactions entres les régresseurs obtenus aux points a) et b).