2.2 Modèles linéaires généralisés (GLM)
Les GLM, comme pour la régression linéaire, sont utilisés pour déterminer et quantifier la relation entre une variable réponse et des variables explicatives incluses dans le paramètre de moyenne de la distribution.
Cette modélisation diffère de la régression linéaire classique en deux points majeurs:
- La variable réponse est un membre de la famille exponentielle linéaire;
- On peut utiliser une transformation pour inclure les variables explicatives dans le paramètre de moyenne.
Une conséquence de l’utilisation des distributions de la famille exponentielle linéaire est la présence d’hétéroscédasticité, signifiant que la variance n’est pas nécessairement constante en fonction de la moyenne.
L’utilisation des GLM est importante en assurance non-vie où, comme expliqué précedemment, les données sont rarement normales. De plus, la relation entre la sinistralité et les caractéristiques du risque est rarement additive, mais plutôt multiplicative.
2.2.1 Caractéristiques des GLM
Supposons une variable réponse \(Y\), ainsi la fonction de densité (ou de probabilité) s’exprime comme:
\[ f(y) = c(y, \phi) \exp\left[ \frac{y \theta - a(\theta)}{\phi}\right],\]
avec:
\[ g(\mu) = \mathbf{X}^T {\beta},\]
appelé la fonction de lien, qui est une transformation de la moyenne \(\mu\). La fonction de lien \(g(\mu)\) est, quant à elle, reliée linéairement avec les variables explicatives exprimées dans le vecteur \(\mathbf{X}\).
Pour complètement définir un modèle GLM, deux éléments sont ainsi nécessaires:
Le choix de \(a(\theta)\) déterminera la distribution de la variable réponse;
Le choix de \(g(\mu)\) indiquera comment la moyenne est reliée avec les variables explicatives.
Finalement, pour travailler avec la théorie des GLM lorsque nous travaillons avec un échantillon de \(m\) observations, ces observations seront supposées indépendantes.
2.2.2 Fonction de lien et lien canonique
Si \(g(\mu) = \theta\), alors \(g\) est appelé le lien canonique correspondant à \(a(\theta)\). Dans une telle situation, \(\theta = \mathbf{X}^T {\beta}\). Comme nous le verrons plus tard, choisir le lien canonique dans un modèle GLM comporte plusieurs avantages.
Exemple 2.10 Trouvez le lien canonique \(g(\mu)\) pour une loi de Poisson.
Nous savons que:
\[ Pr[Y=y] = \frac{\lambda^y e^{-\lambda}}{y!} \]
et que:
\[\begin{eqnarray*} c(y, \phi) &=& - \ln(y!)\\ \theta &=& \ln(\lambda) \\ a(\theta) &=& \lambda = \exp(\theta)\\ \phi &=& 1 \end{eqnarray*}\]
Ainsi, puisque la moyenne \(\mu = \lambda\) pour une loi de Poisson:
\[\begin{eqnarray*} \theta &=& \ln(\lambda) = \ln(\mu) \end{eqnarray*}\]
et donc \(g(\mu) = \ln(\mu)\). On appelle ce lien, le lien logarithmique.
Exemple 2.11 Montrez les liens canoniques \(g(\mu)\) suivants:
| Distribution | \(g(\mu)\) | Fonction de lien canonique |
|---|---|---|
| Binomiale | \(\ln \frac{\mu}{1-\mu}\) | logit |
| Poisson | \(\ln \mu\) | logarithmique |
| Normale | \(\mu\) | Identité |
| Gamma | \(\mu^{-1}\) | puissance (-1) |
| Inv.-gaus. | \(\mu^{-2}\) | puissance (-2) |
En exercice à la maison.
2.2.3 Estimation par maximum de vraisemblance
Les estimateurs du maximum de vraisemblance des paramètres $ {}$ se calculent de manière similaire à ce qu’on avait vu plus tôt. La fonction de logvraisemblance s’exprime comme:
\[\begin{eqnarray*} \ell(\beta, \phi) = \sum_{i=1}^n \ln f(y_i; \beta, \phi) &=& \sum_{i=1}^n \left(\ln(c(y_i, \phi)) + \left[ \frac{y_i \theta_i - a(\theta_i)}{\phi}\right] \right) \\ &=& \frac{1}{\phi} \sum_{i=1}^n [y_i \theta_i - a(\theta_i)] + \sum_{i=1}^n \ln(c(y_i, \phi)) \end{eqnarray*}\]
avec \(\eta_i = \mathbf{X}_i^T {\beta}= g(\mu_i)\) pour des variables \(y_i, i=1,...,n\) indépendantes. En utilisant la règle de dérivation en chaîne, on peut estimer le MLE des \(\beta_j, j=1,...,p\) comme:
\[\begin{eqnarray*} \frac{\delta \ell}{\delta {\beta}} &=& \sum_{i=1}^n \frac{\delta \ln f(y_i; \beta, \phi)}{\delta \theta_i} \frac{\delta \theta_i}{\delta {\beta}} \\ &=& \sum_{i=1}^n \frac{1}{\phi} [y_i - a'(\theta_i)] \frac{\delta \theta_i}{\delta {\beta}}. \end{eqnarray*}\]
Puisque nous savons que \(E[Y_i] = \mu_i = a'(\theta_i)\), et que \(Var[Y_i] = \phi a''(\theta_i)\), nous obtenons:
\[\begin{eqnarray*} \frac{\delta \mu_i}{\delta {\beta}} &=& a''(\theta_i) \frac{\delta \theta_i}{\delta {\beta}} = \frac{1}{\phi} Var[Y_i] \frac{\delta \theta_i}{\delta {\beta}}\\ &&\Rightarrow \frac{\delta \theta_i}{\delta {\beta}} = \frac{\delta \mu_i}{\delta {\beta}} \frac{\phi}{Var[Y_i] } \end{eqnarray*}\]
Ainsi:
\[\begin{eqnarray*} \frac{\delta \ell}{\delta {\beta}} &=& \sum_{i=1}^n \frac{(y_i - a'(\theta_i))}{Var[Y_i]} \frac{\delta \mu_i}{\delta {\beta}}. \end{eqnarray*}\]
Le dernière dérivée peut se développer encore une fois selon le principe des dérivations en chaîne:
\[\begin{eqnarray*} \frac{\delta \mu_i}{\delta {\beta}} = \frac{\delta \mu_i}{\delta \eta_i} \frac{\delta \eta_i}{\delta {\beta}} \end{eqnarray*}\]
où:
\[\begin{eqnarray*} \frac{\delta \eta_i}{\delta {\beta}} &=& \mathbf{X}_i\\ \frac{\delta \mu_i}{\delta \eta_i} = \left(\frac{\delta \eta_i}{\delta \mu_i}\right)^{-1} &=& \left( g'(\mu_i) \right)^{-1}. \end{eqnarray*}\]
Ainsi, la condition de premier ordre s’exprime comme:
\[\begin{eqnarray*} \frac{\delta \ell}{\delta \beta_j} &=& \sum_{i=1}^n \frac{(y_i - \mu_i)}{g'(\mu_i) Var[Y_i]} X_{ij} = 0\\ \end{eqnarray*}\]
et puisque \(Var[Y_i] = \phi a''(\theta_i)\), on peut réécrire la formule précédente par:
\[\begin{eqnarray*} \frac{\delta \ell}{\delta \beta_j} &=& \sum_{i=1}^n \frac{(y_i - \mu_i)}{g'(\mu_i) a''(\theta_i)} X_{ij} = 0\\ \end{eqnarray*}\]
et ainsi montrer que les équations de vraisemblance relatives à \(\beta\) peuvent être résolues sans se préoccuper du paramètre \(\phi\).
Dans le cas où le modèle utilise le lien canonique pour \(g(\mu)\), il est possible de simplifier l’équation de premier ordre. En effet, dans ce cas, on sait que \(\theta_i = g(\mu_i)\), ainsi:
\[\begin{eqnarray*} a''(\theta_i) = \frac{\delta a'(\theta_i)}{\delta \theta_i} &=& \frac{\delta a'(\theta_i)}{\delta g(\mu_i)} \\ &=& \frac{\delta a'(\theta_i)}{\delta \mu_i} \frac{\delta \mu_i}{\delta g(\mu_i)}\\ &=& \frac{\delta a'(\theta_i)}{\delta a'(\theta_i)} \frac{\delta \mu_i}{\delta g(\mu_i)}\\ &=& \frac{\delta (\mu_i)}{\delta g(\mu_i)} = 1/g'(\mu_i). \end{eqnarray*}\]
En conséquence, nous avons:
\[\begin{eqnarray*} \frac{\delta \ell}{\delta \beta_j} &=& \sum_{i=1}^n (y_i - \mu_i) X_{ij} = 0. \end{eqnarray*}\]
On peut remarquer que cette relation traduit l’orthogonalité entre les variables explicatives et les résidus (ce qui est similaire à ce qu’on obtient lors d’une régression linéaire classique).
Exemple 2.12 On suppose que \(Y_i \sim Poisson(\lambda_i)\), avec \(\lambda_i = \exp( \mathbf{X}_i^T {\beta})\). Trouvez la condition de premier ordre pour l’estimation par maximum de vraisemblance de $ {}$.
Nous savons que le lien canonique pour une loi de Poisson est le lien logarithmique. Ainsi, \(\mathbf{X}_i^T {\beta} = \log(\mu_i) = \log(\lambda_i)\), et donc \(\lambda_i = \exp( \mathbf{X}_i^T {\beta})\).
Ainsi, la condition de premier ordre est simplement:
\[\begin{eqnarray*} \frac{\delta \ell}{\delta \beta_j} &=& \sum_{i=1}^n (y_i - \mu_i) X_{ij} \\ &=& \sum_{i=1}^n (y_i - \lambda_i) X_{ij} = 0 \end{eqnarray*}\]
ou encore, en notation vectorielle:
\[\begin{eqnarray*} \frac{\delta \ell}{\delta \beta} &=& \sum_{i=1}^n (y_i - \lambda_i) \mathbf{X}_i = 0 \end{eqnarray*}\]
On peut aussi utiliser l’autre forme, plus générale, de la condition de premier ordre:
\[\begin{eqnarray*} \frac{\delta \ell}{\delta \beta_j} &=& \sum_{i=1}^n \frac{(y_i - \mu_i)}{g'(\mu_i) Var[Y_i]} X_{ij} \\ &=& \sum_{i=1}^n \frac{(y_i - \lambda_i)}{\frac{1}{\lambda_i} \lambda_i} X_{ij} \\ &=& \sum_{i=1}^n (y_i - \lambda_i) \mathbf{X}_i = 0 \end{eqnarray*}\]
Exemple 2.13 On suppose encore que \(Y_i \sim Poisson(\lambda_i)\), avec \(\lambda_i = \exp( \mathbf{X}_i^T {\beta})\). Trouvez la condition de premier ordre en utilisant directement la fonction de vraisemblance de la Poisson.
\[\begin{eqnarray*} L(\beta) &=& \prod_{i=1}^n \frac{\lambda_i^{y_i} e^{-\lambda_i}}{y_i !} \\ \ell(\beta) &=& \sum_{i=1}^n \left[ y_i \ln(\lambda_i) - \lambda_i - \ln(y_i!) \right]\\ \ell(\beta) &=& \sum_{i=1}^n \left[ y_i \ln(\exp( \mathbf{X}_i^T {\beta})) - \exp( \mathbf{X}_i^T {\beta}) - \ln(y_i!) \right] \end{eqnarray*}\]
Pour trouver les estimateurs, on dérive par rapport à \(\beta\) et on pose la dérivée égale à zéro pour obtenir le maximum:
\[\begin{eqnarray*} \frac{\delta \ell(\lambda_i)}{ \delta \beta_0} &=& \sum_{i=1}^n (y_i - \lambda_i) \mathbf{X}_{i} = 0 \end{eqnarray*}\]
Nous reverrons plus en détails la loi de Poisson et plusieurs généralisations dans un prochain chapitre.
Exemple 2.14 On suppose encore que \(Y_i \sim Gamma(\mu_i, \nu)\). Trouvez la condition de premier ordre en supposant:
- \(\mu_i = ( \mathbf{X}_i^T {\beta})^{-1}\);
- \(\mu_i = \exp( \mathbf{X}_i^T {\beta})\).
Regardons chacune des situations séparemment:
- \(\mu_i = ( \mathbf{X}_i^T {\beta})^{-1}\) est la fonction de lien canonique. Ainsi, on peut directement utiliser la fonction de premier ordre de résolution des paramètres:
\[\begin{eqnarray*} \frac{\delta \ell}{\delta \beta} &=& \sum_{i=1}^n (y_i - \mu_i) \mathbf{X}_i = 0 \end{eqnarray*}\]
On peut aussi utiliser l’autre forme, plus générale, de la condition de premier ordre:
\[\begin{eqnarray*} \frac{\delta \ell}{\delta \beta_j} &=& \sum_{i=1}^n \frac{(y_i - \mu_i)}{g'(\mu_i) Var[Y_i]} X_{ij} \\ &=& \sum_{i=1}^n \frac{(y_i - \mu_i)}{\frac{-1}{\mu_i^2} \mu_i^2/\nu} X_{ij} \\ &=& \sum_{i=1}^n (y_i - \lambda_i) \mathbf{X}_i = 0 \end{eqnarray*}\]
Finalement, en utilisant directement la fonction de vraisemblance de la gamma, nous avons:
\[\begin{eqnarray*} L(\beta) &=& \prod_{i=1}^n \frac{1}{\Gamma(\nu)} \left(\frac{\nu y_i}{\mu_i} \right)^{\nu} \exp(-\frac{y_i \nu}{\mu_i} ) \frac{1}{y_i}\\ \ell(\beta) &=& \sum_{i=1}^n -\log(\Gamma(\nu)) + \nu \log(\nu y_i) - \nu \log(\mu_i) - \frac{y_i \nu}{\mu_i} - \log(y_i)\\ && \\ \frac{\delta \ell(\beta)}{\delta \beta} &=& \sum_{i=1}^n \frac{\nu}{\mu_i} (\mu_i)^2 \mathbf{X}_i - \frac{y_i \nu}{\mu_i^2} {\mu_i^2} \mathbf{X}_i \\ &=& \sum_{i=1}^n (y_i - \mu_i) \mathbf{X}_i = 0 \end{eqnarray*}\]
- \(\mu_i = \exp( \mathbf{X}_i^T {\beta})\) n’est pas la fonction de lien canonique:
On peut toutefois utiliser la forme plus générale de la condition de premier ordre:
\[\begin{eqnarray*} \frac{\delta \ell}{\delta \beta_j} &=& \sum_{i=1}^n \frac{(y_i - \mu_i)}{g'(\mu_i) Var[Y_i]} X_{ij} \\ &=& \sum_{i=1}^n \frac{(y_i - \mu_i)}{\frac{1}{\mu_i} \mu_i^2/\nu} X_{ij} \\ &=& \sum_{i=1}^n (1 - \frac{y_i}{\mu_i}) \mathbf{X}_i = 0 \end{eqnarray*}\]
En utilisant directement la fonction de vraisemblance de la gamma, nous avons:
\[\begin{eqnarray*} L(\beta) &=& \prod_{i=1}^n \frac{1}{\Gamma(\nu)} \left(\frac{\nu y_i}{\mu_i} \right)^{\nu} \exp(-\frac{y_i \nu}{\mu_i} ) \frac{1}{y_i}\\ \ell(\beta) &=& \sum_{i=1}^n -\log(\Gamma(\nu)) + \nu \log(\nu y_i) - \nu \log(\mu_i) - \frac{y_i \nu}{\mu_i} - \log(y_i)\\ && \\ \frac{\delta \ell(\beta)}{\delta \beta} &=& \sum_{i=1}^n \frac{\nu}{\mu_i} (\mu_i) \mathbf{X}_i - \frac{y_i \nu}{\mu_i^2} {\mu_i} \mathbf{X}_i \\ &=& \sum_{i=1}^n (1 - \frac{y_i}{\mu_i}) \mathbf{X}_i = 0 \end{eqnarray*}\]
2.2.4 Algorithme d’estimation
Nous avons vu que les estimateurs du maximum de vraisemblance \(\hat{\beta}_j\) des paramètres \(\beta_j\) sont les solutions à l’équation:
\[\begin{eqnarray*} \frac{\delta \ell}{\delta \beta_j} &=& \sum_{i=1}^n \frac{(y_i - \mu_i)}{g'(\mu_i) Var[Y_i]} X_{ij} = 0. \end{eqnarray*}\]
De façon générale, cette équation ne possède pas de solutions explicites et doit donc être résolue numériquement. Plusieurs techniques peuvent être utilisées pour résoudre le système d’équations à \(p\) inconnues.
2.2.4.1 Newton-Raphson
À l’origine, la méthode de Newton-Raphson a été développée pour estimer la racine d’une fonction (continue et dérivable) à une seule dimension.
En choisissant une valeur de départ initiale arbitraire (\(x_0\)), l’algorithme trouve la fonction \(f(x_0)\).
L’idée de l’algorithme est de calculer la tangente de la fonction estimée à ce point (pouvant être estimée par la première dérivée de \(f(.)\)), afin de longer la tangente et de trouver la racine de la droite engendrée par cette tangente, générant ainsi une solution à l’algorithme (\(x_1\)).
Si la fonction générée à ce nouveau point (\(f(x_1)\)) n’est pas assez proche de 0, la procédure recommence avec ce nouveau point de départ.
L’algorithme est illustré dans la figure suivante:
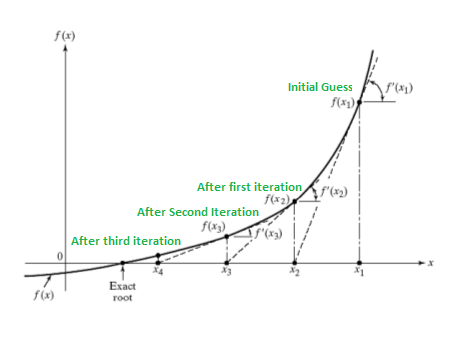
Une version multivariée de cet algorithme pour estimer les paramètres de la fonction. Une autre manière de voir cet algorithme d’estimation est l’approximation linéaire/quadratique de la condition de premier ordre par une série de Taylor.
Avec les GLM, nous devons trouver les racines de la première dérivée de \(\ell\) par rapport à \(\beta\), ce qui correspond à la fonction \(f(.)\) de l’illustration de l’algorithme de Newton-Raphson. Ainsi, nous devons trouver la première dérivée de \(f(.)\) ou, finalement, la seconde dérivée de \(\ell\).
Notons
- \(U(\beta)\) le vecteur gradient de la logvraisemblance, dont la composante \(j\) (pour le \(j^e\) paramètre) est:
\[U(\beta) = \frac{\delta \ell( {\beta})}{\delta \beta_j}, \]
- \(H(\beta)\) la matrice hessienne de \(\ell( {\beta})\), celle dont l’élément \((j,k)\) (la seconde dérivée par rapport aux \(j^e\) et \(k^e\) paramètres) est:
\[H(\beta) = \frac{\delta^2 \ell( {\beta})}{\delta \beta_j \delta \beta_k}.\]
Partant d’une valeur initiale de \(\hat{\beta}^{(0)}\) que l’on espère proche de l’esimtateur du maximum de vraisemblance \(\hat{\beta}\), on définit la \((r+1)\)-ème valeur aprochée de \(\hat{\beta}^{(r+1)}\) de \(\hat{\beta}\) à partir de la \(r\)-ème \(\hat{\beta}^{(r)}\) par:
\[\hat{\beta}^{(r+1)} = \hat{\beta}^{(r)} - H^{-1}(\hat{\beta}^{(r)}) U(\hat{\beta}^{(r)}) .\]
On arrête l’algorithme lorsque :
\[\begin{eqnarray*} \frac{\ell(\hat{\beta}^{(r+1)}) - \ell(\hat{\beta}^{(r)})}{\ell({\hat{\beta}}^{(r)})} \le \epsilon \end{eqnarray*}\]
pour un petit \(\epsilon\).
Exemple 2.15 On suppose que \(Y_i \sim Poisson(\lambda_i)\), avec \(\lambda_i = \exp( \mathbf{X}_i^T {\beta})\). Trouvez \(U(\beta)\) et \(H(\beta)\).
Nous savons que:
\[ \ell( {\beta}) = \sum_{i=1}^n -y_i \log(\lambda_i) - \lambda_i - \log(y_i!)\]
et que:
\[\begin{eqnarray*} U( {\beta}) = \sum_{i=1}^n \mathbf{X}_{i} \left(y_i - \lambda_i \right) \text{, une vecteur } p \times 1\\ \end{eqnarray*}\]
La matrice hessienne se calcule comme:
\[\begin{eqnarray*} H( {\beta}) &=& \frac{\delta^2} {\delta \beta^2} \ell( {\beta}) \\ &=& \frac{\delta} {\delta \beta} \sum_{i=1}^n \mathbf{X}_{i} \left(y_i - \lambda_i \right)\\ &=& - \sum_{i=1}^n \mathbf{X}_i \mathbf{X}_i^T \lambda_i \text{, une matrice } p \times p \end{eqnarray*}\]
Il faut faire attention aux calculs de la matrice hessienne, qui est la seconde dérivée du logvraisemblance et pas seulement la dérivée de l’équation de premier ordre.
2.2.4.2 Exemple numérique: Estimation
Exemple 2.16 On suppose que \(Y_i \sim Poisson(\lambda_i)\), avec \(\lambda_i = \exp( \mathbf{X}_i^T {\beta})\). Trouvez les estimateurs \(\hat{\beta_0}, \hat{\beta_1}, ..., \hat{\beta_p}\) si nous avons les données suivantes:
| Observations (\(i\)) | Territoire | Etat civil | Nb. de sin. (\(y\)) |
|---|---|---|---|
| 1 | Urbain | Celibataire | 1 |
| 2 | Urbain | Divorcé | 0 |
| 3 | Urbain | Marié | 2 |
| 4 | Rural | Marié | 3 |
| 5 | Rural | Divorcé | 1 |
| 6 | Urbain | Marié | 0 |
| 7 | Rural | Celibataire | 1 |
| 8 | Urbain | Celibataire | 2 |
La première étape est de codifier les caractéristiques.
Bien qu’il existe d’autres possibilités, nous codifierons en variables binaires.
\[\begin{align*} X_1 &= \begin{cases} 1 & \text{si le territoire est urbain} \\ 0 & \text{si le territoire est rural} \end{cases},\\ X_2 &= \begin{cases} 1 & \text{si l'assuré est marié} \\ 0 & \text{sinon} \end{cases}, \\ X_3 &= \begin{cases} 1 & \text{si l'assuré est célibataire} \\ 0 & \text{sinon} \end{cases} \end{align*}\]
Remarques:
Le territoire a 2 modalités: urbain et rural. Ainsi, on introduit 2-1=1 variable binaire \(X\) pour codifier l’information.
L’état civil a 3 modalités: marié, célibataire et divorcé. Dans ce cas, on introduit 3-1=2 variables binaires \(X\) pour codifier toutes les possibilités.
- si l’assuré est marié: \(\{X_2 = 1, X_3 = 0 \}\);
- si l’assuré est célibataire: \(\{X_2 = 0, X_3 = 1 \}\);
- si l’assuré est divorcé: \(\{X_2 = 0, X_3 = 0 \}\).
Ainsi, en incluant une valeur de \(X_0 = 1\), qui sera utilisée pour l’intercept \(\beta_0\), notre tableau de données correspond à:
| \(i\) | \(X_0\) | \(X_1\) | \(X_2\) | \(X_3\) | \(y\) |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 | 1 |
| 2 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 1 | 1 | 2 |
| 4 | 1 | 0 | 1 | 1 | 3 |
| 5 | 1 | 1 | 0 | 0 | 1 |
| 6 | 1 | 1 | 1 | 1 | 0 |
| 7 | 1 | 0 | 0 | 1 | 1 |
| 8 | 1 | 1 | 0 | 1 | 2 |
Notre modèle est ainsi, pour l’assuré \(i\):
\[Y_i \sim Poisson(\lambda_i = \exp(\beta_0 X_{0,i} + \beta_1 X_{1,i} + \beta_2 X_{2,i} + \beta_3 X_{3,i})).\]
Nous devons ensuite trouver les paramètres \(\{\beta_0, \beta_1, \beta_2, \beta_3\}\) afin que:
\[\begin{eqnarray*} \mathbf{U}( \mathbf{\hat{\beta}}) = \sum_{i=1}^n \mathbf{X}_{i} \left(y_i - \lambda_i \right) = 0\\ \end{eqnarray*}\]
avec \(\mathbf{X}_{i} = \{X_{0,i}, X_{1,i} , X_{2,i} , X_{3,i} \}\).
Utilisons l’algorithme de Newton-Raphson pour trouver les MLE des \(\beta\):
\[\mathbf{\hat{\beta}}^{(r+1)} = \mathbf{\hat{\beta}}^{(r)} - \mathbf{H}^{-1}( \mathbf{\hat{\beta}}^{(r)}) \mathbf{U}( \mathbf{\hat{\beta}}^{(r)}) .\]
Pour débuter l’algorithme, nous devons commencer avec des valeurs initiales de \(\beta\), i.e. \(\{\beta_0^{(0)}, \beta_1^{(0)}, \beta_2^{(0)}, \beta_3^{(0)} \}\).
Ce choix initial est arbitraire. Mais il est plus simple de débuter avec un effet nul pour \(\{X_{1,i} , X_{2,i} , X_{3,i} \}\), et choisir une valeur de \(\beta_0^{(0)}\) qui fait en sorte que \(\lambda_i^{(0)}= \overline{Y}, \forall i \in \{1, \ldots, 8\}\).
Puisque nous avons une fonction de lien logarithmique, nous avons ainsi:
\[\begin{eqnarray*} (\mathbf{\hat{\beta}}^{(0)})^T &=& \{\log\left( \overline{Y} \right), 0, 0, 0 \}. \end{eqnarray*}\]
Ainsi, tous les \(\lambda_i^{(0)} = \exp( \mathbf{X_i}' \mathbf{\beta}) = \overline{Y} = 1.25\), pour \(i=1,...,8\).
On peut donc estimer la valeur de \(U\) pour la première itération:
\[\begin{align*} U(\hat{\beta}^{(0)}) =& \sum_{i=1}^8 \mathbf{X}_i (n_i - \hat{\lambda}_i^{(0)}) \text{, un vecteur } 4 \times 1 \\ =& \begin{bmatrix} 1 \\ 1 \\ 0 \\ 1 \end{bmatrix} \times \left( \begin{array}{c} 1 - 1.25 \end{array} \right) + \begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix} \times \left( \begin{array}{c} 0 - 1.25 \end{array} \right) + \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} \times \left( \begin{array}{c} 2 - 1.25 \end{array} \right) + \begin{bmatrix} 1 \\ 0 \\ 1 \\ 1 \end{bmatrix} \times \left( \begin{array}{c} 3 - 1.25 \end{array} \right) + \\ & \begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix} \times \left( \begin{array}{c} 1 - 1.25 \end{array} \right) + \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} \times \left( \begin{array}{c} 0 - 1.25 \end{array} \right) + \begin{bmatrix} 1 \\ 0 \\ 0 \\ 1 \end{bmatrix} \times \left( \begin{array}{c} 1 - 1.25 \end{array} \right) + \begin{bmatrix} 1 \\ 1 \\ 0 \\ 1 \end{bmatrix} \times \left( \begin{array}{c} 2 - 1.25 \end{array} \right) \\ =& \begin{bmatrix} 0 \\ -1.50 \\ 1.25 \\ 1.50 \end{bmatrix} \end{align*}\]
alors que:
\[\begin{align*} H(\hat{\beta}^{(0)}) =& - \sum_{i=1}^8 \mathbf{X}_i \mathbf{X}_i^T \hat{\lambda}_i^{(0)} \text{, une matrice } 4 \times 4 \\ =& -\begin{bmatrix} 1 \\ 1 \\ 0 \\ 1 \end{bmatrix} \times \begin{bmatrix} 1 & 1 & 0 & 1 \end{bmatrix} \times 1.25 -\begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix} \times \begin{bmatrix} 1 & 1 & 0 & 0 \end{bmatrix} \times 1.25\\ & -\begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} \times \begin{bmatrix} 1 & 1 & 1 & 1 \end{bmatrix} \times 1.25 -\begin{bmatrix} 1 \\ 0 \\ 1 \\ 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 1 & 1 \end{bmatrix} \times 1.25\\ & -\begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix} \times \begin{bmatrix} 1 & 1 & 0 & 0 \end{bmatrix} \times 1.25 -\begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} \times \begin{bmatrix} 1 & 1 & 1 & 1 \end{bmatrix} \times 1.25\\ & -\begin{bmatrix} 1 \\ 0 \\ 0 \\ 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 & 1 \end{bmatrix} \times 1.25 -\begin{bmatrix} 1 \\ 1 \\ 0 \\ 1 \end{bmatrix} \times \begin{bmatrix} 1 & 1 & 0 & 1 \end{bmatrix} \times 1.25 \\ =& \begin{bmatrix} -10.00 & -7.5 & -3.75 & -7.50 \\ -7.50 & -7.5 & -2.50 & -5.00 \\ -3.75 & -2.5 & -3.75 & -3.75 \\ -7.50 & -5.0 & -3.75 &-7.50 \end{bmatrix} \end{align*}\]
Ainsi:
\[\begin{align*} \hat{\beta}^{(1)} =& \hat{\beta}^{(0)} - H^{-1}(\hat{\beta}^{(0)}) U(\hat{\beta}^{(0)}) \\ =& \begin{bmatrix} log(1.25) \\ 0 \\ 0 \\ 0 \end{bmatrix} - \begin{bmatrix} -10.00 & -7.5 & -3.75 & -7.50 \\ -7.50 & -7.5 & -2.50 & -5.00 \\ -3.75 & -2.5 & -3.75 & -3.75 \\ -7.50 & -5.0 & -3.75 &-7.50 \end{bmatrix}^{-1} \begin{bmatrix} 0 \\ -1.50 \\ 1.25 \\ 1.50 \end{bmatrix} \\ =& \begin{bmatrix} 0.2231 \\ 0 \\ 0 \\ 0 \end{bmatrix} - \begin{bmatrix} 0 \\ 0.6000 \\ -0.2667 \\ -0.4667 \end{bmatrix} = \begin{bmatrix} 0.2231 \\ -0.6000 \\ 0.2667 \\ 0.4667 \end{bmatrix} \end{align*}\]
On peut ainsi recommencer l’algorithme avec ces nouvelles valeurs de \(\hat{\beta}^{(1)}\). Attention, car pour cette nouvelle itération, la valeur des \(\lambda^{(1)}\) ne sera pas la même pour tous les assurés car \(\lambda_i^{(1)} = \exp(\mathbf{X}_i^T \beta^{(1)})\).
| \(i\) | \(X_0\) | \(X_1\) | \(X_2\) | \(X_3\) | \(y\) | \(\lambda^{(1)}\) |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 | 1 | 1.093 |
| 2 | 1 | 1 | 0 | 0 | 0 | 0.686 |
| 3 | 1 | 1 | 1 | 1 | 2 | 1.428 |
| 4 | 1 | 0 | 1 | 1 | 3 | 2.602 |
| 5 | 1 | 1 | 0 | 0 | 1 | 0.686 |
| 6 | 1 | 1 | 1 | 1 | 0 | 1.428 |
| 7 | 1 | 0 | 0 | 1 | 1 | 1.993 |
| 8 | 1 | 1 | 0 | 1 | 2 | 1.094 |
On aurait ainsi:
On peut donc estimer la valeur de \(U\) pour la première itération:
\[\begin{align*} U(\hat{\beta}^{(0)}) =& \sum_{i=1}^8 \mathbf{X}_i (n_i - \hat{\lambda}_i^{(0)}) \text{, un vecteur } 4 \times 1 \\ =& \begin{bmatrix} 1 \\ 1 \\ 0 \\ 1 \end{bmatrix} \times \left( \begin{array}{c} 1 - 1.093 \end{array} \right) + \begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix} \times \left( \begin{array}{c} 0 - 0.686 \end{array} \right) + \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} \times \left( \begin{array}{c} 2 - 1.428 \end{array} \right) + \begin{bmatrix} 1 \\ 0 \\ 1 \\ 1 \end{bmatrix} \times \left( \begin{array}{c} 3 - 2.602 \end{array} \right) + \\ & \begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix} \times \left( \begin{array}{c} 1 - 0.686 \end{array} \right) + \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} \times \left( \begin{array}{c} 0 - 1.428 \end{array} \right) + \begin{bmatrix} 1 \\ 0 \\ 0 \\ 1 \end{bmatrix} \times \left( \begin{array}{c} 1 - 1.993 \end{array} \right) + \begin{bmatrix} 1 \\ 1 \\ 0 \\ 1 \end{bmatrix} \times \left( \begin{array}{c} 2 - 1.094 \end{array} \right) \\ =& ... \end{align*}\]
alors que:
\[\begin{align*} H(\hat{\beta}^{(0)}) =& - \sum_{i=1}^8 \mathbf{X}_i \mathbf{X}_i^T \hat{\lambda}_i^{(0)} \text{, une matrice } 4 \times 4 \\ =& -\begin{bmatrix} 1 \\ 1 \\ 0 \\ 1 \end{bmatrix} \times \begin{bmatrix} 1 & 1 & 0 & 1 \end{bmatrix} \times 1.093 -\begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix} \times \begin{bmatrix} 1 & 1 & 0 & 0 \end{bmatrix} \times 0.686\\ & -\begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} \times \begin{bmatrix} 1 & 1 & 1 & 1 \end{bmatrix} \times 1.428 -\begin{bmatrix} 1 \\ 0 \\ 1 \\ 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 1 & 1 \end{bmatrix} \times 2.602\\ & -\begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix} \times \begin{bmatrix} 1 & 1 & 0 & 0 \end{bmatrix} \times 0.686 -\begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} \times \begin{bmatrix} 1 & 1 & 1 & 1 \end{bmatrix} \times 1.428\\ & -\begin{bmatrix} 1 \\ 0 \\ 0 \\ 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 & 1 \end{bmatrix} \times 1.993 -\begin{bmatrix} 1 \\ 1 \\ 0 \\ 1 \end{bmatrix} \times \begin{bmatrix} 1 & 1 & 0 & 1 \end{bmatrix} \times 1.094 \\ =& ... \end{align*}\]
Ainsi, après convergence, on aurait
\[\begin{align*} \hat{\beta} = \begin{bmatrix} -0.2231 \\ -0.4700 \\ 0.2231 \\ 0.7985 \end{bmatrix} \end{align*}\]
Et donc, on obtiendrait les primes suivantes pour les 6 profils possibles:
| \(profil\) | \(X_0\) | \(X_1\) | \(X_2\) | \(X_3\) | \(\hat{\lambda}\) |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | 0.625 |
| 2 | 1 | 1 | 0 | 1 | 1.111 |
| 3 | 1 | 1 | 0 | 0 | 0.500 |
| 4 | 0 | 1 | 1 | 0 | 1.000 |
| 5 | 0 | 1 | 0 | 1 | 1.778 |
| 6 | 0 | 1 | 0 | 0 | 0.800 |
Il est assez simple de refaire ce dernier exemple en utilisant R.
### entrées les données
x <- matrix(c(1,1,1,1,1,1,1,1,
1,1,1,0,1,1,0,1,
0,0,1,1,0,1,0,0,
1,0,1,1,0,1,1,1),
8, 4)
y <- matrix(c(1,0,2,3,1,0,1,2), 8, 1)
####
ybar <- mean(y)
beta <- matrix(c(log(ybar), 0, 0, 0), 4, 1)
### 10 itérations
for(iter in 0:9){
print(c(iter, beta))
U <-0
for(i in 1:8){
lambda <- as.numeric(exp(x[i,] %*% beta))
U <- U + t(x[i,])*(y[i] - lambda)
}
U
H <-0
for(i in 1:8){
lambda <- as.numeric(exp(x[i,] %*% beta))
H <- H - lambda*(x[i,] %*% t(x[i,]))
}
H
beta <- beta - solve(H) %*% t(U)
}## [1] 0.0000000 0.2231436 0.0000000 0.0000000 0.0000000
## [1] 1.0000000 0.2231436 -0.6000000 0.2666667 0.4666667
## [1] 2.0000000 -0.1688347 -0.4791742 0.2259235 0.7520675
## [1] 3.0000000 -0.2220958 -0.4700478 0.2231551 0.7974987
## [1] 4.0000000 -0.2231430 -0.4700036 0.2231436 0.7985072
## [1] 5.0000000 -0.2231436 -0.4700036 0.2231436 0.7985077
## [1] 6.0000000 -0.2231436 -0.4700036 0.2231436 0.7985077
## [1] 7.0000000 -0.2231436 -0.4700036 0.2231436 0.7985077
## [1] 8.0000000 -0.2231436 -0.4700036 0.2231436 0.7985077
## [1] 9.0000000 -0.2231436 -0.4700036 0.2231436 0.79850772.2.5 Fisher scoring
Au lieu d’utiliser \(\mathbf{H}(\mathbf{\beta})\) dans l’algorithme de Newton-Raphson, il a été suggéré par Ronald Fisher d’utiliser la matrice d’information de Fisher \(\mathbf{I(\beta)}\). En effet, on peut montrer que:
\[\mathbf{H}(\mathbf{\beta}) \approx E[\mathbf{H}(\mathbf{\beta})] = - \mathbf{I(\beta)},\]
Ainsi, nous avons:
\[\mathbf{\hat{\beta}}^{(r+1)} = \mathbf{\hat{\beta}}^{(r)} + \mathbf{I}^{-1}(\mathbf{\hat{\beta}}^{(r)}) \mathbf{U}(\mathbf{\hat{\beta}}^{(r)}) .\]
La substitution de la matrice hessienne par l’information de Fisher dans l’algorithme d’estimation s’appelle le Fisher scoring, ou l’algorithme de score.
Dans le but d’éviter le calcul d’une deuxième dérivée du logvraisemblance, et sachant qu’il peut être montré que:
\[E\left[\frac{\delta^2 \ell(\mathbf{\beta})}{\delta \mathbf{\beta}^2}\right] = - E\left[\left(\frac{\delta \ell(\mathbf{\beta})}{\delta \mathbf{\beta}}\right) \left(\frac{\delta \ell(\mathbf{\beta})}{\delta \mathbf{\beta}}\right)^T \right],\]
il est aussi possible d’utiliser l’espérance du produit croisé de la première dérivée, au lieu de l’espérance de la seconde dérivée dans l’algorithme de score, dans l’algorithme d’estimation.
Exemple 2.17 On suppose que \(Y_i \sim Poisson(\lambda_i)\), avec \(\lambda_i = \exp(\mathbf{X_i}' \mathbf{\beta})\).
Montrez que:
\[E\left[\frac{\delta^2 \ell(\mathbf{\beta})}{\delta \mathbf{\beta}^2}\right] = - E\left[\left(\frac{\delta \ell(\mathbf{\beta})}{\delta \mathbf{\beta}}\right) \left(\frac{\delta \ell(\mathbf{\beta})}{\delta \mathbf{\beta}}\right)^T \right],\]
\[\begin{eqnarray*} E\left[\left(\frac{\delta \ell(\mathbf{\beta})}{\delta \mathbf{\beta}}\right) \left(\frac{\delta \ell(\mathbf{\beta})}{\delta \mathbf{\beta}}\right)^T \right] &=& E\left[\sum_{i=1}^n \left(\mathbf{X}_{i} \left(y_i - \lambda_i \right) \right) \left(\mathbf{X}_{i} \left(y_i - \lambda_i \right)\right)^T \right]\\ &=& \sum_{i=1}^n \mathbf{X}_{i} \mathbf{X}_{i}^T E\left[\left(y_i - \lambda_i \right)^2 \right]\\ &=& \sum_{i=1}^n \mathbf{X}_{i} \mathbf{X}_{i}^T Var[Y_i] \\ &=& \sum_{i=1}^n \mathbf{X}_{i} \mathbf{X}_{i}^T \lambda_i \end{eqnarray*}\]
2.2.6 Variance des estimateurs
Un autre résultat majeur des statistiques mathématiques est qu’il peut être prouvé que la deuxième dérivée du logvraisemblance peut être utilisée pour estimer la variance des MLE. Nous y reviendrons.
Ainsi, nous pouvons donc utiliser l’information de Fisher, ou l’espérance du produit croisé de la première dérivée pour estimer la matrice variance-covariance des MLE. Plus précisément, nous avons:
\[\begin{eqnarray*} \sigma^2(\hat{\beta}) &=& - E\left[\frac{\delta^2 \ell(\mathbf{\beta})}{\delta \mathbf{\beta}^2}\right]^{-1} \end{eqnarray*}\]
ou encore:
\[\begin{eqnarray*} \sigma^2(\hat{\beta}) &=& E\left[\left(\frac{\delta \ell(\mathbf{\beta})}{\delta \mathbf{\beta}}\right) \left(\frac{\delta \ell(\mathbf{\beta})}{\delta \mathbf{\beta}}\right)^T \right]^{-1} \end{eqnarray*}\]
2.2.6.1 Exemple numérique: Variance
Exemple 2.18 En reprenant le modèle et les données indiquées dans l’exemple numérique précédent, obtenez la matrice variance-covariance des estimateurs \(\hat{\beta}\).
Nous avions montré que les MLE de \(\beta\) étaient:
\[\begin{align*} \hat{\beta} = \begin{bmatrix} -0.2231 \\ -0.4700 \\ 0.2231 \\ 0.7985 \end{bmatrix} \end{align*}\]
Comme lors de l’exemple précédent, on peut donc estimer la matrice hessienne:
\[\begin{align*} H(\hat{\beta}) =& \begin{bmatrix} -10.00 & -6.00 & -5.00 & -9.00\\ -6.00 & -6.00 & -2.78 & -5.00\\ -5.00 & -2.78 & -5.00 & -5.00\\ -9.00 & -5.00 & -5.00 & -9.00\\ \end{bmatrix} \end{align*}\]
Ainsi la matrice variance-covariance peut s’exprimer comme:
\[\begin{eqnarray*} \sigma^2(\hat{\beta}) &=& - H(\hat{\beta})^{-1} = \begin{bmatrix} 1.450& -0.450& 0.000& -1.200\\ -0.450& 0.450& 0.000& 0.200 \\ 0.000& 0.000& 0.450& -0.250 \\ -1.200& 0.200& -0.250& 1.339 \\ \end{bmatrix} \end{eqnarray*}\]
Exemple 2.19 En reprenant les résultats de l’exemple précédent, trouvez:
- La variance de \(\hat{\beta}_0\);
- La variance de \(\hat{\beta}_2\);
- La covariance entre \(\hat{\beta}_1\) et \(\hat{\beta}_2\).
Il suffit de voir que la matrice variance-covariance représente:
et donc:
- \(Var[\hat{\beta}_0] = 1.450\);
- \(Var[\hat{\beta}_2] = 0.4500\);
- \(Cov[\hat{\beta}_1, \hat{\beta}_2] = 0.000\).
2.2.7 Déviance
Définition 2.2 Le modèle saturé correspond au modèle contenant autant de paramètres que d’observations et fournissant ainsi une description parfaite des données. Le modèle saturé est caractérisé par \(\hat{\mu}_i = y_i\), pour \(i=1,\ldots,n\).
La fonction de vraisemblance du modèle saturé est notée \(L(y|y)\) et la fonction de logvraisemblance \(\ell(y|y)\). En pratique, ce modèle n’est pas intéressant car il se limite à reproduire exactement les observations passées, sans les résumer.
Définition 2.3 La déviance d’un modèle ajusté par \(\hat{\beta}\), notée \(D\), est définie comme une mesure de distance entre l’ajustement de ce modèle et le modèle saturé. Ainsi:
\[ D = 2\left(\ell(y|y) - \ell(\hat{\mu}|y)\right),\]
où \(\ell(y|y)\) est la fonction logvraisemblance du modèle saturé et \(\ell(\hat{\mu}|y)\) la fonction logvraisemblance du modèle ajusté par \(\hat{\beta}\).
Une grande valeur de \(D\) laisse penser que le modèle ajusté est de piètre qualité. \(D\) est aussi appelé la déviance réduite dans le cadre des modèles linéaires généralisés alors que la déviance non réduite est elle donnée par \(D^* = \phi D\).
En pratique, on jugera le modèle de mauvaise qualité si:
\[ D_{\text{observé}} > \chi^2_{n-p-1; 1-\alpha}\]
où \(\chi^2_{n-p-1; 1-\alpha}\) est le quantile d’ordre \(1-\alpha\) de la loi chi-deux à \(n-p-1\) degrés de liberté, \(n\) le nombre d’observations et $p +1 $ le nombre de paramètres dans le modèle (\(\beta_0, \ldots, \beta_p\)).
2.2.7.1 Exemple numérique: Déviance
Exemple 2.20 Trouvez la déviance dans un modèle de régression Poisson.
Nous savons que la fonction de probabilité d’une loi de Poisson s’exprime comme:
\[\Pr(Y =y) = \frac{\lambda^y e^{-\lambda}}{y!} \]
Ainsi, la fonction logvraisemblance d’un modèle staturé peut s’exprimer comme:
\[\begin{eqnarray*} \ell(y|y) &=& \ln\left( \prod_{i=1}^n \frac{\lambda_i^{y_i} e^{-\lambda_i}}{y_i!} \right), \text{ avec } \lambda_i = y_i \\ &=& \ln\left( \prod_{i=1}^n \frac{y_i^{y_i} e^{-y_i}}{y_i!} \right) \end{eqnarray*}\]
Ainsi:
\[\begin{eqnarray*} D(\boldsymbol{y}, \hat{\beta}) &=& 2 \ln\left( \prod_{i=1}^n \frac{y_i^{y_i} e^{-y_i}}{y_i!} \right) - 2 \ln\left( \prod_{i=1}^n \frac{\widehat{\lambda}_i^{y_i} e^{-\widehat{\lambda_i}}}{y_i!} \right) \\ &=& 2 \left( \left(\sum_{i=1}^n y_i \ln y_i -y_i - \ln(y_i!)\right) - \left(\sum_{i=1}^n y_i \ln \widehat{\lambda}_i - \widehat{\lambda}_i - \ln(y_i!)\right) \right) \\ &=& 2 \sum_{i=1}^n \left( y_i \ln y_i - y_i \ln \widehat{\lambda}_i + y_i - \widehat{\lambda}_i \right) \\ &=& 2 \sum_{i=1}^n \left( y_i \ln\left(\frac{y_i}{\widehat{\lambda}_i}\right) + (y_i - \widehat{\lambda}_i) \right)\\ &=& 2 \sum_{i=1}^n \left( y_i \ln\left(\frac{y_i}{\widehat{\lambda}_i}\right) \right) \end{eqnarray*}\]
car nous savons que le modèle de Poisson suppose un équilibre financier:
\[\begin{eqnarray*} \frac{\delta \ell}{\delta \beta_)} &=& \sum_{i=1}^n (y_i - \widehat{\lambda}_i) X_{i0} = 0\\ &=& \sum_{i=1}^n (y_i -\widehat{\lambda}_i) \\ &\Rightarrow& \sum_{i=1}^n y_i = \sum_{i=1}^n \widehat{\lambda}_i \end{eqnarray*}\] ::::
Exemple 2.21 Trouvez la déviance dans les modèles de régression normal, binomial, gamma et inverse-gaussien.
À faire en exercice.
Exemple 2.22 En reprenant les résultats du modèle de Poisson de l’exemple précédentt, et en supposant que les paramètres ont été estimés par maximum de vraisemblance, trouvez la déviance du modèle.
Nous savons que:
\[\begin{eqnarray*} D(y, \hat{\beta}) &=& 2 \sum_{i=1}^n \left( y_i \ln\left(\frac{y_i}{\widehat{\lambda}_i}\right) \right) = \sum_{i=1}^n D_i(y, \hat{\beta}) \end{eqnarray*}\]
| \(i\) | \(X_0\) | \(X_1\) | \(X_2\) | \(X_3\) | \(y\) | \(\widehat{\lambda}\) | \(D_i\) |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 | 1 | 1.093 | -0.211 |
| 2 | 1 | 1 | 0 | 0 | 0 | 0.686 | 0.000 |
| 3 | 1 | 1 | 1 | 1 | 2 | 1.428 | 1.459 |
| 4 | 1 | 0 | 1 | 1 | 3 | 2.602 | 1.800 |
| 5 | 1 | 1 | 0 | 0 | 1 | 0.686 | 1.386 |
| 6 | 1 | 1 | 1 | 1 | 0 | 1.428 | 0.000 |
| 7 | 1 | 0 | 0 | 1 | 1 | 1.993 | -1.151 |
| 8 | 1 | 1 | 0 | 1 | 2 | 1.094 | 2.351 |
La déviance totale est égale à \(5.635192\).
Pour tester l’ajustement du modèle, il suffit ainsi de comparer cette valeur de la déviance (\(5.635192\)) à une chi-carré avec (\(8-4 = 4\)) degrés de liberté.
A un niveau 95%, un table de chi-carré à 4 degrés de liberté nous donne \(9.488\). On ne peut donc pas rejeter le modèle Poisson à ce niveau.
Autre remarque: on peut aussi voir que \(\sum_{i=1}^8 \widehat{\lambda}_i = \sum_{i=1}^8 y_i = 8\), ce qu’on nommait un équilibre financier.
2.2.8 Autres éléments
Classiquement, dans les ouvrages sur les GLM, beaucoup d’autres éléments sont couverts. Puisqu’ils sont un peu moins importants pour la suite du cours, je laisse la liberté à chacun de lire sur le sujet.
Par contre, au moins deux autres thématiques doivent être couvertes:
1- L’estimation du paramètre de dispersion \(\phi\);
2- Les tests statistiques sur les paramètres.
Nous reviendrons un peu plus en détails sur ces deux thèmes dans un prochain chapitre.