4.2 Applications en R
Utilisons la base de données du cours pour estimer un modèle de régression Poisson, et voir les différents estimés de variance des paramètres.
Par contre au lieu d’utiliser la totalité de la base de données pour faire l’estimation des paramètres du modèle, on divisera cette base de données en 2 parties: la partie TRAIN et la partie TEST. Les paramètres et l’analyse statistique se fera sur la partie TRAIN alors que la comparaison de la qualité de prédiction des modèles se fera sur la partie TEST. Nous élaborerons davantage sur la qualité de prédiction dans un prochain chapitre.
db.train <- db.fictif %>% filter(Type=='TRAIN')
db.test <- db.fictif %>% filter(Type=='TEST')4.2.1 Algorithme Newton-Raphson
Un algorithme de type Newton-Rapshon peut être programmé pour estimer les paramètres de la régression Poisson. Remarquez l’utilisation de la variable expo dans l’évaluation du paramètre \(\lambda\).
### Algorithme Newton-Raphson maison
## Initialisation
# Generer la matrice des X
score.glm <- as.formula(nb.sin ~ couleur + myopie + type_territoire + langue + alimentation)
Matrix.X <- model.matrix(score.glm, db.train)
# Generer le vecteur des Y
Vect.Y <- as.matrix(db.train$nb.sin)
Vect.expo <- as.matrix(db.train$expo)
# Valeur initiale des beta
Beta <- rep(0, ncol(Matrix.X))
Beta[1] <- log(mean(Vect.Y))
## Loops Newton-Raphson
max.U <- 1
arret <- 0
loop <- 0
while (arret < 1){
loop <- loop + 1
## lambda
lambda <- Vect.expo*exp(Matrix.X %*% Beta)
## Vecteur U
U <- t(Matrix.X) %*% (Vect.Y - lambda)
## Matrice H
H <- -t(Matrix.X) %*% (Matrix.X*as.vector(lambda))
## Update beta
Beta <- Beta - solve(H)%*%U
## Criteres d'arret
arret <- ifelse(abs(max(U) - max.U) > 0.0001 & loop < 30, 0, 1)
max.U <- max(U)
}
## Print Results
print(loop)## [1] 6print(abs(max(U) - max.U))## [1] 0print(Beta)## [,1]
## (Intercept) -1.21214965
## couleurRouge -0.02101820
## myopieOui 0.07587350
## type_territoireSemi-urbain -0.09550161
## type_territoireUrbain -0.14857717
## langueF 0.25028395
## alimentationVégétalien -0.24305663
## alimentationVégétarien -0.42802787Un critère d’arrêt de l’algorithme a été placé, autant par rapport à l’amélioration de la fonction de premier ordre, que du nombre d’itérations maximum.
On peut comparer les valeurs estimés de \(\beta\) par rapport à la fonction glm() de R. Remarquez l’introduction du paramètre offset utiliser pour inclure le logarithme de l’exposition au risque.
### Compare avec fonction glm()
score.glm <- as.formula(nb.sin ~ couleur + myopie + type_territoire + langue + alimentation + offset(log(expo)))
Poisson1 <- glm(score.glm, family=poisson(link=log), data=db.train)
cbind(Beta, Poisson1$coefficients)## [,1] [,2]
## (Intercept) -1.21214965 -1.21214965
## couleurRouge -0.02101820 -0.02101820
## myopieOui 0.07587350 0.07587350
## type_territoireSemi-urbain -0.09550161 -0.09550161
## type_territoireUrbain -0.14857717 -0.14857717
## langueF 0.25028395 0.25028395
## alimentationVégétalien -0.24305663 -0.24305663
## alimentationVégétarien -0.42802787 -0.428027874.2.2 Variance des estimateurs
4.2.2.1 MLE
On peut utiliser l’estimation hessienne, équivalente à l’estimation par l’information de Fisher et l’estimateur par produit-croisé. Comparons ces valeurs avec celles obtenues par la fonction glm()
H <- -t(Matrix.X) %*% (Matrix.X*as.vector(lambda))
stderrH <- sqrt(diag(solve(-H)))
OP <- t(Matrix.X) %*% (Matrix.X*as.vector((Vect.Y - lambda)*(Vect.Y - lambda)))
stderrOP <- sqrt(diag(solve(OP)))
cbind(stderrH, stderrOP, summary(Poisson1)$coefficients[, 2])## stderrH stderrOP
## (Intercept) 0.02557011 0.023783653 0.02557011
## couleurRouge 0.01886640 0.017790074 0.01886639
## myopieOui 0.01354869 0.012869358 0.01354869
## type_territoireSemi-urbain 0.01260514 0.011903342 0.01260514
## type_territoireUrbain 0.01221177 0.011439321 0.01221177
## langueF 0.01021171 0.009572906 0.01021171
## alimentationVégétalien 0.01770594 0.016518954 0.01770594
## alimentationVégétarien 0.01683327 0.015712435 0.01683327On peut voir une différence entre l’estimateur par produit-croisé et l’estimateur hessien (ou par l’information de Fisher). On voit que la fonction glm() de R utilise l’estimateur hessien pour le calcul de la variance des estimateurs (ici, l’écart-type est affiché).
4.2.2.2 QMLE
On peut supposer une variance de forme \(\omega_i\) pour l’estimation par quasi-MLE.
Nous avons développé deux estimateurs pour le paramètre \(\phi\) de la NB1.
phi1 <- sum((Vect.Y - lambda)*(Vect.Y - lambda)/lambda)/(nrow(db.train) - length(Beta))
phi2 <- sum((Vect.Y - lambda)*(Vect.Y - lambda))/sum(lambda)
print(c(phi1, phi2))## [1] 1.236228 1.122992stderr.nb1.1 <- sqrt(phi1)*stderrH
stderr.nb1.2 <- sqrt(phi2)*stderrH
Poisson2 <- glm(score.glm, family=quasipoisson(link=log), data=db.train)
summary(Poisson2)##
## Call:
## glm(formula = score.glm, family = quasipoisson(link = log), data = db.train)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.9081 -0.6650 -0.5868 -0.4208 5.6607
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.21215 0.02843 -42.636 < 2e-16 ***
## couleurRouge -0.02102 0.02098 -1.002 0.316
## myopieOui 0.07587 0.01506 5.037 4.74e-07 ***
## type_territoireSemi-urbain -0.09550 0.01402 -6.814 9.50e-12 ***
## type_territoireUrbain -0.14858 0.01358 -10.943 < 2e-16 ***
## langueF 0.25028 0.01135 22.044 < 2e-16 ***
## alimentationVégétalien -0.24306 0.01969 -12.346 < 2e-16 ***
## alimentationVégétarien -0.42803 0.01872 -22.869 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasipoisson family taken to be 1.236228)
##
## Null deviance: 193888 on 270714 degrees of freedom
## Residual deviance: 191556 on 270707 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 6On peut voir que le modèle quasipoisson de la fonction glm() utilise l’estimateur phi1. Bien que la fonction glm() utilise phi1, nous recommandons plutôt d’utiliser phi2 dans l’estimation de la variance d’un modèle QMLE avec variance de forme NB1. En effet, phi1 est plutôt instable lorsqu’il y a présence d’une variable offset.
Au final, nous obtenons les estimés suivants pour la variance des estimateurs, sous la forme d’une variance de type NB1, \(\omega_i = \phi \mu_i\).
cbind(stderr.nb1.1, stderr.nb1.2, summary(Poisson2)$coefficients[, 2])## stderr.nb1.1 stderr.nb1.2
## (Intercept) 0.02843033 0.02709698 0.02843033
## couleurRouge 0.02097675 0.01999297 0.02097675
## myopieOui 0.01506422 0.01435773 0.01506422
## type_territoireSemi-urbain 0.01401513 0.01335784 0.01401513
## type_territoireUrbain 0.01357776 0.01294098 0.01357776
## langueF 0.01135397 0.01082148 0.01135397
## alimentationVégétalien 0.01968649 0.01876322 0.01968649
## alimentationVégétarien 0.01871621 0.01783844 0.01871621Nous avons aussi développé deux estimateurs pour le paramètre \(\alpha\) lorsque nous supposons une forme NB2 de la variance.
alpha1 <- sum(((Vect.Y - lambda)*(Vect.Y - lambda) - lambda)/(lambda*lambda))/(nrow(db.train) - length(Beta))
alpha2 <- sum((Vect.Y - lambda)*(Vect.Y - lambda) - lambda)/sum(lambda*lambda)
print(c(alpha1, alpha2))## [1] 3.7556585 0.5757296La fonction glm() de R ne produit pas d’estimé pour une forme de variance NB2. Comme pour l’estimé de \(\phi\) de la NB1 de la variance, nous recommandons d’utiliser alpha2 dans l’estimation de la variance d’un modèle QMLE avec variance de forme NB2. C’Est encore plus évident ici, mais alpha1 est instable lorsqu’il y a présence d’une variable offset.
Nous obtenons les estimés suivants pour la variance des estimateurs, sous la forme d’une variance de type NB2, \(\omega_i = \mu_i + \alpha \mu_i^2\).
Middle <- t(Matrix.X) %*% (Matrix.X*as.vector((lambda + alpha1*(lambda*lambda))))
Var1 <- solve(-H)%*%(Middle%*%solve(-H))
stderr.nb2.1 <- sqrt(diag(Var1))
Middle <- t(Matrix.X) %*% (Matrix.X*as.vector((lambda + alpha2*(lambda*lambda))))
Var1 <- solve(-H)%*%(Middle%*%solve(-H))
stderr.nb2.2 <- sqrt(diag(Var1))
cbind(stderr.nb2.1, stderr.nb2.2)## stderr.nb2.1 stderr.nb2.2
## (Intercept) 0.03562849 0.02735313
## couleurRouge 0.02554596 0.02003540
## myopieOui 0.01817110 0.01435422
## type_territoireSemi-urbain 0.01736035 0.01344370
## type_territoireUrbain 0.01669169 0.01299912
## langueF 0.01345915 0.01077325
## alimentationVégétalien 0.02549256 0.01910667
## alimentationVégétarien 0.02422435 0.01816256Pour terminer, nous avons vu une modèle QMLE qui ne supposait aucune forme particulière de la variance. On peut comparer tous les estimés des écart-types.
Middle <- t(Matrix.X) %*% (Matrix.X*as.vector(( (Vect.Y - lambda)*(Vect.Y - lambda) )))
Var1 <- solve(-H)%*%(Middle%*%solve(-H))
std.unstr <- sqrt(diag(Var1))
cbind(stderrH, stderrOP, stderr.nb1.1, stderr.nb1.2, stderr.nb2.1, stderr.nb2.2, std.unstr)## stderrH stderrOP stderr.nb1.1 stderr.nb1.2 stderr.nb2.1 stderr.nb2.2 std.unstr
## (Intercept) 0.02557011 0.023783653 0.02843033 0.02709698 0.03562849 0.02735313 0.02750569
## couleurRouge 0.01886640 0.017790074 0.02097675 0.01999297 0.02554596 0.02003540 0.02000922
## myopieOui 0.01354869 0.012869358 0.01506422 0.01435773 0.01817110 0.01435422 0.01426520
## type_territoireSemi-urbain 0.01260514 0.011903342 0.01401513 0.01335784 0.01736035 0.01344370 0.01335507
## type_territoireUrbain 0.01221177 0.011439321 0.01357776 0.01294098 0.01669169 0.01299912 0.01304602
## langueF 0.01021171 0.009572906 0.01135397 0.01082148 0.01345915 0.01077325 0.01089809
## alimentationVégétalien 0.01770594 0.016518954 0.01968649 0.01876322 0.02549256 0.01910667 0.01899002
## alimentationVégétarien 0.01683327 0.015712435 0.01871621 0.01783844 0.02422435 0.01816256 0.01804869La variance non-structurée ne suppose aucune forme particulière de la variance. En ce sens, elle est la forme la plus robuste pour l’estimation de la variance des estimateurs. En comparant avec les autres résultats, on peut faire quelques observations:
Les deux formes de variance de la Poisson MLE, comparativement au résultat obtenu par la variance non-structurée, semble sous-estimer l’écart-type des estimateurs;
On peut voir que les écart-types de la forme NB1, en utilisant phi1, surestime les écart-types. L’écart est encore plus évident avec alpha1 pour la forme NB2.
Entre la forme NB1 et la forme NB2, avec phi2 et alpha2, on voit que la forme NB2 se rapproche peut-être davantage de la forme non-structurée.
On peut voir graphiquement la différence entre les différentes formes de variance.
library(ggplot2)
db.train$lambda <- lambda
db.train$varPoisson <- lambda
db.train$varNB1 <- lambda*phi2
db.train$varNB2 <- lambda + alpha2*lambda^2
ggplot()+
geom_line(aes(x=lambda, y=varPoisson, color='Poisson'), data=db.train) +
geom_line(aes(x=lambda, y=varNB1, color='NB1'), data=db.train) +
geom_line(aes(x=lambda, y=varNB2, color='NB2'), data=db.train) +
scale_color_manual(values=c('blue','red','black')) +
xlab("Espérance") +
ylab("Variance") +
theme(legend.title=element_blank())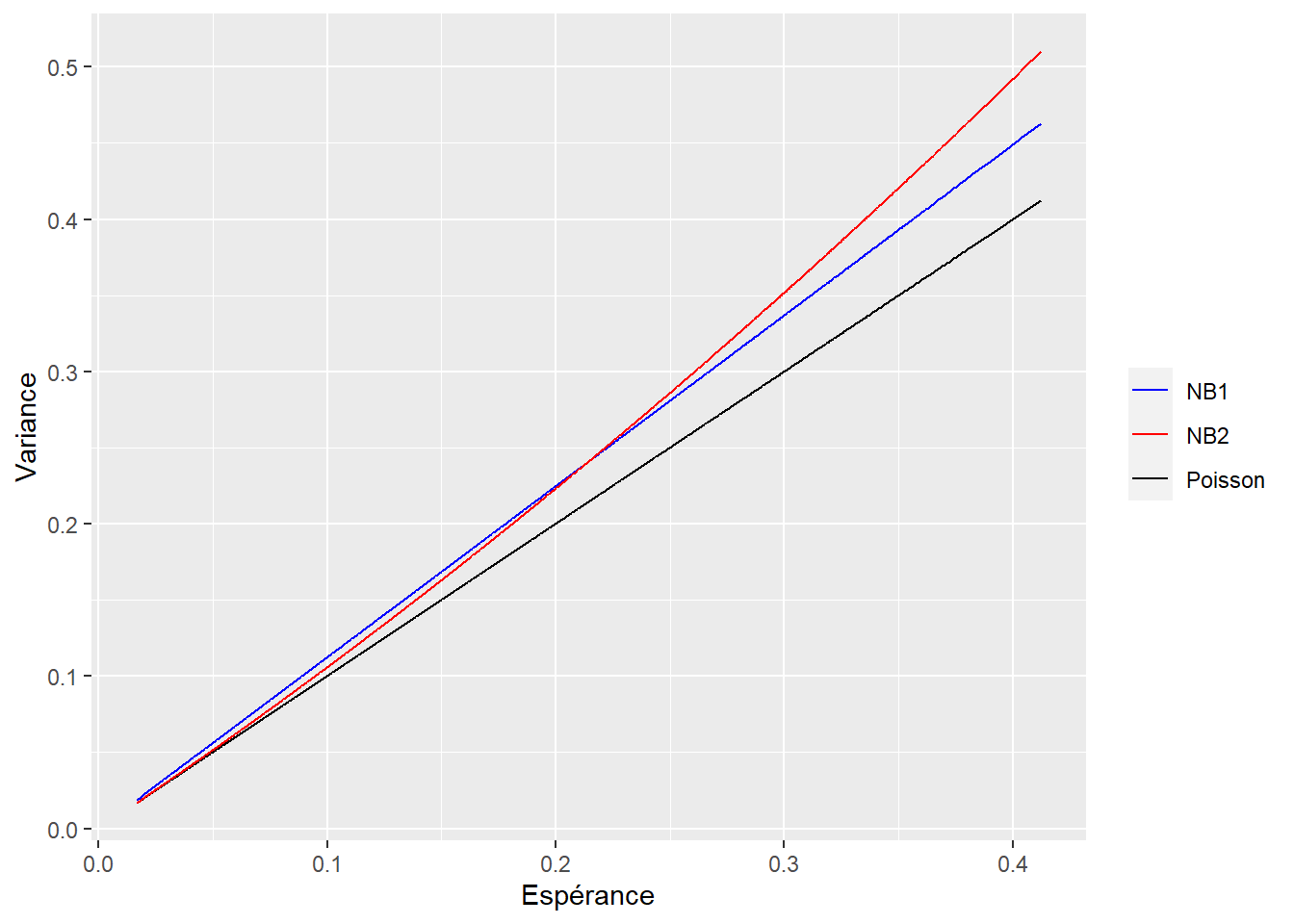
Au lieu de supposer une forme NB1 ou NB2, à l’image de ce que nous avons fait pour la forme non-structuré de la variance des estimateurs, il pourrait être intéressant de développer des méthodes non-paramétriques pour mieux estimer le lien entre la variance et l’espérance.
On peut profiter du fait que \(\hat{\beta}_{MLE}\) soit un estimateur convergent pour faire quelques analyses.
nb.voisin <- 2000
db.train$ind.var <- (db.train$lambda - db.train$nb.sin)^2
lambda.vec <- c(seq(from=0.01, to = 0.4, by=0.01))
nonpar.var <- data.frame()
for(i in 1:length(lambda.vec)){
sel.lambda <- lambda.vec[i]
bd <- db.train %>%
mutate(diff = abs(lambda- sel.lambda)) %>%
arrange(diff) %>%
slice(1:nb.voisin)
var <- sum(bd$ind.var)/(nb.voisin-length(Beta))
result <- cbind(sel.lambda, var)
nonpar.var <- rbind(nonpar.var, result)
}
colnames(nonpar.var) <- c('lambda', 'varUNSTR')
ggplot()+
geom_line(aes(x=lambda, y=varPoisson, color='Poisson'), data=db.train) +
geom_line(aes(x=lambda, y=varNB1, color='NB1'), data=db.train) +
geom_line(aes(x=lambda, y=varNB2, color='NB2'), data=db.train) +
geom_line(aes(x=lambda, y=varUNSTR, color='UNS'), size=1.2, data=nonpar.var) +
scale_color_manual(values=c('blue','red','black', 'darkgreen')) +
xlab("Espérance") +
ylab("Variance") +
theme(legend.title=element_blank())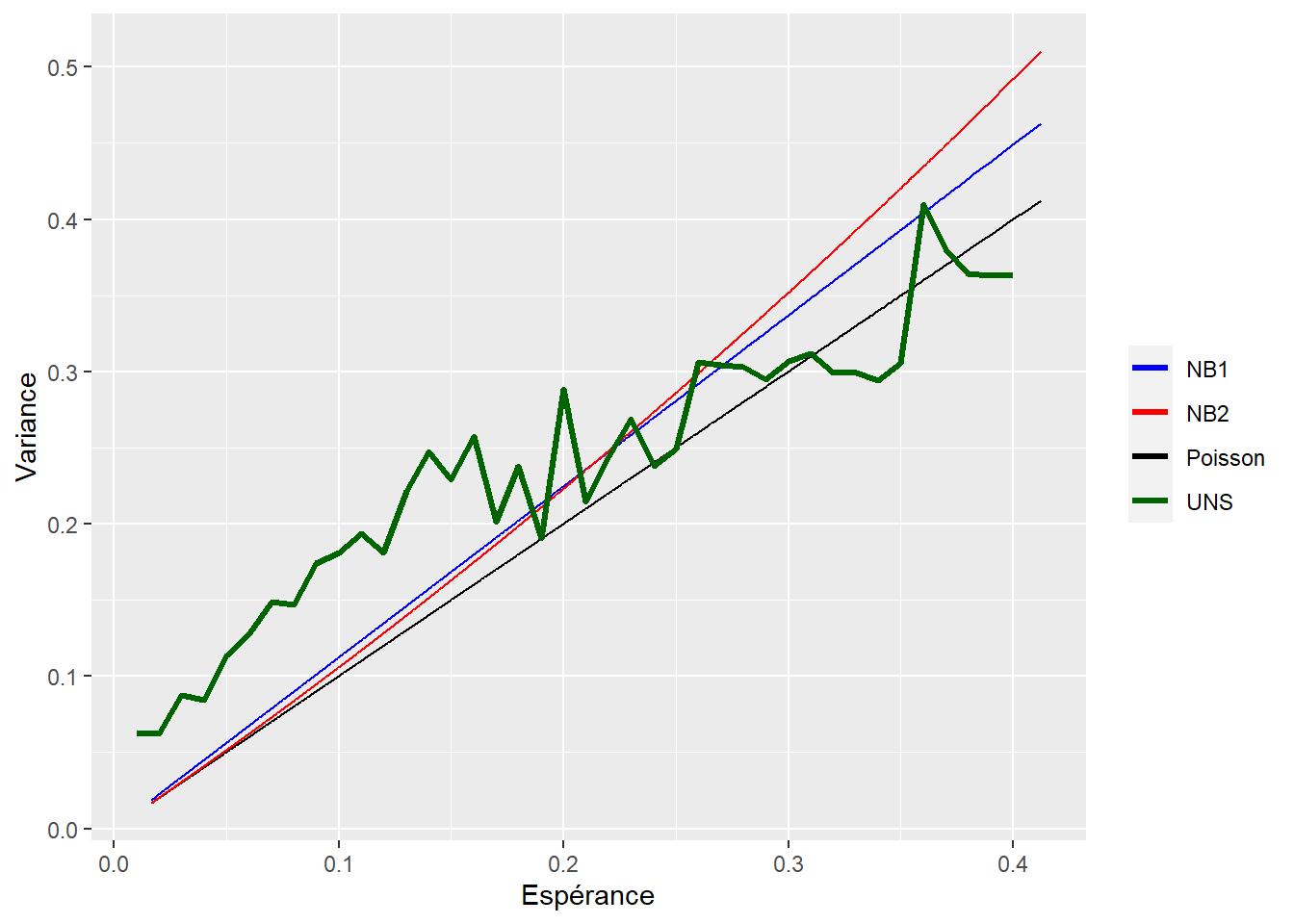
Ceci n’est qu’une première analyse, mais nous pouvons voir que ni la forme paramétrique de la NB1, ou de la NB2, ne semble convenir aux données. Si on voulait aller plus loin et trouver non seulement une meilleure estimation de la variance des paramètres, mais aussi de meilleurs paramètres, on devrait se rabbatre sur une approche appelée Poisson EE (estimating equations).
4.2.3 Poisson EE
On commence la méthode d’estimation en retournant à la condition de premier ordre des modèles GLM:
\[\begin{eqnarray*} \sum_{i=1}^n \frac{(y_i - \mu_i)}{g'(\mu_i) Var[Y_i]} \boldsymbol{X}_{i} &=& \boldsymbol{0}\\ \sum_{i=1}^n \frac{(y_i - \mu_i)}{g'(\mu_i) \omega_i} \boldsymbol{X}_{i} &=& \boldsymbol{0} \end{eqnarray*}\]
On suppose une variance de type \(\omega_i = \omega(\mu_i, \alpha)\), avec un estimateur convergent pour \(\alpha\). Pour une moyenne de forme log-linéaire (i.e. \(\boldsymbol{X}_{i}' \boldsymbol{\beta} = \ln(\mu_i)\)), nous avons ainsi:
\[\begin{eqnarray*} \sum_{i=1}^n \frac{1}{\omega(\mu_i, \alpha)} (y_i - \mu_i) \mu_i \boldsymbol{x_i} = 0\\ \end{eqnarray*}\]
et donc:
\[Var_{EE}[\hat{\beta}_{EE}] = \Big[ \sum_{i=1}^n \frac{1}{\omega(\mu_i, \alpha)} \mu_i^2 \boldsymbol{X}_{i} \boldsymbol{X}_{i}^T \Big]^{-1}\]
Parce que l’estimateur est basé sur les deux premiers moments, on pourrait voir cette approche comme une méthode des moments généralisés (GMM).