7.1 Introduction
Dans les modèles de données transversales, nous supposions que toutes les observations du jeu de données étaient indépendantes. Cela signifiait donc que tous les contrats annuels que nous analysions étaient indépendants.
En réalité, nous voyons que certains contrats annuels sont liés avec le même assuré. Il pourrait ainsi être logique d’imaginer qu’une forme de dépendance pourrait exister entre les contrats d’une même personne:
Il pourrait y avoir une dépendance d’occurence dans le nombre de réclamations: le fait d’avoir eu un sinistre pourrait changer la probabilité de survenance d’un autre sinistre, que ce soit dans le même contrat ou dans un contrat futur;
Il pourrait y avoir une dépendance de survenance dans le nombre de réclamations: le fait d’avoir eu un sinistre pourrait changer le temps de survenance d’un autre sinistre, ce qui affecte les contrats futurs de cet assuré;
s’il y a de l’hétérogénéité provenant d’une segmentation insuffisante, une caractéristique importante de l’assuré qui n’a pas été considérée dans la modélisation affectera tous les contrats de cet assuré.
7.1.1 Forme des données
Une manière simple d’illustrer la forme des données longitudinales serait le tableau suivant. Chaque ligne correspond à un assuré, l’expérience d’un assuré \(i\) pendant chacun des ses contrats \(t, t=1, \ldots,T\) est noté \(s_{i,t}\), et la totalité des caractéristiques est incluse dans le vecteur \(\mathbf{X}_{i,t}\).
Si nous observons \(m\) assurés pour \(T\) contrats, nous avons ainsi:
| Assuré | Contrat 1 | Contrat 2 | … | Contrat T |
|---|---|---|---|---|
| 1 | \(\mathbf{X}_{1,1}, s_{1,1}\) | \(\mathbf{X}_{1,2}, s_{1,2}\) | … | \(\mathbf{X}_{1,T}, s_{1,T}\) |
| 2 | \(\mathbf{X}_{2,1}, s_{2,1}\) | \(\mathbf{X}_{2,2}, s_{2,2}\) | … | \(\mathbf{X}_{2,T}, s_{2,T}\) |
| … | … | … | … | … |
| \(m\) | \(\mathbf{X}_{m,1}, s_{m,1}\) | \(\mathbf{X}_{m,2}, s_{m,2}\) | … | \(\mathbf{X}_{m,T}, s_{m,T}\) |
Une base de données équilibrée correspond à la situation où tous les assurés \(i=1,\ldots,m\) sont observés pendant le même nombre de contrats \(T\). Dans la table ci-dessus, puisque nous observons les \(m\) assurés pendant \(T\) contrats, la base de données est équilibrée.
En pratique, ce n’est évidemment pas le cas: certains assurés ne restent qu’un an chez un assureur, alors qu’un autre assuré peut être chez ce même assureur depuis plus de 30 ans.
Réalistement, nous travaillons ainsi davantage avec des jeux de données qui auraient la forme suivante:
| Assuré | Contrat 1 | Contrat 2 | … | Contrat T |
|---|---|---|---|---|
| 1 | … | \(\mathbf{X}_{1,2}, s_{1,2}\) | … | \(\mathbf{X}_{1,T}, s_{1,T}\) |
| 2 | \(\mathbf{X}_{2,1}, s_{2,1}\) | \(\mathbf{X}_{2,2}, s_{2,2}\) | … | … |
| … | … | … | … | … |
| \(m\) | … | \(\mathbf{X}_{m,2}, s_{m,2}\) | … | … |
Dans les modèles que nous développerons dans ce chapitre, il sera très simple de passer d’un modèle ayant des données équilibrées à un modèle ayant des données non-équilibrées. Ainsi, pour simplifier les notes de cours, nous utiliserons souvent une notation avec données balancées, ce qui signifie que \(T_i = T\), pour \(i = 1,...,m\).
Les tables ci-dessus aident à mieux comprendre la forme longitudinale des données, où nous voyons l’expérience d’un même assuré sur une même ligne. En réalité, avec de vraies bases de données d’assurance, il n’est pas nécessaire d’avoir une telle forme.
On peut prendre exemple sur la base de données db.fictif pour s’en convaincre.
table <- db.fictif[1:7, c("policy_no", "veh.num", "renewal_date", "nb.sin", "Tot.Cost")]
knitr::kable(table)| policy_no | veh.num | renewal_date | nb.sin | Tot.Cost |
|---|---|---|---|---|
| 6000088 | 1 | 2015-11-10 | 0 | 0.00 |
| 6000088 | 1 | 2016-11-10 | 1 | 185.81 |
| 6000274 | 1 | 2011-02-03 | 0 | 0.00 |
| 6000274 | 1 | 2012-02-03 | 0 | 0.00 |
| 6000274 | 1 | 2013-02-03 | 0 | 0.00 |
| 6000274 | 1 | 2014-02-03 | 0 | 0.00 |
| 6000274 | 1 | 2015-02-03 | 0 | 0.00 |
On voit ainsi que le véhicule #1 de la police 6000088 est observé pendant deux contrats, en 2015 et 2016. Le véhicule #1 de la police 60000274, quant à elle, est observée 5 fois. Les colonnes indiquant le nombre de sinistre réclamé, et même la charge totale, sont aussi indiquées.
C’est surtout de cette manière que les bases de données d’assurance sont maintenant structurée. En utilisant la fonction group() du package dplyr, il est assez simple de faire des opérations sur tous les contrats d’un seul véhicule.
L’extrait du jeu de données db.fictif nous permet aussi de voir que la dépendance temporelle en assurance automobile est surtout basée sur le véhicule. Dans les modèles de données de panel, on supposera en effet une dépendance entre les sinistres d’un même véhicule.
Il pourrait être justifié de supposer, aussi, une dépendance entre les véhicules d’un même contrat, par exemple. En effet, puisque les mêmes adultes d’un même ménage conduisent tous les véhicules, des formes de dépendance, ou de l’hétérogénéité non-observée pourrait toucher la sinistralité de tous les véhicules.
Une telle forme de dépendance s’appelle de la dépendance hiérarchique. Nous ne couvrirons pas ces modèles pour ce séminaire, mais on pourra remarquer que certains modèles de données de panel se prêtent parfois à des généralisations pouvant permettre une telle forme de dépendance.
7.1.2 Familles de modèle
Nous verrons ainsi dans ce chapitre que pour les distributions de comptage, il existe 3 possibilités de modélisations distinctes pour les données de panel. Classiquement, on regroupe les approches selon les catégories suivantes:
- Modèles conditionnés sur des réalisations passées (par exemple, des séries chronologiques, ou des modèles de transition).
- Approche avec modèles marginaux (comme les GEE);
- Approche avec paramètres individuels (par exemple, une distribution conditionnée avec effets fixes ou effets aléatoires);
Dans les modèles linéaires, ces mêmes trois généralisations de la régression linéaire classique génèreraient exactement le même modèle, soit une loi gaussienne multivariée.
7.1.3 Tarification prédictive
Nous avons vu que les modèles avec données transversales permettaient de calculer l’espérance du nombre de réclamations en fonction des caractéristiques de l’assuré.
Il s’agit aussi de l’un des objectifs des modèles avec données longitudinales. Par contre, les modèles avec données de panel permettent aussi de faire de la tarification prédictive, c’est-à-dire de tarifer les assurés en fonction de leurs caractéristiques, mais aussi en fonction de leur historique de réclamations.
On cherchera donc, avec ces modèles de données de panel, à calculer \(E[N_{i,t}]\) mais aussi \(E[N_{i,T}|n_{i,1}, \ldots, n_{i,T}]\).
7.1.3.1 Illustration empirique
Il est bien connu dans le milieu de l’assurance que les assurés ayant réclamé dans le passé ont tendance à réclamer davantage dans le futur.
Pour mieux illustrer empiriquement cette situation, on utilise la base de données de cours. On débute par prendre uniquement les polices qui contiennent des contrats annuels ayant une exposition au risque plus grande 0.8.
`%notin%` <- Negate(`%in%`)
remove <- db.fictif[which(db.fictif$expo < 0.8),]
data <- db.fictif[which(db.fictif$policy_no %notin% unique(remove$policy_no)),]Une analyse sommaire de la fréquence de réclamation permet de nous rappeler la fréquence moyenne du portefeuille.
c(mean(data$nb.sin), var(data$nb.sin), var(data$nb.sin)/mean(data$nb.sin), min(data$nb.sin), max(data$nb.sin))## [1] 0.1860964 0.2113058 1.1354641 0.0000000 7.0000000On peut aussi analyser la distribution du nombre de sinistres.
library(janitor)##
## Attaching package: 'janitor'## The following objects are masked from 'package:stats':
##
## chisq.test, fisher.testoptions(scipen = 999)
data %>%
tabyl(nb.sin) %>%
adorn_totals()## nb.sin n percent
## 0 144067 0.839923276043
## 1 23577 0.137455982836
## 2 3368 0.019635736107
## 3 451 0.002629369651
## 4 55 0.000320654835
## 5 3 0.000017490264
## 6 2 0.000011660176
## 7 1 0.000005830088
## Total 171524 1.000000000000On pourrait débuter par analyser le comportement de chaque véhicule en fonction de son historique de réclamations.Analysons la fréquence de réclamations et regardons le nombre de réclamations moyen:
mean(data$nb.sin)## [1] 0.1860964Ainsi, pour la portion fréquence de la prime, on pourrait charger \(0.1860964\) par année à tous les assurés. On aurait ainsi un équilibre financier car la somme des primes serait égale à la somme des sinistres.
data$prime <- 0.1860964
c(sum(data$prime), sum(data$nb.sin))## [1] 31920 31920Maintenant, on pourrait voir si une prime unique à tous les assurés, peu importe leur historique de réclamations, est juste.
data <- data %>%
arrange(policy_no, veh.num, renewal_date) %>%
group_by(policy_no, veh.num) %>%
mutate(contract.no = row_number(),
past.nbclaim = cumsum(nb.sin)- nb.sin) %>%
ungroup()En ayant contrat.no et past.nbclaim, on peut donc vérifier si le nombre de réclamations moyen dépend du nombre de réclamations passées, et si une prime de \(0.1860964\) par année à tous les assurés semble équitable.
sommaire1 <- data %>%
mutate(past.nbclaim = pmin(4, past.nbclaim)) %>%
group_by(contract.no, past.nbclaim) %>%
summarise(nb = n(),
freq = mean(nb.sin), .groups = 'drop') %>%
mutate(pct = freq/0.1860964) %>%
filter(contract.no < 5) %>%
ungroup()Au lieu d’analyser un tableau de chiffres, on peut simplement illustrer le résultat en utilisant une heatmap.
ggplot(sommaire1, aes(as.factor(contract.no), as.factor(past.nbclaim), fill= as.numeric(pct))) +
geom_tile()+
geom_text(aes(label = paste(sprintf("%0.1f", 100*pct),'% (', sprintf("%0.0f", nb), ')') ), color = "black", size = 4) +
scale_fill_gradient2(low = "green", mid = "gray", midpoint = 1, high = "red")+
xlab("No. contrat") + ylab("Nb. réclamations passées")+
theme(legend.position = 'none')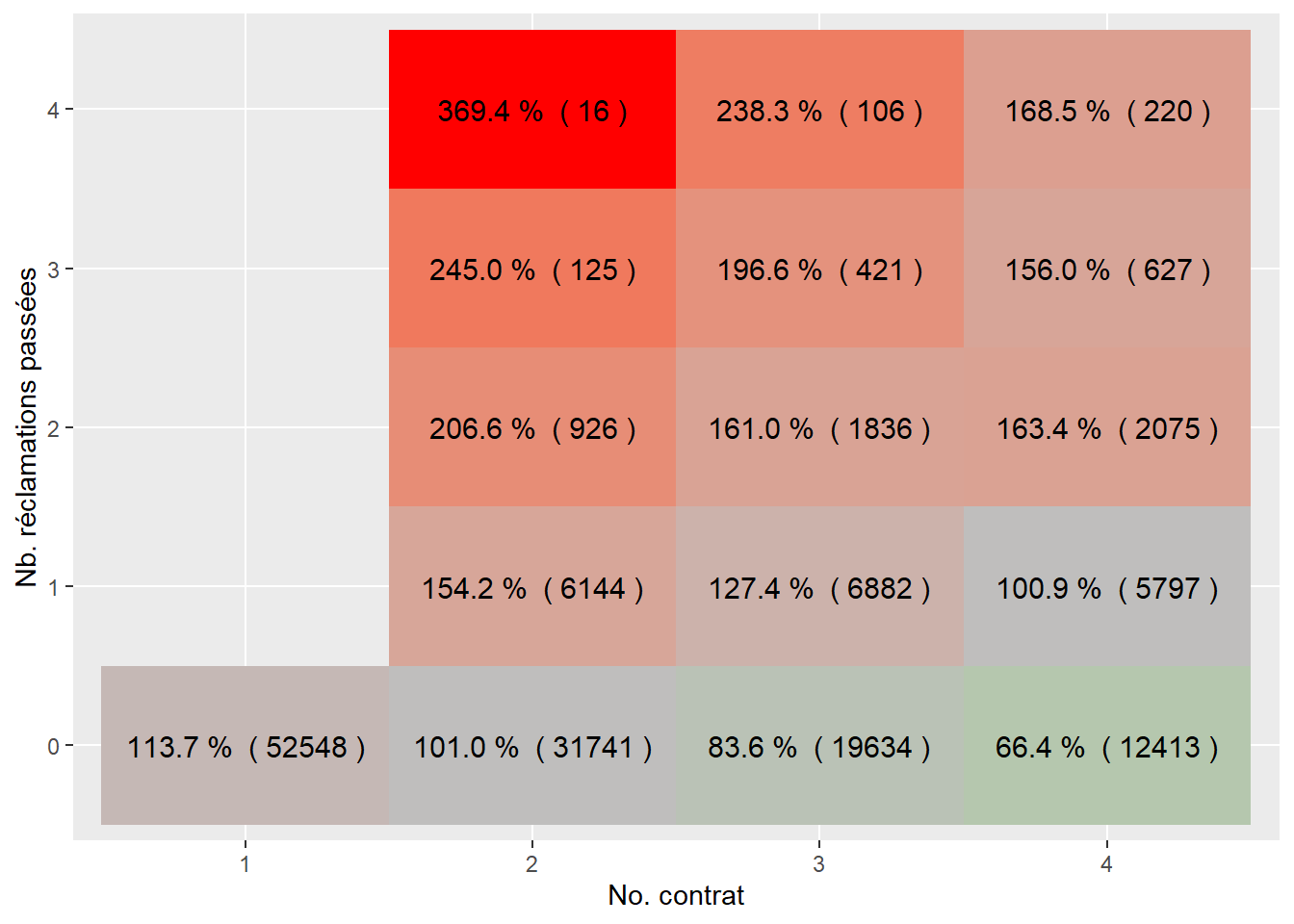
Il faut bien entendu remarquer que l’exposition totale pour chaque tuile n’est pas la même (chiffre entre parenthèses), et que la majorité des assurés ne réclament pas. Par contre, on peut voir certaines tendances assez nettes:
les assurés réclamant dans le passé ont une fréquence de réclamations supérieure à la prime moyenne;
les assurés qui ne réclament pas semblent ont une fréquence de réclamations inférieure à la prime moyenne;
les nouveaux assurés, c’est-à-dire ceux qui n’ont aucune expérience d’assurance, ont une fréquence de réclamations supérieure à la moyenne.