6.4 Ajustement

Même si un modèle semble être meilleur que les tous les autres modèles pour représenter des données de comptage, les techniques que nous venons de voir ne nous permettent pas de conclure néanmois que le modèle ajuste bien les données. Par exemple, le meilleur modèle trouvé par les tests d’ajustement, les critères d’information ou le score de prédiction est peut-être simplement le moins pire. En ce sens, il peut-être le meilleur modèle mais ajuste de manière médiocre les données.

Ainsi, lorsqu’un modèle a été choisi pour représenter les données, et que les paramètres du modèle ont été évalués, il convient de vérifier si les données sont bien ajustées.

6.4.1 Analyse des résidus

Comme nous pouvons le faire avec la régression linéaire, on peut commencer avec l’analyse des résidus, correspondant à la différence entre une observation et sa prédiction:

\[r_i = y_i − \hat{\lambda}_i\]

Pour la Poisson, \(r_i\) est hétéroscédastique car \(Var[r_i] = \lambda_i\) n’est pas constante et dépend de la moyenne \(|lambda_i\), même si l’échantillon est très grand. On peut même voir facilement la forme des résidus en prenant exemple sur nos données.

pred <- predict(Poisson1, newdata=db.train, type="response") 
residus <- db.train$nb.sin - pred
ggplot()+
  geom_point(aes(x=pred, y=residus)) + theme_bw()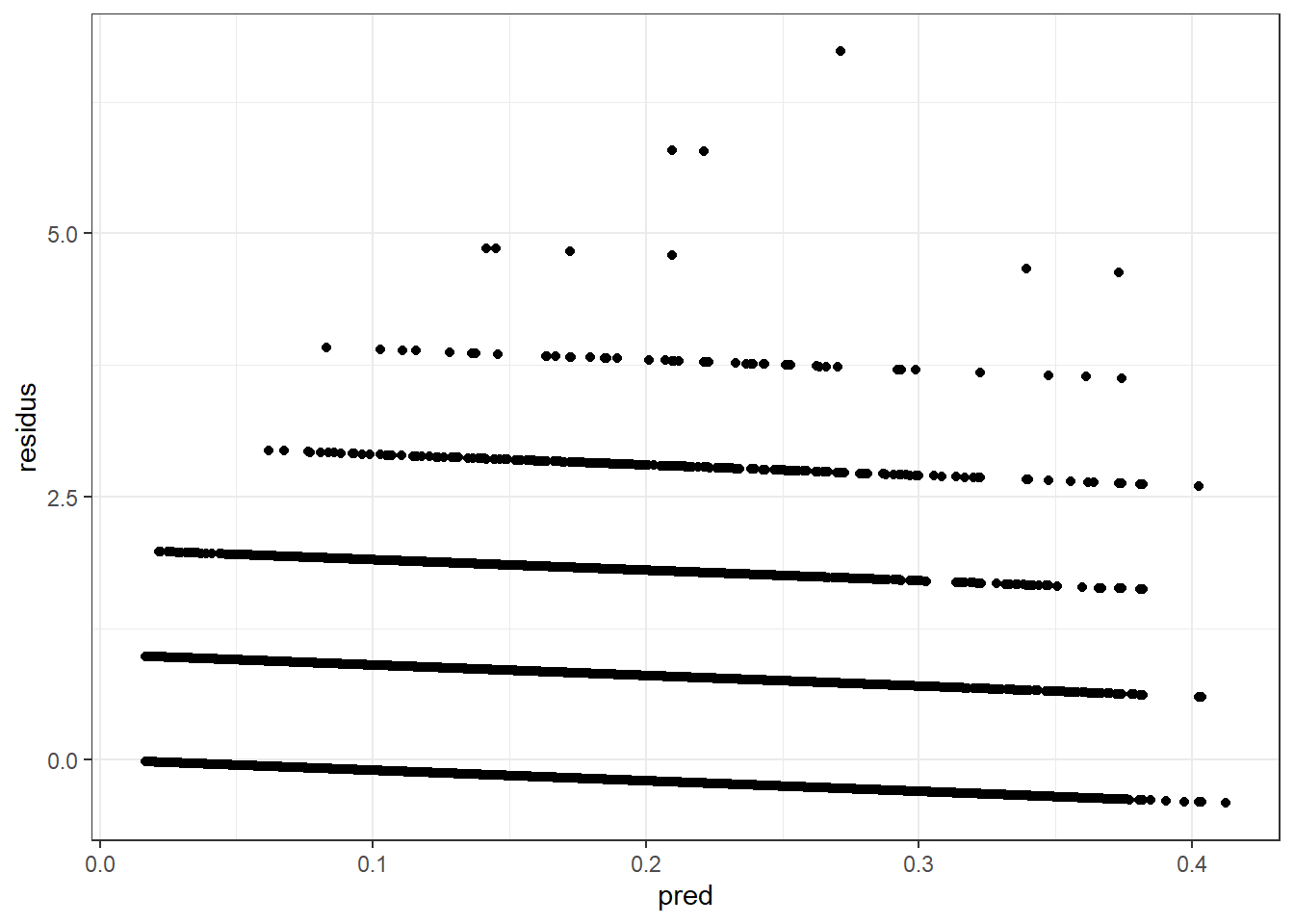

On peut clairement voir 7 (8 en comptant le point) lignes verticales représentant \(0, 1, \ldots, 7\) réclamations. La figure ne nous aide aucunement à conclure quoi que ce soit.

Pour corriger l’hétéroscédasticité, on peut utiliser les résidus de Pearson:

\[r_i^{Pearson} = \frac{y_i − \hat{\lambda}_i}{\sqrt{\hat{\omega_i}}}\] avec \(\omega_i\) représentant la forme de la forme de \(Y\). Pour un large échantillon, les résidus de Pearson ont une moyenne de 0 et son homoscédastiques. Par contre, la distribution n’est pas symétrique.

residusP <- (db.train$nb.sin - pred)/sqrt(pred)
ggplot()+
  geom_point(aes(x=pred, y=residusP)) + theme_bw()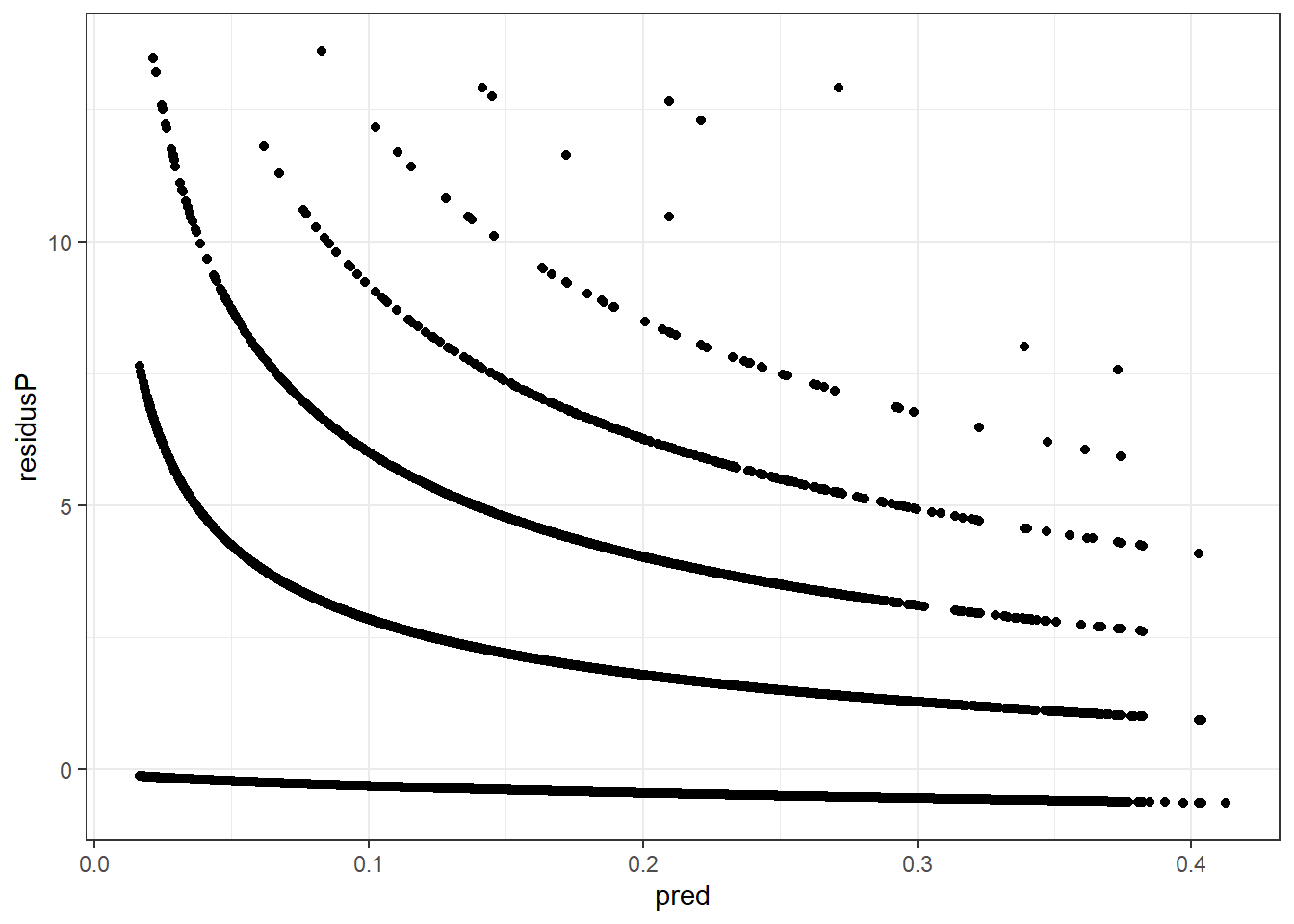

Bien que l’hétéroscédasticité ait été corrigée, on remarque toujours les 8 lignes, et contrairement à ce que nous pouvons faire avec les résidus d’une régression normale, on ne peut pratiquement rien conclure de l’analyse visuelle de ce graph.

6.4.2 Mesures Pseudo-\(R^2\)

Un outil fortement utilisé en régression linéaire est le \(R^2\):

\[ \sum_{i=1}^n (y_i - \overline{y})^2 = \sum_{i=1}^n (y_i - \hat{\mu}_i)^2 + \sum_{i=1}^n (\hat{\mu}_i- \overline{y})^2 + \sum_{i=1}^n (y_i - \hat{\mu}_i)(\hat{\mu}_i- \overline{y})\]

avec:

le premier élément est la somme des carrés totale (TSS);
le second est la somme des carrés des résidus (RSS);
le troisième est la somme des carrés prédits (ESS), et est égal à 0 s’il y a une ordonnées à l’origine (intercept) dans le modèle.

Étant donné que la statistique \(R^2\) est intuitive, facile d’utilisation et permet de juger rapidement de la qualité du modèle, la communauté scientifique a longtemps tenté de développer l’équivalent du \(R^2\) pour les régressions de comptage.

Par contre, il n’y a pas de définition universelle pour les \(R^2\) des modèles non-linéaires car \(R^2 = 1 - RSS/TSS\) ou \(R^2 = ESS/TSS\) ne sont pas équivalents pour les distributions qui ne sont pas gaussiennes.

Un autre problème est que l’objectif d’une régression Poisson n’est pas la minimisation de RSS. Ainsi, l’ajout d’un régresseur ne minimise pas nécessairement le \(R^2\).

Afin d’adapter cette statistique, plusieurs propositions ont été faites, comme le \(R^2\) de déviance, tel qu’en ayant:

\[D(y, \bar{y}) = D(y, \hat{\mu}) + D(\hat{\mu}, \bar{y})\]

nous pouvons obtenir:

\[R^2_{Dev} = 1 - \frac{D(y, \hat{\mu})}{D(y, \bar{y})}\]

Un \(R^2\) basé sur la logvraisemblance, ou même un \(R^2\) basé sur les résidus de Pearson ont aussi été développés. Dans tous les cas, nous ne recommandons pas vraiment l’utilisation des ces pseudo-\(R^2\).

6.4.3 Tableau de prédiction

Une dernière analyse est similaire à ce que nous avons déjà dans un chapitre précédent, soit de calculer

\[\hat{n}_j = \sum_{i=1}^n \frac{e^{-\hat{\lambda}_i} \hat{\lambda}_i^j}{j!}, \text{ pour } j=0,1,\ldots\] et de comparer avec la vraie distribution observée. Il a été montré que la différence entre le prédit et l’observé pourrait suivre une distribution \(\chi^2\). Malgré que nous ayons en mains un test formel statistique entre le prédit et l’observé, le test est basé sur la somme des prédictions et non sur les prédictions individuelles, ce que le rend peu intéressant.

### Compare avec fonction glm()
db.train$lambda <- predict(Poisson1, newdata=db.train, type='response')

table <- data.frame()
for(i in 0:5){
  pred <- sum(dpois(i, db.train$lambda))
  obs  <- sum(ifelse(db.train$nb.sin == i, 1, 0))
  res  <- c(i, pred, obs)
  table <- rbind(table, res)
}
colnames(table) <- c('NbSin', 'Predicted', 'Observed')
table$Diff <- table$Predicted - table$Observed  

knitr::kable(table, digits = c(0, 2, 0, 2))

NbSin	Predicted	Observed	Diff
0	224270.51	226272	-2001.49
1	41708.93	38272	3436.93
2	4383.69	5338	-954.31
3	330.92	739	-408.08
4	19.90	85	-65.10
5	1.01	6	-4.99

6.4.4 Conclusion sur l’ajustement

À l’heure actuelle, il ne semble pas exister de tests statistiques formels vérifiant si une certaine distribution de comptage correspond aux données observées. À défaut de pouvoir conclure s’il est probable que les données proviennent réellement d’un modèle spécifique, l’approche actuelle est dans la commnauté scientifique est de:

Bien comprendre les données analysées: présence de surdispersion, sur-représentation de zéros, etc. Une compréhension fine du phénomène étudié est évidemment recommandé. Cette compréhension pourrait justifier l’utilisation de certains modèles, par exemple.
Essayer une série de modèles à comparer par des tests d’hypothèse (modèles liés), par les critères d’information, et le scores de prédiction;
Utiliser des algorithmes de sélection de variables (type stepwise, GLM-net, forêts aléatoires, boosting, etc.);
Supposer que les modèles testés couvrent un large spectre de possibilités, et choisir le meilleur modèle disponible.