Chapter 14 Bootstrapping to Re-estimate Parameters in Small Samples

This week, our goals are to…

  1. Identify quantitative analyses that have small sample sizes.

  2. Determine when to apply methods such as bootstrapping to calculate alternate inferential estimates for regressions with small sample sizes.

  3. Apply a bootstrapped model to a linear regression analysis with a small sample size.

  4. Witness how an increasingly smaller sample relates to inferential capability in a regression analysis.

Announcements and reminders

We have reached our final week of new content in this course.

Here are the remaining tasks to do, if you have not done so already:

  • Complete and submit the assignment from this chapter
  • Schedule and pass your Oral Exam #3.
  • Submit your final project (into its own D2L dropbox)
  • Complete course evaluation (you should have received an email from IHP with an evaluation link)

I recommend reviewing the course calendar as well as the final project requirements. The final deadline for everything—if you are following the standard course schedule—is Monday April 24 2023.

Please look out for additional announcements and reminders over email.

14.1 Bootstrapping introduction

In this chapter, we will learn a little bit about bootstrapping, which is a technique we can use when we are estimating parameters—such as regression coefficients—from our sample and our sample size is very small.221 In basic terms, bootstrapping involves re-sampling your existing sample and using those additional samples to make estimates.

Whenever we have a sample of less than approximately 30 observations drawn from a population, this sample may be too small for us to reliably make inferences about the entire population. One way to address this problem is by using a method called bootstrapping, which involves telling the computer to “re-sample” the observations in your data and “reuse” them to calculate confidence intervals for regression coefficient estimates.

While this method may be and sound controversial in some ways, it has also been found to be legitimate and useful in some situations. If you do have an extremely small sample, my usual recommendation is to run your analysis the usual way and then run it again with bootstrapping to see if you get the same result. If you do get the same result, you can be more confident that the finding is trustworthy. If you do not get the same result, you should be transparent when reporting your results and note that there is some evidence that the trends found in your sample may not be the case in the population.

In this chapter, we will use bootstrapping to help us estimate regression coefficients, since regression analysis is the main focus of this course. However, bootstrapping can be used to estimate a number of population parameters using a small sample, such as the mean and standard deviation of a variable. Some of the examples and explanations of bootstrapping that you may read will use mean and standard deviation as examples.

Please watch the following video to begin learning about how bootstrapping works:

The video above uses some code that we have not reviewed before and that you will not need to know or use yourself. The overall concepts are all that you need to follow along with in the video, especially the diagrams at the start.

The next section will go through a few of the key concepts of bootstrapping, before we move into an example of how to use and interpret bootstrapping in R.

14.1.1 Key concepts

In this section, we’ll review a few key concepts or reminders to keep in mind as you do a bootstrapping analysis. Most of these notes are taken from the following resource, which is optional (not required) for you to read:

Once again, reading the resource above is not required. You should consider referring to it only if you are using bootstrapping for a project of your own.

Here is an introduction from Fox and Weisberg:

The bootstrap is a general approach to statistical inference based on building a sampling distribution for a statistic by resampling repeatedly from the data at hand. The term “bootstrapping,” due to Efron (1979), is an allusion to the expression “pulling oneself up by one’s bootstraps,” in this case, using the sample data as a population from which repeated samples are drawn. At first blush, the approach seems circular, but has been shown to be sound.

To be clear, when we use bootstrapping, we have a sample of data that is taken from a broader population. We want to use the sample to make inferences about the population, just like we have wanted to do with samples of data throughout this course. Since the sample is small, we generate additional data by re-sampling our own sample to create what we call a bootstrap sample. This is called sampling with replacement.222

Here is how Fox and Weisberg suggest thinking about the population, sample, and bootstrap sample:

The population is to the sample as the sample is to the bootstrap samples223

As you’ll see in the example that follows, we use the bootstrap sample to help us make inferences about the population.

14.2 Example

Now that you have read and listened a little bit about bootstrapping, we will go through an example. Please note that, especially given this shorter final week of the course, we will just be picking out a few concepts from bootstrapping to focus on this week. This lesson does not include everything you need to know to do a complete bootstrapping analysis. Our goal is just to get a basic sense for what is happening.

Before we see an example of bootstrapping, and as we have done so many times before, we will begin by running an OLS linear regression to demonstrate a result that we would get if we used a basic analytic method and had a larger sample.

We will use the very same example that we used in the previous chapter on missing data! Read on for a re-introduction to this data and to see how we will modify in a slightly different way this week.

14.2.1 Load data

We will refer to an example to demonstrate a simple bootstrapping technique. For this example, we will use the diabetes.sav dataset that we have used before in our course. You can click here to download the dataset.

Then run the following code to load the data into R, so that you can follow along:

if (!require(foreign)) install.packages('foreign')
library(foreign)

diabetes <- read.spss("diabetes.sav", to.data.frame = TRUE)

Our research question of interest is:

  • What is the relationship between total cholesterol and age, controlling for weight and gender?

These are the variables we will use:

  • Dependent variable: total_cholesterol
  • Independent variables: weight, age, gender

We will use an ordinary least squares (OLS) linear regression throughout this chapter. However, keep in mind that bootstrapping could possibly be used on other types of regression models too.

Let’s continue to prepare the data for use throughout this chapter.

We will extract the variables we want, using the following technique that we have used before:

if (!require(dplyr)) install.packages('dplyr')
library(dplyr)

d <- diabetes %>%
  dplyr::select(total_cholesterol, age, gender, weight)

Now, the name of our dataset is d and it only contains the variables that we will use in this example. Here are the variables remaining in the data:

names(d)
## [1] "total_cholesterol" "age"               "gender"           
## [4] "weight"

Next, let’s look at how many observations are in the dataset d:

nrow(d)
## [1] 403

There are 403 observations in d. Since this week’s topic is small sample sizes, we will also remove the majority of this data and pretend that we only had a sample of 5% of the data that we actually have. Below, we’ll make a new dataset to help us mimic this situation:

d5 <- d[sample(nrow(d), 20), ]

Above, we did the following:

  • d5 <- – Create a new dataset called d5. This is called d5 because it contains approximately 5% of the amount of data that is in d.
  • d[R,C] – Choose a subset of the data that is in d. Where R is written is where we select rows. Where C is written is where we select columns. In this case, we are selecting a subset of d by selecting a subset of its rows; we use the sample function to do this selection. We are not subsetting its columns (we want to keep all of the original columns), so we leave C blank (you can see in the code above that there is nothing after the comma within the square brackets).
  • sample(nrow(d), 20) – Sample (randomly select) 20 values that fall between 1 and 403. We know that 403 is the result of the nrow(d) command (which you saw just earlier in this chapter), so we can pretend the number 403 is written where nrow(d) is written.

The code above randomly selected 20 observations for us and put them into a new dataset called d5. Let’s confirm that d5 only has 20 observations:

nrow(d5)
## [1] 20

20 is approximately 5% of 403, so dataset d5 contains approximately 5% of the observations that dataset d contains. We will use both of these datasets to run regressions throughout this chapter and illustrate how bootstrapping is used. Sometimes you will be in a situation in which you only have about 20 observations in your dataset (like d5) and you do not have a larger dataset (like d) that you can refer to.

Remember that last week, when we looked at missing data, our practice dataset retained all 403 rows, but 30% of the data was missing in the data. This week, our rows have complete data (no variables are missing for any observations), but we simply have way fewer rows than we had last week (now we only have 20 rows). That is what this week is all about: what to do when you don’t have a large sample.

14.2.2 True effect – initial regression analysis

As a reminder, we will try to answer the following research question in this example:

  • What is the relationship between total cholesterol and age, controlling for weight and gender?

And here, once again, are the variables we will use:

  • Dependent variable: total_cholesterol
  • Independent variables: weight, age, gender

Let’s finally run an OLS regression model—called reg.true—to get an initial answer to our research question:

reg.true <- lm(total_cholesterol ~ weight + age + gender, data = d)
summary(reg.true)
## 
## Call:
## lm(formula = total_cholesterol ~ weight + age + gender, data = d)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -136.198  -26.684   -4.697   22.822  225.533 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  158.67383   12.48237  12.712  < 2e-16 ***
## weight         0.09251    0.05380   1.719   0.0863 .  
## age            0.66441    0.13206   5.031 7.41e-07 ***
## genderfemale   3.16853    4.38681   0.722   0.4705    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 42.97 on 397 degrees of freedom
##   (2 observations deleted due to missingness)
## Multiple R-squared:  0.06438,    Adjusted R-squared:  0.05731 
## F-statistic: 9.107 on 3 and 397 DF,  p-value: 7.663e-06

Above, we see that there is a predicted increase in total cholesterol of 0.66 units for every one year increase in age, controlling for weight and gender. It has a very low p-value, which tells us that we can be extremely confident about this estimate, if all of the assumptions of OLS linear regression are true for this model.

Since we used the dataset d—which is the full original dataset—in the regression above, let’s call 0.66 the true effect (or true association or relationship) of age on total cholesterol.

We can look at the confidence intervals of the estimates for our true effect:

confint(reg.true)
##                     2.5 %      97.5 %
## (Intercept)  134.13402961 183.2136322
## weight        -0.01326627   0.1982839
## age            0.40477257   0.9240392
## genderfemale  -5.45575669  11.7928201

The 95% confidence interval for age—the estimate of most interest to us—ranges from 0.405 to 0.924.

In the rest of this chapter, we will use the other dataset, d5—which is a version of d that has only 5% of the original dataset’s observations—to see if we can still use it to calculate the true effect of 0.66 that we found above.

14.2.3 Re-estimate With limited data

Next, we will re-estimate the regression using OLS regression (without using bootstrapping yet for anything), but only on the limited n = 20 sample in d5. We will run the regression model—called reg.lim—and the confidence intervals all at once:

summary(reg.lim <- lm(total_cholesterol ~ weight + age + gender, data = d5))
## 
## Call:
## lm(formula = total_cholesterol ~ weight + age + gender, data = d5)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -71.531 -21.074   1.844  22.338  74.409 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)
## (Intercept)   55.3963    72.1326   0.768    0.454
## weight         0.5498     0.3531   1.557    0.139
## age            0.7604     0.6188   1.229    0.237
## genderfemale  29.6706    19.8295   1.496    0.154
## 
## Residual standard error: 41.56 on 16 degrees of freedom
## Multiple R-squared:  0.2484, Adjusted R-squared:  0.1075 
## F-statistic: 1.763 on 3 and 16 DF,  p-value: 0.1947
confint(reg.lim)
##                    2.5 %     97.5 %
## (Intercept)  -97.5179033 208.310474
## weight        -0.1988786   1.298391
## age           -0.5513594   2.072194
## genderfemale -12.3660990  71.707287

Above, when we only have a sample of 20 observations, we estimate an age slope of 0.76 units of cholesterol, with a 95% confidence interval of -0.551–2.072. This does not provide us with any evidence about the relationship between total_cholesterol and age.

Now that we have this OLS result, let’s see how we can re-estimate it with bootstrapping.

14.2.4 Bootstrapped confidence intervals with limited data

To use bootstrapping to re-calculate the regression we just ran above, we will only be re-calculating the confidence intervals of our regression estimates. To do this, we will use the Boot() function in the car package:

library(car)
reg.lim <- lm(total_cholesterol ~ weight + age + gender, data = d5)
reg.boot <- Boot(reg.lim, R=10000)
## Warning: package 'car' was built under R version 4.2.3

Here’s what we did above:

  • library(car) – Load the car package, which contains the Boot() function.
  • reg.lim <- lm(... – We re-ran the reg.lim regression that we had already run earlier on our small d5 sample of 20 observations. It is best to re-run the model right before you do the bootstrapping.224
  • reg.boot <- – Create a new regression result object called reg.boot.
  • Boot( – Call the Boot() function from the car package.
  • reg.lim – This is the first argument in the Boot() function, which is the old regression result that you want to bootstrap.
  • R=10000 – This is the second argument in the Boot() function, which is the number of bootstrap samples that you want the computer to draw to calculate your new regression estimates. Now that we have run our bootstrap model and saved it as reg.boot, we can look at the results:
print(confint(reg.boot, level=.95, type="norm"))
## Loading required namespace: boot
## Bootstrap normal confidence intervals
## 
##                     2.5 %    97.5 %
## (Intercept)  -118.3480053 247.79228
## weight         -0.4974841   1.51247
## age            -0.3849342   1.80150
## genderfemale   -2.8424331  60.59761

Above, we see the estimates (which are the same as before) and the 95% confidence intervals for these estimates (which are different than before). These are the new 95% confidence intervals after we bootstrapped.

Remember: the computer took our data in d5 and it re-sampled it to create 10,000 additional samples. These 10,000 samples are all different from each other since they randomly re-sampled d5 with replacement. This means that the results of bootstrapping will be different each time you do it.

We can look at this visually by running the hist() command on our bootstrapped regression result:

hist(reg.boot)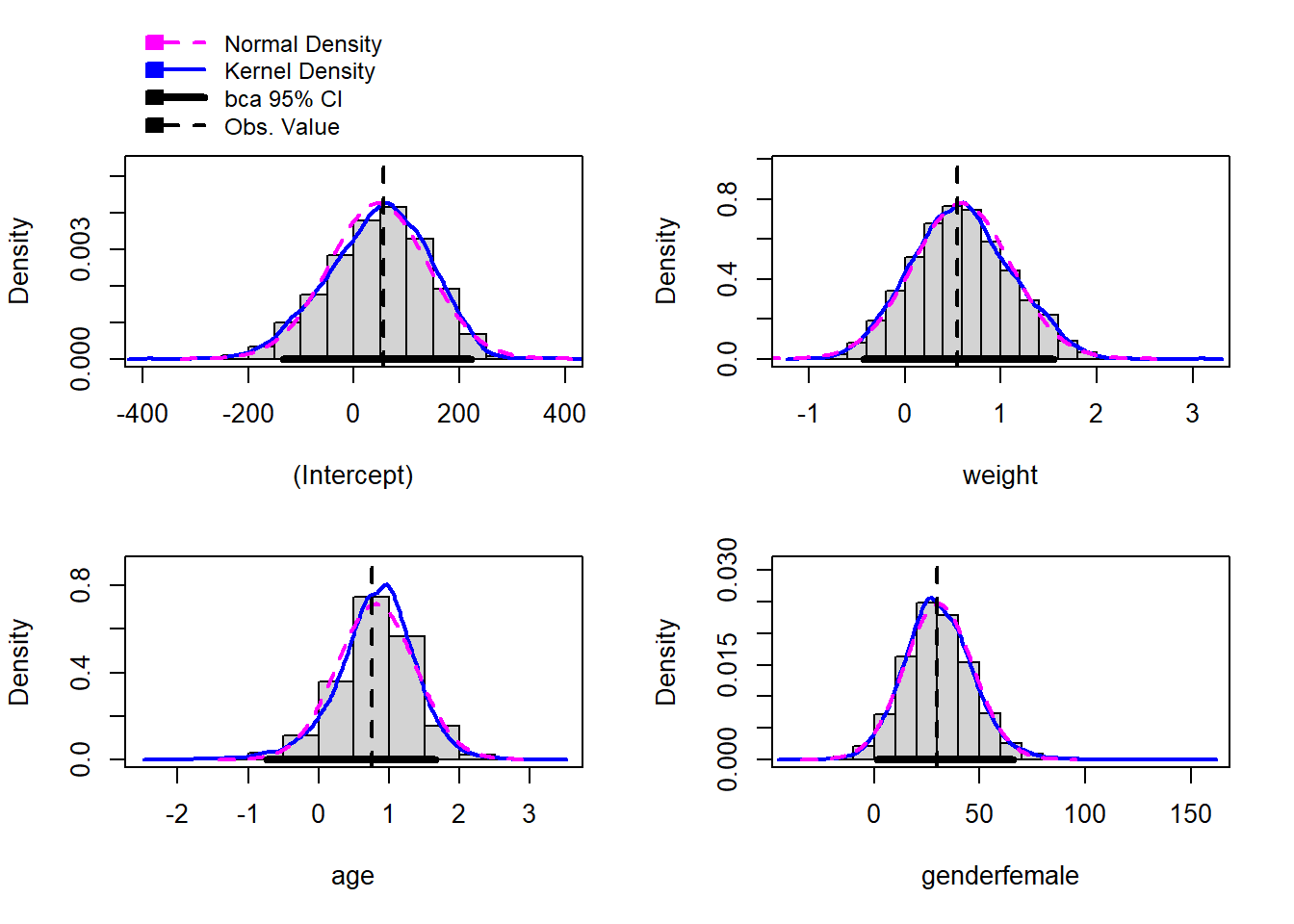

Here is how Fox and Weisberg describe these histograms:

There is a separate histogram for each bootstrapped quantity, here each coefficient. In addition to the histograms we also get kernel density estimates and the normal density based on the bootstrap mean and standard deviation. The vertical dashed line marks the original point-estimate, and the thick horizontal line gives a confidence interval based on the bootstrap.

For example, The computer did 10,000 different regressions and calculated the slope of age for each of these regressions. In the histogram for age, we see all of these different slope estimates plotted. The dotted vertical line is at 0.76, which is the original slope estimate, and the thick black horizontal line indicates the bootstrapped confidence interval for this estimate.

Keep reading to see a comparison of all of the regression models in this chapter.

14.2.5 Comparing the models

In this chapter, we have run three different regression models:

  1. reg.true, which is what we are pretending is the true estimate of age on total_cholesterol with a total sample of 403 observations.
  2. reg.lim, which is a 20-observation sample of our full data. This is an example of the situation we face when we only have a small dataset and only use OLS.
  3. reg.boot, which is a bootstrapped version of reg.lim in which we took 10,000 bootstrapped samples.

The table below summarizes the results we got from these three regressions:

Model Model Details Age Estimate Age 95% C.I.
reg.true Full n=403 dataset, OLS 0.66 0.405 – 0.924
reg.lim n=20 dataset, OLS 0.76 -0.551 – 2.072
reg.boot n=20 dataset, bootstrapped OLS 0.76 -0.385 – 1.802

Notes:

  • Above, all estimates of age are in units of total_cholesterol.
  • The confidence intervals will not be the same in all bootstrapped analyses, so if you run the same analysis twice, you might get different results each time.

Above, we see that the bootstrapped confidence interval for the age coefficient in the bootstrapped model is narrower (more confident) than that in the limited model. However, it did not get narrow enough to tell us if the effect of age on total_cholesterol is negative, zero, or positive.

14.3 Assignment

Since this is the final week of classes and a bit shorter than a usual week, this assignment is meant to be shorter and quicker than the other assignments.

In this assignment, you will look at a single dataset in both full and limited form, to practice using the bootstrapping method that was demonstrated in this chapter.

Just like this chapter has modeled, you will run one regression that represents the true relationship between your dependent variable and independent variable. Then, you will create a small sub-sample of your data and run the analysis again using bootstrapping.

This assignment is a good opportunity to use your own data, if you wish. If you do want to use your own data, just replace the variables in the instructions below with variables from your own dataset.

If you want to use data provided by me, you should once again use the diabetes dataset that was used throughout this chapter. This is the same data and question that we used last week! Of course, our results will be different this time.

You can click here to download the dataset. Then run the following code to load the data into R:

if (!require(foreign)) install.packages('foreign')
library(foreign)

diabetes <- read.spss("diabetes.sav", to.data.frame = TRUE)

Our research question of interest is:

  • What is the relationship between stabilized glucose and BMI, controlling for age and gender?

These are the variables you will use:

  • Dependent variable: stabilized.glucose
  • Independent variables: BMI, age, gender

You will use OLS to estimate this regression model. (If you are using your own data, then you do not necessarily have to use a linear regression model; any kind of regression model is fine in that case.)

Using this data and this research question, you will follow a progression that is similar to that demonstrated in this chapter. Be sure to show the code you use for each task below, even if you are not asked to give any interpretation (unless otherwise noted).

14.3.1 Calculate true relationship

Task 1: Using the complete dataset, calculate the true relationship between your dependent variable and independent variables. We will refer to this regression model as the true result or true relationship. Interpret the result. This is the same as last week! Just copy your answer here, if you are using the same data that you used last week.

14.3.2 Create a small sample

Task 2: Make a new dataset called d20, which contains a random sample of just 20 rows from the data you are using.

Task 3: Use the nrow() command to make sure that you successfully created d20.

Task 4: Inspect d20 visually to check for any clearly-visible errors. Do not show this in your submitted assignment.

14.3.3 Limited Model

Task 5: Run a “limited model” in which you run the same regression model you ran to calculate the true effect, but this time just on your smaller sample dataset, d20. Interpret the results of this model with respect to your research question. Make sure you also calculate and interpret the 95% confidence interval for the key independent variable in our research question.

14.3.4 Bootstrapping

In this part of the assignment—since you will use bootstrapping, which does involve some randomness—the numbers in your output might change each time you run your code. It is completely fine for the numbers in your written answers to the tasks to not match the numbers in the computer output.

Task 6: Bootstrap the limited regression model with 10, 100, and 1000 bootstrapped samples. To do this, you will make three separate bootstrapped regression models, each time changing the R= argument within the Boot function. Show the estimates and confidence intervals for each one.

Task 7: Make histograms for the R=1000 bootstrapped estimates. Interpret these histograms.

Task 8: Compare the results of all five regression models with each other: true effect model, limited model without bootstrapping, and the three bootstrapped models. How close were the bootstrapped models to the true model? How did the bootstrap estimates change as the number of samples increased?

14.3.5 Reflect on course and think to the future

Since this is the final chapter of our course, we will review and reflect a little bit. Click here to read a list of key points that you should always remember. Then, please address the tasks below.

Task 9: After reading the list carefully, which single item on the list do you think you are personally most likely to forget?

Task 10: After reading the list carefully, which single item on the list do you think you are personally most likely to remember well?

Task 11: If you have not done so already, please consider filling out the evaluation survey for this course. You should have received a link to the evaluation by email (please check your MGHIHP email inbox). Your feedback is extremely valuable to us. We read it carefully and often make changes to the course based on it.

Task 12: If you disseminate or publish any work that you did during this class, please be sure to give credit to members of this class from whom you received feedback and ideas. You can do this in an acknowledgments section, for example. If a member of this class made a more substantial intellectual and/or practical contribution to the work, you should consider inviting them to be a co-author on your work. Additionally, please be sure to read and adhere to the journal authorship guidelines related to work you submit for publication. Does this reminder about academic integrity make sense to you? Please answer yes or no. Feel free to include any follow-up questions.

Task 13: In the future, if you are working on quantitative research tied to your dissertation or another part of the PhD program, we heavily recommend that you use R and RStudio for your data analysis. If you find yourself thinking about not using R and RStudio in the future, we strongly recommend that you contact one of us (the instructors of HE-902) to discuss an alternate plan. We are here to support you in your quantitative analysis until you graduate (and often beyond). Please use us as a resource when you plan your dissertation or other projects. Did you read and understand this recommendation? Please answer yes or no. Feel free to include any follow-up questions. We give you this recommendation based on experience. In the past, when PhD candidates have used alternate software (not R and RStudio) for their analyses, they or their dissertation committee have encountered challenges. We then needed to rush to re-do the analysis in R and RStudio. It’s almost always more productive to just use R and RStudio from the start.

14.3.6 Additional items

You have now reached the end of this week’s assignment. The tasks below will guide you through submission of the assignment, remind you of any other items you need to complete this week, and allow us to gather questions and/or feedback from you.

Task 14: You are required to complete 15 quiz question flashcards in the Adaptive Learner App by the end of this week.

Task 15: Please schedule a time for your Oral Exam #3 if you have not done so already.

Task 16: Please write any questions you have for the course instructors (optional).

Task 17: Please write any feedback you have about the instructional materials (optional).

Task 18: Knit (export) your RMarkdown file into a format of your choosing.

Task 19: Please submit your assignment to the D2L assignment drop-box corresponding to this chapter and week of the course. And remember that if you have trouble getting your RMarkdown file to knit, you can submit your RMarkdown file itself. You can also submit an additional file(s) if needed.

  1. While there may be other applications of bootstrapping techniques, we will only use bootstrapping in the context of estimating regression coefficients and their confidence intervals.↩︎

  2. Replacement is a concept from probability. The following resource explains and gives an example: “Sampling With Replacement / Sampling Without Replacement” in Practically Cheating Statistics Handbook. Statistics How To. https://www.statisticshowto.com/sampling-with-replacement-without/.↩︎

  3. Emphasis has been added and text has been reformatted.↩︎

  4. If you don’t re-run the model before you bootstrap, you might get an error message like the following when you run the Boot() function: Error incontrasts<-(tmp, value = contr.funs[1 + isOF[nn]]) : contrasts can be applied only to factors with 2 or more levels↩︎