Chapter 34 Random effects

Motivating scenario: We want to estimate the variability among groups or the repeatability within subjects, or we want to include nonindependence in our model.

34.1 Review

34.1.1 Linear models

Remember, linear models predict Y as a deviation from some constant, a, as a function of a bunch of stuff.

\[\widehat{Y_i} = a + b_1 \times y_{1,i} + b_2 \times y_{2,i} + \dots\]

34.1.2 Analysis of Variance (ANOVA)

We can test for the significance of factors in linear model in an ANOVA framework.

In Chapter 20, we saw that the total estimate of the variance among groups included that attributable to true differences between groups and those attributable to random sampling error.

Both of these measures go into \(MS_{groups}\) but we expect that that induced by sampling will be roughly equal to \(MS_{error}\).

This is why we test the one-tailed null hypothesis that F (i.e. \(\frac{MS_{groups}}{MS_{error}}\)) equals one, when we ask if the variance among groups is non zero.

34.1.2.1 Assumptions & Common Violations of Linear models

Linear models assume that: (1) Data points are independent, and (2) unbiased, and can be modeled as a linear combination of predictors. With (3) error with a mean and variance that is independent of predictors (4) and normally distributed.

Biology breaks assumptions of the linear models

We have addressed binomial and count data with Logistic and Poisson regression from the generalized linear model.

We are now moving towards addressing what to do when we violate the assumption of independence. This is important because this is among the most commonly broken assumptions in biological data.

34.2 Intro to Random effects

In biology we are rarely interested in specific individuals. Rather we are often interested in variability. Variability over space, or individuals etc.

For example, the response to natural selection depends critical on the genetic variability a population.

In addition to the biological importance of variability, we are often interested as scientists in how repeatable (or reliable) someone is. For example, if we measure the same individual twice how similar will our measurements be relative to the variability in our broader sample.

Finally, sometimes we don’t even care specifically about this variability, but rather we think it will make our data non-independent. For example, if I grow plant in a bunch of plots and want to see the effect of fertilizer on plant growth, I want to model the non-independence of plants in a plot.

All the examples above have something in common – we don’t care about specific individuals or locations, rather we want to know about the variability across them.

34.2.1 Fixed vs random effects

Up to this point we have considered “fixed effects” e.g. fertilizer choice, experimental treatment etc… For these cases, we want to predict the effects of these treatments, and we don’t generalize to other treatments – for example if I looked at how three fertilizers of interest impacted plant growth, I wouldn’t go and predict the effect of a totally different fertilizer I hadn’t seen before.

However, in the examples above, we did not care about the “fixed effect”. Rather, we were interested in random effects the variability we find across “random” individuals (or locations etc.) in our population. For these cases, we don’t aim to predict the value of individuals, but rather we aim to describe the expected variability we expect across random individuals in our population. Thus, we hope to generalize to a larger population of sample units.

34.2.1.1 How do we know if we have a fixed or random effect?

Some is inherent to the experimental design:

• Are levels of a predictor chosen intentionally (e.g. temperature treatments)? Fixed
  
• Do we want to make inferences about the levels of a predictor (e.g. mean separation)? Fixed
  
• Can we reasonably expect covariance between levels of a predictor? Random

Some of this is inherent to the predictor:

• Are the levels of a predictor sampled from some distribution of possible levels? Random
  
• Can we borrow information across levels of a predictor? Random

34.2.2 Motivating Example:

Huey and Dunham (1987) were interested in the variability of running speed of the lizard Sceloporus merriam in Big Bend National Park in Texas. So, they built a a two meter raceway, grabbed some lizards and measured their speed. But they were concerned that this would measure something about the lizards motivation to run or the speed at that time etc… so they replicate this and ran each lizard twice.

The data, presented below, can be accessed from this link

34.2.3 Estimating variance components

ggplot(lizard_runs, aes(x = factor(lizard), y = speed, group = lizard)) +
  geom_point()+
  geom_line()

With random effects, we are interested in two sources of variation – that that is between individuals (or locations or whatever) and that that is within them. This sounds a lot like a fixed effects ANOVA, so that will be our starting place. Let’s look at this output, but ignore F and P as we don’t care about them for random effects.

lizard_runs <- lizard_runs %>% mutate( lizard = as.factor(lizard)) # we don't want R thinking lizard 3 is two more than lizard one   
lizard_runs_lm <- lm(speed ~ lizard, data = lizard_runs)
anova(lizard_runs_lm)

## Analysis of Variance Table
## 
## Response: speed
##           Df Sum Sq Mean Sq F value  Pr(>F)    
## lizard    33  11.32   0.343    7.45 3.4e-08 ***
## Residuals 34   1.57   0.046                    
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

We see that the mean squared error (the average squared difference between lizard means and the overall mean) is 0.34309.

Now some of this is due to variability among lizards and some of this is due to chance sampling! How much variability among groups do we expect to arise by chance? – well we know this, it’s the mean squared error!!!!

So, we estimate the variance among groups as this difference divided by the number of individuals per group, because each one contributed to our MS_{group} estimate. Overall, our estimate of the variance among groups, \(s_A^2\) is:

\[s_A^2 = \frac{MS_{group} - MS_{error}}{n_{per group}}\].

For this example, the variance among groups is \(\frac{0.34309 - 0.04607}{2}\) = 0.1485. That is, we think that if we raced each lizard MANY (like an infinite number of) times the variance in average running speeds across lizards would be 0.1485.

34.2.3.1 With lme4

For simple models like this example, we can use an ANOVA table to estimate \(s_A^2\). But as we get to more complex models that “mix” random and fixed effects this get harder. We can therefore use the lmer() function in the lme4 package to run random and mixed effect (next class) models for us. This syntax of lmer is a lot like lm() with the caveat that we need a language for specifying random effects. We specify that we want to estimate variance (or more precisely standard deviations) in means for a model where groups are random samples from a population as follows

library(lme4) # install lme4 first if you have not already
lizard_runs_rand <- lmer(speed ~ (1|lizard), data = lizard_runs)
lizard_runs_rand

## Linear mixed model fit by REML ['lmerMod']
## Formula: speed ~ (1 | lizard)
##    Data: lizard_runs
## REML criterion at convergence: 54.42
## Random effects:
##  Groups   Name        Std.Dev.
##  lizard   (Intercept) 0.385   
##  Residual             0.215   
## Number of obs: 68, groups:  lizard, 34
## Fixed Effects:
## (Intercept)  
##        2.14

Here

• The “REML criterion at convergence:” is two times the log likelihood of this model 2 * logLik(lizard_runs_rand) = r2 * logLik(lizard_runs_rand) %>% as.numeric()`.
  
• The Std.Dev for lizard is the square root of our estimate of the variance among lizards, \(s_A^2\), above (\(\sqrt{0.1485} = 0.385357\)).
  
• The Std.Dev Residual our estimate for the expected variability within groups is the square root of the mean square error, above (\(\sqrt{0.04607} = 0.2146\)).
  
• The Fixed effect for the overall intercept is our guess at the mean: summarize(lizard_runs, mean(speed)) = 2.1391.

34.2.4 Hypothesis testing for random effects

We can use a likelihood ration test to test the null hypothesis that the among subject variance is zero. We do this by

• Finding two times the difference in log likelihoods of the random effects and null models
  
• Comparing this value to the \(\chi^2\) distribution with one degree of freedom (because we only estimate one parameter – the variance).
  
• Because we use Restricted maximum likelihood - (REML) to fit the random effects model, we need to calculate the log likelihood of both the null and random effects model by REML.

log_lik_rand <- lmer(speed  ~ (1|lizard), data = lizard_runs) %>% logLik(REML = TRUE)
log_lik_null <- lm(speed  ~ 1 , data = lizard_runs)           %>% logLik(REML = TRUE)
d <- 2 * (log_lik_rand - log_lik_null)
p <-pchisq(q = d, df = 1, lower.tail = FALSE)                                          

## log_lik_rand  log_lik_nul            d            p 
##   -2.721e+01   -4.196e+01    2.950e+01    5.594e-08

Or we can have R do this for us with the ranova() function in the lmerTest package

library(lmerTest)
ranova(lizard_runs_rand)

## ANOVA-like table for random-effects: Single term deletions
## 
## Model:
## speed ~ (1 | lizard)
##              npar logLik  AIC  LRT Df Pr(>Chisq)    
## <none>          3  -27.2 60.4                       
## (1 | lizard)    2  -42.0 87.9 29.5  1    5.6e-08 ***
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

34.2.5 Repeatability

In a random effects model, we estimate the variance among groups \(s_A^2\). But we might wonder what proportion of the variance in our population do we think is among groups. This is known as “repeatability” or “the interclass correlation” and equals

\[\frac{s_A^2}{s_A^2 + MS_{error}}\]

A repeatability of zero means that measuring the same sample twice is about as reliable as taking two random samples, while a repeatability of one would imply no variation within an individual.

The repeatability for our lizard running example is = 0.763, so this is pretty repeatable.

34.2.5.1 Repeatability vs \(R^2\)

Repeatability measures how repeatable our measure is – that is what is how similar do we expect two measurements from a random lizard to be. This is only meaningful for random effects, but is super useful because this parameter has meaning outside of our model.

This is very different than \(r^2\) the proportion of variance “explained by our model” (\(SS_{groups}/SS_{total}\)). \(r^2\) is not a parameter we can interpret outside of the scope of a single experiment. In our example \(r^2\) equals \(11.3219 / ( 11.3219 +1.5664) = 0.8785\) a number that clearly differs from our estimated repeatability.

34.2.6 Shrinkage

We know from our background on “regression to the mean” that exceptional values are likely overestimates. A ice benefit of the random effects approach is that we share information across individuals. That is, our estimate for an individual is “shrunk” towards the overall population mean.

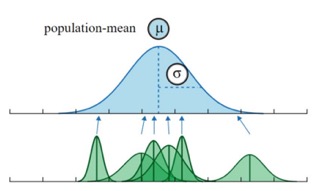
Shrinkage depends on:

• How variable the coefficients are across clusters
  
• The degree of uncertainty associated with individual estimates

Let’s explore this for our lizard data:

First, lets grab predictions from our fixed effect model

fixed_predicted_means <- augment(lizard_runs_lm) %>%
  dplyr::select(lizard, .fitted) %>%
  dplyr::distinct(lizard,.fitted)%>%
  mutate(effect = "fixed")

Now let’s grab predictions from our random effect model

rand_predicted_means <- broom.mixed::augment(lizard_runs_rand) %>%
  dplyr::select(lizard, .fitted) %>%
  dplyr::distinct(lizard,.fitted)%>%
  mutate(effect = "random")

Now let’s combine them and plot. We see this “shrinkage” as extreme estimates are pulled toward the mean in the random-effect based estimates.

bind_rows(fixed_predicted_means,rand_predicted_means) %>%
  mutate(lizard = fct_reorder(lizard, .x = .fitted, .fun = mean)) %>%
  ggplot(aes(x = lizard, y = .fitted, color = effect))+
  geom_point()+
  geom_hline(yintercept =  2.139)

34.2.7 Assumptions of random effects models

Random effects models make our standard linear model assumptions and also assumes that groups (e.g. individuals, sites, etc.) are sampled at random and that group means are normally distributed.

But, we see in the next chapter that by modeling random effects we can model non-independence of observations.

34.2.8 Random effects Quiz

34.3 Mixed effects models

Of course, we can overcome this assumption of independence by modelling the dependence structure of the data. For example, if results of student’s tests are nondependent because they are in a class in a school we can put school and class into our model.

When we aren’t particularly interested in school or class themselves, these are called nuisance parameters.

When school (or class, or whatever “cluster” we’re concerned with) is chosen at random we can model it as a random effect. If not, we can use various other models, including generalized least squares (GLS), which we are not covering right now, but which have similar motivations.

34.3.1 Thinking about mixed effects models

How do we test for some fixed effect, like if type of math instruction increases math scores, in the presence of this nonindependence (like students in the same class learn from the same teacher etc…)?

In a mixed effect model, we model both fixed and random effects!!!!

34.3.1.1 Random Intercepts

With a “random intercept” each cluster gets its own intercept, which it drawn from some distribution. This on its own is much like the example in Chapter ??.

If we assume a random intercept only, we assume that each cluster draws an intercept from some distribution, but that clusters have the same slope (save what is specified in the fixed effect).

34.3.1.2 Random Slopes

With a “random slope” each cluster gets its own slope, which it drawn from some distribution.

If we assume a random slope only, we assume that each cluster draws a slope from some distribution, but that cluster have the same intercepts (save what is specified in the fixed effect).

34.3.1.3 Random Slopes and Random Intercepts

We can, in theory model both random slopes and random intercepts. But sometimes these are hard to estimate together, so be careful.

34.3.1.4 Visualizing Random Intercepts and Random Slopes

I find it pretty hard to explain random slopes and intercepts in words, but that pictures really help!

Read and scroll through the example below, as it is the best description I’ve come across (for some reason, the embedded app has been finicky, so if it doesn’t show up go directly to the website here.

34.3.2 Mixed model: Random intercept example

Selenium, is a bi-product of burning coal. Could Selenium bioaccumulate in fish, suchb that fish from lakes with more selenium have more selenium in them?

Let us look at data (download here) from 98 fish from nine lakes, with 1 to 34 fish per lake.

34.3.2.1 Ignoring nonindependence is inappropriate

What if we just ignored lake and assumed each fish was independent???

selenium     <- read_csv("https://drive.google.com/uc?export=download&id=1UAkdZYLJPWRuFrq9Dc4StxfHCGW_43Ye")
selenium_lm1 <- lm(Log_fish_Se ~  Log_Water_Se, data = selenium)

summary(selenium_lm1)

## 
## Call:
## lm(formula = Log_fish_Se ~ Log_Water_Se, data = selenium)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -0.757 -0.311 -0.179  0.430  0.818 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    1.1635     0.0639   18.22  < 2e-16 ***
## Log_Water_Se   0.2648     0.0586    4.52  2.1e-05 ***
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.43 on 81 degrees of freedom
## Multiple R-squared:  0.201,  Adjusted R-squared:  0.192 
## F-statistic: 20.4 on 1 and 81 DF,  p-value: 2.08e-05

anova(selenium_lm1)

## Analysis of Variance Table
## 
## Response: Log_fish_Se
##              Df Sum Sq Mean Sq F value  Pr(>F)    
## Log_Water_Se  1   3.79    3.79    20.4 2.1e-05 ***
## Residuals    81  15.01    0.19                    
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

ggplot(selenium, aes(x = Log_Water_Se, y = Log_fish_Se, label = Lake)) +
  geom_point(aes(color = Lake), alpha = .5, size = 3) +
  geom_smooth(method = "lm")

That would be a big mistake – as each fish is not independent. There could be something else about the lake associated with levels of Selenium in fish that is not in our model. This seems likely, as we see below, that residuals differ substantially by lake.

bind_cols( selenium , 
           augment(selenium_lm1)  %>%    dplyr::select(.resid))%>%
  ggplot(aes(x = Lake, y = .resid, color = Lake)) +
  geom_jitter(width = .2, size = 3, alpha =.6, show.legend = FALSE)+
  geom_hline(yintercept = 0, color = "red")+
  stat_summary(data = . %>% group_by(Lake) %>% mutate(n = n()) %>% dplyr::filter(n>1), color = "black")

So why is this so bad? It’s because we keep pretending each fish is independent when it is not. So, our certainty is WAY bigger than it deserves to be. This means that our p-value is WAY smaller than it deserves to be.

34.3.2.2 We can’t model lake as a fixed effect

And even if we could it would be wrong.

Putting lake into our model as a fixed effect would essentially take the average of Fish Selenium content for each lake. Since each lake has only one Selenium content, we then have nothing to model.

lm(Log_fish_Se ~  Lake + Log_Water_Se, data = selenium) 

## 
## Call:
## lm(formula = Log_fish_Se ~ Lake + Log_Water_Se, data = selenium)
## 
## Coefficients:
##  (Intercept)         Lakeb         Lakec  
##       1.1619       -0.0895        1.1707  
##        Laked         Lakee         Lakef  
##       0.0863        0.7049       -0.6349  
##        Lakeg         Lakeh         Lakei  
##       0.7480       -0.0710        0.3786  
## Log_Water_Se  
##           NA

But even when this is not the case, this is not the appropriate modelling strategy.

34.3.2.3 Taking averages is a less wrong thing

What if we just took the average selenium content over all fish for every lake, and then did our stats?

selenium_avg <- selenium %>% 
  group_by(Lake, Log_Water_Se) %>%
  summarise(mean_log_fish_Se = mean(Log_fish_Se), n = n()) 

selenium_lm2 <- lm(mean_log_fish_Se ~  Log_Water_Se, data = selenium_avg)
summary(selenium_lm2)

## 
## Call:
## lm(formula = mean_log_fish_Se ~ Log_Water_Se, data = selenium_avg)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.5066 -0.3654  0.0346  0.4287  0.5542 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)   
## (Intercept)     1.131      0.209    5.40    0.001 **
## Log_Water_Se    0.367      0.181    2.03    0.082 . 
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.465 on 7 degrees of freedom
## Multiple R-squared:  0.371,  Adjusted R-squared:  0.281 
## F-statistic: 4.13 on 1 and 7 DF,  p-value: 0.0816

anova(selenium_lm2)

## Analysis of Variance Table
## 
## Response: mean_log_fish_Se
##              Df Sum Sq Mean Sq F value Pr(>F)  
## Log_Water_Se  1  0.894   0.894    4.13  0.082 .
## Residuals     7  1.515   0.216                 
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

ggplot(selenium_avg, aes(x = Log_Water_Se, y = mean_log_fish_Se, label = Lake)) +
  geom_point(aes(size = n)) +
  geom_text_repel(aes(color = Lake), show.legend = FALSE) +
  geom_smooth(method = "lm",se = FALSE)

This approach isn’t too bad, but there are some shortcomings –

1. It takes all means as equally informative, even though some come from large and others from large samples.
   
2. It ignores variability within each lake,
   
3. It surrenders so much of our hard-won data.

34.3.2.4 Accounting for Lake as a Random Effect is our best option

Rather, we can model Lake as a random effect – this allows us to model the non-independence of observations within a Lake, while using all of the data.

selenium_lme <- lmer(Log_fish_Se ~   (1|Lake) + Log_Water_Se , data = selenium)
summary(selenium_lme)

## Linear mixed model fit by REML. t-tests use
##   Satterthwaite's method [lmerModLmerTest]
## Formula: Log_fish_Se ~ (1 | Lake) + Log_Water_Se
##    Data: selenium
## 
## REML criterion at convergence: -8.8
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.1554 -0.3740  0.0424  0.5495  2.5473 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  Lake     (Intercept) 0.2075   0.455   
##  Residual             0.0355   0.188   
## Number of obs: 83, groups:  Lake, 9
## 
## Fixed effects:
##              Estimate Std. Error    df t value
## (Intercept)     1.132      0.209 6.842    5.42
## Log_Water_Se    0.366      0.179 6.727    2.04
##              Pr(>|t|)   
## (Intercept)    0.0011 **
## Log_Water_Se   0.0825 . 
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr)
## Log_Water_S -0.666

Thus we fail to reject the null, and conclude that there is not sufficient evidence to support the idea that more selenium in lakes is associated with more selenium in fish.

34.3.2.4.1 Extracting estimates and uncertainty

Although we do have model estimates, degrees of freedom and standard deviations above, if ca still be hard to consider and communicate uncertainty. The ggpredict function in the ggeffects package can help!

library(ggeffects)
gg_color_hue <- function(n) {hues = seq(15, 375, length = n + 1); hcl(h = hues, l = 65, c = 100)[1:n]}

selenium_predictions <- ggpredict(selenium_lme, terms = "Log_Water_Se")
selenium_predictions

## # Predicted values of Log_fish_Se
## 
## Log_Water_Se | Predicted |       95% CI
## ---------------------------------------
##        -0.30 |      1.02 | [0.54, 1.51]
##         0.75 |      1.41 | [1.10, 1.71]
##         0.84 |      1.44 | [1.13, 1.74]
##         0.95 |      1.48 | [1.17, 1.79]
##         1.70 |      1.75 | [1.31, 2.20]
##         1.76 |      1.78 | [1.31, 2.24]
##         1.91 |      1.83 | [1.33, 2.33]
## 
## Adjusted for:
## * Lake = 0 (population-level)

plot(selenium_predictions)+
  geom_point(data = selenium, aes(x = Log_Water_Se , y= Log_fish_Se, color = Lake), alpha = .4, size = 3)+
  scale_color_manual(values = gg_color_hue(9))

34.3.2.4.2 Evaluating assumptions

We can now see that by modeling Lake as a random effect, the residuals are now independent.

bind_cols( selenium , 
           broom.mixed::augment(selenium_lme)  %>%    dplyr::select(.resid))%>%
  ggplot(aes(x = Lake, y = .resid, color = Lake)) +
  geom_jitter(width = .2, size = 3, alpha =.6, show.legend = FALSE)+
  geom_hline(yintercept = 0, color = "red")+
  stat_summary(data = . %>% group_by(Lake) %>% mutate(n = n()) %>% dplyr::filter(n>1),color = "black")

Major assumptions of linear mixed effect models are

• Data are collected without bias
  
• Clusters are random
  
• Data can be modelled as a linear function of predictors
  
• Variance of the residuals is independent of predicted values,
  
• Residuals are normally distributed,

Let’s look into the last two for these data. Because we hate autoplot, and it can’t handle random effects output, let’s make out own diagnostic plots.

selenium_qq <- broom.mixed::augment(selenium_lme) %>% 
  ggplot(aes(sample = .resid))+ 
  geom_qq()+
  geom_qq_line()

selenium_std_resid  <- broom.mixed::augment(selenium_lme) %>% 
  mutate(sqrt_abs_std_resid = sqrt(abs(.resid / sd(.resid)) )) %>%
  ggplot(aes(x = .fitted, y = sqrt_abs_std_resid)) + 
  geom_point() 

plot_grid(selenium_qq, selenium_std_resid, ncol = 2)

These don’t look great tbh. We would need to think harder if we were doing a legitimate analysis.

34.3.3 Example II: Loblolly Pine Growth

Let’s try to model the growth rate of loblolly pines!

First I looked at the data (a), and thought a square root transform would be a better linear model (b), especially if I began my model after three years of growth (c).

Loblolly <- mutate(Loblolly, Seed = as.character(Seed))
a <- ggplot(Loblolly, aes(x = age, y = height, group = Seed, color = Seed))+ geom_line()
b <- ggplot(Loblolly, aes(x = sqrt(age), y = height, group = Seed, color = Seed))+ geom_line()
c <- ggplot(Loblolly %>% filter(age > 3), aes(x = sqrt(age), y = height, group = Seed, color = Seed))+ geom_line()
top  <- plot_grid(a+theme(legend.position = "none"),     
                  b+theme(legend.position = "none"),  
                  c+theme(legend.position = "none") , 
                  labels = c("a","b","c"), ncol = 3)
legend<- get_legend(a+ guides(color = guide_legend(nrow=2)) + theme(legend.position = "bottom", legend.direction = "horizontal") ) 
plot_grid(top, legend, ncol =1, rel_heights = c(8,2))

34.3.3.1 Random Slopes

loblolly_rand_slope <- lmer(height ~ age + (0+age|Seed), data = filter(Loblolly, age>3))
summary(loblolly_rand_slope)

## Linear mixed model fit by REML. t-tests use
##   Satterthwaite's method [lmerModLmerTest]
## Formula: height ~ age + (0 + age | Seed)
##    Data: filter(Loblolly, age > 3)
## 
## REML criterion at convergence: 348.6
## 
## Scaled residuals: 
##    Min     1Q Median     3Q    Max 
## -1.611 -0.959  0.195  0.704  1.813 
## 
## Random effects:
##  Groups   Name Variance Std.Dev.
##  Seed     age  0.00578  0.076   
##  Residual      7.11659  2.668   
## Number of obs: 70, groups:  Seed, 14
## 
## Fixed effects:
##             Estimate Std. Error      df t value
## (Intercept)   0.7312     0.7478 55.0000    0.98
## age           2.4839     0.0495 61.4194   50.22
##             Pr(>|t|)    
## (Intercept)     0.33    
## age           <2e-16 ***
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##     (Intr)
## age -0.825

broom.mixed::augment(loblolly_rand_slope) %>% mutate(Seed = as.character(Seed))  %>%
  ggplot(aes(x = age, y = .fitted, color = Seed)) + 
  geom_line() + theme(legend.position = "none")

34.3.3.2 Random Intercepts

loblolly_rand_intercept <- lmer(height ~ age + (1|Seed), data = filter(Loblolly, age>3))
summary(loblolly_rand_intercept)

## Linear mixed model fit by REML. t-tests use
##   Satterthwaite's method [lmerModLmerTest]
## Formula: height ~ age + (1 | Seed)
##    Data: filter(Loblolly, age > 3)
## 
## REML criterion at convergence: 349.6
## 
## Scaled residuals: 
##    Min     1Q Median     3Q    Max 
## -1.939 -0.984  0.264  0.769  1.806 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  Seed     (Intercept) 1.32     1.15    
##  Residual             7.38     2.72    
## Number of obs: 70, groups:  Seed, 14
## 
## Fixed effects:
##             Estimate Std. Error      df t value
## (Intercept)   0.7312     0.8208 63.4741    0.89
## age           2.4839     0.0459 55.0000   54.11
##             Pr(>|t|)    
## (Intercept)     0.38    
## age           <2e-16 ***
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##     (Intr)
## age -0.839

broom.mixed::augment(loblolly_rand_intercept) %>% mutate(Seed = as.character(Seed))  %>%
  ggplot(aes(x = age, y = .fitted, color = Seed)) + 
  geom_line() + theme(legend.position = "none")

34.3.4 Mixed effects quiz

34.4 Additional related topics

Sadly our term is coming to an end, as we are just beginning to explore these more complex, flexible, and realistic models. In this brief section, I will show you a few fun directions for more complex models. If you are interested in these problems, I highly recommend John Fieberg’s fantastic course – FW8051 Statistics for Ecologists.

34.4.1 Generalized Least Squares

We can still run into issues of heteroscedasticity and hierarchical model structure with non-random groups. For such cases, we can use generalized least squares. In R, we can do this with the gls() function in the nlme package.

34.4.2 More complex covariance structures

We have considered a simple random effect where individuals are in one group or another. Sometimes the world i more complicated – for example if we have random families, individuals within the family are not equally related. We therefore want to specify more realistic covariances of residuals. In R, we can do this with the lme() function in the nlme package.

34.4.3 Generalized Linear Mixed Effect Models

In Chapters 32 and ?? we saw that we could generalize a linear model to nonlinear distributions. We can do the same for mixed effects models. We can do this with the glmer() function in lme4. These can be a bit tricky, so proceed with caution.