Chapter 14 Associations between continuous variables

This text (roughly) follows Chapter 16 of our textbook. The reading below is required, Whitlock and Schluter (2020) is not.

Motivating scenarios: We are interested to estimate an association between two continuous variables, and test if this association is differs from zero.

Learning goals: By the end of this chapter you should be able to

Summarize the association between to continuous variables as
- Covariance AND
- Correlation
Estimate uncertainty in these estimates by
- By bootstrapping AND
- Naively taking R’s output at face value.
Test the null hypothesis of no association by
- A permutation test
- Naively accepting R’s output at face value.

No additional reading is assigned. But this paper by my colleague here (Fieberg, Vitense, and Johnson 2020) helped lays out why this is a good way to do and teach statistics.

14.1 Associations between continuous variables

One of the most common statistical questions we come across is “are the two variables associated?”

For instance, we might want to know if people who study more get better grades.

Such an association would be quite interesting, and if it arises in a randomized controlled experiment, it would suggest that studying caused this outcome.

What confounds could explain an association (or lack thereof) if this was an observational study?

14.2 Example: Disease and sperm viability

It is hypothesized that there is a trade off between investment in disease resistance and reproduction. To look into this, Simmons and Roberts (2005), assayed sperm viability and lysozyme activity (a measure of defense against bacteria) in 39 male crickets. Let’s use this to explore associations between continuous variables.

ggplot(crickets , aes(x = spermViability, y = lysozyme))+
  geom_point()+
  labs(x = "Sperm viability (%)", y = expression(paste("Lysozyme activity (",mm^2,")")))

Association between reproduction (measured as sperm viability) and immunity (measured as the diameter of lysozyme). Data from @simmons2005 are available [here](https://whitlockschluter3e.zoology.ubc.ca/Data/chapter16/chap16q12CricketImmunitySpermViability.csv). One extreme outlier was removed to simplify the analysis for purposes of explanation (it would not be removed in a real study).

FIGURE 14.1: Association between reproduction (measured as sperm viability) and immunity (measured as the diameter of lysozyme). Data from Simmons and Roberts (2005) are available here. One extreme outlier was removed to simplify the analysis for purposes of explanation (it would not be removed in a real study).

14.3 Summarizing associations between two categorical variables

We focus on two common summaries of associations between two continuous variables, X and Y, the covariance and the correlation.

Both these summaries describe the tendency for values of X and Y to jointly deviate from the mean.

If larger values of X tend to come with larger values of Y the covariance (and correlation) will be positive.
If smaller values of X tend to come with larger values of Y the covariance (and correlation) will be negative.
A covariance (or correlation) of zero means that – on average – X and Y don’t predictably deviate from their means in the same direction. This does not guarantee that X and Y are independent – if they are related by a curve rather than a line, X could predict Y well even if the covariance (or correlation) was zero. It does mean that the best fit line between X and Y will be flat.

For both these summaries X and Y are arbitrary - the covariance between sperm viability and lysozyme activity is the same as the covariance between lysozyme activity and sperm viability.

14.3.1 Covariance

The covariance quantifies the shared deviation of X and Y from the mean as follows:

\[\begin{equation} \begin{split} \text{Sample covariance between X and Y} = Cov(X,Y) &=\frac{\sum{\Big((X_i-\overline{X})\times (Y_i-\overline{Y})\Big)}}{n-1}\\ \end{split} \tag{14.1} \end{equation}\]

The numerator in Eq. (14.1) is known as the ‘Sum of Cross Products’. This should remind you of the numerator in the variance calculation (Sum of squares = $\sum(X-\overline{X})(X-\overline{X})$) – in fact the covariance of X with itself is its variance. The covariance can range from $-\infty$ to $\infty$, but in practice cannot exceed the variance in X or Y.

Some algebra can rearrange Eq. (14.1) to become Eq. (14.2). These two different looking equations are identical. Often, computing the covariance from (14.1) is more convenient, but this isn’t always true, sometimes dealing with Eq. (14.2) is more convinient.

\[\begin{equation} \begin{split} \text{Sample covariance between X and Y} = Cov(X,Y) &= \frac{n-1}{n}(\overline{XY} - \overline{X} \times \overline{Y})\\ \end{split} \tag{14.2} \end{equation}\]

We can calculate the covariance by explicitly writing our math out in R or by using the cov() function:

crickets %>%
  mutate(x_prods = (spermViability-mean(spermViability)) * (lysozyme-mean(lysozyme))) %>%
  summarise(n = n(),
            sum_x_prods = sum(x_prods),
            cov_math_a  = sum_x_prods / (n-1),
            cov_math_b  = (n/(n-1)) * sum(mean(spermViability * lysozyme) -
                                mean(spermViability) * mean(lysozyme)), 
            cov_r       = cov(spermViability, lysozyme))

## # A tibble: 1 × 5
##       n sum_x_prods cov_math_a cov_math_b cov_r
##   <int>       <dbl>      <dbl>      <dbl> <dbl>
## 1    40       -54.1      -1.39      -1.39 -1.39

Reassuringly we get the same result for all derivations– higher quality sperm come from parents with less lysozyme activity.

Covariance - a visual explanation

Some people have trouble intuiting a covariance, as the mean of the product of the difference X and Y and their means (just typing it is a mouthful).

So I’m hoping the visuals in Fig 14.2 help – if they don’t then skip them. To calculate the covariance,

Draw a rectangle around a given data point and the means of X and Y.
Find the area of that rectangle.
If X is less than its mean and Y is greater than its mean (or vice versa) put a negative sign in front of this area.
Do this for all data points.
Add this all up and divide by $n - 1$.

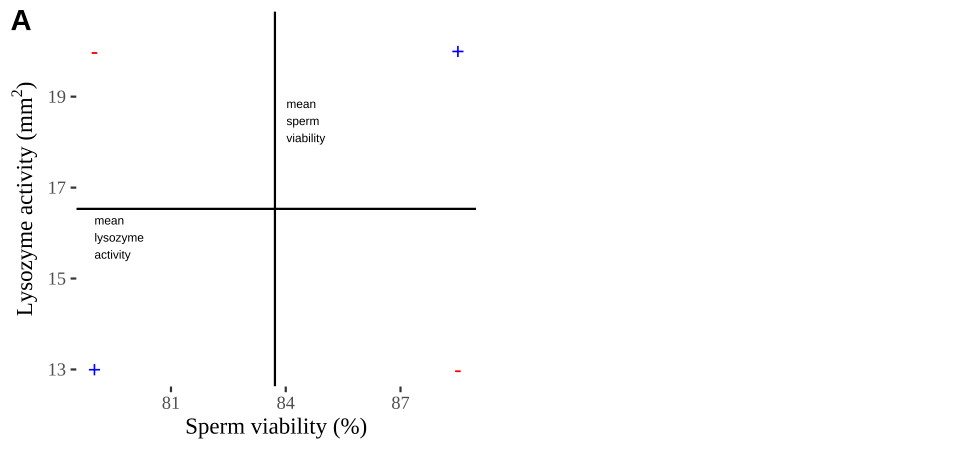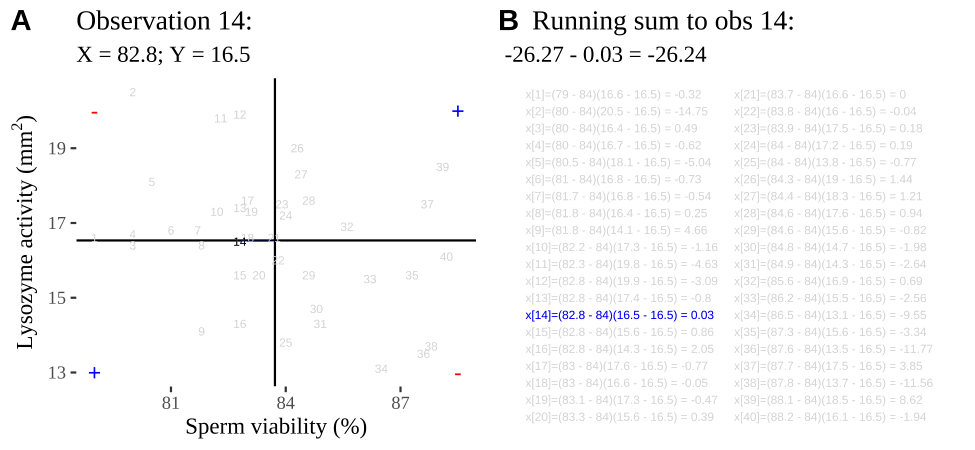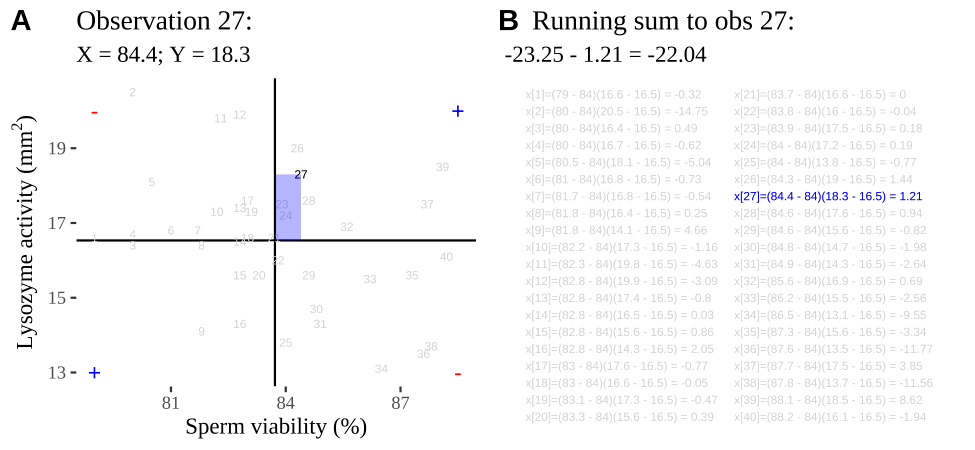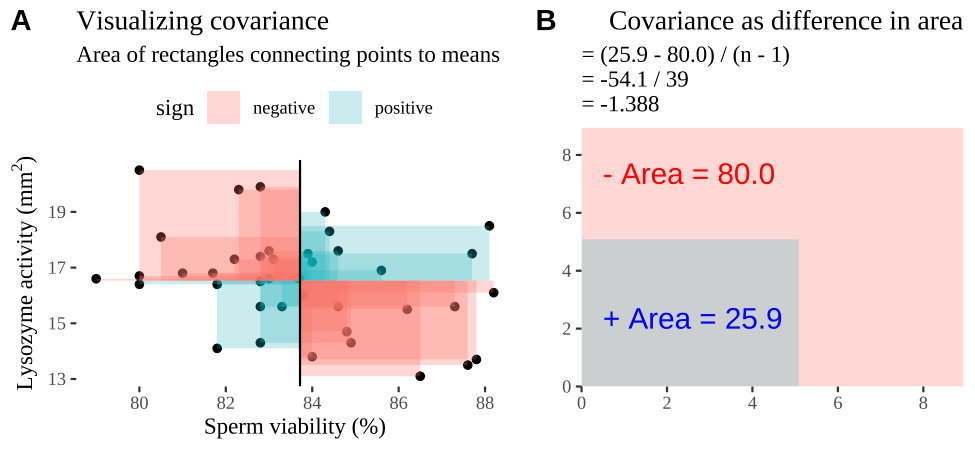
$Visualizing covariance as areas from the mean. **A)** Animation of a rectangles around the $i^{th}$ data point and the mean sperm motility (x), and lysozyme activity (y), looped over all *n* observations. Values in the top left and bottom right quadrants are colored in red because x and y deviate from their means in different directions. Values in the bottom right and top left quadrants are colored in blue because they deviate from their means in the same direction. **B)** The area of the $i^{th}$ rectangle, with a running sum of cross products. **C)** All rectangles in **A** shown at the same time. **D)** The sum of positive (blue) and negative (red) areas.$

FIGURE 14.2: Visualizing covariance as areas from the mean. A) Animation of a rectangles around the $i^{th}$ data point and the mean sperm motility (x), and lysozyme activity (y), looped over all n observations. Values in the top left and bottom right quadrants are colored in red because x and y deviate from their means in different directions. Values in the bottom right and top left quadrants are colored in blue because they deviate from their means in the same direction. B) The area of the $i^{th}$ rectangle, with a running sum of cross products. C) All rectangles in A shown at the same time. D) The sum of positive (blue) and negative (red) areas.

14.3.2 Correlation

We found a covariance in sperm viability and lysozyme activity of -1.388. Is this large or small – I don’t know.

We therefore usually present a more interpretable summary of the association between variables – the correlation, which standardizes the covariance by dividing through by the product of the standard deviations in X and Y, $s_X$ and $s_Y$, respectively:

\[\begin{equation} \begin{split} \text{Sample corelation between X and Y} = Cor(X,Y) &= \frac{Cov(X,Y)}{s_X \times s_Y}\\ \end{split} \tag{14.2} \end{equation}\]

Again we can push through with math, or use the cor() function in R to find the correlation

crickets %>%
  summarise(n = n(),
            cov_r       = cov(spermViability, lysozyme),
            cor_math    = cov_r / (sd(spermViability) * sd(lysozyme)),
            cor_r       = cor(spermViability, lysozyme))

## # A tibble: 1 × 4
##       n cov_r cor_math  cor_r
##   <int> <dbl>    <dbl>  <dbl>
## 1    40 -1.39   -0.328 -0.328

So the correlation is -0.328. It’s not clear if this is a substantial correlation – as this depends on our field and expectations etc. But we can meaningfully compare this to correlations between any other traits to put it in a broader context.

14.4 Bootstrap to quatify uncertainty

Like all estimates, a sample correlation (or covariance) can deviate from the population parameter by chance.

Again we can use the bootstrap – resampling from our sample with replacement to approximate the sampling distribution — to quantify the impact of sampling error on our estimates.

Bootstrap to quatify uncertainty: Step 1. Resample.

We first make a bootstrap replicates by resampling our data with replacement to make a new potential data set (the same size as our data).

crickets_one_resample <- crickets %>%
  slice_sample(prop = 1, replace = TRUE)

So, we now have a data set of 40 combinations of sperm viability and lysozyme activity resampled with replacement from our actual data set.

Bootstrap to quantify uncertainty: Step 2. Summarize a bootstrapped resample.

We then summarize our bootstrap replicate with our estimate of interest – for now we’ll focus on the correlation, but we could have chosen the covariance if we wanted.

crickets_one_boot <- crickets_one_resample  %>% 
  summarise(cor_vals = cor(spermViability, lysozyme))

crickets_one_boot

## # A tibble: 1 × 1
##   cor_vals
##      <dbl>
## 1   -0.455

From this resampled data set, we estimate a correlation of -0.455 – as compared to the correlation of -0.328 observed in the real data.

Bootstrap to quantify uncertainty: Step 2. Repeat many times to approximate the sampling distribution.

So, we resampled our data with replacement and estimated a correlation from this bootstrapped data set to imagine what other results we could have gotten by sampling error. Let’s repeat steps 1 and 2 a bunch of times (lets say ten thousand) to generate a sampling distribution!

n_reps <- 1e4

crickets_boots <- replicate(n = n_reps,simplify = FALSE, 
            expr =crickets %>%
              slice_sample(prop = 1, replace = TRUE)%>% 
              summarise(mean_spermViability = mean(spermViability),
                        mean_lysozyme = mean(lysozyme),
                        cor_vals = cor(spermViability, lysozyme)))%>%
  bind_rows()

So, this is the bootstrapped sampling distribution. (I only show the first thousand values in table below).

Bootstrap to quantify uncertainty: Step 4. Summarize the bootstrap distribution.

Now that we’ve approximated the sampling distribution for the correlation, we can use it to summarize the uncertainty in our estimate of the correlation. Remember our common summaries of uncertainty:

The standard error which describes the expected deviation between a parameter and an estimate of as the standard deviation of the sampling distribution.

crickets_SE_cor <- summarise(crickets_boots, se = sd(cor_vals)) 
crickets_SE_cor

## # A tibble: 1 × 1
##      se
##   <dbl>
## 1 0.143

A confidence interval which puts reasonable bounds on our estimate.

crickets_CI_cor <- crickets_boots %>%
    summarise(CI = quantile(cor_vals, prob = c(0.025,.975))) %>%
    mutate( bound = c("lower","upper"))

crickets_CI_cor

## # A tibble: 2 × 2
##        CI bound
##     <dbl> <chr>
## 1 -0.581  lower
## 2 -0.0240 upper

We can visualize the bootstrapped distribution, with red dashed lines denoting 95% confidence intervals.

ggplot(crickets_boots, aes(x = cor_vals)) +
  geom_histogram(bins = 100, color = "white", size = .3)+
  geom_vline(data = crickets_CI_cor, aes(xintercept = CI), 
             color = "red", lty = 2 )+
  theme_light()+
  scale_y_continuous(expand = c(0,0))+
  scale_x_continuous(limits  = c(-1,1), expand = c(0,0))+ 
  labs(title = "Bootstrap distribution of correlations",
       subtitle = "Sperm viability & lysozyme size in crickets.")

So we find find a negative correlation between sperm motility and lyzosyme activity, with an estimated correlation coefficient of -0.328, and Standard error of 0.1433, and a 95% confidence interval between -0.581 and -0.024.

14.5 Testing the null hypothesis of no association

So, we estimate a negative correlation between sperm viability and lysozyme activity. As our 95% confidence interval excluded zero, it seems unlikely that the data came from a null population with a true correlation of zero. Now, let’s formally test the null hypothesis that such an association could easily be generated by chance sampling from a null population with a true correlation of zero. Here’s how we do it!

State the null hypothesis and its alternative.
- Null hypotheses: There is NO linear association between our two variables. e.g. Crickets with more viable sperm do not have more or less lysozyme activity, on average, than crickets with less viable sperm.
- Alternate hypotheses: There is a linear association between our two variables. e.g. Crickets with more viable sperm do have more or less lysozyme activity, on average, than crickets with less viable sperm.
Calculate a test statistic to summarize our data.
Compare the observed test statistic to the sampling distribution of this statistic from the null model.
Interpret these results. If the test statistic is in an extreme tail of this sampling distribution, we reject the null hypothesis, otherwise we do not.

14.5.1 By permutation

First let’s test this null by permutation. Remember in permutation we generate a sampling distribution under the null by shuffling explanatory and response variables. We need a test statistic – so let’s take the correlation. (p-values and conclusions will be the same if we chose the covariance).

14.5.1.1 Shuffle labels

Unlike the bootstrap – which aims to approximate the sampling distribution around our data, we permute to generate a sampling distribution under the null of no association.
So we now shuffle the association between our explanatory and response variables. We do so by reasigning the explanatory variable (sperm viability) o to a resampling of its values without replacement with the sample() function (the orders will be shuffled, but all data will be there and associations will be maintained).

# shuffle the relationship between explanatory and response variable
crickets_one_perm <- crickets %>%
  mutate(spermViability = sample(spermViability, replace = FALSE))

14.5.1.2 And summarize permuted data

Now let us summarize our permuted data. Again we’ll focus on the correlation, but we could have used a different test statistic, like the covariance.

crickets_one_perm_cor <- crickets_one_perm  %>% 
  summarise(cor_vals = cor(spermViability, lysozyme))

crickets_one_perm_cor

## # A tibble: 1 × 1
##   cor_vals
##      <dbl>
## 1  -0.0639

So, our permutation yielded a correlation of -0.064 which is greater than to correlation of -0.328 found in the data. We can’t make much of this one sample, so we need to build a sampling distribution under the null to see if our result is indeed an unusual outcome of the null model.

14.5.1.3 Permute and summarize the data many times to generate a sampling distribution for the null model

So, we now replicate what we did a bunch of times to generate a sampling distribution under the null.

n_reps <- 1e4 
# shuffle the relationship between explanatory and response variable
crickets_perms<- replicate(n = n_reps, simplify = FALSE, 
    expr = crickets %>%
       mutate(spermViability = sample(spermViability, replace = FALSE))%>%
       summarise(cor_vals = cor(spermViability, lysozyme))) %>%
  bind_rows()

Unlike bootstrapping, here every observation in our initial data set is present in each permuted sample - but we’ve randomly swapped spermViability across individuals with known lysozyme activity. The permutation thus reflects the null model of no association because we’ve randomly associated X and Y many times. So, we now have a data set of ten thousand estimates of the correlation between sperm viability and lysozyme activity, if there was no correlation between these variables (constraining our data to have the same values for each variable as we observed initially).

14.5.1.4 Let’s compare the correlations of permuted data to what we found in the real data

crickets_cor <- crickets %>% 
  summarise(obs_cor = cor(spermViability, lysozyme)) %>%
  pull()
          
          
crickets_perms <- crickets_perms  %>% 
  mutate(actual_cor = crickets_cor, 
         as_or_more_extreme = (abs(cor_vals) >= abs(crickets_cor)))

Let’s have a look at these permuted summaries and how they compare to the actual data. (I only show the first thousand values in table below).

We can then find the p-value as the proportion of permutations that were as or more extreme than the estimate from the data.

crickets_perms %>%
  summarise(pvalue = mean(as_or_more_extreme))

## # A tibble: 1 × 1
##   pvalue
##    <dbl>
## 1 0.0389

Think. Why did we take the absolute values of the observed and permuted correlations to ask if the permutated results were as or more extreme than actual observations?

14.5.1.5 Plot the permuted data

ggplot( crickets_perms , aes(x = cor_vals, fill = as_or_more_extreme))+
  geom_histogram() +
  scale_fill_manual(values = c("grey","black"))+
  theme_tufte()+
  theme(legend.position = "bottom")+
  labs(title = "Permuted distribution of cricket data.")+
  annotate(x = -.5,y =1000, label = sprintf("p = %s", pull(cricket_p_val)%>%round(digits = 3)), geom = "text")

Distribution of permuted correlation coefficients in cricket data. Fewer than five percent of permutations generate correlations as or more extreme then the actual correlation of -0.328 (P < 0.05).

FIGURE 14.3: Distribution of permuted correlation coefficients in cricket data. Fewer than five percent of permutations generate correlations as or more extreme then the actual correlation of -0.328 (P < 0.05).

14.5.1.6 Find a p-value

Remember the p-value is the probability that we would observe our test statistic, or something more extreme if the null were true. While it is clear from Figure 14.3 that it would be quite strange to see a result as extreme as we did if the null were true, we want to quantify this weirdness with a p-value.

We can approximate a p-value as the proportion of permutations with a correlation as or more extreme as our observed correlation:

cricket_p_val <- crickets_perms %>%
  summarise(pvalue = mean(as_or_more_extreme))

cricket_p_val

## # A tibble: 1 × 1
##   pvalue
##    <dbl>
## 1 0.0389

14.5.2 With math

The permutation above did the job. We came to a solid conclusion. But there are a few downsides

It can be a bit slow – it takes my computer like ten seconds to permute this data set 100,000 times. While ten seconds isn’t a lot of time it would add up if for example we wanted to do this for large datasets with millions of variables.
It is influenced by chance. Ever permutation will have a slightly different p-value due to the chance outcomes of random shuffling. While this shouldn’t impact our conclusions it’s a bit unsatisfying.

For these reasons, we usually only apply a permutation to cases where data do not meet the assumptions of the more traditional mathematical approach.

Later in this term we will think a lot about the t-distribution, which is a common and handy statistical distribution. A t-value of one means our estimate is one standard error away from the parameter specified by the null, a t-value of two means our estimate is one standard error away… etc.. etc… etc…

For now know:

We can approximate the standard error of the correlation, $SE_r$, as $\sqrt{\frac{1-r^2}{n-2}}$, where $r$ is our estimated correlation coefficient. So for the cricket data - we can approximate the standard error as $\sqrt{\frac{1- (-0.328)^2}{40-2}} = 0.153$, a value similar to but not identical to the SE of pull(crickets_SE) %>%round(digits = 3) we estimated from the permutation. Don’t stress about this slight difference – this is statistics – we want to be approximately right.
We can find $t$ as $r / SE_r$ – approximately -0.328/0.153 = -2.14 in our case.
In many cases we can use this $t$ value and the sample size to estimate significance. We’ll track this down in a later class.
Calculating the confidence interval is gross.
R can do stats for us.

We can test the null hypothesis of zero correlation with the cor.test() function in R. The cor.test() function needs x and y as vectors so we have to pull() them out of our tibble.

cor.test(x = crickets %>% pull(spermViability),
         y = crickets %>% pull(lysozyme))

## 
##  Pearson's product-moment correlation
## 
## data:  crickets %>% pull(spermViability) and crickets %>% pull(lysozyme)
## t = -2.1, df = 38, p-value = 0.04
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.58012 -0.01822
## sample estimates:
##     cor 
## -0.3279

We find a P-value nearly identical to what we got by permutation and a confidence interval pretty close to ours…. WoooHooo stats works.

Note that R’s test output is easy for humans to read but hard for us to analyze further. The tidy() function in the broom package can tidy this output.

library(broom)
cor.test(x = crickets %>% pull(spermViability),
         y = crickets %>% pull(lysozyme)) %>%
  tidy()

## # A tibble: 1 × 8
##   estimate statistic p.value parameter conf.low
##      <dbl>     <dbl>   <dbl>     <int>    <dbl>
## 1   -0.328     -2.14  0.0389        38   -0.580
## # … with 3 more variables: conf.high <dbl>,
## #   method <chr>, alternative <chr>

14.5.3 Care in interpreting (and running) correlation coefficients.

The correlation looks at how $X$ and $Y$ jointly deviate from their means. As such, interpreting a correlation is only meaningful when both $X$ and $Y$ are random.

Additionally, correlations summarize linear relationships and will fail to capture more complex relationships between variables.

Finally, the $t$ test-based approach assumes that both variable come from a normal distribution… more on this later.

14.6 Attenuation: Random noise in X and/or Y brings correlations closer to zero.

We rarely measure all values of X and Y perfectly. In this example

Each measurement of sperm viability will differ from the individual’s true sperm viability % because of sampling error.
Lysozyme activity will be off because of both sampling error and imprecision of the ruler etc…
If we are lucky this imprecision is randomly distributed across the true values for each data point.

Such random imprecision impacts our estimate of the correlation because random noise will impact each observation of $X$ and $Y$ independently. As such their measured association will be, on average weaker (i.e. closer to zero), than the actual correlation in the real world. This is called attenuation. Two consequences of attenuation are

Even if imprecision in each value of $X$ and $Y$ is unbiased, our estimated correlation will biased to be closer to zero than the actual correlation. Therefore measured correlations are, on average underestimates of true correlations.
The more precise each measurement, the less bias in our estimate of the correlation coefficient.

We do not see such attenuation for our estimates of the mean or difference in means etc. As random noise will result in our estimates bouncing around the true mean without bias.

14.6.1 Attenuation demonstration

Don’t take my word for the reality of attenuation - let’s simulate it! To do so (details in this chapters appendix), I take our crickets data set with an actual correlation of, -0.328, and pretend this is a real population. I copy this data set a bunch of times with the rep_sample_n() function in the infer package, and use the jitter() function to add

Random noise in $X$, spermViability.
Random noise in $Y$, lysozyme
Random noise in both variables,

And compared our estimated correlation in these noisier estimates to our initial estimate of the correlation.

Doing so, I generated the tibble, noisy_crickets, below

The density plots below show that both noise in x and noise in y bring our estimated correlation closer to zero, and noise in both bring this estimate closer still. Thus noise in our measurements of x or y bias our estimated correlation to be closer to zero.

ggplot(noisy_crickets, aes(x = est_cor , fill = noisy))                    +
  facet_wrap(~noisy, labeller = "label_both", ncol = 1)      +
  geom_density(show.legend = FALSE)                          +
  geom_vline(xintercept = crickets %>% summarise(cor(spermViability, lysozyme)) %>% pull() ) +
  geom_vline(data = . %>% group_by(noisy) %>% summarise(est_cor = mean(est_cor)), 
             aes(xintercept = est_cor), color = "white")+
  annotate(x = crickets %>% summarise(cor(spermViability, lysozyme)) %>% pull() ,
           y = 6, label = "correlation in data", geom = "text", hjust = 1.1)+
  geom_label(data = . %>% group_by(noisy) %>% summarise(est_cor = mean(est_cor)),
            aes(y=6),label = "Avg. noisy correlation",  hjust = 0, color = "white", show.legend = FALSE)+
  scale_y_continuous(limits = c(0,6.5))

14.7 Two binary variables:

Above we focused on describing and evaluating associations between two continuous variables. What if we are looking into associations between two categorical variables? If there are only two categories for each variable (i.e. the variables are binary) we don’t need to do anything new.

For example, we can meaningfully describe the association between genotypes, known as linkage disequilibrium, at two biallelic loci (in which we arbitrarily call one allele at each locus “0”, and the other “1”) as a covariance (we call this standard measure of linkage disequilibrium, $D$) or a correlation (another common quantification of linkage disequilibrium, $r^2$). Again we can describe uncertainty by bootstrapping and conduct null hypothesis significance testing by permutation.

Specialized summaries and tests for associations between categorical variables:

Although we can go on and treat associations between categorical variables as correlations and covariances, there are other specialized approaches for these sorts of data. This is not a focus of this course, but I provide the bare bones here for completeness. Feel free to skip everything in this section. For more information check out the Associations Between Categorical Variables section of my previous edition of this book.

14.7.1 Quantifying associations Between Categorical Variables

Quantifying associations as the relative risk

The best summary of an association between two categorical variables is the relative risk, $\widehat{RR}$. The relative risk is the probability of a bad outcome conditional on being in scenario one divided by the probability of that bad outcome conditional on being in the other scenario. For example if 10 of 100 smokers die of lung cancer and 1 of 100 non-smokers die of lung cancer, the relative risk of dying of lung cancer given that you’re a smoker is $\frac{10/100}{1/100} = 10$ times great than that given that you’re a non-smoker. Note that hats $\hat{ }$ over p and RR indicate that these are estimates, not parameters.

\[\widehat{RR} = \frac{\widehat{p_1}}{\widehat{p_2}} \text{ , where } \widehat{p_1} = \frac{n_\text{bad outcomes in scenario one}}{n_\text{individuals in scenario one}}\]

Quantifying associations as the log odds

While the relative risk is a simple summary to communicate it suffers from two challenges

We often cannot study rare outcomes without some selection bias.
It has some non-desirable properties for statistical modeling.

For these reasons, we often deal with the less intuitive (log) Odds Ratio, rather than the simpler relative risk😭. Jason Kerwin argues that odds ratios are so confusing that they are basically useless, do you agree?

The odds of an outcome is the estimated probability of that outcome, $\widehat{p}$, divided by the estimated probability of not that outcome, $1 - \widehat{p}$. That is $\text{Odds} = \frac{\widehat{p}}{1-\widehat{p}}$.
The odds ratio is the odds of an outcome in scenario one divided by the odds of an outcome in the other scenario.

For example if 10 of 100 smokers die of lung cancer and 1 of 100 non-smokers die of lung cancer, the odds ratio of dying of lung cancer for smokers relative to non-smokers is $\frac{(10/100)/(90/100)}{(1/100)/(99/100)} = \frac{1/9}{1/99} = 99/11 = 9$. This shows

The odds ratio does not equal the relative risk.
The denominator drops out of the top and bottom – meaning this will work even if we don’t have true absolute probabilities. This will be the case in studies of rare outcomes in which it makes sense to increase the number of these rare outcomes we see (as we do in case-control studies).

14.7.2 Testing for associations between categorical variables

$\chi^2$ tests for associations between categorical variables

$\chi^2$ is a test statistic that quantifies the difference between observed and expected counts. That is, $\chi^2$ summarizes the fit of categorical data to expectations. We calculate $\chi^2$ as

\[\begin{equation} \chi^2 = \sum \frac{(\text{Observed}_i - \text{Expected}_i)^2}{\text{Expected}_i} \tag{14.3} \end{equation}\]

Where each $i$ is a different potential outcome (in our example: lung cancer with smoking, lung cancer without smoking, no lung cancer with smoking, no lung cancer without smoking), as observations and expectations are counts not proportions.

We use the multiplication rule $P_{A \text{ AND } B} = P_{A} \times P_B$ to find null expectations (i.e. assuming independence) for proportions. We then convert these expected proportions to counts by multiplying by sample size.

We then compare the observed $\chi^2$ value to its sampling distribution under the null (which depends on something called the degrees of freedom, which we will explain later, but which equals one for the case of associations between to binary variables). In R we can find our p-value as pchisq(q = my_chi2_value, df = my_df, lower.tail = TRUE). We type lower.tail = TRUE because the lower tail of this distribution includes all directions of exceptional associations.

The null distribution of $\chi^2$ values is only appropriate when the expected number of counts are not too low (all categories have an expected count greater than one and no more than 20% of categories have an expected count of less than five). If our expectations are too low, we use a better test.

Fisher’s exact test for associations between categorical variables

Fisher’s exact test is basically a permutation-based test of the null in which all possible associations are enumerated in their expected frequencies and the observed association is compared to this null distribution.

14.8 Homework

14.8.1 Guess the correlation

Play three games of Guess the Correlation, and report your high score.

14.8.2 Quiz

Be sure to check out all the topics!

14.8.3 Correlation appendix:

14.8.3.1 Code to make noisy data

library(infer)
n_reps <- 10000

many_crickets <-  crickets %>%
  rep_sample_n(size = nrow(crickets), replace = FALSE, reps = n_reps)

noisy_x <- many_crickets                                                        %>%
  mutate(spermViability = jitter(spermViability, amount = sd(spermViability) )) %>%
  summarise(est_cor = cor(spermViability, lysozyme))                            %>%
  mutate(noisy = "x")

noisy_y <- many_crickets                                       %>%
  mutate(lysozyme = jitter(lysozyme, amount = sd( lysozyme) )) %>%
  summarise(est_cor = cor(spermViability, lysozyme))           %>%
  mutate(noisy = "y")

noisy_xy <- many_crickets                                                       %>%
  mutate(lysozyme = jitter(lysozyme, amount = sd( lysozyme)),
         spermViability = jitter(spermViability, amount = sd(spermViability) )) %>%
  summarise(est_cor = cor(spermViability, lysozyme))                            %>%
  mutate(noisy = "xy")

### Combine the data 
noisy_crickets <- bind_rows(noisy_x, noisy_y, noisy_xy)                       %>%
  mutate(noisy = fct_reorder(noisy, est_cor))

References

Fieberg, John R, Kelsey Vitense, and Douglas H Johnson. 2020. “Resampling-Based Methods for Biologists.” PeerJ 8: e9089.

Simmons, Leigh W., and Benjamin Roberts. 2005. “Bacterial Immunity Traded for Sperm Viability in Male Crickets.” Science 309 (5743): 2031–31. https://doi.org/10.1126/science.1114500.

Whitlock, Michael C, and Dolph Schluter. 2020. The Analysis of Biological Data. Third Edition.