Chapter 21 Linear Models

This text (roughly) follows Chapter 18 of our textbook. The reading below is required, Whitlock and Schluter (2020) is not.

Motivating scenarios: We feel like we have a solid grounding in the ideas behind how we do statistics and now want to actually do them! Here we have a look into linear modeling – an approach that makes up most of the statistics we encounter in the world.

Learning goals: By the end of this chapter you should be able to

• Describe what a linear model is, and what makes a model linear.
  
• Connect the math of a linear model to a visual representation of the model.
  
• Use the lm() function in R to run a linear model and interpret its output to make predictions.
• Understand what a residual is
  • Be able to calculate a residual.
    
  • Visually identify residuals in a plot.
    
• Describe and evaluate the assumptions of a linear model.
  
• Recognize the limitations of predictions form a linear model.

21.1 What is a linear model?

A statistical model describes the predicted value of a response variable as a function of one or more explanatory variables. The predicted value of the response variable of the \(i^{th}\) observation is \(\hat{Y_i}\), where the hat denotes that this is a prediction. This prediction, \(\hat{Y_i}\) is a function of values of the explanatory variables for observation \(i\) (Equation (21.1)).

\[\begin{equation} \hat{Y_i} = f(\text{explanatory variables}_i) \tag{21.1} \end{equation}\]

A linear model predicts the response variable by adding up all components of the model. So, for example, \(\hat{Y_i}\) equals the parameter estimate for the “intercept”, \(a\) plus its value for the first explanatory variable, \(y_{1,i}\) times the effect of this variable, \(b_1\), plus its value for the second explanatory variable, \(y_{2,i}\) times the effect of this variable, \(b_2\) etc all the way through all predictors (Eq. (21.2)).

\[\begin{equation} \hat{Y_i} = a + b_1 y_{1,i} + b_2 y_{2,i} + \dots{} \tag{21.2} \end{equation}\]

Linear models can include e.g. squared, and geometric functions too, so long as we get out predictions by adding up all the components of the model. Similarly, explanatory variables can be combined, too so we can include cases in which the effect of explanatory variable two depends on the value of explanatory variable one, by including an interaction in the linear model.

Predictions are hard – especially outside of our data. Its worth recognizing that the “prediction” we make in a linear model apply only to the range of values in, and conditions of our study. Extrapolating beyond this range or to differing conditions is generally not a great idea.

Optional: A view from linear algebra

If you have a background in linear algebra, it might help to see a linear model in matrix notation.

The first matrix in Eq (21.3) is known as the design matrix. Each row corresponds to an individual, and each column in the \(i^{th}\) row corresponds to this individual \(i\)’s value for the explanatory variable in this row. We take the dot product of this matrix and our estimated parameters to get the predictions for each individual. Equation (21.3) has \(n\) individuals and \(k\) explanatory variables. Note that every individual has a value of 1 for the intercept.

\[\begin{equation} \begin{pmatrix} 1 & y_{1,1} & y_{2,1} & \dots & y_{k,1} \\ 1 & y_{1,2} & y_{2,2} & \dots & y_{k,2} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & y_{1,n} & y_{2,n} & \dots & y_{k,n} \end{pmatrix} \cdot \begin{pmatrix} a \\ b_{1}\\ b_{2}\\ \vdots \\ b_{k} \end{pmatrix} = \begin{pmatrix} \hat{Y_1} \\ \hat{Y_2}\\ \vdots \\ \hat{Y_n} \end{pmatrix} \tag{21.3} \end{equation}\]

21.2 The one sample t-test as the simplest linear model

We’re going to see some complex linear models in the coming weeks. For now, let’s start with the simplest – let’s view the one sample t-test as a linear model. In this case,

• All predicted values \(\hat{Y_i}\) will be the same for all observations because we are not including any explanatory variables.
  
• We are testing the null that the “intercept” \(a\) equals its predicted value under the null \(\mu_0=0\).

So, our design matrix is simple – every individual’s prediction is one times the intercept. We tell R that we want to run this linear model with the lm() function. Because we have no explanatory variables, we type lm(<response_var> ~ 1, data= <dataset>). We the get a summary of the linear model by piping its output to summary().lm

For example, take the the elevations range change data from Chapter 18:

range_shift_file <- "https://whitlockschluter3e.zoology.ubc.ca/Data/chapter11/chap11q01RangeShiftsWithClimateChange.csv"
range_shift      <- read_csv(range_shift_file)
range_shift_lm   <- lm(elevationalRangeShift  ~ 1, data = range_shift)

range_shift_lm %>% summary.lm()

## 
## Call:
## lm(formula = elevationalRangeShift ~ 1, data = range_shift)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -58.63 -23.38  -3.53  24.12  69.27 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    39.33       5.51    7.14  6.1e-08 ***
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 30.7 on 30 degrees of freedom

Let’s focus on the line under coefficients, as that is the most relevant one. Reassuringly, our answers match the output of the t.test() function (Section 18.5.4). Our t-value is still 7.141 , and our p-value is still \(6.06 \times 10^{-8}\). That’s because all calculations are the exact same – the t-value is still the distance, in standard errors, between the null and our estimate.

Again, we can tidy the results of this model with the tidy() function in the broom package.

library(broom)
tidy(range_shift_lm )

## # A tibble: 1 × 5
##   term        estimate std.error statistic      p.value
##   <chr>          <dbl>     <dbl>     <dbl>        <dbl>
## 1 (Intercept)     39.3      5.51      7.14 0.0000000606

So here \(\hat{Y_i} = a = 39.329\) – that is, we predict that a given species range moved 39.329 meters upwards.

21.3 Residuals describe the difference between predictions and observed values.

Of course, most observations will not exactly equal their predicted value. Rather, an observation \(Y_i\) will differ from its predicted value, \(\hat{Y_i}\) by some amount, \(e_i\), called the residual.

\[\begin{equation} \begin{split}Y_i &= \hat{Y_i} + e_i\\ e_i&=Y_i-\hat{Y_i} \end{split} \tag{21.4} \end{equation}\]

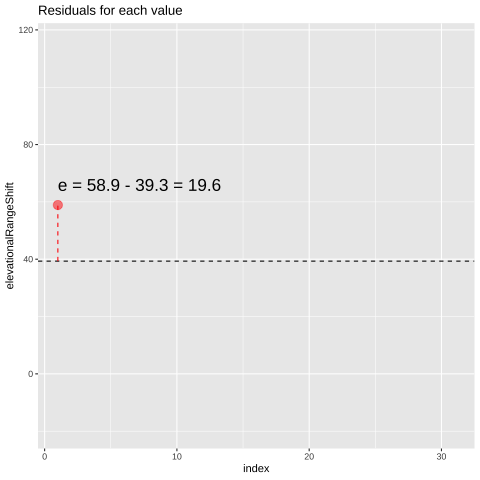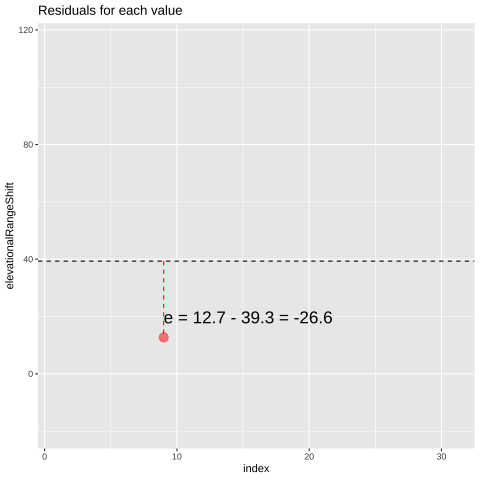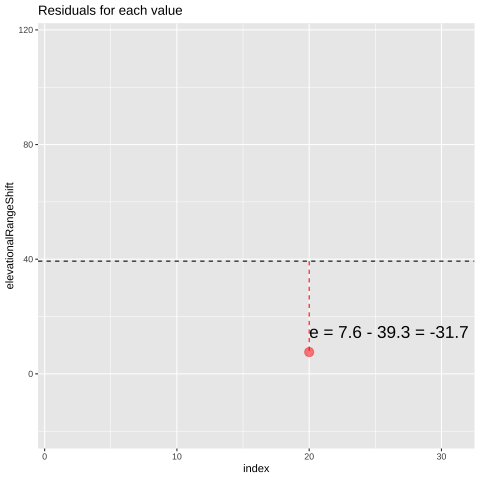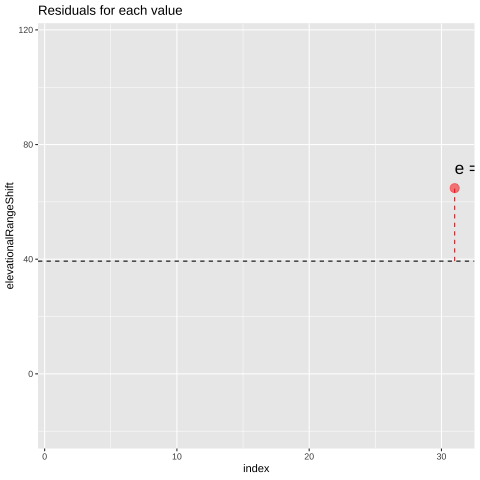
FIGURE 21.1: Change in elevational range, arbitrarily ordered by species ID. All data are shown in the plot on the left. The plot on the right calculates residuals as the difference between expectation and observation.

The augment() function in the broom package is awesome in that it shows us our values (elevationalRangeShift) the prediction (.fitted) and residual (.resid) for each observation.

library(broom)
range_shift_lm %>%
  augment()    %>%
  dplyr::select(elevationalRangeShift, .fitted, .resid)

## # A tibble: 31 × 3
##    elevationalRangeShift .fitted .resid
##                    <dbl>   <dbl>  <dbl>
##  1                  58.9    39.3  19.6 
##  2                   7.8    39.3 -31.5 
##  3                 109.     39.3  69.3 
##  4                  44.8    39.3   5.47
##  5                  11.1    39.3 -28.2 
##  6                  19.2    39.3 -20.1 
##  7                  61.9    39.3  22.6 
##  8                  30.5    39.3  -8.83
##  9                  12.7    39.3 -26.6 
## 10                  35.8    39.3  -3.53
## # … with 21 more rows

21.4 More kinds of linear models

Some common linear models include a two-sample t-test, an ANOVA, a regression, and an ANCOVA. We will go over these in coming weeks, so for now let’s just have a quick sneak preview of the two sample t-test and the regression.

21.4.1 A two-sample t-test as a linear model

We often want to know the difference in means between two (unpaired) groups, and test the null hypothesis that these means are identical. For this linear model,

• \(a\) is the estimate mean for one group,
• \(b_1\) is the average difference between individuals in that and the other group.
  
• \(y_{1,i}\) is an “indicator variable” equaling zero for individuals in group 1 and one for individuals in the other group.

So, the equation \(\hat{Y_i} = a + Y_{1,i} \times b_1\) is

\[\begin{equation} \hat{Y_i}= \begin{cases} a + 0 \times b_1 & = a, &\text{if }\ i \text{ is in group 1}\\ a + 1 \times b_1 & = a +b_1, &\text{if }\ i\text{is in group 2} \end{cases} \end{equation}\]

21.4.1.1 Example: Lizard survival

Could long spikes protect horned lizards from being killed by the loggerhead shrike? The loggerhead shrike is a small predatory bird that skewers its victims on thorns or barbed wire. Young, Brodie, and Brodie (2004) compared horns from lizards that had been killed by shrikes to 154 live horned lizards. The data are plotted below.

lizards <- read_csv("https://whitlockschluter3e.zoology.ubc.ca/Data/chapter12/chap12e3HornedLizards.csv")  %>% na.omit()
ggplot(lizards, aes(x = Survival, y = squamosalHornLength, color = Survival))  +
  geom_jitter(height = 0, width = .2, size = 3, alpha = .5, show.legend = FALSE)  +
  stat_summary(fun.data = "mean_cl_normal", color = "black")

Lizard summary stats

The means for each group are

lizards %>%
  group_by(Survival) %>%
  summarise(mean_squamosalHornLength = mean(squamosalHornLength))

## # A tibble: 2 × 2
##   Survival mean_squamosalHornLength
##   <chr>                       <dbl>
## 1 killed                       22.0
## 2 living                       24.3

Lizard linear model

We can represent this as a linear model

lizard_lm <- lm(squamosalHornLength ~ Survival, data = lizards)
lizard_lm

## 
## Call:
## lm(formula = squamosalHornLength ~ Survival, data = lizards)
## 
## Coefficients:
##    (Intercept)  Survivalliving  
##          21.99            2.29

We can see that the intercept is the mean squamosal Horn Length for killed lizards, and Survivalliving is how much longer, on average horn length is in surviving lizards.

We can look at the output of the linear model, below.

lizard_lm %>% summary.lm()

## 
## Call:
## lm(formula = squamosalHornLength ~ Survival, data = lizards)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -11.181  -1.281   0.269   1.719   6.019 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)
## (Intercept)      21.987      0.483   45.56  < 2e-16
## Survivalliving    2.295      0.528    4.35  2.3e-05
##                   
## (Intercept)    ***
## Survivalliving ***
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.64 on 182 degrees of freedom
## Multiple R-squared:  0.0942, Adjusted R-squared:  0.0892 
## F-statistic: 18.9 on 1 and 182 DF,  p-value: 2.27e-05

From this, we estimate \(\text{horn length}_i = 22.99 + 2.29 \times \text{living}_i\) where living is 0 for killed lizards and 1 for living lizards.

The t value and p-value for the intercept for (Intercept) describe the difference between estimated horn length and zero. This is a very silly null hypothesis, and we ignore that \(t\) and p-value, but we do care about this estimate and uncertainty.

By contrast the t value and p-value for the Survivalliving describe the difference between estimated horn length of surviving and dead lizards. This is an interesting null hypothesis – we conclude that the difference between the extreme 2.3mm difference in the horn lengths of killed and surviving lizards is unexpected by chance (\(t = 4.35\), \(df = 182\), \(p = 2.27 \times 10^{-5}\)).

Lizard residuals

Again, we can look at this in more detail with the augment function in the broom package.

lizard_lm %>% 
  augment() %>%
  dplyr::select(squamosalHornLength, Survival, .fitted, .resid)

## # A tibble: 184 × 4
##    squamosalHornLength Survival .fitted .resid
##                  <dbl> <chr>      <dbl>  <dbl>
##  1                22.4 living      24.3 -1.88 
##  2                26.5 living      24.3  2.22 
##  3                24.5 living      24.3  0.219
##  4                21.7 living      24.3 -2.58 
##  5                23   living      24.3 -1.28 
##  6                25.5 living      24.3  1.22 
##  7                21.4 living      24.3 -2.88 
##  8                17.2 killed      22.0 -4.79 
##  9                22.4 living      24.3 -1.88 
## 10                22.4 living      24.3 -1.88 
## # … with 174 more rows

This shows the residuals (.resid), as the difference between the predicted values, \(\hat{Y_i}\) (.fitted) and the observed values, \(Y_i\) (squamosalHornLength). Note that the \(\hat{Y_i}\) differs for living and killed lizards.

21.4.1.2 Two-sample t-test as an ANOVA

Alternatively, we can consider a two sample t-test as an ANOVA. We basically do everything as in the previous chapter, without the need for post-hoc tests.

We can run this in R as anova(lizrd_lm) [not aov]. Notice that our p-values don’t change, so which you do / report is not particularly meaningful and will all result in the same conclusions. However, the linear model output might make a bit more sense because the t values and standard errors are more readily interpretable.

anova(lizard_lm)

## Analysis of Variance Table
## 
## Response: squamosalHornLength
##            Df Sum Sq Mean Sq F value  Pr(>F)    
## Survival    1    132     132    18.9 2.3e-05 ***
## Residuals 182   1272       7                    
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

21.4.2 An ANOVA as a linear model

Returning to our extended example from the previous chapter – can ambient temperature can influence body temperature in Spermophilus tereticaudus. In this experiment, Wooden and Walsberg (2004) put squirrels in environments that where 10°C (cold), 35°C (warm), and 45°C (hot), and measured their body temperature. The data are plotted in

21.4.2.1 ANOVA as a linear model: The math model

We can, and will, think about this like a linear model.

sqrl_lm <- lm( body_temp ~ ambient_temp, data = sqrl)
sqrl_lm

## 
## Call:
## lm(formula = body_temp ~ ambient_temp, data = sqrl)
## 
## Coefficients:
##      (Intercept)  ambient_tempwarm   ambient_temphot  
##            30.96              6.25             10.00

We can write down the linear equation as follows:

\[\begin{equation} \begin{split}\text{body temp}_i = 30.960 + 6.254 \times WARM + 10 \times hot \end{split} \tag{21.5} \end{equation}\]

And we can find the predicted body temperature for each ambient temperature as follows:

\[\begin{equation} \begin{split} \hat{Y}_\text{Cold ambient} &= 30.960 + 6.254 \times WARM + 10 \times HOT. \\ &= 30.960 + 6.254 \times 0 + 10 \times 0 . \\ &= 30.960 \\ \\ \hat{Y}_\text{Warm ambient} &= 30.960 + 6.254 \times WARM + 10 \times HOT. \\ &= 30.960 + 6.254 \times 1 + 10 \times 0 . \\ &= 30.960 + 6.254 \\ & =37.214\\ \\ \hat{Y}_\text{Hot ambient} &= 30.960 + 6.254 \times WARM + 10 \times HOT. \\ &= 30.960 + 6.254 \times 0 + 10 \times 1 . \\ &= 30.960 + 10 \\ & =40.960 \\ \end{split} \tag{21.6} \end{equation}\]

So that’s all good, and equals the means, as we would like

sqrl %>%
  group_by(ambient_temp) %>%
  summarise(mean_body_temp = mean(body_temp))                                                                           %>% kable(digits = 4)

ambient_temp	mean_body_temp
cold	30.96
warm	37.21
hot	40.96

21.4.2.2 ANOVA as a linear model: You may be looking at the wrong t and p-values

But the t-values and p-values from summary and tidy are weird

tidy(sqrl_lm)                                                                                     %>% kable(digits = 4)

term	estimate	std.error	statistic	p.value
(Intercept)	30.960	0.1157	267.47	0
ambient_tempwarm	6.254	0.1617	38.67	0
ambient_temphot	10.000	0.1637	61.09	0

Specifically, we have three pairs of p and t values.

• t and p values associated with(Intercept) (\(t = 267\), \(2.32 \times 10^{-91}\)), describe the nonsense null hypothesis that mean temperature in cold is 0°C.
• t and p values associated withambient_tempwarm (\(t = 39.7\), \(4.16 \times 10^{-43}\)), describe the null hypothesis that would be useful to evaluate – that mean body temperature does not differ in cold vs. warm environments.
  
• t and p values associated withambient_temphot (\(t = 61.1\), \(2.40 \times 10^{-54}\)), describe the null hypothesis that would be useful to evaluate – that mean body temperature does not differ in warm vs. hot environments.

What’s wrong with the p-values above?

1. We have not compared body temperatures at warm vs hot ambient temperatures.
   
2. We have conducted “multiple tests” on the same data set. That is because we have two p-values we’re looking at, the probability that we incorrectly reject at least one true null is no longer \(\alpha\), but is the probability of not rejecting any null hypotheses \(1-(1 -\alpha)^\text{n tests}\). So with the two interesting null hypotheses to test, with a traditional \(\alpha = 0.05\) the probability of not reject any true null hypotheses is \(1-(1 -.05)^2 = 0.0975\). This is way bigger than the \(\alpha\) of \(0.05\) we claim to have.

21.4.2.3 Find correct values with anova()

Now try anova(sqrl_lm). You will see that our answers match those from the previous chapter that we got with summary() of the aov() output.

summary(sqrl_lm)

## 
## Call:
## lm(formula = body_temp ~ ambient_temp, data = sqrl)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -1.014 -0.414  0.040  0.440  0.940 
## 
## Coefficients:
##                  Estimate Std. Error t value Pr(>|t|)
## (Intercept)        30.960      0.116   267.5   <2e-16
## ambient_tempwarm    6.254      0.162    38.7   <2e-16
## ambient_temphot    10.000      0.164    61.1   <2e-16
##                     
## (Intercept)      ***
## ambient_tempwarm ***
## ambient_temphot  ***
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.518 on 58 degrees of freedom
## Multiple R-squared:  0.985,  Adjusted R-squared:  0.984 
## F-statistic: 1.91e+03 on 2 and 58 DF,  p-value: <2e-16

21.4.3 A regression as a linear model

Let’s revisit our example in which we looked at the correlation by disease and sperm viability from Chapter 14. Remember, we looked into the hypothesis that there is a trade off between investment in disease resistance and reproduction using data from Simmons and Roberts (2005), who assayed sperm viability and lysozyme activity (a measure of defense against bacteria) in 39 male crickets.

In Chapter 14, we looked into a correlation, which showed us how the two variables changed together but did not allow us to make quantitative predictions. Now we will look into interpreting the regression as a linear model. We will consider how to make a regression later, but for now just know that we are modeling y (in this case, lysozyme activity) as a function of x (in this case, sperm viability), by a simple line.

FIGURE 21.2: Lysozyme activity deceases with sperm viability in crickets. Data from Simmons and Roberts (2005).

As usual, we can generate the linear model with the lm() function, here predicting lysozyme activity as a function of sperm viability.

cricket_lm <- lm(lysozyme  ~ spermViability, data = crickets)
cricket_lm 

## 
## Call:
## lm(formula = lysozyme ~ spermViability, data = crickets)
## 
## Coefficients:
##    (Intercept)  spermViability  
##          36.64           -0.24

So from this model, we predict that an individual’s lysozyme activity equals 36.64 minus 0.24 times his sperm viability. This prediction corresponds to the line in figure 21.2 and is mathematically:

\[\text{lysozyme activity}_i = 36.64 -0.24 \times \text{sperm viability}_i+e_i\] Again, we can use the augment function in the broom package to look at actual values (\(Y_i\)), predicted values (\(\hat{Y_i}\)) and residuals \(e_i\). In this case, there are a bunch of different predictions because there are a bunch of different sperm viability scores.

augment(cricket_lm) %>%
  dplyr::select(lysozyme, spermViability, .fitted, .resid)

## # A tibble: 40 × 4
##    lysozyme spermViability .fitted .resid
##       <dbl>          <dbl>   <dbl>  <dbl>
##  1     16.6           79      17.7 -1.07 
##  2     20.5           80      17.4  3.07 
##  3     16.4           80      17.4 -1.03 
##  4     16.7           80      17.4 -0.725
##  5     18.1           80.5    17.3  0.795
##  6     16.8           81      17.2 -0.385
##  7     16.8           81.7    17.0 -0.217
##  8     16.4           81.8    17.0 -0.593
##  9     14.1           81.8    17.0 -2.89 
## 10     17.3           82.2    16.9  0.403
## # … with 30 more rows

We can look at this significance of our predictions with summary.lm()

cricket_lm %>% summary.lm()

## 
## Call:
## lm(formula = lysozyme ~ spermViability, data = crickets)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -2.893 -1.041 -0.161  0.839  3.147 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)
## (Intercept)      36.640      9.403    3.90  0.00038
## spermViability   -0.240      0.112   -2.14  0.03889
##                   
## (Intercept)    ***
## spermViability *  
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.69 on 38 degrees of freedom
## Multiple R-squared:  0.107,  Adjusted R-squared:  0.084 
## F-statistic: 4.58 on 1 and 38 DF,  p-value: 0.0389

As above, the p-value for the intercept is silly – of course crickets have non-zero sperm viability. The more interesting result is that the 0.24 decrease in lysozyme activity with every percent increase in sperm viability is significant at the \(\alpha = 0.05\) level (\(t = -2.139\), \(df = 38\), \(p = 0.0389\)), so we reject the null hypothesis, and conclude that lysozyme activity decreases with increasing sperm viability.

21.4.3.1 A regression as an ANOVA

Alternatively, we can consider a regression as an ANOVA. Here We estimate two parameters (slope and intercept), so we have n - 2 df error, and 2-1 = 1 df model. We get

• Sum of squares model is the difference between predicted values \(\hat{Y_i}\) and the grand mean \(\overline{\overline{Y}}\). That is, \(SS_\text{model} = \Sigma(Y_i-\overline{\overline{Y}})^2\).

• Sum of squares error is the difference between predicted values \(\hat{Y_i}\) and observed values \(Y\). That is, \(SS_\text{error} = \Sigma(Y_i-\hat{Y_i})^2\).

We can run this in R as anova(cricket_lm) [not aov]. Notice that our p-values don’t change, so which you do / report is not particularly meaningful and will all result in the same conclusions

anova(cricket_lm)

## Analysis of Variance Table
## 
## Response: lysozyme
##                Df Sum Sq Mean Sq F value Pr(>F)  
## spermViability  1     13   13.00    4.58  0.039 *
## Residuals      38    108    2.84                 
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

21.5 Assumptions of a linear model

A linear model assumes

• Linearity: That is to say that our observations are appropriately modeled by adding up all predictions in our equation. We can evaluate this by seeing that residuals are independent of predictors.
  
• Homoscedasticity: The variance of residuals is independent of the predicted value, \(\hat{Y_i}\) is the same for any value of X.
  
• Independence: Observations are independent of each other (aside from the predictors in the model).
  
• Normality: That residual values are normally distributed.
  
• Data are collected without bias as usual.

These vary in how hard they are to diagnose. But the autoplot() function in the ggfortify package helps us evaluate assumptions of

• Making sure the residuals are independent of predictors (a diagnosis for linearity). A Residuals vs Fitted plot with a slope near zero is consistent with this assumption.
  
• Making sure that the mean and variance in residuals are independent of predictors. A Scale-location plot with a slope near zero is consistent with this assumption.
  
• Normality of residuals. A qq plot with a slope near one is consistent with this assumption.

Have a look at the diagnostic plots from our models to see if they look ok!

library(ggfortify)
autoplot(lizard_lm)

autoplot(cricket_lm)

21.6 Predictions from linear models

Linear models can be used to predict new results. However, predictions only apply to the range of values investigated in the initial regression and to cases with similar conditions.

21.7 Quiz

References

Simmons, Leigh W., and Benjamin Roberts. 2005. “Bacterial Immunity Traded for Sperm Viability in Male Crickets.” Science 309 (5743): 2031–31. https://doi.org/10.1126/science.1114500.

Whitlock, Michael C, and Dolph Schluter. 2020. The Analysis of Biological Data. Third Edition.

Wooden, K. Mark, and Glenn E. Walsberg. 2004. “Body Temperature and Locomotor Capacity in a Heterothermic Rodent.” Journal of Experimental Biology 207 (1): 41–46. https://doi.org/10.1242/jeb.00717.

Young, Kevin V., Edmund D. Brodie, and Edmund D. Brodie. 2004. “How the Horned Lizard Got Its Horns.” Science 304 (5667): 65–65. https://doi.org/10.1126/science.1094790.