Chapter 8 Practical Sheets

8.1 Practical 1 - Contingency Tables

In this practical, we consider exploring practical application of some of the techniques learnt in the lectures in R. This practical may seem long, however, some of it should be a nice refresher of R techniques already learnt, and some other parts are hopefully gentle and straightforward to read about and follow (although the odd more challenging exercise is thrown in!). You are encouraged to work through to the end in your own time. I would also like to note that Data Science and Statistical Computing II (DSSC II) was not a prerequisite for this course, and hence is not necessary. However, if you did take that course, you are welcome to play around with using some of the exciting skills picked up in that course in conjunction with what you learn in this course (particularly surrounding the visualisation side of things).

Finally, whilst solutions to the practical sheets will be provided, it is by attempting to answer the exercises yourself first that your practical coding skills will be developed!

8.1.1 Construction of Contingency Tables

8.1.1.1 Construction from Matrices

We here consider entering \(2 \times 2\) contingency tables manually into R. We do this as follows for the data in Table 2.3.

DR_data <- matrix( c(41, 9, 
                     37, 13 ), byrow = TRUE, ncol = 2 )
dimnames( DR_data ) <- list( Dose = c("High", "Low"),
                             Result = c("Success", "Failure") )

DR_data

##       Result
## Dose   Success Failure
##   High      41       9
##   Low       37      13

We can add row and column sum margins as follows

DR_contingency_table <- addmargins( DR_data )
DR_contingency_table

##       Result
## Dose   Success Failure Sum
##   High      41       9  50
##   Low       37      13  50
##   Sum       78      22 100

8.1.1.2 Contingency Tables of Proportions

Proportions can be obtained using prop.table.

DR_prop <- prop.table( DR_data )
DR_prop_table <- addmargins( DR_prop )
DR_prop_table

##       Result
## Dose   Success Failure Sum
##   High    0.41    0.09 0.5
##   Low     0.37    0.13 0.5
##   Sum     0.78    0.22 1.0

The row conditional proportions are derived by prop.table(DR_data, 1). Analogously, column conditional proportions can be obtained using prop.table(DR_data, 2).
The addmargins function also provides versatility for specifying margins for particular dimensions. We here specify that margins only be added for each row (trivially yielding 1 in each case as expected).

DR_prop_1 <- prop.table( DR_data, 1 )
DR_prop_1_table <- addmargins( DR_prop_1, margin = 2 )
DR_prop_1_table

##       Result
## Dose   Success Failure Sum
##   High    0.82    0.18   1
##   Low     0.74    0.26   1

We can amend the function argument FUN so that an alternative operation is performed. Since both rows contain the same total number of subjects, we can obtain the overall proportion in each column by amending the function argument FUN as follows⁷³:

DR_prop_2_table <- addmargins( DR_prop_1_table, margin = 1, FUN = mean )
DR_prop_2_table

##       Result
## Dose   Success Failure Sum
##   High    0.82    0.18   1
##   Low     0.74    0.26   1
##   mean    0.78    0.22   1

Notice that

DR_prop_3_table <- addmargins( DR_prop_1, 
                               margin = c(1,2), 
                               FUN = list(mean, sum) )

## Margins computed over dimensions
## in the following order:
## 1: Dose
## 2: Result

DR_prop_3_table

##       Result
## Dose   Success Failure sum
##   High    0.82    0.18   1
##   Low     0.74    0.26   1
##   mean    0.78    0.22   1

yields the same result. Argument margin dictates the order of dimensions over which operations are applied over, and the function list FUN dictates which function should be applied in each case. So here, R first performs mean over dimension 1 (the rows, in this case Dose), and then sum over dimension 2 (the columns, in this case Result), as is confirmed by the additional information R fed back (setting argument quiet=TRUE would remove this).

8.1.1.3 Construction from Dataframes

Here we suppose we have our data collated in a dataframe that we wish to cross-classify into a contingency table. We demonstrate doing this on the penguins dataset in library palmerpenguins (remember to install this library using install.packages("palmerpenguins") if you have not already done so).

library(palmerpenguins)
head(penguins)

## # A tibble: 6 × 8
##   species island    bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
##   <fct>   <fct>              <dbl>         <dbl>             <int>       <int>
## 1 Adelie  Torgersen           39.1          18.7               181        3750
## 2 Adelie  Torgersen           39.5          17.4               186        3800
## 3 Adelie  Torgersen           40.3          18                 195        3250
## 4 Adelie  Torgersen           NA            NA                  NA          NA
## 5 Adelie  Torgersen           36.7          19.3               193        3450
## 6 Adelie  Torgersen           39.3          20.6               190        3650
## # ℹ 2 more variables: sex <fct>, year <int>

You will notice that the penguins data is in the dataframe format known in R lingo as a tibble. For those of you that did not take DSSC II, a tibble is a user-friendly type of dataframe that works with the user-friendly R set of libraries tidyverse. For our purposes, a tibble can just be viewed as any other dataframe.

Firstly, find out information about the dataset using ?penguins.

We are interested in whether different types of penguin typically reside on different islands, hence we wish to tabulate the dataframe as follows.

penguins_data <- table( Species = penguins$species, Island = penguins$island )
penguins_data

##            Island
## Species     Biscoe Dream Torgersen
##   Adelie        44    56        52
##   Chinstrap      0    68         0
##   Gentoo       124     0         0

In this case we may be fairly certain that there is a connection between these variables…but we can test out some techniques using this contingency table nonetheless.

8.1.1.4 Exercises

These questions involve using the contingency table from the penguin data introduced in Section 8.1.1.3.

Use addmargins to add row and column sum totals to the contingency table of penguin data.
Use prop.table to obtain a contingency table of proportions.
Display the column-conditional probabilities, and use addmargins to add the column sums as an extra row at the bottom of the matrix (note: this should be a row of \(1\)’s).
Suppose I want the overall proportions of penguin specie to appear in a final column on the right of the table. How would I achieve this?

8.1.2 Chi-Square Test of Independence

Run the command chisq.test on DR_data with argument correct set to FALSE.

chisq.test( DR_data, correct = FALSE )

## 
##  Pearson's Chi-squared test
## 
## data:  DR_data
## X-squared = 0.9324, df = 1, p-value = 0.3342

chisq.test runs a \(\chi^2\) test of independence, and setting the argument correct to FALSE tells R not to use continuity correction. Look at the help file for chisq.test, and you will see that the default is for R to use Yates’ continuity correction (see Section 2.4.3.5).

chisq.test( DR_data )

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  DR_data
## X-squared = 0.52448, df = 1, p-value = 0.4689

Notice that the \(p\)-value with continuity correction is larger, as expected. The ML estimates of the expected cell frequencies can be obtained by running

chisq.test( DR_data )$expected

##       Result
## Dose   Success Failure
##   High      39      11
##   Low       39      11

8.1.2.1 Exercise

For the penguin data, apply the \(\chi^2\) test of independence between penguin specie and island of residence, and interpret the results.

8.1.3 Data Visualisation

Here we introduce several types of data visualisation methods for categorical data presented in the form of contingency tables, and apply them to the Dose-Result contingency table.

8.1.3.1 Barplots

The exercises in this section should introduce you to (or refresh your memory of, if you have seen it before) the barplot function, as well as refresh your memory of generic R plotting function arguments.

Run barplot( DR_prop ). What do the plots show?
Investigate the density argument of the function barplot by both running the commands below, and also looking in the help file.

barplot( DR_prop, density = 70 )
barplot( DR_prop, density = 30 )
barplot( DR_prop, density = 0 )

Add a title, and x- and y-axis labels, to the plot above.
Use the help file for barplot to find out how to add a legend to the plot.
How would we alter the call to barplot in order to view dose proportion levels conditional on result (instead of the overall proportions corresponding to each cell). You may wish to use some of the table manipulation commands from Section 8.1.1.
Suppose instead that we wish to display each dose level in a bar, with the proportion of successes and failures illustrated by the shading in each bar. How would we do that?

8.1.3.2 Fourfold plots

Try running the following to obtain the plot shown in Figure 8.1.

fourfoldplot( DR_data )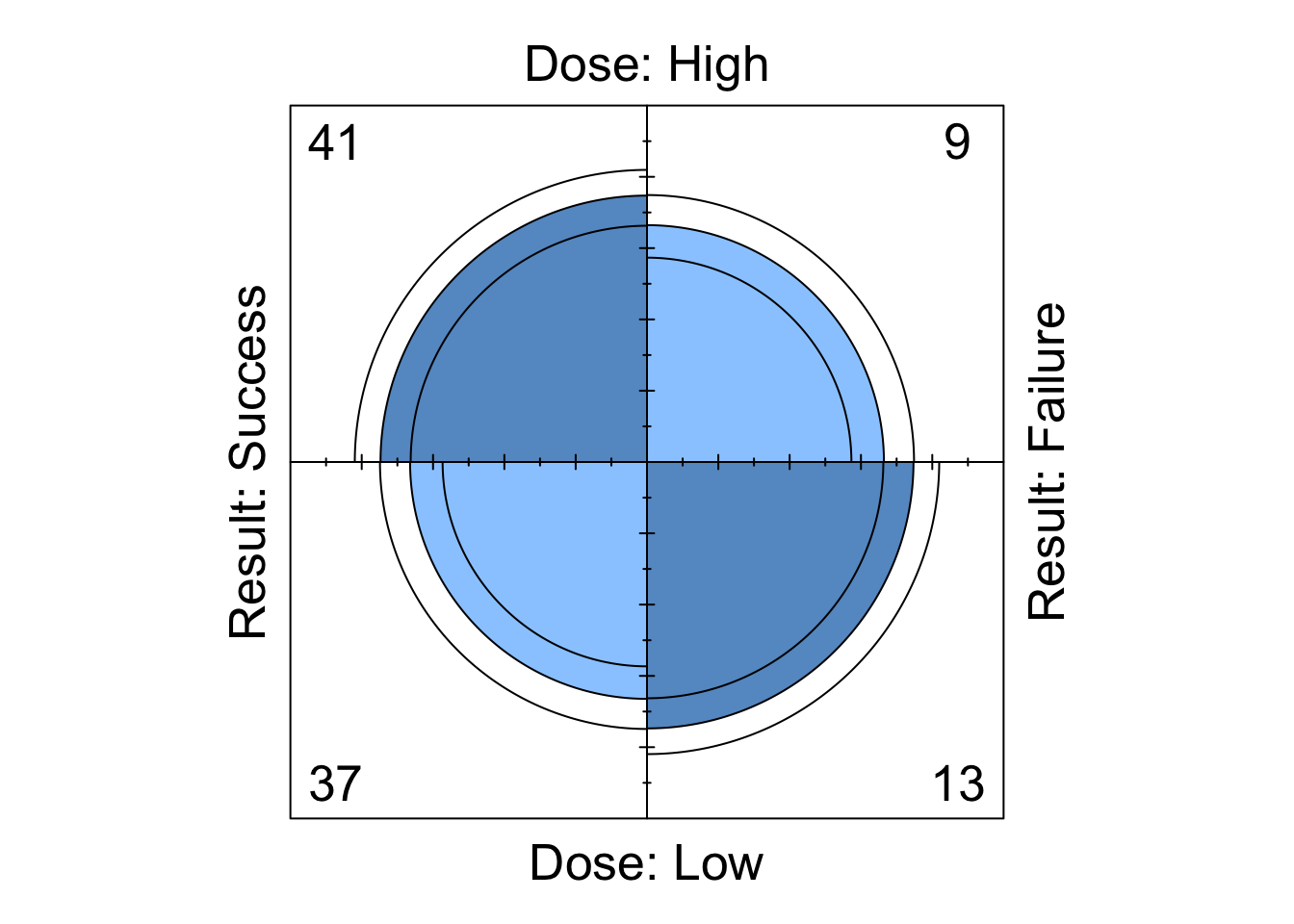

Figure 8.1: Fourfoldplot of the Dose-Result contingency table data.

A fourfold plot provides a graphical expression of the association in a \(2 \times 2\) contingency table, visualising the odds ratio. Each cell entry is represented as a quarter-circle (denoted by the middle of the three rings).

We see that the shaded diagonal areas are represented by quarter-circles with greater area than the off-diagonal areas, hence the association between the two binary classification variables in positive, that is, the odds ratio \(r_{12}\) is greater than 1. The strength of association can be visually strengthened by choice of colour (although it is subjective which colour scheme is best…). For example, to obtain a red/blue colour scheme, we can run the following to obtain the plot shown in Figure 8.2

fourfoldplot( DR_data, color = c("red", "blue") )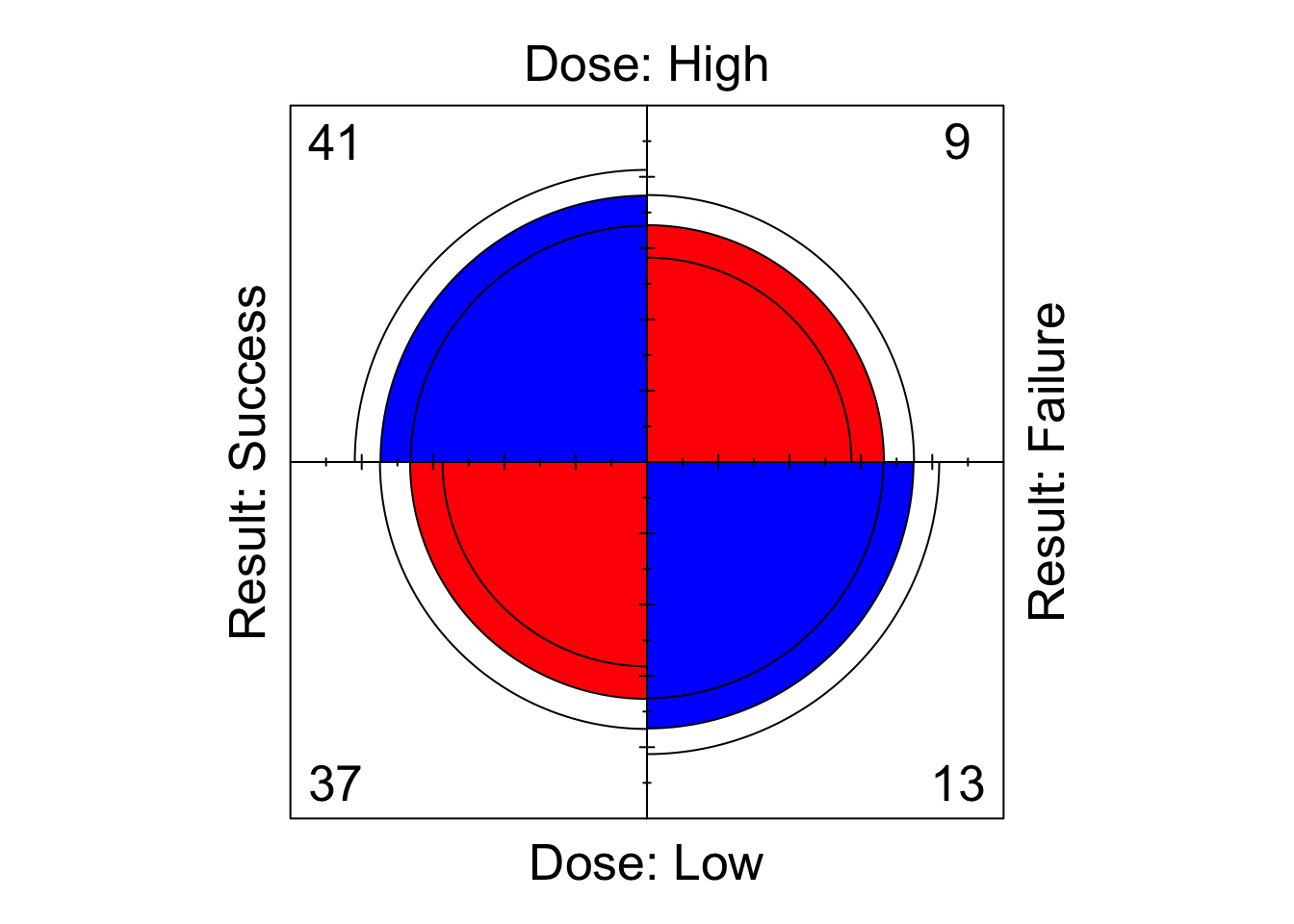

Figure 8.2: Fourfoldplot of the Dose-Result contingency table data.

The inner and outer rings of the quarter-circles correspond to confidence rings. The observed frequencies support the null hypothesis of no association between the variables if the rings for adjacent quarters overlap (we will explore this hypothesis test in the lectures…).

8.1.3.3 Sieve Diagrams

We here investigate the sieve plotting function of library vcd. Remember to look at the help file to help you understand the various arguments for this function.

library(vcd)
sieve( DR_data )

What is shown?

Now run

library(vcd)
sieve( DR_data, shade = T )

Does this make the data easier or harder to visualise?

Finally, run

sieve( DR_data, sievetype = "expected", shade = T )

What is shown now?

8.1.3.4 Mosaic Plots

Run

mosaic( DR_data )

Mosaic plots for two-way tables display graphically the cells of a contingency table as rectangular areas of size proportional to the corresponding observed frequencies. Were the classification variables independent, then the areas would be perfectly aligned in rows and columns. The worse the alignment is, the stronger the lack of fit for independence. Furthermore, specific locations of the table that deviate from independence the most may be identified and thus the pattern of underlying association attempt to be explained.

8.1.4 Odds Ratios in R

This section seeks to test your understanding of odds ratios for \(2 \times 2\) contingency tables, as well as your ability to write simple functions in R.

Write a function to compute the odds ratio of the success of event A with probability pA against the sucess of event B with probability pB.
Write a function to compute the odds ratio for a \(2 \times 2\) contingency table. Test it on the Dose-response data above.
Will there be an issue running your function from part (b) if exactly one of the cell counts of the supplied matrix is equal to zero?
What about if both cells of a particular row or column of the supplied matrix are equal to zero?
We consider two possible options for amending the function in this case.

1. First option: ensure that your function terminates and returns a clear error message of what has gone wrong and why when a zero would be found to be in both the numerator and denominator of the odds ratio. Hint: The command stop can be used to halt execution of a function and display an error message.
1. Second option: in the case that a row or column of zeroes is found, add 0.5 to each cell of the table before calculating the odds ratio in the usual way. Make sure that your function returns a clear warning (as opposed to error) message explaining that an alteration to the supplied table was made before calculating the odds ratio because there was a row or column of zeroes present. Hint: The command warning() can be used to display a warning message (but not halt execution of the function).

8.1.5 Further Exploration: Mushrooms

Consider the mushrooms data in Table 2.7 of Section 2.4.3.4 (note that this is the table after combining cells). Explore further the topics covered in this practical session. You will need to manually enter the data from the lecture notes as a matrix to get started.

8.2 Practical 2 - Contingency Tables

This practical gives you the opportunity to develop the techniques learnt in Practical 1 by utilising the functions presented there, as well as providing a base for exploration of new ones.

Each of the three sections below considers exploring one of three datasets. You are encouraged to explore each of these datasets using the array of techniques previously discussed, as well as utilising the presented questions and suggestions to help you learn new ones.

8.2.1 Mushrooms

We begin by returning to the mushrooms data (Table 2.7, introduced in Section 2.4.3.4). This dataset was the basis for the open-ended final exercise of Practical 1. You may have explored this dataset in some, or all, of the following ways, amongst others:

Manually input the data into R.
Investigated adding relevant margins to the tables and exploring corresponding contingency tables of proportions.
Performed a \(\chi^2\) test of independence.
Generated visual representations of the data in the form of barplots, sieve diagrams and mosaic plots.

You are encouraged to keep exploring this dataset. In particular, the following sections prompt analysis of residuals, a GLR test, and investigation into nominal odds ratios.

8.2.1.1 Residual Analysis

Pearson and Adjusted residuals can be obtained from the output of chisq.test(). Use the help file for this function to find out how.

8.2.1.2 GLR Test

The function below uses the appropriate parameters provided from the output of a call to chisq.test() to perform a GLR test.

Read through the code and try to understand what each line does.
What information/results are being returned at the end of the function?
Apply the function on the mushroom data and interpret the results.

G2 <- function( data ){
  # computes the G2 test of independence 
  # for a two-way contingency table of
  # data: IxJ matrix
  X2 <- chisq.test( data )
  Ehat <- X2$expected
  df <- X2$parameter
  
  term.G2 <- data * log( data / Ehat ) 
  term.G2[data==0] <- 0 # Because if data == 0, we get NaN
  
  Gij <- 2 * term.G2 # Individual cell contributions to G2 statistic.
  dev_res <- sign( data - Ehat ) * sqrt( abs( Gij ) )
  G2 <- sum( Gij ) # G2 statistic
  p <- 1 - pchisq( G2, df ) 
  return( list( G2 = G2, df = df, p.value = p, 
                Gij = Gij, dev_res = dev_res ) ) 
}

8.2.1.3 Nominal Odds Ratios

In Section 8.1.4, you were encouraged to write a function to calculate the odds ratio for a \(2 \times 2\) contingency table. Such a function (without concern for zeroes occurring) may be given by

OR <- function( M ){ ( M[1,1] * M[2,2] ) / ( M[1,2] * M[2,1] ) }

Based on this, what does the following function do? Test the function out on the mushrooms data and interpret the results.

nominal_OR <- function( M, ref_x = nrow( M ), ref_y =  ncol( M ) ){
  
  # I and J
  I <- nrow(M)
  J <- ncol(M)
  
  # Odds ratio matrix.
  OR_reference_IJ <- matrix( NA, nrow = I, ncol = J )
  for( i in 1:I ){
    for( j in 1:J ){
      OR_reference_IJ[i,j] <- OR( M = M[c(i,ref_x), c(j,ref_y)] )
    }
  }
  
  OR_reference <- OR_reference_IJ[-ref_x, -ref_y, drop = FALSE]
  
  return(OR_reference)
  
}

8.2.1.4 Visualisation and Residuals

We can add residual information to mosaic plots as follows:

mosaic( mushroom_data, 
        gp = shading_hcl, 
        residuals_type = "Pearson" )

Alternatively, residuals can be directly specified using the residuals argument (see the help file).

8.2.2 Dose-Result

Manually input into R the hypothetical data presented in Table 2.15. You may wish to attempt some or all of the following.

Utilise previously introduced skills on this dataset.
Amend the function presented in Section 8.2.1.3 to write two new functions
- one to compute the set of \((I-1) \times (J-1)\) local odds ratios for \(i = 1,...,I-1\) and \(j = 1,...,J-1\); and
- one to compute the set of \((I-1) \times (J-1)\) global odds ratios for \(i = 1,...,I-1\) and \(j = 1,...,J-1\).
Write a function that produces an \((I-1) \times (J-1)\) matrix of fourfold plots, each corresponding to the submatrices associated with each of the \((I-1) \times (J-1)\) local odds ratios for \(i = 1,...,I-1\) and \(j = 1,...,J-1\).
Perform a linear trend test on the data, either by writing your own code to calculate the relevant quantities, or by utilising the following function, courtesy of Kateri (2014).

linear.trend <- function( table, x, y ){
  # linear trend test for a 2-way table
  # PARAMETERS:
  # freq: vector of the frequencies, given by rows
  # NI: number of rows
  # NJ: number of columns
  # x: vector of row scores
  # y: vector of column scores
  # RETURNS:
  # r: Pearson’s sample correlation
  # M2: test statistic
  # p.value: two-sided p-value of the asymptotic M2-test
  NI <- nrow( table )
  NJ <- ncol( table )
  
  rowmarg <- addmargins( table )[,NJ+1][1:NI]
  colmarg <- addmargins( table )[NI+1,][1:NJ]
  n <- addmargins( table )[NI+1,NJ+1]
  
  xmean <- sum( rowmarg * x ) / n
  ymean <- sum( colmarg * y ) / n 
  xsq <- sqrt( sum( rowmarg * ( x - xmean )^2 ) )
  ysq <- sqrt( sum( colmarg * ( y - ymean )^2 ) ) 
  
  r <- sum( ( x - xmean ) %*% table %*% ( y - ymean ) ) / ( xsq * ysq )
  M2 = (n-1)*r^2
  p.value <- 1 - pchisq( M2, 1 ) 
  return( list( r = r, M2 = M2, p.value = p.value ) ) 
}

8.2.3 Titanic

Type ?Titanic into R to learn about the Titanic dataset. You may wish to do this in conjuntion with one or more of the following

Titanic
dim( Titanic )
dimnames( Titanic )

We will explore this dataset further in Practical 3. For now, you are encouraged to explore associations between the variables in the contingency table. Some ideas and questions to get you started are:

Generate some partial tables.
Generate some marginal tables. You can do this using the function margin.table (look at the help file).
Calculate partial and marginal odds ratios, and interpret the results.
Perform a \(\chi^2\)-test of independence between Class and Survival, marginalising over Sex and Age.
Can we perform a linear trend test between Class and Survival, having marginalised over Sex and Age? If you think we can, give it a go!
Produce a sieve or mosaic plot of the Titanic data and interpret.

8.3 Practical 3 - Contingency Tables and LLMs

8.3.1 Contingency Tables: Titanic

We revisit the Titanic dataset introduced in Section 8.2.3.

Run the following command to generate an alternative \(2 \times 2 \times 4\) Titanic contingency table, called TitanicA. What does the command do?

TitanicA <- aperm( margin.table( Titanic, margin = c(1,2,4) ), c(2,3,1) )

Use the command mantelhaen.test to perform a Mantel-Haenszel Test on the TitanicA dataset for the conditional independence of Sex and Survived given Class.
Use fourfoldplot() to produce a matrix of fourfoldplots for the TitanicA dataset, each corresponding to one of the K layers for Class. Hint: look in the help file for fourfoldplot and you may find that this question is easier than you think!
Run the following command to obtain another alternative Titanic contingency table, called TitanicB. What does the command do?

TitanicB <- margin.table( Titanic[3:4,,,], c(1,2,4) )

Using the table TitanicB, calculate the marginal (over Sex) odds ratio between Class and Survived. Interpret the result.
Using the table TitanicB, calculate the conditional (on each level of Sex) odds ratio between Class and Survived. Interpret the result and compare with the result to part (e). Do you notice anything initially counter-intuitive? Explain how this comes about.

8.3.2 LLMs: Dose-Result Data

The package for fitting LLMs in R is MASS:

library(MASS)

We will learn how to implement LLMs in R using the Dose-Result data from Table 2.15, manually input into R in Section 9.2.2.

We fit the independence LLM to the Dose-Result data as shown. Note that this function assumes use of zero-sum constraints.

( I.fit <- loglm( ~ Dose + Result, data = DoseResult ) )

## Call:
## loglm(formula = ~Dose + Result, data = DoseResult)
## 
## Statistics:
##                       X^2 df     P(> X^2)
## Likelihood Ratio 25.96835  4 3.211303e-05
## Pearson          25.17856  4 4.631705e-05

Likelihood Ratio shows the \(G^2\) GLR goodness-of-fit test against the fully saturated model of dimension \(q\), where \(q\) is the number of variables (in this case \(q=2\)).
Pearson \(\chi^2\) test: in this case that arising from the \(\chi^2\) test of independence such as derived for 2-way tables in Section 2.4.3.3.

In this case, the goodness-of-fit tests suggest to reject the independence model in favour of the fully saturated model. We thus conclude that there is an association between the Dose level and treatment Result. We therefore decide to fit the saturated model, which we do as follows (note that we only need the highest level interaction terms included when we define the model, as it is assumed the LLM is hierarchical):

( sat.fit <- loglm( ~ Dose*Result, data = DoseResult ) )

## Call:
## loglm(formula = ~Dose * Result, data = DoseResult)
## 
## Statistics:
##                  X^2 df P(> X^2)
## Likelihood Ratio   0  0        1
## Pearson            0  0        1

where clearly now the statistics will be \(0\) (as the model is being compared with itself).

The parameters’ ML estimates, satisfying the zero-sum constraints, are saved in the fitted model objects under param.

( I_param <- I.fit$param )

## $`(Intercept)`
## [1] 3.493314
## 
## $Dose
##       High     Medium        Low 
## -0.1729852 -0.2730687  0.4460540 
## 
## $Result
##     Success     Partial     Failure 
##  0.17502768  0.02757495 -0.20260263

( sat_param <- sat.fit$param )

## $`(Intercept)`
## [1] 3.437124
## 
## $Dose
##       High     Medium        Low 
## -0.2524803 -0.2488126  0.5012929 
## 
## $Result
##     Success     Partial     Failure 
##  0.27862253  0.03096394 -0.30958647 
## 
## $Dose.Result
##         Result
## Dose        Success      Partial     Failure
##   High    0.3868817  0.003268524 -0.39015024
##   Medium  0.1165854 -0.128232539  0.01164718
##   Low    -0.5034671  0.124964015  0.37850305

\(\lambda\) ((Intercept)) is equal to the mean log expected cell count (under the specified model).
\(\lambda_i^X\) (Dose) is the difference between the mean log expected cell count for category \(i\) over \(j\) in \(1,...,J\) and the overall mean log expected cell count (under the specified model).
\(\lambda_j^Y\) (Result) is the difference between the mean log expected cell count for category \(j\) over \(i\) in \(1,...,I\) and the overall mean log expected cell count (under the specified model).
\(\lambda_{ij}^{XY}\) (Dose.Result) correspond to the differences between log expected cell count for cell \((i,j)\) and the sum of the three contributions above (under the two-way interaction model).

For example, we can verify that

exp( I_param$`(Intercept)` + I_param$Dose[2] + I_param$Result[1])

##   Medium 
## 29.82278

is equal to the expected-under-independence count for cell \((2,1)\) of the contingency table

DoseResultTable[2,4] * DoseResultTable[4,1] / DoseResultTable[4,4]

## [1] 29.82278

which can incidentally be calculated for all cells via

fitted(I.fit)

## Re-fitting to get fitted values

##         Result
## Dose      Success  Partial  Failure
##   High   32.96203 28.44304 22.59494
##   Medium 29.82278 25.73418 20.44304
##   Low    61.21519 52.82278 41.96203

For the saturated model, we can verify that

exp( sat_param$`(Intercept)` + sat_param$Dose[2] 
     + sat_param$Result[1] + sat_param$Dose.Result[2,1] )

## Medium 
##     36

is precisely equal to cell \((2,1)\) of the observed table

DoseResult[2,1]

## [1] 36

Recall that the local odds ratios can be directly derived from the interaction parameters (Equation (4.4)). For example, for cell \((2,1)\), we have that

lambdaXY <- sat_param$Dose.Result
lambdaXY[2,1] + lambdaXY[3,2] - lambdaXY[2,2] - lambdaXY[3,1]

## [1] 0.873249

which we can verify is equivalent to cell \((2,1)\) of the following log local OR matrix for the contingency table (obtained using the function from Solutions Section 9.2.2).

log( local_OR( DoseResult ) )

##           [,1]      [,2]
## [1,] 0.1387953 0.5332985
## [2,] 0.8732490 0.1136593

8.3.3 LLMs: Extended Dose-Result Data

Consider an extended Dose-Result dataset that now cross-classifies Treatment (Success or Failure) against presence of a prognostic factor (Yes or No) at each of six possible clinics (A-F), which we enter into R as follows:

dat <- array(c(79, 68, 5, 17,
               89, 221, 4, 46,
               141, 77, 6, 18,
               45, 26, 29, 21,
               81, 112, 3, 11,
               168, 51, 13, 12), c(2,2,6))
dimnames(dat) <- list(Treatment=c("Success","Failure"),
                        Prognostic_Factor=c("Yes","No"),
                        Clinic=c("A","B","C","D","E","F"))

We fit the homogeneous associations and conditional independence (of Prognostic_Factor and Treatment on Clinic) models as follows:

( hom.assoc <- loglm(~ Treatment*Prognostic_Factor 
                   + Prognostic_Factor * Clinic 
                   + Treatment * Clinic, 
                   data=dat )  )

## Call:
## loglm(formula = ~Treatment * Prognostic_Factor + Prognostic_Factor * 
##     Clinic + Treatment * Clinic, data = dat)
## 
## Statistics:
##                       X^2 df  P(> X^2)
## Likelihood Ratio 7.949797  5 0.1590242
## Pearson          7.894439  5 0.1621501

( cond.ind.TF <- loglm(~ Prognostic_Factor * Clinic 
                       + Treatment * Clinic, data=dat ) )

## Call:
## loglm(formula = ~Prognostic_Factor * Clinic + Treatment * Clinic, 
##     data = dat)
## 
## Statistics:
##                       X^2 df     P(> X^2)
## Likelihood Ratio 42.79483  6 1.280709e-07
## Pearson          41.07145  6 2.803322e-07

The GLR test statistic of a model against the fully saturated model can also be obtained by

hom.assoc$deviance

## [1] 7.949797

By subtracting the test statistic for \(\mathcal{M}_1\) from \(\mathcal{M}_0\), where \(\mathcal{M}_0\) is nested in \(\mathcal{M}_1\), we obtain the GLR test statistic between \(\mathcal{M}_0\) and \(\mathcal{M}_1\) (See Equation (4.23)).

( DG2 <- cond.ind.TF$deviance - hom.assoc$deviance )

## [1] 34.84504

The p-value for testing \(\mathcal{H}_0: \, \mathcal{M}_0\) against alternative \(\mathcal{H}_1: \, \mathcal{M}_1\) is then given by

( p.value <- 1 - pchisq(DG2, 1) )

## [1] 3.570184e-09

Finally, backwards stepwise model selection using AIC is obtained using

sat <- loglm(~ Prognostic_Factor * Clinic * Treatment, data=dat )
step( sat, direction="backward", test = "Chisq" )

## Start:  AIC=48
## ~Prognostic_Factor * Clinic * Treatment
## 
##                                      Df   AIC    LRT Pr(>Chi)
## - Prognostic_Factor:Clinic:Treatment  5 45.95 7.9498    0.159
## <none>                                  48.00                
## 
## Step:  AIC=45.95
## ~Prognostic_Factor + Clinic + Treatment + Prognostic_Factor:Clinic + 
##     Prognostic_Factor:Treatment + Clinic:Treatment
## 
##                               Df     AIC     LRT  Pr(>Chi)    
## <none>                            45.950                      
## - Prognostic_Factor:Treatment  1  78.795  34.845 3.570e-09 ***
## - Prognostic_Factor:Clinic     5 117.315  81.366 4.346e-16 ***
## - Clinic:Treatment             5 217.461 181.511 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

## Call:
## loglm(formula = ~Prognostic_Factor + Clinic + Treatment + Prognostic_Factor:Clinic + 
##     Prognostic_Factor:Treatment + Clinic:Treatment, data = dat, 
##     evaluate = FALSE)
## 
## Statistics:
##                       X^2 df  P(> X^2)
## Likelihood Ratio 7.949788  5 0.1590247
## Pearson          7.895029  5 0.1621165

where inclusion of test = "Chisq" results in the GLR test statistic and corresponding p-value information being included in the output. In this case we stop after dropping just the three-way interaction term.

8.3.4 Log linear Models: Titanic

Explicitly fit several models (i.e. without using the step function) to the Titanic dataset, including the independence model and the fully saturated model. Comment on your findings.
Pick two distinct nested models, and calculate the \(G^2\) likelihood ratio test statistic testing the hypothesis \(\mathcal{H}_0: \, \mathcal{M}_0\) against alternative \(\mathcal{H}_1: \, \mathcal{M}_1\).
Use backwards selection to fit a log-linear model using AIC. Which model is chosen? What does this tell you?
Use Forwards selection to fit a log-linear model using BIC (look in the help file for step if you are unsure how to do this). Do you get a different model to that found in part (c)? If so, is this due to the change in model selection criterion or stepwise selection direction?

8.4 Practical 4 - Binary Regression

In this practical, there are two tasks. The first tests your understanding of binary regression as discussed in the lectures, both in terms of R coding and also general understanding. The second question goes further into the R coding side of things, touching upon topics we haven’t yet covered in lectures but which will be a useful taster for things to come. Before you start this practical, you may wish to review the practical example of Section 5.3.5.1.

You can find the datasets required for this practical on Ultra under Other Material.

8.4.1 Space Shuttle Flights

The dataset shuttle describes, for \(n = 23\) space shuttle flights before the Challenger disaster in 1986, the temperature in \(\,^{\circ}F\) at the time of take-off, as well as the occurrence or non-occurrence of a thermal overstrain of a certain component (the famous O-ring). The data set contains the variables:

flight - flight number
temp - temperature in \(\,^{\circ}F\)
td - thermal overstrain (\(1=\)yes, \(0=\)no)

You can read in the Shuttle data as follows.

## shuttle <- read.table("shuttle.asc", header=TRUE)

where we need shuttle.asc to be in the working directory (or else we set as argument to read.table the location of the file).

Fit a linear model (with the temperature as covariate) using the R function lm. Produce a plot which displays the data, as well as the fitted probabilities of thermal overstrain. Why does this model not provide a satisfactory description of the data?
Fit a logistic regression model to these data, with logit link function, using function glm.
Extract the model parameters from the logistic regression model. Write a function for the expected probability of thermal overstrain td in terms of temp explicitly (that is, \(\hat{P}(\textrm{td|temp})\)) using your knowledge of logistic regression models, and add its graph to the plot created in part (a).
According to this model, at what temperature is the probability of thermal overstrain exactly equal to \(0.5\)?
On the day of the Challenger disaster, the temperature was \(31^{\circ}F\). Use your model to predict the probability of thermal overstrain on that day.
Replace the logit link by a probit link, and repeat the above analysis for this choice of link function.

8.4.2 US Graduate School Admissions

The dataset binary.csv contains data on the chances of admission to US Graduate School. We are interested in how GRE (Graduate Record Exam scores), GPA (grade point average) and prestige of the undergraduate institution (rated from 1 to 4, highest prestige to lowest prestige), affect admission into graduate school. The response variable is a binary variable, 0 for don’t admit, and 1 for admit.

The question is to find a model which relates the response to the regressor variables.

First read the data in as follows…

graduate <- read.csv("binary.csv")

where we need binary.csv to be in the working directory (or else we set as argument to read.csv the location of the file). Start to examine it with the following commands

head(graduate)
summary(graduate)

As the response is binary, a natural first step is to try logistic regression. We must first tell R that rank is a categorical variable (for example, we must tell R that rank=2 is not twice as big as rank=1).

graduate$rank <- factor(graduate$rank)
graduate.glm <- glm(admit ~ gre + gpa + rank, data = graduate, 
                                          family = "binomial")

Look at summary(graduate.glm). You should see that all the terms are significant, as well as some information about the deviance and the AIC.

The logistic regression coefficients in the R output give the change in the log odds of the outcome for a one unit increase in the predictor variable. For example, for a one unit increase in GPA, the log odds of being admitted to graduate school increases by 0.804. As rank is a factor (categorical variable) the coefficients for rank have a slightly different interpretation. For example, having attended an undergraduate institution with rank of 2, versus an institution with a rank of 1, changes the log odds of admission by -0.675.

Use the command exp(coef(graduate.glm)) to get the odds ratios. This will tell you, for example, that a one point increase in GRE increases the odds of admittance to Grad school by a factor of 1.0023.
Use the following command in order to use this model to predict the probability of admission for a student with GRE 700, GPA 3.7, to a rank 2 institution.

predData <- with(graduate, data.frame(gre = 700, gpa = 3.7, rank = factor(2)))
predData$prediction <- predict(graduate.glm, newdata = predData,
                                type = "response")

Look at the predData dataframe to find your predicted value.

We haven’t formally covered AIC in the context of logistic regression, but try removing terms from the model to see if it results in a significantly worse AIC value?
Repeat the analysis of parts a), b), d) and e) above for the probit link function (note that exp(coef(graduate.glm)) will no longer give us the odds ratios in this case). Is the model better or worse? Does the predicted admission probability of a student with GRE 700, GPA 3.7, to a rank 2 institution change?

References

Kateri. 2014. Contingency Table Analysis - Methods and Implementation Using r. New York: Birkhauser.

This example serves to demonstrate how to change the function FUN - I would like to reiterate that the mean function works for our purposes here (to get overall proportions for each column) only because the row totals are both the same.↩︎