CHAPTER 3 Estimation Procedures

Click for quick review

The Linear Model

\[ \underset{n\times1}{\textbf{Y}} = \underset{n\times (k+1)}{\textbf{X}}\underset{(k+1)\times1}{\boldsymbol{\beta}} + \underset{n\times 1}{\boldsymbol{\varepsilon}}\\\begin{bmatrix} Y_1 \\ Y_2 \\ \vdots\\ Y_n \end{bmatrix} =\begin{bmatrix} 1 & X_{11} & X_{12} & \cdots & X_{1k} \\ 1 & X_{21} & X_{12} & \cdots & X_{2k} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & X_{n1} & X_{n2} & \cdots & X_{nk} \end{bmatrix}\begin{bmatrix}\beta_0 \\ \beta_1 \\ \beta_2 \\ \vdots\\ \beta_k \end{bmatrix} + \begin{bmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \vdots\\ \varepsilon_n\end{bmatrix} \]

where

  • \(\textbf{Y}\) is the response vector.
  • \(\textbf{X}\) is the design matrix.
  • \(\boldsymbol{\beta}\) is the regression coefficients vector.
  • \(\boldsymbol{\varepsilon}\) is the error term vector.

Assumptions

  • the expected value of the unknown quantity \(\varepsilon_i\) is 0 for every observation \(i\)

  • the variance of the errors term is the same for all observations

  • the error terms and observations are uncorrelated

  • the error terms follow a normal distribution

  • the independent variables are not strongly correlated to each other

Reasons for Having Assumptions

  • to make sure that the parameters are estimable
  • to make sure that the solution to the estimation problem is unique
  • to aid in the interpretation of the model parameters
  • to derive more important results that can be used for further analyses

GENERAL PROBLEM:

Given the following model, for observation \(i=1,...,n\) \[ Y_i=\beta_0+\beta_1X_{i1}+\beta_2 X_{i2}+\dots+\beta_kX_{ik}+\varepsilon_i \] or the matrix form \[ \textbf{Y} = \textbf{X}\boldsymbol{\beta}+\boldsymbol{\varepsilon} \] How do we estimate the \(\beta s\)?

There are several estimation procedures that can be used in linear models. The course will focus on least squares, but others are presented as well.

Scatterplot with fitted line

Figure 3.1: Scatterplot with fitted line

One criterion of the fitted line: have all points to be close to it. That is, we want to have small \(\varepsilon_i\)

3.1 Method of Least Squares

Objective function: Minimize \(\sum_{i=1}^n\varepsilon_i^2\) or \(\boldsymbol{\varepsilon}'\boldsymbol{\varepsilon}\) , the inner product of the error term vector.

In simple linear regression \(y_i=\beta_0 +\beta x_i+\varepsilon_i\), the estimator for \(\beta_0\) and \(\beta\) can be derived as follows:
\[ \hat{\beta_0}=\underset{\beta_0}{\arg \min}\sum_{i=1}^n \varepsilon_i^2 \quad \hat{\beta}=\underset{\beta}{\arg \min}\sum_{i=1}^n \varepsilon_i^2 \]

Full solution

GOAL: Find value of \(\beta_0\) and \(\beta\) that minimizes \(\sum_{i=1}^n\varepsilon_i^2\), which are the solutions to the equations \[ \frac{d}{d\beta_0}\sum_{i=1}^n\varepsilon_i^2=0\quad\text{and}\quad\frac{d}{d\beta}\sum_{i=1}^n\varepsilon_i^2=0 \]

For the Intercept

\[\begin{align} \frac{d}{d\beta_0}\sum_{i=1}^n\varepsilon_i^2 &= \frac{d}{d\beta_0}\sum_{i=1}^n(y_i-\beta_0-\beta x_i)^2 \\ &= -2\sum_{i=1}^n(y_i-\beta_0-\beta x_i) \end{align}\]

Now, equate to \(0\) and solve for \(\hat{\beta_0}\)

\[\begin{align} 0&=-2\sum_{i=1}^n(y_i-\hat{\beta_0}-\hat{\beta} x_i)\\ 0&=\sum_{i=1}^ny_i - n\hat{\beta_0}-\hat{\beta} \sum_{i=1}^nx_i\\ n\hat{\beta_0} &= \sum_{i=1}^ny_i -\hat{\beta} \sum_{i=1}^nx_i \\ \hat{\beta_0} &= \bar{y} -\hat{\beta} \bar{x} \end{align}\]

For the Slope
Since there is already an estimate for \(\beta_0\), we can already plug it in the equation before solving for \(\hat{\beta}\).

\[\begin{align} \frac{d}{d\beta}\sum_{i=1}^n\varepsilon^2 &= \frac{d}{d\beta}\sum_{i=1}^n[y_i-\hat{\beta_0}-\beta x_i]^2 \\ &= \frac{d}{d\beta}\sum_{i=1}^n[y_i-(\bar{y}-\beta\bar{x})-\beta x_i]^2 \\ &= \frac{d}{d\beta}\sum_{i=1}^n[(y_i-\bar{y})-\beta( x_i-\bar{x})]^2 \\ &= -2\sum_{i=1}^n\left\{[(y_i-\bar{y})-\beta( x_i-\bar{x})]( x_i-\bar{x})\right\} \\ &= -2\sum_{i=1}^n[(y_i-\bar{y})( x_i-\bar{x})-\beta( x_i-\bar{x})( x_i-\bar{x})] \end{align}\]

Equating to \(0\) to solve for \(\hat{\beta_0}\)

\[\begin{align} 0 &= -2\sum_{i=1}^n[(y_i-\bar{y})( x_i-\bar{x})-\hat{\beta}( x_i-\bar{x})( x_i-\bar{x})] \\ 0 &= \sum_{i=1}^n[(y_i-\bar{y})( x_i-\bar{x})]- \hat{\beta}\sum_{i=1}^n( x_i-\bar{x})^2 \\ \hat{\beta}&= \frac{\sum_{i=1}^n[(y_i-\bar{y})( x_i-\bar{x})]}{\sum_{i=1}^n( x_i-\bar{x})^2} \end{align}\]

Therefore, we have \(\hat{\beta_0} = \bar{y} -\hat{\beta} \bar{x}\) and \(\hat{\beta} = \frac{\sum_{i=1}^n(y_i-\bar{y})(x_i-\bar{x})}{\sum_{i=1}^n( x_i-\bar{x})^2}\) \(\blacksquare\)

 
How do we generalize this for the multiple linear regression?

 

The Normal Equations

Definition 3.1 The normal equation is a closed-form solution used to find an estimated value of the parameter that minimizes an objective function.

In the least squares method, the objective function (or the cost function) is \(\boldsymbol{\varepsilon}'\boldsymbol{\varepsilon}=(\textbf{Y}-\textbf{X}\boldsymbol{\beta})'(\textbf{Y}-\textbf{X}\boldsymbol{\beta})\).

If we minimize this with respect to the parameters \(\beta_j\), we will obtain the normal equations \(\frac{\partial\boldsymbol{\varepsilon}'\boldsymbol{\varepsilon}}{\partial\beta_j} = 0, \quad j =0,...,k\). Expanding this, we have the following normal equations:

 

In \((k+1)\) equations form : \(\frac{\partial\sum_{i=1}^n\varepsilon_i^2}{\partial\beta_j} = 0, \quad j =0,...,k\)

\[\begin{align}1st :&\quad \hat\beta_0n +\hat\beta_1\sum X_{i1} + \hat\beta_2\sum X_{i2} + \cdots + \hat\beta_k\sum X_{ik}&=\quad&\sum Y_i \\2nd :&\quad \hat\beta_0\sum X_{i1} + \hat\beta_1\sum X_{i1}^2 + \hat\beta_2\sum X_{i1}X_{i2} + \cdots + \hat\beta_k\sum X_{i1}X_{ik} &=\quad& \sum X_{i1} Y_i \\ \vdots\quad & &&\quad\vdots \\ (k+1)th :&\quad \hat\beta_0\sum X_{ik} + \hat\beta_1\sum X_{i1} X_{ik} + \hat\beta_2\sum X_{i2}X_{ik} + \cdots + \hat\beta_k\sum X_{ik}^2 &=\quad& \sum X_{ik} Y_i\end{align}\]

 

In matrix form: \(\frac{\partial\boldsymbol{\varepsilon}'\boldsymbol{\varepsilon}}{\partial{\boldsymbol{\beta}}} = \textbf{0}\)

\[ \textbf{X}'\textbf{X}\hat{\boldsymbol{\beta}} = \textbf{X}'\textbf{Y} \]

\[ \begin{bmatrix}n & \sum X_{i1} & \sum X_{i2} & \cdots & \sum X_{ik} \\\sum X_{i1} & \sum X_{i1}^2 & \sum X_{i1}X_{i2} & \cdots & \sum X_{i1}X_{ik} \\\vdots & \vdots & \vdots & \ddots & \vdots \\\sum X_{ik} & \sum X_{i1} X_{ik} & \sum X_{i2}X_{ik} & \cdots & \sum X_{ik}^2 \\\end{bmatrix}\begin{bmatrix} \hat{\beta_0}\\ \hat\beta_1\\ \hat\beta_2\\ \vdots \\ \hat\beta_k\end{bmatrix}= \begin{bmatrix} \sum Y_i \\ \sum X_{i1} Y_i \\ \vdots\\ \sum X_{ik} Y_i\end{bmatrix} \]

 

The solution to these equations is unique, and will be the ordinary least squares estimator for \(\boldsymbol{\beta}\).

All of these normal equations are unconditionally true under method of least squares.

The OLS Estimator

Theorem 3.1 (Ordinary Least Squares Estimator)

  If \((\textbf{X}'\textbf{X})^{-1}\) exists, the estimator of \(\boldsymbol{\beta}\) that will minimize \(\boldsymbol{\varepsilon}'\boldsymbol{\varepsilon}\) is given by

\[ \boldsymbol{\hat{\beta}}=(\textbf{X}'\textbf{X})^{-1}(\textbf{X}'\textbf{Y}) \]

Remarks:

  • \((\textbf{X}'\textbf{X})^{−1}\) exists when \(\textbf{X}\) is of full column rank.

  • This implies that the independent variables should be independent from each other.  

  • Furthermore, if \(n < p\), then \(\textbf{X}\) cannot be full column rank. Therefore, there should be more observations than the number of regressors.

 

Since the estimator \(\hat{\boldsymbol{\beta}}\) is a random vector, we also want to explore its mean and variance.

Theorem 3.2 The OLS estimator \(\hat{\boldsymbol\beta}\) is an unbiased estimator for \(\boldsymbol{\beta}\)

Theorem 3.3 The variance-covariance matrix of \(\hat{\boldsymbol{\beta}}\) is given by \(\sigma^2(\textbf{X}'\textbf{X})^{-1}\)

Remark: \(Var(\hat{\beta}_j)\) is the \((j+1)^{th}\) diagonal element of \(\sigma^2(\textbf{X}'\textbf{X})^{-1}\)

More properties regarding the method of least squares will be discussed in Section 4.5 , where we also explain that the OLS estimator for \(\boldsymbol{\beta}\) is also the BLUE, MLE, and UMVUE for \(\boldsymbol{\beta}\)

Q: What does it mean when the variance of an estimator \(\hat{\beta}_j\) is large?

Exercises

Exercise 3.1 Prove Theorem 3.1

  Show that the least squares estimator for the coefficient vector \(\boldsymbol{\beta}\) is \(\boldsymbol{\hat{\beta}} = (\textbf{X}'\textbf{X})^{-1}(\textbf{X}'\textbf{Y})\).
  Assume that \((\textbf{X}'\textbf{X})^{-1}\) exists.
Hints
  • Minimize \(\boldsymbol{\varepsilon}'\boldsymbol{\varepsilon}\) with respect to \(\boldsymbol{\beta}\).
  • Note that \(\boldsymbol{\varepsilon}=\textbf{Y}-\textbf{X}\boldsymbol{\beta}\).
  • Recall matrix calculus.
  • You will obtain the normal equations, then solve for \(\boldsymbol{\beta}\).

Exercise 3.2 Prove Theorem 3.2

Hint
  • Show \(E(\hat{\boldsymbol{\beta}})=\boldsymbol{\beta}\)

Exercise 3.3 Prove Theorem 3.3

Hint
  • Show \(Var(\hat{\boldsymbol{\beta}})= \sigma^2(\textbf{X}'\textbf{X})^{-1}\)

The following exercises will help us understand some requirements before obtaining the estimate \(\hat{\boldsymbol{\beta}}\)

Exercise 3.4 Let \(\textbf{X}\) be the \(n\times p\) design matrix. Prove that if \(\textbf{X}\) has linearly dependent columns, then \(\textbf{X}'\textbf{X}\) is not invertible

Hints

The following should be part of your proof. Do not forget to cite reasons.

  • highest possible rank of \(\textbf{X}\)
  • highest possible rank of \(\textbf{X}'\textbf{X}\)
  • order of \(\textbf{X}'\textbf{X}\)
  • determinant of \(\textbf{X}'\textbf{X}\)

Exercise 3.5 Prove that if \(n < p\), then \(\textbf{X}'\textbf{X}\) is not invertible.

Hints
Almost same hints as previous exercise.

3.2 Other Estimation Methods

As mentioned, we will focus on the least squares estimation in this course. The following are just quick introduction of other methods in estimating the coefficients or the equation that predicts \(Y\)

Method of Least Absolute Deviations

Objective function: Minimize \(\sum_{i=1}^n|\varepsilon_i|\)

  • Solution is quantile regression model.
  • Solution is robust to extreme observations. The method places less emphasis on outlying observations than does the method of least squares.
  • This method is one of a variety of robust methods that have the property of being insensitive to both outlying data values and inadequacies of the model employed.
  • The solution may not be unique.
Backfitting Method

Assuming an additive model \[ Y_i=\beta_0+ \beta_1X_{i1}+\beta_2X_{i2}+\cdots+\beta_kX_{ik}+\varepsilon_i \] with constraints \(\sum_{i=1}^n\beta_jX_{ij}=0\) for $j=1,…,k$ and \(\quad \beta_0=\frac{1}{n\sum_{i=1}^nY_i}\)

  • Fit the coefficient of the most important variable.
    Compute for residuals: \(Y_1 = Y − \hat{\beta}_1 X_1\)

  • Fit the coefficient for the next important variable.
    Compute for residuals: \(Y_2 = Y_1 − \hat{\beta}_2 X_2\)

  • Continue until last coefficient is computed.

Gradient Descent

Gradient Descent is an optimization algorithm for finding a local minimum of a differentiable function. This is one of the first algorithms that you will encounter if you will study machine learning.

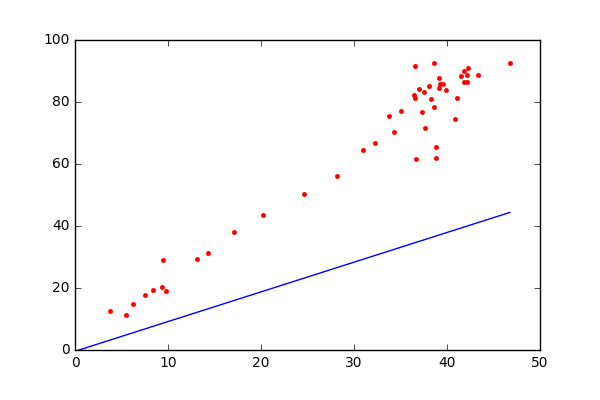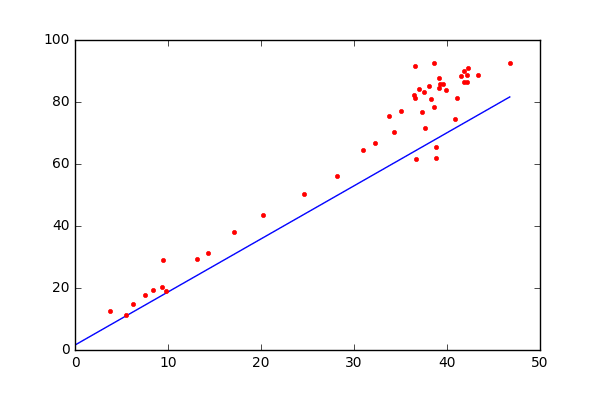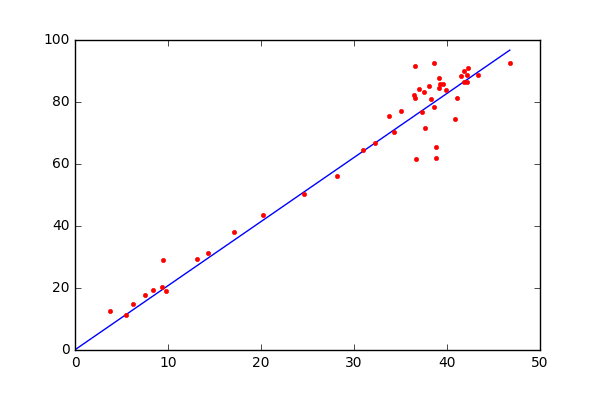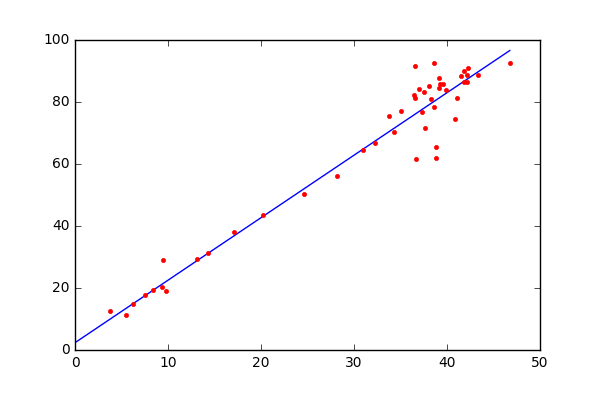
  1. Initialize the parameters of the model randomly
  2. Compute the gradient of the cost function with respect to each parameter. It involves making partial differentiation of cost function with respect to the parameters.
  3. Update the parameters of the model by taking steps in the opposite direction of the model. Choose a hyperparameter learning rate which is denoted by alpha. It helps in deciding the step size of the gradient.
  4. Repeat steps 2 and 3 iteratively to get the best parameter for the defined model.

If the cost function is the sum of squares of errors, then OLS is better.

But if the cost function has no closed form solution, then gradient descent may become useful.

Source: https://www.geeksforgeeks.org/gradient-descent-in-linear-regression/

Nonparametric Regression

Fit the model \(Y = f (X_1, X2, \cdots , X_k ) + \varepsilon_i\) where the function \(f\) is has no parameters.

It is the unknown function \(f\) being estimated, not just the parameters as what we do in parametric fitting.

Some examples:

  • Kernel Estimation
  • Projection Pursuit
  • Spline Smoothing
  • Wavelets Fitting
  • Iterative Backfitting
Example(Anscombe dataset): predict per capita income based on budget for education of a state.
education income young urban
ME 189 2824 350.7 508
NH 169 3259 345.9 564
VT 230 3072 348.5 322
MA 168 3835 335.3 846
RI 180 3549 327.1 871
CT 193 4256 341.0 774
NY 261 4151 326.2 856
NJ 214 3954 333.5 889
PA 201 3419 326.2 715
OH 172 3509 354.5 753
IN 194 3412 359.3 649
IL 189 3981 348.9 830
MI 233 3675 369.2 738
WI 209 3363 360.7 659
MN 262 3341 365.4 664
IO 234 3265 343.8 572
MO 177 3257 336.1 701
ND 177 2730 369.1 443
SD 187 2876 368.7 446
NE 148 3239 349.9 615
KA 196 3303 339.9 661
DE 248 3795 375.9 722
MD 247 3742 364.1 766
DC 246 4425 352.1 1000
VA 180 3068 353.0 631
WV 149 2470 328.8 390
NC 155 2664 354.1 450
SC 149 2380 376.7 476
GA 156 2781 370.6 603
FL 191 3191 336.0 805
KY 140 2645 349.3 523
TN 137 2579 342.8 588
AL 112 2337 362.2 584
MS 130 2081 385.2 445
AR 134 2322 351.9 500
LA 162 2634 389.6 661
OK 135 2880 329.8 680
TX 155 3029 369.4 797
MT 238 2942 368.9 534
ID 170 2668 367.7 541
WY 238 3190 365.6 605
CO 192 3340 358.1 785
NM 227 2651 421.5 698
AZ 207 3027 387.5 796
UT 201 2790 412.4 804
NV 225 3957 385.1 809
WA 215 3688 341.3 726
OR 233 3317 332.7 671
CA 273 3968 348.4 909
AK 372 4146 439.7 484
HI 212 3513 382.9 831 
# Least Squares
lm(income ~ education, data = Anscombe)
## 
## Call:
## lm(formula = income ~ education, data = Anscombe)
## 
## Coefficients:
## (Intercept)    education  
##    1645.383        8.048
# Least Absolute Deviation (Quantile Regression)
library(quantreg)
rq(income ~ education, data = Anscombe)
## Call:
## rq(formula = income ~ education, data = Anscombe)
## 
## Coefficients:
## (Intercept)   education 
##  1209.67290    10.25234 
## 
## Degrees of freedom: 51 total; 49 residual

3.3 Interpretation of the Coefficients

In general, ceteris paribus(all things being the same)

  • \(\hat{\beta_j}\) = change in the estimated mean of \(Y\) per unit change in variable \(X_j\) holding other independent variables constant.

  • \(\hat{\beta_0}\) = value of the estimated mean of \(Y\) when all independent variables are set to 0.

We don’t always interpret the intercept, but why include it in the estimation?

Figure 3.2: Fitted line if estimated intercept is forced to be 0

  • Intercept is only interpretable if a value of 0 is logical for all independent variables included in the model.
  • Regardless of its interpretability, we still include it in the estimation. That is why in the design matrix \(\textbf{X}\), the first column is a vector of \(1\)s
  • If we force to have an intercept of equal to 0, then the fitted line is the line that passes through the center of the points and the origin.

Caution on the Interpretation of the Coefficients

  • Coefficients are partial. Assume that other effects are held constant.
  • Validity of interpretation depends on whether the assumption of uncorrelatedness among the \(X_j\)s holds
  • Affected by the range of \(X\) used in estimation

Example

© 2024 UP School of Statistics. All rights reserved.