Part 8 Variable Selection
Here we discuss a few different approaches to variable selection in R.
8.1 Data: Airbnb listings
We will use the airbnb_small.csv dataset, which contains information on 50 Airbnb listings in Florence, Italy from 2021. There are 24 variables for each listing, which includes information on hosts, location, price, property details, and reviews. Our goal will be to build a model that predicts the price of the Airbnb property from the remaining variables.
Two useful packages are olsrr and glmnet, which have convenient built-in methods for variable selection. Let’s start by loading these packages, setting our working directory, and reading in the file:
8.2 Stepwise regression
When we have a large number of potential variables to choose from for regression, simply throwing all of them into the model might make the model too complex. High model complexity has two drawbacks:
- it makes interpreting and explaining the model to others more complicated, and
- it risks overfitting the model to data, which can erode predictive performance.
One way of controlling model complexity in linear regression is called stepwise regression.
The key to stepwise regression is a performance metric called the Akaike information criterion (AIC). The AIC of a regression model measures how well the model balances complexity (i.e., the number of variables included in the regression) and goodness-of-fit (i.e., how well the chosen set of variables fit the data). In general, a regression model with a lower AIC is viewed as achieving a “better” balance between complexity and goodness-of-fit. The AIC is therefore widely used as a guide for finding a small number of variables with high explanatory power.
8.2.1 Stepwise regression with forward selection
One approach to stepwise regression is called forward selection. The general idea is that we start with a “blank” model, add whichever variable improves (i.e., decreases) the AIC the most, and repeat until the AIC can’t be improved any further.
Building a stepwise model in R is similar to building a standard linear regression model, but takes one extra step. Using the airbnb.csv First we run a regular linear regression using lm(), with Price as the dependent variable:
As a benchmark, let’s look at the results of the full linear regression model:
##
## Call:
## lm(formula = Price ~ ., data = airbnb)
##
## Residuals:
## Min 1Q Median 3Q Max
## -56.613 -10.105 -0.221 12.286 49.415
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 13516.3486 56832.9384 0.238 0.8144
## HostResponseTimewithin a day -475.6676 213.3597 -2.229 0.0374 *
## HostResponseTimewithin a few hours -493.5318 203.8891 -2.421 0.0251 *
## HostResponseTimewithin an hour -455.0459 207.1368 -2.197 0.0400 *
## HostResponseRate 390.4220 220.2179 1.773 0.0915 .
## HostAcceptRate 31.5768 39.6043 0.797 0.4346
## Superhost -7.6700 13.5703 -0.565 0.5782
## HostListings 0.7634 0.2810 2.716 0.0133 *
## NeighbourhoodCentro Storico 4.9871 37.1483 0.134 0.8945
## NeighbourhoodGavinana Galluzzo -186.4095 1012.4128 -0.184 0.8558
## NeighbourhoodIsolotto Legnaia -103.9420 83.4928 -1.245 0.2276
## NeighbourhoodRifredi -28.8847 43.0517 -0.671 0.5099
## Latitude 60.4395 1238.8568 0.049 0.9616
## Longitude -1464.6477 1062.1974 -1.379 0.1832
## RoomTypeHotel room 50.2613 33.7877 1.488 0.1525
## RoomTypePrivate room -5.8018 24.4563 -0.237 0.8149
## Accomodates 12.1546 6.7288 1.806 0.0859 .
## Bathrooms -19.7126 13.0087 -1.515 0.1453
## Bedrooms 29.1729 15.6235 1.867 0.0766 .
## Beds -2.6974 10.8947 -0.248 0.8070
## MinNights 1.0589 2.6414 0.401 0.6928
## AvgRating -51.2645 75.8444 -0.676 0.5068
## RatingAccuracy -31.8468 35.4207 -0.899 0.3793
## RatingClean 11.9607 63.9980 0.187 0.8536
## RatingCheckIn 22.1832 88.4108 0.251 0.8044
## RatingCommunication 85.7820 75.2299 1.140 0.2676
## RatingLocation -55.6150 43.7572 -1.271 0.2183
## RatingValue 102.3121 55.8141 1.833 0.0817 .
## InstantBook -17.9653 16.8469 -1.066 0.2990
## ReviewsPerMonth -4.2126 6.0649 -0.695 0.4953
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 32.55 on 20 degrees of freedom
## Multiple R-squared: 0.8794, Adjusted R-squared: 0.7045
## F-statistic: 5.028 on 29 and 20 DF, p-value: 0.0002066Then we send our stored model to the ols_step_forward_aic() function (which comes from the olsrr package), which will automatically perform the stepwise regression:
To see the full set of results and the variables that are added at each step, we simply use print():
##
##
## Stepwise Summary
## ------------------------------------------------------------------------------
## Step Variable AIC SBC SBIC R2 Adj. R2
## ------------------------------------------------------------------------------
## 0 Base Model 554.125 557.949 409.858 0.00000 0.00000
## 1 Bedrooms 531.846 537.583 387.393 0.38465 0.37183
## 2 HostListings 518.117 525.765 374.034 0.55074 0.53163
## 3 Accomodates 515.520 525.080 371.373 0.59021 0.56348
## 4 Bathrooms 511.999 523.471 368.259 0.63305 0.60043
## 5 Neighbourhood 509.511 528.631 361.779 0.70248 0.64443
## 6 ReviewsPerMonth 503.142 524.174 357.944 0.74834 0.69171
## 7 MinNights 502.423 525.368 358.631 0.76165 0.70054
## ------------------------------------------------------------------------------
##
## Final Model Output
## ------------------
##
## Model Summary
## ----------------------------------------------------------------
## R 0.873 RMSE 28.942
## R-Squared 0.762 MSE 837.642
## Adj. R-Squared 0.701 Coef. Var 36.115
## Pred R-Squared -Inf AIC 502.423
## MAE 18.964 SBC 525.368
## ----------------------------------------------------------------
## RMSE: Root Mean Square Error
## MSE: Mean Square Error
## MAE: Mean Absolute Error
## AIC: Akaike Information Criteria
## SBC: Schwarz Bayesian Criteria
##
## ANOVA
## ----------------------------------------------------------------------
## Sum of
## Squares DF Mean Square F Sig.
## ----------------------------------------------------------------------
## Regression 133837.507 10 13383.751 12.463 0.0000
## Residual 41882.113 39 1073.900
## Total 175719.620 49
## ----------------------------------------------------------------------
##
## Parameter Estimates
## ----------------------------------------------------------------------------------------------------------------
## model Beta Std. Error Std. Beta t Sig lower upper
## ----------------------------------------------------------------------------------------------------------------
## (Intercept) 42.093 24.588 1.712 0.095 -7.642 91.827
## Bedrooms 22.657 10.726 0.288 2.112 0.041 0.961 44.352
## HostListings 0.495 0.129 0.314 3.832 0.000 0.234 0.756
## Accomodates 11.967 4.473 0.384 2.676 0.011 2.920 21.014
## Bathrooms -31.706 9.829 -0.280 -3.226 0.003 -51.587 -11.826
## NeighbourhoodCentro Storico 23.629 16.649 0.179 1.419 0.164 -10.047 57.306
## NeighbourhoodGavinana Galluzzo 832.596 512.196 1.966 1.626 0.112 -203.419 1868.610
## NeighbourhoodIsolotto Legnaia -39.923 29.538 -0.132 -1.352 0.184 -99.668 19.823
## NeighbourhoodRifredi -8.569 22.240 -0.043 -0.385 0.702 -53.554 36.415
## ReviewsPerMonth -10.633 3.577 -0.261 -2.973 0.005 -17.867 -3.398
## MinNights -2.117 1.434 -1.816 -1.476 0.148 -5.018 0.784
## ----------------------------------------------------------------------------------------------------------------The output above tells us that the first variable added to the model is Bedrooms, and that this one-variable achieves \(AIC = 532\) and \(R^2 = 0.385\). Then a two-variable linear model with both Bedrooms and HostListings achieves \(AIC = 518\) and \(R^2 = 0.551\), and so on. Note that the output above lists only 7 out of the 23 possible independent variables we could have used.
Next, visualizing AIC is straightforward using plot():
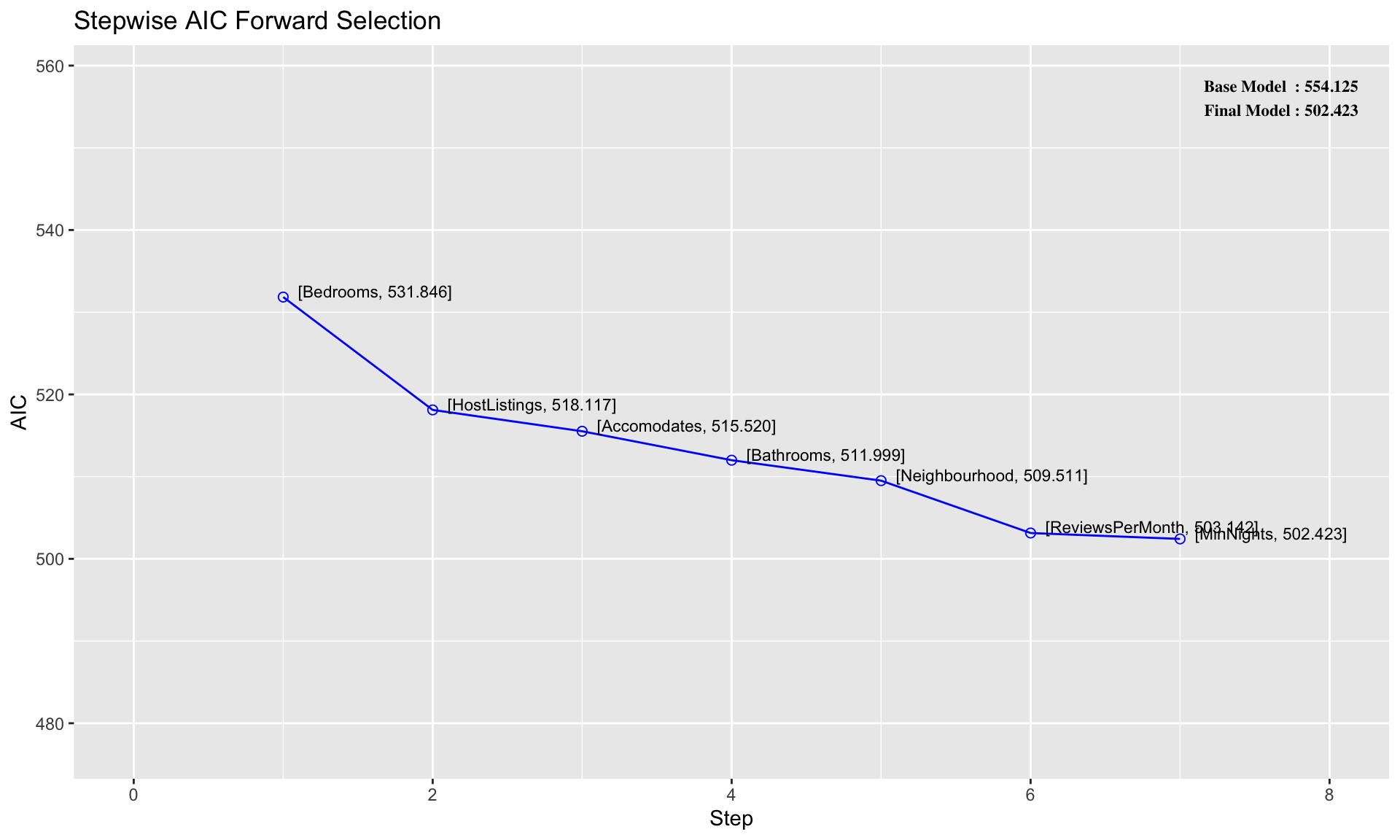
8.2.2 Stepwise regression with backward elimination
Another way of performing stepwise regression is backward elimination, which is conceptually similar to forward selection. In backward elimination, we start with a “full” model that contains all possible variables, and then we identify the variable whose removal from the model improves the AIC the most, and repeat until the AIC cannot be improved further.
The R code for backward elimination is similar: first we run the full linear regression model using lm(), and then we use ols_step_backward_aic():
Like in forward selection, we can print the model to see the result of each step:
##
##
## Stepwise Summary
## -----------------------------------------------------------------------------
## Step Variable AIC SBC SBIC R2 Adj. R2
## -----------------------------------------------------------------------------
## 0 Full Model 506.367 565.639 419.973 0.87939 0.70450
## 1 Latitude 504.373 561.733 410.189 0.87937 0.71854
## 2 RatingClean 502.458 557.907 401.324 0.87917 0.73087
## 3 Beds 500.568 554.105 393.223 0.87890 0.74200
## 4 RatingCheckIn 499.030 550.655 386.123 0.87777 0.75046
## 5 MinNights 497.612 547.324 379.718 0.87635 0.75764
## 6 AvgRating 496.242 544.043 373.875 0.87478 0.76400
## 7 HostAcceptRate 495.231 541.119 368.848 0.87228 0.76821
## 8 Superhost 494.898 538.875 364.913 0.86794 0.76890
## -----------------------------------------------------------------------------
##
## Final Model Output
## ------------------
##
## Model Summary
## ----------------------------------------------------------------
## R 0.932 RMSE 21.543
## R-Squared 0.868 MSE 464.097
## Adj. R-Squared 0.769 Coef. Var 31.726
## Pred R-Squared -Inf AIC 494.898
## MAE 15.842 SBC 538.875
## ----------------------------------------------------------------
## RMSE: Root Mean Square Error
## MSE: Mean Square Error
## MAE: Mean Absolute Error
## AIC: Akaike Information Criteria
## SBC: Schwarz Bayesian Criteria
##
## ANOVA
## ---------------------------------------------------------------------
## Sum of
## Squares DF Mean Square F Sig.
## ---------------------------------------------------------------------
## Regression 152514.786 21 7262.609 8.763 0.0000
## Residual 23204.834 28 828.744
## Total 175719.620 49
## ---------------------------------------------------------------------
##
## Parameter Estimates
## ------------------------------------------------------------------------------------------------------------------------
## model Beta Std. Error Std. Beta t Sig lower upper
## ------------------------------------------------------------------------------------------------------------------------
## (Intercept) 16248.212 7816.138 2.079 0.047 237.579 32258.845
## HostResponseTimewithin a day -478.262 166.018 -1.581 -2.881 0.008 -818.334 -138.190
## HostResponseTimewithin a few hours -503.945 160.664 -2.950 -3.137 0.004 -833.050 -174.840
## HostResponseTimewithin an hour -465.391 162.138 -3.353 -2.870 0.008 -797.515 -133.267
## HostResponseRate 428.393 167.135 1.497 2.563 0.016 86.033 770.753
## HostListings 0.860 0.166 0.546 5.196 0.000 0.521 1.199
## NeighbourhoodCentro Storico -1.922 24.825 -0.015 -0.077 0.939 -52.773 48.930
## NeighbourhoodGavinana Galluzzo 239.102 93.577 0.565 2.555 0.016 47.418 430.787
## NeighbourhoodIsolotto Legnaia -114.779 61.572 -0.379 -1.864 0.073 -240.903 11.345
## NeighbourhoodRifredi -34.656 31.113 -0.175 -1.114 0.275 -98.389 29.076
## Longitude -1467.268 693.156 -0.385 -2.117 0.043 -2887.134 -47.403
## RoomTypeHotel room 48.958 24.015 0.162 2.039 0.051 -0.234 98.150
## RoomTypePrivate room 1.278 17.652 0.006 0.072 0.943 -34.880 37.437
## Accomodates 11.259 4.644 0.362 2.424 0.022 1.746 20.772
## Bathrooms -25.234 8.778 -0.223 -2.875 0.008 -43.215 -7.253
## Bedrooms 28.714 10.491 0.365 2.737 0.011 7.224 50.205
## RatingAccuracy -33.234 26.964 -0.384 -1.233 0.228 -88.467 21.998
## RatingCommunication 67.552 33.123 0.630 2.039 0.051 -0.298 135.401
## RatingLocation -39.816 32.630 -0.439 -1.220 0.233 -106.655 27.024
## RatingValue 80.270 32.846 0.906 2.444 0.021 12.988 147.552
## InstantBook -18.073 11.221 -0.148 -1.611 0.118 -41.058 4.912
## ReviewsPerMonth -5.342 4.291 -0.131 -1.245 0.223 -14.133 3.448
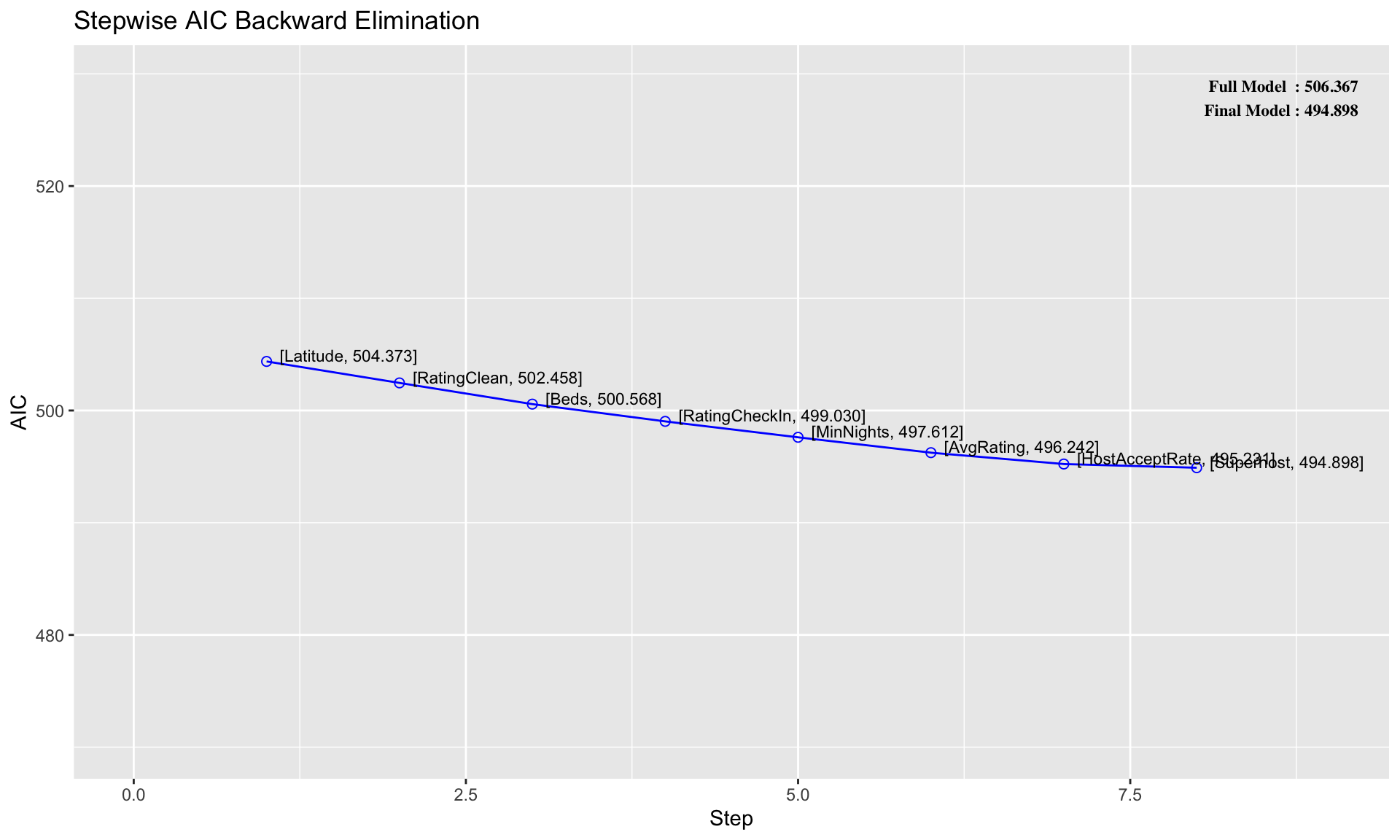
## ------------------------------------------------------------------------------------------------------------------------In the table above, we can see the names of 8 variables that are eliminated from the model. In this example, the final model from backward elimination achieves \(AIC = 495\) and \(R^2 = 0.868\). Note that backward elimination arrives at a different final model than forward selection in this case.
Similar to before, we can use plot() to visualize the result of the stepwise regression based on backward elimination:
8.3 LASSO regression
Another popular method for variable selection is LASSO regression. In general, LASSO is used when dealing with a huge number of potential variables, in which case stepwise regression can be very slow. (There are other differences that we won’t get into here).
8.3.1 Building a LASSO regression model
LASSO regression can be done in R using the glmnet() function. In order to apply it to the Airbnb data, we first need to do a little bit of data manipulation. In particular, we need to manually convert the columns with character strings (i.e., words) into R factors, and then convert the factors into 0 or 1 binary variables using “one-hot” encoding. The code below does this:
airbnb$HostResponseTime <- as.factor(airbnb$HostResponseTime)
airbnb$RoomType <- as.factor(airbnb$RoomType)
airbnb$Neighbourhood <- as.factor(airbnb$Neighbourhood)
airbnbone <- one_hot(as.data.table(airbnb))If we take a look at the new data frame, we can see that it now has 34 columns, due to the conversion of the factor variables into 0-1 dummy variables. (It is commented out below to simplify HTML output, but you can run it in R Markdown to preview the new data frame).
Next, we need to split the dataframe into independent and dependent variables. (We have to do this because the glmnet() function we will use for LASSO regression expects the data to be in a different format from the stepwise regression functions we used above). For simplicity we will use x and y to denote the independent and dependent variables, respectively:
x <-as.matrix(subset(airbnbone, select=-c(Price)))
y <-as.matrix(subset(airbnbone, select=c(Price)))Now that the data is formatted, we can call glmnet() to run a lasso regression:
Printing the results displays the number of variables selected at each value of \(\lambda\) (Df = degrees of freedom):
##
## Call: glmnet(x = x, y = y)
##
## Df %Dev Lambda
## 1 0 0.00 36.770
## 2 2 7.19 33.500
## 3 2 13.22 30.520
## 4 2 18.24 27.810
## 5 3 23.99 25.340
## 6 3 29.94 23.090
## 7 3 34.88 21.040
## 8 3 38.98 19.170
## 9 3 42.38 17.470
## 10 3 45.21 15.920
## 11 3 47.55 14.500
## 12 3 49.50 13.210
## 13 4 51.49 12.040
## 14 5 53.80 10.970
## 15 7 56.68 9.995
## 16 7 59.60 9.108
## 17 8 62.07 8.298
## 18 9 64.32 7.561
## 19 9 66.40 6.889
## 20 9 68.13 6.277
## 21 9 69.57 5.720
## 22 9 70.76 5.212
## 23 10 71.76 4.749
## 24 12 72.66 4.327
## 25 13 73.62 3.942
## 26 15 74.55 3.592
## 27 16 75.50 3.273
## 28 16 76.37 2.982
## 29 16 77.09 2.717
## 30 17 77.70 2.476
## 31 17 78.33 2.256
## 32 17 78.85 2.056
## 33 18 79.32 1.873
## 34 18 79.76 1.707
## 35 18 80.13 1.555
## 36 18 80.43 1.417
## 37 18 80.68 1.291
## 38 18 80.89 1.176
## 39 18 81.07 1.072
## 40 19 81.24 0.977
## 41 19 81.45 0.890
## 42 19 81.63 0.811
## 43 20 81.78 0.739
## 44 21 81.96 0.673
## 45 23 82.12 0.613
## 46 24 82.58 0.559
## 47 25 82.94 0.509
## 48 25 83.25 0.464
## 49 26 83.52 0.423
## 50 25 84.08 0.385
## 51 25 84.57 0.351
## 52 27 84.97 0.320
## 53 26 85.37 0.291
## 54 27 85.69 0.266
## 55 27 86.02 0.242
## 56 27 86.30 0.220
## 57 27 86.54 0.201
## 58 27 86.79 0.183
## 59 27 86.97 0.167
## 60 26 87.12 0.152
## 61 26 87.24 0.138
## 62 26 87.34 0.126
## 63 26 87.42 0.115
## 64 26 87.49 0.105
## 65 27 87.55 0.095
## 66 28 87.61 0.087
## 67 28 87.66 0.079
## 68 28 87.70 0.072
## 69 28 87.73 0.066
## 70 28 87.76 0.060
## 71 28 87.78 0.055
## 72 28 87.80 0.050
## 73 28 87.82 0.045
## 74 28 87.84 0.041
## 75 28 87.85 0.038
## 76 28 87.86 0.034
## 77 28 87.87 0.031
## 78 28 87.87 0.028
## 79 28 87.88 0.026
## 80 28 87.89 0.024
## 81 28 87.89 0.022
## 82 28 87.89 0.020
## 83 28 87.90 0.018
## 84 28 87.90 0.016
## 85 28 87.90 0.015
## 86 28 87.90 0.014
## 87 30 87.91 0.012
## 88 30 87.91 0.011
## 89 30 87.91 0.010
## 90 30 87.91 0.009
## 91 30 87.91 0.008
## 92 30 87.91 0.008
## 93 30 87.91 0.007
## 94 30 87.91 0.006The table above represents 94 different regression models obtained for 94 different values of \(\lambda\). The R function glmnet() automatically decides which values of \(\lambda\) to test. For example, we can see that when \(\lambda\) is around 5, the LASSO selects 9 variables, and when \(\lambda\) is around 1, the regression selects 19 variables. (The middle column (%Dev) is a measure of goodness-of-fit that we won’t worry about.)
To actually see the model output for each value of \(\lambda\), we use the coef() function. For example, if we want to see the results of the LASSO regression using \(\lambda = 10\), we can write
## 33 x 1 sparse Matrix of class "dgCMatrix"
## s=10
## (Intercept) 30.8880917
## HostResponseTime_a few days or more .
## HostResponseTime_within a day .
## HostResponseTime_within a few hours -7.7209538
## HostResponseTime_within an hour .
## HostResponseRate .
## HostAcceptRate .
## Superhost .
## HostListings 0.3786573
## Neighbourhood_Campo di Marte .
## Neighbourhood_Centro Storico 2.0365337
## Neighbourhood_Gavinana Galluzzo .
## Neighbourhood_Isolotto Legnaia .
## Neighbourhood_Rifredi .
## Latitude .
## Longitude .
## RoomType_Entire home/apt .
## RoomType_Hotel room .
## RoomType_Private room .
## Accomodates 7.4069029
## Bathrooms -0.4116008
## Bedrooms 18.6908176
## Beds .
## MinNights .
## AvgRating .
## RatingAccuracy .
## RatingClean .
## RatingCheckIn .
## RatingCommunication .
## RatingLocation .
## RatingValue .
## InstantBook .
## ReviewsPerMonth -1.2924361The variables selected are those with non-zero coefficients. You can try varying the \(\lambda\) parameter in coef() to see how it changes the variables that are selected along with their coefficients.
8.3.2 Cross-validation of LASSO regression
It is important to remember that \(\lambda\) is a parameter that we need to choose before building a LASSO regression model. The glmnet() function builds many different regression models by varying \(\lambda\) (in our case, the variable lasso is storing the results of 78 different regression models).
Of course, usually we want to identify one good model, and the output doesn’t tell us anything about what value of \(\lambda\) we should use. So how do we select the “best” value of \(\lambda\) in the first place?
The standard approach to picking \(\lambda\) is cross-validation. Recall that the main idea behind cross-validation is as follows:
- Pick a value of \(\lambda\),
- Randomly split the dataset into 10 different segments called folds,
- Build the LASSO regression model using data from 9 folds, and measure its prediction error on the 10th fold that was “left out” from the model building phase,
- Repeat by rotating through all 10 folds, and then calculate the average prediction error over the 10 folds. This produces a single number – the cross-validation error – which we can interpret as a measure of model performance (under the value of \(\lambda\) that we have selected).
- Repeat steps 1 through 4 for many different values of \(\lambda\), and pick the value that achieves the desired balance between predictive performance and model complexity (discussed more below).
Luckily, the glmnet package comes with a built-in function for cross validation, so we can perform the above steps in a single line!
Next, we can use plot() to visualize the cross-validation errors:
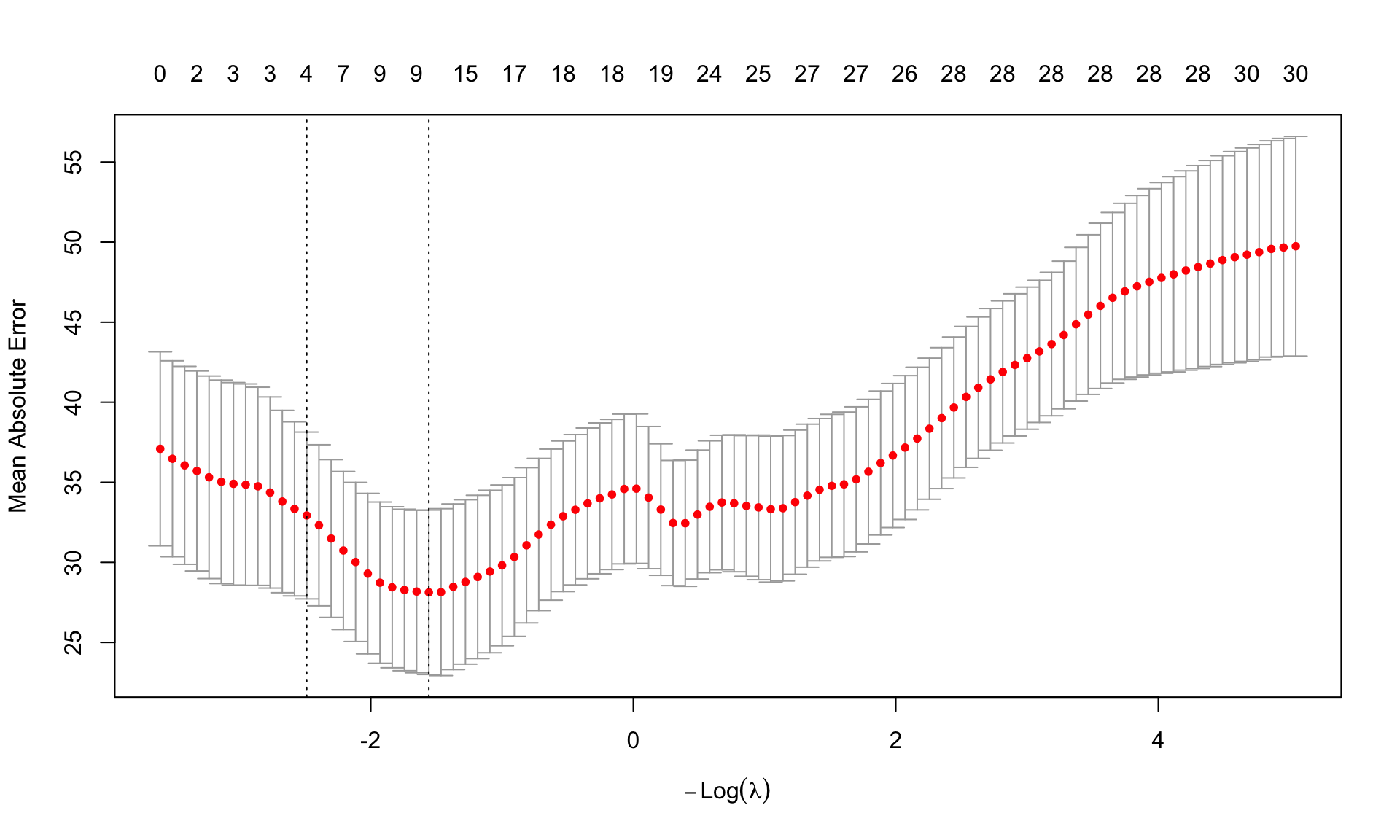
The horizontal axis of the plot shows different values of \(\lambda\) (by default, this is given in terms of \(log(\lambda)\) instead of \(\lambda\), which just makes the results easier to visualize). The vertical axis reports the associated cross-validation error. Across the top of the plot, we can also see the number of variables that are selected at each value of \(\lambda\). The dashed line on the left indicates the value of \(\lambda\) that achieves the minimum cross-validation error, which is what we would usually choose as our “final” model.
To print the values of \(\lambda\) corresponding to the minimum cross-validation error, we write
##
## Call: cv.glmnet(x = x, y = y, type.measure = "mae")
##
## Measure: Mean Absolute Error
##
## Lambda Index Measure SE Nonzero
## min 4.749 23 28.13 5.133 10
## 1se 12.040 13 32.93 5.209 4The table above shows that the cross-validation error is minimized at a value of \(\lambda = 4.7\), which produces a mean absolute error of $28 and selects 10 variables. A general rule of thumb is to select the value of \(\lambda\) that minimizes the error, but ultimately, the decision of which value of \(\lambda\) to use for the final model depends on your preference for how to balance model complexity and prediction error.
Forward selection, backward elimination, and LASSO regression are three common approaches to variable selection. An advantage of forward selection and backward elimination is that they do not require choosing a value of \(\lambda\) through cross-validation, which LASSO does. An advantage of LASSO is that it can be computationally much faster than stepwise regression when there are a large number of variables to choose from.
Regardless of which approach we use, it is important to remember there is no “one-size-fits-all” approach to variable selection. These methods should be used as helpful guides only, and we should always aim to incorporate background knowledge and domain expertise into the variable selection process wherever possible.