6 Review: Margins & Graph Design (Stata)
6.1 Lab Overview
This lab reviews two fundamentals: mastering margins and graph design!
Research Question: What characteristics of passengers are associated with survival on the Titanic?
Lab Files
Data:
Download titanic_df.dta
Script File:
Download lab3_F1_margins_graphs.do
6.2 Margins
When we are talking about margins, we are really talking about two separate commands we can do within this one command: predicted values OR marginal effects. These two commands help us illustrate the effects that we have found in our model for our reader. It can help convey effect size or interactions. If you master the margins command, you can use it to highlight a particular finding for your reader. You can list the values or marginal effects as numbers or plot it. I will display each of the examples via plots.
What is a predicted value?
Remember, all the models we run are based on equations that are trying to predict our dependent variable (aka our outcome - Y). Once we run the model, we actually get an equation we can use. If we plug in specific values for our independent variables (our X’s), then we can predict the value of our outcome. In a linear regression, that outcome is some continuous variable: income, years in the NBA, life expectancy, etc. In a regression with a binary outcome, the predicted value is actually a predicted probability. In a regression with a count outcome, the predicted value is, you guessed it, a count.
To get a predicted value out of the margins command, you don’t have to add anything special! This is the default for the margins command.
What is a marginal effect?
A marginal effect tells us how much our outcome (Y) changes based on a one unit change in X. This hopefully sounds familiar to you. That’s because it’s how we interpret coefficients in a linear regression. Basically, a marginal effect is a slope. In a linear regression, the slope is constant. A one unit change in X causes the same change in Y for any X value. In other models, the slope changes as you go up the range of X. It’s actually the instantaneous rate of change, meaning the slope at a particular point. This is harkening back to your calculus classes. In the image below, the dashed line shows you the slope at the point where the arrow ends.
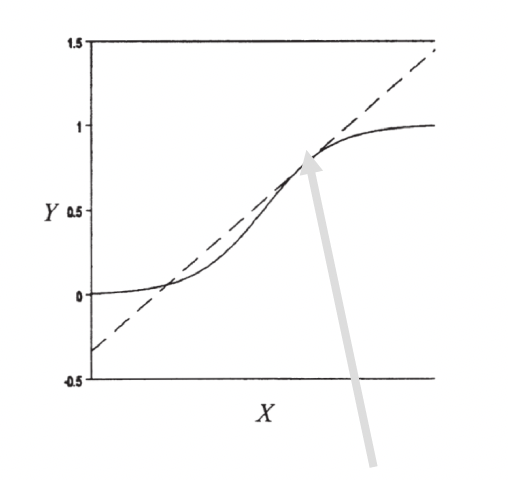
To get a marginal effect out of the margins command, you need to include
dydx()to your margins command. That’s that calculus terminology.
Now what makes the margins command difficult is that there are so so many options we can add to the command. Do we want to focus on one of our independent variables or two? Are we holding the other variables at means or at representative values? Are we working with continuous or categorical variables? This overview today is hopefully going to help you understand the grammar of this command and how to bend it to your will when you need to use it on your project.
There are four decisions you will need to make when producing margins. These four decisions form the basics of the many variations of the margins command. All of these examples will be from a logistic regression so they will be predicted probabilities or changes in probability.
To use the margins command, we need to run a regression first. This is the regression we’ll be basing the following commands off of:
logistic survived i.port i.female log_fare parchDecision 1: Categorical or Continuous?
The first decision you will need to make when using margins, is what independent (X) variable to focus on. Remember, you as the analyst are using the margins or margins plot to visualize some finding, usually relating to a key independent variable in your analysis. For example, in our titanic analysis our key variable was port of boarding. With the margins command, the syntax for the command will change depending on whether your X variable of focus is categorical or continuous.
For a categorical variable, the variable name will be listed BEFORE the comma if other options are specified or don’t include any comma at all.
Here is the margins command and margins plot, focusing on port of entry.
margins port
marginsplot 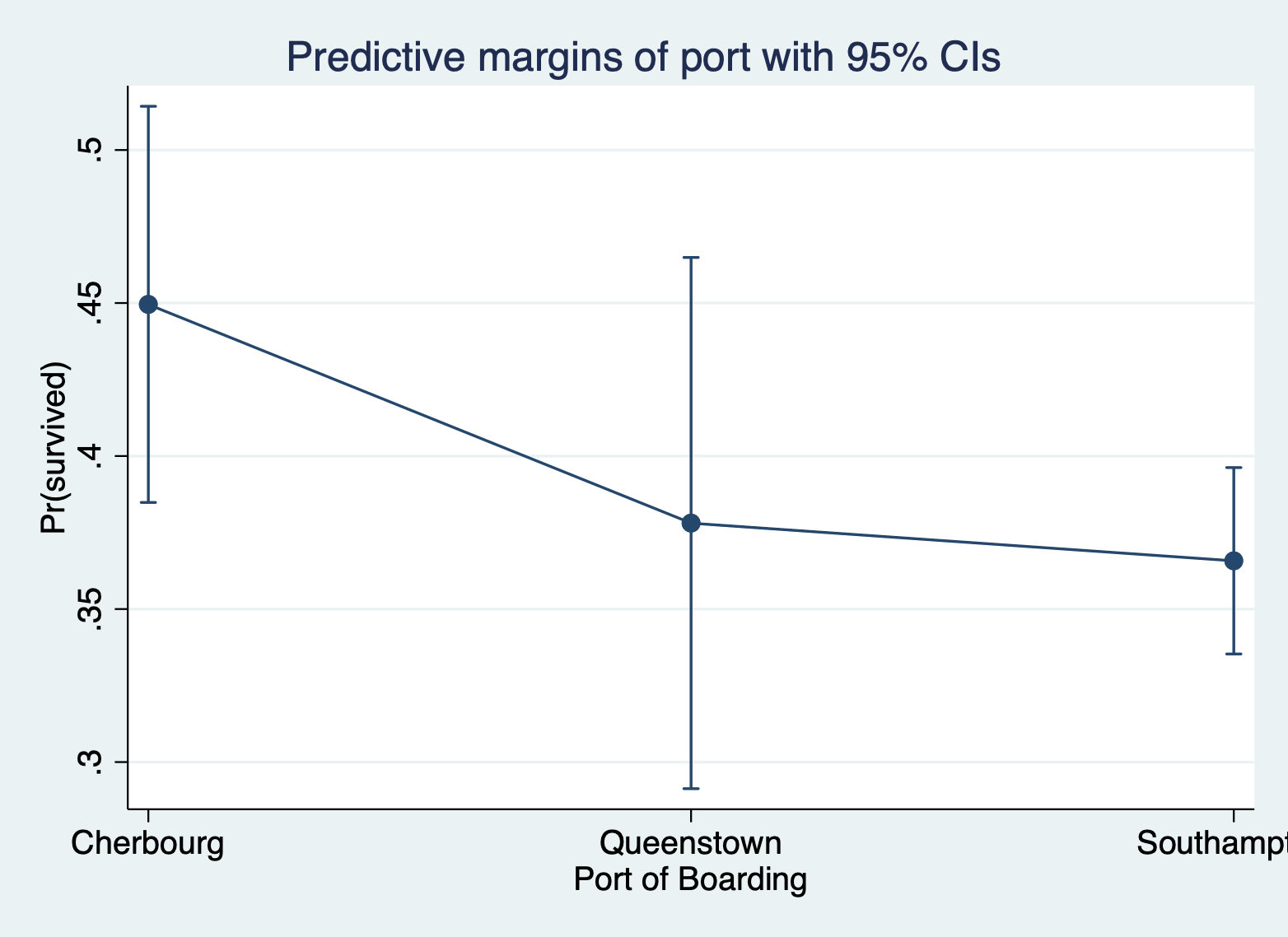
For a continuous variable, the variable name will be listed AFTER the comma inside of an
at()option statement and you must specify which values of X Stata should calculate/plot the margins for.
Here is the margins command and margins plot, focusing on ticket fare (logged to address skew).
margins, at(log_fare = (0 2 4 6))
marginsplot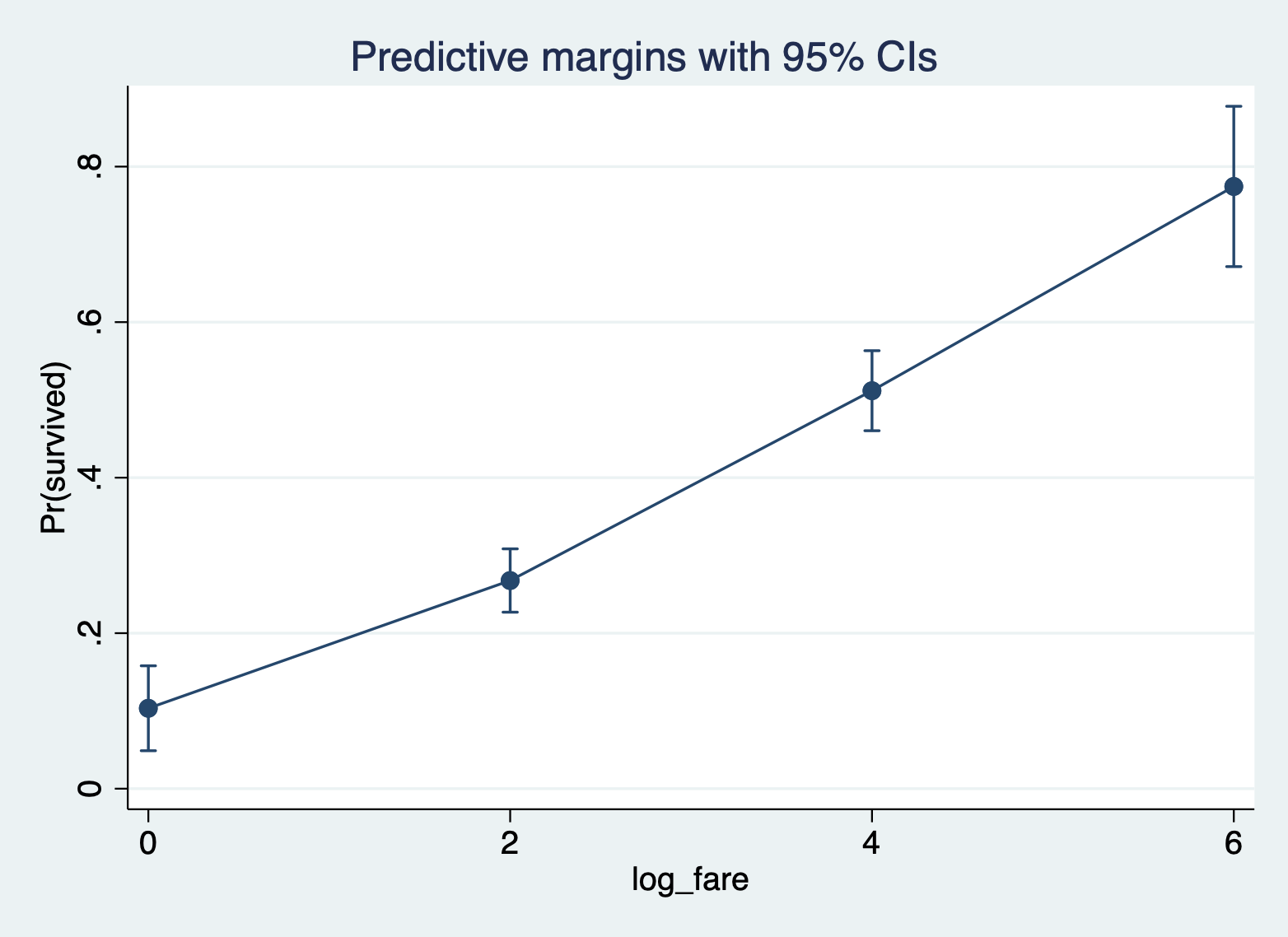
Decision 2: Add a second variable?
The second decision you will need to make is whether you want to add a second variable to focus on. Any more than two X variables of focus will lead to a complicated plot that doesn’t communicate much to your reader. But adding a second variable can help you show not only the effect of your first variable, but how that effect varies across groups. It can illustrate interactions. Again, whether your variables are continuous or categorical will affect how you do this command.
Continuous and Continuous You will specify both variables AFTER the comma inside of the same
at()and you must specify the multiple values of each variable to calculate/plot. The first variable will plot on the X axis and the second variable will be plotted as different lines.
Here is the margins command and margins plot for ticket fare and number of parents/children on board.
margins, at(log_fare = (0 2 4 6) parch = (0 3 6))
marginsplot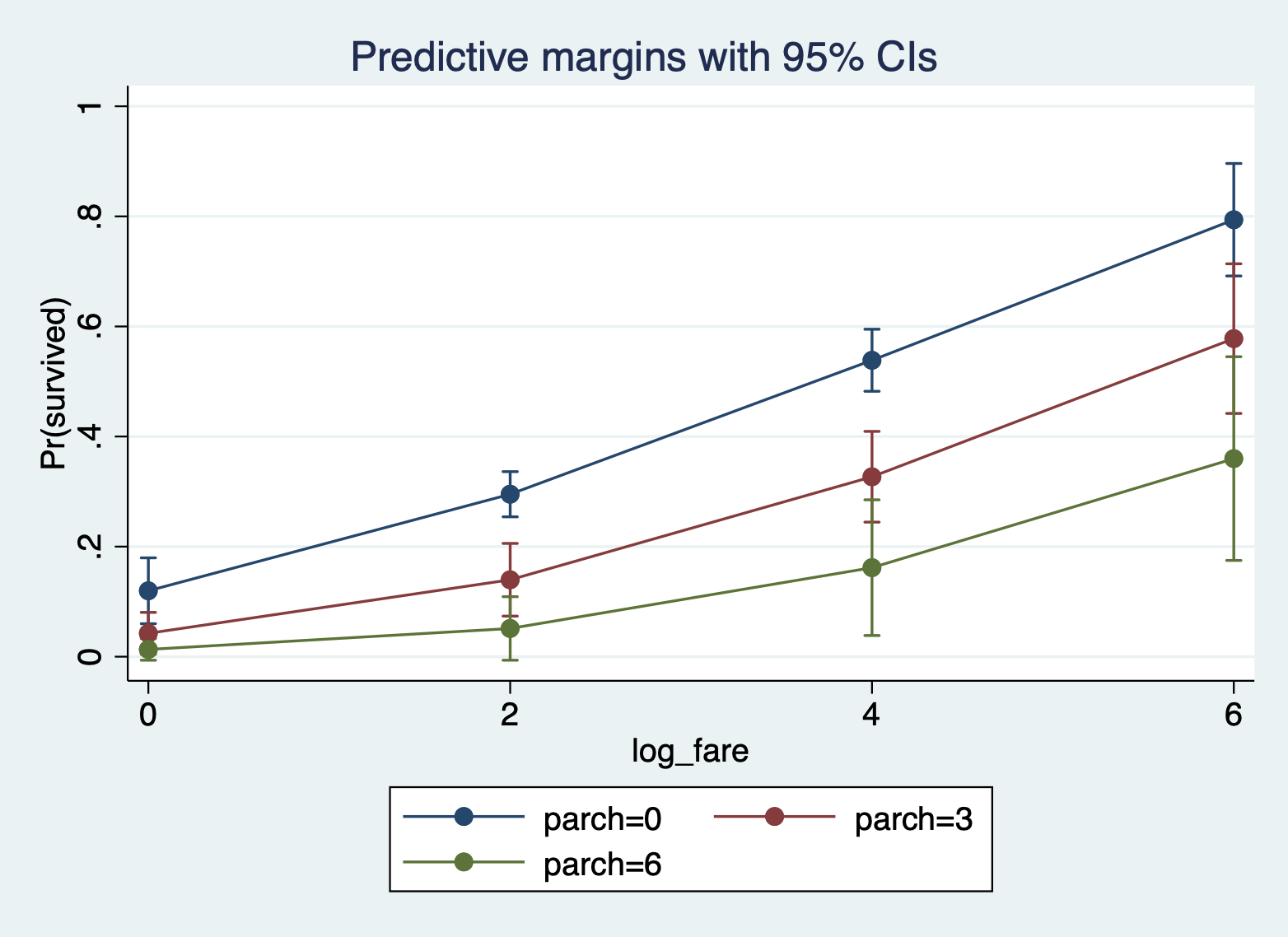
Continuous and Categorical You will specify the categorical variable BEFORE the comma and the continuous variable AFTER the comma within the
at()option statement. If you only want to include certain categories, you can move the categorical variable into the at() statement and specify the categories to include.
Here is the margins command and margins plot for ticket fare and port of boarding.
margins port, at(log_fare = (0 2 4 6))
marginsplot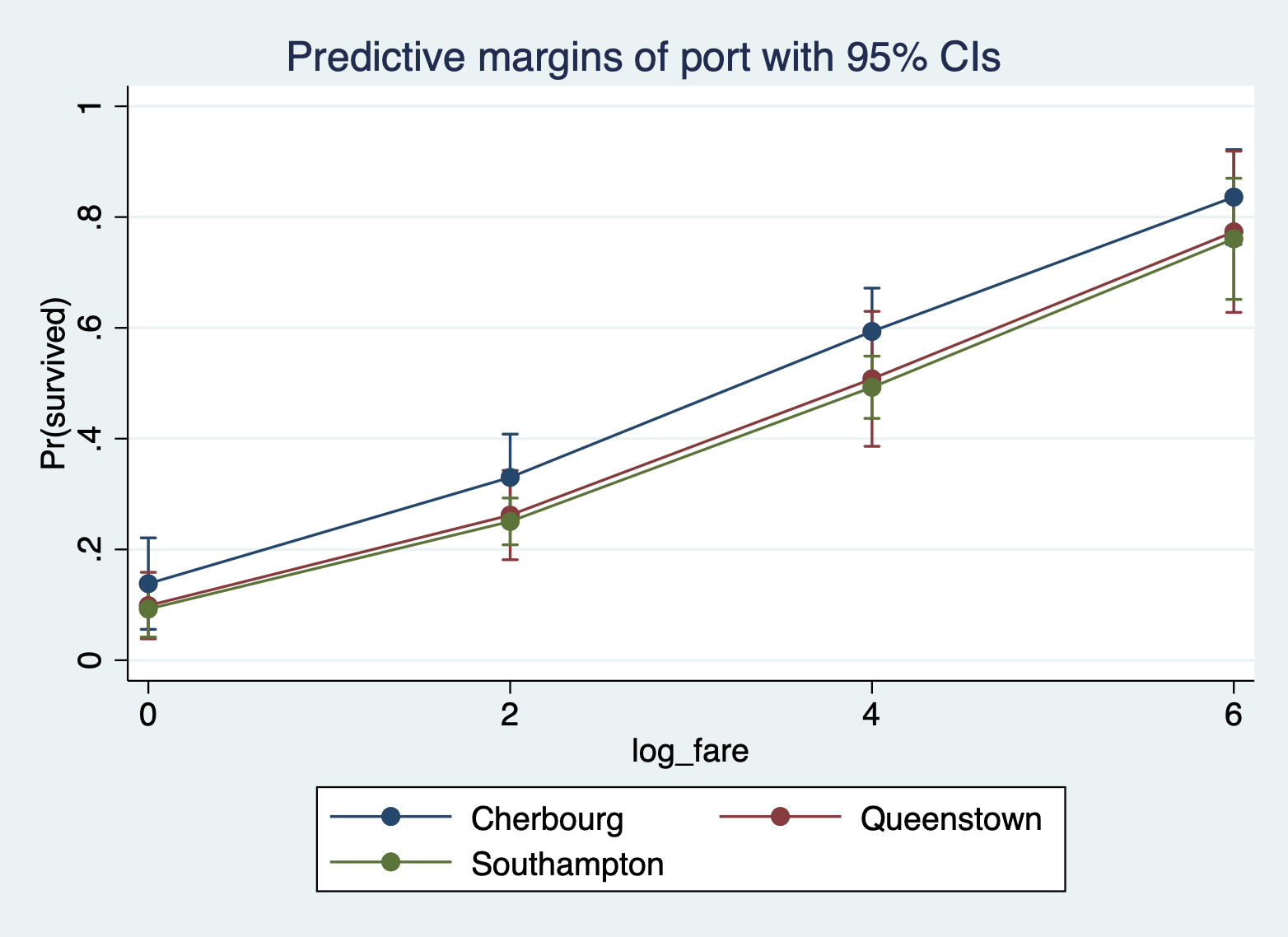
And here is the same plot, but with only Cherbourg and Queenstown.
margins, at(log_fare = (0 2 4 6) port = (1 2))
marginsplot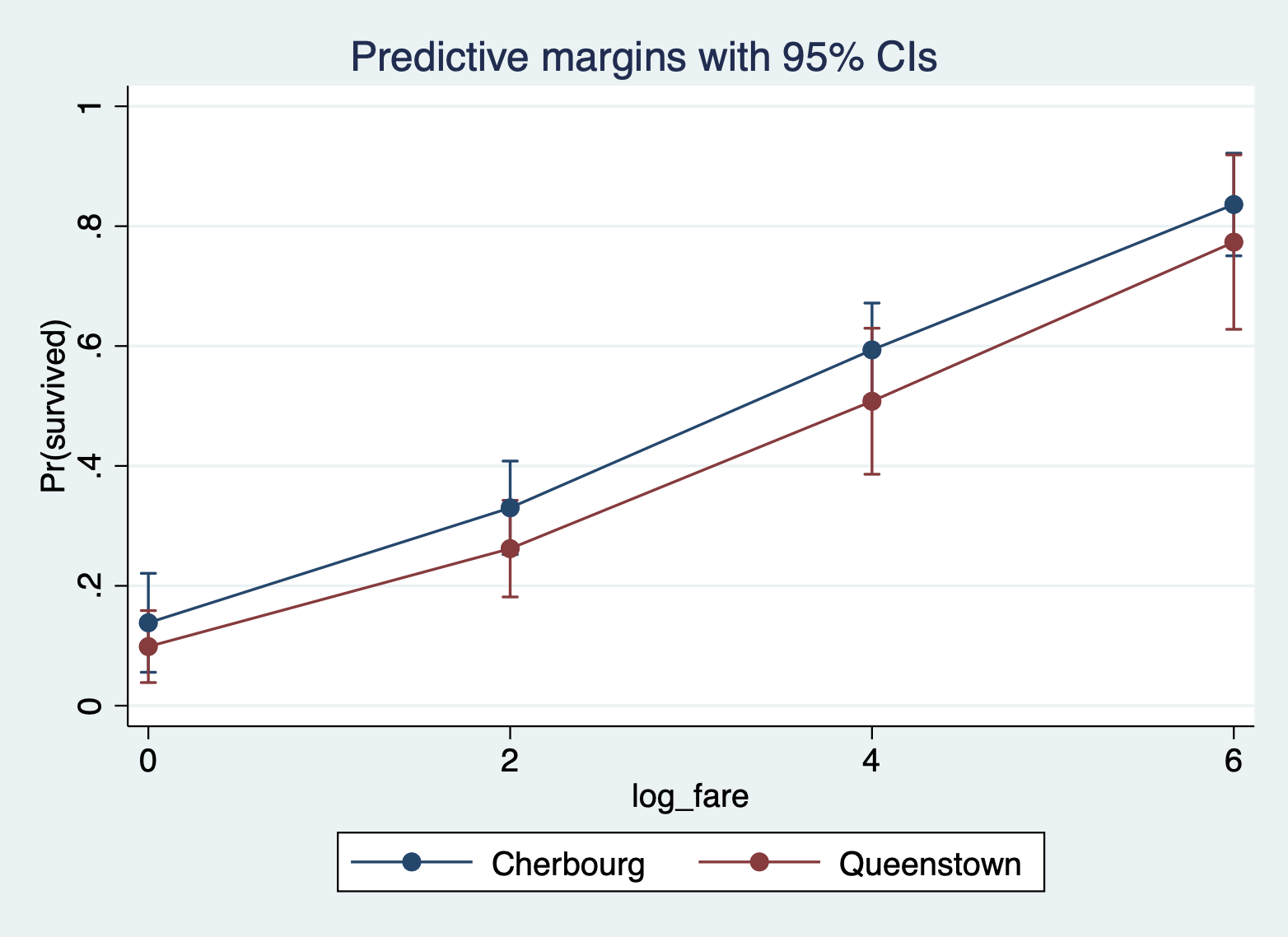
Categorical and Categorical You will specify the variable you want on the X axis BEFORE the comma and the variable you want split across different lines AFTER the comma in the over() optional statement.
Here is the margins command margins plot for port of boarding and sex of passenger with port on the X axis and sex as lines.
margins port, over(female)
marginsplot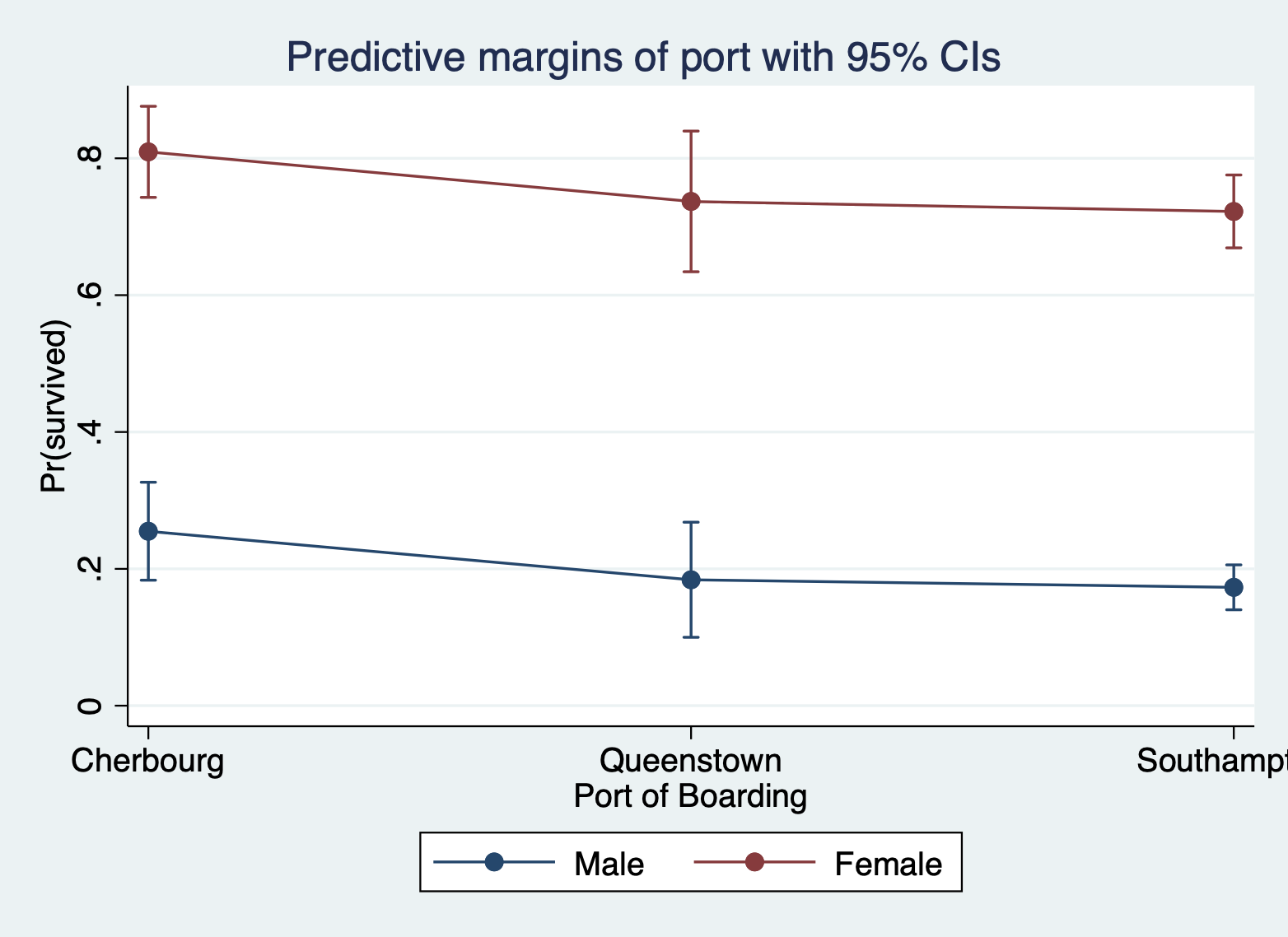
Decision 3: How will you handle the other X variables?
This is a review from last week. There are three approaches to handling the other X variables (aka the ones that are NOT the X variable you want to highlight):
- Hold other variables AT MEANS
- Hold other variables AT REPRESENTATIVE VALUES
- Run everything with observed values and compute the AVERAGE predicted value/effect.
NOTE: For these I want you to note how the actual predicted values change, so I am not going to include the margins plot. Look at the actual calculated margins for each approach.
At means: You just have to add an
at meansafter the comma
Here are the margins for port with the other variables at means.
margins port, atmeansAdjusted predictions Number of obs = 889
Model VCE: OIM
Expression: Pr(survived), predict()
At: 1.port = .1889764 (mean)
2.port = .0866142 (mean)
3.port = .7244094 (mean)
0.female = .6490439 (mean)
1.female = .3509561 (mean)
log_fare = 2.959024 (mean)
parch = .3824522 (mean)
------------------------------------------------------------------------------
| Delta-method
| Margin std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
port |
Cherbourg | .453225 .049525 9.15 0.000 .3561577 .5502923
Queenstown | .3466006 .0648861 5.34 0.000 .2194261 .4737751
Southampton | .3286141 .02262 14.53 0.000 .2842797 .3729486
------------------------------------------------------------------------------At representative values: You have to specify the specific values of the other variables within the
at()option, but only ONE value per variable.
Here are the margins for port with the other variables at representative values.
margins port, at(female = 1 log_fare = 2 parch = 2)Adjusted predictions Number of obs = 889
Model VCE: OIM
Expression: Pr(survived), predict()
At: female = 1
log_fare = 2
parch = 2
------------------------------------------------------------------------------
| Delta-method
| Margin std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
port |
Cherbourg | .5240158 .0825546 6.35 0.000 .3622117 .6858199
Queenstown | .4133268 .0845754 4.89 0.000 .247562 .5790915
Southampton | .3939654 .0596048 6.61 0.000 .2771421 .5107888
------------------------------------------------------------------------------Average predicted values/marginal effects: Don’t do a damn thing! This is the default.
Here are the average predicted probabilities for port of boarding.
margins portPredictive margins Number of obs = 889
Model VCE: OIM
Expression: Pr(survived), predict()
------------------------------------------------------------------------------
| Delta-method
| Margin std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
port |
Cherbourg | .4495649 .033027 13.61 0.000 .3848331 .5142967
Queenstown | .3781069 .0442857 8.54 0.000 .2913085 .4649054
Southampton | .3657791 .0155409 23.54 0.000 .3353196 .3962387
------------------------------------------------------------------------------Decision 4: Predicted values or Marginal effects
And finally, we can specify whether we want the predicted values or the marginal effects. All of the above examples were predicted values. Specifically they were predicted probabilities because we’re working with logistic regression.
Predicted values: Again, don’t do a damn thing! This is the default for the margins command.
Here again are the average predicted probabilities at different values of ticket fare (logged).
margins, at(log_fare = (2 4 6)) Predictive margins Number of obs = 889
Model VCE: OIM
Expression: Pr(survived), predict()
1._at: log_fare = 2
2._at: log_fare = 4
3._at: log_fare = 6
------------------------------------------------------------------------------
| Delta-method
| Margin std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
_at |
1 | .2676895 .0207842 12.88 0.000 .2269532 .3084257
2 | .5118238 .0262607 19.49 0.000 .4603537 .5632939
3 | .7744947 .0526051 14.72 0.000 .6713907 .8775987
------------------------------------------------------------------------------Marginal effects: When you do marginal effects, you move your variable of focus, regardless of whether it is categorical or continuous, AFTER the comma inside the
dydx()option statement.
Here is the marginal effect for ticket fare (logged).
margins, dydx(log_fare)Average marginal effects Number of obs = 889
Model VCE: OIM
Expression: Pr(survived), predict()
dy/dx wrt: log_fare
------------------------------------------------------------------------------
| Delta-method
| dy/dx std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
log_fare | .1111977 .0158007 7.04 0.000 .0802289 .1421665
------------------------------------------------------------------------------You can get one marginal effect for a continuous variable OR get the marginal effects across the range if you so choose:
margins, dydx(log_fare) at(log_fare = (2 4 6))Average marginal effects Number of obs = 889
Model VCE: OIM
Expression: Pr(survived), predict()
dy/dx wrt: log_fare
1._at: log_fare = 2
2._at: log_fare = 4
3._at: log_fare = 6
------------------------------------------------------------------------------
| Delta-method
| dy/dx std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
log_fare |
_at |
1 | .1043584 .0131838 7.92 0.000 .0785187 .1301981
2 | .1365486 .0224777 6.07 0.000 .092493 .1806041
3 | .1116513 .0047204 23.65 0.000 .1023996 .1209031
------------------------------------------------------------------------------6.3 Basics of Graphing Aesthetics
This lab will not review in detail all of the many different ways you can change the graphs you produce in Stata. However, I will provide you with this reference do file for graph formatting in Stata. It covers:
- Titles, subtitles, and captions
- Changing axis and tick mark options
- Color of markers, lines, and the fill area
- Style of markers and lines
- Background colors for the plot area and graph area
- Labelling specific values
Here is a resource just to learn more about adjusting plots with grstyle:
Download grstyle_StataGraphsMadeEasy.pdf
6.4 Good Graph Design
Basic Principles of Good Graph Design
These principles are from the online The Fundamentals of Data Visualization. book. I highly recommend this book if you want to dive deeper into making great graphs. It is not written for any one statistical software, though the examples in the book are made in R. These examples plots are also taken from the book.
- Keep the background and grid lines of your plot light and simple. Your default should be a white background and light gray grid lines. In the graphs below the first is too busy, the second doesn’t have enough grid lines, and the third is just right.
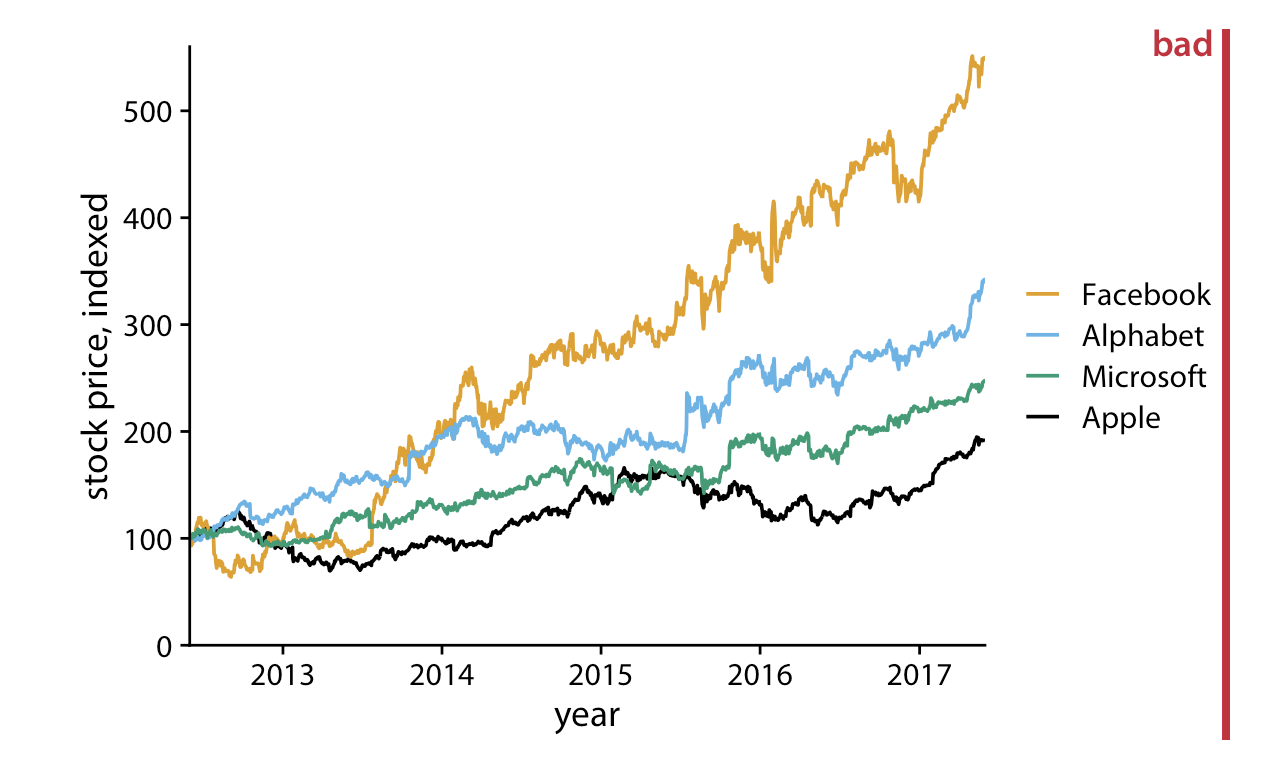
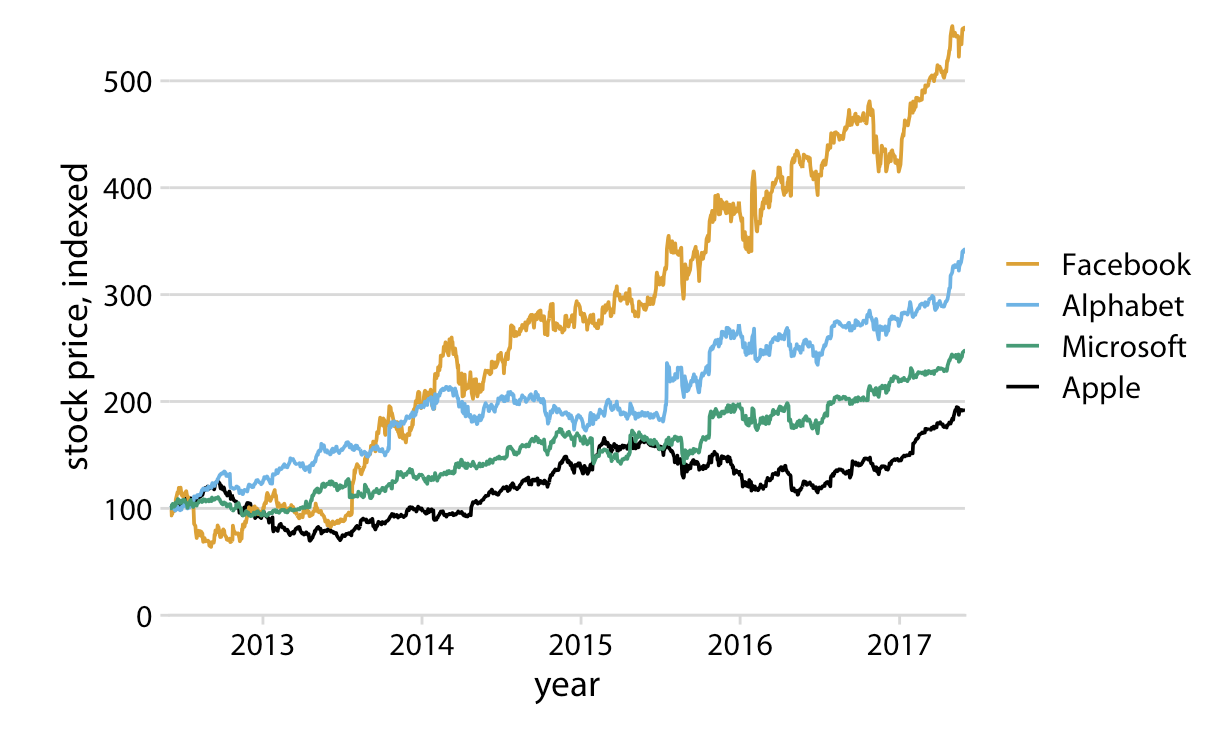
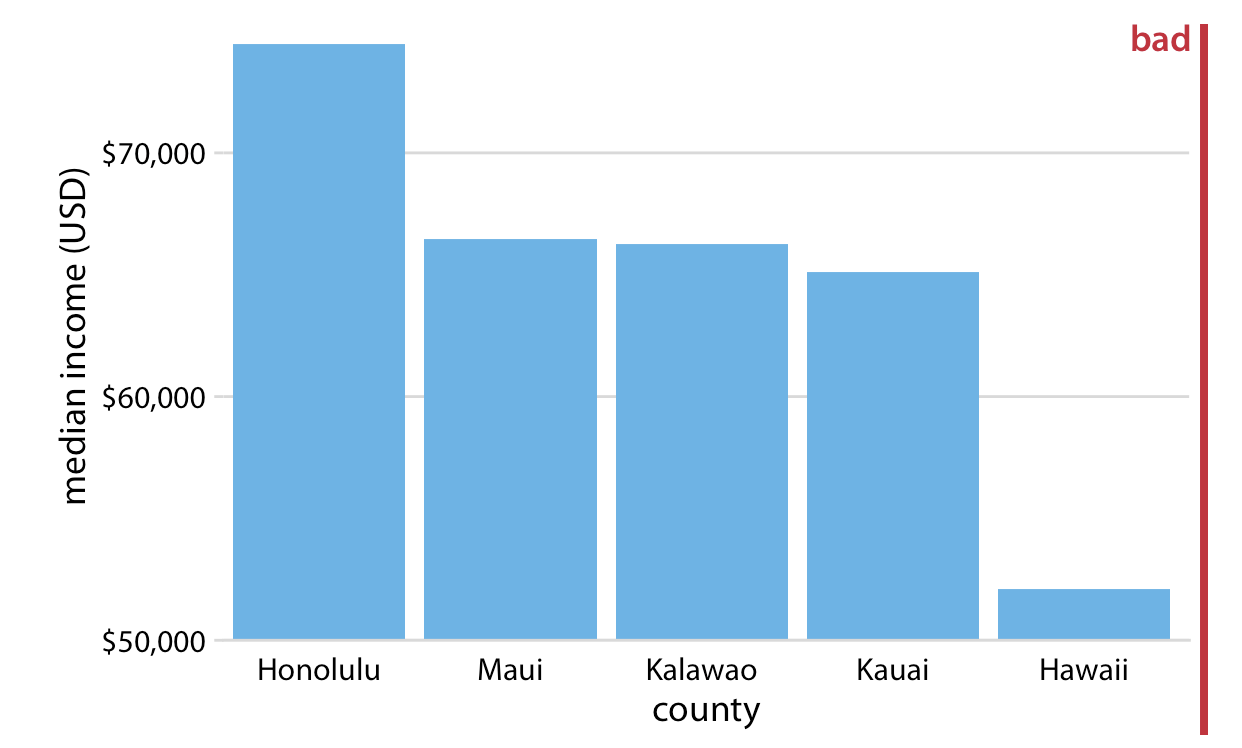
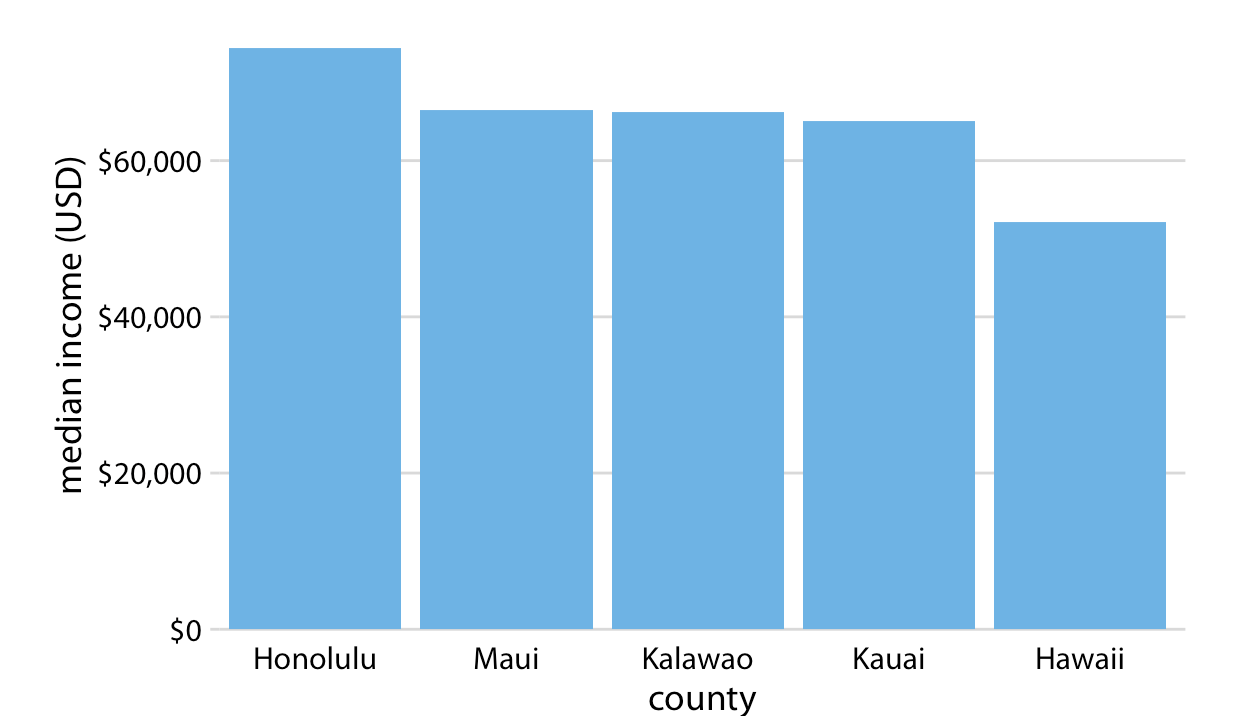
- Make sure the differences between lines, bars, points are proportional to the data. Aka. Don’t lie with your graph!.
- Color should serve a purpose in your graph. Keep it simple, and limit the total number of colored categories to 3 to 5.
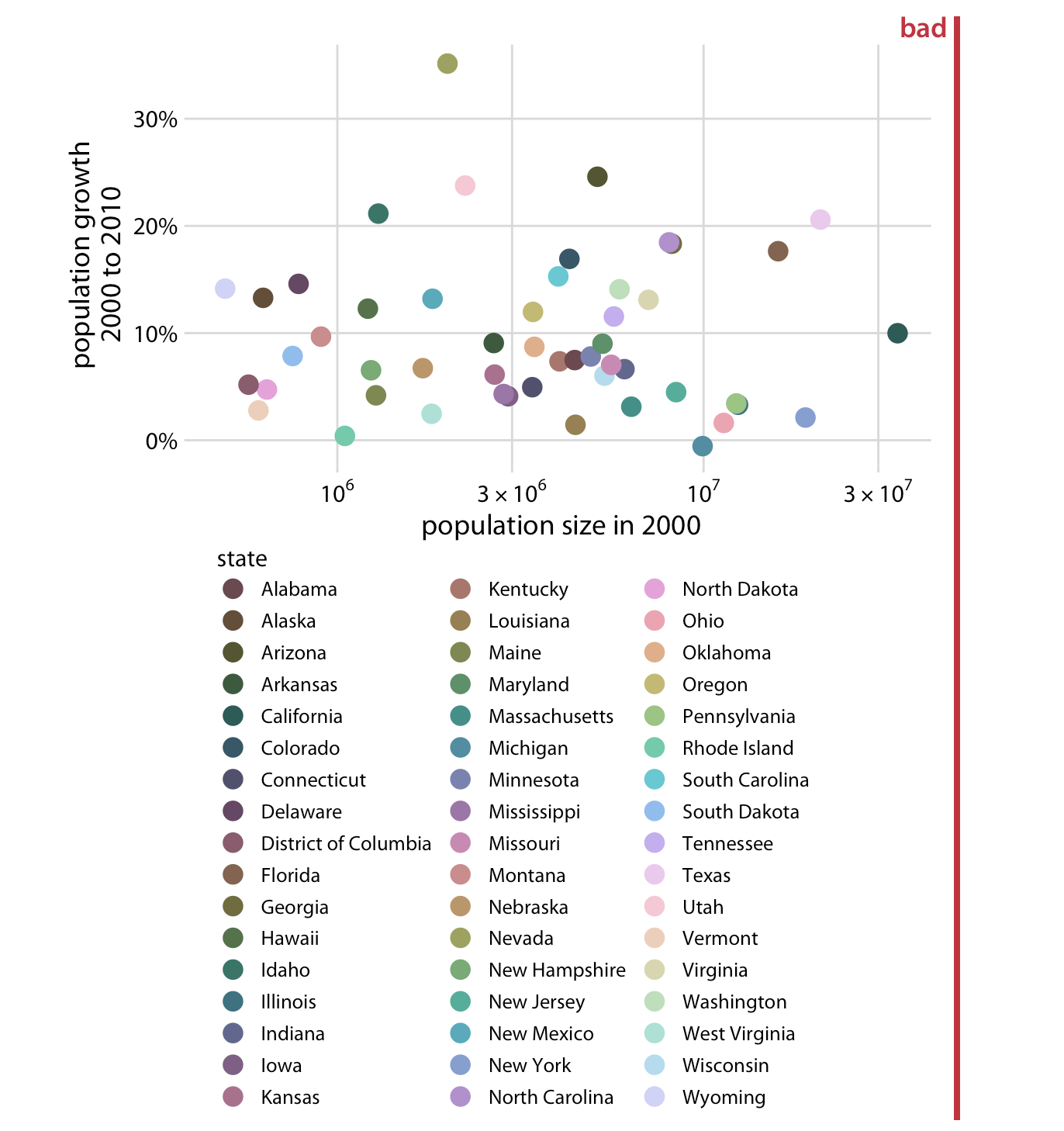
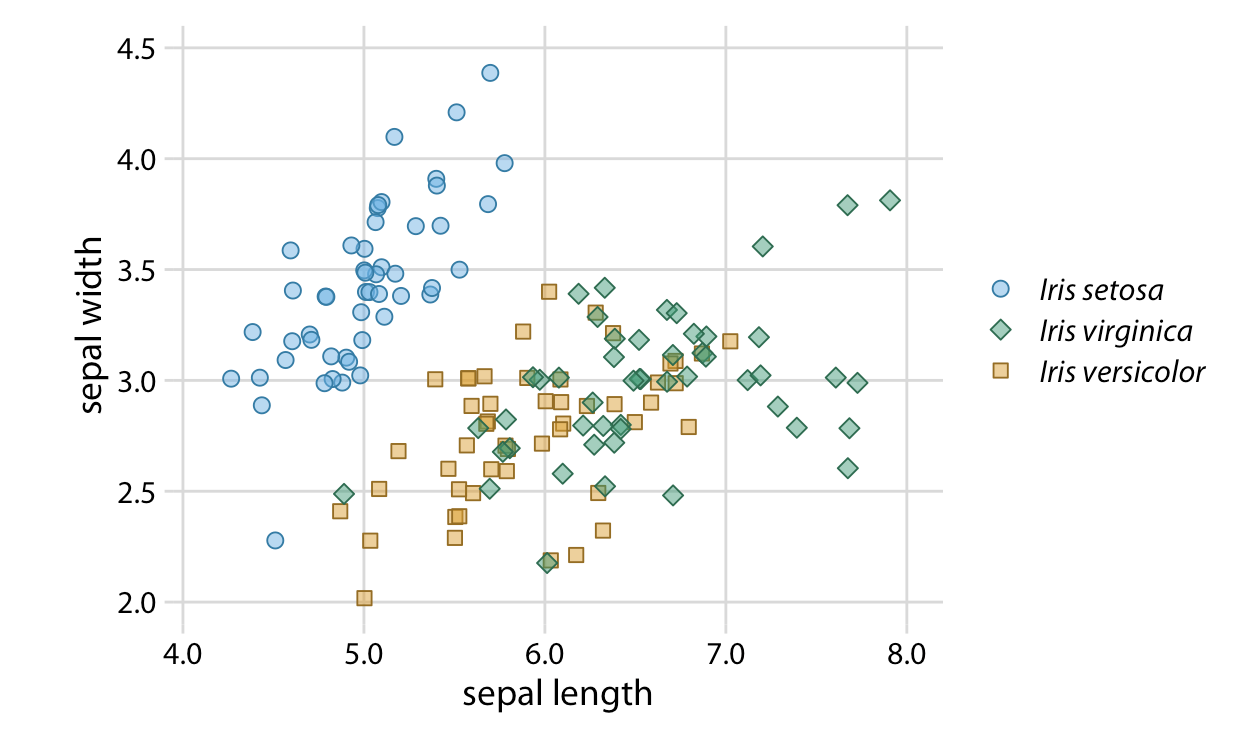
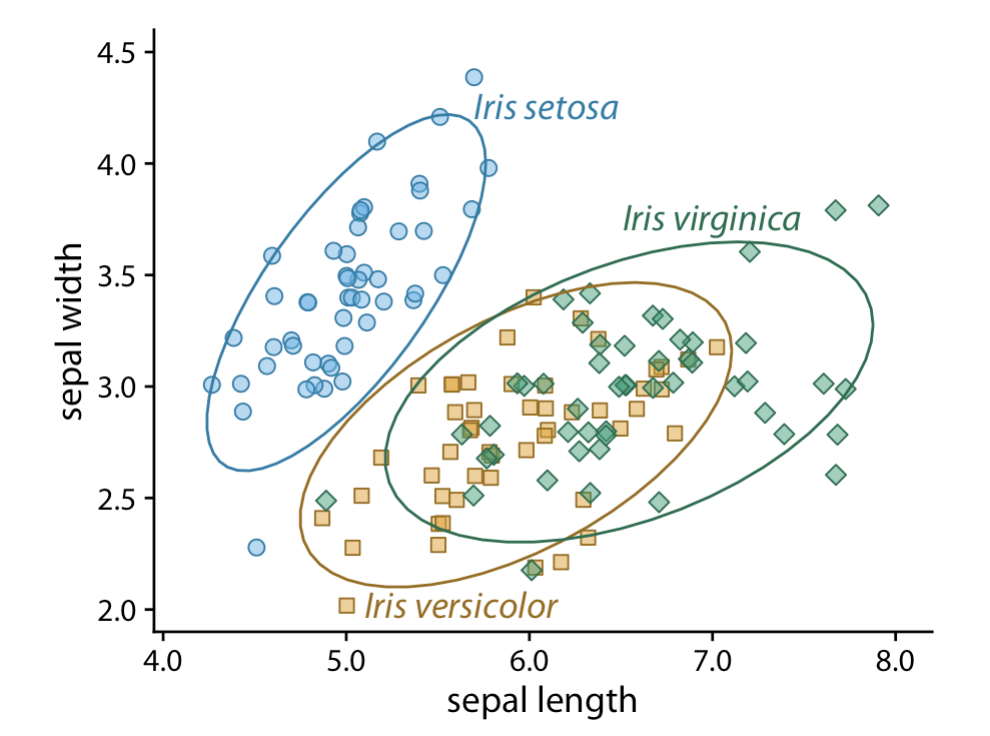
- Design clear legends with clear visual differences between categories. You can show different groups with different colors, symbol, or order on the plot. When possible, design your figure so it doesn’t need a legend.
An example where color and symbol are used to distinguish between categories.
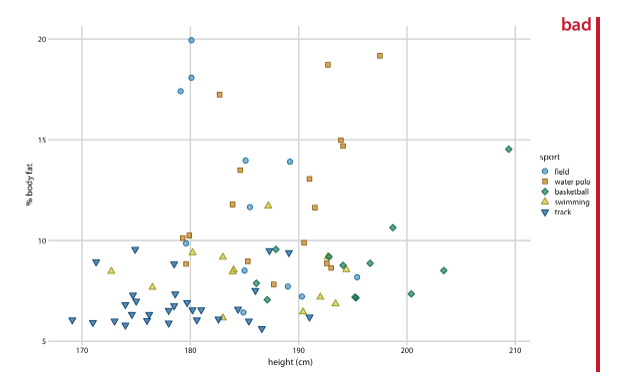
- Use larger axis labels. Always look at scaled down versions of your figures to make sure that your axes are still readable.
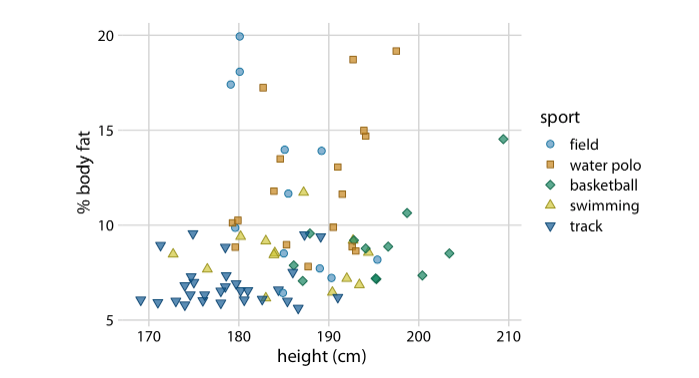
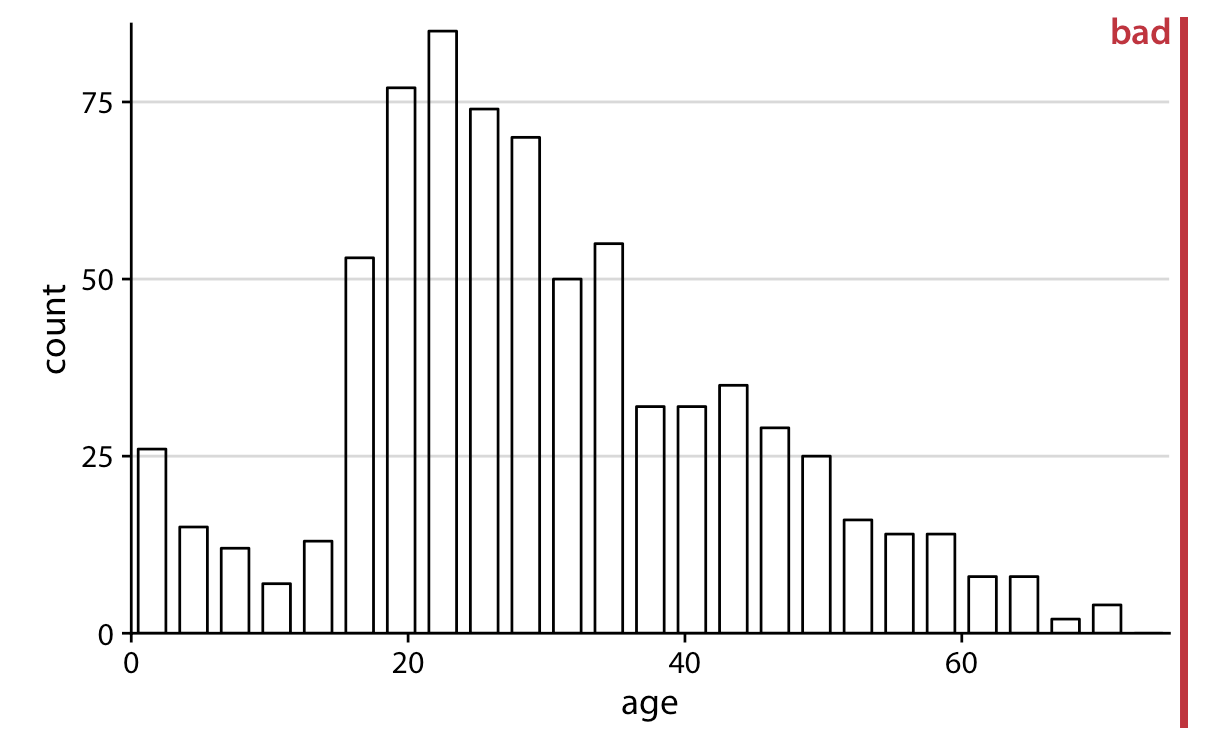
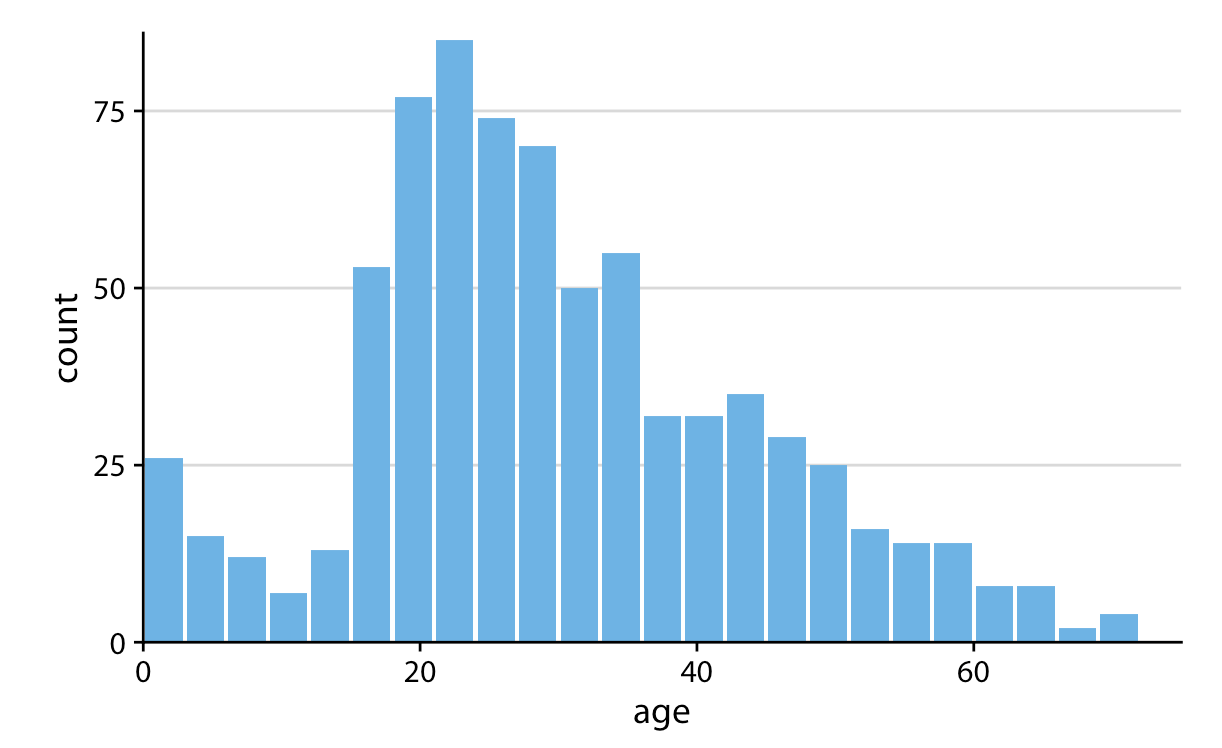
- Don’t use lined drawings. Whenever possible shade in the figures on your graph. Line drawings make it harder to visually detect patterns.
Example: A journal ready predicted values plot
Here is one example of a journal ready plot. This is code you can tweak and save to be your default style when producing plots for papers. I pulled this shortcut formatting from various places online, and it is in the reference .do file I put above.
We will use the grstyle shortcuts for changing the default settings for graphs. This is going to do the bulk of the formatting work for you, and would make your plot style consistent if you wanted to make several graphs for the same paper.
* Install some helper commands (if you haven't already installed them)
net install http://www.stata-journal.com/software/sj18-3/gr0073/
ssc install grstyle
ssc install palettes
ssc install colrspace
* Set the new default styles for your graph
grstyle clear // clear the grstyle settings
set scheme s2color // sets the color scheme
grstyle init // initiates the gr style command
grstyle set plain, box // create a plain style, with a box around the plot
* 'grid' is another good option you can play with
grstyle color background white // turn the background white
grstyle set color mono // set a monochrome color scheme for points/lines
grstyle set color Dark2, n(3) // set a color scheme for colored lines/points
* other color schemes include Set1, Set2, RdYlGn, Dark1, Dark2
* I set the number of colors I need in the plot in ', n(3)'
grstyle yesno draw_major_hgrid yes // include major grid lines
grstyle yesno draw_major_ygrid yes // include major grid lines
grstyle set legend 10, box inside // move the legend inside the plot area
* for this last command the number after legend refers to the corner
* of the plot (1 to at least 12 like a clock). I wanted it in the upper
* left. I just played around with numbers til I got it where I wanted.
grstyle set size 14pt: axis_title // change the size of axis text I will calculate the margins quietly:
quietly margins, at(log_fare = (0 2 4 6) parch = (0 3 6))And then here is the final plot. I don’t have to change many options, because all the grstyle options I used above did that work. I left plot title blank, because often you will manually title plots in your manuscript. You can add a title in if you wish.
marginsplot, ///
title("") ///
ytitle("Predicted Probabilities") ///
xtitle("Ticket Fare (logged)") ///
legend (order(1 "0 parents/children" 2 "3 parents/children" ///
3 "6 parents/children"))
graph export figs_output/probplot.png // save plot to your files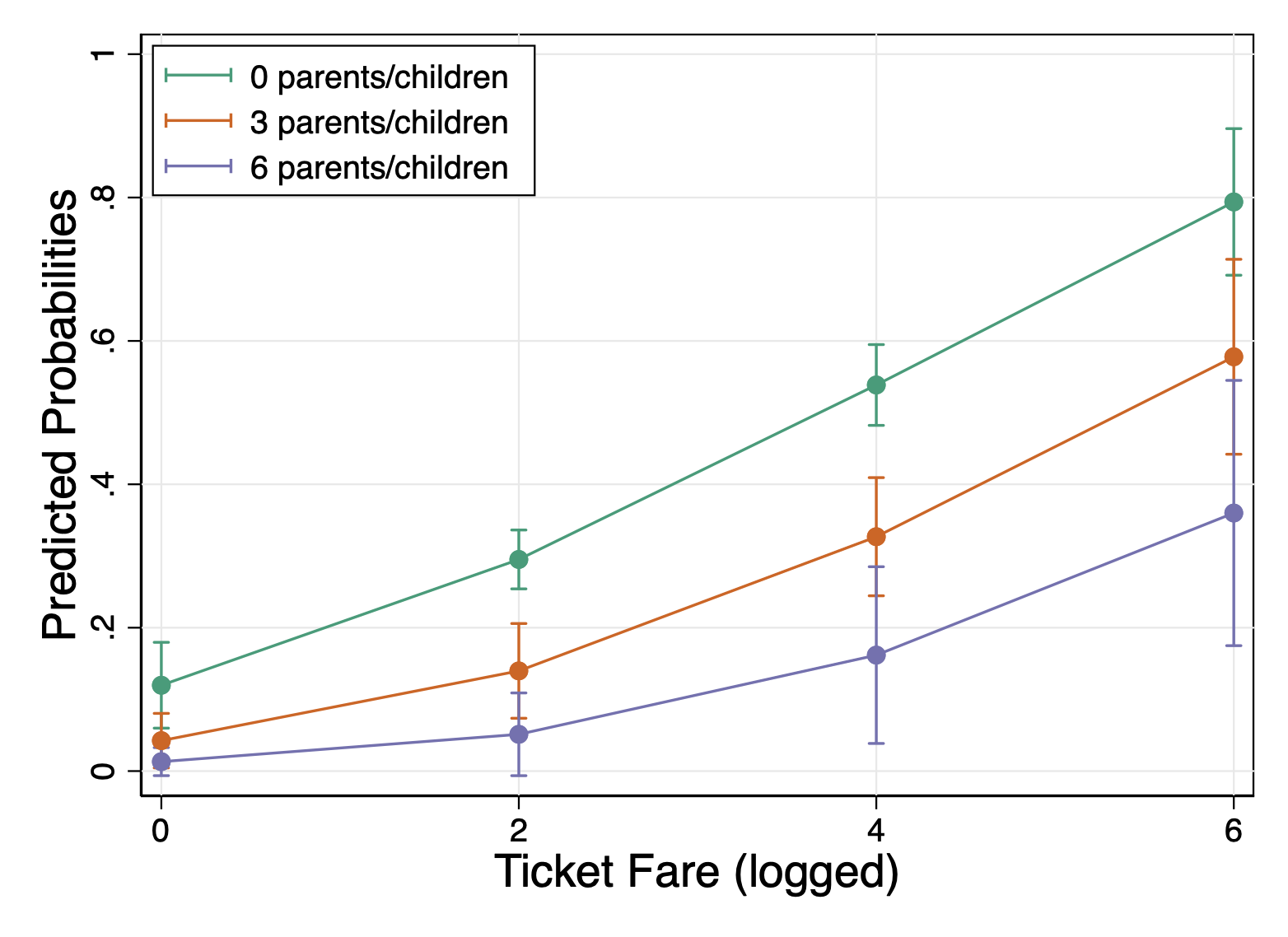
Here is a resource just to learn more about adjusting plots with grstyle:
Download grstyle_StataGraphsMadeEasy.pdf
6.5 Lab Assignment
From this logistic regression, produce a journal ready predicted probability plot with two X variables of focus (you can choose any two X variables from the regression). You can play around with grstyle or the direct commands from the reference file.