Capítulo 7 Genética

7.1 Genética de populações

No estudo de genética de populações, alguns cálculos básicos são as frequências alélicas e genotípicas, verificar se está em equilíbrio de Hardy-Weinberg e também verificar o desequilíbrio de ligação.

Esses cálculos podem ser feitos com o pacote genetics (Warnes et al. 2021).

Vamos carregar alguns dados de exemplo:

dados<-read.table("dados/genotipagem.txt", head=T)
head(dados)
##   AMOSTRAS rs1800977 rs2230806 rs3764650 rs2279796 rs692383 rs3827225 grupo
## 1    AHC01       G/G       C/C       G/T       A/G      A/G       G/G     1
## 2    AHC02       G/G       C/T       G/T       G/G      A/A       A/G     1
## 3    AHC03       G/G       T/T       T/T       A/G      A/A       G/G     1
## 4    AHC04       A/A       C/C       T/T       G/G      A/G       A/G     1
## 5    AHC06       A/G       C/C       T/T       A/A      A/A       A/A     1
## 6    AHC07       A/G       C/C       T/T       A/G      A/G       A/A     1

Vamos carregar o pacote genetics:

library(genetics)
snp<-"rs1800977"  #substituir  pelo gene/SNP de interesse

Agora vamos usar a função genotype, onde em sep informamos o separador de alelos nos dados.

genotipos1<-na.omit(genotype(dados$rs1800977, sep="/")) 
genotipos1
##   [1] "G/G" "G/G" "G/G" "A/A" "G/A" "G/A" "G/A" "G/A" "G/A" "G/G" "G/A" "G/G"
##  [13] "G/A" "G/G" "G/G" "G/A" "G/G" "G/A" "G/A" "G/A" "G/A" "A/A" "G/G" "G/G"
##  [25] "G/A" "G/G" "G/A" "G/A" "G/A" "G/A" "G/A" "G/G" "G/G" "G/G" "G/A" "G/G"
##  [37] "G/A" "G/A" "G/G" "A/A" "G/G" "G/A" "G/A" "G/G" "G/G" "G/G" "G/A" "A/A"
##  [49] "G/A" "G/A" "G/G" "G/G" "G/A" "A/A" "A/A" "G/G" "A/A" "G/G" "G/A" "G/G"
##  [61] "A/A" "A/A" "G/A" "G/G" "G/A" "G/A" "G/A" "G/A" "G/G" "G/A" "G/G" "G/A"
##  [73] "G/A" "G/G" "G/A" "G/A" "G/A" "G/A" "G/A" "G/A" "G/A" "G/G" "G/G" "G/G"
##  [85] "G/G" "G/A" "A/A" "G/A" "G/A" "G/A" "G/G" "G/G" "G/G" "G/A" "G/A" "G/A"
##  [97] "G/A" "G/G" "G/G" "G/A" "G/G" "G/G" "G/A" "G/A" "G/A" "G/G" "G/G" "G/G"
## [109] "G/G" "G/G" "G/A" "G/G" "G/A" "G/G" "G/A" "A/A" "A/A" "G/A" "G/A" "G/G"
## [121] "A/A" "G/A" "G/G" "G/A" "G/A" "G/G" "G/G" "G/A" "A/A" "A/A" "G/G" "G/A"
## [133] "G/A" "G/G" "G/G" "G/A" "G/G" "G/G" "G/A" "G/A" "G/G" "G/G" "G/A" "A/A"
## [145] "G/G" "G/A" "A/A" "G/G" "G/A" "G/G" "G/G" "G/G" "G/G" "G/A" "G/G" "G/A"
## [157] "G/G" "G/G" "G/A" "G/A" "G/G" "G/A" "G/G" "G/A" "G/G" "G/G" "G/G" "G/A"
## [169] "G/G" "G/A" "G/A" "G/A" "G/A" "G/A" "A/A" "G/A" "G/G" "G/A" "G/A" "G/A"
## [181] "G/G" "A/A" "G/A" "G/G" "G/A" "G/G" "G/A" "A/A" "G/A" "G/A" "G/A" "G/A"
## [193] "G/G" "G/A" "A/A" "G/G" "G/A" "G/G" "A/A" "G/A" "G/A" "G/A" "G/G" "G/G"
## [205] "G/A" "G/G" "G/G" "G/A" "G/G" "G/A" "G/A" "G/A" "G/A" "G/A" "G/A" "G/A"
## [217] "G/G" "G/A" "G/A" "A/A" "G/G" "G/G" "G/A" "G/G" "G/G" "G/G" "G/A" "G/A"
## [229] "G/A" "G/A" "G/G" "G/A" "G/G" "G/A" "G/G" "G/G" "G/A" "G/G" "G/G" "G/A"
## [241] "G/G" "G/A" "G/A" "G/A" "G/G" "G/G" "G/G" "G/G" "G/G" "G/A" "G/A" "G/A"
## [253] "G/A" "A/A" "G/G" "G/A" "G/G" "G/A" "G/A" "G/A" "G/A" "G/A" "G/A" "G/A"
## [265] "G/A" "G/A" "G/G" "G/A" "G/G" "G/G" "G/G" "G/G" "A/A" "G/G" "G/G" "G/G"
## [277] "G/A" "G/G" "G/G" "G/A" "G/A" "G/G" "G/G" "G/A" "A/A" "G/A" "A/A" "G/A"
## [289] "G/G" "G/A" "G/G" "G/A" "G/G" "G/A" "A/A" "A/A" "G/A" "G/G" "G/G" "G/A"
## [301] "G/G" "G/G" "G/G" "G/G" "G/A" "G/G" "G/G" "G/A" "G/A" "G/A" "G/G" "G/A"
## [313] "G/G" "G/G" "G/G" "G/G" "G/A" "G/A" "G/A" "G/A" "G/G" "G/G" "G/A" "G/A"
## [325] "A/A"
## Alleles: G A

Podemos ver os resultados de frequências usando summary:

resultado1<-summary(genotipos1)
resultado1
## 
## Number of samples typed: 325 (100%)
## 
## Allele Frequency: (2 alleles)
##   Count Proportion
## G   430       0.66
## A   220       0.34
## 
## 
## Genotype Frequency:
##     Count Proportion
## G/G   135       0.42
## G/A   160       0.49
## A/A    30       0.09
## 
## Heterozygosity (Hu)  = 0.4485007
## Poly. Inf. Content   = 0.3475435

Para verificar o equilíbrio de Hardy-Weinberg usamos a função HWE.chisq:

eqhw1<-HWE.chisq(genotipos1)
eqhw1
## 
##  Pearson's Chi-squared test with simulated p-value (based on 10000
##  replicates)
## 
## data:  tab
## X-squared = 3.2089, df = NA, p-value = 0.08419

Podemos salvar os resultados em um arquivo txt, onde vamos usar o objeto snp para especificar de qual SNP são os resultados:

write("Frequencias alelicas e genotipicas.", file="res.genes.txt",append=T)
write(snp, file="res.genes.txt", append=T)
capture.output(resultado1, file="res.genes.txt",append = T)
capture.output(eqhw1, file="res.genes.txt", append = T)

Também podemos gerar figuras com as frequências:

plot(genotipos1, type="allele", what="percentage")

plot(genotipos1, type="genotype", what="percentage")

Para salvar as figuras com as frequências, onde filename=paste(snp,“alelo.jpg”, sep=““: serve para criar o nome do arquivo juntando o conteúdo de snp + alelo.jpg, sem espaço, definido por sep sem nada:

jpeg(filename=paste(snp,"alelo.jpg", sep=""))
plot(genotipos1, type="allele", what="percentage")
dev.off()
## png 
##   2
jpeg(filename=paste(snp,"genotipo.jpg", sep=""))
plot(genotipos1, type="genotype", what="percentage")
dev.off()
## png 
##   2

Desequilíbrio de ligação

Também podemos calcular o desequilíbrio de ligação entre 2 SNPs com a função LD, mas primeiro criamos os objetos com os dados dos SNPs com a função genotype:

rs1800977<-na.omit(genotype(dados$rs1800977, sep="/"))
rs2230806<-na.omit(genotype(dados$rs2230806, sep="/"))
ld<-LD(rs1800977,rs2230806)
ld
## 
## Pairwise LD
## -----------
##                      D       D'        Corr
## Estimates: -0.01494381 0.146423 -0.06881552
## 
##               X^2    P-value   N
## LD Test: 3.078125 0.07935198 325

7.2 Genotipagem com genetics e loop

Vamos juntar os conhecimentos de loops, que já aprendemos, para genotipar vários SNPs e criar um arquivo de saída mais elaborado:

No arquivo que estamos usando, tem uma coluna grupo (caso e controle). Usaremos essa coluna para criar 2 objetos:

library(dplyr)
caso<-filter(dados, grupo==1)   
controle<-filter(dados, grupo==2)

Precisamos detalhar o que tem em resultados1:

names(resultado1)
## [1] "allele.names"  "allele.freq"   "genotype.freq" "Hu"           
## [5] "pic"           "n.typed"       "n.total"       "nallele"

Em allele.fre e genotype.freq temos uma matriz com os resultados:

resultado1$allele.freq
##   Count Proportion
## G   430  0.6615385
## A   220  0.3384615
resultado1$genotype.freq
##     Count Proportion
## G/G   135 0.41538462
## G/A   160 0.49230769
## A/A    30 0.09230769

Com base nisso, precisamos definir quais dados queremos salvar e criar uma tabela com as variáveis. Aqui criamos o objeto tabela.saida, que é um data.frame e especificamos as colunas:

tabela.saida<-data.frame(grupo=as.character(NA),SNP=as.character(NA),genot1=as.character(NA), N1=NA, F1=NA,genot2=as.character(NA), N2=NA, F2=NA,genot3=as.character(NA),N3=NA,F3=NA,alelo1=as.character(NA),N4=NA,F4=NA,alelo2=as.character(NA),N5=NA,F5=NA,hw=NA,qui_genot=NA,qui_alel=NA,stringsAsFactors = F)

Agora vamos criar o loop, usando for, para fazer a genotipagem e equilíbrio de HW, de cada SNP, no grupo caso e no grupo controle, depois compare por qui-quadrado as frequências alélicas e genotípica entre casos e controles.

nomes<-colnames(dados) #nomes dos SNPs
i<-2 #número da coluna inicial para genotipar
snp<-7 # número da coluna final para genotipar
j<-1

for (i in i:snp) {
  nome_snp<-nomes[i]
  genotipos1<-na.omit(genotype(caso[,i], sep="/"))#genotipagem
  resultado1<-summary(genotipos1)#sumariza resultados
  eqhw1<-HWE.chisq(genotipos1)#equilíbrio de HW
  nome_genot<-rownames(resultado1$genotype.freq)
  nome_alelos<-rownames(resultado1$allele.freq)
  
  
  tabela.saida[j,]<-data.frame(grupo=as.character("caso"),SNP=as.character(nome_snp),genot1=as.character(nome_genot[1]), N1=resultado1$genotype.freq[1,1], F1=resultado1$genotype.freq[1,2],genot2=as.character(nome_genot[2]), N2=resultado1$genotype.freq[2,1],F2=resultado1$genotype.freq[2,2], genot3=as.character(nome_genot[3]),N3=resultado1$genotype.freq[3,1],F3=resultado1$genotype.freq[3,2],alelo1=as.character(nome_alelos[1]),N4=resultado1$allele.freq[1,1],F4=resultado1$allele.freq[1,2],alelo2=as.character(nome_alelos[2]),N5=resultado1$allele.freq[2,1],F5=resultado1$allele.freq[2,2],hw=eqhw1$p.value,qui_genot=NA,qui_alel=NA,stringsAsFactors = F)
  j<-j+1
  
  genotipos2<-na.omit(genotype(controle[,i], sep="/"))#genotipagem
  resultado2<-summary(genotipos2)#sumariza resultados
  eqhw2<-HWE.chisq(genotipos2)#equilíbrio de HW
  
  #qui-quadrado alelo
  a<-resultado1$allele.freq[1,1]
  b<-resultado1$allele.freq[2,1]
  c<-resultado2$allele.freq[1,1]
  d<-resultado2$allele.freq[2,1]
  quadrado<-rbind(c(a,c),c(b,d))
  quadrado
  res_qui<-chisq.test(quadrado,correct=F)
  
  #qui-quadrado genotipo
  g<-resultado1$genotype.freq[1,1]
  h<-resultado1$genotype.freq[2,1]
  l<-resultado1$genotype.freq[3,1]
  k<-resultado2$genotype.freq[1,1]
  m<-resultado2$genotype.freq[2,1]
  o<-resultado2$genotype.freq[3,1]
  quadrado2<-rbind(c(g,k),c(h,m),c(l,o))
  res_qui2<-chisq.test(quadrado2,correct=F)
  
  tabela.saida[j,]<-data.frame(grupo=as.character("controle"),SNP=as.character(nome_snp),genot1=as.character(nome_genot[1]), N1=resultado2$genotype.freq[1,1], F1=resultado2$genotype.freq[1,2],genot2=as.character(nome_genot[2]), N2=resultado2$genotype.freq[2,1],F2=resultado2$genotype.freq[2,2], genot3=as.character(nome_genot[3]),N3=resultado2$genotype.freq[3,1],F3=resultado2$genotype.freq[3,2],alelo1=as.character(nome_alelos[1]),N4=resultado2$allele.freq[1,1],F4=resultado2$allele.freq[1,2],alelo2=as.character(nome_alelos[2]),N5=resultado2$allele.freq[2,1],F5=resultado2$allele.freq[2,2],hw=eqhw2$p.value,qui_genot=res_qui2$p.value,qui_alel=res_qui$p.value,stringsAsFactors = F)
  
  
  
  i<-(i+1)
  j<-j+1
}

Verificando os resultados:

library(flextable)
flextable(tabela.saida)

grupo

SNP

genot1

N1

F1

genot2

N2

F2

genot3

N3

F3

alelo1

N4

F4

alelo2

N5

F5

hw

qui_genot

qui_alel

caso

rs1800977

G/G

79

0.4030612

G/A

96

0.4897959

A/A

21

0.10714286

G

254

0.6479592

A

138

0.3520408

0.3501650

controle

rs1800977

G/G

56

0.4341085

G/A

64

0.4961240

A/A

9

0.06976744

G

176

0.6821705

A

82

0.3178295

0.1065893

0.5055572

0.3671365

caso

rs2230806

C/C

91

0.4642857

C/T

90

0.4591837

T/T

15

0.07653061

C

272

0.6938776

T

120

0.3061224

0.3173683

controle

rs2230806

C/C

67

0.5193798

C/T

48

0.3720930

T/T

14

0.10852713

C

182

0.7054264

T

76

0.2945736

0.2920708

0.2505753

0.7535973

caso

rs3764650

T/T

135

0.7758621

T/G

36

0.2068966

G/G

3

0.01724138

T

306

0.8793103

G

42

0.1206897

1.0000000

controle

rs3764650

T/T

79

0.8061224

T/G

16

0.1632653

G/G

3

0.03061224

T

174

0.8877551

G

22

0.1122449

0.1042896

0.5473538

0.7691475

caso

rs2279796

A/A

55

0.2777778

A/G

91

0.4595960

G/G

52

0.26262626

A

201

0.5075758

G

195

0.4924242

0.2571743

controle

rs2279796

A/A

31

0.2460317

A/G

69

0.5476190

G/G

26

0.20634921

A

131

0.5198413

G

121

0.4801587

0.2820718

0.2845827

0.7607357

caso

rs692383

A/A

83

0.4234694

A/G

85

0.4336735

G/G

28

0.14285714

A

251

0.6403061

G

141

0.3596939

0.4345565

controle

rs692383

A/A

53

0.4140625

A/G

59

0.4609375

G/G

16

0.12500000

A

165

0.6445312

G

91

0.3554688

1.0000000

0.8488922

0.9126687

caso

rs3827225

G/G

103

0.5282051

G/A

76

0.3897436

A/A

16

0.08205128

G

282

0.7230769

A

108

0.2769231

0.7174283

controle

rs3827225

G/G

74

0.5692308

G/A

49

0.3769231

A/A

7

0.05384615

G

197

0.7576923

A

63

0.2423077

0.6277372

0.5623675

0.3261360

Para terminar vamos salvar os resultados em um arquivo xlsx:

library(openxlsx)
write.xlsx(tabela.saida, file="genotipagem.xlsx")

7.3 Heredogramas

Também podemos gerar heredogramas usando o R, para isso usamos o pacote kinship2 (Sinnwell and Therneau 2022) e carregar o arquivo de exemplo:

library(kinship2)
familia<-read.xlsx("dados/familia.xlsx", sheet=1, colNames = T)
head(familia)
##   ids dad mom sex dead caract
## 1   1  NA  NA   1    0      0
## 2   2  NA  NA   2    1      0
## 3   3  NA  NA   1    0      0
## 4   4   1   2   2    0      0
## 5   5   1   2   1    0      0
## 6   6  NA  NA   2    0      0

Nessa planilha temos uma coluna com a identificação única de de cada indivíduo (ids), duas colunas identificando os pais (dad e mom), uma coluna para o sexo, uma coluna com a informação se o indivíduo está vivo ou não (dead) e uma última coluna (caract) que indica se o indivíduo tem a característica de interesse.

Usando a função pedigree:

family <- pedigree(id=familia$ids, dadid=familia$dad, momid=familia$mom, affected=familia$caract, sex=familia$sex, status=familia$dead)

E plotando o heredograma:

plot.pedigree(family,cex = 0.8, col = c("red","blue","green","red","blue","green","red","blue","green","black"))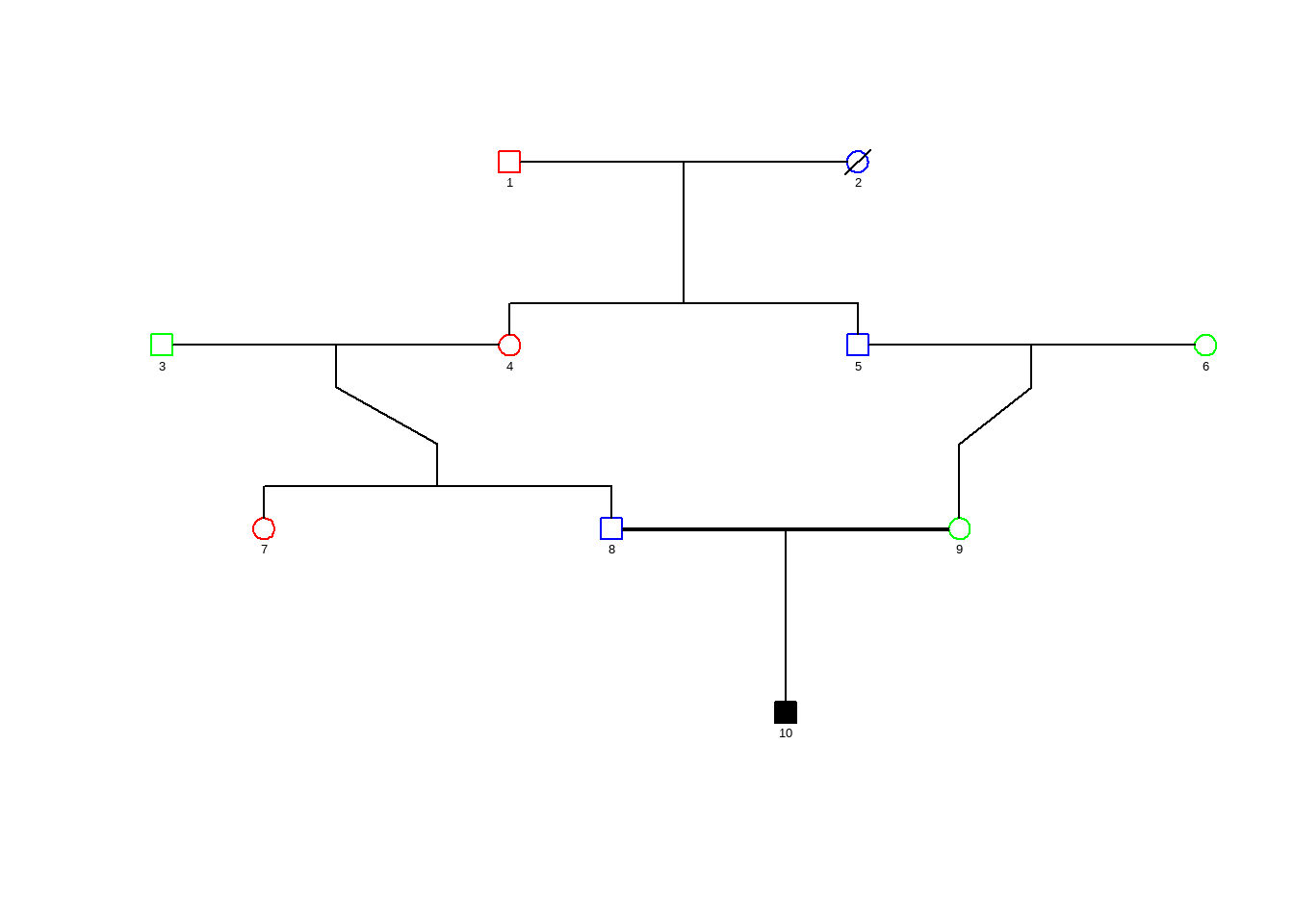

7.4 Análises filogenéticas

O pacote APE (Analysis of Phylogenetics and Evolution) (paradis2019?) permite fazer vários tipos de análises (http://ape-package.ird.fr/).

Podemos pegar sequências de DNA diretamente do Genbank:

library(ape)

id_seq<-c("NM_001081850.1","NM_000055.3","NM_009738.3")
seq_bche<-read.GenBank(id_seq)
seq_bche
## 3 DNA sequences in binary format stored in a list.
## 
## Mean sequence length: 3495.333 
##    Shortest sequence: 1809 
##     Longest sequence: 6209 
## 
## Labels:
## NM_001081850.1
## NM_000055.3
## NM_009738.3
## 
## Base composition:
##     a     c     g     t 
## 0.315 0.192 0.194 0.299 
## (Total: 10.49 kb)

Também é possível ler um arquivo fasta:

pon<-read.FASTA("dados/PON123.fas")
pon
## 13 DNA sequences in binary format stored in a list.
## 
## All sequences of same length: 1065 
## 
## Labels:
## PON1Hsapie
## PON1Ptrogl
## PON1Mmulat
## PON1Mmuscu
## PON2Hsapie
## PON2Ptrogl
## ...
## 
## Base composition:
##     a     c     g     t 
## 0.284 0.215 0.228 0.274 
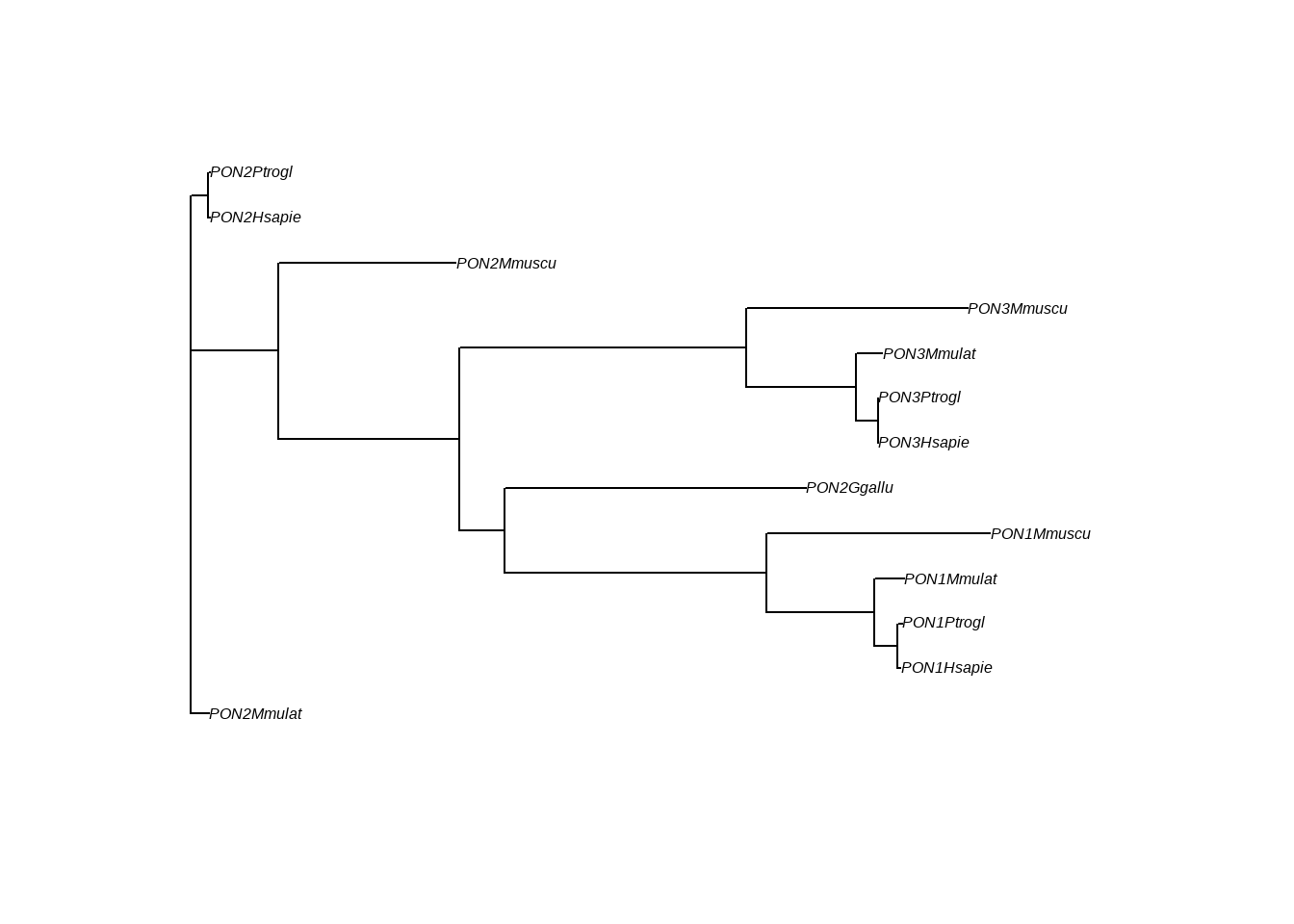
## (Total: 13.85 kb)

E com a função nj podemos fazer uma árvore pelo método neighbor-joining (Trees 1987).

pon.trw<-nj(dist.dna(pon))
plot(pon.trw)

References

Sinnwell, Jason, and Terry Therneau. 2022. Kinship2: Pedigree Functions. https://CRAN.R-project.org/package=kinship2.
Trees, Reconstructing Phylogenetic. 1987. “The Neighbor-Joining Method: A New Method For.” Mol. Biol. Evol 4 (4): 406–25.
Warnes, Gregory, with contributions from Gregor Gorjanc, Friedrich Leisch, and Michael Man. 2021. Genetics: Population Genetics. https://CRAN.R-project.org/package=genetics.