Capítulo 5 Estatística
5.1 Estatística descritiva
O R permite fazer qualquer teste estatístico. No R base já temos o pacote stats que possibilita fazer vários testes estatísticos. Além disso temos muitos outros pacotes estatísticos.
Primeiro vamos fazer uma estatística descritiva, obtendo os valores de média, mediana, desvio padrão, máximo, mínimo.
Os dados que vamos usar estão no pacote palmerpenguins.
## species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
## 1 Adelie Torgersen 39.1 18.7 181 3750
## 2 Adelie Torgersen 39.5 17.4 186 3800
## 3 Adelie Torgersen 40.3 18.0 195 3250
## 4 Adelie Torgersen NA NA NA NA
## 5 Adelie Torgersen 36.7 19.3 193 3450
## 6 Adelie Torgersen 39.3 20.6 190 3650
## sex year
## 1 male 2007
## 2 female 2007
## 3 female 2007
## 4 <NA> 2007
## 5 female 2007
## 6 male 2007## [1] 43.92193## [1] 44.45## [1] 5.459584## [1] 59.6## [1] 32.1## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 32.10 39.23 44.45 43.92 48.50 59.60 25.2 Testes estatísticos
Tipos de testes estatísticos
Existem testes paramétricos e não paramétricos. Primeiro passo: verificar como é a distribuição dos nossos dados. Podemos fazer um gráfico assim:
m<-mean(dados$bill_length_mm ,na.rm=TRUE)
std<-sd(dados$bill_length_mm ,na.rm=TRUE)
hist(dados$bill_length_mm , prob=TRUE)
curve(dnorm(x, mean=m, sd=std),
col="darkblue", lwd=2, add=TRUE, yaxt="n")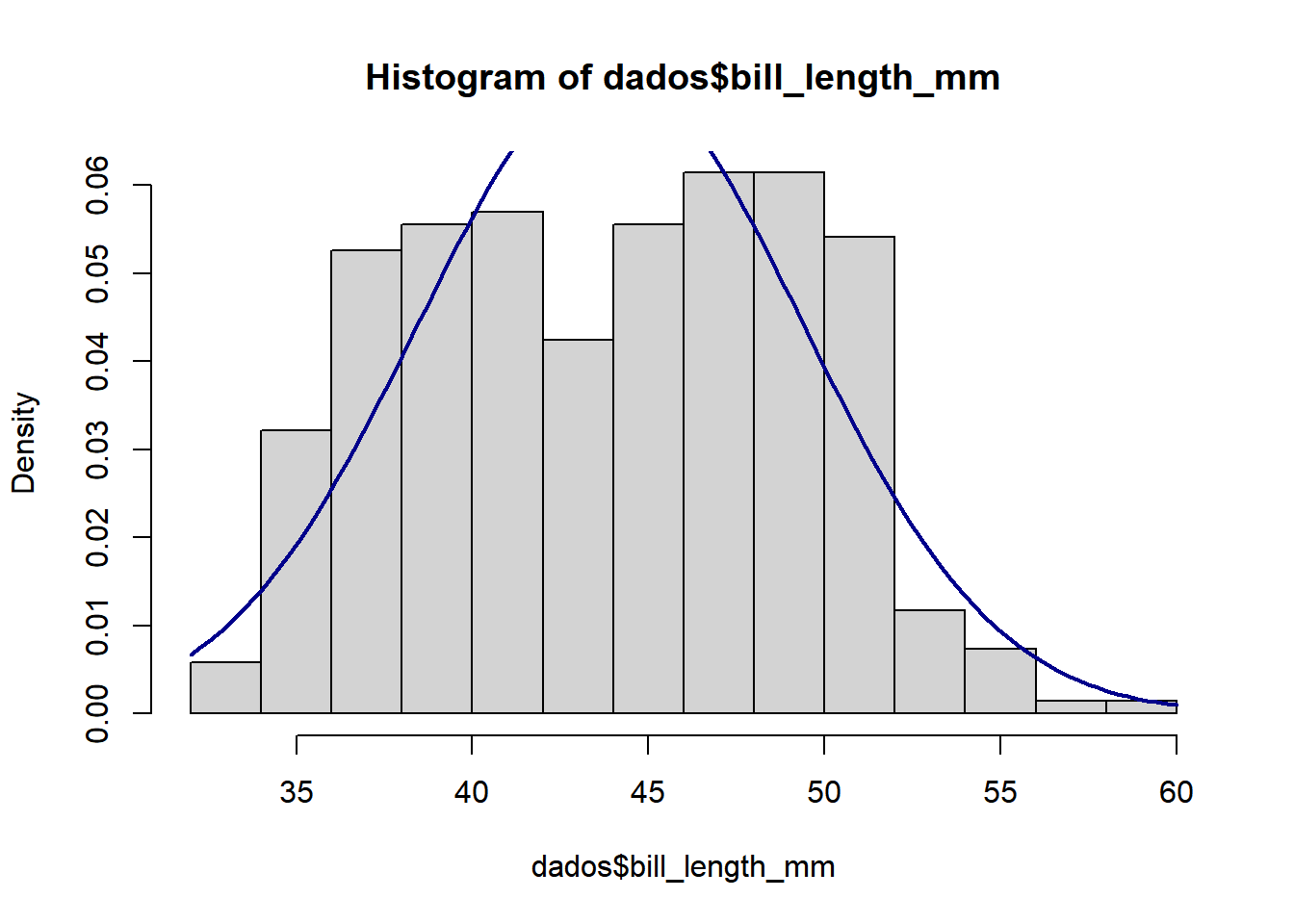
Ou podemos fazer um gráfico qq plot:
library(ggplot2)
library(dplyr)
p <- dados %>%
ggplot(aes(sample= bill_length_mm))
params <- dados %>%
summarize(mean = mean(bill_length_mm, na.rm = T), sd = sd(bill_length_mm, na.rm=T))
p + geom_qq(dparams = params)+
geom_abline()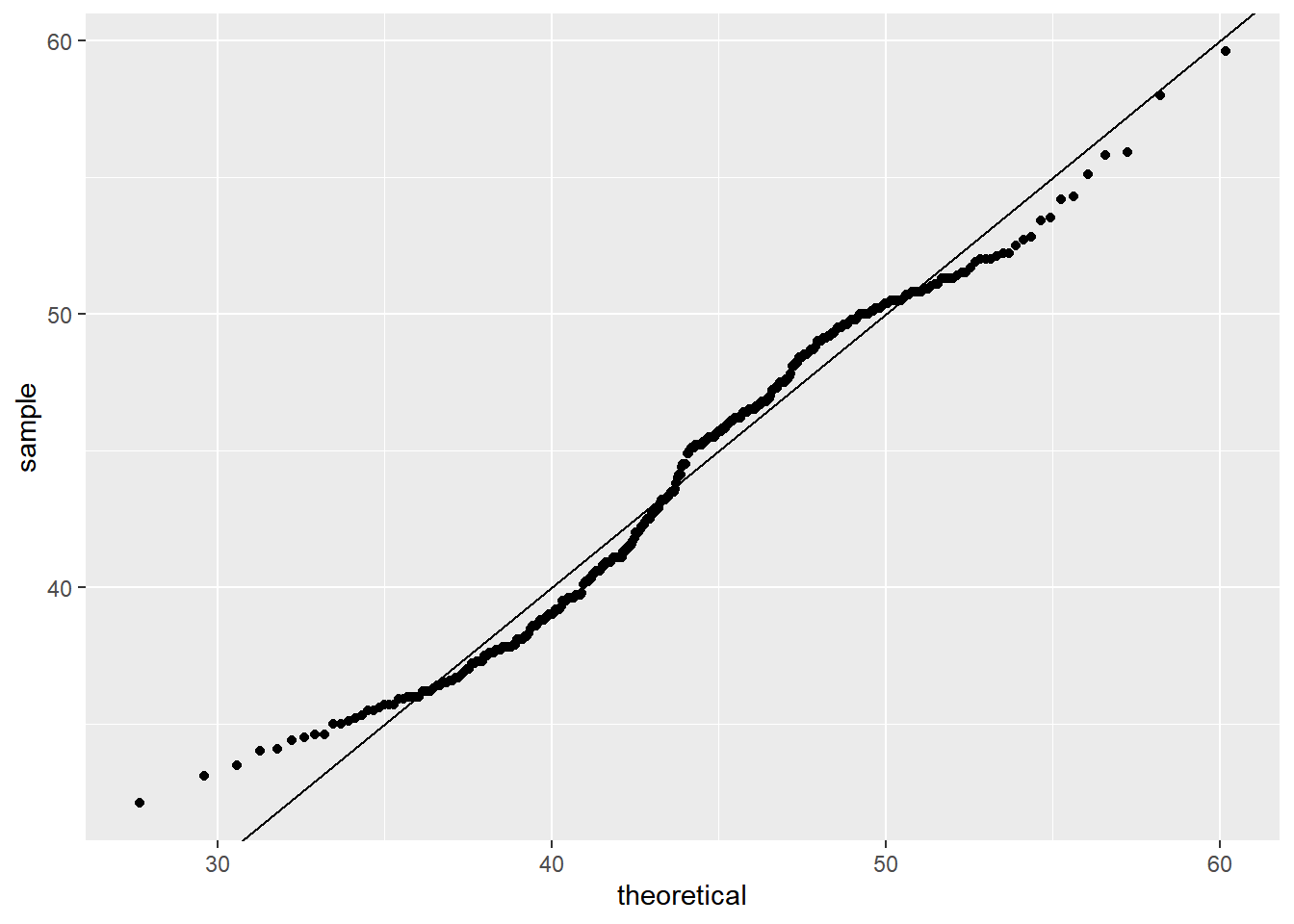
5.2.1 Normalidade
Através dos gráficos podemos ter uma ideia da distribuição dos dados, mas isso não é um teste estatístico. Para testar a normalidade podemos usar o teste Kolmogorov-Smirnov com correção de Lilliefors, para isso precisamos instalar ativar o pacote nortest (Gross and Ligges 2015):
##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: dados$bill_length_mm
## D = 0.069803, p-value = 0.0003883Esses dados são de diferentes espécies, então devemos testar a normalidade em cada grupo:
library(dplyr)
adelie<-filter(dados, species=="Adelie")
gentoo<-filter(dados, species=="Gentoo")
chinstrap<-filter(dados, species=="Chinstrap")
lillie.test(adelie$bill_length_mm)##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: adelie$bill_length_mm
## D = 0.042489, p-value = 0.7254##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: gentoo$bill_length_mm
## D = 0.062001, p-value = 0.2929##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: chinstrap$bill_length_mm
## D = 0.093769, p-value = 0.1459Também podemos usar o teste de Shapiro-Wilk para testar a normalidade:
##
## Shapiro-Wilk normality test
##
## data: adelie$bill_length_mm
## W = 0.99336, p-value = 0.7166##
## Shapiro-Wilk normality test
##
## data: gentoo$bill_length_mm
## W = 0.97272, p-value = 0.01349##
## Shapiro-Wilk normality test
##
## data: chinstrap$bill_length_mm
## W = 0.97525, p-value = 0.19415.2.2 Assimetria e curtose
Em estatística, assimetria (skewness) e curtose (kurtosis) são duas maneiras de medir a forma de uma distribuição.
A assimetria é uma medida da assimetria de uma distribuição. Este valor pode ser positivo ou negativo.
Um valor de zero indica que não há assimetria na distribuição, o que significa que a distribuição é perfeitamente simétrica.
Curtose mede a concentração ou dispersão dos valores de um conjunto de valores em relação às medidas de tendência central.
A curtose de uma distribuição normal é 3. Se uma dada distribuição tem uma curtose menor que 3, ela tende a produzir menos outliers e menos extremos do que a distribuição normal. Se uma dada distribuição tem uma curtose maior que 3, ela tende a produzir mais outliers do que a distribuição normal. Para fazer esses testes vamos utilizar o pacote moments (Komsta and Novomestky 2022).
## [1] 0.1600638##
## D'Agostino skewness test
##
## data: adelie$bill_length_mm
## skew = 0.16006, z = 0.83425, p-value = 0.4041
## alternative hypothesis: data have a skewness## [1] 2.80848##
## Anscombe-Glynn kurtosis test
##
## data: adelie$bill_length_mm
## kurt = 2.80848, z = -0.28403, p-value = 0.7764
## alternative hypothesis: kurtosis is not equal to 3Se os dados tem distribuição normal podemos comparar as médias usando o teste t, mas precisamos saber se as variâncias são iguais:
##
## F test to compare two variances
##
## data: adelie$bill_length_mm and gentoo$bill_length_mm
## F = 0.74688, num df = 150, denom df = 122, p-value = 0.08894
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.5303445 1.0455238
## sample estimates:
## ratio of variances
## 0.74687745.2.3 Teste t
##
## Two Sample t-test
##
## data: adelie$bill_length_mm and gentoo$bill_length_mm
## t = -25.095, df = 272, p-value < 2.2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -9.397060 -8.029915
## sample estimates:
## mean of x mean of y
## 38.79139 47.50488Se o teste de variância não foi significativo, usamos var.equal=T, caso contrário, usamos var.equal=F
Para dados não paramétricos temos o teste Mann-Whitney (para duas amostras) ou Wilcoxon (para uma amostra pareada: paired = T):
##
## Wilcoxon rank sum test with continuity correction
##
## data: adelie$bill_length_mm and gentoo$bill_length_mm
## W = 224.5, p-value < 2.2e-16
## alternative hypothesis: true location shift is not equal to 05.2.4 Teste qui-quadrado
chisq.test(x, correct = TRUE, simulate.p.value = FALSE, B = 2000)
correct = T: faz correção de Yates (subtrae 0,5 de todas as diferenças |O - E|. Deve ser usado quando o n está entre 20 e 40 e tiver só um grau de liberdade. simulate.p.value = T: calcula o valor de p através de simulação de Monte Carlo. Ideal principalmente para amostras pequenas. B: quando usar simulação de Monte Carlo, especificar o número de replicatas (sugestão, use um valor de 10000).
Exemplos:
## [,1] [,2]
## [1,] 163 147
## [2,] 109 125##
## Pearson's Chi-squared test
##
## data: x
## X-squared = 1.9198, df = 1, p-value = 0.1659## [,1] [,2] [,3]
## [1,] 163 147 130
## [2,] 109 125 125##
## Pearson's Chi-squared test
##
## data: x
## X-squared = 4.4321, df = 2, p-value = 0.109##
## Pearson's Chi-squared test with simulated p-value (based on 10000
## replicates)
##
## data: x
## X-squared = 4.4321, df = NA, p-value = 0.1045.2.5 Correlação
cor(x, use=, method= )
use: como tratar dados faltantes. Options are all.obs (sem NA), complete.obs (listwise deletion), pairwise.complete.obs (pairwise deletion) method tipo de correlação. Options are pearson, spearman or kendall.
Pearson (entre duas variáveis contínuas), que é um teste paramétrico. Spearman (ou rho) ? uma correlação de “rankings” ou “postos”, # e por isso é um teste não-paramétrico Kendall (ou tau) vai na mesma linha não-paramétrica da correlação de Spearman
## [1] 0.5488658A função cor da apenas o valor da correlação, por outro lado, podemos usar a função chart.Correlation do pacote PerformanceAnalytics (Peterson and Carl 2020), com a qual teremos o valor da correlação, a significância e o gráfico.
# plot the data
library(PerformanceAnalytics)
mydata<-select(adelie, bill_length_mm :body_mass_g)
chart.Correlation(mydata, method = "pearson")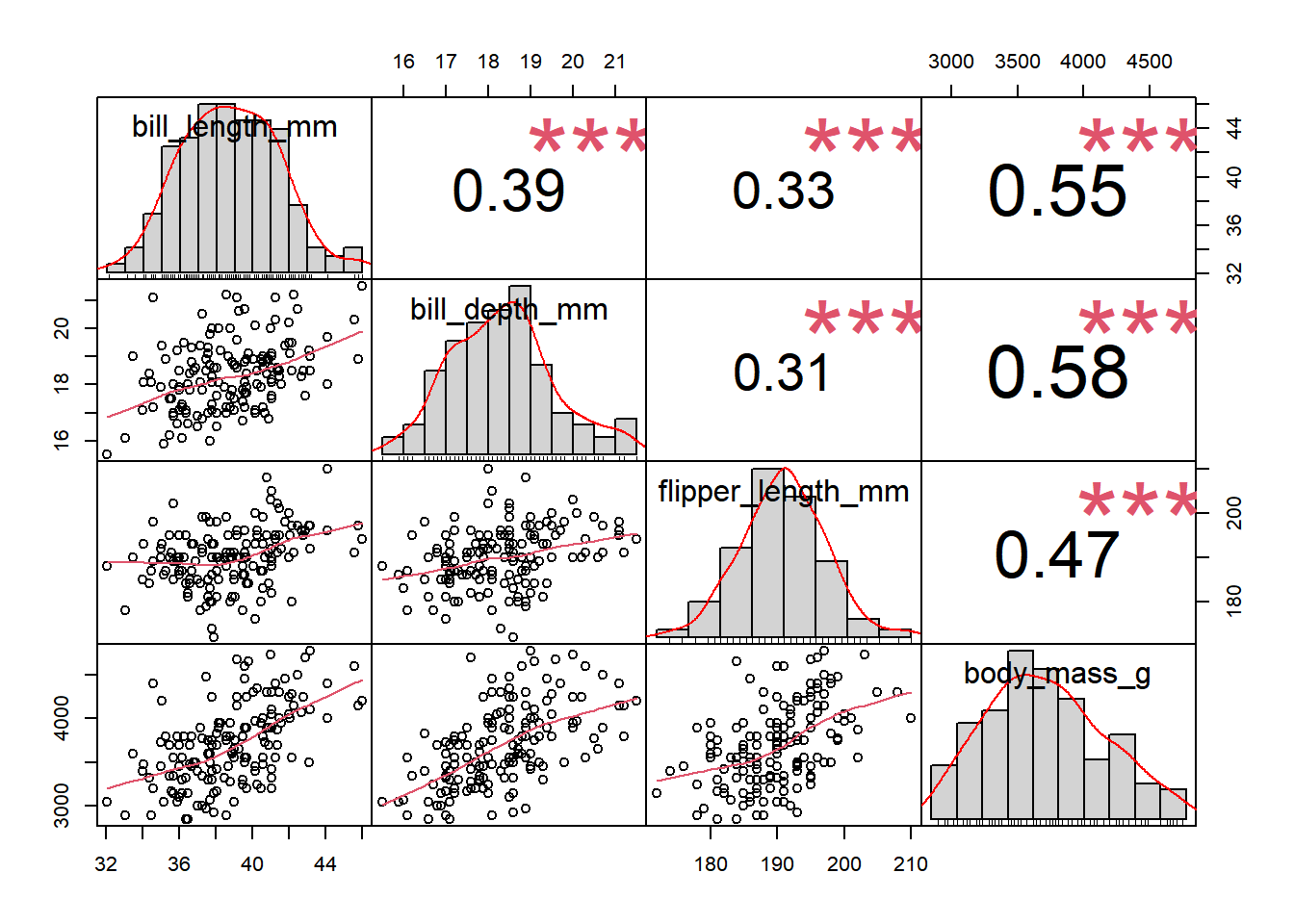
5.2.6 Regressão
A regressão linear é uma análise que avalia se uma ou mais variáveis preditoras explicam a variável dependente. A regressão tem cinco pressupostos principais:
Relação linear Normalidade Nenhuma ou pouca multicolinearidade Sem auto-correlação Homocedasticidade (Homogeneidade de Variância)
Na regressão linear requer pelo menos 20 casos por variável independente na análise.
Vamos transformar as variáveis species e island em uma variável numérica, utilizando mutate e ifelse:
dados<-mutate(dados, especie= ifelse(grepl("Adelie",species), 0,
ifelse(grepl("Gentoo", species),1,2)))
dados<-mutate(dados, ilha= ifelse(grepl("Torgersen",island), 0,
ifelse(grepl("Biscoe", island),1,2)))
head(dados)## species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
## 1 Adelie Torgersen 39.1 18.7 181 3750
## 2 Adelie Torgersen 39.5 17.4 186 3800
## 3 Adelie Torgersen 40.3 18.0 195 3250
## 4 Adelie Torgersen NA NA NA NA
## 5 Adelie Torgersen 36.7 19.3 193 3450
## 6 Adelie Torgersen 39.3 20.6 190 3650
## sex year especie ilha
## 1 male 2007 0 0
## 2 female 2007 0 0
## 3 female 2007 0 0
## 4 <NA> 2007 0 0
## 5 female 2007 0 0
## 6 male 2007 0 0O grepl é uma função que procura correspondências de uma string ou vetor de string. O método grepl() pega um padrão e retorna TRUE se uma string contiver o padrão, caso contrário, FALSE.
No R temos duas funções para fazer a regressão:
lm, Usada para ajustar modelos lineares
lm(formula, data, …)
fórmula: (y ~ x1 + x2)
glm, Usada para ajustar modelos lineares generalizados. glm(formula, family=gaussian, data, …) family: A família estatística a ser usada para ajustar o modelo. O padrão é gaussiano, mas outras opções incluem binomial, gama e poisson, entre outros.
Fazendo a regressão com a função glm, como variável dependente body_mass_g e como variáveis independentes especie e ilha:
##
## Call:
## glm(formula = body_mass_g ~ especie + ilha, family = gaussian,
## data = dados)
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4415.04 82.42 53.568 < 2e-16 ***
## especie 390.51 59.15 6.602 1.57e-10 ***
## ilha -419.48 66.06 -6.350 6.92e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for gaussian family taken to be 552729.2)
##
## Null deviance: 219307697 on 341 degrees of freedom
## Residual deviance: 187375185 on 339 degrees of freedom
## (2 observations deleted due to missingness)
## AIC: 5497.7
##
## Number of Fisher Scoring iterations: 25.2.7 ANOVA
Análise de variância (ANOVA)
A análise da variância (ou ANOVA, de “ANalysis Of VAriance”) é uma poderosa técnica estatística desenvolvida por R.A. Fisher. Ela consiste em um procedimento que decompõe, em vários componentes identificáveis, a variação total entre os valores obtidos no experimento. Cada componente atribui a variação a uma causa ou fonte de variação diferente: o número de causas de variação ou “fatores” depende do delineamento da investigação.
Um dos modelos mais simples de ANOVA é o que analisa os dados de um delineamento completamente casualizado ou ANOVA a um critério de classificação (One way ANOVA). Neste modelo, a variação global é subdividida em duas frações. A primeira é a variação entre as médias dos vários grupos, quando comparadas com a média geral de todos os indivíduos do experimento e representa o efeito dos diferentes tratamentos. A outra é a variação observada entre as unidades experimentais de um mesmo grupo ou tratamento, com relação à média desse grupo: tratam-se das diferenças individuais, ou aleatórias, nas respostas.
Resumidamente:
Variação total = Variação entre tratamentos + Variação dentro dos tratamentos.
A variação entre grupos experimentais ou tratamentos é estimada pela variância entre tratamentos ou simplesmente Variância Entre. A variação dentro do mesmo tratamento é estimada pela média das variâncias de cada grupo: é por isso chamada variancia média dentro dos grupos ou Variância Dentro. Como ela representa também a fração da variabilidade que não é explicada pelo efeito dos tratamentos, é também chamada Variância Residual ou, ainda, Variância do Erro Experimental.
O teste de comparação entre os efeitos dos tratamentos baseia-se na pressuposição de que os k tratamentos A,B,… podem originar médias diferentes, mas a entre os indivíduos (o) é igual em todas as populações que estão sendo comparadas. Em outras palavras, deseja-se testar a hipótese de igualdade estre médias.
Antes de fazer a ANOVA, vamos fazer o teste de Bartlett para verificar a variância, utilizando o pacote car (Fox and Weisberg 2019):
##
## Bartlett test of homogeneity of variances
##
## data: bill_length_mm by species
## Bartlett's K-squared = 5.6179, df = 2, p-value = 0.06027Como não foi significativo, vamos fazer a ANOVA com a função aov:
## Df Sum Sq Mean Sq F value Pr(>F)
## species 2 7194 3597 410.6 <2e-16 ***
## Residuals 339 2970 9
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 2 observations deleted due to missingnessO resultado foi significativo, mas com a ANOVA sabemos que tem diferença, mas não sabemos entre quais grupos,então podemos usar o teste de Duncan do pacote agricolae (de Mendiburu 2023):
##
## Study: res_anova ~ "species"
##
## Duncan's new multiple range test
## for bill_length_mm
##
## Mean Square Error: 8.760732
##
## species, means
##
## bill_length_mm std r se Min Max Q25 Q50 Q75
## Adelie 38.79139 2.663405 151 0.2408694 32.1 46.0 36.75 38.80 40.750
## Chinstrap 48.83382 3.339256 68 0.3589349 40.9 58.0 46.35 49.55 51.075
## Gentoo 47.50488 3.081857 123 0.2668810 40.9 59.6 45.30 47.30 49.550
##
## Groups according to probability of means differences and alpha level( 0.05 )
##
## Means with the same letter are not significantly different.
##
## bill_length_mm groups
## Chinstrap 48.83382 a
## Gentoo 47.50488 b
## Adelie 38.79139 cPara vizualizar essas diferenças podemos fazer gráficos. Para esse exemplo, vamos usar o pacote ggpubr (Kassambara 2023):
library("ggpubr")
ggline(dados, x = "species", y = "bill_length_mm",
add = c("mean_se", "jitter"),
ylab = "bill_length_mm", xlab = "espécies",color = "species")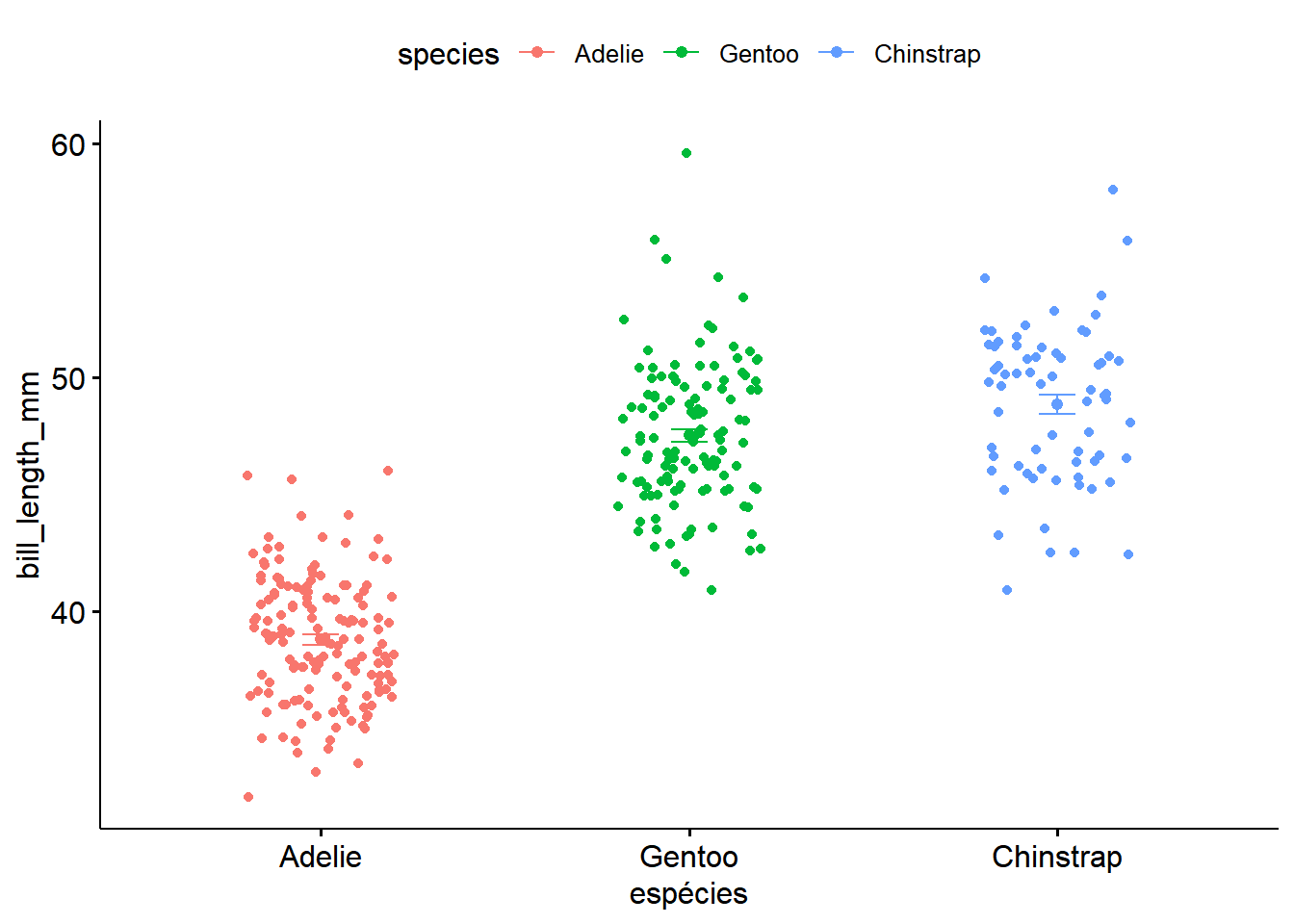
ggboxplot(dados, x = "species", y = "bill_length_mm",
color = "species", palette = c("#00AFBB", "#E7B800", "#FC4E07"),
ylab = "bill_length_mm", xlab = "species")
Para dados não paramétricos, podemos usar o teste de Kruskal-Wallis
##
## Kruskal-Wallis rank sum test
##
## data: bill_length_mm by species
## Kruskal-Wallis chi-squared = 244.14, df = 2, p-value < 2.2e-16Para esse caso, podemos o usar o teste de Dunn, do pacote FSA (Ogle et al. 2023) para identificar as diferenças:
## Comparison Z P.unadj P.adj
## 1 Adelie - Chinstrap -12.753511 2.980163e-37 4.470244e-37
## 2 Adelie - Gentoo -13.135630 2.057716e-39 6.173147e-39
## 3 Chinstrap - Gentoo 1.767498 7.714481e-02 7.714481e-025.3 Visualização de resultados estatísticos
Vamos usar alguns pacotes que vão ajudar na análise de dados e também gerar um relatório com tabelas e gráficos em um documento html ou doc.
O pacote DataExplorer (Cui 2020) permite fazer diversas análises. Podemos ter uma visão inicial dos dados com a função introduce
## Warning: package 'DataExplorer' was built under R version 4.3.3## rows columns discrete_columns continuous_columns all_missing_columns
## 1 344 10 3 7 0
## total_missing_values complete_rows total_observations memory_usage
## 1 19 333 3440 31032Também podemos ver na forma de gráficos:
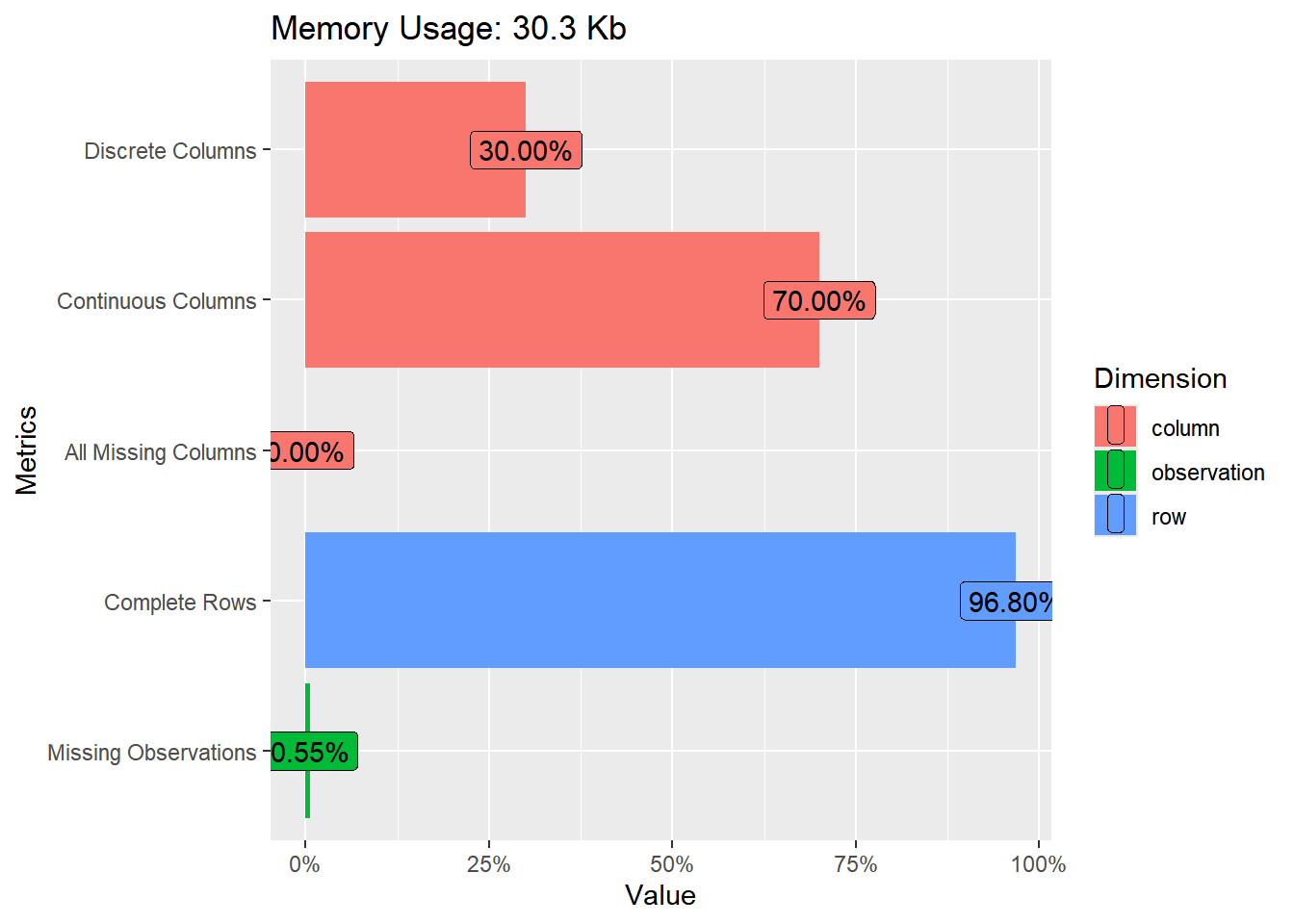
Os dados categóricos podem ser plotados:
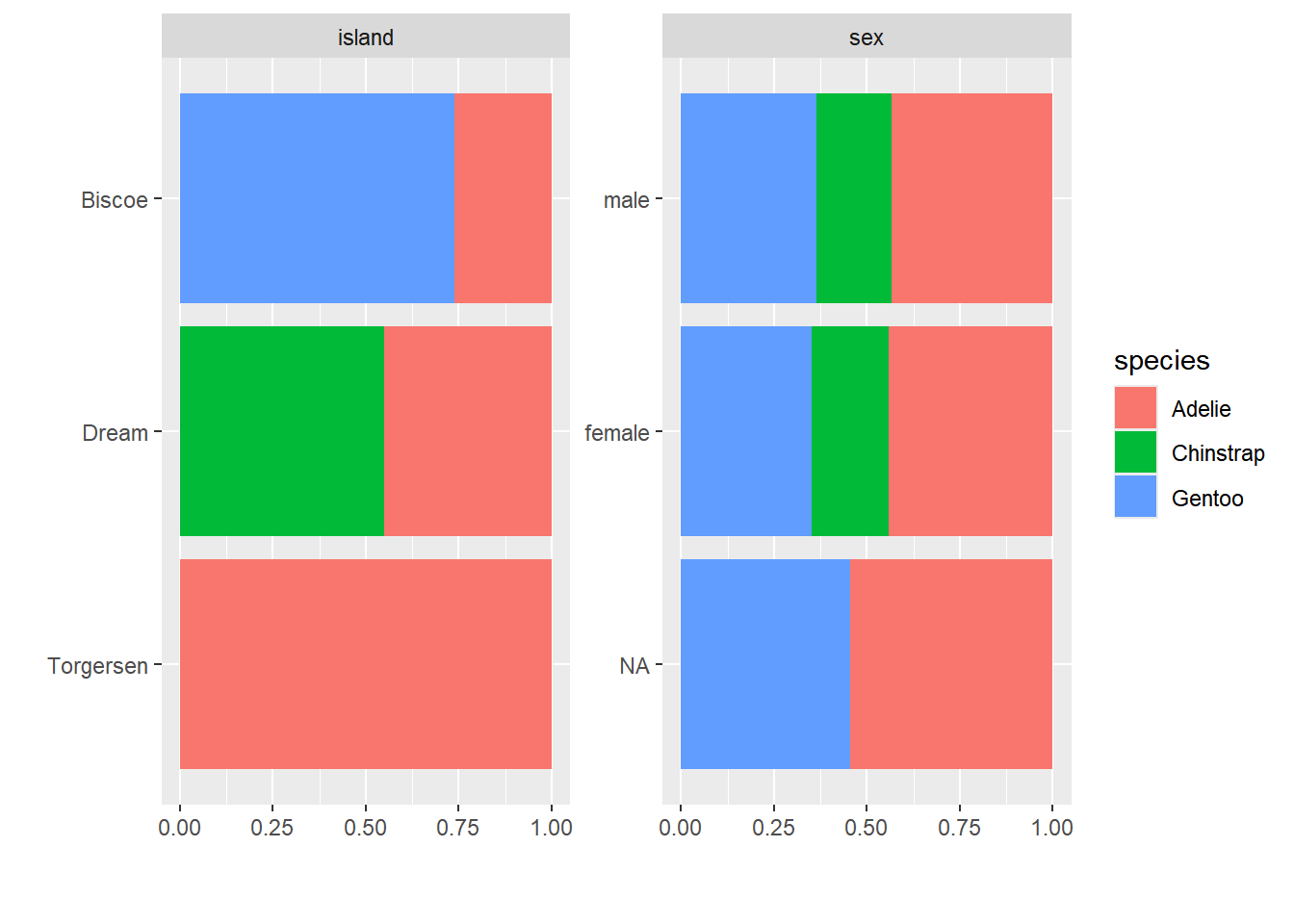
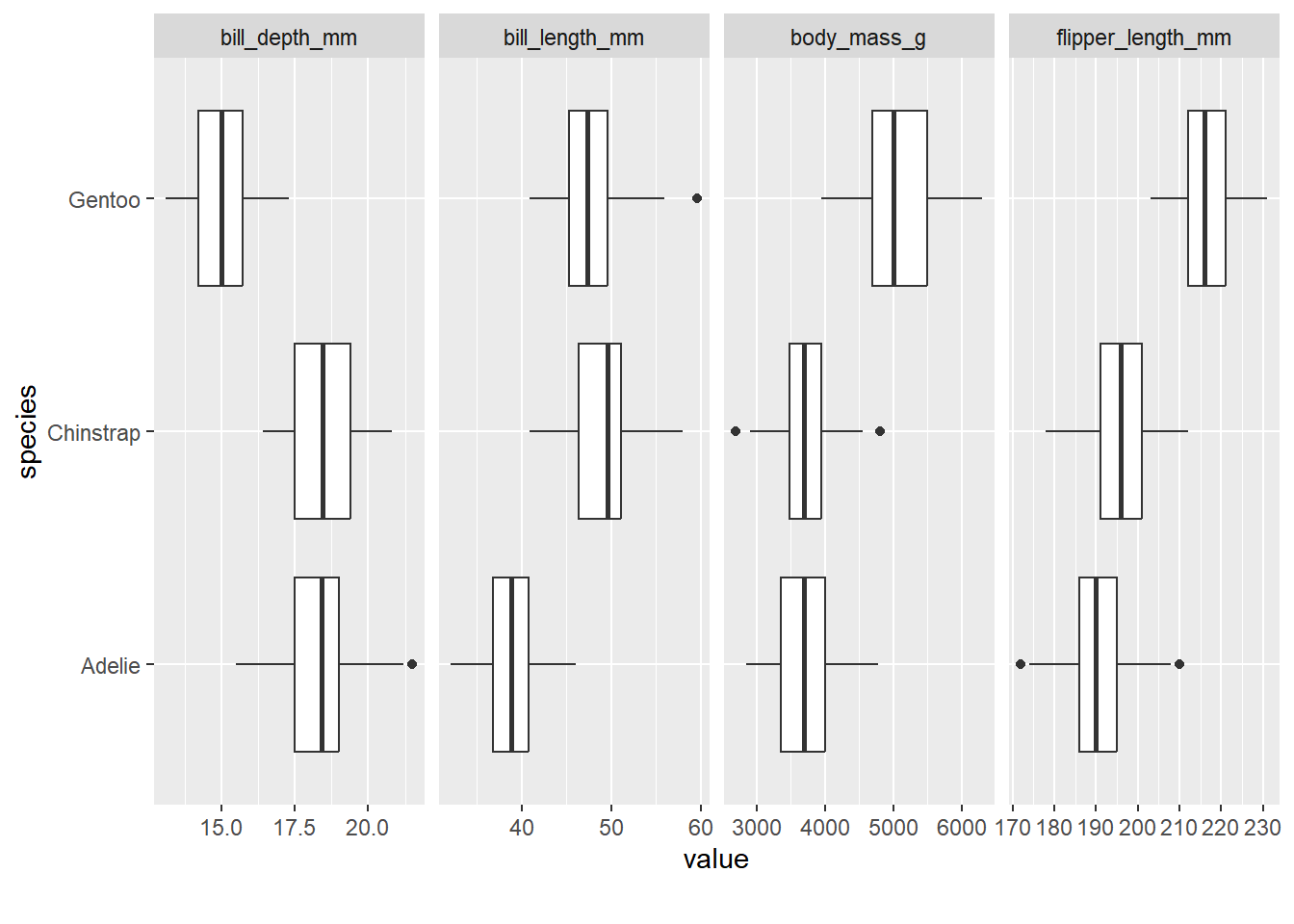
Outro pacote muito útil é o ggstatsplot (Patil 2021), com o qual podemos unir gráficos e análises estatísticas. Por exemplo, para dados categóricos:
## Warning: package 'ggstatsplot' was built under R version 4.3.3## You can cite this package as:
## Patil, I. (2021). Visualizations with statistical details: The 'ggstatsplot' approach.
## Journal of Open Source Software, 6(61), 3167, doi:10.21105/joss.03167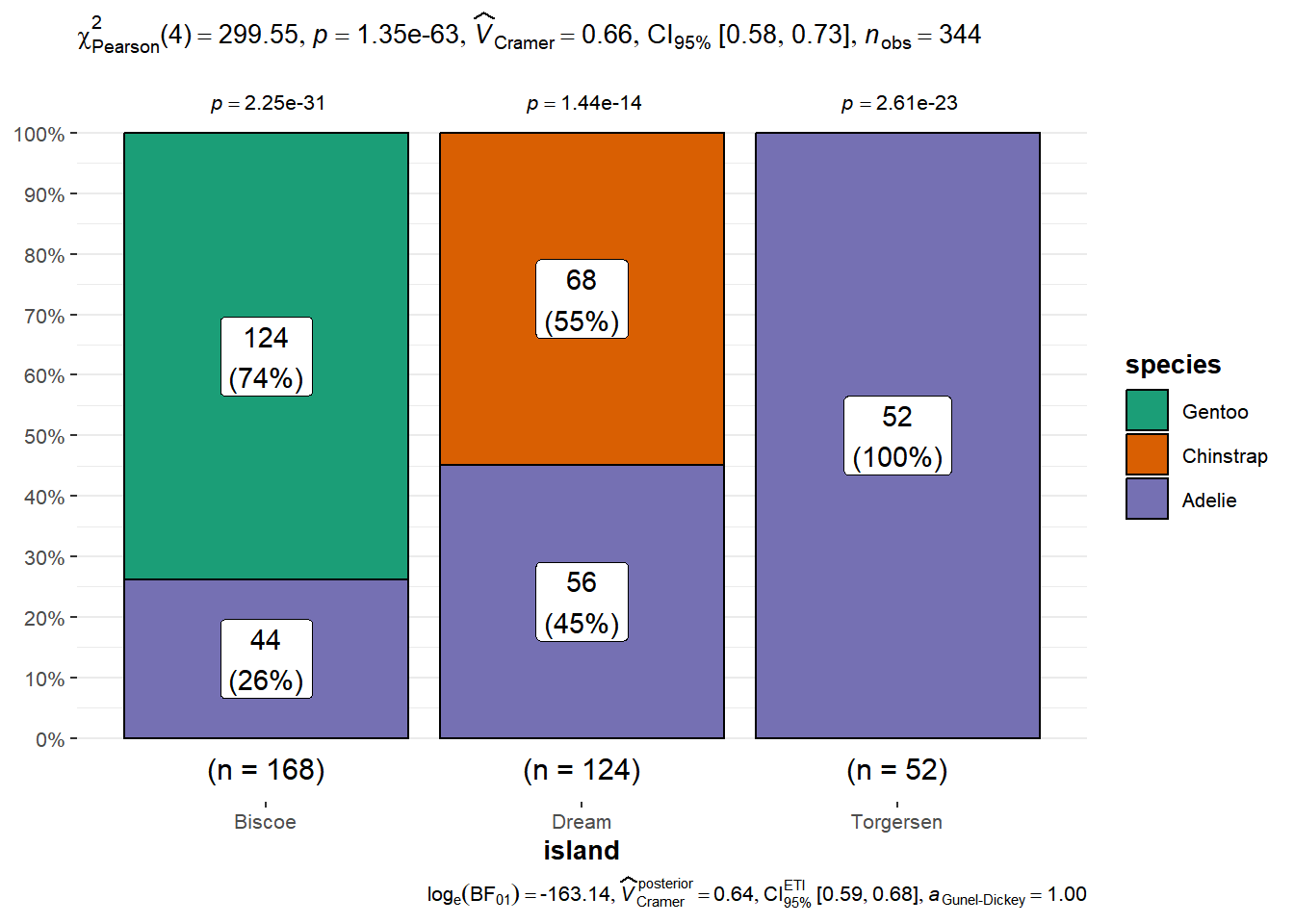
Ou para dados numéricos:
## Warning in min(x): nenhum argumento não faltante para min; retornando Inf## Warning in max(x): nenhum argumento não faltante para max; retornando -Inf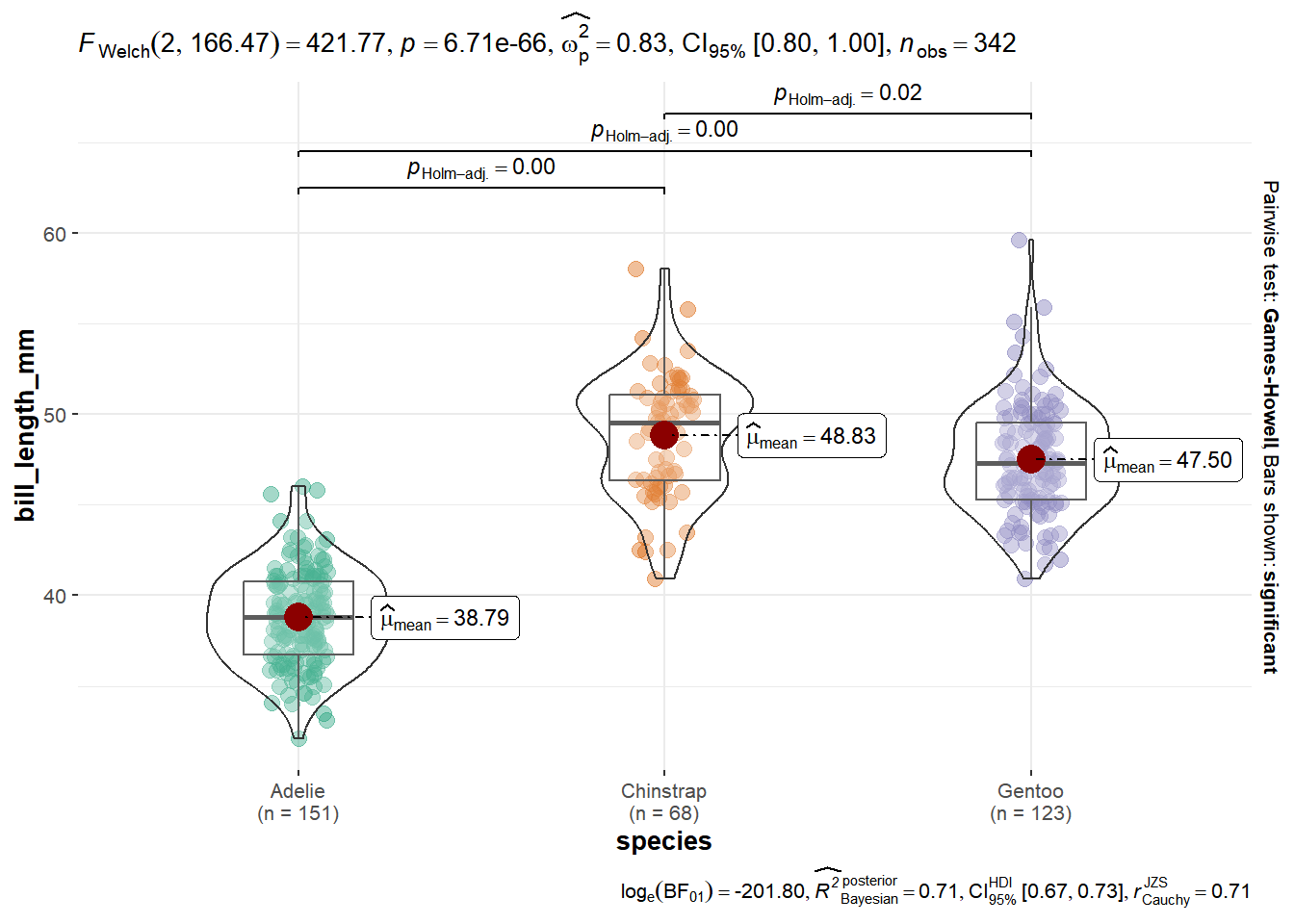
Onde em type temos as seguintes opções: p (parametric), np (non parametric), r (robust), bf (bayes).
O pacote dlookr (Ryu 2023) descreve cada variável e o pacote flextable (Gohel and Skintzos 2023) permite criar tabelas com os resultados. Podemos fazer diversas análises usando a função describe.
described_variables | n | na | mean | sd | se_mean | IQR | skewness | kurtosis | p00 | p01 | p05 | p10 | p20 | p25 | p30 | p40 | p50 | p60 | p70 | p75 | p80 | p90 | p95 | p99 | p100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
bill_length_mm | 342 | 2 | 43.921930 | 5.4595837 | 0.29522048 | 9.275 | 0.05311807 | -0.8760270 | 32.1 | 34.041 | 35.7 | 36.6 | 38.34 | 39.225 | 40.20 | 42.0 | 44.45 | 46.0 | 47.37 | 48.5 | 49.38 | 50.8 | 51.995 | 55.513 | 59.6 |
bill_depth_mm | 342 | 2 | 17.151170 | 1.9747932 | 0.10678458 | 3.100 | -0.14346463 | -0.9068661 | 13.1 | 13.441 | 13.9 | 14.3 | 15.00 | 15.600 | 15.93 | 16.8 | 17.30 | 17.9 | 18.50 | 18.7 | 18.90 | 19.5 | 20.000 | 21.100 | 21.5 |
flipper_length_mm | 342 | 2 | 200.915205 | 14.0617137 | 0.76037039 | 23.000 | 0.34568183 | -0.9842729 | 172.0 | 178.000 | 181.0 | 185.0 | 188.00 | 190.000 | 191.00 | 194.0 | 197.00 | 203.0 | 210.00 | 213.0 | 215.00 | 220.9 | 225.000 | 230.000 | 231.0 |
body_mass_g | 342 | 2 | 4,201.754386 | 801.9545357 | 43.36473482 | 1,200.000 | 0.47032933 | -0.7192219 | 2,700.0 | 2,900.000 | 3,150.0 | 3,300.0 | 3,475.00 | 3,550.000 | 3,650.00 | 3,800.0 | 4,050.00 | 4,300.0 | 4,650.00 | 4,750.0 | 4,950.00 | 5,400.0 | 5,650.000 | 5,979.500 | 6,300.0 |
year | 344 | 0 | 2,008.029070 | 0.8183559 | 0.04412279 | 2.000 | -0.05372777 | -1.5049366 | 2,007.0 | 2,007.000 | 2,007.0 | 2,007.0 | 2,007.00 | 2,007.000 | 2,007.00 | 2,008.0 | 2,008.00 | 2,008.0 | 2,009.00 | 2,009.0 | 2,009.00 | 2,009.0 | 2,009.000 | 2,009.000 | 2,009.0 |
especie | 344 | 0 | 0.755814 | 0.7626262 | 0.04111805 | 1.000 | 0.44393545 | -1.1582383 | 0.0 | 0.000 | 0.0 | 0.0 | 0.00 | 0.000 | 0.00 | 0.0 | 1.00 | 1.0 | 1.00 | 1.0 | 1.00 | 2.0 | 2.000 | 2.000 | 2.0 |
ilha | 344 | 0 | 1.209302 | 0.6849703 | 0.03693113 | 1.000 | -0.29384888 | -0.8699712 | 0.0 | 0.000 | 0.0 | 0.0 | 1.00 | 1.000 | 1.00 | 1.0 | 1.00 | 1.0 | 2.00 | 2.0 | 2.00 | 2.0 | 2.000 | 2.000 | 2.0 |
Também podemos usar a função diagnose_numeric:
variables | min | Q1 | mean | median | Q3 | max | zero | minus | outlier |
|---|---|---|---|---|---|---|---|---|---|
bill_length_mm | 32.1 | 39.225 | 43.921930 | 44.45 | 48.5 | 59.6 | 0 | 0 | 0 |
bill_depth_mm | 13.1 | 15.600 | 17.151170 | 17.30 | 18.7 | 21.5 | 0 | 0 | 0 |
flipper_length_mm | 172.0 | 190.000 | 200.915205 | 197.00 | 213.0 | 231.0 | 0 | 0 | 0 |
body_mass_g | 2,700.0 | 3,550.000 | 4,201.754386 | 4,050.00 | 4,750.0 | 6,300.0 | 0 | 0 | 0 |
year | 2,007.0 | 2,007.000 | 2,008.029070 | 2,008.00 | 2,009.0 | 2,009.0 | 0 | 0 | 0 |
especie | 0.0 | 0.000 | 0.755814 | 1.00 | 1.0 | 2.0 | 152 | 0 | 0 |
ilha | 0.0 | 1.000 | 1.209302 | 1.00 | 2.0 | 2.0 | 52 | 0 | 0 |
O pacote SmartEDA (Dayanand Ubrangala et al. 2022) também faz um resumo descritivo das variáveis numéricas
## Warning: package 'SmartEDA' was built under R version 4.3.3Vname | Group | TN | nNeg | nZero | nPos | NegInf | PosInf | NA_Value | Per_of_Missing | sum | min | max | mean | median | SD | CV | IQR | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
bill_depth_mm | All | 344 | 0 | 0 | 342 | 0 | 0 | 2 | 0.58 | 5,865.7 | 13.1 | 21.5 | 17.15 | 17.30 | 1.97 | 0.12 | 3.10 | -0.14 | -0.91 |
bill_length_mm | All | 344 | 0 | 0 | 342 | 0 | 0 | 2 | 0.58 | 15,021.3 | 32.1 | 59.6 | 43.92 | 44.45 | 5.46 | 0.12 | 9.27 | 0.05 | -0.88 |
body_mass_g | All | 344 | 0 | 0 | 342 | 0 | 0 | 2 | 0.58 | 1,437,000.0 | 2,700.0 | 6,300.0 | 4,201.75 | 4,050.00 | 801.95 | 0.19 | 1,200.00 | 0.47 | -0.73 |
flipper_length_mm | All | 344 | 0 | 0 | 342 | 0 | 0 | 2 | 0.58 | 68,713.0 | 172.0 | 231.0 | 200.92 | 197.00 | 14.06 | 0.07 | 23.00 | 0.34 | -0.99 |
Em by temos as opções A: All, G: by group e GA: by group e Overall:
Vname | Group | TN | nNeg | nZero | nPos | NegInf | PosInf | NA_Value | Per_of_Missing | sum | min | max | mean | median | SD | CV | IQR | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
bill_depth_mm | species:Adelie | 152 | 0 | 0 | 151 | 0 | 0 | 1 | 0.66 | 2,770.3 | 15.5 | 21.5 | 18.35 | 18.40 | 1.22 | 0.07 | 1.50 | 0.32 | -0.10 |
bill_depth_mm | species:Gentoo | 124 | 0 | 0 | 123 | 0 | 0 | 1 | 0.81 | 1,842.8 | 13.1 | 17.3 | 14.98 | 15.00 | 0.98 | 0.07 | 1.50 | 0.32 | -0.61 |
bill_depth_mm | species:Chinstrap | 68 | 0 | 0 | 68 | 0 | 0 | 0 | 0.00 | 1,252.6 | 16.4 | 20.8 | 18.42 | 18.45 | 1.14 | 0.06 | 1.90 | 0.01 | -0.90 |
bill_length_mm | species:Adelie | 152 | 0 | 0 | 151 | 0 | 0 | 1 | 0.66 | 5,857.5 | 32.1 | 46.0 | 38.79 | 38.80 | 2.66 | 0.07 | 4.00 | 0.16 | -0.19 |
bill_length_mm | species:Gentoo | 124 | 0 | 0 | 123 | 0 | 0 | 1 | 0.81 | 5,843.1 | 40.9 | 59.6 | 47.50 | 47.30 | 3.08 | 0.06 | 4.25 | 0.64 | 1.20 |
bill_length_mm | species:Chinstrap | 68 | 0 | 0 | 68 | 0 | 0 | 0 | 0.00 | 3,320.7 | 40.9 | 58.0 | 48.83 | 49.55 | 3.34 | 0.07 | 4.73 | -0.09 | -0.05 |
body_mass_g | species:Adelie | 152 | 0 | 0 | 151 | 0 | 0 | 1 | 0.66 | 558,800.0 | 2,850.0 | 4,775.0 | 3,700.66 | 3,700.00 | 458.57 | 0.12 | 650.00 | 0.28 | -0.59 |
body_mass_g | species:Gentoo | 124 | 0 | 0 | 123 | 0 | 0 | 1 | 0.81 | 624,350.0 | 3,950.0 | 6,300.0 | 5,076.02 | 5,000.00 | 504.12 | 0.10 | 800.00 | 0.07 | -0.74 |
body_mass_g | species:Chinstrap | 68 | 0 | 0 | 68 | 0 | 0 | 0 | 0.00 | 253,850.0 | 2,700.0 | 4,800.0 | 3,733.09 | 3,700.00 | 384.34 | 0.10 | 462.50 | 0.24 | 0.46 |
flipper_length_mm | species:Adelie | 152 | 0 | 0 | 151 | 0 | 0 | 1 | 0.66 | 28,683.0 | 172.0 | 210.0 | 189.95 | 190.00 | 6.54 | 0.03 | 9.00 | 0.09 | 0.28 |
flipper_length_mm | species:Gentoo | 124 | 0 | 0 | 123 | 0 | 0 | 1 | 0.81 | 26,714.0 | 203.0 | 231.0 | 217.19 | 216.00 | 6.48 | 0.03 | 9.00 | 0.39 | -0.60 |
flipper_length_mm | species:Chinstrap | 68 | 0 | 0 | 68 | 0 | 0 | 0 | 0.00 | 13,316.0 | 178.0 | 212.0 | 195.82 | 196.00 | 7.13 | 0.04 | 10.00 | -0.01 | -0.04 |
Vname | Group | TN | nNeg | nZero | nPos | NegInf | PosInf | NA_Value | Per_of_Missing | sum | min | max | mean | median | SD | CV | IQR | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
bill_depth_mm | species:All | 344 | 0 | 0 | 342 | 0 | 0 | 2 | 0.58 | 5,865.7 | 13.1 | 21.5 | 17.15 | 17.30 | 1.97 | 0.12 | 3.10 | -0.14 | -0.91 |
bill_depth_mm | species:Adelie | 152 | 0 | 0 | 151 | 0 | 0 | 1 | 0.66 | 2,770.3 | 15.5 | 21.5 | 18.35 | 18.40 | 1.22 | 0.07 | 1.50 | 0.32 | -0.10 |
bill_depth_mm | species:Gentoo | 124 | 0 | 0 | 123 | 0 | 0 | 1 | 0.81 | 1,842.8 | 13.1 | 17.3 | 14.98 | 15.00 | 0.98 | 0.07 | 1.50 | 0.32 | -0.61 |
bill_depth_mm | species:Chinstrap | 68 | 0 | 0 | 68 | 0 | 0 | 0 | 0.00 | 1,252.6 | 16.4 | 20.8 | 18.42 | 18.45 | 1.14 | 0.06 | 1.90 | 0.01 | -0.90 |
bill_length_mm | species:All | 344 | 0 | 0 | 342 | 0 | 0 | 2 | 0.58 | 15,021.3 | 32.1 | 59.6 | 43.92 | 44.45 | 5.46 | 0.12 | 9.27 | 0.05 | -0.88 |
bill_length_mm | species:Adelie | 152 | 0 | 0 | 151 | 0 | 0 | 1 | 0.66 | 5,857.5 | 32.1 | 46.0 | 38.79 | 38.80 | 2.66 | 0.07 | 4.00 | 0.16 | -0.19 |
bill_length_mm | species:Gentoo | 124 | 0 | 0 | 123 | 0 | 0 | 1 | 0.81 | 5,843.1 | 40.9 | 59.6 | 47.50 | 47.30 | 3.08 | 0.06 | 4.25 | 0.64 | 1.20 |
bill_length_mm | species:Chinstrap | 68 | 0 | 0 | 68 | 0 | 0 | 0 | 0.00 | 3,320.7 | 40.9 | 58.0 | 48.83 | 49.55 | 3.34 | 0.07 | 4.73 | -0.09 | -0.05 |
body_mass_g | species:All | 344 | 0 | 0 | 342 | 0 | 0 | 2 | 0.58 | 1,437,000.0 | 2,700.0 | 6,300.0 | 4,201.75 | 4,050.00 | 801.95 | 0.19 | 1,200.00 | 0.47 | -0.73 |
body_mass_g | species:Adelie | 152 | 0 | 0 | 151 | 0 | 0 | 1 | 0.66 | 558,800.0 | 2,850.0 | 4,775.0 | 3,700.66 | 3,700.00 | 458.57 | 0.12 | 650.00 | 0.28 | -0.59 |
body_mass_g | species:Gentoo | 124 | 0 | 0 | 123 | 0 | 0 | 1 | 0.81 | 624,350.0 | 3,950.0 | 6,300.0 | 5,076.02 | 5,000.00 | 504.12 | 0.10 | 800.00 | 0.07 | -0.74 |
body_mass_g | species:Chinstrap | 68 | 0 | 0 | 68 | 0 | 0 | 0 | 0.00 | 253,850.0 | 2,700.0 | 4,800.0 | 3,733.09 | 3,700.00 | 384.34 | 0.10 | 462.50 | 0.24 | 0.46 |
flipper_length_mm | species:All | 344 | 0 | 0 | 342 | 0 | 0 | 2 | 0.58 | 68,713.0 | 172.0 | 231.0 | 200.92 | 197.00 | 14.06 | 0.07 | 23.00 | 0.34 | -0.99 |
flipper_length_mm | species:Adelie | 152 | 0 | 0 | 151 | 0 | 0 | 1 | 0.66 | 28,683.0 | 172.0 | 210.0 | 189.95 | 190.00 | 6.54 | 0.03 | 9.00 | 0.09 | 0.28 |
flipper_length_mm | species:Gentoo | 124 | 0 | 0 | 123 | 0 | 0 | 1 | 0.81 | 26,714.0 | 203.0 | 231.0 | 217.19 | 216.00 | 6.48 | 0.03 | 9.00 | 0.39 | -0.60 |
flipper_length_mm | species:Chinstrap | 68 | 0 | 0 | 68 | 0 | 0 | 0 | 0.00 | 13,316.0 | 178.0 | 212.0 | 195.82 | 196.00 | 7.13 | 0.04 | 10.00 | -0.01 | -0.04 |
Podemos ter os dados de saída de diversas análises estatísticas organizados com o pacote report (Makowski et al. 2023).
library(report)
dados2<-na.omit(dados)
flextable(report_table(wilcox.test(dados2$bill_length_mm~dados2$sex))) Parameter1 | Parameter2 | W | p | Method | Alternative | r_rank_biserial | rank_biserial_CI_low | rank_biserial_CI_high |
|---|---|---|---|---|---|---|---|---|
dados2$bill_length_mm | dados2$sex | 8,178 | 0.00000000009901184 | Wilcoxon rank sum test | two.sided | -0.4099567 | -0.5078078 | -0.301662 |
Também podemos personalizar as tabelas geradas pelo pacote flextable.
flextable(report_table(wilcox.test(dados2$bill_length_mm~dados2$sex)))%>%
colformat_double(digits = 2)%>%
style(i = 1, j = 4, pr_t = fp_text_default(bold = T))Parameter1 | Parameter2 | W | p | Method | Alternative | r_rank_biserial | rank_biserial_CI_low | rank_biserial_CI_high |
|---|---|---|---|---|---|---|---|---|
dados2$bill_length_mm | dados2$sex | 8,178.00 | 0.00 | Wilcoxon rank sum test | two.sided | -0.41 | -0.51 | -0.30 |