Chapter 2 Theory
A necessity theory is a theory that employs causal necessity logic for describing the causal relationships between all, or a selection of the concepts of a theory (Bokrantz & Dul, 2023). Necessity theorizing is formulating necessity theory using necessity logic when describing causal relationships between concepts.
2.1 The four parts of a theory
A theory –including a necessity theory– consists of four parts: concepts, propositions, focal unit and theoretical domain. The concepts are the variable parts of a theory that can increase or decrease. In NCA the independent concepts are called ‘conditions’ and the dependent concepts ‘outcomes’. A proposition describes the causal relationship between the concepts. In NCA the causal relationship is a necessity relationship: ‘\(X\) is necessary for \(Y\)’. The focal unit is the object to which the theory applies: country, person, firm, project. etc. The theoretical domain is the set of cases of the focal unit where the theory is supposed to hold. A case is one particular example of the focal unit: a specific country, a specific person, etc.
The four characteristics of theory on which the nca.example data set of the NCA software is based are:
Focal unit: country.
Concepts:
Independent concepts (conditions): Individualism, Risk taking.
Dependent concept (outcome): Innovation performance.
Propositions: Individualism is necessary for Innovation performance. Risk taking is necessary for Innovation performance.
Theoretical domain: all countries of the world.
In theory testing research, empirical data are used to test the propositions. The theoretical concepts are operationalized into variables that can be measured, the propositions are operationalized into hypotheses consisting of variables with their expected relationship, the focal unit becomes the unit of analysis, and cases are selected from the theoretical domain. For the case selection usually a population of cases is identified in the theoretical domain and a sample is taken from this population, but purposive selection of cases is possibe as well. From the sample a dataset is obtained with variables scores of the cases.
2.2 Formulation of necessity hypotheses
The propositions (or the operationalized hypotheses) are the core elements of a theory. They describe the expected causal relationships between the concepts. Most theories express the causal relationship in terms of probabilistic sufficiency: cause \(X\) likely changes effect \(Y\). Such cause contributes to the outcome ‘on average’. Other theories express the causal relationship deterministically or typically : cause \(X\) is (typically) necessary or sufficient for \(Y\). These different causal perspectives are discussed in Dul (2024a). NCA employs a deterministic (no exceptions) or typicality (with exceptions) causal perspective about necessity.
NCA starts with formulating a hypothesis that a condition is a necessary cause for the outcome. In some fields the existence of a causal necessity relationship is widely known and accepted. An example is the psychological theory that intelligence is necessary for creativity. This hypothesis was proposed in the 1960’s (Guilford, 1967) and is still widely around. Until recently, this theory could not be tested with a specific necessity method. When NCA became available it was possible to ensure theory-method fit by testing the hypothesis with NCA, as was done by Karwowski et al. (2016).
In other fields, theories that are broadly accepted include systematic formulations of necessity. Some of these establised theories were recently tested with NCA. Examples are the Ability Motivation, Opportunity model – AMO (or Motivation, Opportunity, Ability model - MOA) of human behavior (e.g., Tuuli & Rhee, 2021), the Theory of Planned Behavior – TPB (Frommeyer et al., 2022), the Technology Acceptance Model – TAM (e.g., Richter, Schubring, et al., 2020) and the Self-Determination Theory – SDT (e.g., Cassia & Magno, 2024). Other established necessity theories have never been tested with NCA, including Porter’s theory on competitive advantage of nations (Porter, 1985), Wernerfelt’s resource-based view of the firm (Wernerfelt, 1984), Teece’s theory on dynamic capabilities (Teece et al., 1997), Rogers’ theory on person-centered psychotherapy (Rogers, 1957) and Turner’s framework for project management success (Turner, 2009).
Yet, necessity causality (even if explicitly formulated) is not widely recognized and when these theories are being tested, probabilistic sufficiency causality is (implicitly) assumed. NCA gives the opportunity to test such theories while ensuring theory-method fit.
In most research fields necessity formulations of the relationships of interest are scattered around in the literature. Although necessity causality exists in virtually all research areas, and necessity statements are commonly made, the necessity statements are usually not part of the theories. NCA gives the researcher an opportunity to formalize the theoretical necessity statements and test them with an appropriate method.
2.2.1 Sources with potential necessary conditions
Four sources can be used for formulating necessary condition hypotheses. First, existing necessity statements in the literature can be identified. Although several necessity statements may use the word ‘necessity’ rather loosely as synonym for ‘important’, many necessity statements refer to necessity logic and causality. Common words referring to a condition that is necessity for an outcome are listed in Table 2.1. Several words reflect that the necessary condition must be present to have the outcome (enablers); other words reflect that the absence of the necessary conditions guarantees the absence of the outcome (constaints).
| Enablers (The presence of X …) | Constraints (The absence of X …) |
|---|---|
| X is necessary for Y | X constrains Y |
| X is needed for Y | X limits Y |
| X is critical for Y | X blocks Y |
| X is crucial for Y | X bounds Y |
| X is essential for Y | X restricts Y |
| X is indispensable for Y | X is a barrier for Y |
| X is a prerequisite for Y | X is a bottleneck for Y |
| X is a requirement for Y | Without X there cannot be Y |
| X is a conditio sine qua non for Y | |
| X is a pre-condition for Y | |
| X allows Y | |
| X enables Y | |
| There must be X to have Y | |
| Y requires X |
Second, when ‘important’ contributing causal factors for a outcome of interest have been identified with conventional methods, several of them could also be necessary conditions. For example, when a researcher formulates an additive theory with generic causes (to be analysed with regression analysis) arguments are provided why a concept is an important contributor to an outcome. As a standard, the arguments imply sufficiency logic (‘\(X\) produces \(Y\)’), but as an alternative, the relationship could also be described with necessity logic: an important factor that cannot be compensated for. Not only independent concepts but also mediator and moderator concepts in additive theories could be candidate necessary conditions. In other words, when current additive theories state that concepts are ‘important’ contributing concepts they may or may not (also) be necessary. But also contributing concepts that are considered ‘unimportant’ according to additive theories could be necessary.
Third, ‘critical’ and ‘bottleneck’ factors in practice could be candidate necessary conditions to be included in the theory. Practitioners commonly act upon ‘critical success factors’ or ‘must have’ factors (versus ‘nice to have’ factors). When such factor does not have the required level it can become a bottleneck on which the practitioner must act to ensure a desired outcome. Practitioners often have a ‘theory in use’ (Dul & Hak, 2008) in which they argue why a factor is related to an outcome. Often the arguments imply necessity logic.
Fourth, the researcher may have ideas about necessary conditions in a specific based the researcher’s knowledge about that field. Such ideas could be discussed with other experts in the field.
2.2.2 Thought experiment
When a potential necessary condition is selected the researcher can do a ‘thought-experiment’ to test if necessity is possible1. Thus for testing necessity the researcher can ask the question “Can I imagine cases with outcome \(Y\), but without condition \(X\)?”. When such cases are relatively common, the conclusion is that the condition is not necessary. When cases with the outcome \(Y\) and without the condition \(X\) are impossible or rare, the hypothesis may generally hold. The rare cases can be used to define the context where the hypothesis holds and where not, and thus to define the theoretical domain of the theory. Defining the theoretical domain –where the theory is supposed to hold– is important for all theories, because theories do rarely hold universally.
To illustrate the thought-experiment and the process of defining the theoretical domain, assume that a researcher wants to test the hypothesis ‘understanding English is necessary for reading this book’. This statement is generally correct, but it is possible to imagine cases (persons) with the outcome (reading the book) but without the condition (not mastering English). Such exception is possible when someone translates the book in the language other than English, such that a reader who does not master English can read the translated book. This exception helps to specify the theoretical domain of the hypothesis: ‘persons reading the original version of book’. Further exploration of exceptions can help to specify the theoretical domain. This process continues until the theoretical domain is precisely specified where the hypotheses is expected to hold virtually always. For testing this hypothesis, cases are selected from this specified theoretical domain. This can help to avoid sampling error (see section 3.8).
It is also possible that the necessary condition is rejected in the thought experiment because the condition is formulated too narrow. For example, ‘green apple’ is not necessary for an apple pie, and also red apple is not necessary for an apple pie. However, the higher-order construct (apple) is necessary. Then it would make sense to formulate the necessary condition hypothesis with the higher order concept. In general, attractive theories are supposed to be valid in a broad set of contexts, not only in very specific situations.
2.2.3 Direction of necessity
A hypothesis is usually only generally and semantically described as a theoretical statement. In NCA the common hypothesis is a qualitative theoretical statement like “X is necessary for Y” (in kind). A hypothesis usually is not described as a quantitative statement like “a specific level of X is necessary for a specific level of Y” (in degree). A hypothesis usually includes or implies a ‘direction’ of the causal relationship. In NCA four ‘directions’ are possible: the presence/high value of \(X\) is necessary for the presence/high value of \(Y\) (+ +), the absence/low value of \(X\) is necessary for the presence/high value of \(Y\) (- +), the presence/high value of \(X\) is necessary for the absence/low value of \(Y\) (+ -), and the absence/low value of \(X\) is necessary for the absence/low value of \(Y\) (- -). This is shown in Figure 2.1, where the empty space is in different corners.
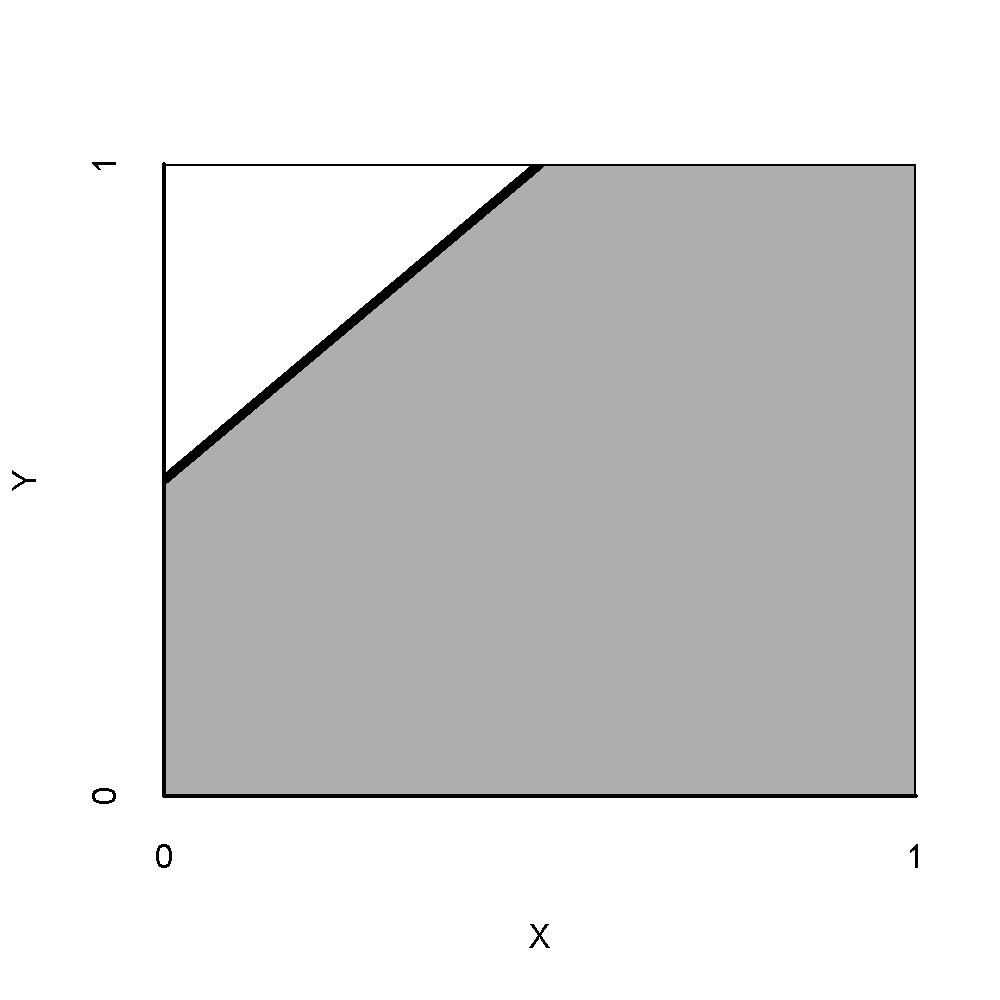
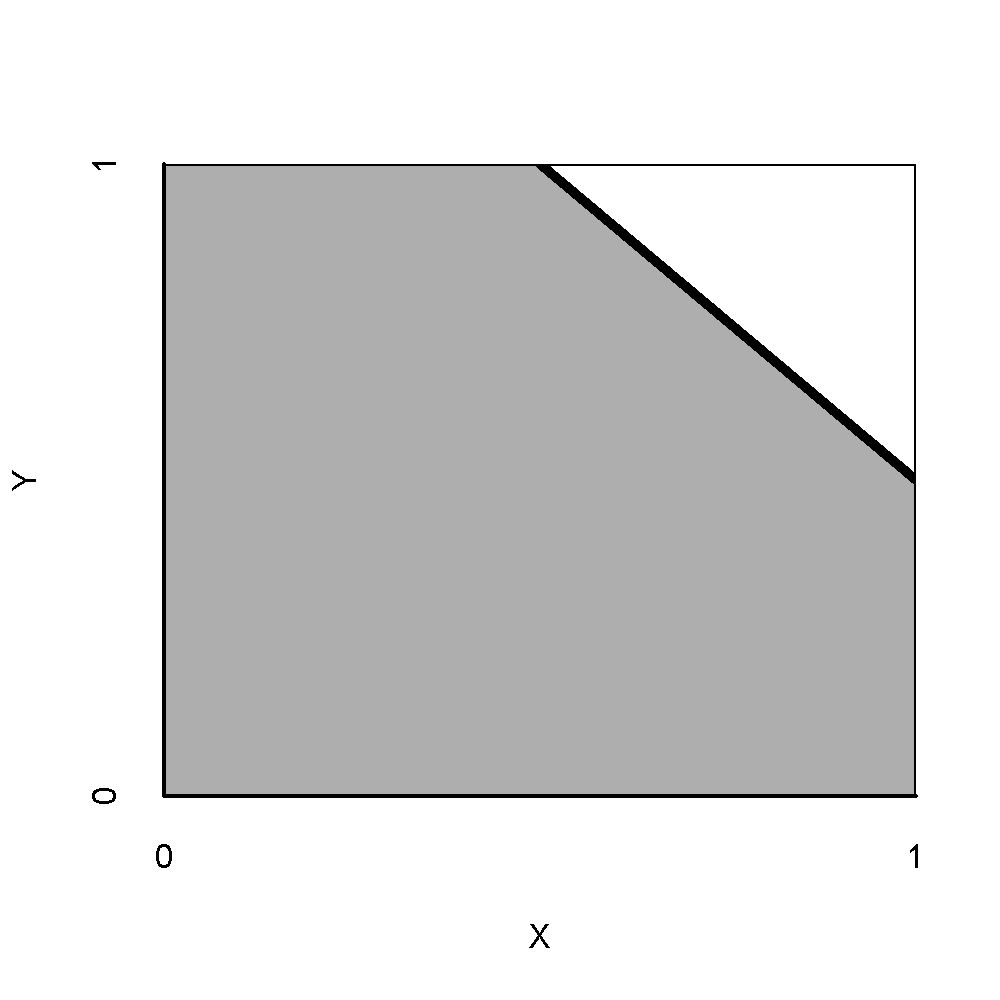
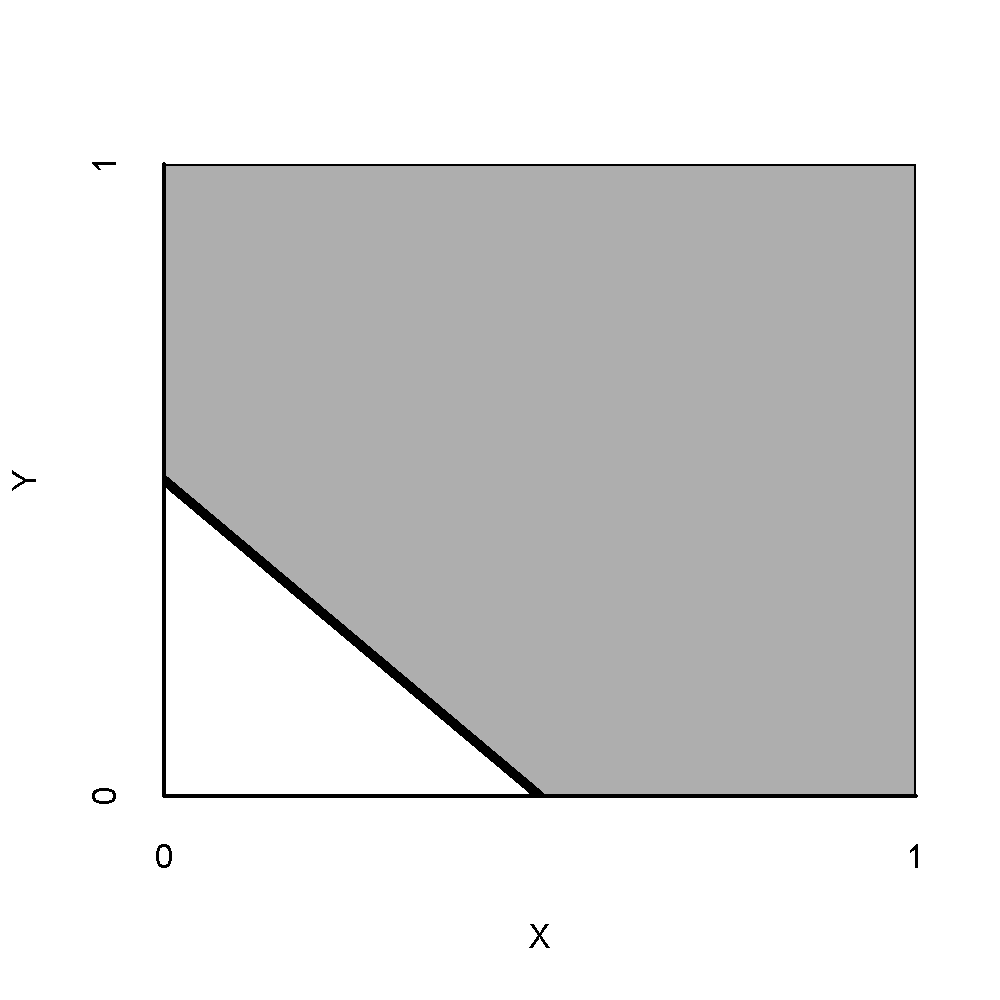
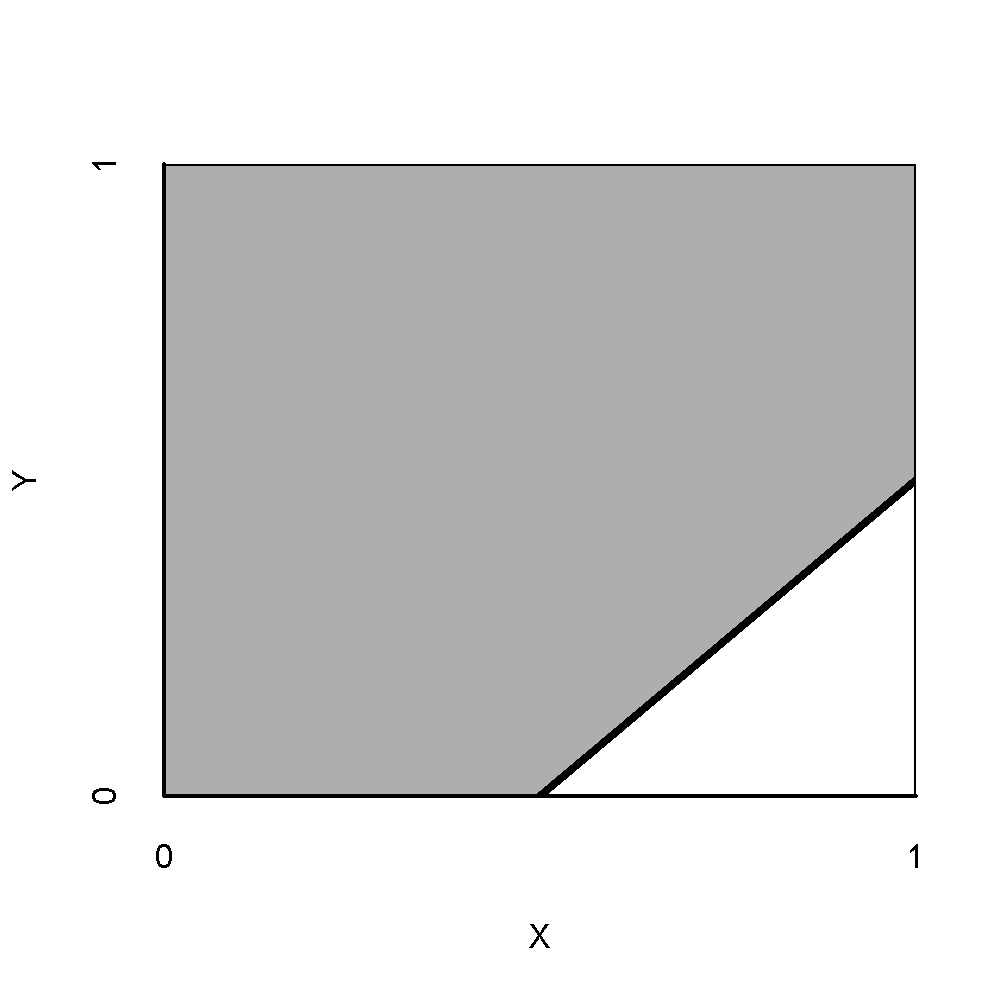
Figure 2.1: ‘Direction’ of necessary conditions. Upper-left: a high value of \(X\) is necessary for a high value of \(Y\) (+ +). Upper-right: a low value of \(X\) is necessary for a high value of \(Y\) (- +). Lower-left: a high value of \(X\) is necessary for a low value of \(Y\) (+ -). Lower-right: a low value of \(X\) is necessary for a low value of \(Y\) (- -).
Figure 2.2 shows conceptual models in which the arrows suggest a necessity causal relationship using the symbol (“nc” = ‘necessary condition’ or ‘necessary cause’), and the ‘direction’ of causality is specified as well.
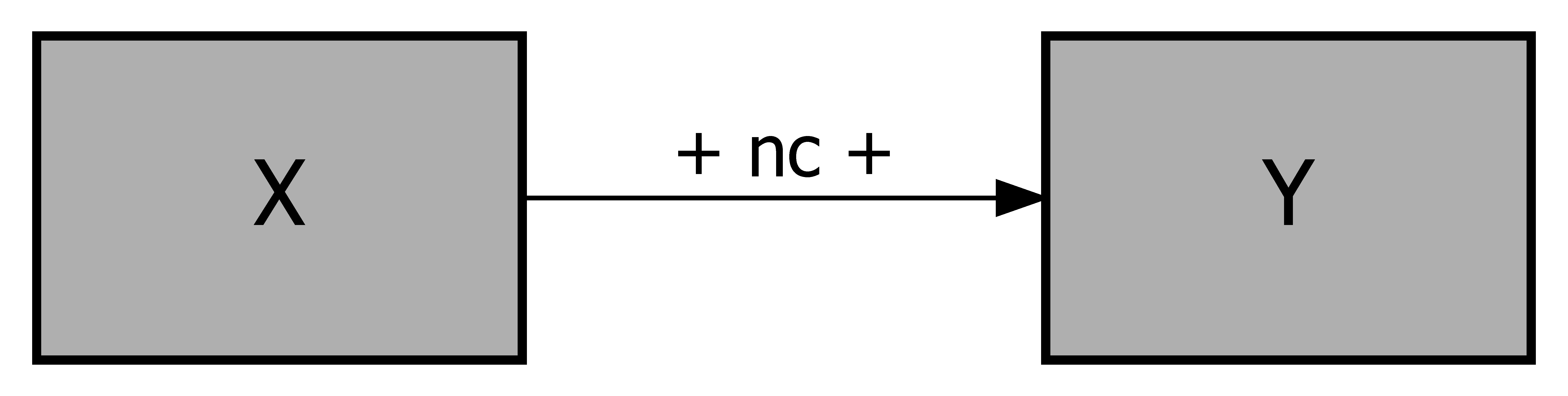
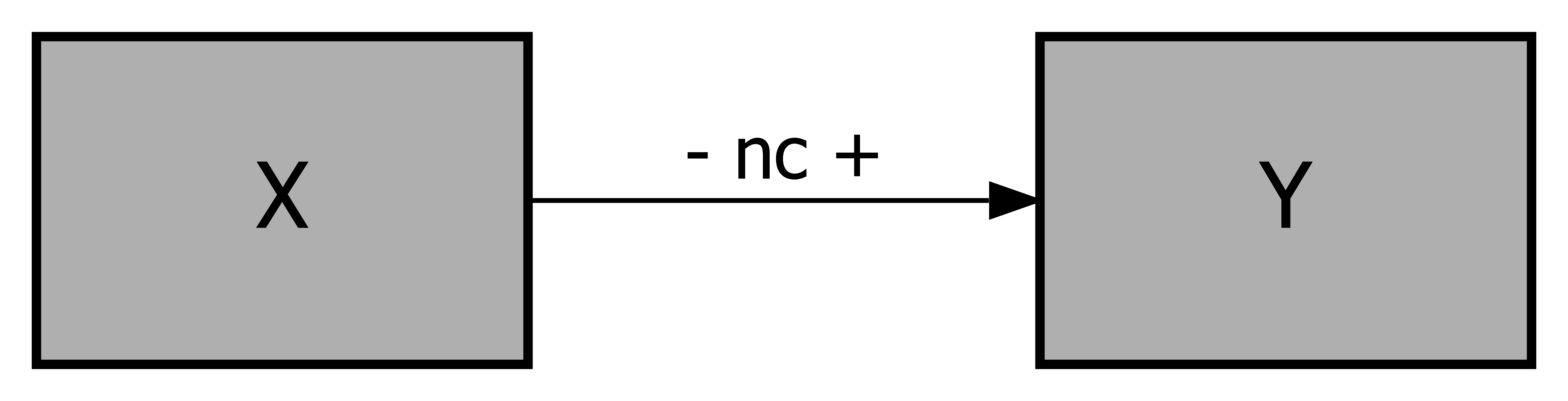
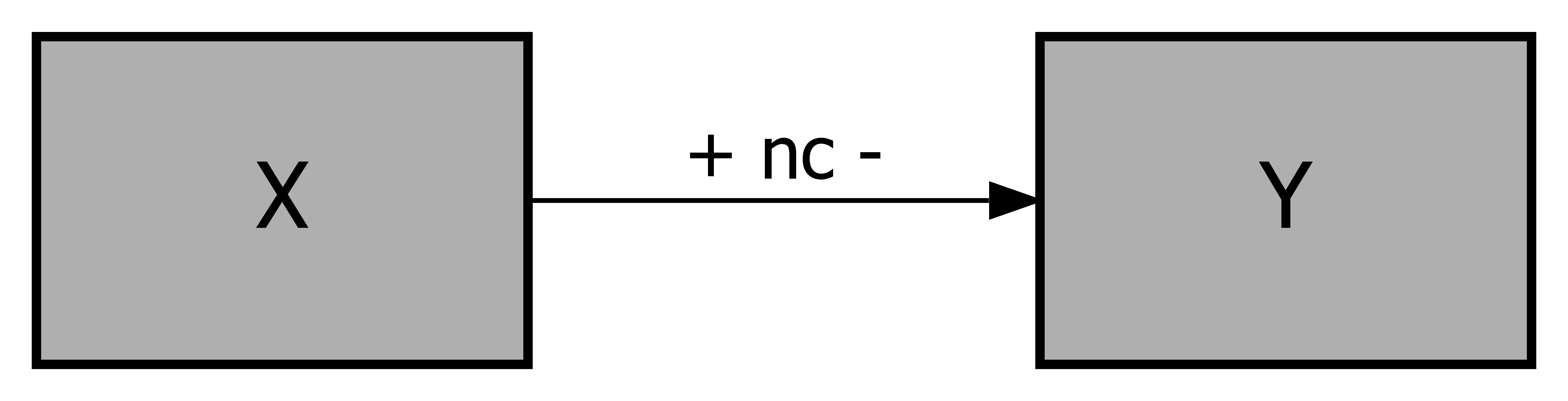
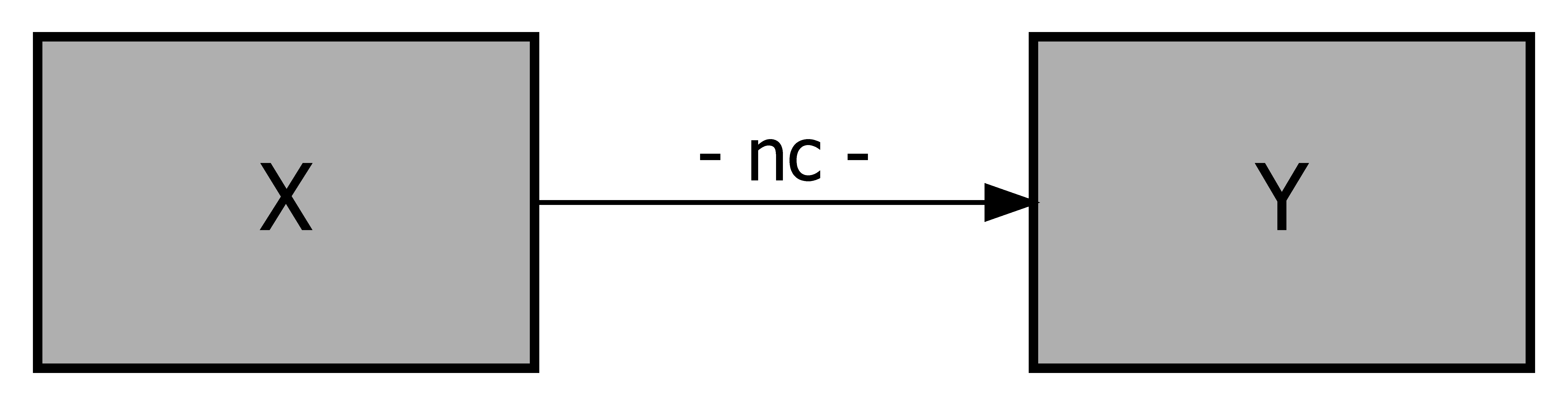
Figure 2.2: Conceptual models for necessary conditions. Top-Left: presence of \(X\) is necessary for presence of \(Y\). Top-Right: absence of \(X\) is necessary for presence of \(Y\). Bottom-Left: presence of \(X\) is necessary for absence of \(Y\). Bottom-Right: absence of \(X\) is necessary for absence of \(Y\).
If the direction is not specified, the + + direction is implied. Note that in NCA the hypothesis is not described by a verb like in ‘\(X\) increases \(Y\)’ or ‘\(X\) has a positive effect on \(Y\)’, which are common formulations to express probabilistic sufficiency (average effect) relationships. In NCA a noun or adverb is used to describe levels of \(X\) and \(Y\) as for example in ‘the absence of \(X\) is necessary for the presence of \(Y\)’ or ‘low \(X\) is necessary for high \(Y\)’. Note also that the two ‘ceiling lines’ in the lower part of the plot can be considered as ‘floor lines’. An empty space in the lower-left corner represents that a high value of \(X\) is necessary for a low value of \(Y\). This is logically equivalent to the statement that a not-high level of \(X\) is sufficient for a not-low level of \(Y\). The floor line in this corner suggests therefore that a low level of \(X\) is sufficient for a not so high level of \(Y\). Similarly, an empty space in the lower-right corner suggests that a high level of \(X\) is sufficient for a not so high level of \(Y\).
2.3 Justification of necessity hypotheses
A theory is more than a set of hypotheses. It is also important to describe the mechanism why \(X\) is necessary for \(Y\).
2.3.1 Temporal order
A first requirement for claiming causality is that condition occurs before the outcome: first the condition, then the outcome. If an empty spaces is observed in the upper left corner of the \(XY\) plot, this could not only indicate that the presence of \(X\) is necessary for the presence of \(Y\) (first \(X\) then \(Y\)), but also that the presence of \(Y\) is sufficient for the presence of \(X\) (first \(Y\) then \(X\)). Often it is easy to theorize that the second temporal order does not exist. For example if \(X\) is oxigen and \(Y\) is being alive, the empty space could support the claim that being alive is a sufficient causal condition for having oxigen, but theoretically this does not make sense. If the causal direction is not immediately clear, the temporal order should be part of the theoretical justification of the necessity hypothesis.
2.3.2 Causal mechinism
The causal mechanism of a necessity relationship can be argued by answering three why questions. Assuming that the presence of \(X\) is necessary or the presence of \(Y\) these questions are:
- Why if \(X\) is absent also \(Y\) is absent? This can be done by imagining a case without \(X\) and without \(Y\) and describing why without \(X\), \(Y\) cannot be produced.
- Why if \(Y\) is present also \(X\) is present? This can be done by imagining a case with \(X\) and with \(Y\) and describing why \(Y\) would disappear when \(X\) disappears, thus why \(Y\) could not have happened without \(X\)?
- Why the absence of \(X\) cannot be compensated by another concept? This can be done by imagining a case without \(X\) and with \(Y\).
If in any of these situations a case can be imagined, the consequence for the theory’s domain (smaller?) or for the concept definition \(X\) (higher order concept?) should be considered. It is also possible that such imagined case is very exceptional, and ignored from the perspective of typicality necessity.
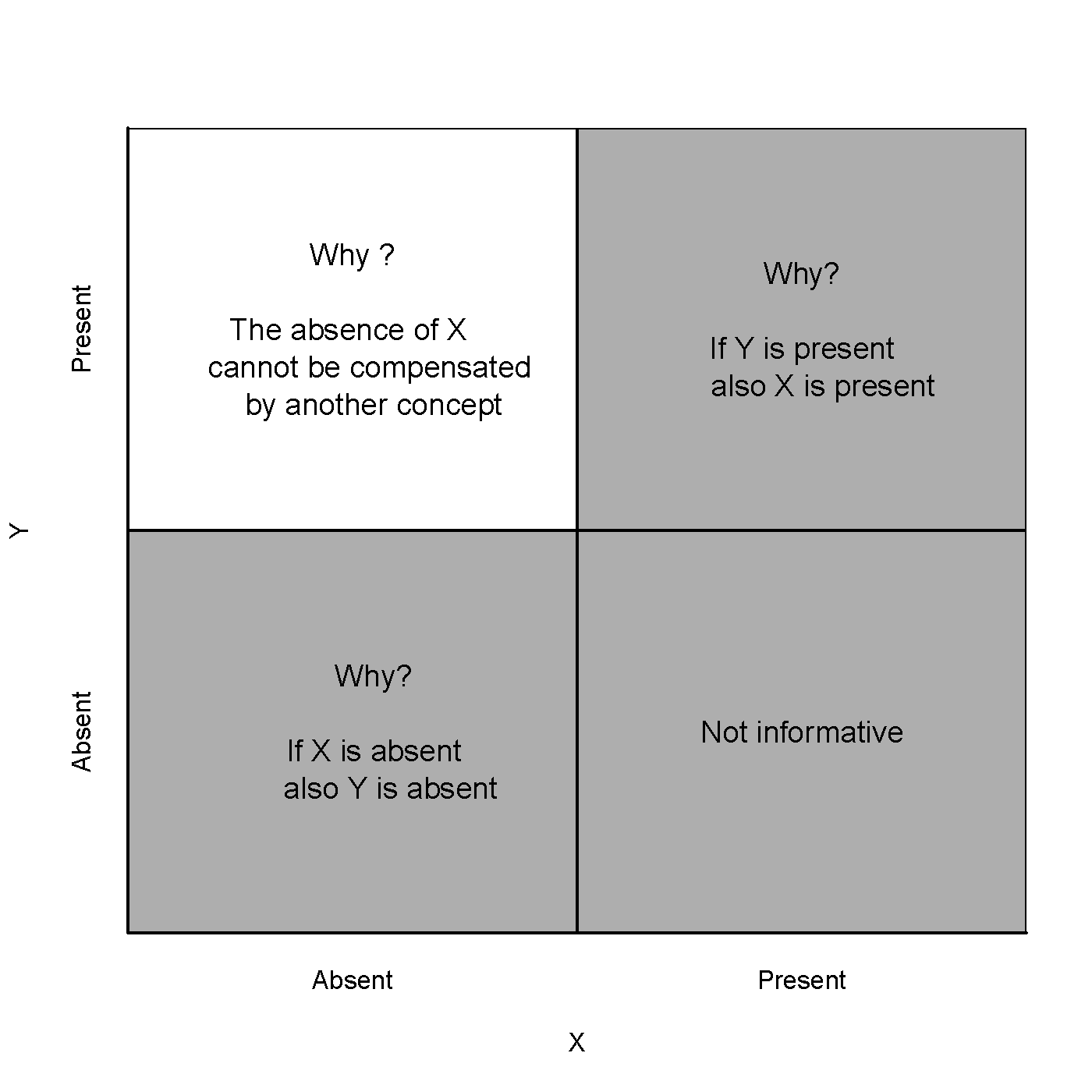
Figure 2.4: Questions to justify a ‘++’ necessity hypothesis.
Figure 2.4 shows that these questions relate to three cells of the 2x2 table that are compatible with the ‘++’ necessary condition hypothesis: where cases are possible or impossible when the necessary condition ‘the presence of \(X\) is necessary for the presence of \(Y\)’ holds. Note that the lower right cell is not informative about necessity.
Describing the causal mechanism is often difficult. It is a creative process inspired by the three questions. The answers can be based on exploring and combining knowledge from the literature, from practice and from the researcher’s own experience. In the literature, researchers may partly use necessity arguments when describing the causal mechanism why an ‘important’ factor produces an outcome. Practitioners may tell stories why a ‘must have’ factor is ‘critical’ or a ‘bottleneck’ for the outcome and why he acts upon them for getting the outcome.
2.4 Theoretical contribution
[Acknowledgement: Stefan Breet contributed to this section].
According to Campbell & Aguilera (2022) scholars are expected to contribute the a ‘conversation’ about a certain topic in the academic literature. Based on Lange & Pfarrer (2017), suggestions can be made for formulating a contribution with a necessity theory. The conversation starts with a ‘common ground’. The primary literature with the ongoing conversation about the problem/topic, and to which new insights with NCA will contribute, is identified (i.e., what do we know?). Next, an interesting ‘complication’ in the literature is highlighted. This can be a missing element or failure in the literature, something that is missing in the conversation, or how the conversation falling short (i.e., what we don’t know?). Afterwards, it should be explained why this complication is a ‘concern’ (i.e., so what?). Next, in the ‘course of action’ it is explained how the complication is addressed with NCA. Finally, the ‘contribution’ is described showing how and why the new insights are now part of the ongoing conversation.
I give two examples of possible formulations of a contribution with NCA:
- A contribution to a conversation on causal relationships of a phenomenon (e.g., Knol, 2022).
- A contribution to conversation on a necessity relationship of a phenomenon (e.g., Karwowski et al., 2016).
Tables 2.2 and 2.3 provide details about how these contributions can be formulated.
| Topic |
|---|
| Common Ground (What do we know?) |
| Several contributing factors to the outcome of interest are identified in the primary literature that describes a complex multicausal phenomenon. |
| Complication (What don’t we know?) |
| We do not know which factors are essential. |
| Concern (So what?) |
| If the essential factor is not known, we do not know if it is present. If it is not present the outcome will not occur no matter the other factors. Acting on other factors than the bottleneck factor is a waste of effort. |
| Course of action |
| We analyse the phenomenon from the causal perspective of necessity by formulating a necessity theory and testing it with NCA to ensure theory-method fit. |
| Contribution |
| The phenomenon is now described in more detail by distinguishing between factors that contribute to the outcome and can be substituted (as commonly done), and essential factors that must be in place. |
| Topic |
|---|
| Common Ground (What do we know?) |
| A necessity relationship is suggested in the primary literature that describes a complex multicausal phenomenon (i.e., what do we know?) |
| Complication (What don’t we know?) |
| But necessity logic was not used when empirically testing that relationship so we do not know if it is a true necessity relationship(i.e., what don’t we know?) |
| Concern (So what?) |
| Whether or not the relationship is a necessary relationship makes a big difference for theoretical understanding and practical action. If necessary, the factor is essential in theory and practice; if not the factor ‘only’ contributes and can be substituted (i.e., so what?) |
| Course of action |
| We test the necessity relationship with NCA to ensure theory-method fit. |
| Contribution |
| There is now empirical evidence (or not) of a claim of a necessity relationship. |
2.5 Types of necessity theories
Bokrantz & Dul (2023) distinguish two types of necessity theories. First, Pure necessity theories are theories that consist only of necessary condition relationships between \(X\)’s and \(Y\)’s. Because necessary conditions operate in isolation from the rest of the causal structure, such theories can be parsimonious with only one or a few necessary conditions. An example of a pure necessity theory with one condition and one outcome is the early theory of Guilford (1967) that intelligence is ‘necessary-but-not-sufficient’ for creativity. Shortly after NCA was introduced (Dul, 2016b), this theory was empirically tested with NCA by Karwowski et al. (2016). Other examples of pure necessity theories that have been proposed and tested with NCA and that are described in well-cited articles are theories about necessary conditions for lean manufacturing (Knol et al., 2018), for workplace spirituality (Garg, 2017), and innovation in buyer-supply relationships (Van der Valk et al., 2016). Also the established Theory of Planned Behavior (TPB) has been revisited by Frommeyer et al. (2022) from the perspective of necessity, showing with NCA that intention is a necessary but not sufficient condition for behavior. Other established theories could be revisited as well, and tested with NCA. For example, the Resource Based View of the firm (RBV) is a framework that is often described in terms of necessity (e.g., Wernerfelt, 1984) but has not yet been tested accordingly. One theory about the necessary conditions for success of start-up firms was developed based on literature and common beliefs, but this necessity theory was rejected after empirical testing with NCA (Arenius et al., 2017).
Second, Embedded necessity theories are theories that consist of a mix of necessity relations and common additive relations where all factors are supposed to contribute to producing the outcome, but some factors (additionally) may also be necessary. These theories are usually complex as their main goal is to describe how the outcome is produced (sufficiency). One of the first embedded necessity theories is an extension of the Technology Acceptance Model (TAM). Richter, Schubring, et al. (2020) first described TAM as a structural (sufficiency) model including the classical antecedents ‘perceived usefulness’ and ‘perceived ease of use’ and analysed this model with Partial Least Squares Structural Equation Modeling (PLS-SEM). Subsequently, the relations were described as necessity conditions, and analysed with NCA. The results show that, for example the two classical antecedents not only help to produce technology acceptance on average, but they are also necessary.
2.6 Two empty corners
It is possible that a researcher formulates a theory that a single factor has two necessity relations with the outcome at the same time, implying that more than one corner is empty.
First, a researcher may theorize that an optimum (not low, not high) level of \(X\) is necessary for a high level of \(Y\). Then the upper left and the upper right corners are expected to be empty (Figure 2.5, left). Similarly, a researcher may theorize that an optimum (not low, not high) level of \(X\) is necessary for a low level of \(Y\). Then the lower left and the lower right corners are expected to be empty (Figure 2.5, right).
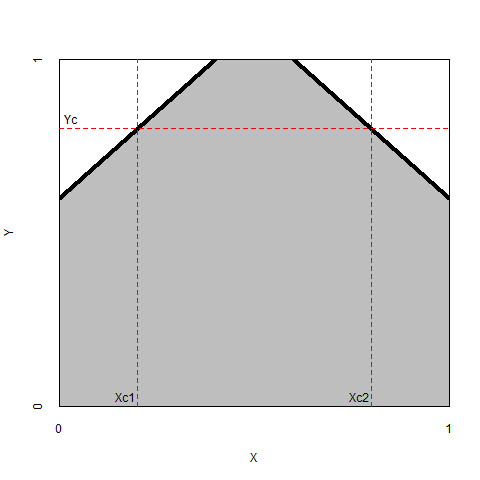
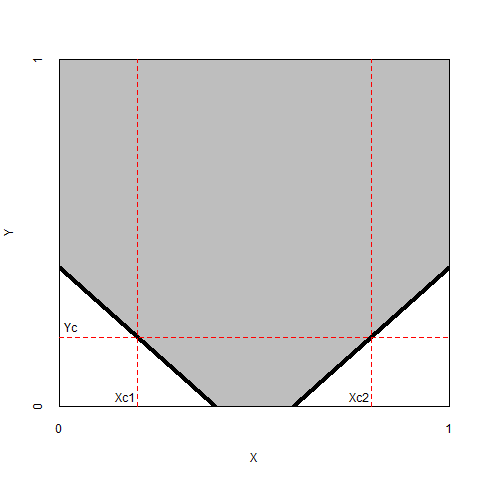
Figure 2.5: Left: The necessity of an optimum level of \(X_{c1} < X < X_{c2}\) for a high level of \(Y = Y_c\). Right: The necessity of an optimum level of \(X_{c1} < X < X_{c2}\) for a low level of \(Y = Y_c\).
In the NCA software, it is possible to do a combined test of the two necessity relations of a single factor by using the argument effect_aggregation in the nca_analysis function. The software can estimate the aggregate effect size of two adjacent corners, which is the sum of the effect sizes of the separate empty spaces, and its p value. For example, with an expectation that and optimum level of \(X\) is necessary for a high level of \(Y\), it is expected that the upper-left and the upper-right corners are empty, and the total empty zone can be aggregated and tested for randomness.
It is also possible that a researcher theorizes that a high level of \(X\) is necessary for an extreme (low or high) level of \(Y\). Then the upper left and the lower left corners are expected to be empty (Figure 2.6, left). Similarly, a researcher may theorize that a low level of \(X\) is necessary for an extreme (low or high) level of \(Y\). Then the upper right and the lower right corners are expected to be empty (Figure 2.6, right).
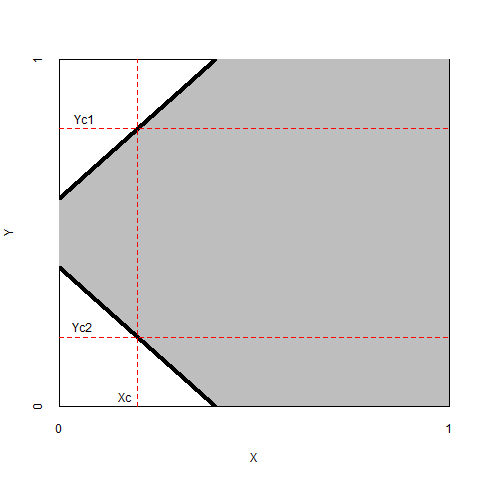
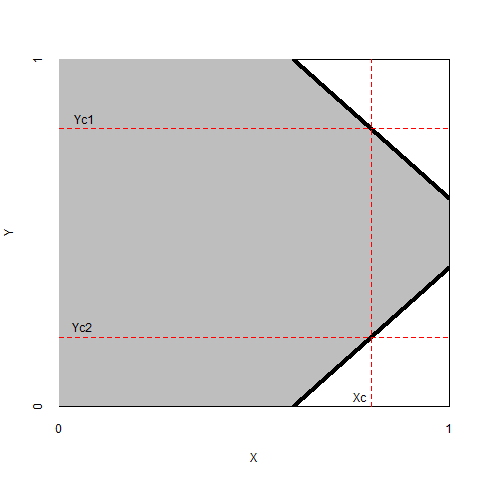
Figure 2.6: Left: The necessity of a high level of \(X > X_c\) for an extreme (low or high) level of \(Y = Y_{c1}\) or \(Y = Y_{c2}\). Right: The necessity of a low level of \(X < X_c\) for an extreme (low or high) level of \(Y = Y_{c1}\) or \(Y = Y_{c2}\).
The final possible situation with two empty corners is that a researcher theorizes that a high level of \(X\) is necessary for a high level of \(Y\) and a low level of \(X\) is necessary for a low level of \(Y\) (Figure 2.7, left). Similarly, a researcher may theorize that a low level of \(X\) is necessary for a high level of \(Y\) and that a high level of \(X\) is necessary for a low level of \(Y\). Then two opposite corners are empty (Figure 2.7, right).
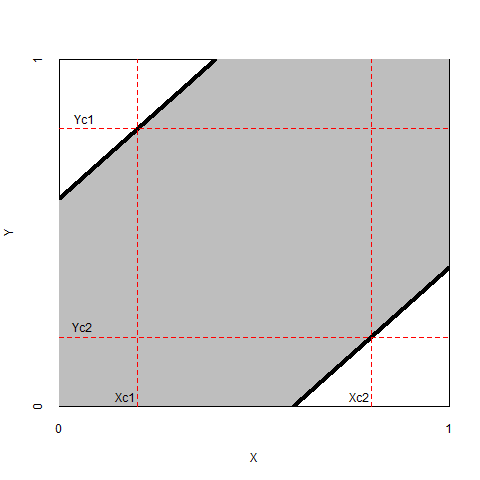
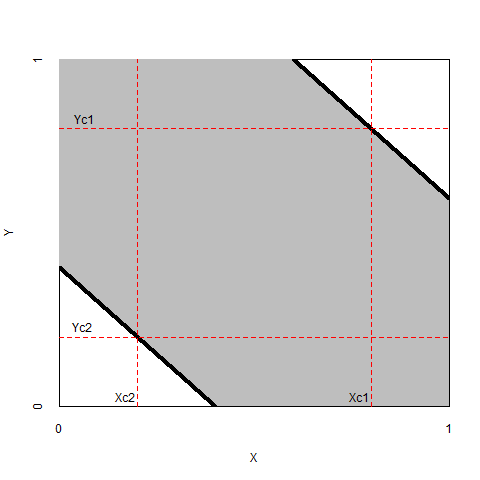
Figure 2.7: Left: The necessity of a high level of \(X > X_{c1}\) for a high level of \(Y = Y_{c1}\), and the necessity of low level of \(X < X_{c2}\) for a low level of \(Y = Y_{c2}\). Right: The necessity of low level of \(X < X_{c1}\) for a high level of \(Y = Y_{c1}\), and the necessity of high level of \(X > X_{c2}\) for a low level of \(Y = Y_{c2}\).
.
–>
2.7 The meaning of ‘necessary but not sufficient’
Figure 2.1 shows a single factor with a one necessity relationship, and Figures 2.5, 2.6, and 2.7 show a single factor with two necessity relationships. In all figures, consistent with necessity, there are no observations in the empty space and observations in the grey area. If the necessity relationship holds, and no observations were in the grey area, all observations would be exactly on the border line. Then, the necessary condition is also a sufficient conditions. However this is not realistic as single necessary conditions are seldom also sufficient. This implies that the words ‘but not sufficient’ can normally be added to all necessity statements.
For example, upper left Figure 2.1, shows a single factor with one necessary condition: only the upper left corner is empty. This corresponds to the statement “a high level of \(X\) is necessary for a high level of \(Y\)”. If all points were on the border line (ceiling line) the condition is also sufficient resulting in the statement: “a high level of \(X\) is necessary and sufficient for a high level of \(Y\)”. In practice, observations will appear below the ceiling line. This justifies the statement that “a high level of \(X\) is necessary but not sufficient for a high level of \(Y\)”.
Figure 2.5, left is an example of a factor with two necessity relations, “a high level of \(X\) is necessary for a high level of \(Y\)” and “a low level of \(X\) is necessary for a high level of \(Y\)” (thus an optimum level of \(X\) is necessary for a high level of \(Y\)). If all observations were on the two ceiling lines, the words ‘and sufficient’ could be added to the word ‘necessary’. Again, in practice observations show up below the border lines such that the words “but not sufficient” can be added to the word ‘necessary’. The same holds for any other necessity relationship shown in Figures 2.1, 2.5, 2.6, and 2.7.
Any necessity statement can be rephrased as a sufficiency statement by formulating its logical complement. For example, the upper left corner of Figure 2.5 left (ignoring the upper right corner) indicates that a high level of \(X\) is necessary but not sufficient for a high value of \(Y\). This can be reformulated as ‘the absence of a high level of \(X\) is sufficient but not necessary for the absence of a high value of \(Y\)’. This means that a level of \(X < X_{c1}\) guarantees (is sufficient for) \(Y < Y_c\).
Similarly, the lower right corner of Figure 2.5 right (ignoring the lower left corner) indicates that a low level of \(X\) is necessary but not sufficient for a low value of \(Y\). This can be reformulated as: ‘the absence of a low level of \(X\) is sufficient but not necessary for the absence of a high level of \(Y\)’. A value of \(X > X_{c2}\) guarantees that \(Y > Y_c\).
When a single factor has two necessary relationships, it is possible to use the necessity formulation for one necessary condition, and the sufficiency formulation for the other. For example, in Figure 2.7, left the double necessity formulation is: ‘a high level of \(X > X_{1c}\) is necessary but not sufficient for a high level of \(Y = Y_{c1}\)’, and ‘the absence or low level of \(X < X_{c2}\) is necessary but not sufficient for the absence or low level of \(Y = Y_{2c}\)’. When the necessity formulation is used for the upper left necessity relation, and the sufficiency formulation for the lower right necessity relation, the new equivalent statement is: ‘a high level of \(X > X_{1c}\) is necessary but not sufficient for a high level of \(Y = Y_{c1}\)’, and ‘a high level of \(X < X_{c2}\) is sufficient but not necessary for a high level of \(Y = Y_{2c}\)’.
Note that dual statements cannot be combined into a single statement, because the two border lines have a different location. This means that for a given \(Y\) there are different levels of \(X\) (see Figures 2.5, and 2.7) and for a given \(X\) there different levels of \(Y\) (see Figures 2.6, and 2.7).
Sometimes, the situation in Figure 2.7, left is formulated ‘in kind’ as ‘\(X\) is necessary and sufficient for \(Y\)’, which implies that the upper left necessity relationship is formulated in terms of necessity, and the lower right in terms of sufficiency. However, this formulation is problematic when the actual necessity relationships are ‘in degree’. The ‘in degree’ formulation of the situation is not: ‘a high level of \(X\) is necessary and sufficient for a high level of \(Y\)’, but instead: ‘\(X > X_{c1}\) is necessary for \(Y = Y_{c1}\) and \(X > X_{c2}\) is sufficient for \(Y = Y_{c2}\)’. There is no common \(X\) that is necessary and sufficient for a common \(Y\) and no common \(Y\) for which a common \(X\) is necessary and sufficient.
Only when the two borderlines overlap, the ‘in kind’ statement also holds in an ‘in degree’ situation: ‘a certain level of \(X\) is necessary and sufficient for a certain level of \(Y\)’. At best, the ‘in kind’ formulation could be re-formulated as ‘a high level of \(X\) is necessary for a high level of \(Y\) and sufficient for a not so high level of \(Y\)’, or similar. The theoretical meaning is that a high level of \(X\) is necessary for (enables) a high level of \(Y\) (border line = ceiling line) and is sufficient for (ensures) a low level of \(Y\) (border line = floor line).
References
Doing a though experiment is a type of counterfactual reasoning. A counterfactual is a hypothetical scenario that describes what could have happened, but didn’t. It can be used not only for theorizing about necessity but also for sufficiency. In counterfactual reasoning for necessity it is first assumed that \(X\) and \(Y\) occurred and subsequently the question is raised “what would have happened if \(X\) had not occurred?” If \(Y\) would still be there, \(X\) is not necessary for \(Y\). If \(Y\) would disappear, \(X\) is necessary for \(Y\). In counterfactual reasoning for sufficiency it is first assumed that \(X\) and \(Y\) did not occur and subsequently the question is raised “what would have happened if \(X\) would have happened if X had occurred?” If \(Y\) would still not be there, \(X\) is not sufficient for \(Y\). If \(Y\) would appear, \(X\) is sufficient for \(Y\).↩︎
