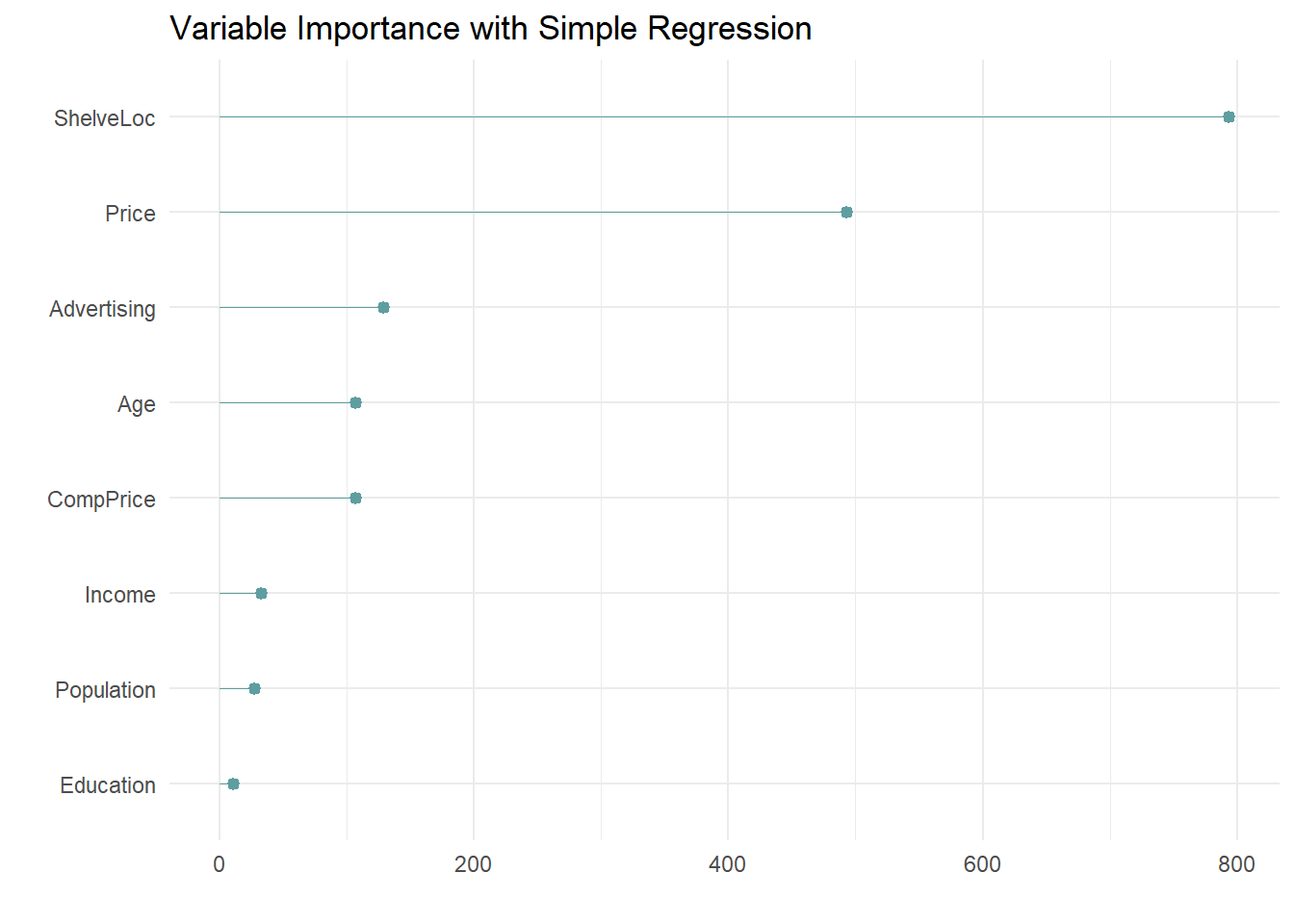2.7 Hypergeometric

If \(X\) is the count of successful events in a sample of size \(n\) without replacement from a population of size \(N\) containing \(K\) successes and \(N-K\) non-successes, then \(X\) is a random variable with a hypergeometric distribution

\[f(x|N,K,n) = \frac{{{K}\choose{k}}{{N-K}\choose{n-k}}}{{N}\choose{n}}.\]

with \(E(X) = n\frac{K}{N}\) and \(Var(X) = n \frac{K}{N} \cdot \frac{N-n}{N} \cdot \frac{N-K}{N-1}\).

The formula follows from the frequency table of the possible outcomes.

	Sampled	Not Sampled	Total
success	k	K-k	K
non-success	n-k	(N-K)-(n-k)	N-K
Total	n	N-n	N

If \(X\) is the count of successful events in a sample of size \(k\) without replacement from a population containing \(M\) successes and \(N\) non-successes, then \(X\) is a random variable with a hypergeometric distribution

\[f(x|m,n,k) = \frac{{{m}\choose{x}}{{n}\choose{k-x}}}{{m+n}\choose{k}}.\]

with \(E(X)=k\frac{m}{m+n}\) and \(Var(X) = k\frac{m}{m+n}\cdot\frac{m+n-k}{m+n}\cdot\frac{n}{m+n-1}\).

phyper returns the cumulative probability (percentile) p at the specified value (quantile) q. qhyper returns the value (quantile) q at the specified cumulative probability (percentile) p.

Example

What is the probability of selecting \(X = 14\) red marbles from a sample of \(k = 20\) taken from an urn containing \(m = 70\) red marbles and \(n = 30\) green marbles?

Function dhyper() calculates the hypergeometric probability.

x = 14
m = 70
n = 30
k = 20

dhyper(x = x, m = m, n = n, k = k)

## [1] 0.21

The expected value is 14 and variance is 3.39.

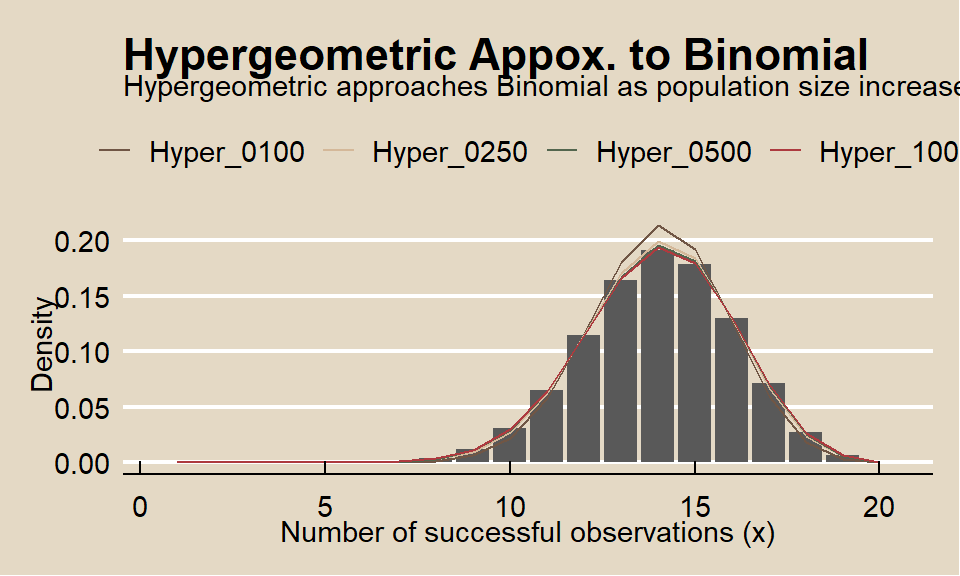
The hypergeometric random variable is similar to the binomial random variable except that it applies to situations of sampling without replacement from a small population. As the population size increases, sampling without replacement converges to sampling with replacement, and the hypergeometric distribution converges to the binomial. What if the total population size is 250? 500? 1000?