2.6 Geometric

If \(X\) is the count of Bernoulli trials of success probability \(p\) required to achieve the first successful event, then \(X\) is a random variable with a geometric distribution \(X \sim G(p)\). The probability of \(X = x\) trials is

\[f(x; p) = p(1-p)^{x-1}.\]

with \(E(X)=\frac{{n}}{{p}}\) and \(Var(X) = \frac{(1-p)}{p^2}\). The probability of \(X<=n\) trials is

\[F(X=n) = 1 - (1-p)^n.\]

Examples

What is the probability a marketer encounters x = 3 people on the street who did not attend a sporting event before the first success if the population probability is p = 0.20?

\[f(4; 0.20) = 0.20(1-0.20)^{4-1} = 0.102.\]

Function dgeom() calculates the geometric distribution probability. Parameter x is the number of failures, not the number of trials.

dgeom(x = 3, prob = 0.20)

## [1] 0.1

data.frame(cnt = rgeom(n = 10000, prob = 0.20)) %>%
  count(cnt) %>%
  top_n(n = 15, wt = n) %>%
  ungroup() %>%
  mutate(pct = round(n / sum(n), 3),
         X_eq_x = cnt == 3) %>%
  ggplot(aes(x = as.factor(cnt), y = n, fill = X_eq_x, label = pct)) +
  geom_col(alpha = 0.8) +
  scale_fill_mf() +
  geom_text(size = 3) +
  theme_mf() +
  theme(legend.position = "none") +
  labs(title = "Distribution of trials prior to first success",
       subtitle = paste("P(X = 3) | X ~ G(.2) = ", round(dgeom(2, .2), 3)),
       x = "Unsuccessful trials",
       y = "Count",
       caption = "simulation of n = 10,000 samples from geometric dist.")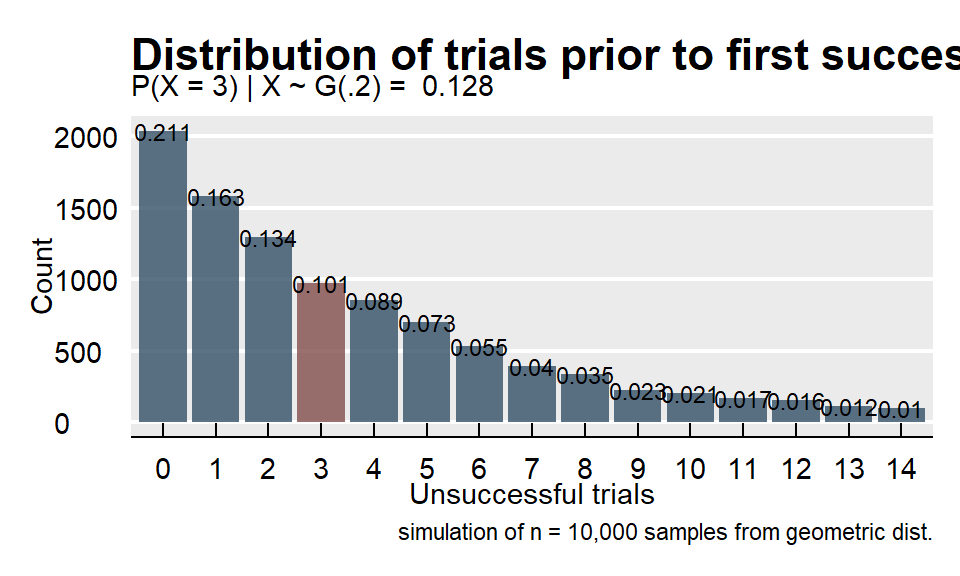 

What is the probability the marketer fails to find someone who attended a game in x <= 5 trials before finding someone who attended a game on the sixth trial when the population probability is p = 0.20?

p = 0.20
n = 5
# exact
pgeom(q = n, prob = p, lower.tail = TRUE)

## [1] 0.74

# simulated
mean(rgeom(n = 10000, prob = p) <= n)

## [1] 0.74

What is the probability the marketer fails to find someone who attended a game on x >= 5 trials before finding someone who attended a game on the next trial?

p = 0.20
n = 5
# exact
pgeom(q = n, prob = p, lower.tail = FALSE)

## [1] 0.26

# simulated
mean(rgeom(n = 10000, prob = p) > n)

## [1] 0.26

The expected number of trials to achieve the first success is 1 / 0.20 = 5, Var(X) = (1 - 0.20) / 0.20^2 = 20?

p = 0.20
# mean
# exact
1 / p

## [1] 5

# simulated
mean(rgeom(n = 10000, prob = p)) + 1

## [1] 5

# Variance
# exact
(1 - p) / p^2

## [1] 20

# simulated
var(rgeom(n = 100000, prob = p))

## [1] 20