Kapitel 9 Umrichtertechnologie
In der klassischen leistungselektronik sind verschiedene Topologien und Methoden bekannt, um Gleich- und Wechselspannung ineinander umzuformen. Je nach Art und Weise der Umwandlung wird zwischen Umrichter, Gleichrichter, Wechselrichter und Steller unterschieden (vgl. Abb. 9.1.
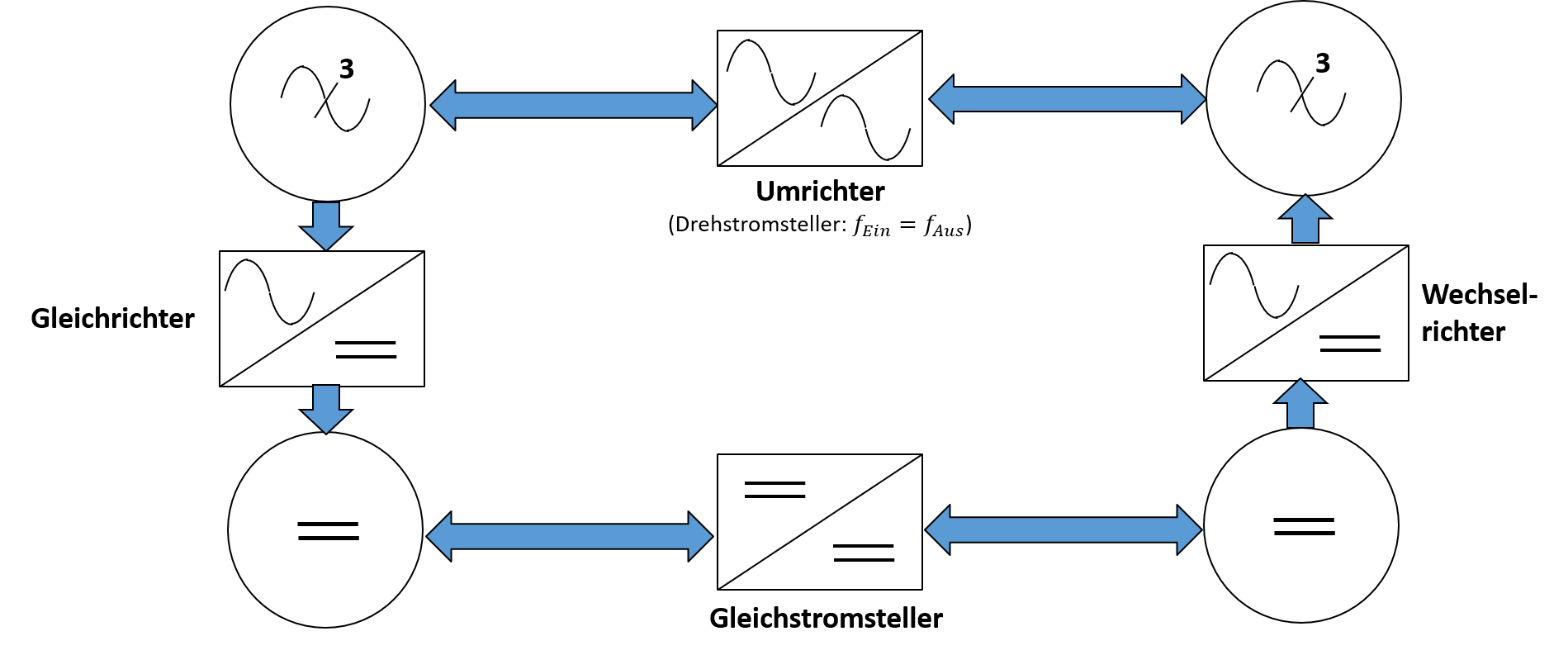
Abbildung 9.1: Möglichkeiten der Umwandlung von elektrischer Energie mittels Leistungselektronik
Je nach Anwendung und Topologie ergeben sich somit eine Vielzahl unterschiedlicher leistungselektronischer Stellglieder (Stromrichter), die in der Abbildung 9.2 dargestellt werden.
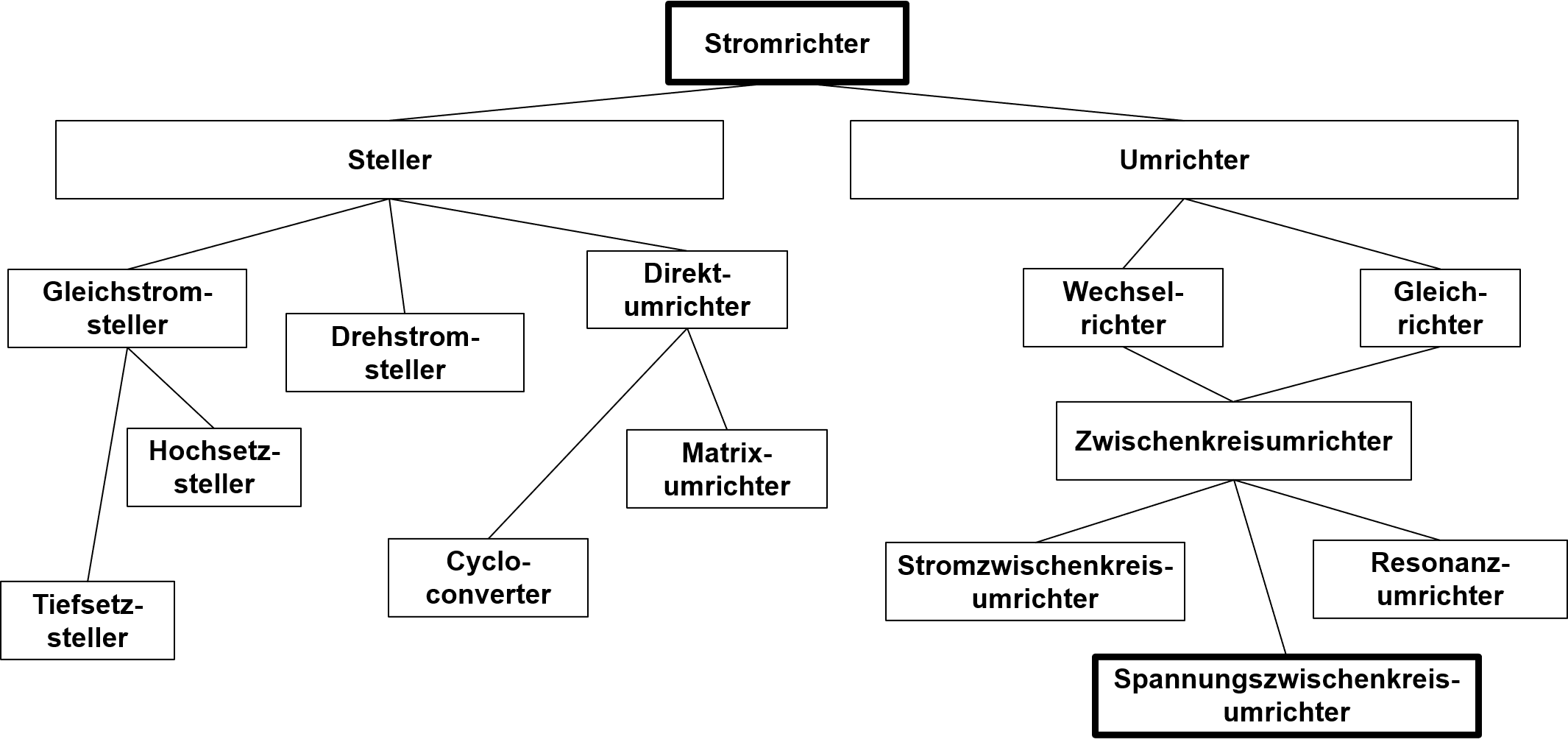
Abbildung 9.2: Darstellung verschiedener Stromrichtertypen
Heutzutage wird der grösste Teil der Drehstrommotoren über Umrichter aus einer Gleichspannungsquelle gespeist. Diese Gleichspannungsquelle wird durch den sogenannten Spannungszwischenkreis gebildet, welcher einen Spannungszwischenkreis-Umrichter auszeichnet (englisch: voltage source inverter VSI). Im Falle sehr grosser Leistungen von über 10MW kommen auch Stromzwischenkreisumrichter (englisch: current souce inverter CSI) sowie Direktumrichter und Matrixumrichter zum Einsatz. In den folgenden Kapiteln soll sich jedoch auf den gleichspannungsgespeisten Umrichter, den sog. Pulswechselrichter, beschränkt werden.
9.1 Pulswechselrichter
Der Pulswechselrichter erhält seine Energie über eine dreisträngige Brückenschaltung (B6), wie in Abbildung 9.3) dargestellt.
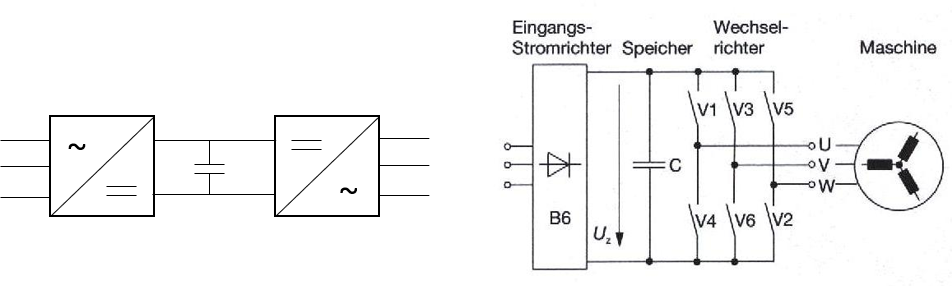
Abbildung 9.3: Indealisiertes Grundprinzip eines Spannungszwischenkreisumrichters
Bei den elektronischen Schaltern handelt es sich um abschaltbare Leistungshalbleiter (MOSFET, IGBT oder IGCT), die aufgrund der stark induktiven Last (Motorwicklungen) und der damit verbundenen Spannungsinduktion im Abschaltmoment mit antiparallel angeordneten Freilaufdioden versehen werden (mit Ausnahme des MOSFET aufgrund der internen Body Diode).
Wird davon ausgegangen, das die Schalter eines gemeinsamen Zweiges immer wechselseitig angesteuert werden (was eine notwendige Bedingung ist um einen Kurzschluss zu vermeiden), kann das Funktionsprinzip mit Hilfe von idealen Schaltern wie in Abbildung 9.4 gezeigt vereinfacht werden.
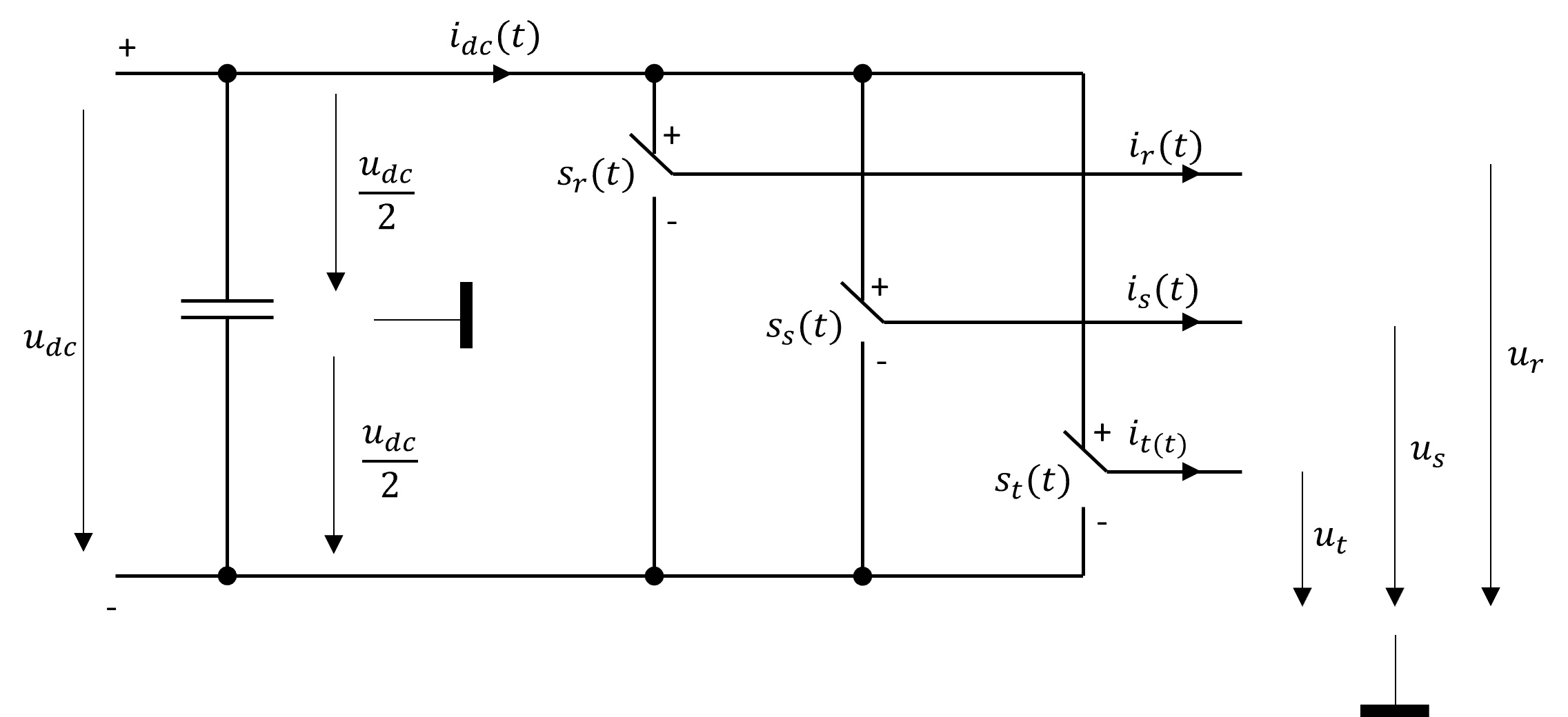
Abbildung 9.4: Indealisierter Umrichter mit Spannungszwischenkreis
In Abbildung 9.4 wird als Bezugspotential für die Ausgangsspannungen die halbe Zwischenkreisspannung \(\frac{u_{dc}}{2}\) definiert. Dieser Punkt existiert in der realen Schaltung üblicherweise nicht. Es erfolgt folglich auch kein Stromausgleich über dieses Potential. Da der angeschlossene Motor immer im Stern oder im Dreieck geschaltet ist, ergibt die Stromsumme zu jedem Zeitpunkt null.
\[ \sum_{r,s,t}{i_{k}(t)}=0 \]
Um die Schalterpositionen zu definieren, werden die Schaltfunktionen \(s_{r,s,t}(t)\) definiert. Befindet sich ein Schalter in der dem höheren Potential zugeordneten (oberen) Position gilt \(s_{r,s,t}=1\). Befindet er sich hingegen in einer dem niedrigeren Potential zugeordneten (unteren) Position gilt \(s_{r,s,t}=-1\). Über die induktiven Motorwicklungen werden sich von der aktuellen Schalterposition abhängige Ströme \(i_{r,s,t}(t)\) einstellen. Da die Ausgangsspannung \(u_{r,s,t}(t)\) ebenfalls auf die halbe Zwischenkreisspannung \(\frac{u_{dc}}{2}\) bezogen werden, können die drei Ausgangsspannungen folgendermassen bestimmt werden.
\[ u_{r,s,t}(t)=s_{r,s,t}(t) \frac{u_{dc}(t)}{2} \]
Der eingangsseitige Gleichstrom \(i_{dc}(t)\) ergibt sich aus der Summe der drei Wicklungsströme.
\[ i_{dc}(t)=\frac{1}{2}\sum_{r,s,t}{s_{k}(t)\cdot i_{k}(t)} \]
Da der idealisierte Umrichter drei Schalter mit jeweils zwei denkbaren Schalterpositionen aufweist, ergeben sich \(2^{3}=8\) mögliche Schaltzustände. Um gleichzeitig eine Verbindung zu den, in der Antriebstechnik sehr wichtigen Raumzeigern, herstellen zu können. kann davon ausgegangen werden, das jeder der 8 Schaltzustände einem Raumzeiger zugeordnet werden kann. Diese Zuordnung beruht, wie bereits gezeigt, auf der räumlich um 120 Grad versetzten Anordnung der drei Wicklungen. Da die drei Ausgangsspannungen mit eben diesen Wicklungen in Verbindung stehen, ist es zulässig die Clarke Transformation, unter Berücksichtigung der entsprechenden Transformationsmatrix \(T_{C}\), zu verwenden, um die Spannungsraumzeiger \(\underline{u}_{i}^{s}\) im statorfesten \((\alpha, \beta)\)-Koordinatensystem zu bestimmen (siehe Kapitel 6.1.3).
\[ \underline{u}_{i}^{s} = c\cdot T_{C}\left[\begin{matrix}u_{ri}\\ u_{si} \\ u_{ti} \end{matrix} \right]= \frac{u_{dc}}{2}\cdot c\cdot T_{C}\left[\begin{matrix}s_{ri}\\ s_{si} \\ s_{ti} \end{matrix} \right] \]
Berücksichtigt man den Skalierungsfaktor \(c=\frac{2}{3}\) können die elementaren Spannungsvektoren im statorfesten Koordinatensystem bestimmt werden.
\[ \underline{u}_{i}^{s}= \frac{u_{dc}}{3}\cdot \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix}\cdot \left[\begin{matrix}s_{ri}\\ s_{si} \\ s_{ti} \end{matrix} \right] \]
| Vektor | \(s_{r}\) | \(s_{s}\) | \(s_{t}\) | \(u_{i\alpha}\) | \(u_{i\beta}\) | \(u_{i0}\) |
|---|---|---|---|---|---|---|
| \(u_{0}\) | -1 | -1 | -1 | 0 | 0 | \(-\frac{u_{dc}}{\sqrt{2}}\) |
| \(u_{1}\) | 1 | -1 | -1 | \(\frac{2}{3}u_{dc}\) | 0 | \(-\frac{u_{dc}}{3\sqrt{2}}\) |
| \(u_{2}\) | 1 | 1 | -1 | \(\frac{u_{dc}}{3}\) | \(\frac{u_{dc}}{\sqrt{3}}\) | \(\frac{u_{dc}}{3\sqrt{2}}\) |
| \(u_{3}\) | -1 | 1 | -1 | \(-\frac{u_{dc}}{3}\) | \(\frac{u_{dc}}{\sqrt{3}}\) | \(-\frac{u_{dc}}{3\sqrt{2}}\) |
| \(u_{4}\) | -1 | 1 | 1 | \(-\frac{2}{3}u_{dc}\) | \(0\) | \(\frac{u_{dc}}{3\sqrt{2}}\) |
| \(u_{5}\) | -1 | -1 | 1 | \(-\frac{u_{dc}}{3}\) | \(-\frac{u_{dc}}{\sqrt{3}}\) | \(-\frac{u_{dc}}{3\sqrt{2}}\) |
| \(u_{6}\) | 1 | -1 | 1 | \(\frac{u_{dc}}{3}\) | \(-\frac{u_{dc}}{\sqrt{3}}\) | \(\frac{u_{dc}}{3\sqrt{2}}\) |
| \(u_{7}\) | 1 | 1 | 1 | \(0\) | \(0\) | \(\frac{u_{dc}}{\sqrt{2}}\) |
Normiert man alle Spannungsvektoren auf die halbe Zwischenkreisspannung ergibt sich folgende Darstellung.
| Vektor | \(s_{r}\) | \(s_{s}\) | \(s_{t}\) | \(u_{i\alpha}\) | \(u_{i\beta}\) | \(u_{i0}\) |
|---|---|---|---|---|---|---|
| \(u_{0}\) | -1 | -1 | -1 | 0 | 0 | \(-\sqrt{2}\) |
| \(u_{1}\) | 1 | -1 | -1 | \(\frac{4}{3}\) | 0 | \(-\frac{\sqrt{2}}{3}\) |
| \(u_{2}\) | 1 | 1 | -1 | \(\frac{2}{3}\) | \(\frac{2}{\sqrt{3}}\) | \(\frac{\sqrt{2}}{3}\) |
| \(u_{3}\) | -1 | 1 | -1 | \(-\frac{2}{3}\) | \(\frac{2}{\sqrt{3}}\) | \(-\frac{\sqrt{2}}{3}\) |
| \(u_{4}\) | -1 | 1 | 1 | \(-\frac{4}{3}\) | \(0\) | \(\frac{\sqrt{2}}{3}\) |
| \(u_{5}\) | -1 | -1 | 1 | \(-\frac{2}{3}\) | \(-\frac{2}{\sqrt{3}}\) | \(-\frac{\sqrt{2}}{3}\) |
| \(u_{6}\) | 1 | -1 | 1 | \(\frac{2}{3}\) | \(-\frac{2}{\sqrt{3}}\) | \(\frac{\sqrt{2}}{3}\) |
| \(u_{7}\) | 1 | 1 | 1 | \(0\) | \(0\) | \(\sqrt{2}\) |
Stellt man alle elementaren Spannungsvektoren grafisch in der \(\alpha/ \beta\) Ebene dar, ergibt sich ein Sechseck (vgl. Abb. 9.5).
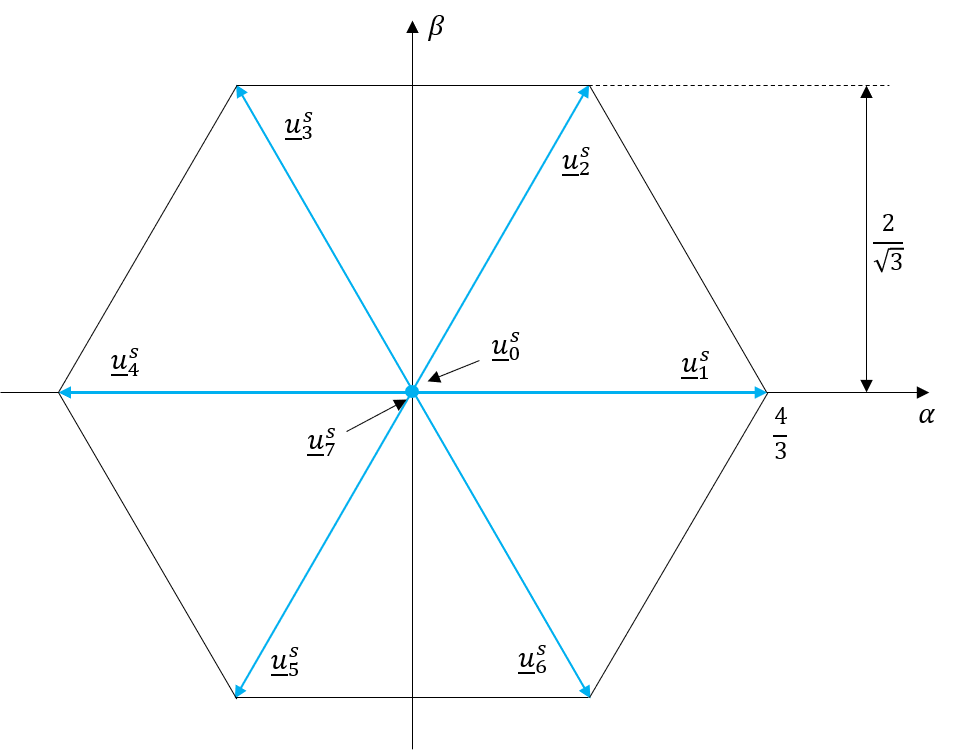
Abbildung 9.5: Normierte elementare Spannungsvektoren im statorfesten KOS
Es ergeben sich zwei Nullspannungsvektoren \(\underline{u}_{0}\) und \(\underline{u}_{7}\), die sich damit begründen lassen, dass bei diesen Schalterstellungen alle drei Ausgänge des Umrichters auf dem gleichen Potential liegen. Das Gleichtaktverhalten der Umrichter-Ausgangsspannungen wird durch die Nullkomponente beschrieben. Da die Motorwicklungen üblicherweise isoliert betrieben werden und alle drei Motorpotentiale somit im Gleichtakt verschoben werden, kann die Nullkomponente für die Regelung vernachlässigt werden. Allerdings verursacht die Nullkomponente Verschiebungsströme über parasitäre Komponenten zwischen den Motorwicklungen und dem Gehäuse sowie der Schirmung.
9.2 Pulsweitenmodulation
Da der Umrichter lediglich 8 Schaltzustände und 7 unterschiedliche Spannungen an seinen Ausgängen erzeugen kann, muss man sich einer speziellen Methode bedienen, um Spannungszwischenwerte zu erzeugen. Eine der möglichen Methoden ist die Pulsweitenmodulation, bei der der Mittelwert der Ausgangsspannung durch zeitlich unterschiedlich langes Verweilen in den Schaltpositionen beeinflusst werden kann.
9.2.1 Einphasige Pulsweitenmodulation
Zur Verdeutlichung soll die Funktionsweise der einpasigen Pulsweitenmodulation beschrieben werden. Bei der Pulsweitenmodulation wird ein Spannungssollwert (\(U_{Ref}\)) als Eingangsgrösse betrachtet, welches mit einem linearen Modulationssignal (üblicherweise ein Dreieckssignal \(d(t)\)) definierter Frequenz verglichen wird. Das Ergebnis dieses Vergleiches wird direkt dazu verwendet die Schaltfunktion \(s(t)\) zu erzeugen. Dieses Prinzip ist in Abbildung 9.6 für einen konstanten Spannungs-Sollwert dargestellt.
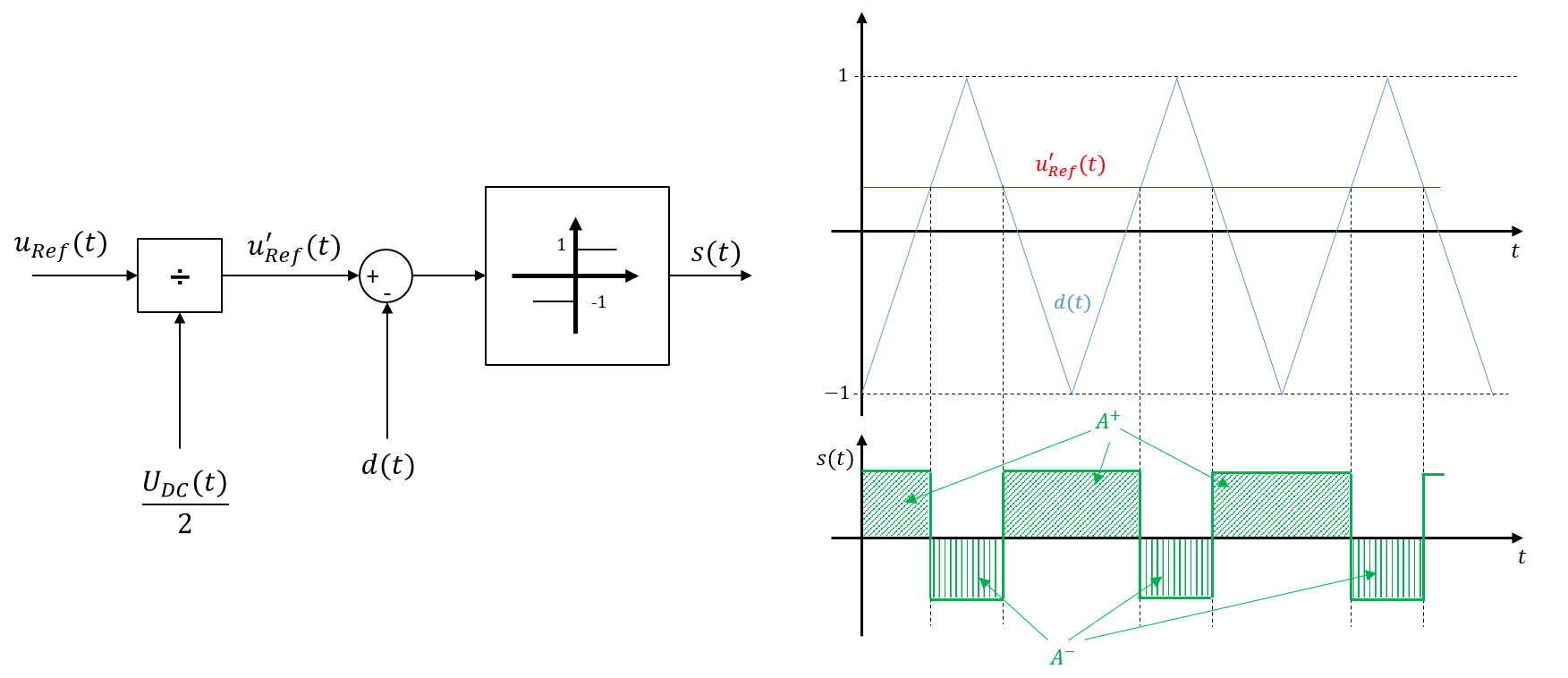
Abbildung 9.6: Funktionsprinzip der Pulsweitenmodulation mit konstantem Spannungs-Sollwert
Der zeitliche Mittelwert (respräsentiert durch die positiven (\(A^{+}\)) bzw. negativen (\(A^{-}\)) Schaltfunktions-Zeitflächen) entspricht dabei dem normierten Spannungs-Sollwert. Es sei darauf hingewiesen, dass das Modulationssignal auch von der Dreiecksform abweichen kann. Lediglich die Forderung nach einem abschnittsweise linearen Verlauf des Modulationssignals (z.B. Sägezahnsignal) bleibt bestehen. Da als Modulationssignal sehr häufig auf die Dreiecksfunktion zurückgegriffen wird, wird dieses Verfahren auch als Dreieckmodulation bezeichnet. Dieses Verfahren kann für beliebige (z.B. sinusförmige) Sollwerte angewandt werden (vgl. Abbildung 9.7), wobei die Frequenz des Sollwertsignals mindestens um den Faktor 10 kleiner sein sollte als die Frequenz des Modulationssignals. In Zusammenhang mit einem sinusförmigen Spannungs-Sollwert, spricht man häufig auch von der Sinus-Dreieck Modulation oder dem Unterschwingungsverfahren.
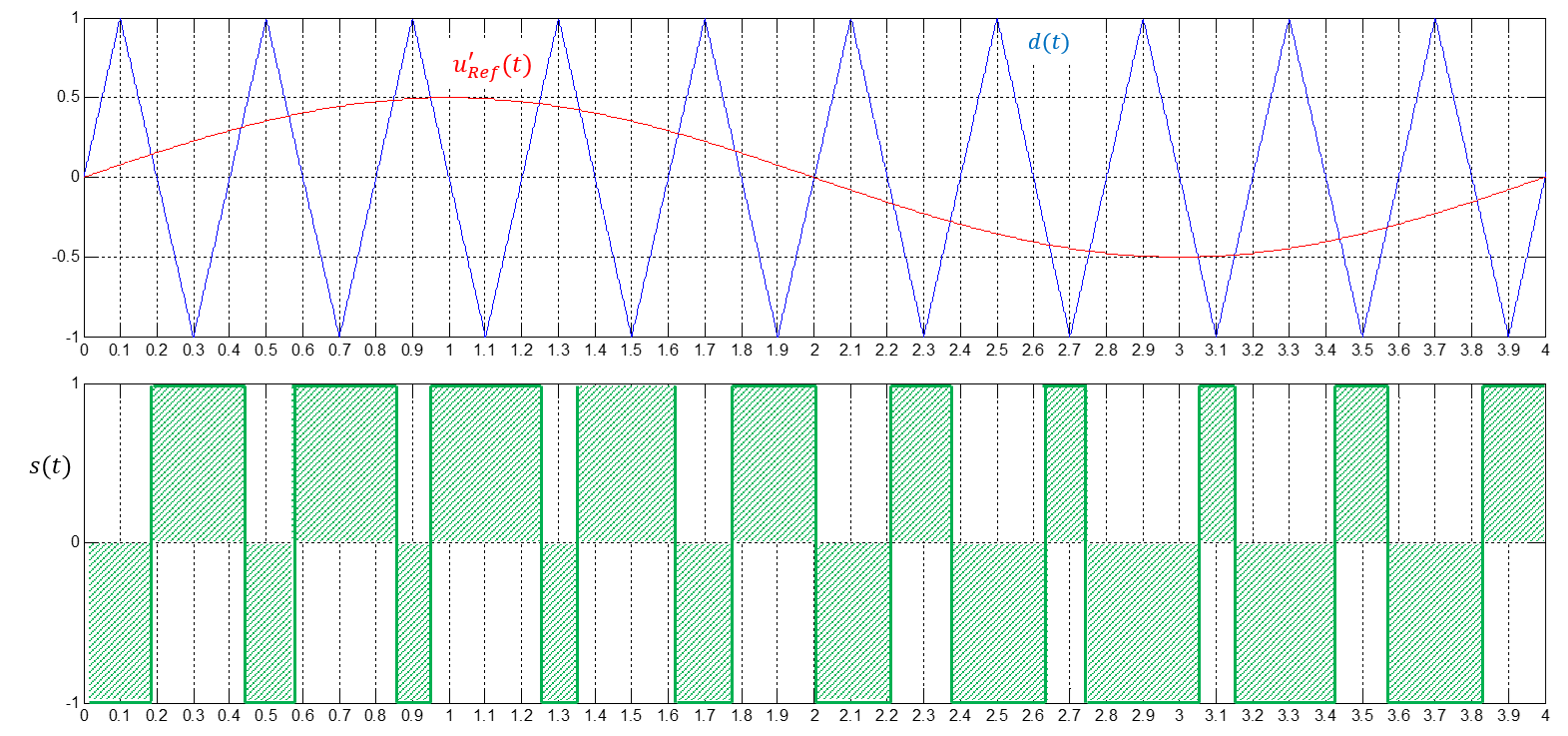
Abbildung 9.7: Funktionsprinzip der Pulsweitenmodulation sinusförmigen Spannungs-Sollwert
Um eine Aussage zur Amplitude des Spannungs-Sollwertes machen zu können, wird üblicherweise von der Aussteuerung \(A\) des Umrichters gesprochen, welche den Scheitelwert des normierten Referenzwertes beschreibt.
\[ A=max\left| \frac{u_{Ref}(t)}{\frac{U_{DC}(t)}{2}}\right| = max\left| u_{Ref}^{'}\right| \leq 1 \]
Die Abbildungen 9.6 bzw. 9.7 machen deutlich, dass die Schaltfrequenz des Umrichters durch die Frequenz des Modulationssignals (\(d(t)\)) gegeben ist. Die Frequenz kann dabei, je nach Leistung des Antriebssystems, im Bereich weniger hundert Hertz (grosse Leistungen) bis zu mehreren 10kHz (geringere Leistungen) liegen. Die geringere Frequenz bei grossen Leistungen lässt sich damit begründen, dass die Schaltverluste der Leistungshalbleiter mit der Schaltfrequenz zunehmen.
9.2.2 Dreiphasige Pulsweitenmodulation
Das in Kapitel 9.2.1 beschriebene Prinzip der Sinus-Dreieck Modulation lässt sich sehr einfach auch für dreiphasige Anwendungen, wie beispielsweise Umrichter, anwenden, indem das in Abbildung 9.6 dargestellte Verfahren zur Erzeugung der Schaltfunktion \(s(t)\) um zwei weitere sinusförmige Sollwerte, die um jeweils 120° zeitlich versetzt angeordnet sind, erweitert.
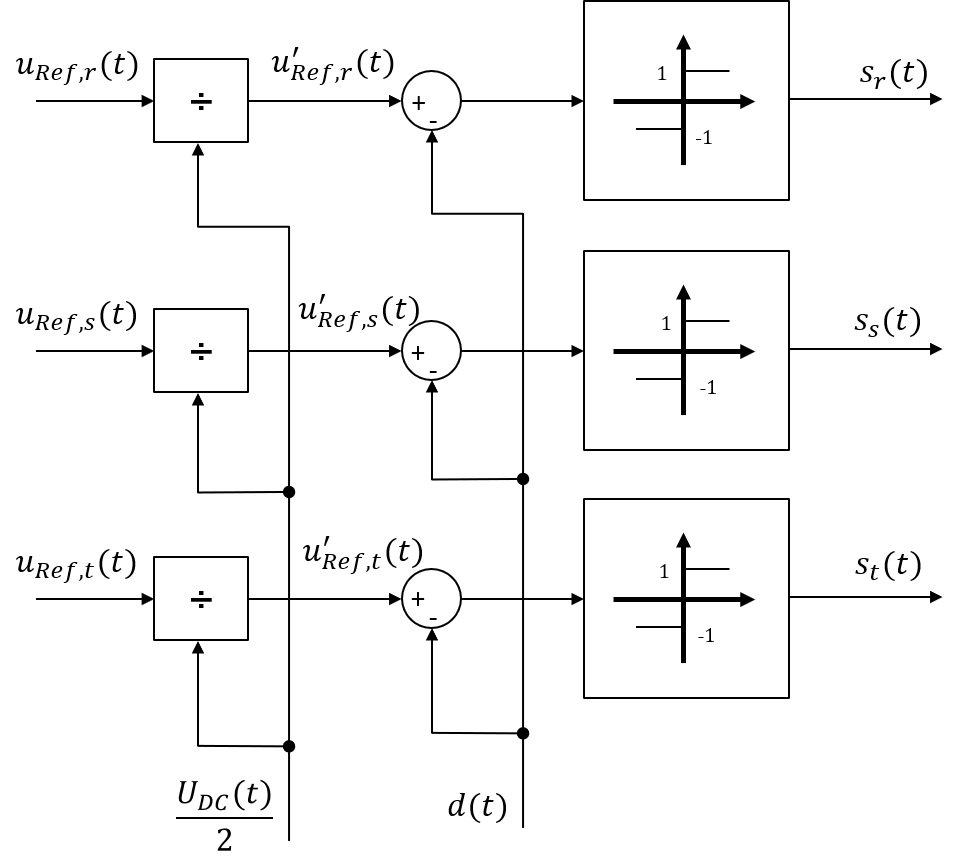
Abbildung 9.8: Funktionsprinzip der dreiphasigen Pulsweitenmodulation
Die Erzeugung der drei Schaltfunktionen \(s_{r,s,t}(t)\), welche sich aus dieser Methode ergibt, ist in Abbildung 9.9 dargestellt. Die Ausstereung jeder einzelnen Phase kann dabei maximal den Wert \(A_{r,s,t}=1\) erreichen.
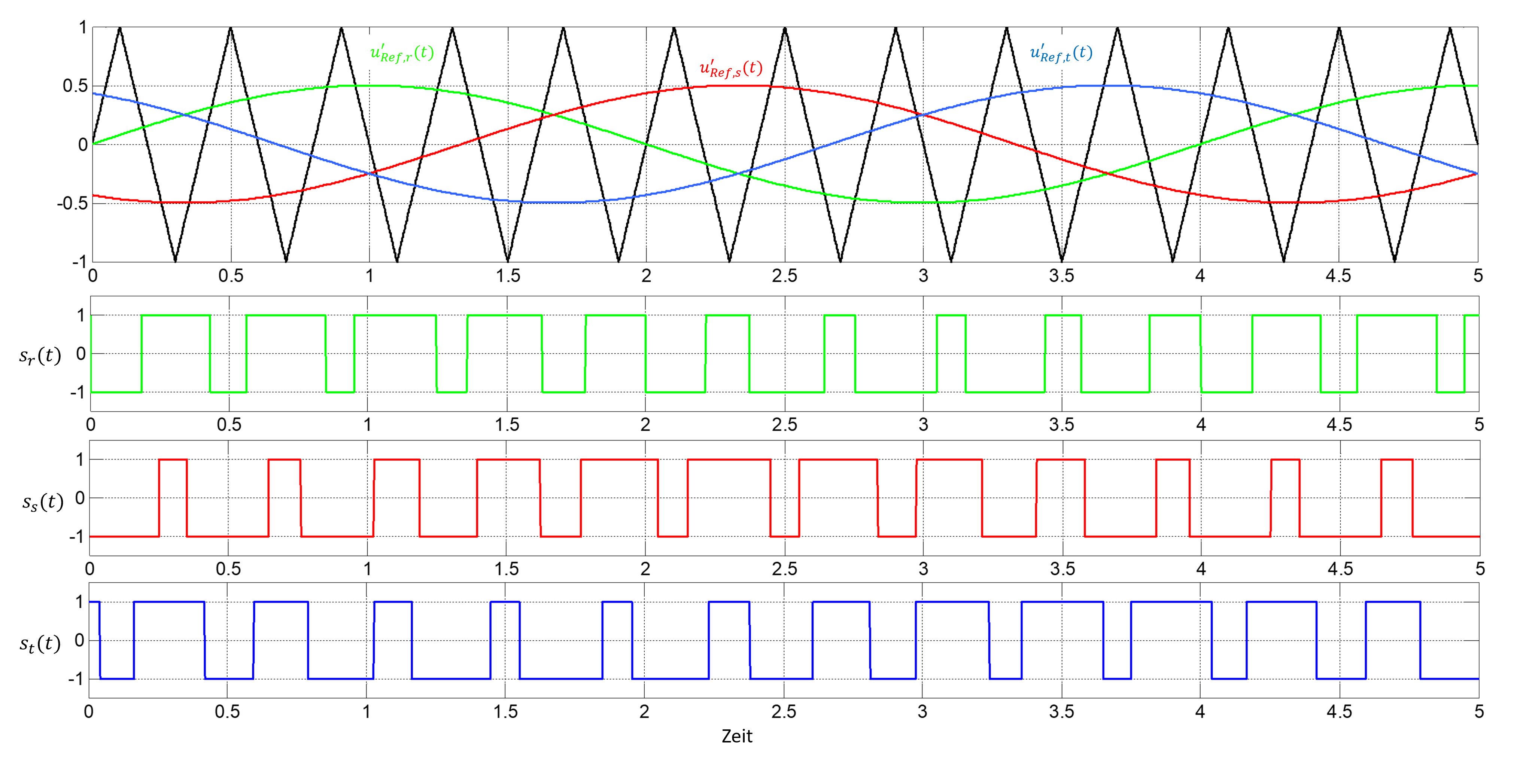
Abbildung 9.9: Erzeugung der Schaltfunktionen für ein sinusförmiges Drehspannungssystem mit einer Aussteuerung von A=0.5
Der Nachteil dieses Verfahrens besteht darin, dass die maximale verkettete Spannung zwischen zwei Strängen, die vom Umrichter auf den Motor geschaltet werden können, nie den theoretisch denkbaren Maximalwert von \(U_{DC}\) erreicht. Dies ist auch in Abbildung 9.10 ersichtlich.
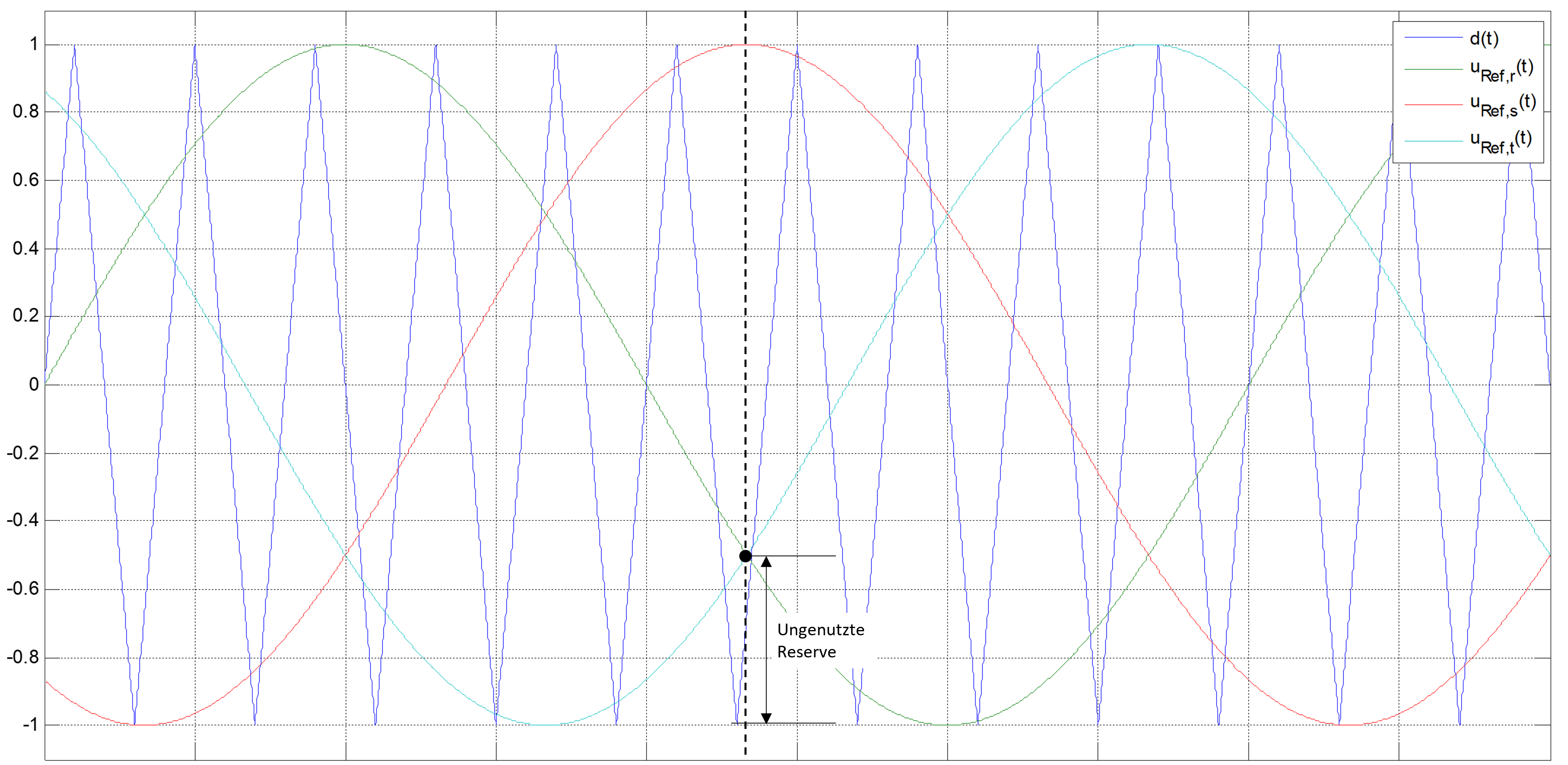
Abbildung 9.10: Spannungsreserve bei der dreiphasigen Pulsweitenmodulation
Um diesen Nachteil zu eliminieren, wird das Bezugspotential durch Addition einer Nullkomponente verschoben. Diese verschiebung hat keinen Einfluss auf die verketteten Spannungen, erhöht allerdings den Aussteuerbereich. Die Amplitude dieser Nullkomponente kann bestimmt werden, indem zu jedem Zeitpunkt die Summe des grössten und des kleinsten normierten Referenzwertes bestimmt wird und mit dem Faktor 0.5 multipliziert wird.
\[ u_{0}(t) = -\frac{1}{2}\left[max\left(u_{Ref,r}^{'}(t),u_{Ref,s}^{'}(t),u_{Ref,t}^{'}(t)\right)+min\left(u_{Ref,r}^{'}(t),u_{Ref,s}^{'}(t),u_{Ref,t}^{'}(t)\right)\right] \]
Da es sich um eine Nullkomponente handelt, muss diese zu jedem einzelnen normierten Spannungsreferenzwert addiert werden und es ergeben sich drei modifizierte Spannungsreferenzwerte (\(u_{Ref,i}^{''}(t)\)).
\[ \begin{matrix} u_{Ref,r}^{''}(t) = u_{Ref,r}^{'}(t) + u_{0}(t) \\ u_{Ref,s}^{''}(t) = u_{Ref,s}^{'}(t) + u_{0}(t) \\ u_{Ref,t}^{''}(t) = u_{Ref,t}^{'}(t) + u_{0}(t) \end{matrix} \]
Aufgrund dessen, kann das Blockschaltbild zur Erzeugung der Schaltfunktionen (vgl. Abb. 9.8) modifiziert werden und liefert das Blockschaltbild in Abbildung 9.11.
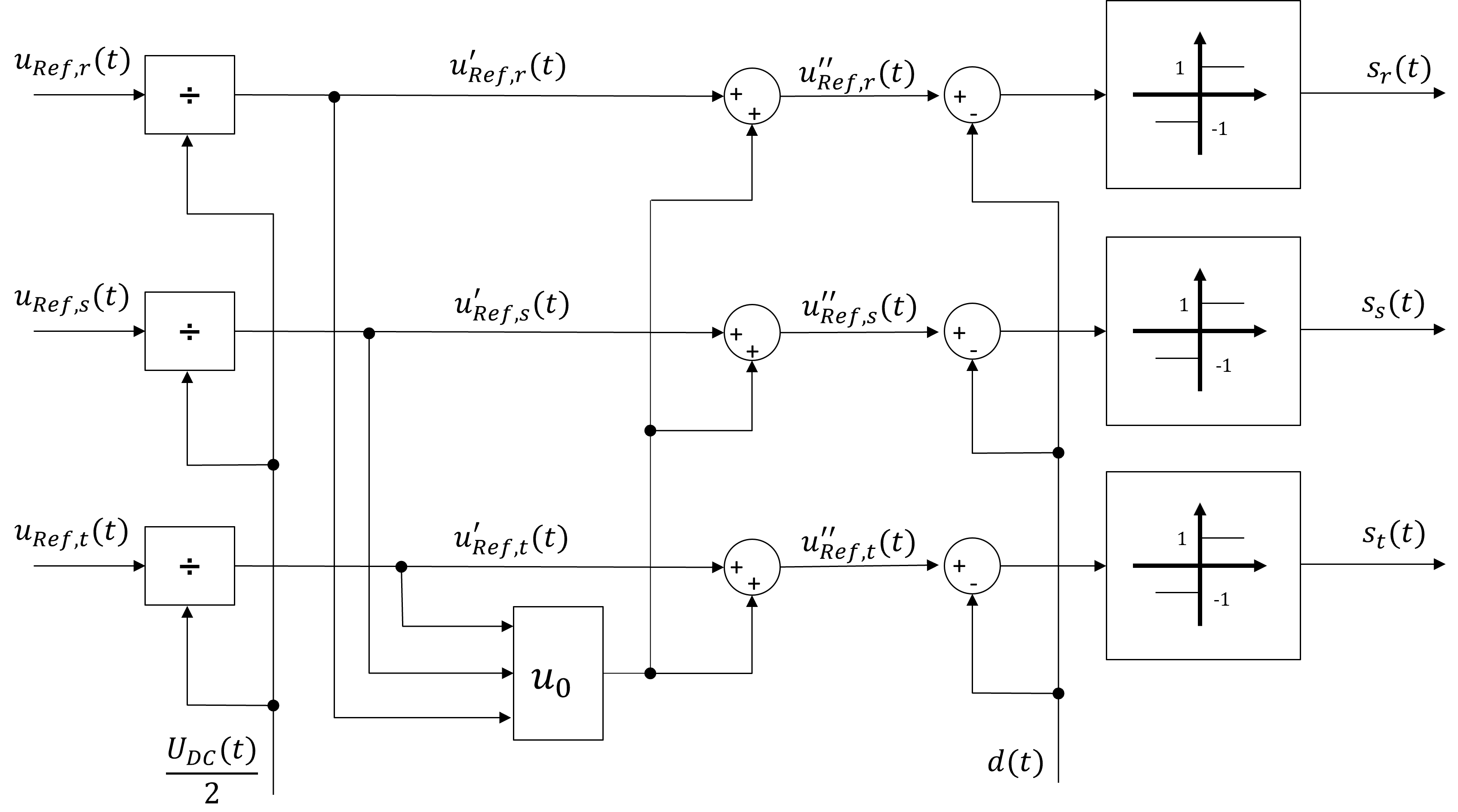
Abbildung 9.11: Spannungsreserve bei der dreiphasigen Pulsweitenmodulation
Durch diese Modifikation verlieren die Strangsollwerte, im Gegensatz zu den verketteten Spannungen, ihre Sinusform (vgl. Abb. 9.12).
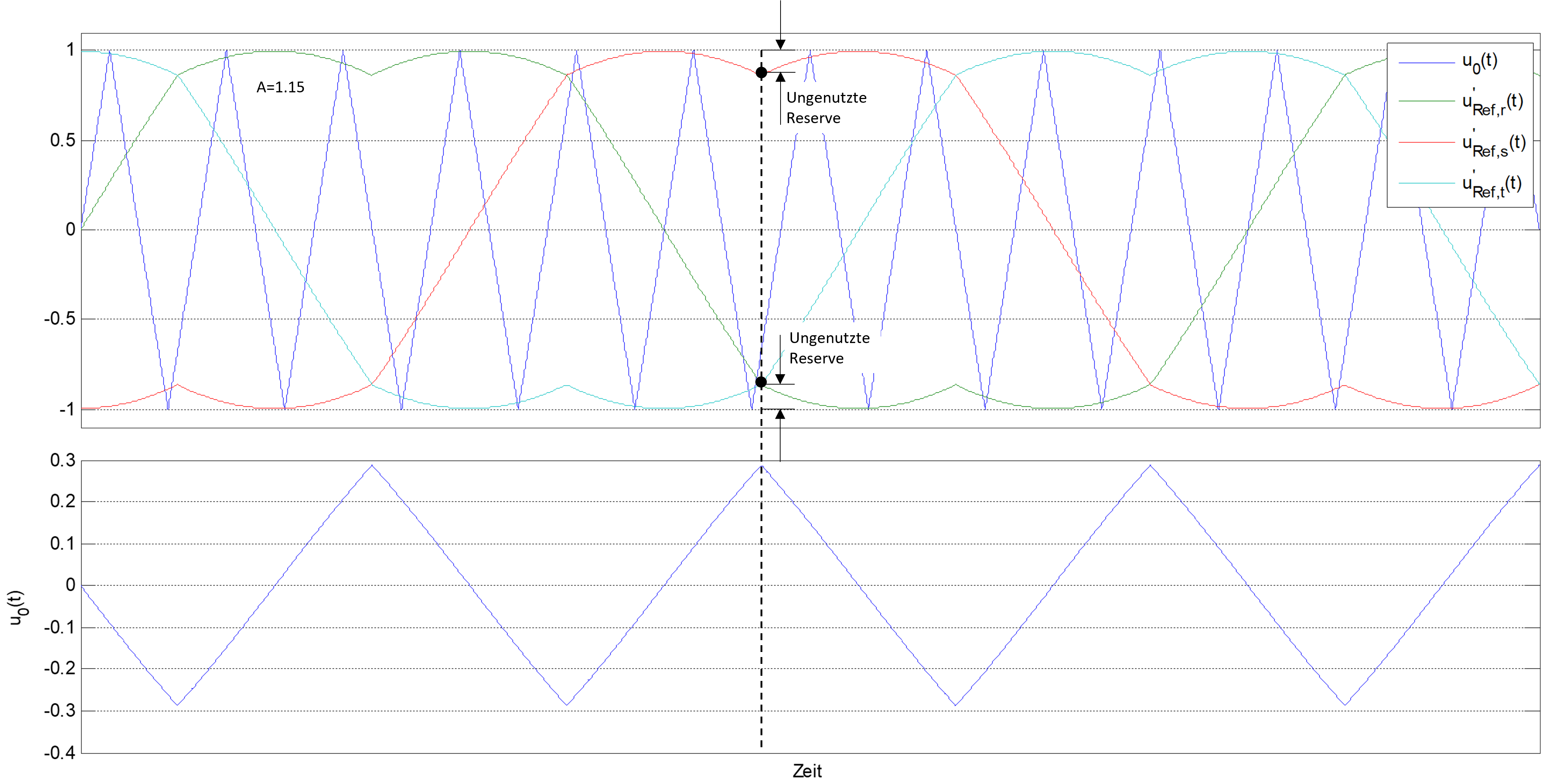
Abbildung 9.12: Modifizierte dreiphasigen Pulsweitenmodulation mit Nullpunktverschiebung bei einer Aussteuerung von A=1.15 (oben: modifizierte Referenzwerte, unten: Nullkomponente)
Da die Frequenz der Nullkomponente die dreifache Frequenz der Sollwertesignale besitzt, wird diese Methode auch als Injektion der dritten Harmonischen bezeichnet. Die Verschiebung ermöglicht somit die Ausnutzung des maximal möglichen Aussteuerungsbereiches für die verketteten Spannungen. Da die maximale Ausgangsspannung des Umrichter zwischen zwei Phasen der verketteten Spannung entspricht, kann die Amplitude des Sollwert für die verketteten Spannungen in folgendem Bereich liegen:
\[ \left|u_{Ref_{rs,st,tr}}(t)\right| \leq U_{DC} \iff \frac{\left|u_{Ref_{rs,st,tr}}(t)\right|}{U_{DC}} \leq 1 \]
Wird der Verkettungsfaktor \(\sqrt{3}\), zur Umrechnung zwischen Strangspannung und verketteter Spannung, berücksichtigt,
\[ u_{Ref_{r,s,t}}(t) = \frac{u_{Ref_{rs,st,tr}}(t)}{\sqrt{3}} = \frac{k\cdot U_{DC}}{\sqrt{3}}, \space k\leq 1 \]
kann die Aussteuerung für die Pulsweitenmodulation mit Injektion der dritten Harmonischen bestimmt werden:
\[ A=max\left| \frac{u_{Ref_{r,s,t}}(t)}{\frac{U_{DC}(t)}{2}}\right| = max\left| \frac{k\cdot U_{DC}}{\frac{\sqrt{3}\cdot U_{DC}}{2}}\right| = \frac{2}{\sqrt{3}}k \] Der Faktor \(k\) beschreibt dabei die Amplitude des Sollwertes und kann maximal den Wert 1 annehmen. Folglich kann die maximale Aussteuerung \(A_{max}\) (bei \(k=1\)) einen Wert von
\[ A_{max} = \frac{2}{\sqrt{3}}=1.15 \]
erreichen. Das Hinzufügen der Nullkomponente erhöht die maximale Aussteuerung also um 15 Prozent. Dieser Zusammenhang ist nochmals grafisch in Abbildung 9.13 dargestellt.
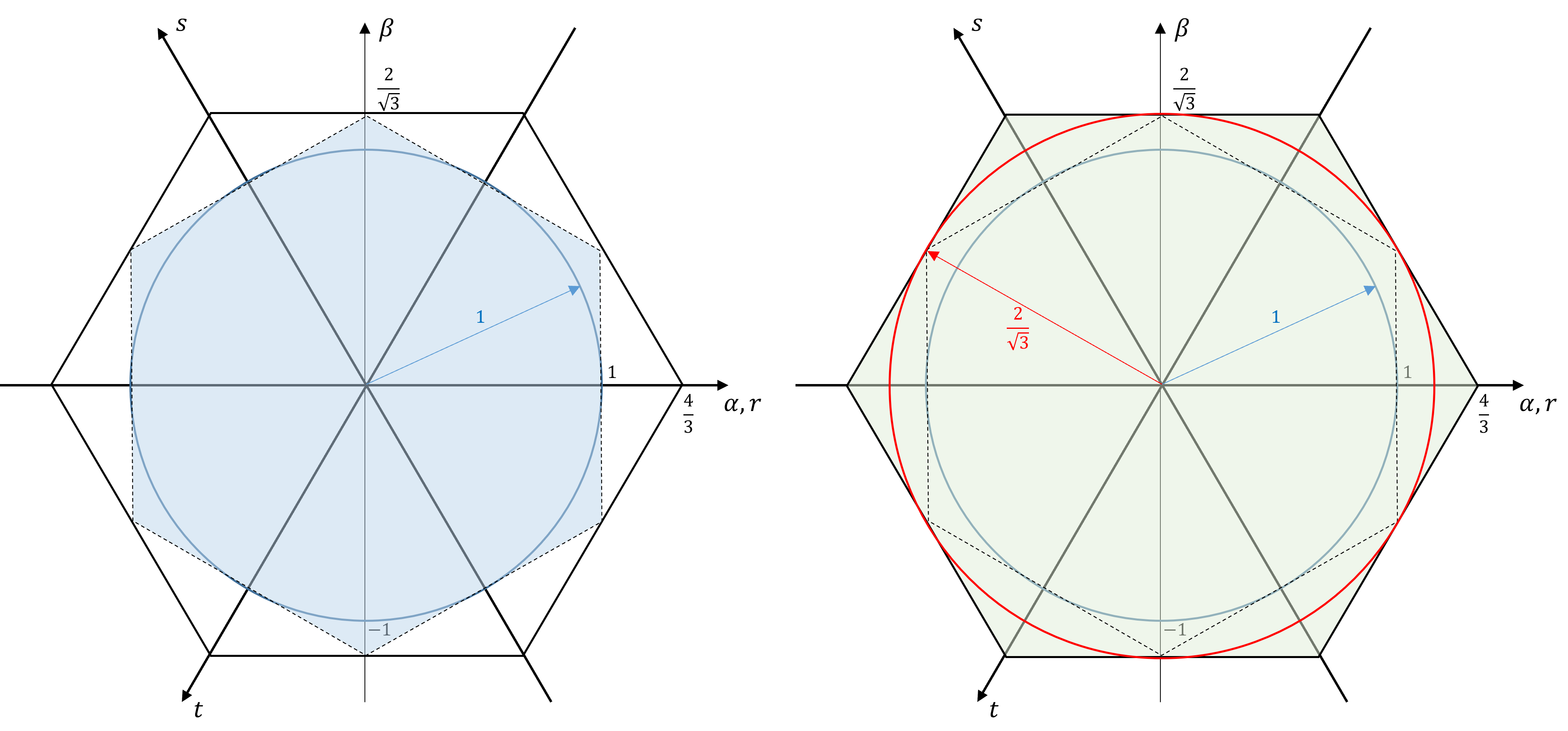
Abbildung 9.13: Vergleich der durch Dreiecksmodulation realisierbaren Spannungsvektoren (links: ohne Nullpunktverschiebung, rechts: mit Nullpunktverschiebung)
9.3 Raumzeigermodulation
Bei der Dreiecksmodulation werden die drei Stränge einzeln moduliert. Bei der Raumzeigermodulation, die auch als Vektormodulation (eng. space vector modulation) bezeichnet wird, wird stattdessen von einem Spannungssollwert-Raumzeiger \(\underline{u}_{Ref,s}^{s}\) in Statorkoordinaten ausgegangen. Der Grundgedanke besteht dabei darin, den Mittelwert des Umrichterausgangsspannungs-Raumzeigers mit Hilfe einer geeigneten zeitlichen Abfolge von elementaren Spannungsvektoren \(u_{i}\) innerhalb eines definierten Zeitintervalls \(T_{a}\) dem Spannungsreferenz-Raumzeiger anzupassen. Dazu wird ein Zeitintervall \(T_{a}\) definiert, in dem diese zeitlichen Abfolge der elementaren Spannungsvektoren untergebracht werden soll. Da es grundsätzlich acht elementare Spannungsvektoren gibt (vgl. Abb 9.5), wäre es denkbar all diese für einen gewissen Zeitraum \(t_{i}\leq T_{a}\) am Ausgang des Umrichters anzulegen.
\[ \underline{u}_{Ref,s}^{s}(i) = \frac{1}{T_{a}} \int_{iT_{a}}^{(i+1)T_{a}}{u(t)\ dt}= \frac{1}{T_{a}} \sum_{i=0}^{7}{t_{i}\underline{u}_{i}} \]
Die Summe der einzelnen Zeiten \(t_{i}\) muss dabei die Bedingung
\[ \sum_{i}{t_{i}} = T_{a}, \space t_{i} \geq 0 \]
Die Summe aller Zeiten muss also exakt dem definierten Zeitintervall \(T_{a}\) entsprechen. In der Literatur werden die Zeiten \(t_{i}\) häufig noch auf die Abtastzeit \(T_{a}\) normiert,
\[ \tau_{i} = \frac{t_{i}}{T_{a}} \]
wodurch sich obige Gleichung verändert.
\[ \underline{u}_{Ref,s}^{s}(i) = \sum_{i=0}^{7}{\tau_{i}\underline{u}_{i}} \]
Dabei gilt es auch die Nebenbedingung, das die Summe aller Zeitkomponenten exakt dem Abtastintervall \(T_{a}\) entsprechend muss, anzupassen.
\[ \sum_{i}{\tau_{i}} = 1, \space \tau_{i} \geq 0 \]
Da, je nach Position des Sollspannungs-Raumzeigers \(\underline{u}_{Ref,s}^{s}(i)\), maximal drei der acht verfügbaren elementaren Spannungsvektoren ausreichen, um den Raumzeiger abzubilden, kann obige Geichung zur Bestimmung der Einschaltzeiten der elementaren Spannungsvektoren vereinfacht werden.
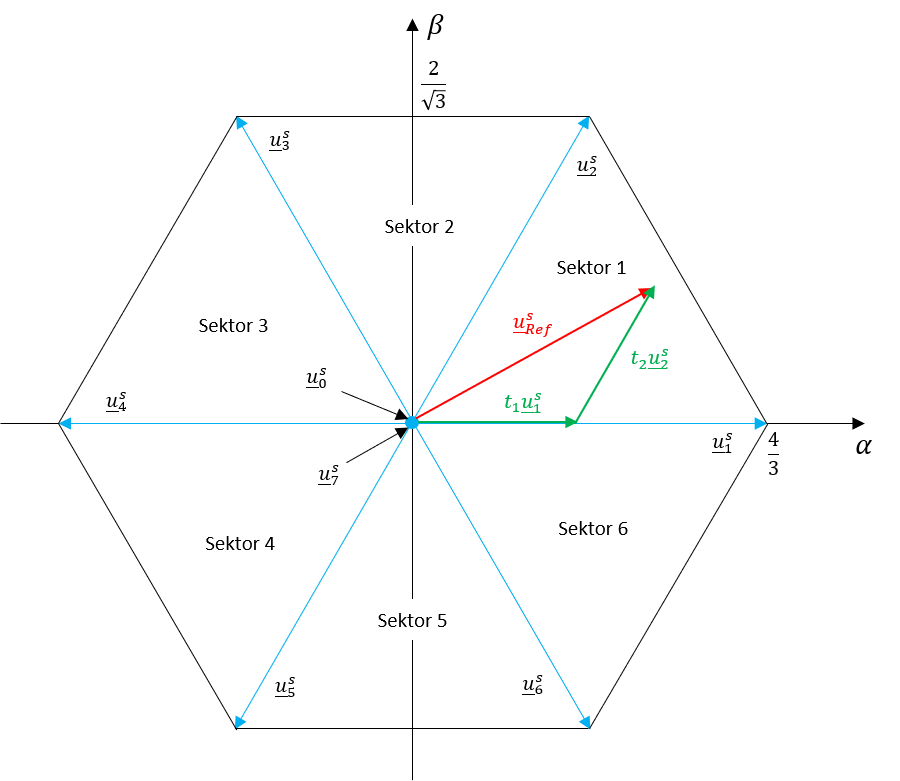
Abbildung 9.14: Funktionsprinzip der Raumzeigermodulation für einen Sollspannungs-Raumzeiger im Sektor 1
Dazu werden, je nachdem in welchem Sektor sich der Sollspannungs-Raumzeiger befindet, die den jeweiligen Sektor begrenzenden elementaren Spannungsvektoren (\(u_{li}\) bzw. \(u_{re}\)) und die Nullspannungsvektoren (\(u_{0}\) oder \(u_{7}\)) verwendet (siehe Abb. 9.14). Rein geometrisch betrachtet lassen sich die normierten Zeiten \(\tau_{i}\) als duale Koordinaten interpretieren, welche an den Achsen abgelesen werden können, die senkrecht auf den elementaren Vektoren stehen (vgl. Abb. 9.15).
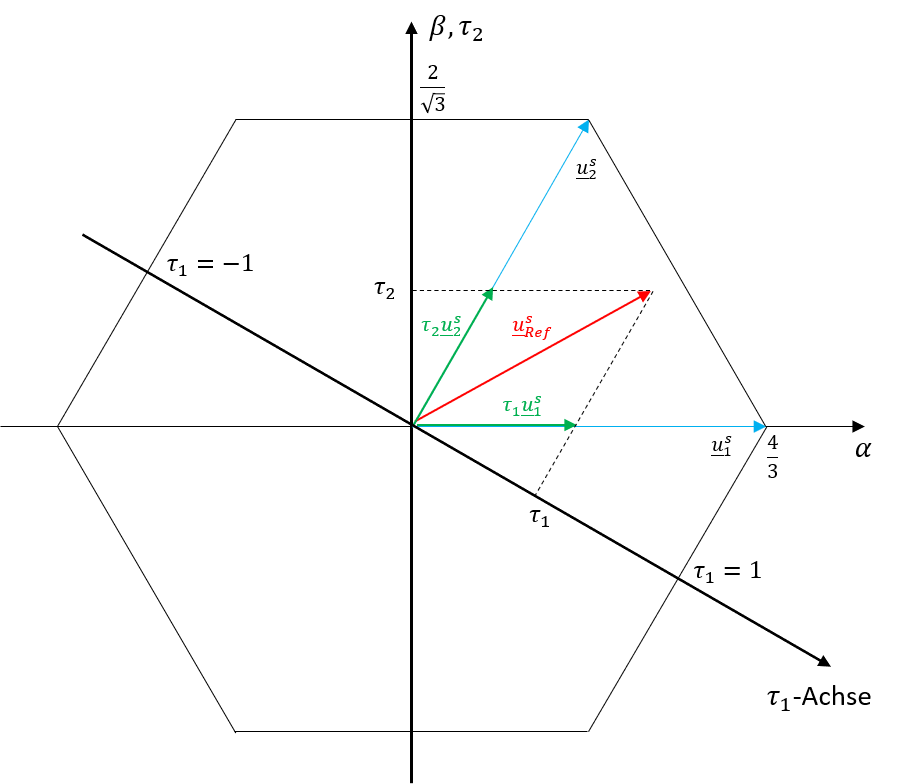
Abbildung 9.15: Beispiel zur geometrischen Interpretation der Zeiten \(\tau_{i}\) durch duale Koordinaten
\[ \begin{matrix} \underline{u}_{Ref,s}^{s}(i) = \frac{1}{T_{a}} \int_{iT_{a}}^{(i+1)T_{a}}{u(t)\ dt} = \frac{1}{T_{a}}\left(t_{0,7}\cdot \underline{u}_{0,7}+t_{re}\cdot\underline{u}_{re}+t_{li}\cdot\underline{u}_{li} \right) \\ = \tau_{0,7}\cdot\underline{u}_{0,7}+\tau_{re}\cdot\underline{u}_{re}+\tau_{li}\cdot\underline{u}_{li} \end{matrix} \]
Ist der Sollspannungs-Raumzeiger \(\underline{u}_{Ref,s}^{s}(i)\) gegeben, dann kann dieses Gleichungssystem nach den normierten Zeiten \(\tau_{li}\) und \(\tau_{re}\) aufgelöst werden.
\[ \left(\begin{matrix}u_{Ref_\alpha} \\ u_{Ref_\beta} \end{matrix}\right) = \tau_{re} \left(\begin{matrix}u_{re_\alpha} \\ u_{re_\beta} \end{matrix}\right) + \tau_{li} \left(\begin{matrix}u_{li_\alpha} \\ u_{li_\beta} \end{matrix}\right) \]
Der Term \(\tau_{0,7}\cdot\underline{u}_{0,7}\) wurde in obiger Gleichung weggelassen, da die Komponenten der Nullspannungsvektoren Null sind. Werden die entsprechenden \(\alpha,\beta\)-Komponenten der links- und rechtsseitig begrenzenden elementaren Spannungsvektoren in obige Gleichung eingesetzt, dann kann eine Berechnungsvorschrift für die Zeiten gefunden werden.
\[ \begin{matrix} \tau_{re} = \frac{u_{Ref_\beta}\cdot u_{li_\alpha} - u_{Ref_\alpha}\cdot u_{li_\beta}}{u_{re_\beta}\cdot u_{li_\alpha} - u_{re_\alpha}\cdot u_{li_\beta}} \\ \tau_{li} = \frac{1}{u_{li_\alpha}}\left(u_{Ref_\alpha}-u_{re_\alpha} \frac{u_{Ref_\beta}\cdot u_{li_\alpha} - u_{Ref_\alpha}\cdot u_{li_\beta}}{u_{re_\beta}\cdot u_{li_\alpha} - u_{re_\alpha}\cdot u_{li_\beta}} \right) \\ \tau_{0,7} = 1-\tau_{re}-\tau_{li} \end{matrix} \]
Mit Hilfe der Raumzeigermodulation lassen sich alle Sollspannungsvektoren, die innerhalb des durch die sechs elementaren Spannungsvektoren aufgespannten Hexagons liegen, realisieren. Folglich entspricht der Aussteuerungsbereich der Raumzeigermodulation dem der Pulsweitenmodulation mit Nullpunktverschiebung.
\[ \left|\underline{u}_{Ref,s}^{s} \right| \leq \frac{2}{\sqrt{3}} \]
Trotz der eindeutigen Definition der Einschaltzeiten für die beiden rechts- und linksseitig begrenzenden elementaren Spannungsvektoren und des Nullspannungsvektors, ergeben sich dennoch gewisse Freiheitsgrade bei der schlussendlichen Umsetzung der Raumzeigermodulation. Es kann beispielsweise zwischen zwei Nullspannungsvektoren \(\underline{u}_{0}\) bzw. \(\underline{u}_{7}\) gewählt werden. Ausserdem kann die Reihenfolge der begrenzenden, elementaren Spannungsvektoren frei gewählt werden. In der Praxis wird die Aktivierungsdauer des Nullspannungsvektors gern hälftig auf den Beginn und das Ende des Abtastintervall \(T_{a}\) gelegt. Da jeder Schaltvorgang mit Verlusten einhergeht, wird somit üblicherweise der Nullspannungsvektor ausgewählt, der weniger Schalthandlungen nach sich zieht. Es ist auch zulässig die Aktivierungsdauern der einzelnen elementaren Spannungsvektoren in mehrere Zeitblöcke aufzuteilen und dann gemischt über das Abtastintervall zu verteilen. Dieses Vorgehen hat eine höhere Schaltfrequenz, bei gleichzeitiger Reduktion des Stromrippels, zu Folge. Um die Anzahl der Schalthandlungen beim Übergang von einem zum nächsten elementaren Spannungsvektor beurteilen zu können, wird häufig das in Abbildung 9.16 dargestellte Transitionsdiagramm verwendet.
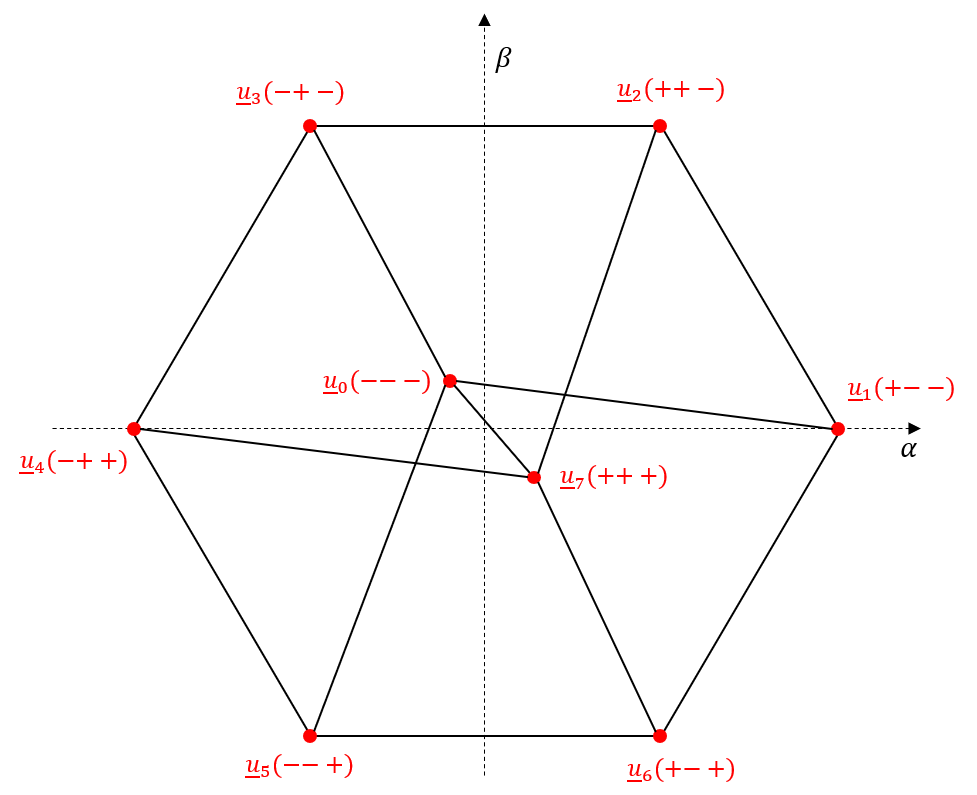
Abbildung 9.16: Übergangsdiagramm der elementaren Spannungsvektoren