Kapitel 8 Asynchronmaschine

8.1 Aufbau und Eigenschaften

Aufgrund seines recht einfachen, robusten und wartungsarmen (Wegfall der Schleifkontakte) Aufbaus ist der Asynchronmotor der am häufigsten eingesetzte Elektromotor (ca. 85% der industriellen Antriebe). Er deckt einen Leistungsbereich von wenigen Watt bis hin zu mehreren 10MW ab.

Abbildung 8.1: Schnittmodell einer ASM (Bildquelle: www.wikipedia.org)

Abbildung 8.1 zeigt einen aufgeschnittenen Asynchronmotor der Firma ABB.

Um die Wirbelstromverluste zu minimieren, werden sowohl der stillstehende Ständer als auch der rotierende Läufer geblecht ausgeführt. Beide Hauptteile sind durch einen kleinen Luftspalt voneinander getrennt. Die Ständerwicklung wird üblicherweise als symmetrische Drehstromwicklung, bestehend aus drei einzelnen Wicklunsgsträngen, ausgeführt, wie dies bereits in Kapitel 6 dargestellt wurde.

Abbildung 8.2: Einzelne Lamelle eines Eisenblechpaketes eines Läufers und Ständers (Bildquelle: www.wikipedia.org)

Bei Maschinen mit einer Polpaarzahl von \(p=1\) beträgt der räumliche Versatz der einzelnen Wicklungsstränge 120 Grad. Bei Maschinen höherer Polpaarzahl beträgt der räumliche Versatz hingegen \(\tau=\frac{120°}{p}\). Die drei Wicklungsstränge des Ständers werden in Stern- oder Dreieckschaltung an das Drehstromnetz oder einen Frequenzumrichter angeschlossen.

Man unterscheidet zwei Ausführungsformen:

• Schleifringläufer-Asynchronmaschine
• Kurzschlussläufer-Asynchronmaschine

Bei der Schleifringläufer-ASM weist der Läufer ebenfalls eine in Stern- oder Dreieck geschaltete Drehstromwicklung auf, deren Enden von aussen über isolierte, auf der Welle befindliche, Schleifringe zugänglich sind. Bei der Kurzschlussläufer-ASM hingegen besteht die Läuferwicklung aus einem sogenannten Kurzschlusskäfig (bestehend aus Aluminium- oder Kupferstäben mit beidseitig angebrachten Kurzschlussringen), der nach aussen hin nicht zugänglich ist.

Abbildung 8.3: Gegenüberstellung der Läufer von Kurz- (links) bzw. Schleifringläufern (Bildquellen: http://www.betz-simon.homepage.t-online.de/ba/ASM.pdf bzw. https://docplayer.org/70773305-5-antriebe-mit-asynchronmaschine.html)

8.2 Wirkungsweise

Betrachtet man vereinfacht einen elektrischen Leiter, der sich mit der Geschwindigkeit \(\vec{v}\) durch ein magnetisches Feld mit konstanter Induktion \(\vec{B}\) bewegt, dann werden die Ladungsträger (Elementarladungen), die sich im Leiter befinden, durch den Einfluss der Lorentzkraft \(\vec{F}_{L}\) voneinander getrennt. Die Richtung der Kraftwirkung hängt davon ab, ob es sich um eine positive oder um eine negative Elementarladung handelt. Dieser Zusammenhang ist in Abbildung 8.4 dargestellt.

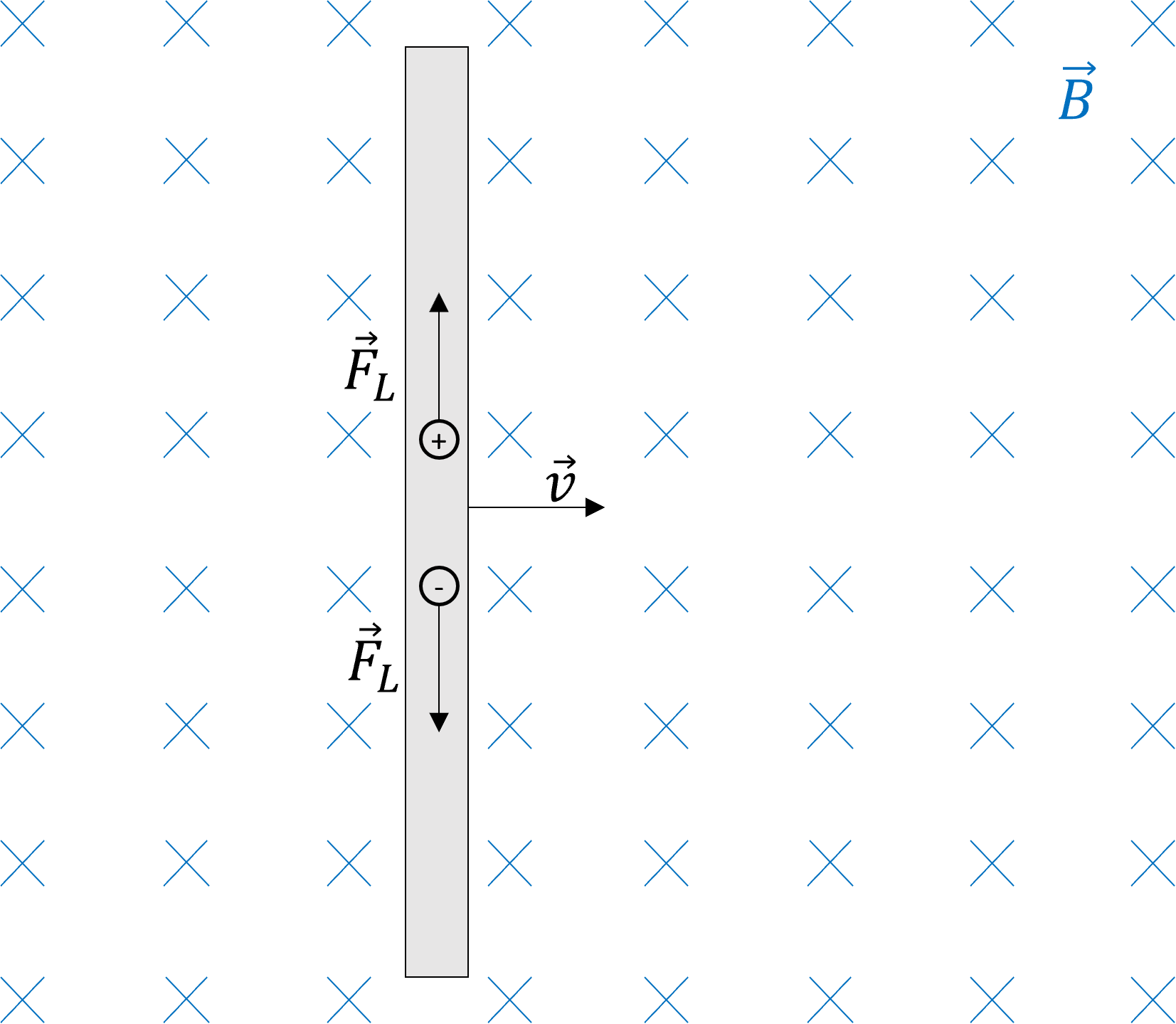
Abbildung 8.4: Kraftwirkung auf Elementarladungen eines im Magnetfeld bewegten Leiters

Die Lorentzkraft kann folgendermassen bestimmt werden.

\[ \vec{F}_{L}=q\cdot \vec{v} \times \vec{B} \]

Da, wie in der Abbildung 8.4 dargestellt, im Falle elektrischer Maschinen alle Vektoren orthogonal zueinander angeordnet sind, kann von der Vektorschreibweise abgewichen werden.

\[ F_{L}=q\cdot v\cdot B \]

Die von der Lorentzkraft hervorgerufene, örtliche Trennung der Elementarladungen ruft allerdings eine entgegengesetzt wirkende Couloumbkraft \(\vec{F}_{C}\) hervor, da sich zwischen den getrennten Elementarladungen ein elektrostatisches Feld mit der elektrischen Feldstärke \(\vec{E}\) ausbildet.

\[ \vec{F}_{C}=q\cdot \vec{E} \]

Auch hier kann, aufgrund der räumlichen Anordnung auf die Vektordarstellung verzichtet werden. Der Betrag der elektrischen Feldstärke ergibt sich dabei aus der Spannung \(U\), die sich zwischen den örtlich getrennten Ladungsträgern ausbildet und deren Abstand \(l\) zueinander (gleichbedeutend mit der Länge des Leiterstückes). Somit wirken beide Kräfte entgegengesetzt zueinander und es stellt sich ein Kräftegleichgewicht ein.

\[ F_{L}=F_{C} \iff q\cdot v\cdot B=q\cdot E = q\cdot \frac{U}{l} \]

Dieser Zusammenhang lässt sich, im Falle der Asynchronmaschine, dahingehend verwenden, dass sich die Läuferstäbe in einem rotierenden magnetischen Feld (Drehfeld) befinden. Es ergibt sich folglich eine Relativbewegung des magnetischen Feldes gegenüber der Läuferstäbe. Je nach Winkelgeschwindigkeiten des Drehfeldes und des Läufers fällt die Differenz beider Winkelgeschwindigkeiten unterschiedlich gross aus. Oben beschriebene Wirkungskette wird somit im Falle einer Asynchronmaschine ebenfalls zutreffen und in den einzelnen Läuferstäben Spannungen \(U_{ind}\) hervorrufen. Dieser Vorgang wird als Spannungsinduktion bezeichnet. Die Höhe der induzierten Spannung kann mit Hilfe obiger Gleichung bestimmt werden.

\[\begin{equation} U_{ind}=l\cdot v\cdot B \tag{8.1} \end{equation}\]

Da die Enden der einzelnen Läuferstäbe über den Kurzschlussring (in Falle einer Kurzschlussläufer-ASM) bzw. über die Schleifringe und mögliche externe Beschaltung (im Falle der Schleifringläufer-ASM) miteinander verbunden sind, führen die induzierten Spannungen zu Läuferströmen. Die Amplitude der Läuferströme ist dabei proportional zur Amplitude der induzierten Spannungen.

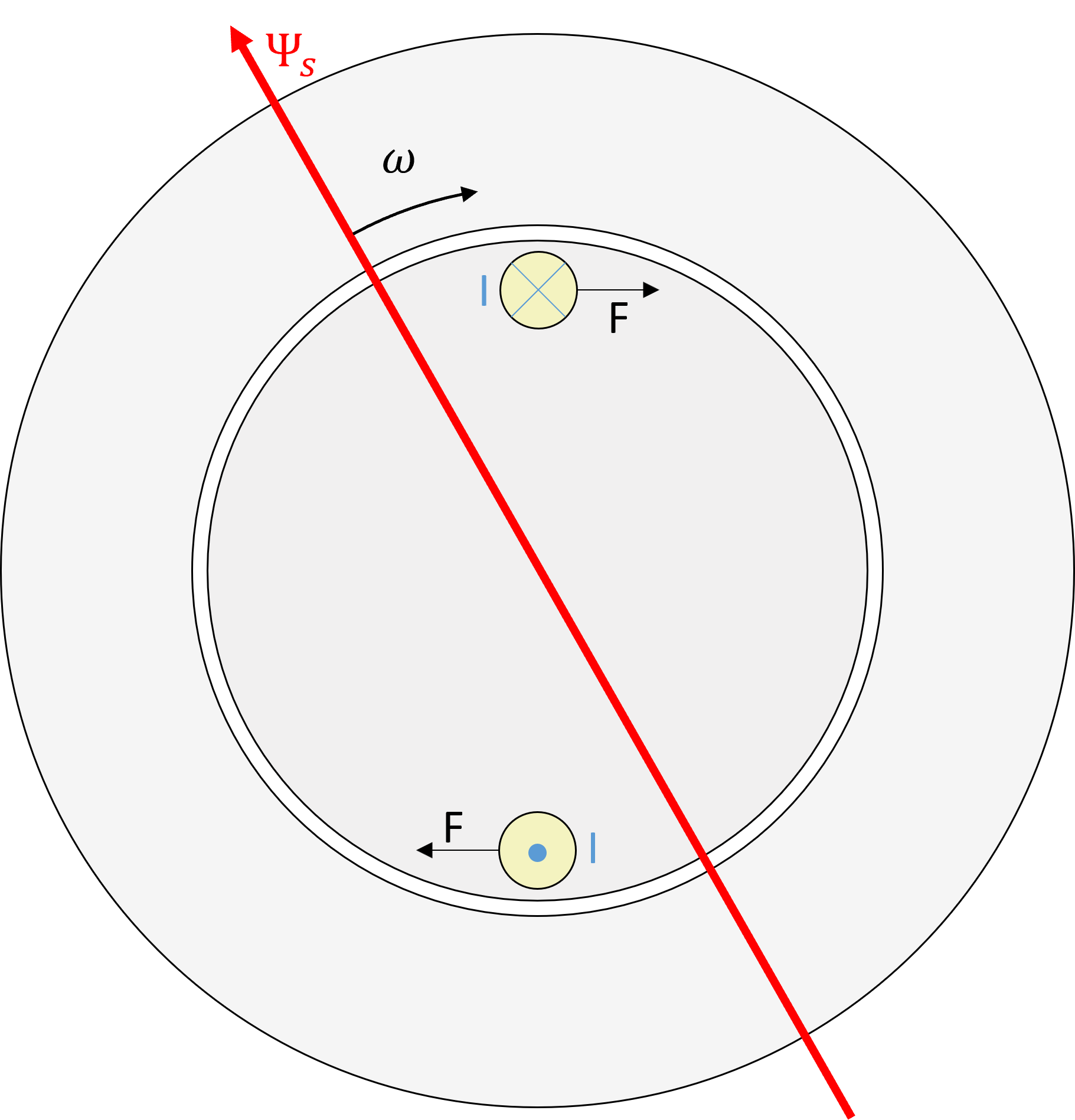
Abbildung 8.5: Simplifizierte Darstellung der Spannungsinduktion in eine einzelne Leiterschleife des Läufers

Die Abbildung 8.5 stellt, als Schnittdarstellung, eine einzelne Leiterschleife des Läufers dar, die sich in einem Drehfeld befindet (Rotation im Uhrzeigersinn). Geht man davon aus, dass sich der Läufer (und somit auch die Leiterschleife) mit einer geringeren Winkelgeschwindigkeit bewegt als das Drehfeld, dann bewegt sich die Leiterschleife relativ zum Drehfeld im Gegenuhrzeigersinn. Dies hat zur Folge, dass die positiven Ladungsträger im oberen Leiter der Leiterschleife in die Zeichenebene hinein- und im unteren Leiter der Leiterschleife aus der Zeichenebene heraus bewegt werden. Da die Bewegungsrichtung der positiven Ladungsträger mit der technischen Stromrichtung übereinstimmt, bedeutet dies, dass sich ein Stromfluss einstellt, der im oberen Teil der Leiterschleife in die Zeichenebene hinein und im unteren Leiter heraus verläuft. Dieser Stromfluss wiederum ruft eine tangential zur Schnittebene wirkende Kraft \(F\) hervor, die auf die, jetzt bewegten, Ladungsträger und somit auf die Leiterschleife wirkt. Die Kraft, die auf jeden einzelnen Läuferstab wirkt, kann mit Hilfe der Gleichung für die Lorentzkraft eines stromdurchflossenen Leiters bestimmt werden.

\[ F_{L}=I\cdot l\cdot B \]

Geht man in erster Näherung davon aus, dass die Leiterschleife lediglich einen ohmschen Widerstand \(R\) besitzt, dann kann die Stromamplitude mit Hilfe der Gleichung (8.1) zum Ausdruck gebracht werden.

\[ F_{L}=\frac{U_{ind}}{R}\cdot l\cdot B = \frac{l^{2}\cdot B^{2}\cdot v}{R} \]

Wird ausserdem berücksichtigt, dass die Relativgeschwindigkeit \(v\) mit Hilfe einer Winkelgeschwindigkeit \(\omega_{Diff}\) und dem Abstand der Leiterschleife von deren Drehachse \(r\) ausgedrückt werden kann,

\[ F_{L}=\frac{U_{ind}}{R}\cdot l\cdot B = \frac{l^{2}\cdot B^{2}\cdot r\cdot \omega_{Diff}}{R} \]

dann sind die massgeblichen Einflussfaktoren, die für die Drehmomentbildung bekannt. Hierbei gilt es zu berücksichtigen, dass die Winkelgeschwindigkeit \(\omega_{Diff}\) die Differenz zwischen der Winkelgeschwindigkeit des Drehfeldes \(\omega_{D}\) und der mechanischen Winkelgeschwindigkeit des Läufers \(\omega_{m}\) beschreibt.

\[\begin{equation} \omega_{Diff}=\omega_{D}-\omega_{m} \tag{8.2} \end{equation}\]

Da die Kraft sowohl auf den Hin- als auch den Rückleiter (oberer und unterer Leiter in obiger Darstellung) der Leiterschleife im Läufer wirkt, lässt sich eine Gleichung formulieren, die das zur Verfügung stehende Drehmoment einer einzelnen Leiterschleife beschreibt.

\[ M=2\cdot F\cdot r=2\cdot \frac{l^{2}\cdot B^{2}\cdot r^{2}\cdot \left(\omega_{D}-\omega_{m} \right)}{R} \]

Da eine Asynchronmaschine aus mehreren Läuferstäben besteht, müsste dies bei der Bestimmung des Drehmomentes berücksichtigt werden. Obige Gleichung lässt hingegen einige Rückschlüsse auf das Verhalten der Maschine zu. Die wichtigste Erkenntnis bezieht sich auf die Differenz der Winkelgeschwindigkeiten. Drehen Läufer und Drehfeld mit der gleichen Winkelgeschwindigkeit, dann wird das Drehmoment zu Null. Dieser Zusammenhang wird auch durch die Namensgebung dieses Maschinentyps zum Ausdruck gebracht, indem von einer Asynchronität ausgegangen wird. Soll von der Maschine ein von Null verschiedenes Drehmoment aufgebracht werden, müssen sich die Winkelgeschwindigkeiten von Drehfeld und Läufer unterscheiden. Es sei weiterhin darauf hingewiesen, dass die magnetische Flussdichte \(B\) massgeblich von der Ständerspannung abhängt. Die Differenzdrehzahl zwischen Drehfeld und Läufer bezogen auf die Drehfelddrehzahl \(n_{s}=\frac{f_{N}}{p}\) wird als Schlupf \(s\) bezeichnet.

\[\begin{equation} s=\frac{n_{s}-n_{m}}{n_{s}}= \frac{\omega_{s}-p\omega_{m}}{\omega_{s}}= \frac{\omega_{r}}{\omega_{s}} \tag{8.3} \end{equation}\]

Der Schlupf stellt eine der wichtigsten Systemgrössen des Asynchronmotors dar. Ein zweiter Effekt, der bei der Drehmomentbildung der ASM berücksichtigt werden muss, sind die parasitären Induktivitäten der Leiterschleifen im Läufer. Diese führen einerseits dazu, dass sich eine zeitliche Verzögerung (Phasenverschiebung) zwischen den induzierten Spannungen und den Läuferströmen einstellt. Dies führt dazu, dass der Läuferstrom in dem Moment, in dem die magnetische Flussdichte des Drehfeldes über dem Leiter ihr Maximum erreicht noch nicht seine maximale Amplitude aufweist und das resultierende Drehmoment folglich verringert wird. Ausserdem bedingt die parasitäre Induktivität des Läufers eine grundsätzliche Reduktion der Läuferstromamplitude, da bei der Berechnung der Stromamplitude die Impedanz \(Z\) anstelle der Resistanz \(R\) berücksichtigt werden muss.

\[ \frac{U}{R}>\frac{U}{Z}=\frac{U}{\sqrt{R^{2}+X^{2}}} \]

Die Reaktanz \(X\) ist ausserdem frequenzabhängig \(\left(X=2\cdot \pi\cdot f\cdot L\right)\), wodurch der Einfluss der parasitären Induktivität massgeblich von der Frequenz der induzierten Spannung \(U_{ind}\) abhängt. Die Frequenz der induzierten Spannung \(f_{m}\) entspricht der Differenz der Winkelgeschwindigkeiten von Drehfeld und Läufer und entspricht bei Stillstand des Läufers der Drehfeldfrequenz \(f_{s}\).

\[ f_{ind}=\frac{n_{Diff}}{60}=\frac{n_{s}-n_{m}}{60} \]

Der begrenzende Einfluss der Reaktanz auf die Läuferstromamplitude nimmt also mit steigender Drehzahl des Motors ab. Die Zusammenhänge zwischen der Amplitude sowie der Frequenz der induzierten Spannung und dem Schlupf sind in der Abbildung 8.6 dargestellt.

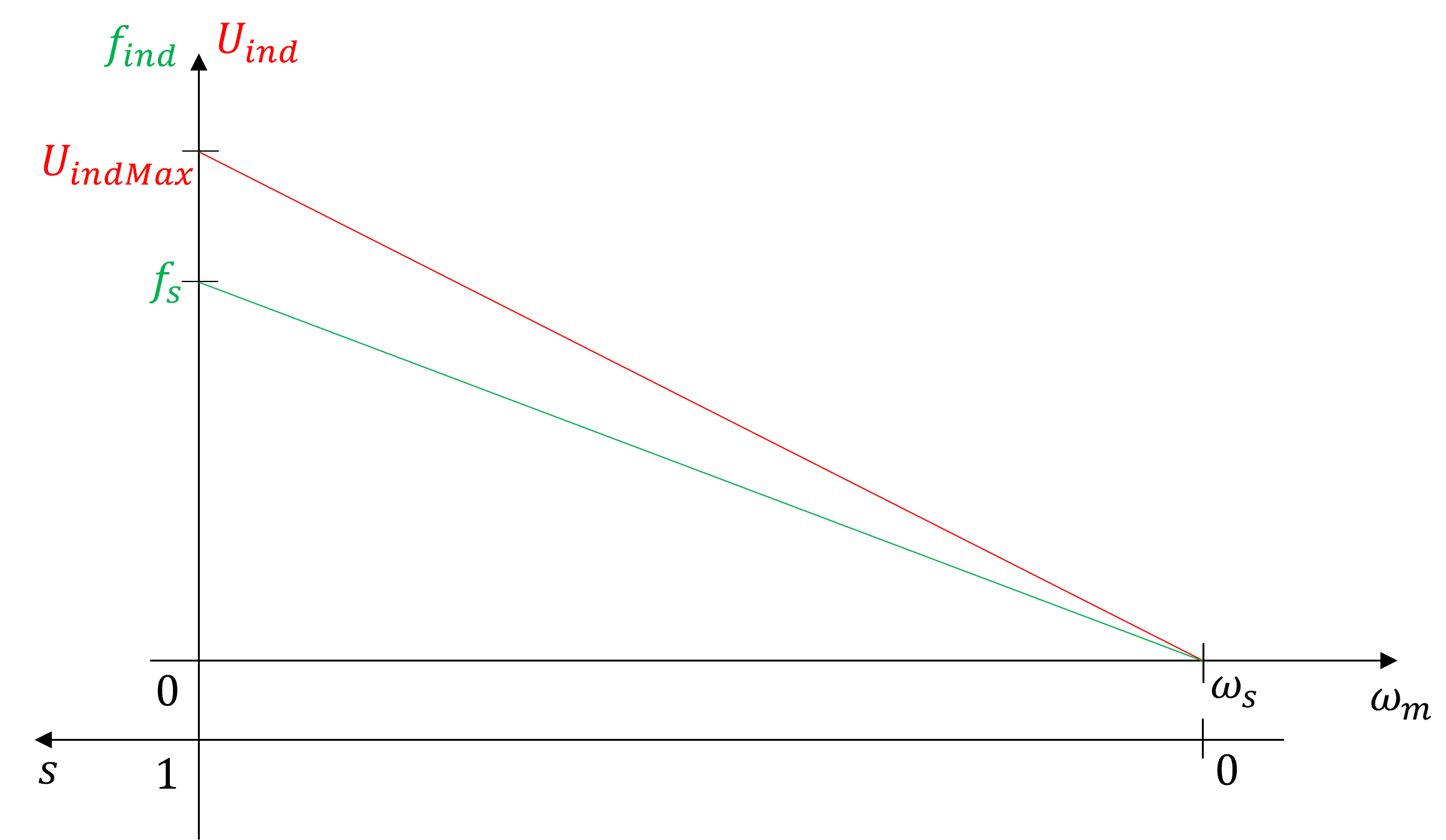
Abbildung 8.6: Abhängigkeit von Frequenz sowie Amplitude der induzierten Läuferspannung vom Schlupf der ASM

Die beschriebenen Effekte resultieren in der typischen Drehzahl-Drehmomentkennlinie der netzgespeisten ASM im motorischen Betrieb (\(M>0, n_{m}>0\)), die in der Abbildung 8.7 dargestellt ist.

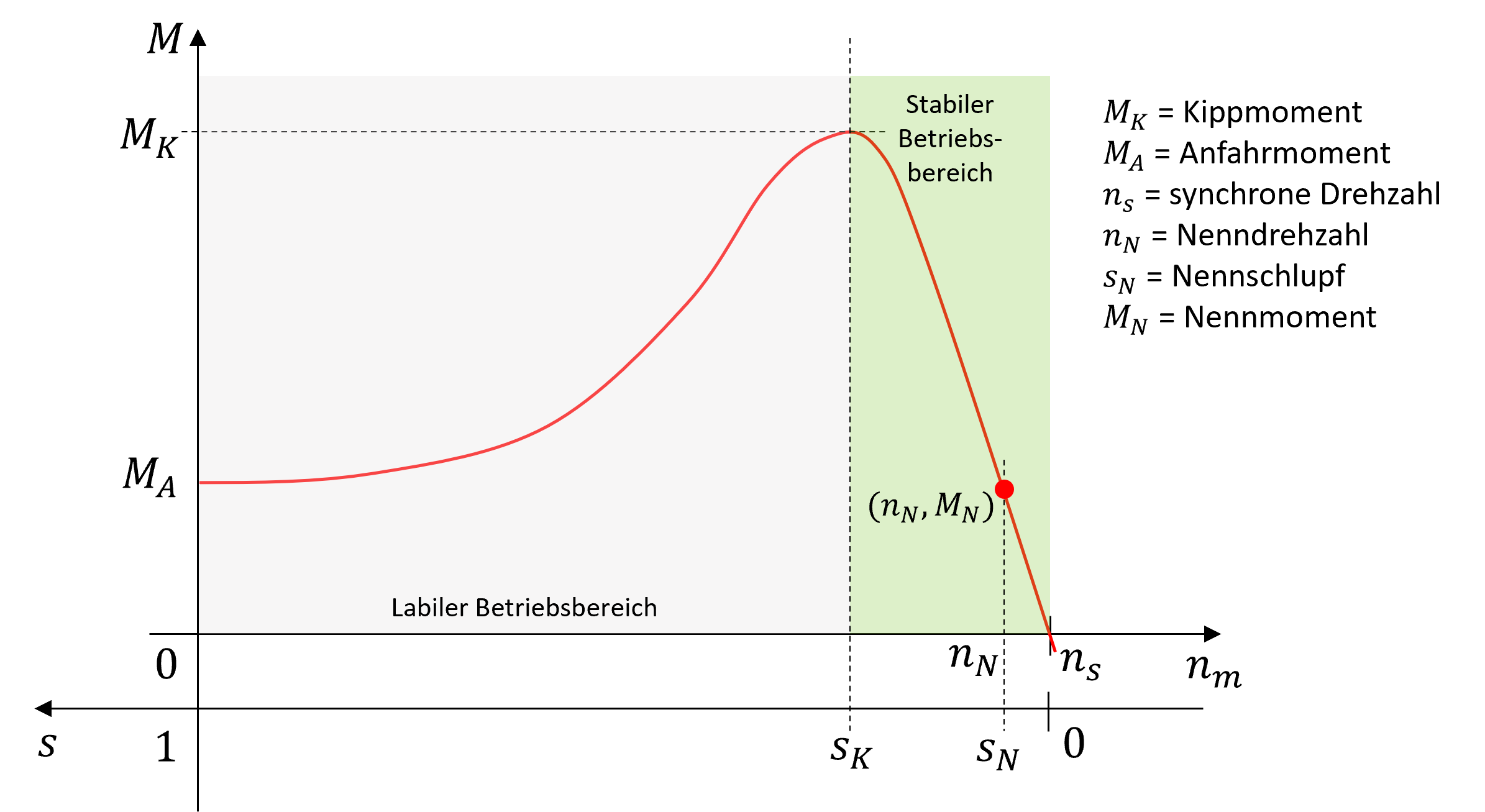
Abbildung 8.7: Charakteristischer Verlauf der Drehzahl-Drehmoment-Kennlinie der ASM bei Netzspeisung

Da das Drehmoment vom Betrag des magnetischen Flusses sowie von Betrag und Phasenlage des Läuferstromes abhängt und der Betrag des magnetischen Flusses bei konstanter Netzspannung praktisch konstant ist, wird der Betrag des Läuferstromes mit wachsendem Schlupf (zunehmender Belastung), aufgrund der Zunahme der induzierten Spannung, immer grösser. Allerdings steigt mit der Frequenz des Läuferstromes (wachsender Schlupf) der Blindwiderstand des Läufers, was zu einer Vergrösserung des Phasenwinkels zwischen induzierter Läuferspannung und Läuferstrom führt. Aufgrund dessen ergibt sich ein Drehmomentoptimum (Kippmoment \(M_{K}\)) bei einem bestimmten Schlupfwert (Kippschlupf \(s_{K}\)). Das Kippmoment übersteigt das Nennmoment um das 2- bis 3-fache. Beim Anlauf aus dem Stillstand (\(n_{m}=0\)) entwickelt der ASM das sogenannte Anlaufmoment, welches im Vergleich zum Kippmoment recht gering ausfällt, obwohl der Anlaufstrom sehr hohe Wert (bis zum 8-fachen des Nennstromes) erreicht. Um diesem Effekt entgegenzuwirken, wird die Stromverdrängung der Läuferstäbe beim Käfigläufer durch konstruktive Massnahmen (z.B. Doppel- oder Hochstäbe) erhöht, was zu einer Vergrösserung des Anlaufmomentes und einer Reduktion des Anlaufstromes führt. Bei Schleifringläufermaschinen hingegen kann durch gezieltes Einschalten von zusätzlichen ohmschen Widerständen im Läuferkreis das Anfahrmoment bis auf das Kippmoment erhöht werden, da die zusätzlichen Widerstände den Phasenwinkel zwischen Läuferspannung und Läuferstrom reduzieren. Diese Variante des Anlassens von Schleifringläufer-ASM ist jedoch durch hohe Verluste (Stromwärme in den Zusatzwiderständen) geprägt und wird somit heutzutage nur noch selten bzw. bei speziellen Anwendungen angewandt. Ein signifikanter Nachteil der ASM ist deren starke Bindung an die, durch die Speisefrequenz gegebene, synchrone Drehzahl, da der Wirkungsgrad der ASM nur bei kleinen Schlupfwerten hohe Werte annimmt. Durch Fortschritte in der Halbleitertechnik ist es möglich verlustarme elektronische Frequenzumrichter zu bauen, die den Einsatz von ASM in drehzahlvariablen Antrieben ermöglichen, indem die Speisefrequenz variabel gestaltet werden kann (siehe Abbildung 8.8).

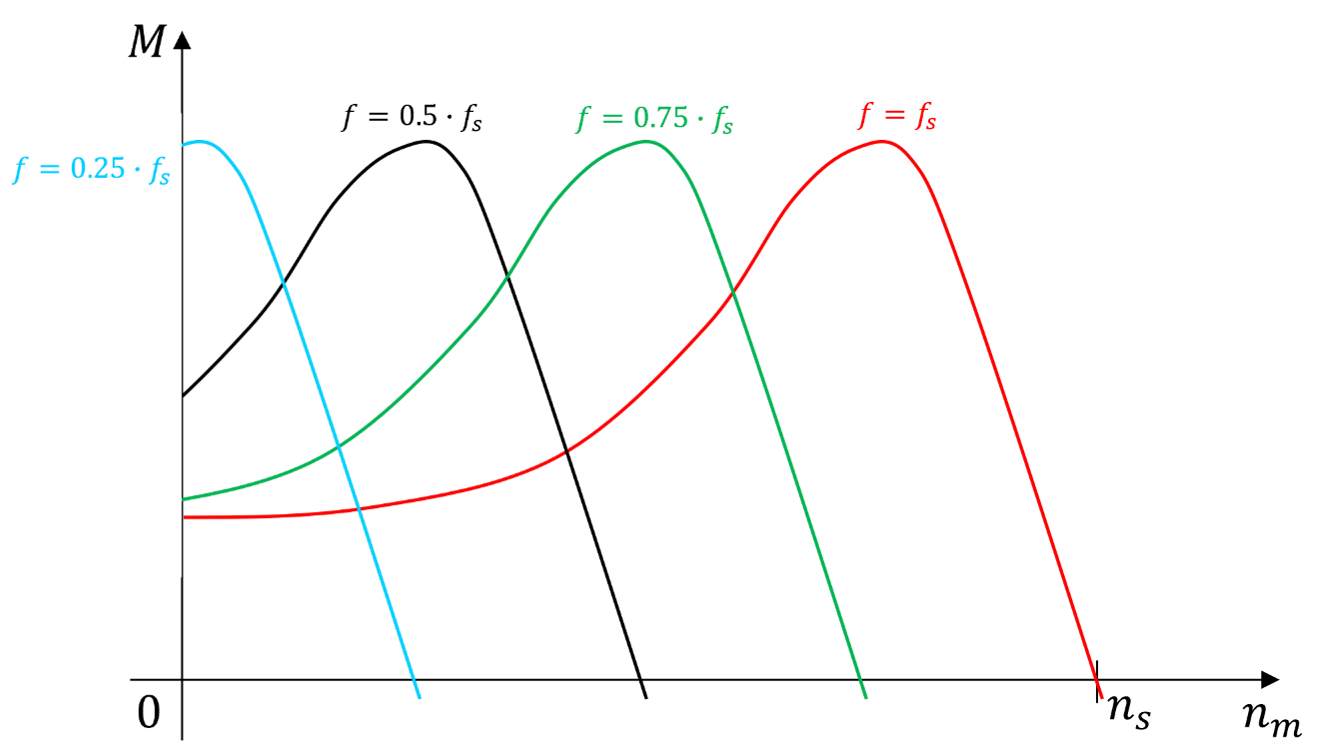
Abbildung 8.8: Charakteristische Verläufe der Drehzahl-Drehmoment-Kennlinie der ASM bei Umrichterspeisung

Um bei unterschiedlichen Drehzahlen stets das volle Drehmoment verfügbar zu machen, muss dafür gesorgt werden, dass die Amplitude der magnetischen Flussdichte und somit des magnetischen Flusses konstant bleibt. Dies ist dadurch zu erreichen, dass der Ständerstrom konstant bleibt. Da der stromdurchflossene Läufer, vergleichbar mit den Verhältnissen in einer Gleichstrommaschine, eine geschwindigkeitsproportionale Spannung im Ständerkreis induziert, muss die Ständerspannung proportional mit der Frequenz geändert werden. Diese Betreibsart wird als Spannungs-Frequenz-Steuerung bezeichnet. Es sei darauf verwiesen, dass bei dieser Art der Drehzahlsteuerung, die Ständerspannung bei niedrigen Frequenzen leicht angehoben werden muss (Boost), da der Spannungsabfall über dem Ständerwiderstand \(R_{S}\) deutlicher ins Gewicht fällt, als bei hohen Frequenzen, da die Ständerreaktanz \(X_{h}\) eine frequenzproportionale Grösse ist.

8.3 Ersatzschaltbilder der Asynchronmaschine

Der Ständer- und Läuferkreis einer ASM sind induktiv gekoppelt, wodurch das Verhalten der ASM mit dem eines Drehstromtransformators zu vergleichen ist. Insbesondere bei festgebremsten Läufer ist dies leicht vorstellbar. Aufgrund dieser Ähnlichkeit, lässt sich analog zum Drehstromtransformator ein T-Ersatzschaltbild für den stationären Betrieb (eingeschwungene Zustände der Ströme, Spannungen und Flüsse) herleiten. Dabei ist es üblich die beiden Dreiphasenwicklungssysteme (Läufer und Ständer) jeweils durch 3 einphasige zu ersetzen. Dies ist zulässig unter der Voraussetzung, dass sie symmetrisch durchflutet werden. Eine solche symmetrische Durchflutung ist im störungsfreien Betrieb gewährleistet (Wechselfelder und Gegensystem Null und keine Oberwellen im Drehfeld). Im stationären Betrieb sind die Raumzeiger in der Amplitude als auch in der Phasenlage zeitinvariant, wodurch es zulässig ist sie als komplexe Zeitzeiger aufzufassen. Wie bereits in Kapitel 6.2.1 beschrieben, bestehen die Läufer- und Ständerinduktivitäten (\(L_{s}\) bzw. \(L_{r}\)) jeweils aus einer Haupt- und einer Streuinduktivität.

\[ \begin{matrix} L_{s}=L_{h}+L_{\sigma s} \\ L_{r}=L_{h}+L_{\sigma r} \\ \end{matrix} \]

Die Hauptinduktivität stellt dabei den Zusammenhang zwischen den Strömen beider Wicklungssysteme und dem verketteten Fluss her. Da sich Ströme und Spannungen zwischen Ständer- und Läuferseite der ASM aufgrund der möglicherweise unterschiedlichen Wicklungszahlen in ihren Beträgen unterscheiden, ist es üblich die Grössen der Läufer- auf die Ständerseite umzurechnen, indem das Übersetzungsverhältnis berücksichtigt wird. Die umgerechneten Grössen werden in der Literatur üblicherweise mit dem Superskript (\('\)) versehen.

\[ \begin{matrix} i = \frac{L_{hs}}{L_{M}}=\frac{L_{M}}{L_{hr}} \\ U_{r}^{'} = U_{r}\cdot i \\ I_{r}^{'} = \frac{I_{r}}{i} \\ R_{r}^{'} = R_{r}\cdot i^{2} \\ L_{r}^{'} = L_{r}\cdot i^{2} \\ L_{M}^{'} = L_{M}\cdot i = L_{hs} = L_{hr} \\ \end{matrix} \]

Das sich aus diesen Überlegungen ergebende Ersatzschaltbild ist in Abbildung 8.9 dargestellt.

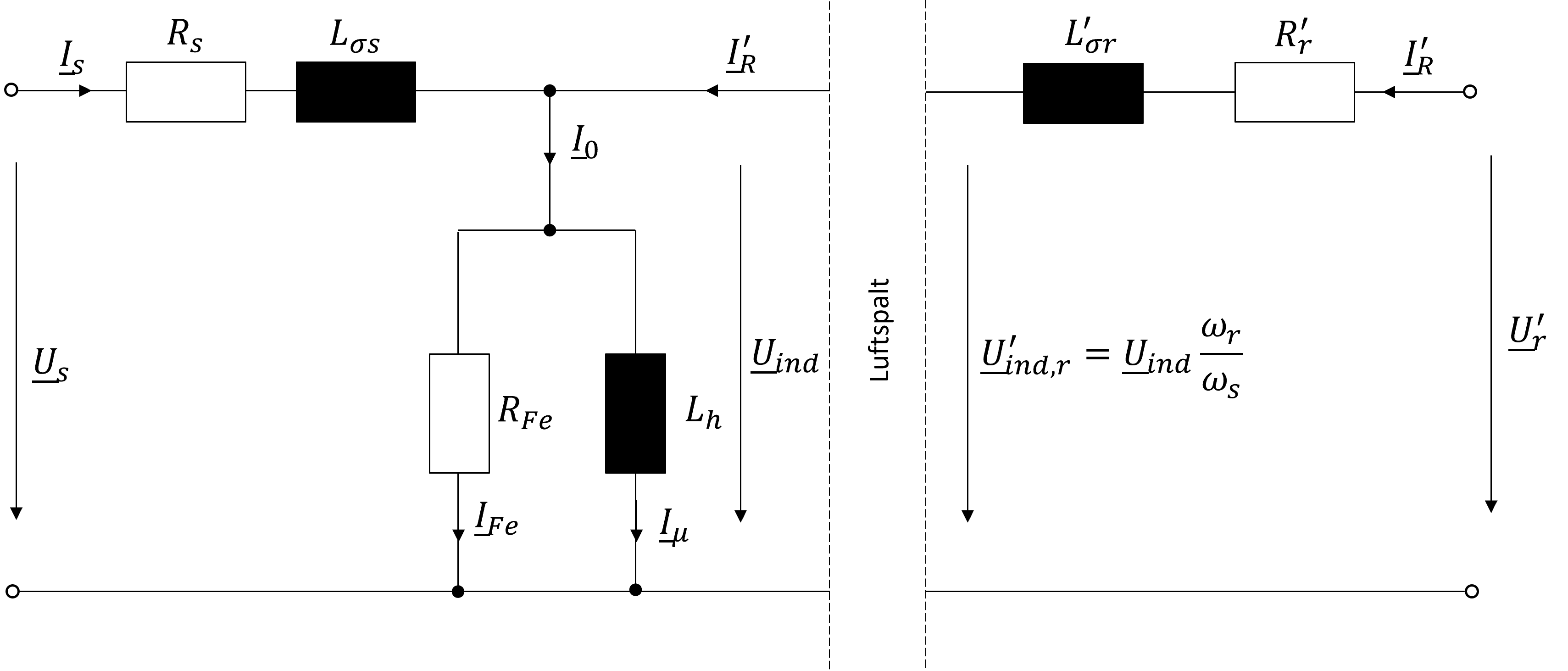
Abbildung 8.9: Ersatzschaltung eines Stranges der ASM mit getrenntem Stator- und Rotorkreis

Da die Übersetzung der Spannung von Stator- auf Rotorseite einem weiteren Einfluss unterliegt, muss dieser ebenfalls berücksichtigt werden. Und zwar ist die, durch den mit der Winkelgeschwindigkeit \(\omega_{s}\) rotierenden Statorfluss, in der Rotorwicklung induzierte Spannung von der Drehgeschwindigkeit \(\omega_{m}\) des Rotors abhängig. Bei stillstehenden Rotor ist die induzierte Spannung maximal. Dreht der Rotor hingegen mit der gleichen Winkelgeschwindigkeit wie das Feld \((\omega_{s}=p\cdot \omega_{m})\) ist die induzierte Spannung hingegen null. Diese Abhängigkeit lässt sich durch die Gleichung

\[ \underline{U}_{ind,r}^{'} = \underline{U}_{ind}\frac{\omega_{s}-p\omega_{m}}{\omega_{s}}=\underline{U}_{ind}\frac{\omega_{r}}{\omega_{s}} \]

berücksichtigen. Wird weiterhin die Spannungsgleichung für den Rotorkreis in Abbildung 8.9, unter Berücksichtigung des Rotorstromes, aufgestellt

\[ \underline{U}_{ind,r}^{'} = \underline{U}_{ind}\frac{\omega_{s}-p\omega_{m}}{\omega_{s}}= -\underline{I}_{r}^{'}\left(j\omega_{r}L_{\sigma r}^{'}+R_{r}^{'}\right) + \underline{U}_{r}^{'} \]

und nach \(\underline{U}_{ind}\) aufgelöst, so kann diese Drehzahlabhängigkeit der rotorseitig induzierten Spannung durch einen schlupfabhängigen Rotorwiderstand und eine schlupfabhängige Rotorspannung repräsentiert werden.

\[\begin{equation} \underline{U}_{ind}= -\underline{I}_{r}^{'}\left(j\omega_{s}L_{\sigma}^{'}+R_{r}^{'}\frac{\omega_{s}}{\omega_{r}}\right) + \underline{U}_{r}^{'}\frac{\omega_{s}}{\omega_{r}}= -\underline{I}_{r}^{'}\left(j\omega_{s}L_{\sigma r}^{'}+\frac{R_{r}^{'}}{s}\right) + \frac{\underline{U}_{r}^{'}}{s} \tag{8.4} \end{equation}\]

Durch diese Modifikation wurden sowohl der Rotorwiderstand \(R_{r}^{'}\) als auch eine möglicherweise vorhandene Rotorspannung \(\underline{U}_{r}^{'}\) (im Falle von Schleifringläufermaschinen) auf die statorseite transformiert und die Ersatzschaltbildung in Abb. 8.9, die einen getrennten Stator- und Rotorkreis aufweist, kann in einem gemeinsamen Ersatzschaltbild dargestellt werden (vgl. Abb. 8.10).

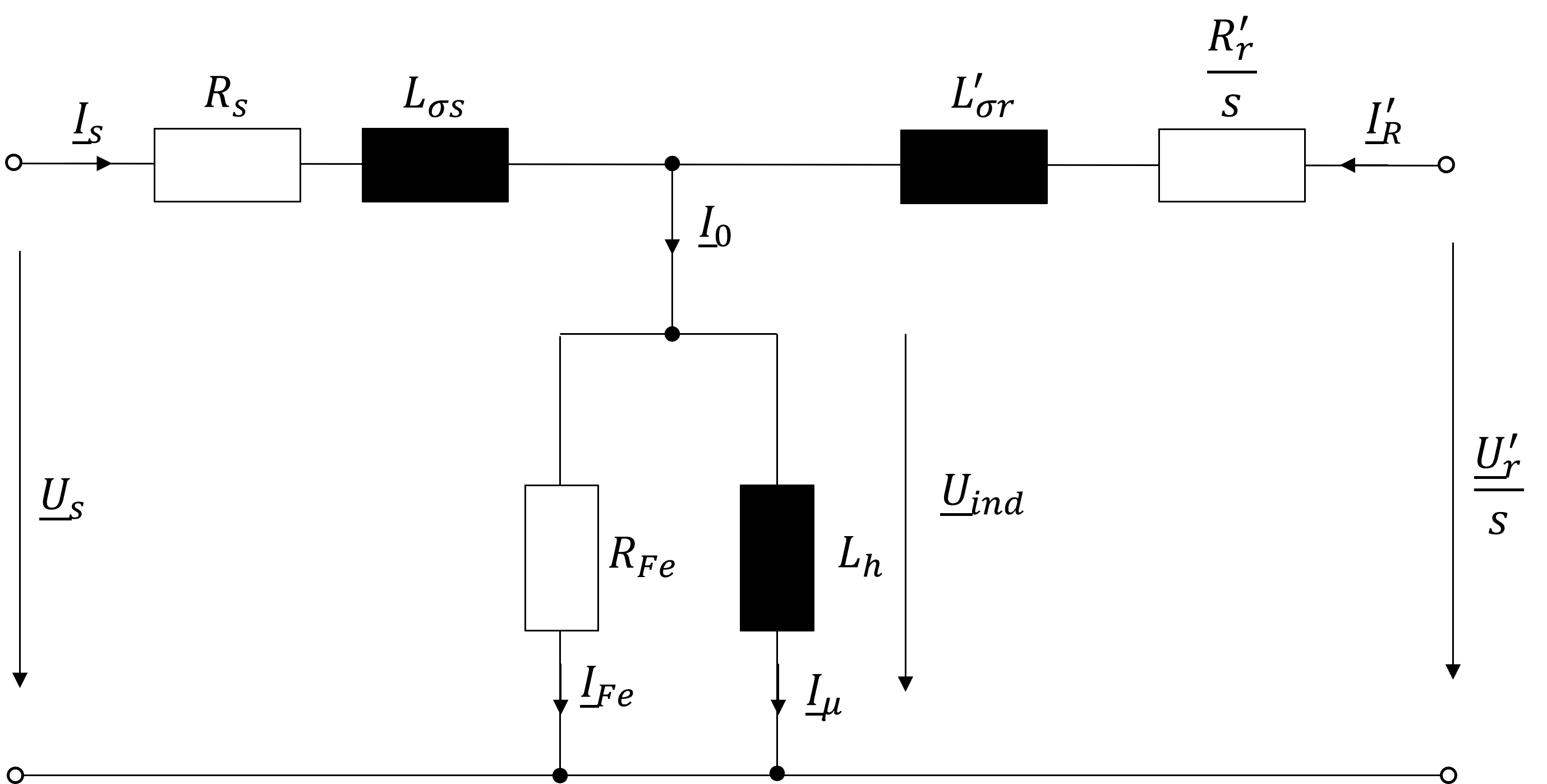
Abbildung 8.10: Transformator-Ersatzschaltbild eines Stranges der ASM

Aus der Gleichung (8.4) kann gleichzeitig der Rotorstrom berechnet werden.

\[ \underline{I}_{r}^{'}= \frac{\underline{U}_{r}^{'}-\frac{\underline{U}_{r}^{'}}{s}}{j\omega_{s}L_{\sigma r}^{'}+\frac{R_{r}'{'}}{s}} \]

In Kapitel 6.2.1 wurde bereits erläutert, dass bei der Bestimmung der Flussverkettungen der Wicklungsstränge sowohl das Haupt- als auch das Streufeld zu berücksichtigen sind, welche durch den Strom im betracheteten Wicklungsstrang selbst erzeugt werden. Allerdings gilt es auch zu berücksichtigen, dass alle benachbarten stromdurchflossenen Wicklungen ebenfalls Luftspaltfelder aufbauen, die je nach Verdrehwinkel (Läuferstellung) unterschiedlich stark miteinander verkoppelt sind. Berücksichtigt man, wie vereinbart, nur die Grundwellen, dann lassen sich die Beiträge aller stromdurchflossenen Wicklungen zur Flussverketung einer anderen Wicklung durch Sinusfunktion repräsentieren, da sich die Verkettung mit dem Cosinus des Winkels zwischen beider Achsen berücksichtigen lässt. Bei Streufeldern wird definiert, dass diese nur mit der Wicklung verkettet sind, von der sie erzeugt wurden. Somit lässt sich eine Gleichung für die Verkettung einer einzelnen Ständerwicklung (Index a) definieren.

\[\begin{equation} \begin{matrix} \Psi_{sa} = \left(L_{h}+L_{\sigma s} \right)\cdot i_{sa}+ L_{h}\cdot i_{sb}\cdot \underbrace{cos\left(\frac{2\pi}{3} \right)}_{-\frac{1}{2}}+L_{h}\cdot i_{sc}\cdot \underbrace{cos\left(\frac{4\pi}{3} \right)}_{-\frac{1}{2}} \\ + L_{h}\left[i_{ra}\cdot cos\left(\varphi \right)+i_{rb}\cdot cos\left(\varphi+\frac{2\pi}{3} \right)+i_{rc}\cdot cos\left(\varphi+\frac{4\pi}{3} \right)\right] \end{matrix} \tag{8.5} \end{equation}\]

Die Spannungsgleichungen aller sechs Wicklungen mittels des Ersatzschaltbildes 6.9 können mit folgender allgemeinen Gleichung dargestellt werden.

\[ u=u_{r}+u_{i}=i\cdot R + \frac{d\Psi}{dt} \]

Diese Gleichung beschreibt, dass sich die Spannungsabfälle jeder Wicklung auf einen ohmschen Anteil \(u_{r}\) und einen induktiven Anteil \(U_{i}\) aufteilen. Somit lassen sich mit Hilfe der Gleichung (8.5) mathematische Ausdrücke für die 6 Spannungsgleichungen formulieren. Die Ständerspannungsgleichungen lauten:

\[ \begin{matrix} u_{sa}=R_{s}\cdot i_{sa}+\left(L_{h}+L_{\sigma s} \right)\cdot \frac{di_{sa}}{dt}-\frac{L_{h}}{2}\cdot \frac{di_{sb}}{dt}-\frac{L_{h}}{2}\cdot \frac{di_{sc}}{dt} \\ +L_{h}\cdot \frac{d}{dt}\left[i_{ra}\cdot cos\left(\varphi \right)+i_{rb}\cdot cos\left(\varphi+\frac{2\pi}{3} \right)+i_{rc}\cdot cos\left(\varphi-\frac{2\pi}{3} \right) \right] \end{matrix} \]

\[ \begin{matrix} u_{sb}=R_{s}\cdot i_{sb}+\left(L_{h}+L_{\sigma s} \right)\cdot \frac{di_{sb}}{dt}-\frac{L_{h}}{2}\cdot \frac{di_{sb}}{dt}-\frac{L_{h}}{2}\cdot \frac{di_{sc}}{dt} \\ +L_{h}\cdot \frac{d}{dt}\left[i_{ra}\cdot cos\left(\varphi -\frac{2\pi}{3}\right)+i_{rb}\cdot cos\left(\varphi \right)+i_{rc}\cdot cos\left(\varphi+\frac{2\pi}{3} \right) \right] \end{matrix} \]

\[ \begin{matrix} u_{sc}=R_{s}\cdot i_{sc}+\left(L_{h}+L_{\sigma s} \right)\cdot \frac{di_{sc}}{dt}-\frac{L_{h}}{2}\cdot \frac{di_{sa}}{dt}-\frac{L_{h}}{2}\cdot \frac{di_{sb}}{dt} \\ +L_{h}\cdot \frac{d}{dt}\left[i_{ra}\cdot cos\left(\varphi +\frac{2\pi}{3}\right)+i_{rb}\cdot cos\left(\varphi-\frac{2\pi}{3}\right)+i_{rc}\cdot cos\left(\varphi\right) \right] \end{matrix} \]

Die Läuferspannungsgleichungen (bei kurzgeschlossenem Läufer) lauten:

\[ \begin{matrix} u_{ra}=R_{r}\cdot i_{ra}+\left(L_{h}+L_{\sigma r} \right)\cdot \frac{di_{ra}}{dt}-\frac{L_{h}}{2}\cdot \frac{di_{rb}}{dt}-\frac{L_{h}}{2}\cdot \frac{di_{rc}}{dt} \\ +L_{h}\cdot \frac{d}{dt}\left[i_{sa}\cdot cos\left(\varphi \right)+i_{sb}\cdot cos\left(\varphi-\frac{2\pi}{3} \right)+i_{sc}\cdot cos\left(\varphi+\frac{2\pi}{3} \right) \right]=0 \end{matrix} \]

\[ \begin{matrix} u_{rb}=R_{r}\cdot i_{rb}+\left(L_{h}+L_{\sigma r} \right)\cdot \frac{di_{rb}}{dt}-\frac{L_{h}}{2}\cdot \frac{di_{rb}}{dt}-\frac{L_{h}}{2}\cdot \frac{di_{rc}}{dt} \\ +L_{h}\cdot \frac{d}{dt}\left[i_{sa}\cdot cos\left(\varphi \right)+i_{sb}\cdot cos\left(\varphi-\frac{2\pi}{3} \right)+i_{sc}\cdot cos\left(\varphi+\frac{2\pi}{3} \right) \right]=0 \end{matrix} \]

\[ \begin{matrix} u_{rc}=R_{r}\cdot i_{rc}+\left(L_{h}+L_{\sigma r} \right)\cdot \frac{di_{rc}}{dt}-\frac{L_{h}}{2}\cdot \frac{di_{ra}}{dt}-\frac{L_{h}}{2}\cdot \frac{di_{rc}}{dt} \\ +L_{h}\cdot \frac{d}{dt}\left[i_{sa}\cdot cos\left(\varphi-\frac{2\pi}{3} \right)+i_{sb}\cdot cos\left(\varphi+\frac{2\pi}{3} \right)+i_{sc}\cdot cos\left(\varphi \right) \right]=0 \end{matrix} \]

Die hergeleiteten Gleichungen beschreiben das Verhalten der ASM vollständig. Aufgrund der trigonometrischen Terme in diesem Gleichungssystem ist eine geschlossene Lösung allerdings nicht möglich. Es lässt sich allerdings mathematisch begründen, dass sich die obigen Gleichungen im stationören Betrieb und bei symmetrischem Aufbau durch jeweils eine einzelne Gleichung für den Rotor- und den Statorkreis ersetzen lassen.

8.4 Leistungsbilanz und Anlaufstrom

Abbildung 8.11 zeigt den grundsätzlichen Leistungsfluss einer Asynchronmaschine.

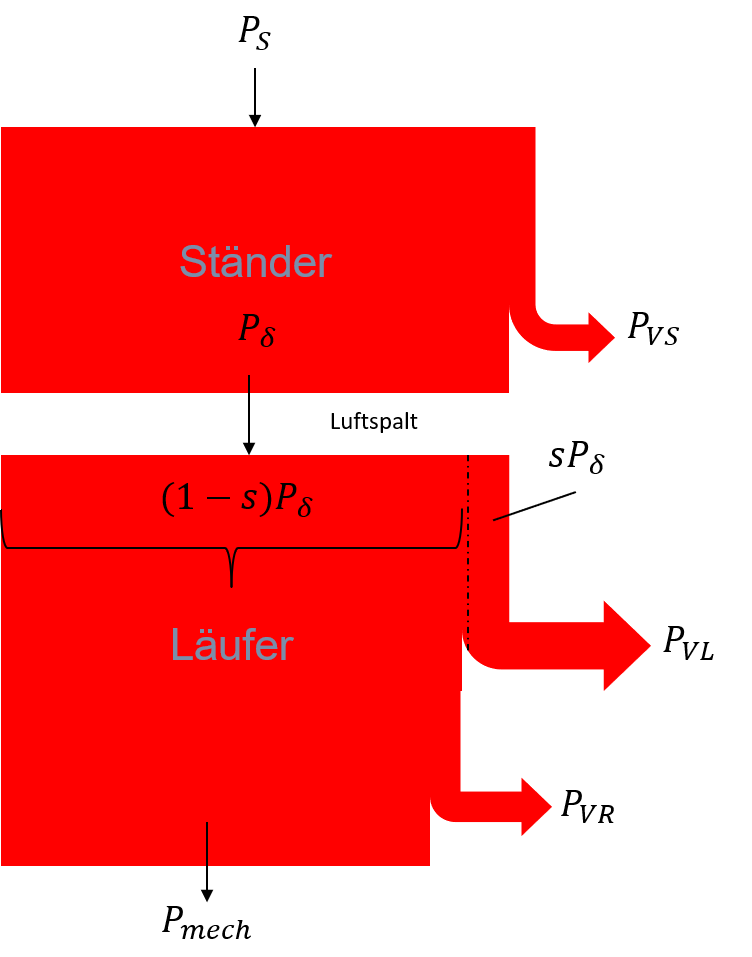
Abbildung 8.11: Leistungsflussdiagramm der Asynchronmaschine

Das Diagramm beinhaltet dabei folgende Grössen:

• Vom Ständer aufgenommene Wirkleistung \(P_{S}\)
• Ständerverluste \(P_{VS}\)
• Luftspaltleistung \(P_{\delta}\) (über den Luftspalt übertragene Wirkleistung)
• Läuferverlustleistung \(P_{VL}=s\cdot P_{\delta}\)
• Lüfter- bzw. Reibungsverluste \(P_{VR}\)
• Abgegebene mechanische Leistung \(P_{mech}\)

Die Ständerverluste \(P_{VS}\) können in die Kupfer- (\(P_{VCu}\)) und die Eisenverlustleistung (\(P_{VFe}\)) aufgeteilt werden.

\[ P_{VS}=P_{VCu}+P_{VFe} \]

Diese Zweiteilung ist ebenfalls auf der Läuferseite denkbar. Bei einer Schleifringläufer-ASM muss ausserdem die vom Läufer abgegebene elektrische Leistung \(P_{L}\) berücksichtigt werden. Beim Kurzschlussläufer gilt \(P_{L}=0\).

\[ P_{VL}=P_{VCu}+P_{VFe}+P_{L} \]

Die Eisenverluste auf Läuferseite werden jedoch üblicherweise vernachlässigt. Die mechanische Leistung ergibt sich aus der aufgenommenen Wirkleistung \(P_{s}\) vermidert um die Eisenverluste \(P_{VFe}\) und die Wicklungsverluste der \(P_{VCu}\) des Ständers.

\[ P_{S}=3\cdot \left(I_{S}^{2}\cdot R_{s}+\frac{U_{s}^{2}}{R_{VFe}}\right)+P_{\delta}= 3\cdot U_{s}\cdot I_{s}\cdot cos{\varphi}=P_{VS}+\omega_{d}\cdot M_{\delta} \]

Die um die Läuferverluste reduzierte Luftspaltleistung \(P_{\delta}\) steht wiederum als mechanische Leistung \(P_{mech}\) zur Verfügung.

\[ P_{\delta}=M_{\delta}\cdot \omega_{d}=3\cdot {I_{r}^{'}}^{2}\cdot R_{L}^{'}+M_{\delta}\cdot \omega=P_{VL}+P_{VR}+P_{mech} \]

Die Läuferverluste \(P_{VL}\) steigen mit der Frequenz der Läuferspannung (Schlupf), weshalb sie sich auch folgendermassen berechnen lassen:

\[ P_{VL}=M_{\delta}\cdot \left(\omega_{d}-\omega\right) \]

Dabei handelt es sich bei \(\omega_{d}\) um die Winkelgeschwindigkeit des Drehfeldes und bei \(\omega\) um die Winkelgeschwindigkeit des Läufers. Somit kann die Luftspaltleistung auch auf andere Art und Weise zum Ausdruck gebracht werden.

\[ P_{\delta}=M_{\delta}\cdot \omega_{d}=\omega_{d}\cdot \frac{P_{VL}}{\omega_{d}-\omega}=\frac{P_{VL}}{s} \]

Diese Gleichung ermöglicht eine Beschreibung der mechanischen Leistung in Abhängigkeit des Schlupfes

\[ P_{mech}=P_{\delta}-P_{VL}=P_{\delta}-s\cdot P_{\delta}=P_{\delta}\cdot \left(1-s\right)=\frac{\left(1-s\right)\cdot\omega_{d}\cdot M_{\delta}}{p} \]

und des inneren Drehmomentes \(M_{\delta}\).

\[ M_{\delta}=\frac{P_{VL}}{\omega_{d}-\omega}=3\cdot \frac{{I_{r}^{'}}^{2}\cdot R_{r}^{'}}{\omega_{d}-\omega} \]

Die Angabe der Nennleistung einer Asynchronmaschine bezieht sich immer auf die abgegebene mechanische Leistung (bei Generatoren elekrische Leistung).

Der Anlaufstrom \(I_{A}\) der ASM kann mit Hilfe des Ersatzschaltbildes bestimmt werden, indem der sowohl der Magnetisierungsstrom \(I_{\mu}\) als auch der Eisenverlusstrom \(I_{Fe}\) vernachlässigt werden und der Schlupf mit \(s=1\) angesetzt wird.

\[ I_{A}=-I_{r}^{'}=I_{s}=\frac{U_{S}}{\sqrt{\left(R_{s}+R_{r}^{'}\right)^{2}+\left(X_{\sigma s}+X_{\sigma r}^{'}\right)^{2}}} \]

Das Anlaufmoment kann erhöht werden, indem der Läuferwiderstand \(R_{r}^{'}\) für Schlupfwerte von 1 erhöht wird. Bei Schleifringläufern ist dies durch Hinzuschalten von zusätzlichen Läuferwiderständen möglich. Bei Käfigläufermaschinen hingegen wird der Stromverdrängungseffekt (Skin-Effekt), durch konstruktive Massnahmen (z.B. Doppelstäbe), ausgenutzt und die Drehzahl-Drehmoment Charaktersitik dahingehend verändert (siehe Abb. 8.12).

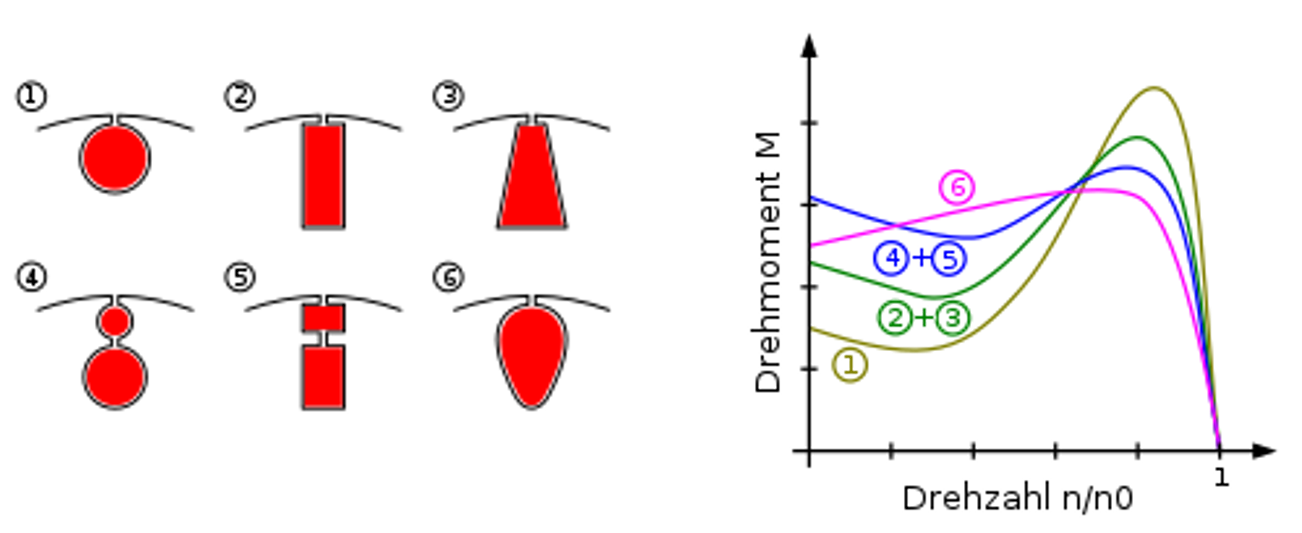
Abbildung 8.12: Einfluss der Läuferstabform auf die Drehzahl-Drehmoment-Charaktersitik der ASM (Bildquelle: www.wikipedia.org)

Diese, durch den Skin-Effekt hervorgerufene Erhöhung des Läuferwiderstandes, reduziert gleichzeitig den Anlaufstrom der Maschine.

8.5 Bestimmung der Maschinenparameter

Um das Verhalten einer Asynchronmaschine simulieren zu und mit realen Systemen vergleichen können, ist es notwendig die notwendigen Parameter zu kennen. Dabei ist nicht immer gewährleistet, dass die benötigten Parameter in den Datenblättern der Hersteller zur Verfügung gestellt werden.

8.5.1 Bestimmung des Massenträgheitsmomentes

Motor Trägheitsmomente sind üblicherweise in Datenblättern angegeben. Last-Trägheitsmomente hingegen müssen häufig experimentell bestimmt werden. Dazu eignet sich folgende Methoden:

• Anlaufversuch
• Auslaufversuch
• Drehkörper mit Pendel

8.5.1.1 Anlaufversuch

Beim normalen Anlaufversuch wird der Antriebsmotor bis zum Erreichen der Nenndrehzahl \(n_{N}\) beschleunigt. Die benötige Beschleunigungsdauer \(t_{a}\) wird dabei gemessen. In diesem Fall kann das gesamte Trägheitsmoment \(J\) mit Hilfe der Gleichung

\[ J=J_{L}+J_{M}=\frac{M_{bmi}\cdot t_{a}}{2\pi\cdot n_{N}} \]

bestimmt werden. Dabei entspricht \(J_{L}\) dem Lasträgheitsmoment, \(J_{M}\) dem Rotorträgheitsmoment und \(M_{bmi}\) dem mittleren Beschleunigungsmoment. Dabei ist zu berücksichtigen, dass das Beschleunigungsmoment auch ein, meist unbekanntes Reibmoment beinhaltet. Bei Anlaufversuch mit Hilfsschwungmasse wird zunächst die Anlaufzeit \(t_{a}\) des normalen Anlaufversuches (ohne Hilfsschwungmasse) bestimmt und anschliessend der versuch mit einer zusätzlichen Hilfsschwungmasse, mit bekanntem Massenträgheitsmoment \(J_{h}\), wiederholt und die längere Anlaufzeit \(t_{ah}\) gemessen. Das Gesamtträgheitsmoment \(J\) erhält man in diesem Fall mit Hilfe der folgenden Gleichung:

\[ J=J_{L}+J_{M}=\frac{J_{h}\cdot t_{a}}{t_{ah}-t_{a}} \]

Voraussetzung für dieses Vorgehen ist, dass das mittlere Beschleunigungsmoment \(M_{bmi}\) in beiden Fällen (mit und ohne Hilfsschwungmasse) identisch ist.

8.5.1.2 Auslaufversuch

Beim normalen Auslaufversuch wird die Zeit bis zum Erreichen des Stillstandes \(t_{br}\) gemessen, während die Stromzufuhr zum Motor unterbrochen und ein bekanntes Bremsmoment \(M_{br}\) ausgeübt wird. Das Gesamtträgheitsmoment \(J\) erhält man in diesem Fall mit Hilfe der folgenden Gleichung:

\[ J=J_{L}+J_{M}=\frac{M_{br}\cdot t_{br}}{2\pi\cdot n} \]

Ist das Bremsmoment hingegen unbekannt kann ein Auslaufversuch mit Hilfsschwungmasse mit bekanntem Trägheitsmoment \(J_{h}\) durchgeführt werden. Dazu wird der Drehkörper mit dem Antrieb gekoppelt und durch Unterbrechen der Energiezufuhr die Auslaufzeit \(t_{brh}\) gemessen. Ein zweites Auslaufen ohne Drehkörper liefert die Auslaufzeit \(t_{br}\). Wenn die Drehzahlen, bei denen die Auslaufversuche gestartet wurden, gleich waren und sich das Reibmoment aufgrund der zusätzlichen Schwungmasse nicht verändert, kann das Trägheitsmoment mit Hilfe der Gleichung

\[ J=J_{L}+J_{M}=\frac{J_{h}\cdot t_{br}}{t_{brh}-t_{br}} \]

bestimmt werden. Bei der Kombination des An- und Ausluafversuches ist es möglich das Last- bzw. Reibungsmoment zu eliminieren und das Gesamtträgheitsmoment lässt sich mit der Gleichung

\[ J=J_{L}+J_{M}=\frac{M_{mi}\cdot t_{a}\cdot t_{b}}{2\pi\cdot n\cdot \left(t_{a}+t_{b}\right)} \]

bestimmen.

8.5.1.3 Drehkörper mit Pendel

Um das Trägheitsmoment von unregelmässig geformten , schwierig zu berechnenden und nicht im Schwerpunkt aufgehängten Körpern zu bestimmen, kann diese Methode verwendet werden. Dabei wird der Körper, dessen Trägheitsmoment \(J\) bestimmt werden soll, mit dem Wellenende des Antriebsmotors verbunden und daran ein Pendel bekannten Gewichts \(F_{G}=m_{P}\cdot g\) im Abstand \(r\) seines Schwerpunktes von der Motorachse angebracht. Dieses Vorgehen basiert auf der, durchaus zulässigen Annahme, dass der Rotor des Motors nahezu reibungslos gelagert ist.

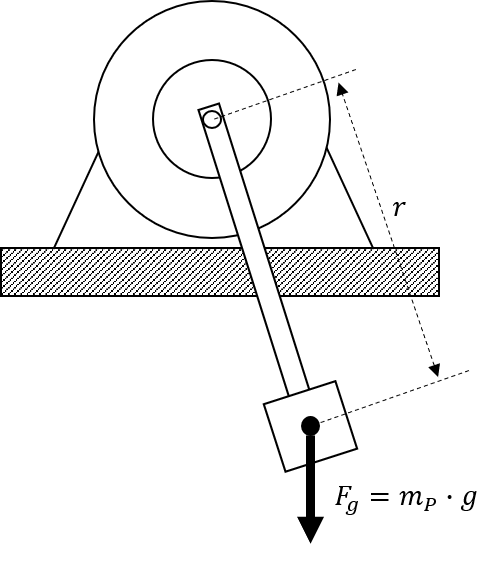
Abbildung 8.13: Antriebssystem mit zusätzlichem Pendel zur Bestimmung des Trägheitsmomentes

Bei der Auslenkung des Pendels werden die trägen Massen durch das enstehende Drehmoment bewegt und das gesuchte Trägheitsmoment des Körpers \(J_{K}\) lässt sich mit Hilfe der Gleichung

\[ J_{K}=m_{P}\cdot g\cdot r\cdot \left(\frac{T}{2\pi}\right)^{2}-J_{M}-J_{P} \] errechnen. Dabei handelt es sich bei \(J_{P}=r^{2}\cdot m_{P}\) um das Trägheitsmoment des Pendels, bei \(J_{M}\) um das Trägheitsmoment des Motors und bei \(T\) um die Schwingungsdauer der gemessenen Schwingung.

8.5.2 Bestimmung elektrischer Parameter

Der ohmsche Ständerwiderstand der Asynchronmaschine kann relativ einfach mit Hilfe einer Widerstandsmessung bestimmt werden. Die Verschaltung der Ständerwicklungen ist dabei allerdings entsprechend zu berücksichtigen. Im Falle eines Schleifringläufers ist auch der Läuferwiderstand messbar. Bei Käfigläufern hingegen ist eine Messung, aufgrund der fehlenden Zugänglichkeit nicht möglich. Zu berücksichtigen gilt es die Temperatur der Wicklung zum Zeitpunkt der Messung, da dieser, je nach Material, stark temperaturabhängig ist. Ausgangspunkt zur Bestimmung der elektrischen Grössen bildet das einsträngige Ersatzschaltbild der ASM für den stationären Betrieb.

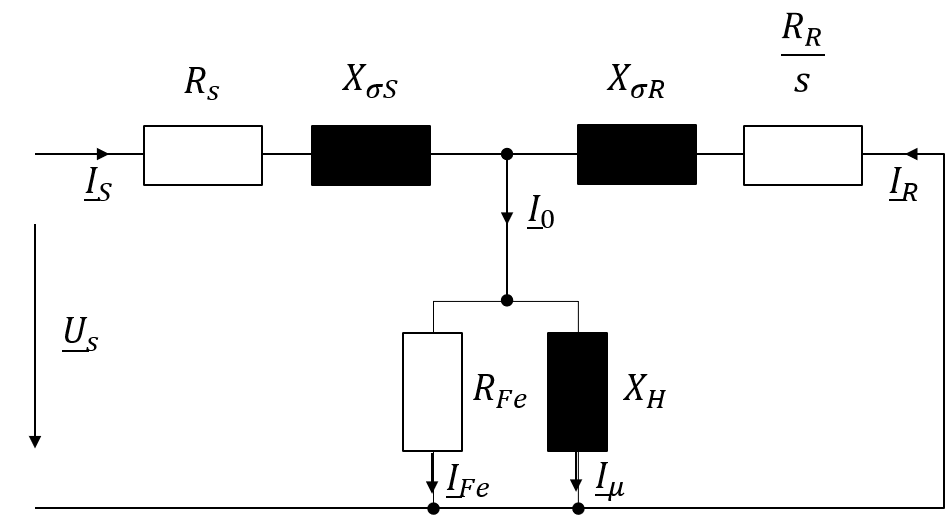
Abbildung 8.14: Zur Parameterbestimmung verwendetes Ersatzschaltbild der ASM

8.5.2.1 Leerlaufmessung

Der Leerlaufversuch der Asynchronmaschine bietet die Möglichkeit die wichtigsten Kenngrössen des magnetischen Kreises und die Verluste zu bestimmen. Die Durchführung erfolgt bei Nennspannung, Nennfrequenz und Nenndrehzahl, indem die Maschine unbelastet betrieben wird. Bei unbelastetem Betrieb wird dem Netz der Magnetisierungsstrom und die für die Eisen- und Reibungsverluste benötigte elektrische Energie entnommen. Mit Hilfe des Leerlaufstromes \(I_{0}\), der Leerlaufspannung \(U_{0}\) und der Leerlaufleistung \(p_{0}\) kann der Leistungsfaktor

\[ cos \varphi_{0}=\frac{P_{0}}{U_{0}\cdot I_{0}} \]

bestimmt werden. Der benötigte Magnetisierungsstrom wiederum kann durch die Gleichung

\[ I_{\mu}=I_{0}\cdot sin(\varphi) \]

bestimmt werden. Mit Hilfe des Leerlaufstromes können ausserdem die Kupferverluste \(V_{Cu}=R_{St}\cdot I_{0}^{2}\) berechnet werden. Es ist auch möglich den Läufer der ASM mit Hilfe einer zweiten Maschine auf die Synchrondrehzahl zu beschleunigen. Auf diese Art und Weise werden die Reibungsverluste eliminiert. Wird auf diese Art und Weise verfahren, gilt es folgende Messwerte zu ermitteln:

• Leerlauspannung \(U_{0}\)
• Leerlaustrom \(I_{0}\)
• Verlustleistung \(P_{0}\)
• Temperatur \(T\)
• Drehzahl \(n\)

Wird die ASM im Leerlauf mit der Synchrondrehzahl betrieben, wird im Läuferkreis keine Spannung induziert, wodurch sich auch kein Läuferstrom einstellt. Aufgrund dessen kann der Läuferstrom in der Ersatzschaltung (vgl. Abb. 8.14) unberücksichtigt bleiben. Desweiteren werden die Statorreaktanz sowie der Statorwiderstand bei der Berechnung der folgenden Parameter vernachlässigt, da sowohl der Statorwiderstand im vergleich zum Ersatzwiderstand für die Eisenverluste \(R_{Fe}\) als auch die Statorstreureaktanz \(X_{\sigma s}\) im Vergleich zur Hauptreaktant \(X_{h}\) sehr gering ausfallen. Der Ersatzwiderstand für die Eisenverluste wird folgendermassen bestimmt:

\[ R_{Fe}=\frac{U_{0}^{2}}{P_{0}} \]

Die Hauptreaktanz \(X_{h}\) ergibt sich aus der Überlegung, dass die gesamte Leerlaufblindleistung \(Q_{0}\) in der Hauptreaktanz umgesetzt wird.

\[ X_{h}=\frac{U_{0}^{2}}{\sqrt{S_{0}^{2}-P_{0}^{2}}}=\frac{U_{0}^{2}}{\sqrt{\left(U_{0}\cdot I_{0}\right)^{2}-P_{0}^{2}}} \]

Mit Hilfe der Hauptreaktanz kann die Hauptinduktivität bestimmt werden:

\[ L_{h}=\frac{X_{h}}{2\pi \cdot f} \]

8.5.2.2 Kurzschlussmessung

Zur Durchführung des Kurzschlussversuches wird der Rotor blockiert und dients zur Bestimmung der Streureaktanzen und der Kurzschlussverluste. Um den Motor thermisch nicht zu überlasten, wird der Versuch bei reduzierter Spannung \(U_{k}\) durchgeführt, indem der Dauerkurzschlusstrom \(I_{k}\) auf den Nennstrom begrenzt wird. Die Höhe des Kurzschlusstromes hängt vom magnetischen Leitwert der Streuwege ab. Umso grösser die Streureaktanz, umso geringer fällt der Kurzschlussstrom aus. Bei der Messung werden folgende Parameter gemessen:

• Kurzschlussspannung \(U_{k}\)
• Kurzschlusstrom \(I_{k}\)
• Verlustleistung \(P_{k}\)
• Temperatur \(T\)

Bei der Kurzschlussmessung werden sowohl der Ersatzwiderstand für die Eisenverlste \(R_{Fe}\) als auch die Hauptreaktanz \(X_{h}\) vernachlässigt, da der auf die Ständerseite transformierte Läuferwiderstand \(R_{r}^{'}\) viel kleiner ist als \(R_{Fe}\) und die Summe der Streureaktanzen \(X_{\sigma s} + X_{\sigma r}^{'}\) deutlich kleiner sind als die Hauptreaktanz \(X_{h}\). Durch Messung der Kurzschlussleistung \(P_{k}\) lässt sich der Leistungsfaktor

\[ cos \varphi_{k}=\frac{P_{k}}{U_{k}\cdot I_{k}} \]

bestimmen. Der auf die Läuferseite transformierte Läuferwiderstand \(R_{r}^{'}\) ergit sich aus der Gleichung:

\[ R_{r}^{'}=\frac{P_{k}^{2}}{I_{k}^{2}}-R_{s}(T) \]

Die Summe der Streureaktanzen kann auf ähnliche Weise bestimmt werden:

\[ X_{\sigma s} + X_{\sigma r}^{'} = \frac{Q_{k}}{I_{k}^{2}}=\frac{\sqrt{\left(U_{k}\cdot I_{k}\right)^{2}-P_{k}^{2}}}{I_{k}^{2}} \]

Mit Hilfe der Summe der Streureaktanzen können die Ständer- und Läuferinduktivitäten bestimmt werden:

\[ L_{r}=L_{s}=\frac{1}{2}\cdot \frac{X_{\sigma s}+X_{\sigma r}^{'}}{2\pi \cdot f}+L_{h} \]

Obige Gleichung macht deutlich, dass die Ständer- und Läuferreaktanzen als gleich gross angenommen werden. Diese Annahme ist in der Praxis üblich, da eine messtechnische Aufspaltung nicht möglich ist.

8.6 Grundidee der feldorientierten Regelung

Wichtig an dieser Stelle zu erwähnen ist, das die Rotorparameter (z.B. Rotorwiderstand und Rotorinduktivität) in den folgenden Kapiteln auf die Statorseite bezogen werden. Es handelt sich folglich um gestrichene Grössen. Es wird lediglich auf einen entsprechenden Superskript verzichtet.

Bei der feldorientierten Regelung versucht man den einfachen Ansatz zur getrennten Regelung von magnetischem Fluss und Drehmoment (Ankerstrom) einer Gleichstrommaschine auf eine Drehfeldmaschine anzuwenden. Die Grundidee besteht darin, ein rotierendes Bezugssystem zu wählen, welches beispielsweise mit dem Flussraumzeiger rotiert. Dieser Ansatz führt dazu, dass sich das magnetische Feld nicht mehr dreht (Sinusgrösse), sondern still steht (Gleichgrösse). Dies lässt sich so interpretieren, dass man mit dem Flussraumzeiger rotiert. Als Bezugs-Koordinatensystem wird üblicherweise der Rotorflussraumzeiger verwendet und man spricht in diesem Zusammenhang von einem rotorflussorientiertem Bezugssystem, welches dem statorflussorientierten (oder luftspaltflussorientierten) Bezugssystem gegenüber gewisse Vorteile bietet. Wird die Gleichung zur Bestimmung des Drehmomentes (vgl. Kapitel 6.3) mit Hilfe von Rotorgrössen ausgedrückt,

\[ \begin{aligned} \underline{M}=\left(\begin{array}{c}M_{d}\\ M_{q}\\ M_{z}\end{array}\right)&=-\frac{3}{2}\cdot p\cdot \left(\underline{\Psi}_{r}^{k}\times\underline{i}_{r}^{k} \right)\\ &= -\frac{3}{2}\cdot p\cdot\left(\Psi_{r}^{d}\cdot i_{r}^{q} - \Psi_{r}^{q}\cdot i_{r}^{d} \right) \end{aligned} \]

Da es sich beim gewählten Koordinatensystem um ein rotorflussorientiertes Koordinatensystem handelt (d-Achse zeigt exakt in Richtung des Rotorflusses), besitzt der Rotorfluss keine q-Komponenten (\(\Psi_{r}^{q}=0\)) und obige Gleichung für das Drehmoment vereinfacht sich.

\[ \underline{M}=-\frac{3}{2}\cdot p\cdot\ \Psi_{r}^{d}\cdot i_{r}^{q} \]

Diese Gleichung ähnelt von der Struktur her eindeutig der Gleichung für das Drehmoment der Gleichstrommaschine und das Drehmoment kann durch die d-Komponente des verketteten Rotorflusses oder die q-Komponente des Rotorstromes beeinflusst werden. Es sei darauf hingewiesen, dass ein ähnliches Vorgehen auch bei Statorflussorientierung möglich ist. Um das Drehmoment anhand obiger Gleichung, durch getrennte Regelung des Flusses und des Stromes, regeln zu können, werden die Systemgleichungen der allgemeinen Drehfeldmaschine in das k-Koordinatensystem umgewandelt. Die Statorspannungsgleichung lautet:

\[ \underbrace{\underline{u}_{s}^{s}}_{T_{P}(\varphi_{k})\cdot \underline{u}_{s}^{k}}= R_{s}\cdot \underbrace{\underline{i}_{s}^{s}}_{T_{P}(\varphi_{k})\cdot \underline{i}_{s}^{k}} + \underbrace{\frac{d\underline{\Psi}_{s}^{s}}{dt}}_{\frac{d\left(T_{P}(\varphi_{k})\cdot \underline{\Psi}_{s}^{k}\right)}{dt}} \]

Bei der zeitlichen Ableitung des Statorflussraumzeigers gilt es zu beachten, dass die Amplitude durch zwei Effekte beeinflusst wird. Zum einen ändert sich die Amplitude mit der Zeit aufgrund der Drehung des Statorflussraumzeigers und zum anderen ändert sich die Amplitude des Statorfluss aufgrund einer Amplitudenänderung selbst. Diese zwei Effekte werden aus mathematischer Sicht berücksichtigt, indem die Kettenregel bei der Bildung der zeitlichen Ableitung berücksichtigt wird.

\[ \frac{d\left(T_{P}(\varphi_{k})\cdot \underline{\Psi}_{s}^{k}\right)}{dt} = \frac{dT_{P}(\varphi_{k})}{dt}\cdot \underline{\Psi}_{s}^{k} + T_{P}(\varphi_{k})\cdot \frac{d\underline{\Psi}_{s}^{k}}{dt} \]

Bildet man die Ableitung der Drehmatrix \(T_{P}(\varphi_{k})\), lässt sich das in der Literatur häufig anzutreffende Ergebnis leicht nachvollziehen.

\[ \begin{aligned} \frac{dT_{P}(\varphi_{k})}{dt}&= \frac{d}{dt}\cdot \left(\begin{matrix} cos(\varphi_{k}) & -sin(\varphi_{k}) \\ sin(\varphi_{k}) & cos(\varphi_{k})\end{matrix} \right) \\ &= \left(\begin{matrix} \dot \varphi_{k} \cdot (-1)\cdot sin(\varphi_{k}) & \dot \varphi_{k} \cdot(-1)\cdot cos(\varphi_{k}) \\ \dot \varphi_{k} \cdot cos(\varphi_{k}) & \dot \varphi_{k} \cdot (-1)\cdot sin(\varphi_{k})\end{matrix} \right) \\ &=\underbrace{\dot \varphi_{k}}_{\omega_{k}} \cdot \left(\begin{matrix} -sin(\varphi_{k}) & - cos(\varphi_{k}) \\ cos(\varphi_{k}) & -sin(\varphi_{k})\end{matrix} \right) \\ &=\omega_{k}\cdot T_{P}(\varphi_{k})\cdot J \end{aligned} \]

Werden diese Modifikationen in die Ausgangsgleichung eingesetzt, lässt sich die Statorspannungsgleichung im k-Koordinatensystem darstellen.

\[ \begin{aligned} T_{P}(\varphi_{k})\cdot \underline{u}_{s}^{k}&= R_{s}\cdot T_{P}(\varphi_{k})\cdot \underline{i}_{s}^{k} + \omega_{k}\cdot T_{P}(\varphi_{k})\cdot J\cdot \underline{\Psi}_{s}^{k} + T_{P}(\varphi_{k})\frac{d\underline{\Psi}_{s}^{k}}{dt} \iff \\ \underline{u}_{s}^{k}&= R_{s}\cdot \underline{i}_{s}^{k} + \omega_{k}\cdot J\cdot \underline{\Psi}_{s}^{k} + \frac{d\underline{\Psi}_{s}^{k}}{dt} \end{aligned} \]

Um die Rotorspannungsgleichung im rotorflussorientierten Koordinatensystem darstellen zu können wird die Rotorspannungsgleichung erst, durch Anwendung der inversen Park-Transformation, in Statorkoordinaten (\(\varphi_{m}\)) dargestellt und anschliessend durch erneute Transformation in das gleiche rotorflussorientierte Koordinatensystem (\(\varphi_{k}\)) transformiert.

\[ \begin{aligned} \underline{u}_{r}^{r}&= R_{r}\cdot \underline{i}_{r}^{r} + \frac{d\underline{\Psi}_{r}^{r}}{dt} \iff \\ T_{P}(-\varphi_{m})\cdot \underline{u}_{r}^{s}&=R_{r}\cdot T_{P}(-\varphi_{m})\cdot \underline{i}_{r}^{s}+\frac{d\left(T_{P}(-\varphi_{m})\cdot \underline{\Psi}_{r}^{s}\right)}{dt} \end{aligned} \]

Die obige Gleichung repräsentiert die Rotorspannungsgleichung im Statorkoordinatensystem. Durch Verwendung der Park-Transformation ergibt sich schlussendlich die Darstellung im rotorflussorientierten Koordinatensystem.

\[ \begin{aligned} T_{P}(\varphi_{k})\cdot T_{P}(-\varphi_{m})\cdot \underline{u}_{r}^{k}&=R_{r}\cdot T_{P}(\varphi_{k})\cdot T_{P}(-\varphi_{m})\cdot \underline{i}_{r}^{k}+\frac{d\left(T_{P}(\varphi_{k})\cdot T_{P}(-\varphi_{m})\cdot \underline{\Psi}_{r}^{k}\right)}{dt} \iff \\ T_{P}(\varphi_{k}-\varphi_{m})\cdot \underline{u}_{r}^{k}&= R_{r}\cdot T_{P}(\varphi_{k}-\varphi_{m})\cdot \underline{i}_{r}^{k} + \frac{d\left(T_{P}(\varphi_{k}-\varphi_{m})\cdot \underline{\Psi}_{r}^{k}\right)}{dt} \iff \\ T_{P}(\varphi_{k}-\varphi_{m})\cdot \underline{u}_{r}^{k} &= R_{r}\cdot T_{P}(\varphi_{k}-\varphi_{m})\cdot \underline{i}_{r}^{k} +\frac{dT_{P}(\varphi_{k}-\varphi_{m})}{dt}\cdot \underline{\Psi}_{r}^{k}+T_{P}(\varphi_{k}-\varphi_{m})\cdot \frac{\underline{\Psi}_{r}^{k}}{dt} \end{aligned} \]

Auch bei dieser Gleichung kann die zeitliche Ableitung der Drehmatrix \(T_{P}(\varphi_{k}-\varphi_{m})\) gebildet werden.

\[ \begin{aligned} \frac{dT_{P}(\varphi_{k}-\varphi_{m})}{dt}&= \frac{d}{dt}\cdot \left(\begin{matrix} cos(\varphi_{k}-\varphi_{m}) & -sin(\varphi_{k}-\varphi_{m}) \\ sin(\varphi_{k}-\varphi_{m}) & cos(\varphi_{k}-\varphi_{m})\end{matrix} \right)\\&= \left(\begin{matrix} -\frac{d(\varphi_{k}-\varphi_{m})}{dt} \cdot sin(\varphi_{k}-\varphi_{m}) & -\frac{d(\varphi_{k}-\varphi_{m})}{dt} \varphi_{k} \cdot cos(\varphi_{k}-\varphi_{m}) \\ \frac{d(\varphi_{k}-\varphi_{m})}{dt} \cdot cos(\varphi_{k}-\varphi_{m}) & -\frac{d(\varphi_{k}-\varphi_{m})}{dt} \cdot sin(\varphi_{k}-\varphi_{m})\end{matrix} \right) \\ &= \underbrace{\frac{d(\varphi_{k}-\varphi_{m})}{dt}}_{\omega_{k}-\omega_{m}} \cdot \left(\begin{matrix} -sin(\varphi_{k}-\varphi_{m}) & - cos(\varphi_{k}-\varphi_{m}) \\ cos(\varphi_{k}-\varphi_{m}) & -sin(\varphi_{k}-\varphi_{m})\end{matrix} \right) \\ &=(\omega_{k}-\omega_{m})\cdot T_{P}(\varphi_{k}-\varphi_{m})\cdot J \end{aligned} \]

Somit kann auch für die Rotorspannungsgleichung eine ähnliche Gleichung verwendet werden wie für die Statorspannungsgleichung.

\[ \begin{matrix} T_{P}(\varphi_{k}-\varphi_{m})\cdot \underline{u}_{r}^{k}= R_{r}\cdot T_{P}(\varphi_{k}-\varphi_{m})\cdot \underline{i}_{r}^{k} + (\omega_{k}-\omega_{m})\cdot T_{P}(\varphi_{k}-\varphi_{m})\cdot J\cdot \underline{\Psi}_{r}^{k}+\\ T_{P}(\varphi_{k}-\varphi_{m})\cdot \frac{\underline{d\Psi}_{r}^{k}}{dt} \iff \\ \underline{u}_{r}^{k}= R_{r}\cdot \underline{i}_{r}^{k} + (\omega_{k}-\omega_{m})\cdot J\cdot \underline{\Psi}_{r}^{k} + \frac{\underline{d\Psi}_{r}^{k}}{dt} \end{matrix} \]

Um das System vollständig beschreiben zu können, müssen auch die Gleichungen für die Flussverkettungen im rotorflussorientierten Koordinatensystem gegeben sein. Die Statorflussverkettung kann mit Hilfe der inversen Park-Transformation und dem Winkel \(\varphi_{k}\) in das k-KOS überführt werden, da die Statorflussverkettung bereits in Statorkoordinaten gegeben ist.

\[ \begin{matrix} T_{P}(-\varphi_{k})\cdot \underline{\Psi}_{s}^{s}=L_{s}\cdot T_{P}(-\varphi_{k})\cdot \underline{i}_{s}^{s} + L_{M}\cdot T_{P}(-\varphi_{k})\cdot \underline{i}_{r}^{s} \iff \\ \underline{\Psi}_{s}^{k}= L_{s}\cdot \underline{i}_{s}^{k} + L_{M}\cdot \underline{i}_{r}^{k} \end{matrix} \]

Auf ähnliche Art und Weise kann die Rotorflussverkettung mit der Park-Transformation \(T_{P}(\varphi_{m}-\varphi_{k})\) angewendet auf die Rotorflussgleichung (6.5) bestimmt werden.

\[ \underline{\Psi}_{r}^{k}= L_{r}\cdot \underline{i}_{r}^{k} + L_{M}\cdot \underline{i}_{s}^{k} \]

8.7 FOR der Käfigläufer-ASM

Die feldorientierte Regelung (FOR) soll anhand einer Käfigläufer-ASM mit Kaskadenregelung vorgestellt werden, um die Analogie zur Gleichstrommaschine zeigen zu können. Für die Rotorspannung gilt im Falle der Käfigläufer ASM:

\[ \underline{u}_{r}^{r} = 0 \]

Die im Kapitel 8.6 hergeleiteten Gleichungen stellen die Systemgleichungen der Käfigläufer-ASM dar.

\[\begin{equation} \begin{matrix} \underline{u}_{s}^{k}= R_{s}\cdot \underline{i}_{s}^{k} + \omega_{k}\cdot J\cdot \underline{\Psi}_{s}^{k} + \frac{d\underline{\Psi}_{s}^{k}}{dt} \\ \underline{0} = R_{r}\cdot \underline{i}_{r}^{k} + (\omega_{k}-\omega_{m})\cdot J\cdot \left(\begin{matrix}\Psi_{r}^{d} \\ 0 \end{matrix}\right) + \left(\begin{matrix}\dot \Psi_{r}^{d} \\ 0 \end{matrix}\right) \\ \underline{\Psi}_{s}^{k}= L_{s}\cdot \underline{i}_{s}^{k} + L_{M}\cdot \underline{i}_{r}^{k} \\ \underline{\Psi}_{r}^{k}= \left(\begin{matrix}\Psi_{r}^{d} \\ 0 \end{matrix}\right)= L_{r}\cdot \underline{i}_{r}^{k} + L_{M}\cdot \underline{i}_{s}^{k} \\ M=\frac{3}{2}\cdot p\cdot \left(\underline{i}_{s}^{k}\right)^{T}\cdot J \cdot \underline{\Psi}_{s}^{k} \\ \omega_{r}=p\cdot \omega_{m} \end{matrix} \tag{8.6} \end{equation}\]

Da der Statorstrom im Vergleich zum Rotorstrom einfach messbar ist, wird empfohlen die entsprechende Momentengleichung zu verwenden. Ähnlich wie bei der Herleitung der allgemeinen Drehfeldmaschine werden die Systemgleichungen verwendet, um ein Blockschaltbild zu erarbeiten, welches das Gesamtsystem beschreibt. Um in der Gleichung für das Drehmoment den Rotor- anstelle des Statorflusses verwenden zu können, wird die Gleichung für den Rotorfluss \(\underline{\Psi}_{r}^{k}\) nach dem Rotorstrom im k-Koordinatenystem (\(\underline{i}_{r}^{k}\)) umgestellt.

\[ \underline{i}_{r}^{k}= \frac{1}{L_{r}}\cdot \left(\underline{\Psi}_{r}^{k} -L_{M}\cdot \underline{i}_{s}^{k} \right) \]

Diese Gleichung lässt sich in die Gleichung für die Statorflussverkettung einsetzen.

\[\begin{equation} \begin{matrix} \underline{\Psi}_{s}^{k}= L_{s}\cdot \underline{i}_{s}^{k} + L_{M}\cdot \underline{i}_{r}^{k} \\ = L_{s}\cdot \underline{i}_{s}^{k}+L_{M}\cdot \frac{1}{L_{r}}\cdot \left(\underline{\Psi}_{r}^{k} -L_{M}\cdot \underline{i}_{s}^{k} \right) \\ = L_{s}\cdot \underline{i}_{s}^{k}+\frac{L_{M}}{L_{r}}\cdot \underline{\Psi}_{r}^{k}- \frac{L_{M}^{2}}{L_{r}}\cdot \underline{i}_{s}^{k} \\ = \left(L_{s} - \frac{L_{M}^{2}}{L_{r}} \right)\cdot \underline{i}_{s}^{k} + \frac{L_{M}}{L_{r}} \cdot \underline{\Psi}_{r}^{k} \\ = L_{s}\cdot\underbrace{\left(1-\frac{L_{M}^{2}}{L_{r}\cdot L_{s}} \right)}_{\sigma}\cdot \underline{i}_{s}^{k} + \frac{L_{M}}{L_{r}} \cdot \underline{\Psi}_{r}^{k} \end{matrix} \tag{8.7} \end{equation}\]

Der Term \(\left(1-\frac{L_{M}^{2}}{L_{r}\cdot L_{s}} \right)=\sigma\) wird, wie bereits in Kapitel 3.2.4 beschrieben, als Blondel’scher Streukoeffizient bezeichnet. Die neu gewonnene Gleichung für die Statorflussverkettung wird anschliessend in die Momentengleichung eingesetzt.

\[ \begin{matrix} M=\frac{3}{2}\cdot p\cdot \left(\underline{i}_{s}^{k}\right)^{T}\cdot J \cdot \underline{\Psi}_{s}^{k} \\ = \frac{3}{2}\cdot p\cdot \left(\underline{i}_{s}^{k}\right)^{T}\cdot J \cdot \left(L_{s}\cdot\sigma\cdot \underline{i}_{s}^{k} + \frac{L_{M}}{L_{r}} \cdot \underline{\Psi}_{r}^{k}\right) \\ = \underbrace{\frac{3}{2}\cdot p\cdot \left(\underline{i}_{s}^{k}\right)^{T}\cdot J\cdot L_{s}\cdot\sigma\cdot \underline{i}_{s}^{k}}_{=0}+\frac{3}{2}\cdot p\cdot \left(\underline{i}_{s}^{k}\right)^{T}\cdot J\cdot \frac{L_{M}}{L_{r}} \cdot \underline{\Psi}_{r}^{k} \end{matrix} \]

Der erste Term obiger Gleichung ist Null, da \(\underline{i}_{s}^{k} \perp J\cdot \underline{i}_{s}^{k}\). Somit vereinfacht sich die Gleichung für das Drehmoment massgeblich.

\[\begin{equation} \begin{matrix} M = \frac{3}{2}\cdot p\cdot \left(\underline{i}_{s}^{k}\right)^{T}\cdot J\cdot \frac{L_{M}}{L_{r}} \cdot \underline{\Psi}_{r}^{k} = \frac{3}{2}\cdot p\cdot\left(\begin{matrix}i_{s}^{d} & i_{s}^{q}\end{matrix}\right) \cdot \underbrace{\left(\begin{matrix}0&-1\\1&0\end{matrix}\right)\cdot \left(\begin{matrix}\Psi_{r}^{d} \\ 0\end{matrix}\right)}_{\left(\begin{matrix}0 \\ \Psi_{r}^{d}\end{matrix}\right)} \\ = \frac{3}{2}\cdot p\cdot \frac{L_{M}}{L_{r}}\cdot i_{s}^{q}\cdot \Psi_{r}^{d} \end{matrix} \tag{8.8} \end{equation}\]

Diese Gleichung lässt eine Darstellung als Blockschaltbild zu (siehe Abb. 8.15) zu.

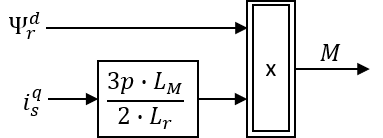
Abbildung 8.15: Blockschaltbild des Drehmomentes der Käfigläufer-ASM in k-Koordinaten

Da die Gleichung für das Drehmoment in k-Koordinaten (vgl. Gleichung (8.8)) die einzelnen Komponenten der Raumzeiger beinhaltet, ist es notwendig diese aus den Systemgleichungen zu bestimmen. Dazu wird die Rotorflussgleichung (Gleichung (8.6)) verwendet und in ihre Komponenten zerlegt.

\[ \begin{matrix} \Psi_{r}^{d}=L_{r}\cdot i_{r}^{d}+L_{M}\cdot i_{s}^{d} \iff i_{r}^{d}=\frac{1}{L_{r}}\cdot(\Psi_{r}^{d}-L_{M}\cdot i_{s}^{d})\\ 0=L_{r}\cdot i_{r}^{q}+L_{M}\cdot i_{s}^{q} \iff i_{r}^{q}=-\frac{L_{M}}{L_{r}}\cdot i_{s}^{q} \end{matrix} \]

Diese Gleichungen werden in die Rotorspannungs-DGL (vgl. Gleichungen (8.6)) eingesetzt.

\[\begin{equation} \begin{matrix} \left(\begin{matrix}0 \\ 0 \end{matrix}\right) = R_{r}\cdot \left(\begin{matrix}i_{r}^{d} \\ i_{r}^{q} \end{matrix}\right) + (\omega_{k}-\omega_{m})\cdot \left(\begin{matrix}0 \\ \Psi_{r}^{d} \end{matrix}\right) + \left(\begin{matrix}\dot \Psi_{r}^{d} \\ 0 \end{matrix}\right) \iff \\ \left(\begin{matrix}0 \\ 0 \end{matrix}\right) = R_{r}\cdot \left(\begin{matrix}\frac{1}{L_{r}}\cdot(\Psi_{r}^{d}-L_{M}\cdot i_{s}^{d}) \\ -\frac{L_{M}}{L_{r}}\cdot i_{s}^{q} \end{matrix}\right) + (\omega_{k}-\omega_{m})\cdot \left(\begin{matrix}0 \\ \Psi_{r}^{d} \end{matrix}\right) + \left(\begin{matrix}\dot \Psi_{r}^{d} \\ 0 \end{matrix}\right) \end{matrix} \tag{8.9} \end{equation}\]

Da das Blockschaltbild (Abb. 8.15) zur Vervollständigung eine Gleichung zur Berechnung der d-Komponente der Rotorflussverkettung benötigt, wird diese Komponente obiger Gleichung berücksichtigt.

\[\begin{equation} 0=\frac{R_{r}}{L_{r}} \cdot(\Psi_{r}^{d}-L_{M}\cdot i_{s}^{d}) + \dot \Psi_{r}^{d} \iff L_{M}\cdot i_{s}^{d}=\frac{L_{r}}{R_{r}}\cdot \dot \Psi_{r}^{d}+\Psi_{r}^{d} \tag{8.10} \end{equation}\]

Diese Gleichung kann durch Laplace-Transformation in den Bildbereich transformiert werden, um das Verhalten der d-Komponente des Rotorflusses in Abhängigkeit der d-Komponente des Statorflusses in Form einer Übertragungsfunktion zum Ausdruck bringen zu können.

\[ L_{M}\cdot i_{s}^{d}=\frac{L_{r}}{R_{r}}\cdot s\cdot \Psi_{r}^{d}+\Psi_{r}^{d} \iff \frac{\Psi_{r}^{d}}{i_{s}^{d}}=\frac{L_{M}}{1+s\cdot \frac{L_{r}}{R_{r}}} \]

Diese Übertragungsfunktion beschreibt ein PT1-Glied mit einer Verstärkung von \(k=L_{M}\) und einer Zeitkonstante \(T=\frac{L_{r}}{R_{r}}\), welche direkt zur Erweiterung des Blockschaltbildes (Abb. 8.15) verwendet werden kann.

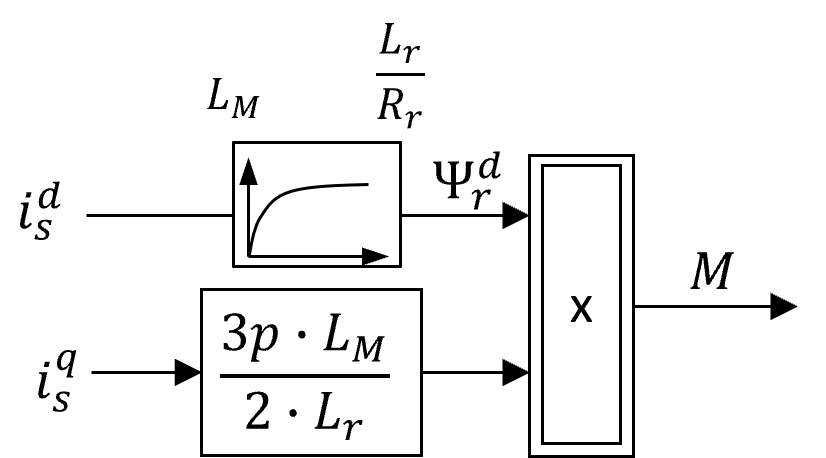
Abbildung 8.16: Erweitertes Blockschaltbild des Drehmomentes der Käfigläufer-ASM in k-Koordinaten

Das Blockschaltbild beinhaltet die zwei Komponenten des Statorstromraumzeigers, welcher jedoch nicht ohne weiteres als Stell- bzw. Eingangsgrösse zur Verfügung steht. Bei Umrichterbetrieb fungiert der Statorspannungsraumzeiger als Eingangsgrösse. Aufgrund dessen ist es notwendig den Statorstromraumzeiger in Abhängigkeit des Statorspannungsraumzeigers darzustellen. Ausgangspunkt dazu bildet die Statorspannungs-DGL der Systemgleichungen (Gleichungen (8.6)), in welcher der Statorflussraumzeiger \(\underline{\Psi}_{s}^{k}\) durch den Ausdruck in Gleichung (8.7) ersetzt werden kann.

\[ \begin{matrix} \underline{u}_{s}^{k}= R_{s}\cdot \underline{i}_{s}^{k} + \omega_{k}\cdot J\cdot \underline{\Psi}_{s}^{k} + \frac{d\underline{\Psi}_{s}^{k}}{dt} \\ = R_{s}\cdot \underline{i}_{s}^{k} + \omega_{k}\cdot J\left( L_{s}\cdot\sigma_{}\cdot \underline{i}_{s}^{k} + \frac{L_{M}}{L_{r}} \cdot \underline{\Psi}_{r}^{k}\right) + \frac{d}{dt}\left( L_{s}\cdot\sigma_{}\cdot \underline{i}_{s}^{k} + \frac{L_{M}}{L_{r}} \cdot \underline{\Psi}_{r}^{k}\right) \\ = R_{s}\cdot \underline{i}_{s}^{k} + \omega_{k}\cdot L_{s}\cdot \sigma \cdot J\cdot \underline{i}_{s}^{k} + L_{s}\cdot \sigma \cdot \frac{d\underline{i}_{s}^{k}}{dt} +\omega_{k}\frac{L_{M}}{L_{r}}\cdot J\cdot \underline{\Psi}_{r}^{k} + \frac{L_{M}}{L_{r}} \dot {\underline{\Psi}}_{r}^{k} \end{matrix} \]

Diese Gleichung wird nach der zeitlichen Ableitung des Statorstromraumzeigers \(\frac{d\underline{i}_{s}^{k}}{dt}\) umgestellt und in seine zwei Komponenten zerlegt.

\[\begin{equation} \begin{aligned} \frac{d\underline{i}_{s}^{k}}{dt} &= \frac{1}{L_{s}\sigma}\left[\underline{u}_{s}^{k}-R_{s}\cdot \underline{i}_{s}^{k}- \omega_{k}\cdot L_{s}\cdot \sigma \cdot J\cdot \underline{i}_{s}^{k}-\omega_{k}\frac{L_{M}}{L_{r}}\cdot J\cdot \underline{\Psi}_{r}^{k}-\frac{L_{M}}{L_{r}} \dot {\underline{\Psi}}_{r}^{k}\right] \frac{d}{dt}\left(\begin{matrix}i_{s}^{d}\\i_{s}^{q} \end{matrix}\right) \\ &=\frac{1}{L_{s}\sigma}\left[\left(\begin{matrix}u_{s}^{d} \\ u_{s}^{q} \end{matrix}\right)-R_{s}\left(\begin{matrix}i_{s}^{d}\\i_{s}^{q} \end{matrix}\right)-\omega_{k}L_{s}\sigma\left(\begin{matrix}-i_{s}^{q}\\i_{s}^{d} \end{matrix}\right)-\omega_{k}\frac{L_{M}}{L_{r}}\left(\begin{matrix}0\\ \Psi_{r}^{d} \end{matrix}\right)-\frac{L_{M}}{L_{r}}\left(\begin{matrix}\dot\Psi_{r}^{d}\\0 \end{matrix}\right) \right] \end{aligned} \tag{8.11} \end{equation}\]

Setzt man in die Gleichung für die d-Komponente des Statorstromraumzeigers noch die, nach der zeitlichen Ableitung der d-Komponente des Rotorfluss \(\dot\Psi_{r}^{d}\) umgestellte, Gleichung (8.10) ein, ergibt sich eine Gleichung, die es ermöglicht die Übertragungsfunktionen der beiden Stromkomponenten zu bestimmen. Die zeitliche Änderung der d-Komponente des Statorstromraumzeigers lautet:

\[ \dot\Psi_{r}^{d} = -\frac{R_{r}}{L_{r}}\Psi_{r}^{d}+\frac{R_{r}\cdot L_{M}}{L_{r}}i_{s}^{d} \]

Wird dieser Ausdruck in obige Gleichung eingesetzt, ergeben sich folgende zwei Gleichungen.

Zeitliche Änderung der d-Komponente des Statorstromraumzeigers:

\[ \begin{matrix} \frac{di_{s}^{d}}{dt} = \frac{1}{L_{s}\sigma}\left[u_{s}^{d}-R_{s}i_{s}^{d}+\omega_{k}L_{s}\sigma i_{s}^{q}-\frac{L_{M}}{L_{r}}\left( -\frac{R_{r}}{L_{r}}\Psi_{r}^{d}+\frac{R_{r}\cdot L_{M}}{L_{r}}i_{s}^{d}\right)\right] \\ =\frac{1}{L_{s}\sigma}\left[u_{s}^{d}-R_{s}i_{s}^{d}+\omega_{k}L_{s}\sigma i_{s}^{q}+\frac{L_{M}R_{r}}{L_{r}^{2}}\Psi_{r}^{d}-\frac{L_{M}^{2}R_{r}}{L_{r}^{2}} i_{s}^{d}\right] \\ \frac{1}{L_{s}\sigma}\left[u_{s}^{d}-\left(R_{s}+ \frac{L_{M}^{2}R_{r}}{L_{r}^{2}}\right)i_{s}^{d} + \underbrace{\omega_{k}L_{s}\sigma i_{s}^{q}+ \frac{L_{M}R_{r}}{L_{r}^{2}}\Psi_{r}^{d}}_{Störterm} \right] \end{matrix} \]

Zeitliche Änderung der q-Komponente des Statorstromraumzeigers:

\[ \frac{di_{s}^{q}}{dt} = \frac{1}{L_{s}\sigma}\left[u_{s}^{d}-R_{s}i_{s}^{q}-\underbrace{\omega_{k}L_{s}\sigma i_{s}^{d}-\omega_{k}\frac{L_{M}}{L_{r}}\Psi_{r}^{d}}_{Störterm}\right] \]

Die Störterme in obigen zwei Gleichungen für die zeitlichen Änderungen des Statorstromraumzeigers enthalten Terme abhängig von der Rotorflussverkettung \(\Psi_{r}^{d}\) als auch Kreuzkoppelterme. Diese Kreuzkoppelterme sind Stromkomponenten, die auf die jeweils andere Stromkomponente zurückwirken (siehe Kapitel 8.7.1). Werden die Störterme in den zwei Gleichungen vernachlässigt, vereinfachen sich die Gleichungen für die Statorstromdynamiken.

\[\begin{equation} \left(\begin{matrix}\frac{di_{s}^{d}}{dt} \\ \frac{di_{s}^{q}}{dt}\end{matrix}\right)= \frac{1}{L_{s}{\sigma}}\left(\begin{matrix}u_{s}^{d}-\left(R_{s}+ \frac{L_{M}^{2}R_{r}}{L_{r}^{2}}\right)i_{s}^{d} \\ u_{s}^{d}-R_{s}i_{s}^{q} \end{matrix}\right) \tag{8.12} \end{equation}\]

Die erarbeiteten Gleichungen zeigen, dass zur Vervollständigung des Blockschaltbildes die elektrische Winkelgeschwindigkeit \(\omega_{k}\) des Rotors benötigt wird. Bei dieser Winkelgeschwindigkeit handelt es sich um Winkelgeschwindigkeit des Transformationswinkels \(\varphi_{k}\). Diese kann mit Hilfe der Gleichung (8.9) für die q-Komponente des Rotorflusses ermittelt werden.

\[ 0=-\frac{R_{r}L_{M}}{L_{r}}i_{s}^{q}+(\omega_{k}-\omega_{m})\Psi_{r}^{d} \iff \omega_{k}=\omega_{m}+\frac{R_{r}L_{M}}{L_{r}}\cdot \frac{i_{s}^{q}}{\Psi_{r}^{d}} \]

Dieser Ausdruck wird auch als Steuerbedingung bezeichnet, da sie besagt, dass die d-Achse exakt zum Rotorfluss ausgerichtet ist. Durch nachträgliche Integration dieser Gleichung über die Zeit kann der Transformationswinkel \(\varphi_{k}\) bestimmt werden.

\[\begin{equation} \varphi_{k}=\varphi_{m}+\frac{R_{r}L_{M}}{L_{r}}\int \frac{i_{s}^{q}}{\Psi_{r}^{d}}dt \tag{8.13} \end{equation}\]

Es gilt zu berücksichtigen, dass die Winkelgeschwindigkeit des Rotors \(\varphi_{m}\) nur bei Maschinen mit einer Polpaarzahl \(p=1\) mit der elektrischen Rotorwinkelgeschwindigkeit übereinstimmt. Für höherpolige Maschinen muss die Winkelgeschwindigkeit des Rotors \(\varphi_{m}\) mit der Polpaarzahl multipliziert werden. Die Gleichung (8.12) kann dazu verwendet werden das Blockschaltbild der ASM ohne Störterme darzustellen, indem die beiden Komponenten in den Laplacebereich transformiert und die Übertragungsfunktionen gebildet werden. Die Übertragungsfunktion für die d-Komponente des Statorstromraumzeiger lautet:

\[\begin{equation} \frac{i_{s}^{d}}{u_{s}^{d}} = \frac{\overbrace{\frac{1}{R_{s}+\frac{R_{r}\cdot L_{M}^{2}}{L_{r}^{2}}}}^{V_{s}^{d}} }{\underbrace{\frac{L_{s}\sigma}{R_{s}+\frac{R_{r}\cdot L_{M}^{2}}{L_{r}^{2}}}}_{T_{s}^{d}}\cdot s+1} \tag{8.14} \end{equation}\]

Die Übertragungsfunktion für die q-Komponente des Statorstromraumzeiger lautet:

\[\begin{equation} \frac{i_{s}^{d}}{u_{s}^{d}} = \frac{\overbrace{\frac{1}{R_{s}}}^{V_{s}^{q}}}{\underbrace{\frac{L_{s}\sigma}{R_{s}}}_{V_{s}^{q}}\cdot s+1} \tag{8.15} \end{equation}\]

Auf diese Art und Weise kann das Blockschaltbild in Abbildung 8.16 erweitert werden.

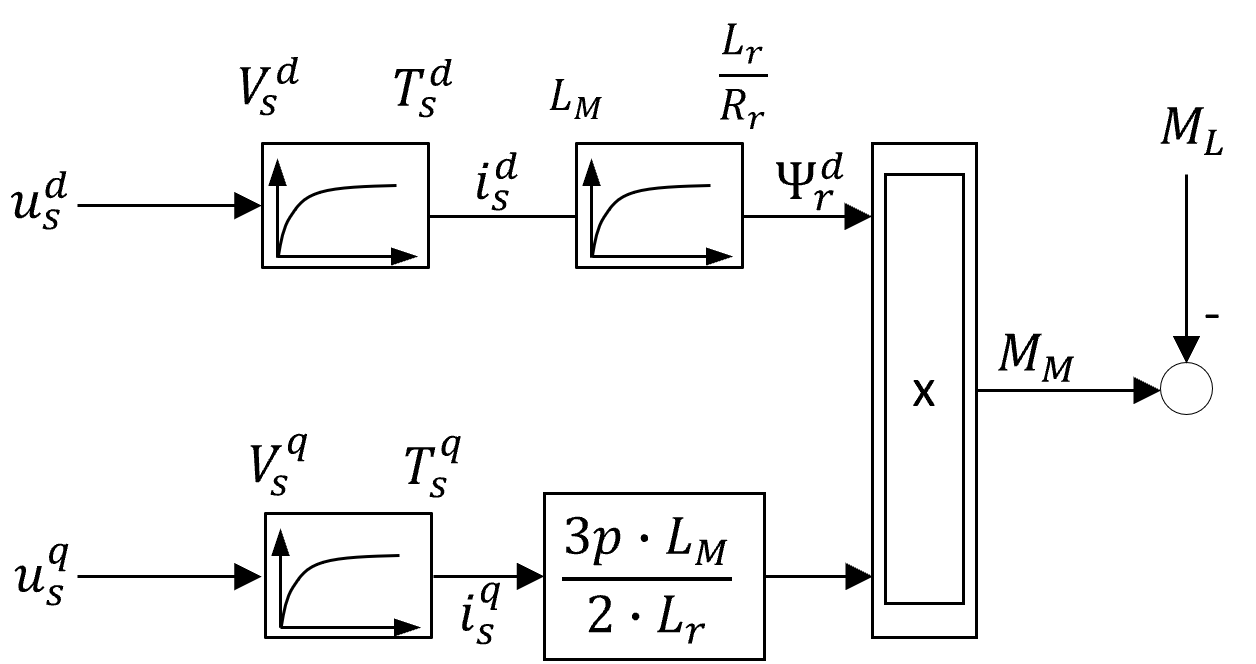
Abbildung 8.17: Blockschaltbild der Käfigläufer-ASM in k-Koordinaten unter Vernachlässigung der Störterme der Statorraumzeigerdynamik

Wie das Blockschaltbild erkennen lässt, wurde die ASM mit Hilfe der vorgestellten Transformationen quasi in eine Gleichstrommaschine transformiert. Die q-Komponente des Statorstromraumzeigers entspricht dem Ankerstrom und die d-Komponente des Statorstromraumzeigers dem Erregerstrom der DC-Maschine. Und auch in diesem Fall ist die Zeitkonstante der Erregerspule deutlich grösser als die des Statorkreises. Somit können die Regler mit der selben Methode ausgelegt werden wie die der DC-Maschine. Auch in diesem Fall muss darauf geachtet werden, dass sich bei der Momentensteuerung bzw. der Drehzahlregelung im Feldschwächebereich die Streckenverstärkung ändert.

8.7.1 Kompensation der Störgrössen durch Störgrössenaufschaltung

Die Wahl einer geeigneten Störgrössenkompensation mit

\[ \underline{u}_{s,komp}^{k}=\left(\begin{matrix}u_{s,komp}^{d}(t) \\ u_{s,komp}^{q}(t)\end{matrix}\right) = -\left(\begin{matrix}\omega_{k}L_{s}\sigma i_{s}^{q}(t)+ \frac{L_{M}R_{r}}{L_{r}^{2}}\Psi_{r}^{d}(t) \\ \omega_{k}L_{s}\sigma i_{s}^{d}(t)-\omega_{k}\frac{L_{M}}{L_{r}}\Psi_{r}^{d}(t)\end{matrix}\right) \]

ermöglicht es diese Kreuzkoppel- bzw. Störterme zu kompensieren unter der Voraussetzung, dass alle Systemparameter bekannt sind. Es sei allerdings darauf hingewiesen, dass aufgrund der Parametersensitivität in der Praxis häufig auf eine solche Kompensation verzichtet wird. Wird auf eine solche Störgrössenkompensation verzichtet, müssen die Regler diese Störungen ausregeln. Desweiteren sollte die Störgrössenaufschaltung aufgrund der Verzögerungszeiten des Umrichters nicht zu stark verzögert einwirken.

8.7.2 Schätzung des Rotorflusses

Wird eine ASM an einem Umrichter betrieben, liegt der Statorstromraumzeiger \(i_{s}^{k}\) im k-Koordinatensystem und die mechanische Winkelgeschwindigkeit des Läufers durch Messung und anschliessend Koordinatentransformation vor. Folglich muss lediglich der verkettete Rotorfluss \(\Psi_{r}^{d}\) mit Hilfe der vorhandenen Messgrössen abgeschätzt werden, um den Transformationswinkel \(\varphi_{k}\) (Gleichung (8.13)) bestimmen zu können. Dazu wird die Gleichung der d-Komponente der Rotorflussdynamik (8.10) verwendet.

\[\begin{equation} \frac{d\hat{\Psi}_{r}^{d}(t)}{dt}= \frac{L_{M}R_{r}}{L_{r}}i_{s}^{d}-\frac{R_{r}}{L_{r}}\hat{\Psi}_{r}^{d}, \quad \hat{\Psi}_{r}^{d}(t=0)=0 \tag{8.16} \end{equation}\]

Somit lässt sich mit Hilfe der gemessenen Statorströme \(\underline{i}_{s}^{s}\) und dem oben beschriebenen Motormodell (Strommodell) der Rotorfluss \(\hat{\Psi}_{r}^{d}\) abschätzen (Kennzeichnung eines geschätzten Wertes durch einen Hut). Auch dieses Modell ist parametersensitiv und es muss berücksichtigt werden, dass diese in der Realität nichtlinear von Strom und Temperatur abhängen. Bei der Implementierung auf einem Mikrocontroller ist darauf zu achten, dass bei der Schätzung des Rotorflusses, zur Bestimmung des Transformationswinkels \(\varphi_{k}\), insbesondere bei der Initialisierung nie durch Null geteilt wird.

8.7.3 Stromregelkreis

Ausgangspunkt für die Reglerauslegung des Stromregelkreises bilden die zwei Übertragungsfunktionen des Statorstromraumzeigers (Gleichungen (8.14) und (8.14)), bei denen die Störterme vernachlässigt wurden. Es müssen also zwei unabhängige PI-regler als sogenannte Stromkomponenten-Regler

\[ \begin{matrix} G_{R,i_{s}^{d}}(s)= V_{r,i_{s}^{d}}\frac{1+sT_{N,i_{s}^{d}}}{sT_{N,i_{s}^{d}}}\\ G_{R,i_{s}^{q}}(s)= V_{r,i_{s}^{q}}\frac{1+sT_{N,i_{s}^{q}}}{sT_{N,i_{s}^{q}}} \end{matrix} \]

ausgelegt werden. Beide PI-Stromregler werden nach dem Betragsoptimum ausgelegt, um ein gutes Führungsverhalten zu gewährleisten.

8.7.4 Drehzahlregelkreis

Ausgangspunkt für die Auslegung des Drehzahlreglers bildet das Blockschaltbild der ASM bei Rotorflussorientierung (vgl. Abb 8.18).

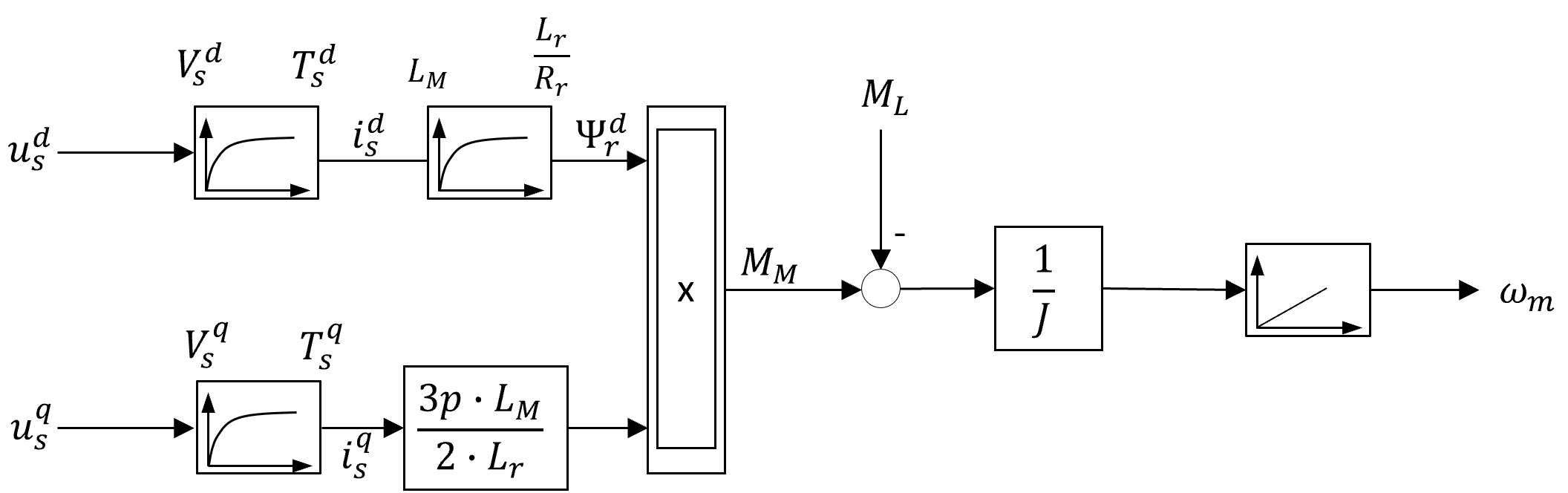
Abbildung 8.18: Signalflussplan der Momentenbildung und der Mechanik einer ASM bei Rotorflussorientierung und Vernachlässigung der Kreuzverkoppelungen

Anhand dieses Signalflussplanes kann das Streckenverhalten der Drehzahlstrecke durch die Übertragungsfunktion \(G_{S,\omega_{m}}(s)\) dargestellt werden, wenn von einer konstanten Rotorflussverkettung \(\Psi_{r}^{d}\) ausgegangen wird.

\[ G_{S,\omega_{m}}(s) = \left .\frac{\omega_{m}(s)}{i_{s}^{q}(s)} \right|_{\Psi_{r}^{d}=konst} = \frac{3p}{2} \frac{L_{M}\Psi_{r}^{d}}{L_{r}\cdot J}\cdot \frac{1}{1+sT_{s}^{q}}\cdot \frac{1}{s} \]

Die Übertragungsfunktion der Strecke beschreibt ein \(IT_{1}\)-System, auf welches ein unbekanntes Lastmoment \(M_{L}\) einwirkt. Wie schon bei der Gleichstrommaschine erfolgt die Auslegung nach dem Symmetrischen Optimum, um ein gutes Störverhalten des Drehzahlregelkreises zu ermöglichen.

8.7.5 Rotorflussregelung

Wie in Kapitel 8.7.2 beschrieben, wird der Rotorfluss \(\hat\Psi_{r}^{d}\), unter Verwendung der gemessenen Strangströme und der geschätzten Maschinenparameter mit Hilfe des Strommodells abgeschätzt. Wird der unterlagerte Stromregelkreis nach dem Betragsoptimum eingestellt, kann die Übertragungsfunktion der d-Komponente des Stromregelkreises, wie bei der DC-Maschine, durch ein PT1-Glied approximiert werden.

\[ \frac{i_{s}^{d}}{i_{s^,Ref}^{d}} = \frac{1}{1+s\cdot 2T_{WR}} \iff i_{s}^{d}=\frac{i_{s^,Ref}^{d}}{1+s\cdot 2T_{WR}} \]

Bei der Zeitkonstante \(T_{WR}\) handelt es sich um die Umrichterverzögerungszeit, die indirekt proportional zur Schaltfrequenz des Umrichters ist. Berücksichtigt man ausserdem den geschätzen Rotorfluss (vgl. Gleichung (8.16)), kann die Übertragungsfunktion des Rotorflussregelkreis bestimmt werden.

\[ G_{R,\Psi_{r}^{d}}(s)= \frac{\hat\Psi_{r}^{d}}{i_{s^,Ref}^{d}}= \frac{1}{1+s\cdot 2T_{WR}}\cdot \frac{L_{M}}{1+\frac{L_{r}}{R_{r}}s} \]

Diese Übertragungsfunktion entspricht einem Verzögerungsglied 2. Ordnung, welches mit einem, nach dem Betragsoptimum eingestellten, PI-Flussregler geregelt werden kann.

Auch hier sei darauf verwiesen, dass es sich bei den Maschinenparametern \((L_{r}, L_{M}, R_{r})\) um geschätzte Werte handelt. Aufgrund dessen kann die reale Regelperformanz von der erwarteten idealen Regelperformanz abweichen.

8.7.6 Sollwertbegrenzung des Stromes

Wie auch bei der DC-Maschine üblich, werden die Strom-Sollwerte auf zulässige Werte begrenzt, um die Maschine vor zu hohen Strömen zu schützen. Im falle der Asynchronmaschine liefern sowohl der Fluss- als auch der Drehzahlregler die d- bzw. q-Strom-Sollwerte. Diese Begrenzung erfolgt üblicherweise durch Bildung der Sollstrom-Vektoramplitude \(||i_{s,Ref}^{k}||\). Dabei wird davon ausgegangen, dass diese Vektoramplitude die maximal zulässige Gesamtstromamplitude \(\hat i_{max}\) nicht überschreiten darf.

\[ ||i_{s,Ref}^{k}|| = \sqrt{\left(i_{s,Ref}^{d}\right)^{2}+\left(i_{s,Ref}^{q}\right)^{2}}\leq \hat i_{max} \]

In einigen Fällen werden die Stromkomponenten auch getrennt voneinander begrenzt.

\[ \begin{matrix} |i_{s,Ref}^{d}|\leq \hat i_{max} \cdot \sqrt{1-\alpha^{2}} \\ |i_{s,Ref}^{q}|\leq \hat i_{max} \cdot \alpha \\ \alpha \in (0,1) \end{matrix} \]

Der Faktor \(\alpha\) kann beispielsweise dem Leistungsfaktor \(cos \varphi\) gleichgesetzt werden. Die flussbildende Stromkomponente \(i_{s}^{d}\) ist üblicherweise deutlich kleiner als die momentbildenden Komponente.