Kapitel 3 Allgemeine Grundlagen der Antriebstechnik

Zum Verständnis der Antriebstechnik sind gewisse physikalische Wechselwirkungen und mathematische Zusammenhänge aller an der Funktion eines Antriebes beteiligten Grössen und Parameter (z.B. Geschwindigkeit, Spannung, Strom, Trägheitsmoment sowie magnetische Grössen) notwendig. Davon ausgehend lassen sich die Gesetzmässigkeiten des statischen und dynamischen Zusammenwirkens innerhalb der Systemprozesse beschreiben. Neben Grundlagen der Mechanik und Elektrotechnik sind ebenfalls die der magnetischen Felder massgeblich.

3.1 Mechanische Grundlagen

Ein elektrischer Antrieb fungiert schlussendlich als elektromechanischer Energiewandler, dessen Aufgabe darin besteht elektrische Energie möglichst verlustlos in mechanische Energie umzuwandeln. Die mechanische Energie kann dabei durch Drehmomente und Drehzahlen mathematisch beschrieben werden. Unter Berücksichtigung der Vorzeichen dieser zwei physikalischen Grössen, ergeben sich vier verschiedene Betriebszustände, die wiederum in einer Drehmoment-Drehzahl-Ebene dargestellt werden können.

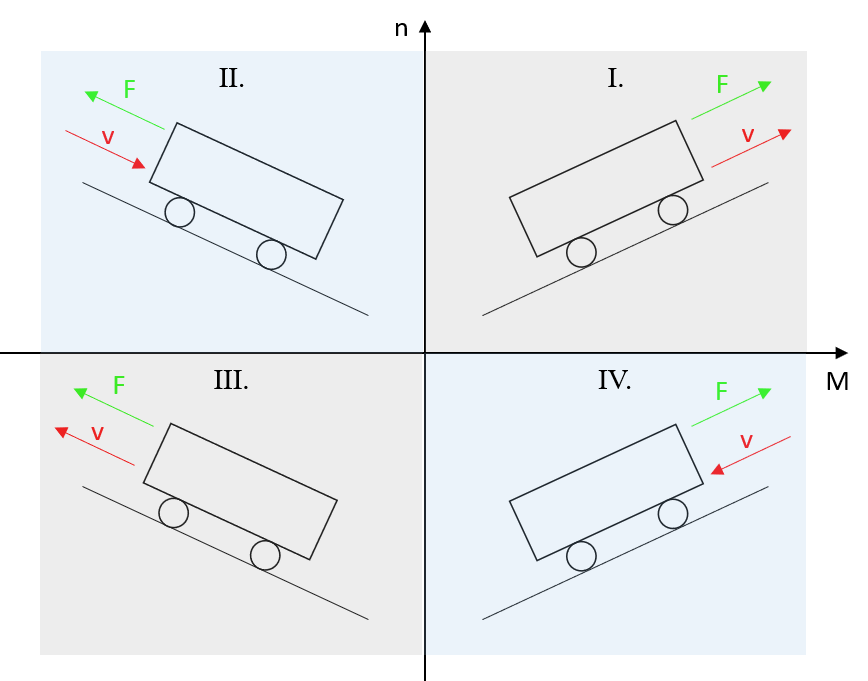
Abbildung 3.1: Die vier Quadranten der Drehmoment-Drehzahl-Ebene

Wird hierbei das Verbraucherzählpfeilsystem angewandt, welches sich dadurch auszeichnet, dass bei positiven Leistungswerten eine Leistungsabgabe an die Last erfolgt, dann können Betriebspunkte, die sich sowohl im ersten als auch im dritten Quadranten befinden als motorische Betriebszustände (Leistungsaufnahme der Last) betrachtet werden. Betriebspunkte im zweiten und vierten Quadranten hingegen werden als generatorische Betriebszustände (Leistungsabgabe der Last) betrachtet. Die mechanische Leistung ergibt sich, je nach Art der Bewegung (Rotation oder Translation) aus dem Produkt von Kraft und Geschwindigkeit bzw. dem Produkt aus Drehmoment und Winkelgeschwindigkeit \(\omega\).

\[ P_{mech} = F\cdot v = M\cdot \omega = M\cdot 2\pi\cdot n \]

Für die mechanische Behandlung eines Antriebsproblems reichen grundsätzlich drei Gesetze aus:

• das dynamische Grundgesetz, das auch den Sonderfall des stationären Betriebs einschliesst,
• das Leistungsgesetz (die Leistungsbilanz) und
• der Energiesatz (die Energiebilanz).

Unabhängig davon ob translatorische oder rotatorische Bewegungen betrachtet werden, lässt sich die Ursache dieser Bewegung durch die Existenz von Kräften bzw. Drehmomenten begründen. Diese Kräfte bzw. Drehmomente können, je nach Vorzeichen und Bezugssystem entweder beschleunigend oder bremsend wirken. Dabei wird im Allgemeinen davon ausgegangen, dass Kräfte \(F_{M}\) bzw. Drehmomente \(M_{M}\), die von Motoren ausgehen beschleunigend wirken. Passive Lasten hingegen wirken den von Motoren erzeugten Kräften bzw. Drehmomenten entgegen (\(F_{Last}\) bzw. \(M_{Last}\)). Abbildung 3.2 stellt schematisch rotatorische und translatorische Bewegungen gegenüber.

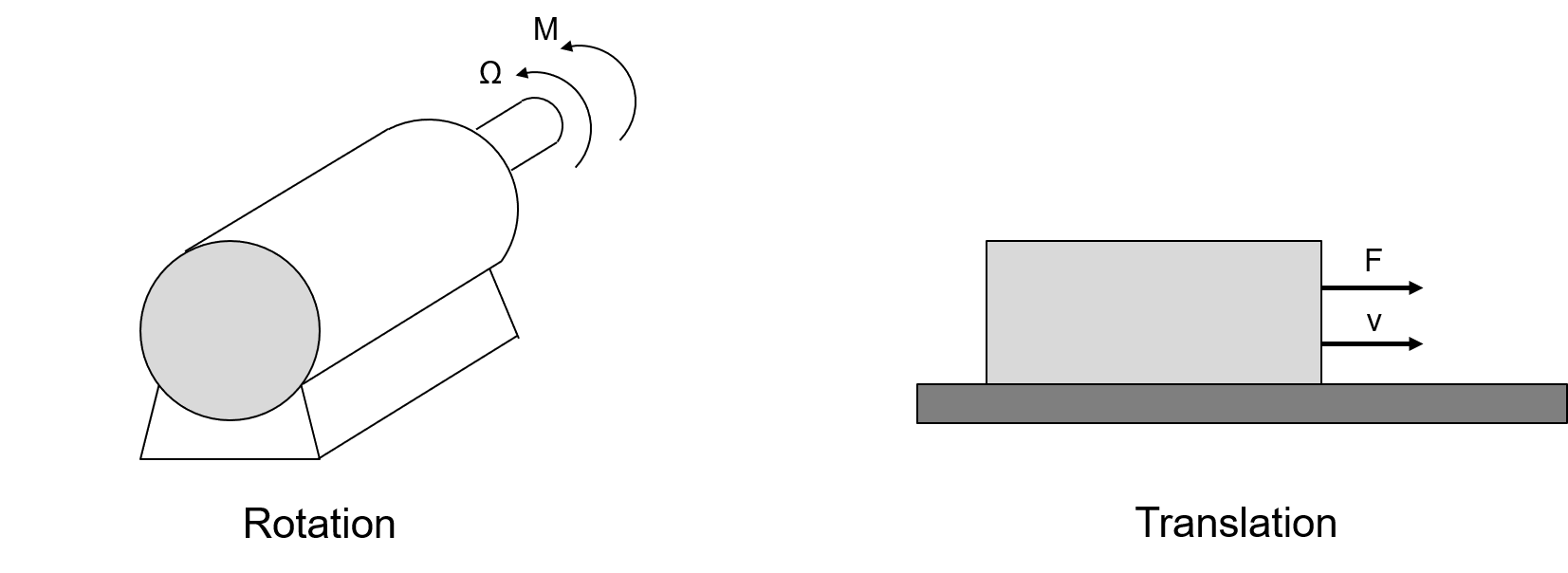
Abbildung 3.2: Gegenüberstellung von Rotation und Translation

In beiden Fällen gilt, dass bei Kräfte- bzw. Momentenungleichgewicht eine beschleunigende Kraft \(F_{B}\) bzw. ein beschleunigendes Drehmoment \(M_{B}\) resultiert, welche auf die Masse \(m\) bzw. die träge Masse (Trägheitsmoment \(J\)) einwirken. Dadurch wird die Masse bzw. das Trägheitsmoment beschleunigt. Diese Beschleunigung kann unter Verwendung der physikalischen Gesetzmässigkeiten in Geschwindigkeit, Weg bzw. Drehwinkel sowie Leistung und Arbeit umgerechnet werden.

Abbildung 3.3: Kräfteverhältnisse bei der translatorischen Bewegung

Wie in Abbildung 3.3 dargestellt wirkt eine antreibende Kraft \(F\) auf eine Masse \(m\) und beschleunigt diese. Die Summe aller Kräfte muss laut Newtonschem Grundgesetz null ergeben.

\[ \sum_{i}{F_{i}} = F-m\cdot a-F_{Reib}\cdot v = F-m\cdot \dot{v}-\mu_{Reib}\cdot v \]

Der Faktor \(\mu_{Reib}\) repräsentiert dabei einen Reibkoeffizienten, der eine geschwindigkeistproportionale Reibkraft erzeugt. Somit führt diese Gleichung zu einer Differentialgleichung erster Ordnung zur Beschreibung des Systemverhaltens.

\[ F=m\cdot \dot{v}+\mu_{Reib}\cdot v \]

Ein ähnliches Bild ergibt sich bei der Betrachtung der rotatorischen Bewegung (siehe Abbildung 3.4). Ein Körper mit einem Trägheitsmoment \(J\) erfährt eine Beschleunigung durch das antreibende Drehmoment \(M\).

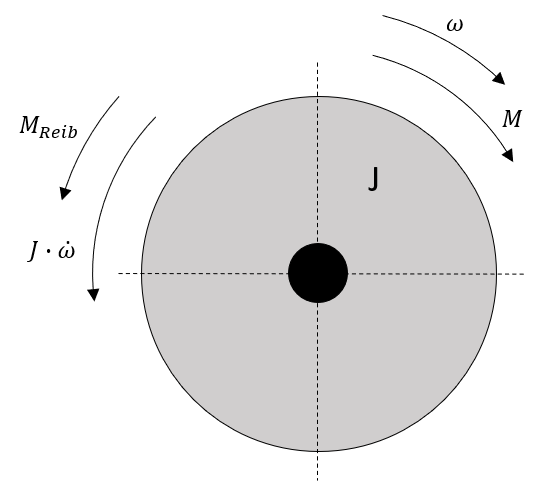
Abbildung 3.4: Momentenverhältnisse bei der rotatorischen Bewegung

In diesem Fall muss die Summe aller Drehmomente null ergeben.

\[ \sum_{i}{M_{i}} = M-J\cdot \alpha-M_{Reib}\cdot v = M-J\cdot \dot{\omega}-\mu_{Reib}\cdot \omega \]

Es ergibt sich auch für diesen Fall eine systembeschreibende DGL erster Ordnung.

\[ M=J\cdot \frac{d\omega}{dt}+\mu_{Reib}\cdot \omega \]

Obige Gleichungen lassen sich auf ähnliche Art und Weise auch in Form von Integralgleichungen ausdrücken, wodurch sich das dynamische Grundgesetz für die Translation ergibt:

\[ F_{B}=F_{M}-F_{Last}=m\cdot a=m\cdot\frac{dv}{dt}=m\cdot \frac{d^{2}s}{dt^{2}} \]

Auf ähnliche Weise entsteht auch das dynamische Grundgesetz der Rotation:

\[ M_{B}=M_{M}-M_{Last}=J\cdot \alpha=J\cdot\frac{d\omega}{dt}=J\cdot \frac{d^{2}\varphi}{dt^{2}} \]

Die Anwendung der Gesetze soll das Antriebsbeispiel in Abb. 3.5 zeigen. Dort ist das allgemeine Schema eines Elektroantriebs abgebildet. Bei diesem Beispiel, einem Hubantrieb, treten Linear- und Drehbewegungen sowie aktive und passive Lasten auf. Bei den meisten Antriebsproblemen ist es sinnvoll, die Maschinenwelle als Bezugswelle zu wählen. Dann müssen alle Massenträgheitsmomente und die Betriebsdaten der angekoppelten Arbeitsmaschine ebenfalls auf diese Welle umgerechnet werden. Mit Hilfe des Satzes von der Erhaltung der Energie werden die realen Antriebsdaten auf die fiktiv wirkenden Daten auf die Maschinenwelle reduziert. Die dabei einmal eingeführten Zählrichtungen gelten auch für alle mathematischen Berechnungen am Antriebsmodell.

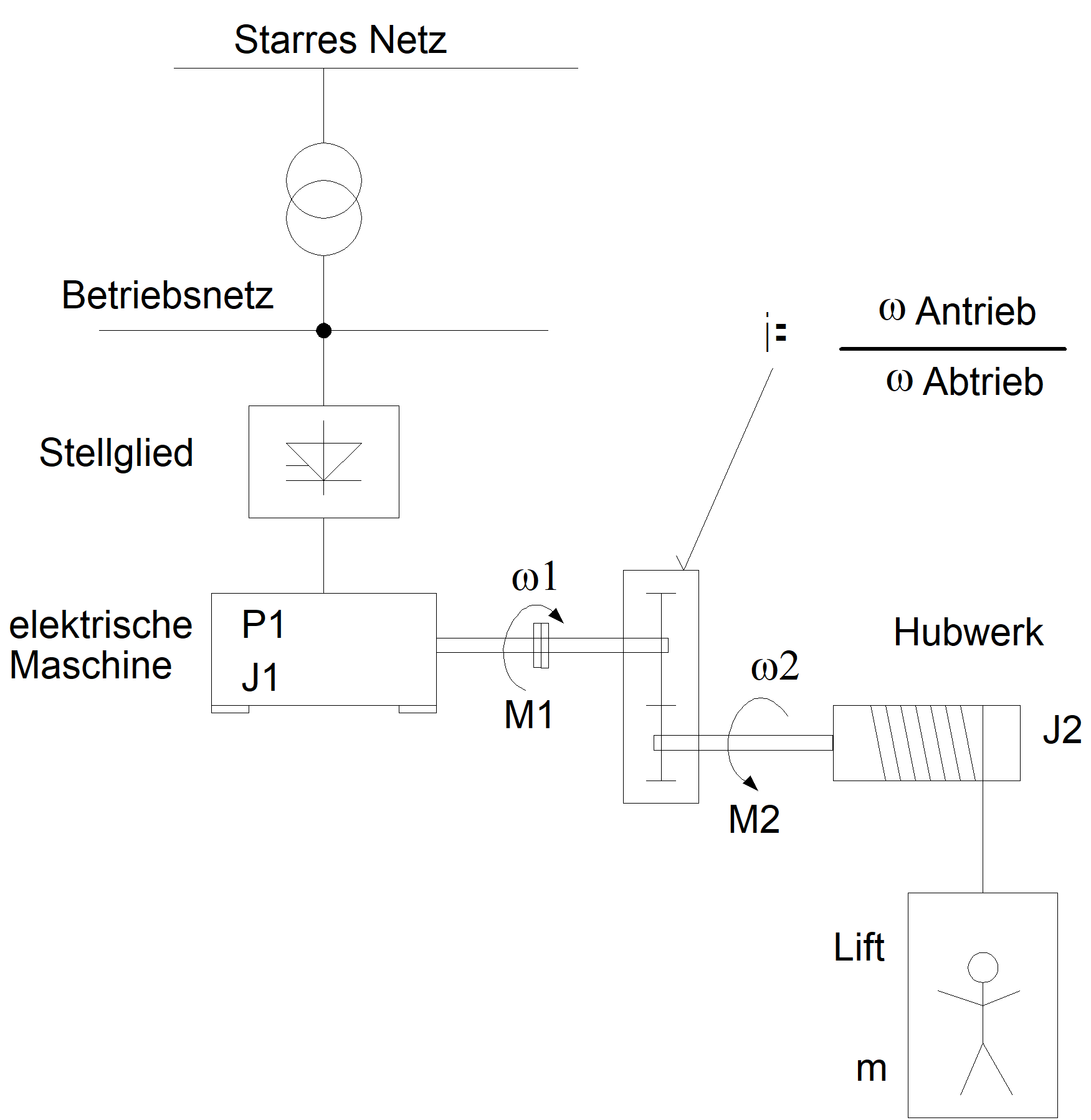
Abbildung 3.5: Beispiel eines Hubantriebs

3.1.1 Umrechnung der auf die Motorwelle reduzierten Drehmomente eines Hubantriebes

Den Ansatz bildet der Energieerhaltungssatz:

\[ \frac{1}{2}\cdot J^{'}_{2} \cdot \omega^{2}_{1}=\frac{1}{2}\cdot J_{2} \cdot \omega^{2}_{2}=\frac{1}{2}\cdot m \cdot v^{2} \]

Dabei repräsentiert \(J^{'}_{2}\) das auf die Motorwelle bezogene Trägheitsmoment auf der Lastseite (Abtriebsseite). Diese Gleichung kann entsprechend umgestellt werden. Dabei ergibt sich für das rotatorische Massenträgheitsmoment (rotierende Massen) der Last bezogen auf die Motorwelle:

\[ J^{'}_{2}=J_{2}\cdot \frac{\omega^{2}_{2}}{\omega^{2}_{1}} = \frac{J_{2}}{i^{2}} \]

Da der Hubantrieb dazu verwendet wird eine rotatorische Bewegung der Motorwelle in eine translatorische Bewegung des Lifts umzuwandeln, muss auch die träge Masse des Lifts berücksichtigt werden. Die träge Masse der translatorisch bewegten Masse wirkt auf Motorseite folglich wie ein zusätzliches Trägheitsmoment \(J^{'}_{Last}\) und kann ebenfalls aus dem obigen Energieerhaltungssatz bestimmt werden:

\[ J^{'}_{Last}=m\cdot \frac{v^{2}}{\omega^{2}_{1}} \]

Betrachtet man also den gesamten Hubantrieb aus Abbildung 3.5, dann müssen drei Anteile bei der Bestimmung des gesamten Trägheitsmomentes \(J_{ges}\), bezogen auf die Motorwelle, berücksichtigt werden:

\[ J_{ges} = J_{1} + J^{'}_{2} + J^{'}_{Last} \]

Aus der Leistungsbilanz lässt sich das Übersetzungsverhältnis \(i\) bestimmen, indem davon ausgegangen wird, dass die Leistung auf Eingangsseite des Getriebes genauso gross ist wie auf Ausgangsseite:

\[ P_{mech}=M_{1}\cdot \omega_{1}=M_{2}\cdot \omega_{2}=F\cdot v \] Aus dieser Gleichung lässt sich das motorseitige Drehmoment \(M_{1}\) bestimmen:

\[ M_{1}=M_{2}\cdot \frac{\omega_{2}}{\omega_{1}} = \frac{M_{2}}{i} \]

Aus der Leistungsbilanz kann gleichzeitig auch die Getriebeübersetzung \(i\) bestimmt werden:

\[ i=\frac{\omega_{1}}{\omega_{2}} = \frac{n_{Antrieb}}{n_{Abtrieb}} = \frac{M_{2}}{M_{1}} \]

Zusammengefasst bedeutet dies, dass ein Getriebeübersetzungsverhältnis \(i>1\) für eine Drehzahlreduktion auf der Abtriebsseite (Getriebeausgangsseite), bei gleichzeitiger Drehmomentzunahme, sorgt.

3.2 Magnetische Felder

Elektrische Maschinen, unabhängig davon ob es sich um rotierende oder statische Maschinen handelt, agieren immer als elektromechanische Energiewandler. Der entsprechende Umwandlungsprozess benötigt immer ein magnetisches Feld. Die Krafterzeugung durch einen magnetischen Strom oder die Spannungsinduktion in einem bewegten elektrischen Leiter sind nur bei Vorhandensein eines magnetischen Feldes möglich.

3.2.1 Der stromdurchflossene Leiter

Ähnlich einem geladenen Kondensator, besitzt ein stromdurchflossener Leiter die Möglichkeit Energie zu speichern. Dieses Speichervermögen wird mit Hilfe der Induktivität \(L\) beschrieben. Die entsprechenden physikalischen Vorgänge lassen sich anhand der folgenden Wirkungskette beschreiben:

Abbildung 3.6: Wirkungskette eines stromdurchflossenen Leiters

Der elektrische Strom \(I\) ruft eine magnetische Durchflutung \(\Theta=f(I)\) hervor, welche wiederum durch den Durchflutungssatz Rückschlüsse auf die magnetische Feldstärke \(H=f(\Theta)\) zulässt. Das Durchflutungsgesetz gilt dabei unabhängig von der umgebenden Materie.

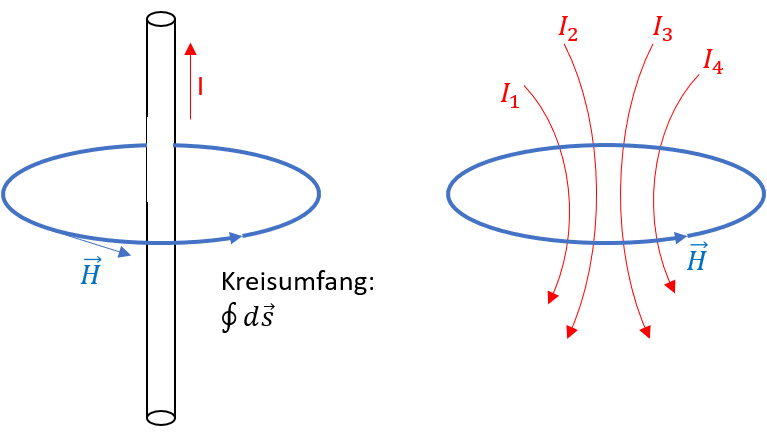
Abbildung 3.7: Durchflutungsgesetz der magnetischen Feldstärke

Berücksichtigt man weiterhin die Materialeigenschaften, lässt sich magnetische Flussdichte (häufig auch als magnetische Induktion bezeichnet) \(B=f(H)\) bestimmen. Die Materialeigenschaften spielen hierbei eine wesentliche Rolle, da insbesondere ferromagnetische Materialien das Magnetfeld verstärken. Dieser Zusammenhang wird durch den Faktor \(\mu\) (Permeabilität) in der folgenden Gleichung, die den Zusammenhang zwischen magnetischer Feldstärke und der magnetischen Flussdichte herstellt, berücksichtigt.

\[ \vec{B}=\mu \vec{H} \] Die Permeabilität wiederum setzt sich dabei aus der Magnetischen Feldkonstante \(\mu_{0}\) und der relativen Permeabilität \(\mu_{r}\) zusammen.

\[ \mu = \mu_{0}\cdot \mu_{r} \] Die Magnetische Feldkonstante beschreibt hierbei das Verhältnis der magnetischen Flussdichte \(\vec{B}\) zur magnetischen Feldstärke \(\vec{H}\) im Vakuum und wird mit \(\mu_{0} = 4\pi \cdot 10^{-7}\frac{N}{A^{2}}\) angegeben. Die relative Permeabilität ist eine dimensionslose Materialkonstante.

Über die durchströmte Fläche lässt sich gleichzeitig der magnetische Fluss \(\Phi=f(B)\) bestimmen.

Aus obiger Wirkungskette lässt sich erkennen, dass der Strom dem Fluss proportional ist (\(I \sim \Phi\)). Die damit zusammenhängende Proportionalitätskonstante wird als Induktivität \(L\) bezeichnet und in Henry [H] gemessen.

\[ \Phi = LI \] Soll der Einfluss mehrerer parallel verlaufender Leiter (Spule) die den gleichen Strom tragen, erfasst werden dann spricht man vom verketteten Fluss \(\Psi=N\cdot \Phi\). Damit ergibt sich die Induktivität einer Spule aus dem Quotienten des verketteten Flusses und dem Strom.

\[ L=\frac{\Psi}{I}=\frac{N\cdot \Phi}{I} \]

3.2.2 Kraftwirkung des magnetischen Feldes

Vergleichbar zur Kraftwirkung im elektrischen Feld, gibt es auch beim Magnetfeld eine Kraftwirkung auf bewegte Ladungen. Dabei gilt es die Bewegungsrichtung postiver Ladungen zu berücksichtigen, welche mit der technischen Stromrichtung übereinstimmt.

Die Lorentzkraft (\(\vec{F}\)) beschreibt die Kraftwirkung bewegter Ladungen (\(Q\)) welche sich mit einer Geschwindigkeit (\(\vec{v}\)) in einem Magnetfeld der Flussdichte (\(\vec{B}\)) befindet.

\[\begin{equation} \vec{F}=Q\cdot(\vec{v}\times \vec{B}) \tag{3.1} \end{equation}\]

Berücksichtigt man weiterhin, dass sich die Ladung aus dem Integral des Stromes (\(Q=\int{I}dt=I\cdot t\)) ergibt und die Geschwindigkeit als Quotient von Weg und Zeit (\(\vec{v}=\frac{d\vec{s}}{dt}\)) ausdrücken lässt, kann die Gleichung noch modifiziert werden, indem die Wegstrecke durch die Länge (\(\vec{l}\)) des Leiters ausgedrückt wird, die unter dem Einfluss des magnetischen Feldes steht.

\[ \vec{F}=I\cdot(\vec{l}\times \vec{B}) \]

3.2.3 Der magnetische Kreis

Spricht man von einem mgnetischen Kreis, bezieht man sich meist auf dreidimensionale Anordnungen von ferromagnetischen Werkstoffen, die an gewissen Stellen mit Leitern umwickelt werden und somit ein Magnetfeld hervorrufen, welches sich, aufgrund des geringen magnetischen Widerstandes (\(R_{m}\)) des Eisenmaterials, hauptsächlich innerhalb dieses magnetischen Leiters ausbreitet. Charakterisiert wird dieser Eisenkreis mit Hilfe des magnetischen Flusses \(\Phi\), welcher sich, je nach Position im Eisenkreis aus der Gesamtzahl der Feldlinien ergibt, die eine entsprechende Querschnittsfläche durchsetzen.

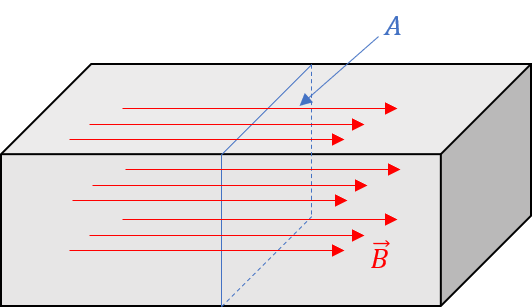
Abbildung 3.8: Magnetischer Fluss

Dies erlaubt eine Analogie zum elektrischen Kreis, bei dem die elektrische Spannung zwischen zwei Punkten im Leiter über einen integralen Ansatz der elektrischen Feldstärke (\(\vec{E}\)) ermöglicht.

\[ U_{12}=\int^{2}_{1}{\vec{E}d\vec{s}} \] Im Falle des magnetischen Feldes kann somit ebenfalls eine sog. magnetische Spannung (\(\Theta\)) als Integralgrösse definiert werden, deren Einheit in Ampere (\(A\)) angegeben wird.

\[ \Theta_{12} = \int^{2}_{1}{\vec{H}d\vec{s}} \] Dieses Betrachtungsweise wird in Abbildung 3.9 in Form einer Gegenüberstellung des elektrischen und des magnetischen Maschensatzes dargestellt.

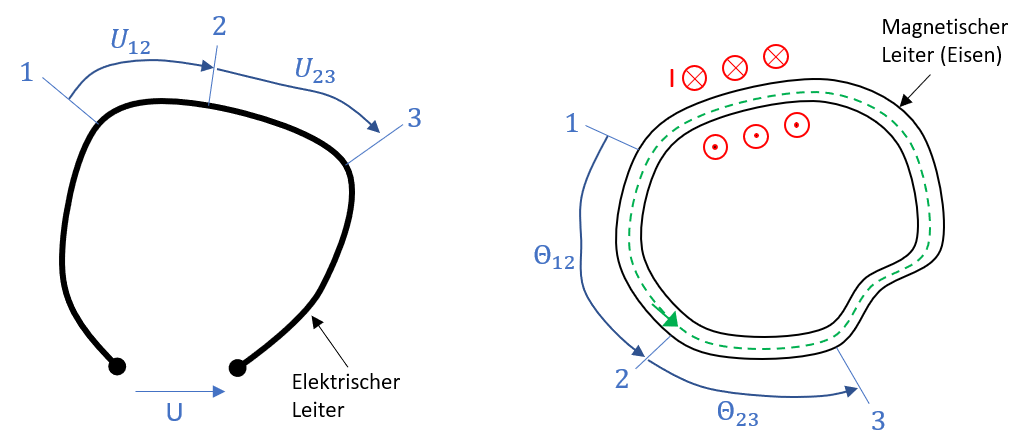
Abbildung 3.9: Elektrischer und magnetischer Maschensatz

Wie die Abbildung zeigt, lässt sich somit, ausgehend vom Durchflutungssatz durch Summation der einzelnen magnetischen Spannungen die gesamte Durchflutung bestimmen. Dies wird als magnetischer Maschensatz bezeichnet.

\[ \Theta=\oint{\vec{H}d\vec{s}}=N\cdot I=\int^{2}_{1}{\vec{H}d\vec{s}}+\int^{3}_{2}{\vec{H}d\vec{s}}+\cdots +\int^{1}_{n}{\vec{H}d\vec{s}} \] Es ergibt sich somit eine Analogie zum elektrischen Feld, wodurch auch der im Falle eines Magnetkreises eine Widerstandsgrösse, der sog. magnetische Widerstand \(R_{m}\) definiert werden kann, der die magnetische Spannung und den magnetischen Fluss miteinander verknüpft.

\[ R_{m}=\frac{\Theta}{\Phi} \]

Die Einheit des magnetischen Widerstandes ist

\[ [R_{m}]=\frac{A}{Wb}=\frac{A}{V\cdot s}=\frac{1}{H} \]

Somit lassen sich auch im Falle des magnetischen Kreises Berechnungen mit den Methoden der Gleichstromtechnik durchführen, was die Kirchhoffschen Gleichungen in Form des magnetischen Maschen- und Knotensatzes (siehe Abb. 3.9 bzw. Abb. 3.10) mit einschliesst. Der magnetische Knotensatz basiert auf der Quellenfreiheit des magnetischen Feldes, welche besagt, dass an keiner Stelle des Raumes Feldlinien verschwinden oder entstehen.

\[ \oint{\vec{B}d\vec{A}}=0 \]

Betrachtet man also eine geschlossene Hüllfläche, wie in der Abbildung 3.10 dargestellt, bedeutet dies, das alle Feldlinien, die in eine geschlossenen Hüllfläche eindringen diese an anderer Stelle auch wieder verlassen.

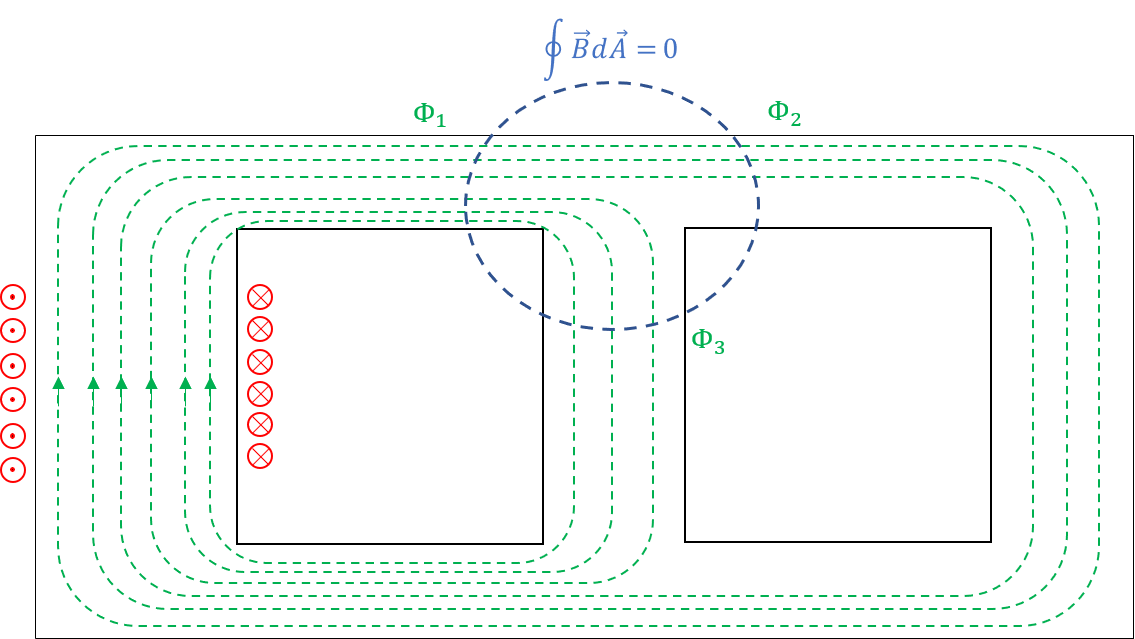
Abbildung 3.10: Vereinfachte Darstellung des magnetischen Knotensatzes

Betrachtet man homogene Magnetfelder, wovon im Falle eine magnetischen Kreises häufig ausgegangen wird, vereinfachen sich die benötigten Integralgleichungen zur Berechnung des magnetischen Widerstandes zu einfachen Produkten und die geometrischen Abmessungen des Eisenkreises sowie die Materialkonstanten können zur Berechnung verwendet werden.

\[ R_{m} = \frac{\Theta}{\Phi} = \frac{H\cdot l}{B\cdot A}=\frac{H\cdot l}{\mu H \cdot A}=\frac{l}{\mu A} \]

Auch hier wird die Analogie zum elektrischen Widerstand sehr deutlich. Es bleibt zu berücksichtigen, dass zur vereinfachten Berechnung magnetischer Kreise lineare magnetische Widerstände vorausgesetzt werden müssen. Diese Voraussetzung ist erfüllt, solange keine Sättigungserscheinungen im magnetischen Kreis auftreten.

3.2.3.1 Sättigungserscheinungen

Wie im Kapitel 3.2.1 beschrieben, fungiert die Induktivität als Proportionalitätskonstante zwischen magnetischem Fluss und dem Strom, welcher einen Leiter durchfliesst. Betrachtet man einen stromdurchflossenen Leiter im Raum ist diese Proportionalität immer gewährleistet, da das umgebende Medium (Luft) eine konstante relative Permeabilität \(\mu_{r}\) besitzt. Betrachtet man allerdings einen stromdurchflossenen Leiter, welcher einen Eisenkreis umfasst, dann bilden sich die Feldlinien, aufgrund des geringen magnetischen Widerstandes, massgeblich im Eisenkreis aus. Dadurch muss die relative Permeabilität des Eisenkreismaterials im Zusammenhang zwischen magnetischer Feldstärke und magnetischer Flussdichte berücksichtigt werden.

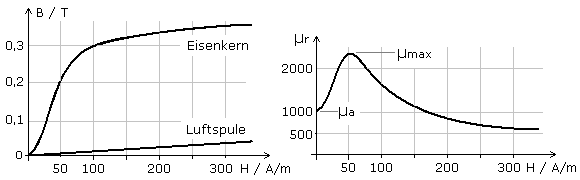
Abbildung 3.11: Typ. Magnetisierungskurve ferromagnetischer Materialien (Quelle: www.elektroniktutor.de)

Wie Abbildung 3.11 zeigt, ist der Zusammenhang von magnetischer Feldstärke und magnetischer Flussdichte eines Eisenkerns nichtlinear. Mit steigender magnetischer Feldstärke nimmt die magnetische Flussdichte ab. Die Ursache dafür ist in der Ausrichtung der Weiss’schen Bezirke unter dem Einfluss des magnetischen Feldes (siehe Abbildung 3.12) zu suchen.

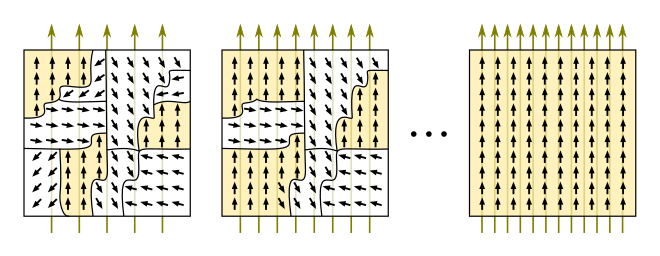
Abbildung 3.12: Weiss-Bezirke unter Einfluss eines Magnetfeldes (Quelle: www.wikipedia.org)

Sind schlussendlich alle Weiss’schen Bezirke bei entsprechend hoher Feldstärke aufgrund des äusseren Magnetfeldes vollständig ausgerichtet, ist dieser unterstützende Effekt nicht mehr gegeben und der Anstieg (\(\frac{d\vec{B}}{d\vec{H}}\)) der Kennlinie fällt deutlich geringer aus. In diesem gesättigten Bereich entspricht der Anstieg der Kennlinie eines stromdurchflossenen Leiters in Luft. Damit lässt sich begründen, dass die Induktivität eines Eisenkreises massgeblich von der Feldstärke abhängig ist. Dieser Effekt äussert sich dadurch, dass eine signifikante Stromerhöhung der magnetfelderzeugenden Spule im gesättigten Bereich nur zu einer marginalen Erhöhung der Flussdichte beiträgt. Damit begründet sich die Notwendigkeit einer sinnvollen Dimensionierung eines magnetischen Kreises durch entsprechende Wahl des Querschnittes (und Länge) eines Eisenkreises.

3.2.4 Gekoppelte magnetische Kreise

Die magnetische Kopplung zweier oder mehrerer Spulen ermöglicht die Übertragung von elektrischer Energie. Da die Kopplung ohne jegliche elektrisch leitende Verbindung erfolgt, spricht man von einer galvanischen Trennung beider Stromkreise. Erfolgt die Kopplung zur Übertragung elektrischer Energie, spricht man üblicherweise von statischen bzw. ruhenden (Transformatoren) und rotierenden elektrischen Maschinen. Dient die magnetische Kopplung der Übertragung von Informationen (Signalen) spricht man von Übertragern. Betrachtet man zwei magnetisch gekoppelte Spulen, dann handelt es sich bei der Spule, die mit der Energie- bzw. Signalquelle in Verbindung steht um die Primärspule und bei der Spule, die als Energie- bzw. Signalsenke fungiert, um die Sekundärspule.

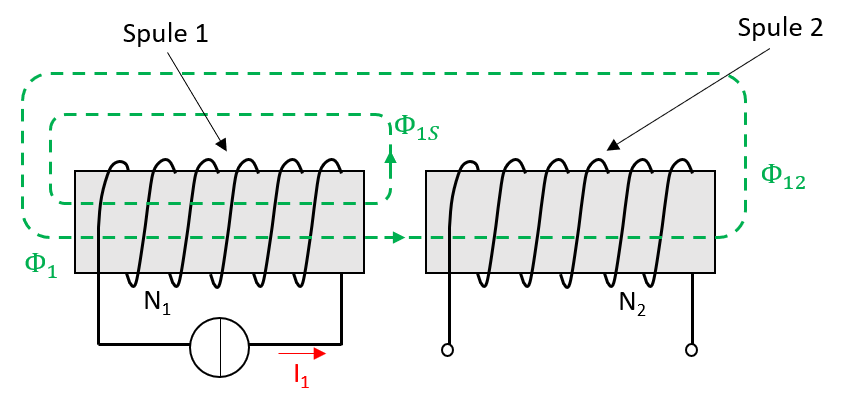
Abbildung 3.13: Magnetische Kopplung der Spule 2

Betrachtet man eine Anordnung wie in Abbildung 3.13 erzeugt eine Spule 1 einen magnetischen Primärfluss \(\Phi_{1}\), welcher sich wiederum in einen Streufluss \(\Phi_{1S}\) und einen Fluss aufteilt, der auch die Sekundärspule durchströmt \(\Phi_{12}\). Die doppelte Indizierung dient dabei zur Unterscheidung zwischen dem Ort der Entstehung (Index 1) und dem Ort der Wirkung (Index 2) des Flusses. Der Fluss, der von beiden Spulen umfasst wird kann, bei idealer Kopplung (\(\Phi_{1S}=0\)), einen Wert erreichen der dem Fluss \(\Phi_{1}\) entspricht. Somit kann ein Kopplungsfaktor \(k_{1}\leq1\) definiert werden, der diese unterschiedlich starke Kopplung berücksichtigt.

\[ \Phi_{12}=k_{1}\cdot \Phi_{1} \] Die induzierte Spannung in der Sekundärspule ist abhängig von der zeitlichen Änderung des Flusses, der von der Sekundärspule umfasst wird und der Wicklungszahl \(N_{2}\) der Sekundärspule.

\[ u_{2}(t)=N_{2}\cdot \frac{d\Phi_{12}(t)}{dt}=N_{2}\cdot k_{1}\cdot \frac{d\Phi_{1}(t)}{dt} \]

Dieser Effekt lässt sich natürlich auch umkehren (siehe Abb. 3.14), indem die Spule zwei von einem Strom durchflossen wird und eine Spannung im Spule 1 induziert.

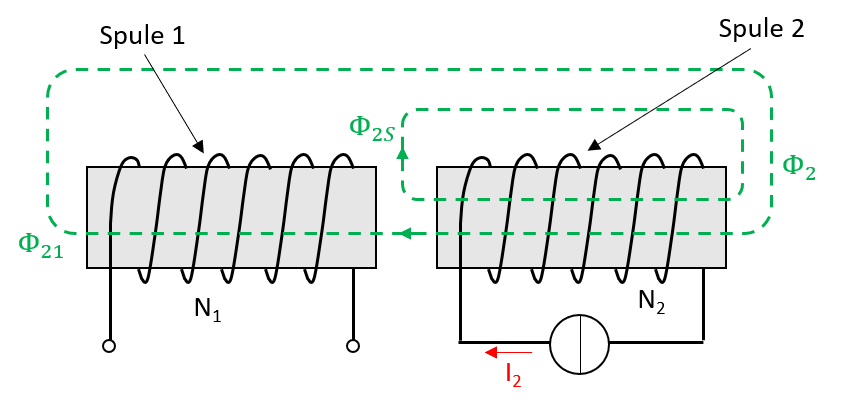
Abbildung 3.14: Magnetische Kopplung der Spule 1

Dabei gelten die gleichen physikalischen Zusammenhänge.

\[ \Phi_{21}=k_{2}\cdot \Phi_{2} \] Die induzierte Spannung lässt sich somit auf gleiche Art und Weise bestimmen.

\[ u_{1}(t)=N_{1}\cdot \frac{d\Phi_{21}(t)}{dt}=N_{1}\cdot k_{2}\cdot \frac{d\Phi_{2}(t)}{dt} \]

Wird in einem der beiden Fälle die Sekundärspule mit einem Widerstand belastet, stellt sich ein Sekundärstrom \(i_{2}(t)=\frac{u_{2}(t)}{R}\) ein. Ein solcher Sekundärstrom ruft seinerseits wiederum ein entsprechendes Magnetfeld hervor und erzeugt somit den Fluss \(\Phi_{2}(t)\) welcher auf oben beschriebene Art und Weise auf die Primärspule rückkoppelt. Dieser Effekt beschreibt anschaulich, dass eine Leistungsentnahme auf der Sekundärseite zu einer entsprechenden Belastung der Primärseite führt. In jeder der beiden Spulen kommt es somit zu einer Überlagerung der beiden Magnetfelder, was im mathematischen Sinne einer Addition entspricht. Diese Überlagerung kann in den Spannungsgleichungen der beiden Spule berücksichtigt werden.

\[\begin{equation} u_{1}(t) = N_{1}\frac{d\Phi_{1}(t)}{dt}+N_{1}\cdot k_{1}\frac{d\Phi_{2}(t)}{dt} \tag{3.2} \end{equation}\]

\[\begin{equation} u_{2}(t) = N_{2}\frac{d\Phi_{2}(t)}{dt}+N_{2}\cdot k_{2}\frac{d\Phi_{1}(t)}{dt} \tag{3.3} \end{equation}\]

Diese Gleichungen werden üblicherweise durch Verwendung der Induktivitäten zum Ausdruck gebracht. Dazu berücksichtigt man den Zusammenhang zwischen Strom und verkettetem Fluss.

\[ \Psi(t)=L\cdot i(t)=N\cdot\Phi(t)\\ \] Wendet man diesen allgemeinen Zusammenhang auf das hier beschriebene Beispiel an, ergeben sich insgesamt vier Induktivitäten, die berücksichtigt werden müssen.

\[\begin{align} L_{1}=\frac{N_{1}\cdot \Phi_{1}}{i_{1}(t)}\\ L_{2}=\frac{N_{2}\cdot \Phi_{2}}{i_{2}(t)}\\ M_{12}=\frac{N_{2}\cdot \Phi_{12}}{i_{1}(t)}=\frac{N_{2}\cdot \Phi_{1}\cdot k_{1}}{i_{1}(t)}=\frac{N_{2}\cdot k_{1}\cdot L_{1}}{N_{1}}\\ M_{21}=\frac{N_{1}\cdot \Phi_{21}}{i_{2}(t)}=\frac{N_{1}\cdot \Phi_{2}\cdot k_{2}}{i_{2}(t)}=\frac{N_{1}\cdot k_{2}\cdot L_{2}}{N_{2}} \end{align}\]

Die Induktivitäten \(L_{1}\) bzw. \(L_{2}\) beschreiben dabei die sog. Selbstinduktivitäten der Spule 1 bzw. 2. Die Induktivitäten \(M_{12}\) bzw. \(M_{21}\) hingegen beschreiben den Einfluss der jeweils anderen, magnetisch gekoppelten Spule. Aufgrund dessen werden diese Induktivitäten häufig als Fremd- bzw. Gegeninduktivität bezeichnet.

Stellt man die Gleichung zur Berechnung der Fremdinduktivität \(M_{21}\) nach der Wicklungszahl \(N_{2}\) um, ergibt sich folgender Ausdruck.

\[ N_{2}=\frac{N_{1}\cdot k_{2}\cdot L_{2}}{M_{21}} \]

Wird dieser in die Gleichung zur Bestimmung Fremdinduktivität \(M_{12}\) eingesetzt, ergibt sich folgender Ausdruck:

\[ M_{12}\cdot M_{21} = k_{1}\cdot k_{2}\cdot L_{1} \cdot L_{2} \]

Da sich beide Spulen in gleichem Masse beeinflussen, kann eine einzelne Gegeninduktivität \(M=M_{12}=M_{21}\) definiert werden, wodurch sich obige Gleichung modifizieren lässt.

\[ M^{2}=k_{1}\cdot k_{2}\cdot L_{1} \cdot L_{2} \Longrightarrow M=\sqrt{k_{1}\cdot k_{2}}\sqrt{L_{1}\cdot L_{2}}=k\cdot\sqrt{L_{1}\cdot L_{2}} \]

Somit lässt sich das folgende Differentialgleichungssystem für die zwei Maschen der galvanisch getrennten elektrischen Kreise formulieren.

\[\begin{align} u_{1}(t) = L_{1}\frac{di_{1}(t)}{dt} + M\frac{di_{2}(t)}{dt}\\ u_{2}(t) = M\frac{di_{1}(t)}{dt} + L_{2}\frac{di_{2}(t)}{dt} \end{align}\]

Dieses DGLS kann durch komplexe Zeiger und in Matrix-Vektor Notation in Form eines linearen Gleichungssystems ausgedrückt werden.

\[ \left[\begin{array}{c} \underline{U}_{1}\\ \underline{U}_{2} \end{array}\right] =\left[\begin{array}{cc} j \omega L_{1} & j\omega \cdot k\cdot \sqrt{L_{1}L_{2}} \\ j\omega \cdot k\cdot \sqrt{L_{1}L_{2}} & j\omega L_{2} \end{array}\right] \cdot \left[\begin{array}{c}\underline{I}_{1} \\ \underline{I}_{2} \end{array}\right] =\left[\begin{array}{cc} j \omega L_{1} & j\omega M \\ j\omega M & j\omega L_{2} \end{array}\right] \cdot \left[\begin{array}{c}\underline{I}_{1} \\ \underline{I}_{2} \end{array}\right] =Z\cdot \left[\begin{array}{c}\underline{I}_{1} \\ \underline{I}_{2} \end{array}\right] \] Dabei wird \(Z\) als Impedanzmatrix der gekoppelten Spulen bezeichnet. Stellt man die Spannungsgleichungen nach den Eingangsgrössen \(\underline{U}_{1}\) bzw. \(\underline{I}_{1}\) um, erhält man die sogenannte Kettenmatrix \(K\) der gekoppelten Spulen.

\[ \left[\begin{array}{c} \underline{U}_{1}\\ \underline{I}_{1} \end{array}\right] =\left[\begin{array}{cc} \frac{1}{k}\sqrt{\frac{L_{1}}{L_{2}}} & \frac{1-k^{2}}{k} j \omega \sqrt{L_{1}L_{2}}\\ \frac{1}{j\omega k\sqrt{L_{1}L_{2}}} & \frac{1}{k}\sqrt{\frac{L_{2}}{L_{1}}} \end{array}\right] \cdot \left[\begin{array}{c}\underline{U}_{2} \\ -\underline{I}_{2} \end{array}\right] =K\cdot \left[\begin{array}{c}\underline{U}_{2} \\ -\underline{I}_{2} \end{array}\right] \]

Der Faktor \(\sigma=1-k^{2}=1-\frac{M^{2}}{L_{1}L_{2}}\) in der Kettenmatrix \(K\) wird als Blondel’scher Streukoeffizient bezeichnet.

3.2.4.1 Ideale Kopplung

Betrachtet man ein, in der Realität nicht existierendes, magnetisch ideal gekoppeltes System (\(k=1\)), bestehend aus zwei Spulen, lassen sich, ausgehend von den oben dargestellten Spannungsgleichungen, viele bekannte Eigenschaften von Übertragern und Transformatoren herleiten. Bei einer solchen idealen Kopplung zweier Spulen lässt sich leicht nachvollziehen, dass die Magentisierung beider Spulen bereits bei verschwindend kleinem Magnetisierungsstrom erfolgt, da es keinerlei Spannungsabfälle an weiteren passiven Bauelementen gibt. Der sich einstellende magnetische Fluss, welcher beide Spulen durchsetzt wird durch die Primärspannung definiert. Dieser Zusammenhang gilt auch, wenn ein zusätzlicher Primärstrom (\(i_{1}(t)\)) bzw. Sekundärstrom (\(i_{2}(t)\)) fliessen, da sich die dadurch einstellenden Flusskomponenten jederzeit in ihren Wirkungen aufheben. Dieser Zusammenhang kann mathematisch folgendermassen berücksichtigt werden:

\[ \Phi_{1}(t)+\Phi_{2}(t)=0 \rightarrow \Phi_{1}(t)=-\Phi_{2}(t) \]

Unter Berücksichtigung der Geometrie- und Materialparameter des Raumes, welcher die ideal gekoppelten Spulen umgibt, kann diese Gleichung weiter modifiziert werden:

\[ \frac{\mu\cdot A\cdot N_{1}\cdot i_{1}(t)}{l}= - \frac{\mu\cdot A\cdot N_{2}\cdot i_{2}(t)}{l} \]

Aufgrund der idealen Kopplung sind die Geometrie- und Materialparameter somit auf der linken und rechten Seite der Gleichung identisch und das Stromübersetzungsverhältnis (\(i\)) kann damit bestimmt werden:

\[\begin{equation} \frac{i_{1}(t)}{i_{2}(t)} = -\frac{N_{2}}{N_{1}}=-\frac{1}{i} \tag{3.4} \end{equation}\]

Das Spannungsübersetzungsverhältnis eines ideal gekoppelten Systems lässt sich basierend auf den Gleichungen (3.2) bzw. (3.3) bestimmen:

\[\begin{equation} i = \frac{u_{1}(t)}{u_{2}(t)}=\frac{2\cdot N_{1}\left(\frac{d\Phi_{1}(t)}{dt}+ \frac{d\Phi_{2}(t)}{dt}\right)}{2\cdot N_{2}\left(\frac{d\Phi_{2}(t)}{dt}+ \frac{d\Phi_{1}(t)}{dt}\right)}=\frac{N_{1}}{N_{2}} \tag{3.5} \end{equation}\]

3.2.5 Ersatzschaltbild ideal gekoppelter Spulen

Die getroffenen Annahmen ermöglichen es entsprechendes Ersatzschaltbild für zwei ideal gekoppelte Spulen zu definieren (siehe Abb. 3.15).

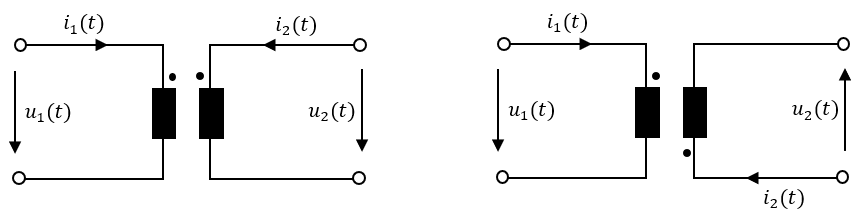
Abbildung 3.15: Ersatzschaltbilder zweier ideal gekoppelter Spulen im Verbraucherzählpfeilsystem (links: gleiche Polarität beider Spulen, rechts: ungleiche Polarität beider Spulen)

Die beiden Punkte an den Spulen repräsentieren den Wicklungssinn und damit die Polarität der Spulen (der Punkt repräsentiert das höhere Potential).

3.2.5.1 Netzwerktransformation

Unter Berücksichtigung der Strom- und Spannungsübersetzungsverhältnisse können Netzwerkgrössen von einer Spulenseite auf die andere (z.B. von der Primär- auf die Sekundärspule) transformiert werden, wodurch ein äquivalentes Ersatzschaltbild entsteht, welches ohne Darstellung der beiden gekoppelten Spulen auskommt. Um eine solche Transformation zu ermöglichen, werden die Auswirkungen (Strom und Spannung) die eine Impedanz auf die jeweilige Seite (Primär- oder Sekundärseite) haben berücksichtigt. Wird beispielsweise eine Impedanz and die Sekundärspule angeschlossen, dann bewirkt diese einen Stromfluss, welcher wiederum aufgrund des vollständig gekoppelten magnetischen Flusses einen Stromfluss auf der primärseitigen Spule hervorruft. Folglich gilt es die sekundärseitig angeschlossene Impedanz durch eine primärseitige Impedanz darzustellen, welche den gleichen Stromfluss verursacht.

\[ \underline{Z}_{1}^{'}=\frac{\underline{U}_{1}}{\underline{I}_{1}}=\frac{i\cdot \underline{U}_{2}}{\frac{-\underline{I}_{2}}{i}} = i^{2}\frac{\underline{U}_{2}}{-\underline{I}_{2}}=i^{2}\cdot \underline{Z}_{2} \] In der Literatur werden physikalische Grössen, die von der Sekundär- auf die Primärseite transformiert werden, häufig durch ein einzelnes Hochkomma (z.B. \(Z^{'}\)) gekennzeichnet. Grössen, die wiederum von der Primär- auf die Sekundärseite transformiert wurden, werden durch zwei Hochkommas (z.B. \(Z^{''}\)) gekennzeichnet. In der Abbildung 3.16 wird ein passiver Zweipol von der Sekundär- auf die Primärseite transformiert.

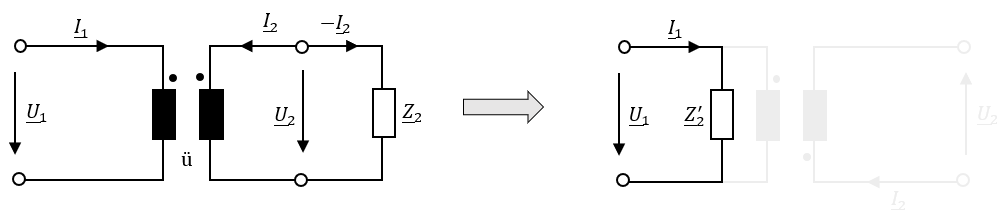
Abbildung 3.16: Transformation eines passiven Zweipols von der Sekundär- auf die Primärseite

3.3 Das Grundsystem des Antriebs

Unabhängig vom Leistungsbereich lässt sich ein elektrischer Antrieb mit einfachen Systemgrössen beschreiben. Wie Abbildung 3.17 zeigt, besteht ein solches System im allgemeinen aus:

• dem elektronischen Stellglied (dem Stromrichter),
• der elektrischen Maschine, hauptsächlich antreibend daher meist Motor genannt und
• der angekuppelten meist passiven Arbeitsmaschine.

Dabei ist es in der Antriebstechnik üblich, die einzelnen Systemkomponenten mit ihren Kennlinien zu beschreiben. Dort sind die mechanischen Grössen in der Drehzahl- Drehmoment- Ebene und die elektrischen in der Spannungs- Strom- Ebene dargestellt. Leider ist die übliche Drehzahlangabe in Umdrehungen/Minute dem System der gesetzlichen SI-Einheiten fremd, jedoch zugelassen. Zum besseren Verständnis wird bei mechanischen Darstellungen und Berechnungen die Winkelgeschwindigkeit \(\omega\) benutzt, während bei den Antrieben praxisnah von der Drehzahl \(n\) gesprochen wird.

Abbildung 3.17: Darstellung der einzelnen Antriebskomponenten vom Netz zur Last

In Abb. 3.18 sind die Kenngrössen für die Beschreibung des Antriebsgrundsystems abgebildet. Die eingetragene positive Zählrichtung ist frei, aber zweckmässig gewählt. Sie gibt die positiven Zählrichtungen für alle eingetragenen elektrischen und mechanischen Grössen an. Damit sind auch die für jeden Antrieb charakteristischen vier möglichen Betriebsquadranten festgelegt. Zwei Betriebsarten der elektrischen Maschine lassen sich unterscheiden:

• Motorbetrieb (treiben) = Abgabe mechanischer Energie an der Motorwelle im 1. und III. Quadranten und
• Generatorbetrieb (bremsen) = Aufnahme mechanischer Energie an der Generatorwelle im II. und IV Quadranten

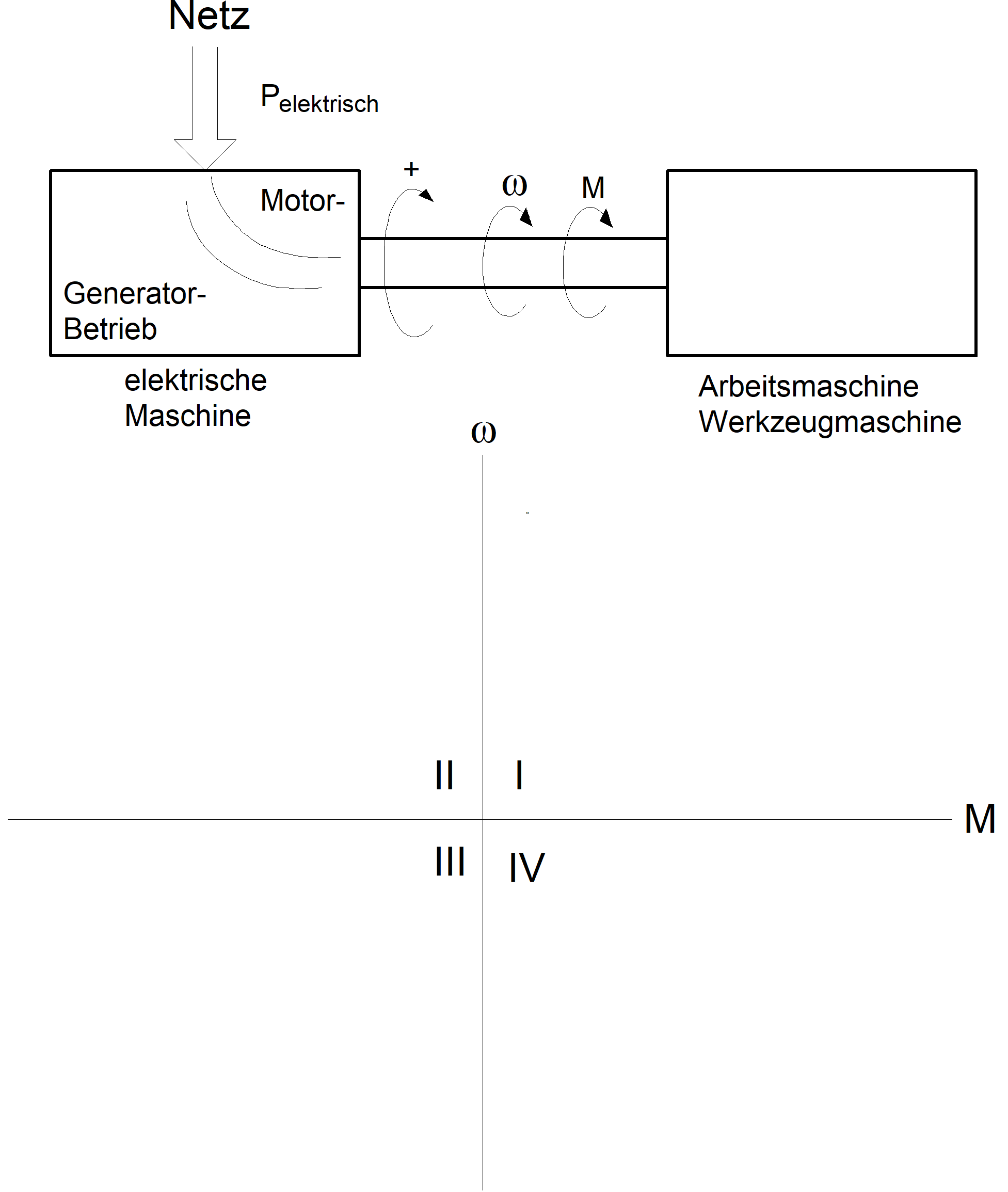
Abbildung 3.18: Kenngrössen und die sich ergebenden Betriebsquadranten

3.3.1 Leistungsflussbetrachtungen

Während des motorischen Betriebs eines elektrischen Antriebes wird dem Antriebssystem elektrische Leistung vom Netz (oder einem entsprechenden Energiespeicher) zugeführt. Die Menge (Amplitude) der zugeführten elektrischen Leistung wird vom leistungselektronischen Stellglied (Stromrichter) geregelt (in seltenen Fällen auch gesteuert), um den Anforderungen der Last hinsichtlich der benötigten mechanischen Leistung gerecht zu werden. Steigt der mechanische Leistungsbedarf auf Lastseite (z.B. durch eine gewünschte Beschleunigung), wird diese entsprechend vom Stromrichter zur Verfügung gestellt. Dieses Prinzip des Leistungsflusses ist in der Abbildung 3.19 dargestellt.

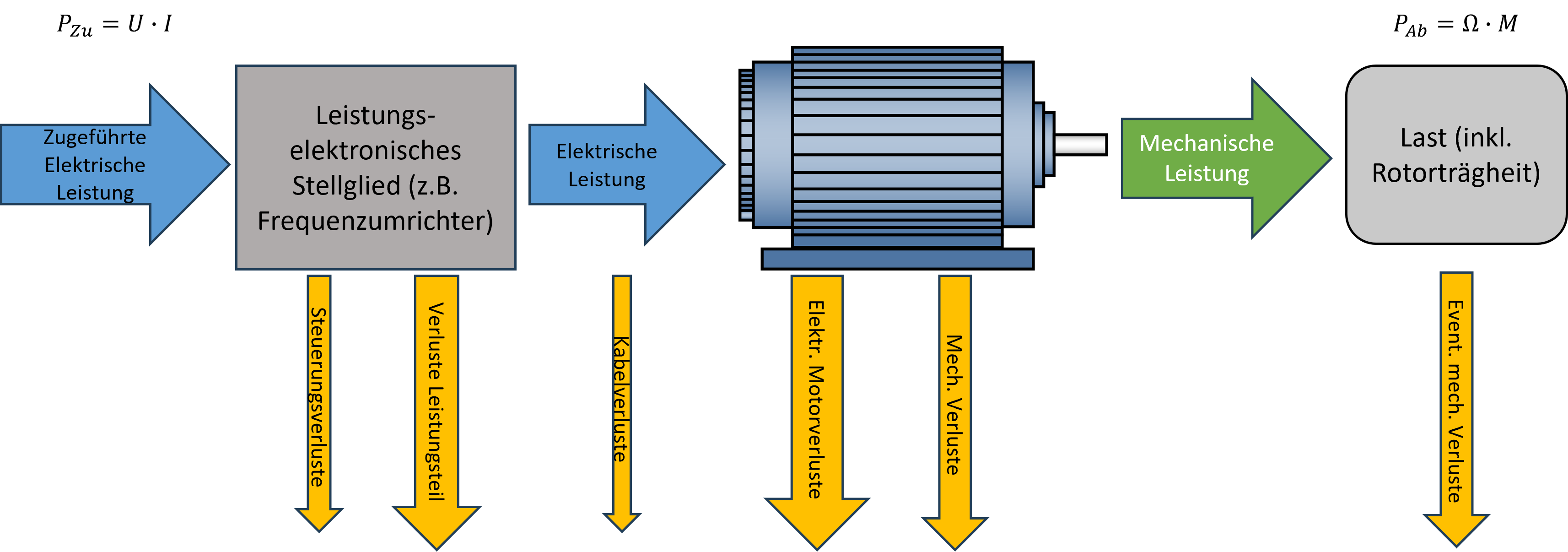
Abbildung 3.19: Leistungsfluss bei motorischem Betrieb

Gleichzeitig entstehen in den einzelnen Bestandteilen eines Antriebsystems Verluste, welche ebenfalls vom Netz zur Verfügung gestellt werden. So entstehen beispielsweise Verluste in der Regeleinrichtung des Antriebs (Versorgung des Steuereinheit), welche auch im Stanbdy-Betrieb anfallen und in Wärme umgewandelt werden. Werden die leistungselektronische Halbleiterbauelemente (z.B. Transistoren oder IGBT’s) angesteuert, dann entstehen sog. Schalt- bzw. Durchlassverluste. Da die Leistung mittels Kabel, welche einen ohmschen Widerstand aufweisen, zum Elektromotor übertragen wird, werden auch in diesem Übertragungselement Verluste entstehen. Der Motor als Wandler von elektrischer zu mechanischer Leistung weist ebenfalls Verluste auf, die in mechanische (z.B. Reibungs- bzw. Vibrationsverluste) und elektrische Verluste (z.B. Kupferverluste) unterteilt werden können. Wird das Antriebssystem generatorisch betrieben, dann drehz sich der Leistungsfluss um (vgl. Abb. 3.20).

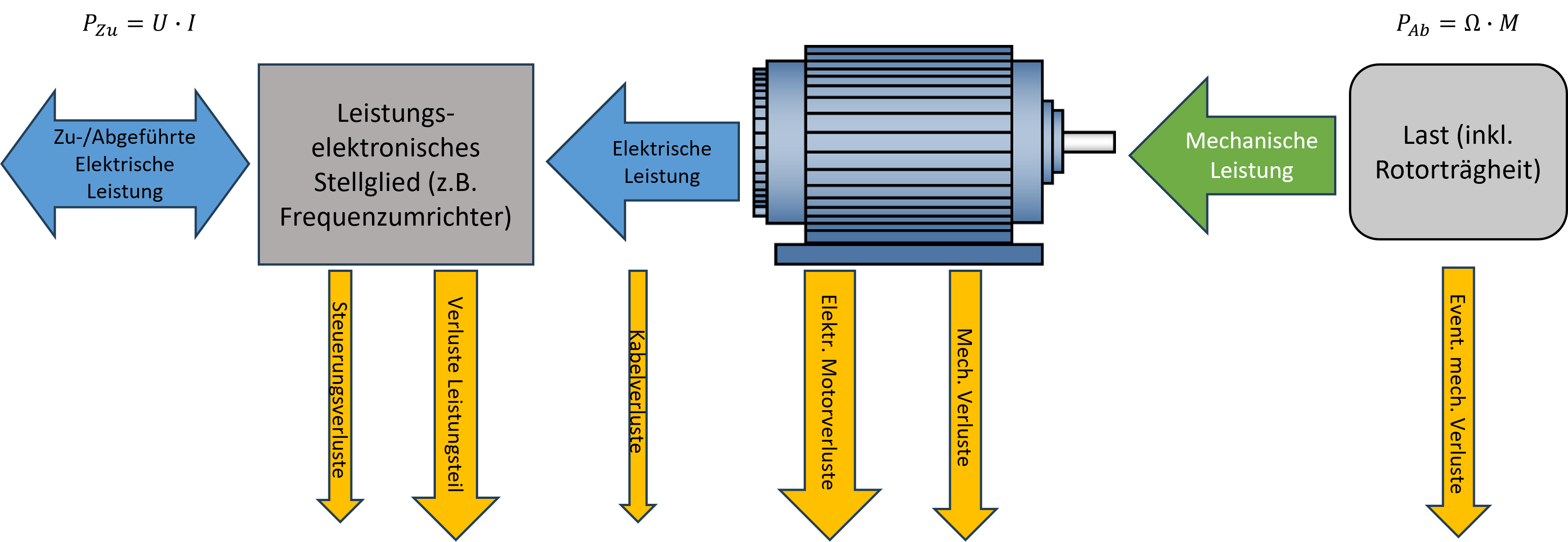
Abbildung 3.20: Leistungsfluss bei generatorischem Betrieb

In diesem Zusammenhang gilt es zu berücksichtigen, dass die Leistung im generatorischen Betrieb, welche nicht im Antriebsystem in Form von Verlusten abgeführt wird, nur dann an das versorgende Netz abgegeben werden kann, wenn der Stromrichter einen bidirektionalen Leistungsfluss zulässt. Im Falle von Stromrichtern, die eingangsseitig aus einfachen Brückengleichrichtern bestehen, ist dies nicht möglich. Da die am meisten verbreiteten Spannungszwischenkreisumrichter (vgl. Abb. 9.2) mit einer konstanten Zwischenkreisspannung arbeiten, führt der generatorische Betrieb zu einem unweigerlichen Ansteigen dieser Zwischenkreisspannung, da die Zwischenkreiskondensatoren vom Strom aufgeladen werden. Ist der vorgeschaltete Gleichrichter nicht rückspeisefähig, kann die Zwischenkreispannung unzulässig hohe Werte annehmen, welche die Sperrspannungen der Leistungshalbleiter übersteigen. Folglich muss diese Art von Stromrichter entsprechend geschützt werden. Bei Antriebssystemen, die nur sehr selten generatorisch betrieben werden, wird diesem Effekt üblicherweise mit sogenannten Bremswiderständen entgegengewirkt. Diese Bremswiderstände werden, in Abhängigkeit der aktuellen Zwischenkreisspannung, mittels Pulsweitenmodulation und einem leistungselektronischen Schaltelement (z.B. MOSFET oder IGBT) dem Zwischenkreis parallel geschaltet. Im Einschaltmoment werden die Zwischenkreiskondensatoren somit über einen oder mehrere solcher Bremswiderstände entladen. Die generatorisch zugeführte Leistung wird somit in Wärme umgewandelt.

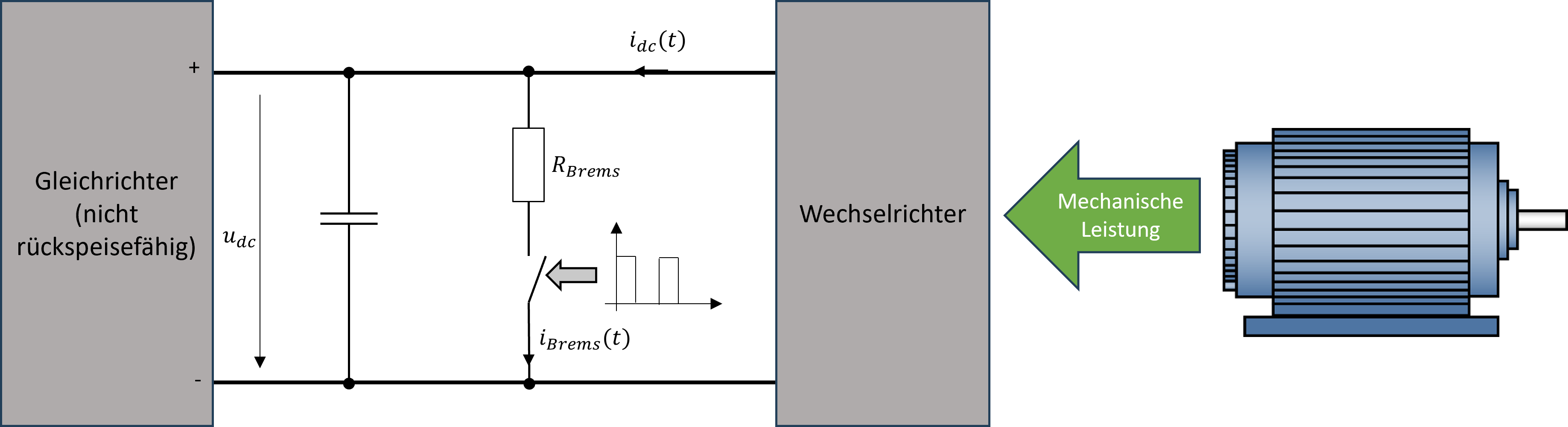
Abbildung 3.21: Funktionsweise eines Bremschoppers bei generatorischem Betrieb (vereinfacht)

Die Kombination aus leistungselektronischem Schalter und Bremswiderstand wird als Bremschopper bezeichnet (vgl. Abb. 3.21). Besteht das Antriebssystem aus mehreren Wechselrichtern, die vom gleichen Zwischenkreis (DC-Link) gespeist werden (z.B. Mehrachsen-Servoantrieb), muss der Bremswiderstand entsprechend dimensioniert werden.

3.3.1.1 Dimensionierung Bremswiderstand

Bei der konservativen Dimensionierung eines Bremswiderstandes wird üblicherweise davon ausgegangen, dass die gesamte Energie zum Verzögern der Last (\(E_{mech}\)) im Bremswiderstand in Wärme umgesetzt wird. Dies bedeutet, dass die Verluste im Antriebssystem (z.B. Kupferverluste im Motor bzw. Kabelverluste) zu Null angenommen werden. Grundlage zur Dimensionierung des Bremswiderstandes bilden die maximale kinetische (\(E_{kin}\)) und potentielle Energie (\(E_{pot}\)) im Antriebssystem.

\[ E_{mech} = E_{kin} + E_{pot} \]

Bei der Bestimmung dieser Grössen müssen die Trägheitsmomente von Motor, möglichen Getrieben und Last berücksichtigt werden. Der Widerstandswert des Bremswiderstandes wird über die max. Zwischenkreisspannung \(\hat{U}_{DC}\) (üblicherweise 10 Prozent oberhalb des Nennwertes) und dem Spitzenwert des Antriebs-Phasenstromes (\(\hat{I}_{Ph}\)) bestimmt. In einigen Fällen geben die Hersteller im Datenblatt des Antriebs einen Bremswiderstands-Stromwert an (\(I_{Brems}\)).

\[ R_{Brems} = \frac{\hat{U}_{DC}}{\hat{I}_{Ph}} = \frac{\hat{U}_{DC}}{I_{Brems}} = \frac{k\cdot U_{DC}}{\hat{I}_{Ph}} \]

Der Faktor \(k\) in der obigen Gleichung beschreibt die max. zulässige Überspannung im Zwischenkreis (üblickerweise ist \(k=1.1\)). Um die Leistung des Bremswiderstandes zu bestimmen, wird die mittlere Bremsleistung \(\overline{P}_{Brems}\), basierend auf der Anzahl notwendiger Bremsvorgänge pro Sekunde \(n_{Brems}\), benötigt.

\[ \overline{P}_{Brems} = E_{mech} \cdot n_{Brems} \] Kann keine Angabe zur Anzahl der Lastzyklen gemacht werden, wird üblicherweise von einer ständigen Einschaltdauer des Bremswiderstandes ausgegangen.

\[ \overline{P}_{Brems} = \frac{\left(\hat{U}_{DC}\right)^{2}}{R_{Brems}} \]

Diese Art der Dimensionierung führt zu einem deutlich überdimensionierten Bremswiderstand. Die Spitzenleistung des Bremswiderstandes \(\hat{P}_{Brems}\) wird unter Berücksichtigung der kürzesten Verzögerungszeitdauer \(t_{Verz_{min}}\) bestimmt.

\[ \hat{P}_{Brems} = \frac{E_{mech}}{t_{Verz_{min}}} \] Da Bremswiderstände einen zusätzlichen Kostenfaktor darstellen und gleichzeitig den Platzbedarf des Umrichters erhöhen, ist es in gewissen Fällen möglich einen Bremswiderstand durch zusätzliche Zwischenkreiskapazität(en) zu ersetzen.

\[ C_{Zus} = \frac{2\cdot E_{mech}}{\Delta U_{DC}} \]

In der obigen Gleichung wird der zulässige Anstieg der Zwischenkreisspannung \(\Delta U_{DC}\) berücksichtigt. Diese Vorgehensweise ist jedoch nur sinnvoll, wenn die Energie zum Verzögern der Last (\(E_{mech}\)) nur sehr gering ausfällt, da andernfalls sehr grosse (und kostspielige) zusätzliche Zwischenkreiskondensatoren notwendig werden.

3.4 Unterteilung von Motoren

Grundsätzlich spielt es für den Anwender kaum eine Rolle welche Motortechnologie er einsetzt. Üblicherweise gelten lediglich die Kosten des Antriebssystems eine massgebliche Rolle bei der Kaufentscheidung. Die Technologie hat aber indirekt Auswirkungen auf die mechanische Gestaltung, die Steuermöglichkeiten und die Kosten. Aufgrund dessen ist es von Vorteil einen Überblick über die Motorentypen und deren Eigenschaften zu haben. Eine Klassifizierung ist dabei nach konstruktiven Aspekten als auch nach ihren Betriebseigenschaften möglich. Konstruktive Gesichtspunkte sind dabei:

• Art der Energieübertragung: bürstenlos bzw. bürstenbehaftet
• Art der Bewegung: Asynchron bzw. Synchron
• Art der Flussführung: Transversalflussmaschinen bzw. Longitudinalflussmaschinen
• Art der Erregung: Permanentmagnete, elektrisch erregt bzw. Induktionsmaschinen
• Art der Wicklung: Konzentrierte Wicklung, Ringwicklung bzw. verteilte Wicklung
• Art der Versorgung: Blockstromspeisung, Drehstromspeisung bzw. Impulsspeisung

Sollen hingegen Betriebseigenschaften zur Klassifizierung herangezogen werden:

• Art der Spannung:
  • Kleinspannung bis 50V AC oder 120V DC
  • Niederspannung bis 1000V AC oder 1500V DC
  • Mittelspannungsantriebe bis ca. 20kV
• Amplitude des Drehmomentes bzw. Drehzahl
  • “High Torque” Antriebe mit geringen Drehzahlen bis ca. 300U/min (oft Direktantriebe)
  • Hochdrehende Antriebe mit Drehzahlen oberhalb von 10000U/min (www.celeroton.com)

3.5 Wirkungsgradbetrachtungen

Die Europäische EG-Verordnung 640/2009 legt die Ökodesignrichtlinie für elektrische Maschinen fest, wobei momentan die IEC 60034-30 als Grundlage für die Festlegung der Effizienzdaten dient. Da laut entsprechender Verordnung ca. 70 Prozent des Stromverbrauches in der Industrie auf die verwendeten Antriebssysteme zurückgehen, spielen elektrische Maschinen in der Ökodesignrichtlinie eine zentrale Rolle. Es wird davon ausgegangen, dass ca. 20-30 Prozent dieser Energie kostengüstig eingespart werden können, indem energieeffiziente Motoren verwendet werden. Somit ergeben sich laut Verordnung die Anforderungen an Elektromotoren, welche für die Inbetriebsetzung erfüllt sein müssen. Dabei werden folgende Motoren berücksichtigt:

• Dreiphasige 50/60Hz Käfigläufer Asynchronmaschinen
• Polpaarzahlen der Maschinen im Bereich 2 bis 6
• Nennspannungen bis 1kV
• Bemessungsleistungen zwischen 0.75 und 375kW
• Auslegung für den Dauerbetrieb S1

Ausnahmen bilden dabei folgende Maschinen:

• Vollständig in ein Produkt integrierte Motoren, die aufgrund dessen nicht unabhängig erfasst werden können
• Vollständig in einer Flüssigkeit betriebene Motoren
• Motoren, die unter speziellen Randbedingungen (Einsatztemperatur, Ex-Sicherheit bzw. Einsatzhöhe) betrieben werden
• Einsatz als Bremsen

Es werden dabei Nenn-Mindesteffizienzen definiert (IE1, IE2 und IE3), welche die vorher vom Europäischen Komitee der Hersteller von elektrischen Maschinen auf freiwilliger Basis verabschiedeten Effizienklassen Eff1, Eff2 und Eff3 ablösen.

Dabei wurde folgender Zeitplan vereinbart:

1. Ab 16.06.2011 müssen Motoren mindesten Effizienniveau IE2 erreichen
2. Ab 01.01.2015 müssen Motoren mit einer Nennausgangsleistung von 7.5-375kW entweder das Niveaus IE3 erreichen oder dem Niveau IE2 entsprechen und mit einer Drehzahlregelung ausgestattet sein.
3. Ab 01.01.2017 müssen alle Motoren mit einer Nennausgangsleistung von 0.75-375kW entweder das Niveaus IE3 erreichen oder dem Niveau IE2 entsprechen und mit einer Drehzahlregelung ausgestattet sein.

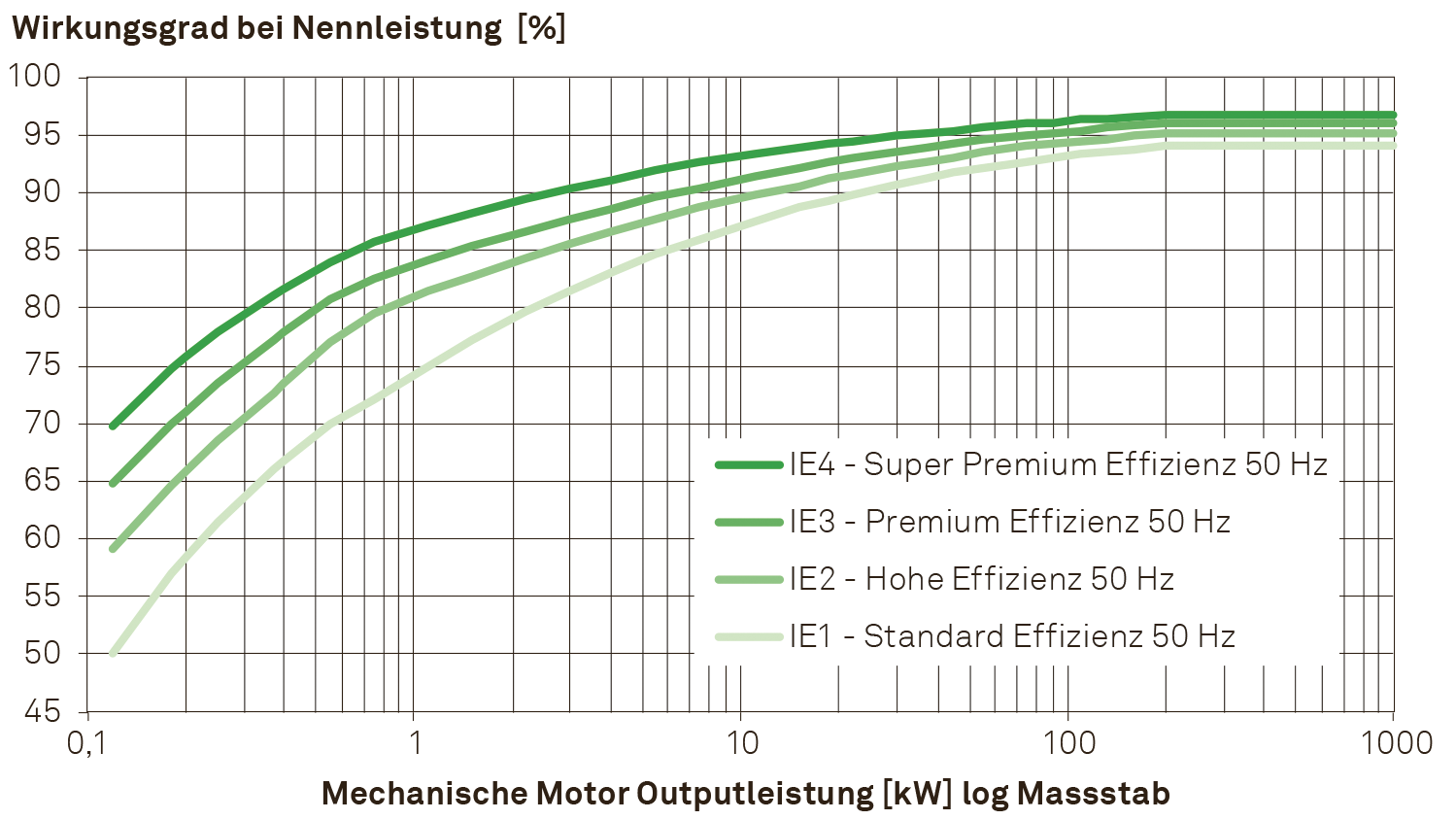
Abbildung 3.22: Effizienklassen für vierpolige Motoren (www.topmotors.ch)

Es wird ausserdem eine weitere Effiziensklasse IE5 mit erhöhten Anforderungen in Aussicht gestellt. Gleichzeitig werden Normen ausgearbeitet, welche das ganze Antriebssystem umfassen.

3.6 Motortechnologie

Wird der Aufbau des Rotors zur Klassifizierung von elektrischen Maschinen gewählt, wird ein möglicher Klassifizierungsbaum nach Abbildung 3.23 möglich.

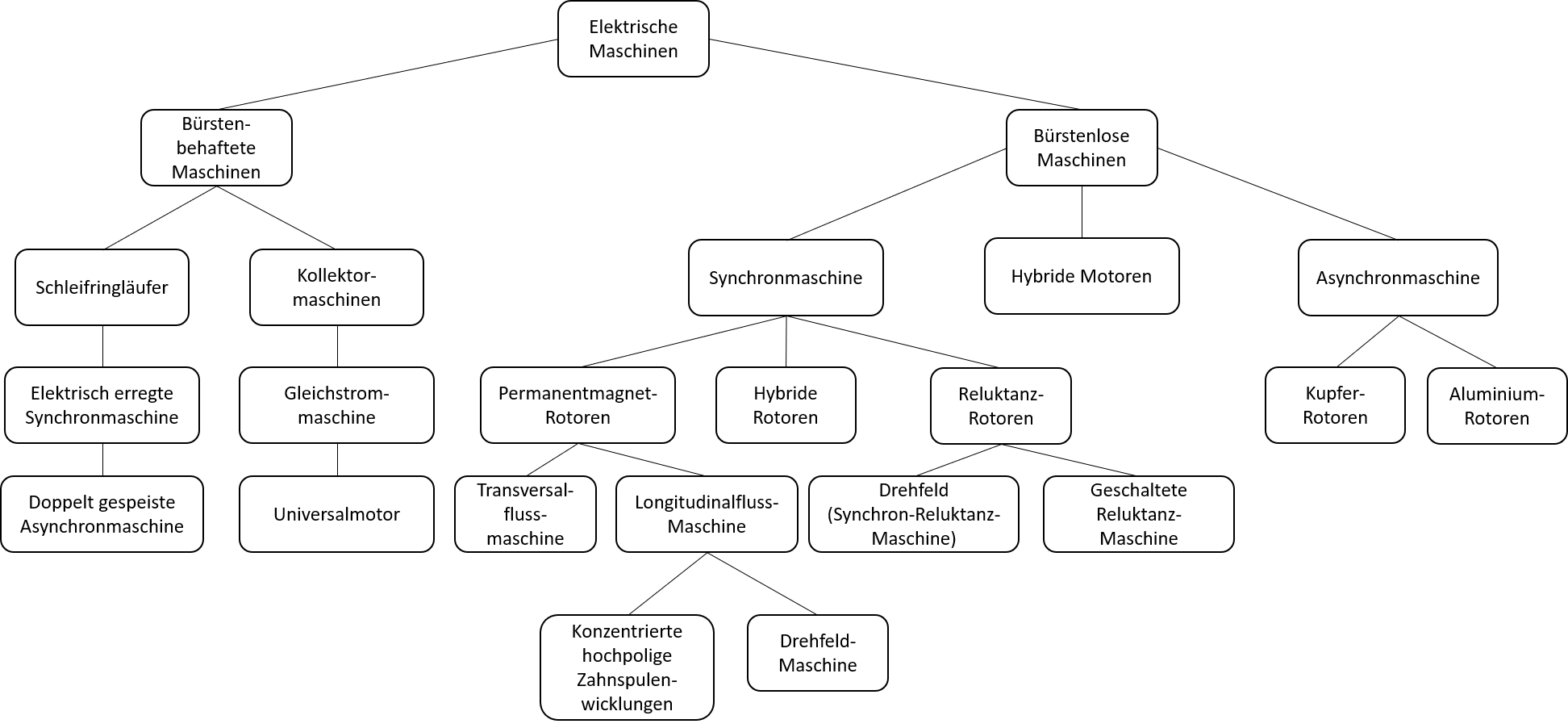
Abbildung 3.23: Klassifizierung nach Art des Rotors

3.7 Antriebsmomente elektrischer Maschinen

Wie bereits erwähnt, arbeiten elektrische Maschinen und Stromrichter als Antriebspaket eng abgestimmt zusammen. Während Gleichstrom- und Drehstrommaschinen herkömmlicher Bauart auch direkt am normalen Netz selbständig laufen, können die neuen Maschinen mit elektronischer Stromwendung oder Schrittmotoren nur zusammen mit dem angepassten Stromrichter arbeiten. Durch die Speisung über Stromrichter kann meist ein grosser Drehzahlbereich genutzt werden. Die am häufigsten eingesetzten elektrischen Maschinen sind:

• Gleichstrommaschinen mit Nebenschlussverhalten, elektrisch oder permanenterregt,
• Reihenschlussmaschinen (Universalmotoren),
• Asynchronmaschinen mit Kurzschluss- oder Schleifringläufer und
• Synchronmaschinen, elektrisch oder permanenterregt.

Alle stationär drehzahlveränderbaren Antriebe werden heute aus dem 50-Hz-Netz über Stromrichter gespeist. Die Stromrichter enthalten den Steuer-, Regel- und Leistungsteil. Je nach Anwendung unterscheidet man dabei:

• Netzgeführte Stromrichter, hauptsächlich in vollgesteuerter Brückenschaltung, zur Speisung des Anker- und Feldkreis.
• Gleichstromsteller mit Spannungszwischenkreis zur Flussteuerung von Gleichstrommaschinen.
• Drehstromsteller mit Anschnittsteuerung für Drehstromasynchronmaschinen und Universalmotoren,
• Frequenzumrichter mit Spannungs- oder Stromzwischenkreis, für Drehstrommaschinen synchroner und asynchroner Bauart und
• Maschinengetaktete Stromrichter für die elektronische Stromwendung, die ähnlich wie Frequenzumrichter aufgebaut sind. Schrittmotoren sind als hochpolige Synchronmaschinen ebenfalls dort einzuordnen.

Die elektrischen Maschinen zeigen unterschiedliches Verhalten und haben spezifische Kennlinien. Vereinfachend unterscheidet man in der Antriebstechnik drei Arten von charakteristischen Maschinenkennlinien:

• Die starre Kennlinie, wie bei der Synchronmaschine und dem Schrittmotor.
• Die harte Kennlinie, wie bei der Gleichstrommaschine mit konstanter Erregung oder der Asynchronmaschine zwischen Leerlauf und Bemessungspunkt.
• Die weiche Kennlinie, wie bei der Gleichstrommaschine im Feldstellbereich oder bei Maschinen mit Reihenschlusserregung.

3.8 Grundtypen der Lastkennlinien (Arbeitsmaschinen)

Nehmen die Belastungsmaschinen Energie über die Welle auf, so wirken sie als reine passive Last auf den Elektromotor zurück. Neben diesen hauptsächlichen Betriebsfällen treten vereinzelt jedoch Fälle auf, bei denen die Energierichtung zeitweise umgekehrt verläuft. Dann wirkt auch die Arbeitsmaschine als aktives Element und speist Energie über die Welle zur elektrischen Maschine zurück. Charakteristische Beispiele hierfür sind Hebezeugantriebe beim Absenken der Last oder Antriebe mit grossen Schwungmassen, z.B. Zentrifugen, beim Abbremsen. In diesen Fällen zeigt sich ein Vorteil des Elektroantriebs: Die elektrische Maschine kann Nutzbremsen, d.h. im Generatorbetrieb die Energie ins Netz zurückspeisen, wenn die Einrichtungen dazu ausgelegt sind. Betrachtet man den Verlauf des Lastdrehmoments, so treten in der Praxis eine Vielzahl von möglichen Betriebsfällen mit einer Fülle von verschiedenen Verläufen des Drehmoments auf. Eingrenzend lassen sich jedoch vier typische Drehmomentverläufe angeben.

• Konstanter Drehmomentverlauf (Trockene Reibung)
• linearer Drehmomentverlauf (Viskose Reibung)
• Quadratischer Drehmomentverlauf
• Hyperbolischer Drehmomentverlauf

In der Praxis treten im allgemeinen Mischformen auf, oder es ergeben sich Abweichungen von dem idealisierten Verlauf, z.B. im Bereich kleiner Drehzahlen durch Losbrechmomente.

3.8.1 Konstantmomentanwendung (Trockene Reibung)

Handelt es sich um eine Anwendung mit konstantem Lastmoment, so stellt sich eine geschwindigkeitsunahängige Kraft

\[F=F_{0}\cdot sgn(v)\] bzw. ein entsprechendes Drehmoment

\[M=M_{0}\cdot sgn(\omega)\] ein. Die vom Antrieb zur Verfügung zu stellende Leistung ergibt sich somit zu

\[P=\omega\cdot M = \omega\cdot M_{0}\cdot sgn(\omega) = M_{0}\cdot \mid\omega\mid.\]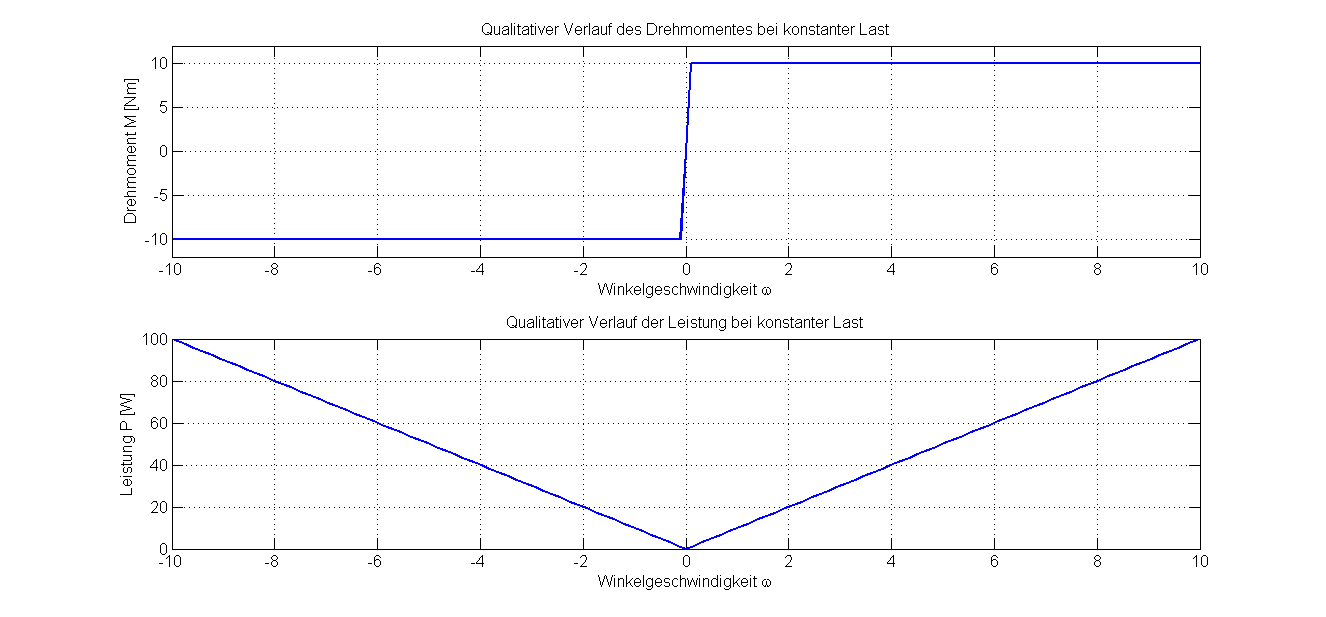

Abbildung 3.24: Drehmoment- u. Leistungsverlauf bei konstantem Lastmoment

Beispiele für Konstantmomentanwendungen sind Hebezeuge, Förderanlagen und Werkzeugmaschinen.

3.8.2 Linearer Drehmomentverlauf (Viskose Reibung)

Bei einem linearen Drehmomentverlauf ergibt sich ein geschwindigkeitsproportionaler Kraft- bzw. Drehmomentverlauf:

\[M=k\cdot \omega\] Folglich ergibt sich ein Leistungsverlauf, der eine quadratische Abhängigkeit von der Winkelgeschwindigkeit aufweist:

\[P=M\cdot \omega = k\cdot \omega^{2}\]

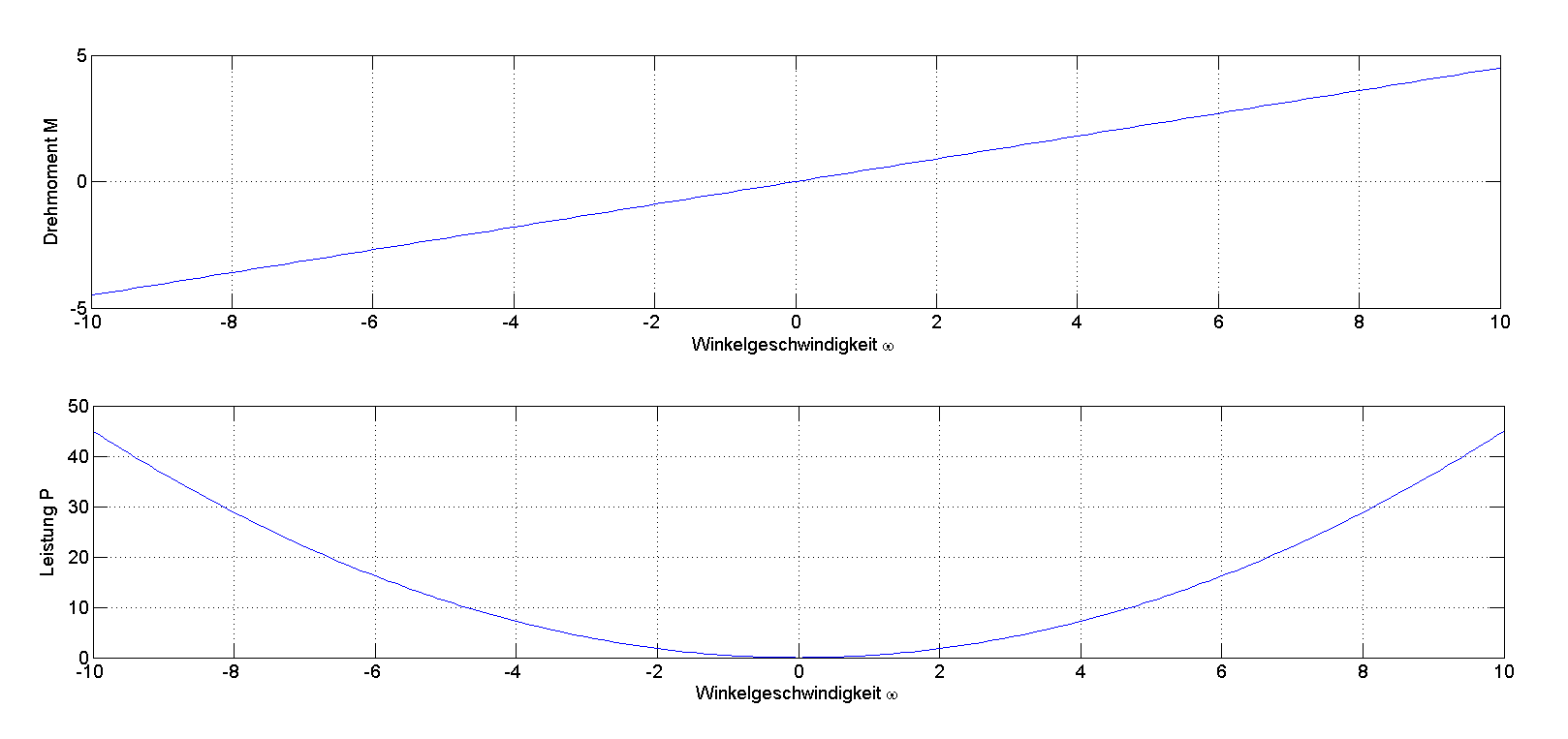
Abbildung 3.25: Drehmoment- u. Leistungsverlauf bei geschwindigkeitsproportionalem Lastmoment (k=0.45)

Beispiele für Lastkennlinien mit linearem Drehmomentverlauf sind Walzanlagen, Schleifmaschinen und hydraulische Pumpen.

3.8.3 Quadratischer Lastkennlinienverlauf

Einen quadratischen Lastkennlinienverlauf weisen insbesondere aero- und hydrodynamische Prozesse auf. Dazu zählen vor allem Lüfteranwendungen, Pumpen und Zentrifugen. Der entsprechende Drehmomentverlauf ergibt sich somit zu:

\[M=c\cdot \omega^{2}\cdot sgn(\omega)\]

Die entsprechende Leistung kann folgendermassen berechnet werden:

\[P=c\cdot \mid \omega^{3} \mid\]

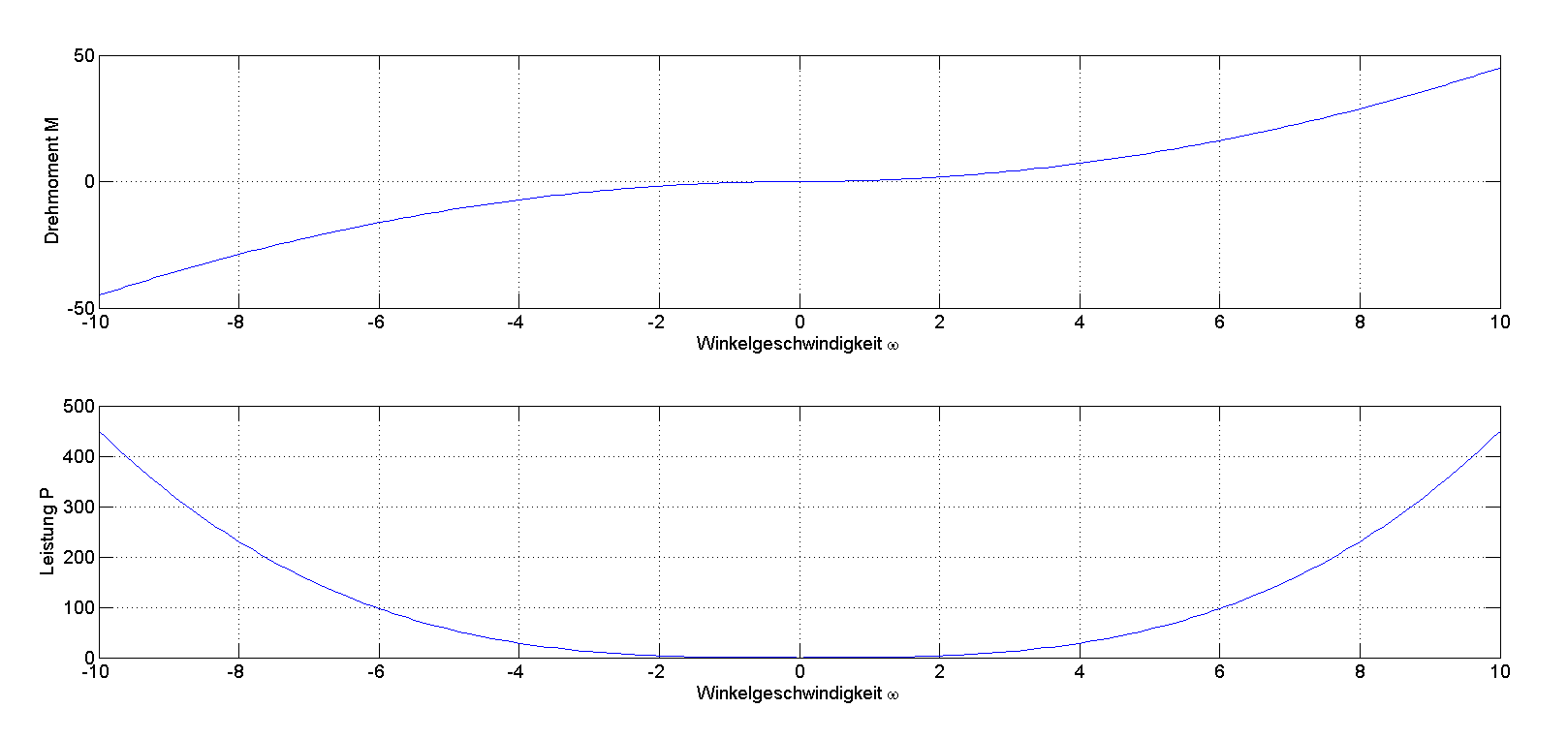
Abbildung 3.26: Drehmoment- u. Leistungsverlauf bei quadratischem Lastmoment (c=0.45)

3.8.4 Komplexitätsbetrachtungen

Die oben genannten Lastkennlinienverläufe stellen ideele Gesetzmässigkeiten dar, die in vielen Fälle, aufgrund der Komplexität eines Antriebssystems, als Mischformen auftreten. Um hier Beispiele zu nennen, sei beispielsweise auf einen Wickler bzw. eine Haspel verwiesen, welcher die Aufgabe hat ein entsprechendes Bandmaterial (z.B. Folien oder Bleche) unter definiertem Zug auf- bzw. abzuwickeln. Dadurch verändert sich der Radius der Rolle im Betrieb, wodurch sich das Massenträgheitsmoment ebenfalls verändert. Ein weiteres Beispiel sei beispielsweise ein Traktions- oder Fahrantrieb, bei dem mehrere Kräfte (Luftwiderstand \(F_{Luft}\), Rollreibung \(F_{Reib}\) sowie die Hangabtriebskraft \(F_{g}\)) die Widerstandskraft \(F_{Last}\) bilden.

\[ F_{Last}=F_{Luft}+f_{Reib}+F_{g}=\frac{\rho_{Luft}}{2}c_{w}Av^{2}+k_{roll}\cdot m_{F}\cdot g \cdot \cos(\alpha)+m_{F}\cdot g\cdot \sin(\alpha) \] Wobei gilt:

• \(\rho_{Luft}\) spezifische Dichte der Luft
• \(A\) wirksame Querschnittsfläche des Fahrzeugs
• \(c_{w}\) Widerstandsbeiwert der Luft
• \(k_{roll}\) Rollwiderstandsbeiwert
• \(g\) Erdbeschleunigung
• \(\alpha\) Steigungswinkel der Fahrbahn
• \(m_{F}\) Masse des Fahrzeugs

Eine Geschwindigkeitsänderung stellt sich nur dann ein, wenn die Differenz zwischen der antreibenden Kraft \(F_{Mot}\) und der Widerstandskraft von Null abweicht (Dynamische Gleichung):

\[ m_{F}\cdot \frac{dv}{dt}=F_{Mot}-F_{Last} \]

Wird der Beharrungszustand (stationärer Fall) betrachtet muss ein entsprechendes Gleichgewicht zwischen den zwei Kraftkomponenten herrschen:

\[ F_{Mot}=F_{Last} \]

3.9 Arbeitspunkte eines Antriebes

Im stationären Betrieb läuft ein Antrieb mit konstanter Winkelgeschwindigkeit (\(\omega_{st}\)), und es herrscht Gleichgewicht zwischen dem treibenden (positiver Zahlenwert) Drehmoment der elektrischen Maschine (\(M_{Mot}\)) und dem (negativer Zahlenwert) Belastungsmoment (\(M_{Last}\)) der Arbeitsmaschine; die Summe der Drehmomente ist 0, sowie die zeitliche Änderung der Winkelgeschwindigkeit.

\[ M_{ot}+M_{Last}=0 \]

Jede kleine Änderung des Lastmomentes (\(\Delta M_{Last}\)) an der Maschinenwelle ruft automatisch auch eine Änderung der Winkelgeschwindigkeit (\(\Delta \omega\)) und damit des Drehmoments bei der elektrischen Maschine hervor. Der Antrieb soll danach im neuen Arbeitspunkt, mit geändertem Drehmoment und mit neuer Winkelgeschwindigkeit, stabil weiterarbeiten. Zur Stabilitätsuntersuchung konstruiert man die resultierende Drehmomentenkennlinie, indem man für jede Winkelgeschwindigkeit die Momentensumme bildet. Die resultierende Kennlinie schneidet die \(\omega\)-Achse bei \(A^{*}\) und \(B^{*}\).

Abbildung 3.27: Bestimmung der Stabilität eines Arbeitspunktes am Beispiel der ASM (a) Systemstruktur b) Bildung Momentensumme c) resultierende Kennlinie

Nun betrachtet man den Betriebspunkt \(A^{*}\) der resultierenden Kennlinie. Der Antrieb arbeitet dort stabil, da bei einem Anstieg des Lastmoments die Drehzahl fällt. Im Betriebspunkt \(B^{*}\) ist dies nicht der Fall, dadurch ist der Antrieb in diesem Punkt instabil! Daraus ergeben sich folgende allgemeingültige Aussagen für einen stabilen Arbeitspunkt:

• Die Summe der stationären Drehmomente muss Null sein
• Die Neigung der resultierenden Drehmomentkennlinie muss negativ sein

3.10 Erwärmung

In der Antriebstechnik spielen Erwärmungsfragen bei der Bemessung elektrischer Maschinen eine entscheidende Rolle. Daher wird kurz auf thermische Probleme eingegangen. Um eine Abschätzung der Temperaturerhöhung zu ermöglichen wird häufig auf das Einkörper-Temperaturmodell (3.28) zurückgegriffen.

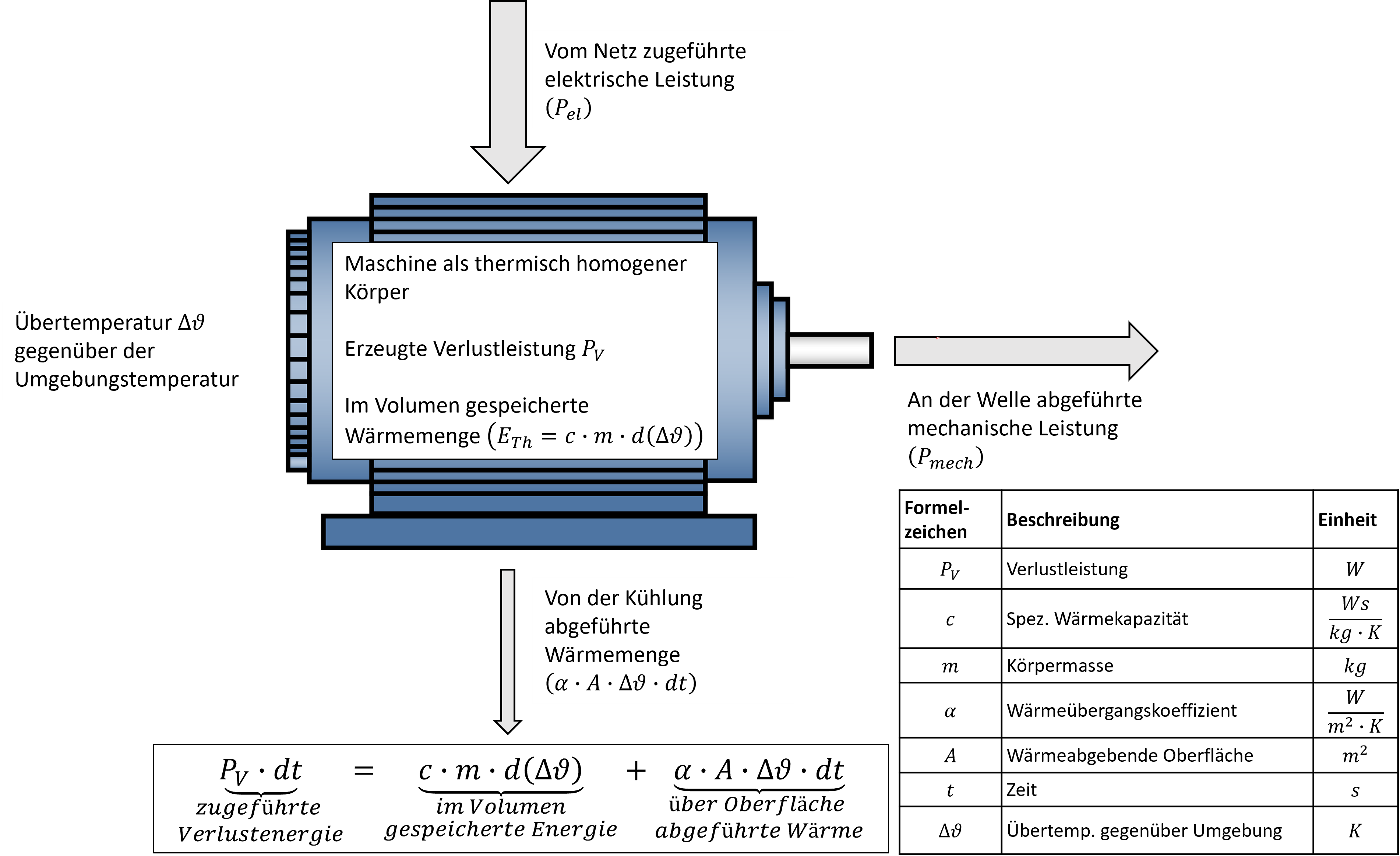
Abbildung 3.28: Einkörper-Temperaturmodell

Für die verschiedenen, in den elektrischen Maschinen benutzten Werkstoffe gelten naturgemäss unterschiedliche Temperaturgrenzen. Je nach eingesetztem Isolierstoff, einschliesslich Tränkmittel, unterscheidet man nach Wärmeklassen mit festgelegten Grenztemperaturen (siehe Tabelle 3.1).

Tabelle 3.1: Wärmeklassen

Isolierstoffgruppe	Wärmeklasse	Kühlmittel- temperatur [°C]	Grenzübertemperatur (nach dem Widerstands-verfahren) [K]	Grenztemperatur [°C]
1	A	40	60	105
2	B	40	80	130
3	F	40	105	155
4	H	40	125	180
5	C	40	noch nicht def.	>180

Gute Ausnutzung der zulässigen Temperatur steigert die Maschinenleistung, begrenzt jedoch andererseits die Isolierstoff-Lebensdauer. Nach dem Lebensdauergesetz bedeutet eine dauernde Temperaturerhöhung von 8 bis 12° K, über die zulässige Grenztemperatur hinaus, eine Halbierung der Lebensdauer und umgekehrt. Beispiele für die in Tabelle 3.1 aufgeführten Isolierstoffgruppen sind:

Gruppe 1:

• Baumwolle
• Naturseide
• Kunstseide
• Pressspan

Gruppe 2:

• Glimmerprodukte
• Drahtlacke auf der Basis von Polyterephthalat
• geschichtete Glasfaser

Gruppe 3:

• Glasfaser
• Asbest
• Drahtlacke auf der Basis von Imid-Polyester bzw. Esterimid

Gruppe 4:

• Glasfaser
• Asbest
• Drahtlacke auf reiner Polyimidbasis

Gruppe 5:

• Glimmer
• Porzellan
• andere keramische Stoffe
• Glas
• Quarz

Aus der allgemeinen thermischen Betrachtung lassen sich vier wichtige Feststellungen ableiten:

• Im stationären Betrieb wird die gesamte Verlustwärme über die Oberfläche durch Kühlung abgeführt.
• Die Endübertemperatur ist um so höher, je grösser der Wärmewiderstand \(R_{th}=\frac{1}{\alpha \cdot A}\) ist.
• Der thermische Beharrungszustand wird um so schneller erreicht, je schärfer die Maschine belüftet wird.
• Ist die Zeit der Energiezufuhr klein gegenüber der Erwärmungszeitkonstanten, dann darf man als Näherung einen linearen Temperaturanstieg annehmen (adiabater Verlauf). So wird z.B. bei einem Hochlauf- oder Bremsvorgang die Wärme überwiegend nur gespeichert und nicht abgegeben.

3.11 Abschätzung der thermischen Zeitkonstante

Eine kurze Rechnung liefert eine Abschätzung der thermischen Zeitkonstante T aus der Leistungsangabe (\(P_{N}\)), dem Wirkungsgrad (\(\eta\)), der Wärmeklasse (\(\Delta \vartheta_{zul}\)), der Maschinenmasse (\(m\)) und der spezifischen Wärmekapazität \(c\):

\[ T=\frac{c \cdot m}{\alpha \cdot A}=\frac{c \cdot m\cdot \eta}{P_{N}(1-\eta)}\cdot \Delta \vartheta_{zul} \]

Der sich ergebende Wert liefert einen Hinweis auf die Grössenordnung der Zeitkonstanten und somit einen Anhaltspunkt bei thermischen Fragestellungen.

Allgemein gilt für den Koeffizienten \(\alpha\):

Tabelle 3.2: Wärmeübergangskoeffizient

Materialpaarung	Strömungsgeschwindigkeit	Wärmeübergangskoeffizient
Stahl - Luft	\(v \leq 5m/s\)	\(\alpha = 5.8+4\cdot v\)
Stahl - Luft	\(v \geq 5m/s\)	\(\alpha = 7.17\cdot v\)

3.11.1 Kühlung

Die im Motor entstehende Verlustwärme muss abgeführt werden. Bei der Kühlung elektrischer Maschinen unterscheidet man nach dem Zustandekommen und der Wirkungsweise der Kühlung. Die Kühlarten werden durch zwei Buchstaben und in der vereinfachten Kennzeichnung mit zwei Ziffern beschrieben. Die Angaben beginnen mit den Buchstaben IC (International Cooling). Für weiterführende Informationen wird auf IEC 60034-6 verwiesen.

Dabei gilt ganz Allgemein folgendes:

• Selbstkühlung: Bei Selbstkühlung wird die Maschine ohne Verwendung eines Lüfters durch Luftbewegung und Strahlung gekühlt.
• Eigenkühlung: Bei Eigenkühlung wird die Luft durch einen am Läufer angebrachten Lüfter bewegt.
• Fremdkühlung: Bei Fremdkühlung wird die Maschine durch einen Lüfter gekühlt, der nicht von der Welle der Maschine angetrieben wird.

Nicht alle Kühlarten sind für Servoantriebe von Bedeutung. Für Servoantriebe kleiner Leistung wird typischerweise die Kühlart IC40 verwendet. Bei grösseren Leistungen kommen, insbesondere bei Asynchronmotoren, auch die Kühlarten IC05 bzw. IC45 zum Einsatz. Bei drehzahlveränderbaren Antrieben wird die Maschine meist durch angebaute Lüfter fremdgekühlt. Somit ist die Wärmeabgabe konstant und unabhängig von der Motordrehzahl. Bei Maschinen mit Selbstkühlung ist die Zeitkonstante etwa 2 bis 3mal grösser als bei fremd- oder eigengekühlten Maschinen. Auch bei abgeschaltetem Lüfter oder bei eigengekühlten Maschinen im Stillstand verdoppelt sich die Zeitkonstante in etwa. Anhaltswerte für die notwendige Drehmoment- und Leistungsreduzierung zeigt Abbildung @ref(fig:Leistungsreduktion-Kühlart) im Prinzip. Oft werden die Wicklungen der Maschinen nach Wärmeklasse F oder H ausgeführt, jedoch nur nach Klasse B ausgenutzt, um Reserven zu haben. Die Leistungsangaben der Maschinen beziehen sich auf eine Kühlmitteltemperatur von 40°C und eine Aufstellungshöhe bis 1000 m über Meer. Bei abweichenden Bedingungen muss die Bemessungsleistung u.U. reduziert werden.

Abbildung 3.29: Von Kühlart abhängige Leistungs- bzw. Drehmomentreduktion

3.11.2 Abführen der anfallenden Wärme

Bei allen stoffverarbeitenden oder stoffverändernden Arbeitsmaschinen wird praktisch die gesamte Antriebsleistung in Wärme umgesetzt. Die Wärme muss über die Raumluft aus dem Betriebsraum abgeführt werden. Damit diese Wärmemengen die Raumluft nicht aufheizen, ist für gute Frischluftzufuhr zu sorgen . Eine überschlagsmässige Berechnung des notwendigen Kühlluftstromes (\(V_{L}\)) kann mit Hilfe der gesamten Verlustleistung (\(P_{V}\)), der spezifischen Wärmekapazität des Kühlmittels (\(c_{p}\)), der Kühlmiteldichte (\(\rho\)) und der Temperaturdifferent (\(\Delta \vartheta\)) zwischen Lufteintritts- und zulässiger Raumtemperatur folgendermassen erfolgen:

\[ V_{L}=\frac{P_{V}}{c_{p}\cdot \rho \cdot \Delta \vartheta} \]

3.12 Zeitkonstanten

In der Antriebstechnik können bei Überschlagsrechnungen und Abschätzungen von Einflüssen, Zeitkonstanten eine wichtige Rolle spielen. Es treten entsprechend der unterschiedlichen Vorgänge verschiedene Zeitkonstanten auf:

• elektromagnetisch
• mechanisch
• thermisch

In der folgenden Tabelle sind die Werte der Zeitkonstanten für elektrische Maschinen grob dargestellt:

Tabelle 3.3: Gegenüberstellung unterschiedlicher Zeitkonstanten

Zeitkonstante	Grössenordnung
\(T_{elektrisch}\)	1ms - 100 (1000)ms
\(T_{mechanisch}\)	10ms - 10s
\(T_{thermisch}\)	1min - 120 min

Ausserdem lässt sich festhalten, dass die Zeitkonstanten elektrischer Maschinen proportional mit der Leistung sowie der Polpaarzahl zunehmen (siehe Abbildung 3.30).

Abbildung 3.30: Abhängigkeit der Zeitkonstanten von der Leistung bei elektrischen Maschinen

Ganz andere Zeitkonstanten ergeben sich bei Leistungshalbleitern in Stromrichtern. Dort liegen die thermischen Zeitkonstanten wegen der geringen Masse der Bauelemente im Millisekunden-Bereich! Halbleiterbauelemente sind kaum thermisch überlastbar. Oft kann man sich bei der Betrachtung eines Problems auf einen Vorgang konzentrieren und darf bei der Untersuchung die anderen Erscheinungen ausklammern, weil davon keine Einflüsse zu erwarten sind. Erfolgt ein Hochlauf eines Maschinensatzes z.B. in 10s, so sind die elektromagnetischen Schaltvorgänge längst im stationären Zustand, wogegen die thermischen Vorgänge praktisch noch gar nicht zu wirken angefangen haben. Allgemein kann man festhalten, dass bei Übergangsvorgängen nur die Einflüsse beachtet zu werden müssen, deren Zeitkonstanten in der gleichen Grössenordnung liegen. Wenn die Zeitkonstanten der anderen Einflussgrössen um gut eine Grössenordnung darüber oder darunter liegen, kann man sie mindestens in erster Näherung vernachlässigen.

3.13 Betriebsarten

Verschiedene Arbeitsverfahren und verschiedene Arten von Arbeitsmaschinen belasten die antreibende elektrische Maschine auch unterschiedlich. Die Anzahl der möglichen Betriebsarten ist rein theoretisch unbegrenzt. Die IEC-Norm 60034-1 ordnet diese Vielfalt von verschiedenen Belastungen in ein System von 9 Betriebsarten (S1 bis S10) ein. Eine richtige Auswahl und Bemessung von Antrieben wird mit Rücksicht auf die Erwärmung der Maschinen durch Einordnen in eine der folgenden Betriebsarten ermöglicht:

Abbildung 3.31: Darstellung der häufigsten Betriebsarten

• S1: Dauerbetrieb mit konstantem Belastungszustand, dessen Dauer ausreicht, den thermischen Beharrungszustand zu erreichen (Betriebsdauer \(t_{B}\) grösser als drei thermische Zeitkonstanten \(T\)).
• S2: Kurzzeitbetrieb mit konstanter Belastung, der aber nicht so lange dauert dass der thermische Beharrungszustand erreicht wird (\(t_{B}\) klein gegen \(T\)). Die nachfolgende Pause, dauert so lange, bis die Maschinentemperatur nicht mehr als 2°K von der Temperatur des Kühlmittels abweicht (Pause grösser \(3\cdot T\)).
• S3: Aussetzbetrieb ohne Einfluss des Anlaufvorgangs, der sich aus einer Folge gleichartiger Spiele zusammensetzt von denen jedes eine Zeit mit konstanter Belastung und einer Pause umfasst wobei der Anlaufstrom die Erwärmung kaum beeinflusst (\(t_{A}\) sehr klein gegen \(T\)).
• S4: Aussetzbetrieb mit Einfluss des Anlaufvorgangs, der sich aus einer Folge gleichartiger Spiele zusammensetzt, von denen jedes eine merkliche Anlaufzeit, eine Zeit mit konstanter Belastung und einer Pause umfasst.
• S5: Aussetzbetrieb mit Einfluss des Anlaufvorgangs und der elektrischen Bremsung, der sich aus einer Folge gleichartiger Spiele zusammensetzt, von denen jedes eine merkliche Anlaufzeit, eine Zeit mit konstanter Belastung, eine Zeit schneller elektrischer Bremsung und einer Pause umfasst.
• S6: Durchlaufbetrieb mit Aussetzbelastung, der sich aus einer Folge gleichartiger Spiele zusammensetzt, von denen jedes eine Zeit mit konstanter Belastung und eine Leerlaufzeit umfasst. Es tritt keine Pause auf.
• S7: Ununterbrochener Betrieb mit Anlauf und elektrischer Bremsung, der sich aus einer Folge gleichartiger Spiele zusammensetzt, von denen jedes eine merkliche Anlaufzeit, eine Zeit mit konstanter Belastung und eine Zeit mit schneller elektrischer Bremsung umfasst. Es tritt keine Pause auf.
• S8: Ununterbrochener Betrieb mit periodischer Drehzahländerung, der sich aus einer Folge gleichartiger Spiele zusammensetzt. Jedes dieser Spiele umfasst eine Zeit mit konstanter Belastung und bestimmter Drehzahl; anschliessend eine oder mehrere Zeiten mit anderer Belastung, denen unterschiedliche Drehzahlen entsprechen.
• S9: Ununterbrochener Betrieb mit nicht periodischer Last- oder Drehzahländerung, bei dem sich i.a. Belastung und Drehzahl innerhalb des zulässigen Betriebsbereichs nicht periodisch ändern. Bei diesem Betrieb treten häufig Belastungsspitzen auf, die weit über den Bemessungswert liegen können. Dieser Betriebsart soll eine passend gewählte Dauerbelastung als Bezugswert für das Lastspiel zugrunde gelegt werden.
• S10: Betrieb mit einzelnen konstanten Belastungen. Ein Betrieb mit einem Lastspiel, das nicht mehr als vier einzelne Belastungswerte enthält, von denen jede einzelne über eine so lange Zeit aufrechterhalten bleibt, dass die Maschine den thermischen Beharrungszustand erreicht. Die grösste Belastung darf die 1,2 fache Bemessungsleistung nicht übersteigen. Die kleinste Belastung darf den Wert Null (Stillstand, Leerlauf) besitzen. Jedes Lastspiel muss integral auf die gleiche thermische Lebenserwartung führen.

Dabei gilt folgende Definition:

• Bei S2, S3 und S6 ist eine Leistungserhöhung gegenüber S1 möglich.
• Bei S4, S5, S7 bis S9 ist eine Leistungsreduktion gegenüber S1 erforderlich.

In der Praxis treten die oben beschriebenen idealen Belastungsfälle ausser bei Dauerbetrieb S1 kaum auf. Ein erheblicher Teil der Maschinen wird jedoch mit einer vom Dauerbetrieb abweichenden Betriebsart gefahren. Da die hierbei zu erzielende Leistungsausbeute von der Dauerbetriebsleistung erheblich abweichen kann, benötigt man zum Projektieren eine genaue Beschreibung der Betriebsart. Für den realen Lastfall kann man eine Bemessungsbetriebsart immer so auswählen, dass sie der zeitlichen Belastung der Maschine am besten entspricht.

3.14 Äquivalente Belastung

Die Endübertemperatur einer Maschine hängt von den Verlusten und somit in erster Näherung vom Quadrat des Maschinenstroms ab. Geht man davon aus, dass der für den konkreten Lastfall ermittelte äquivalente Strom gleich oder kleiner dem Bemessungsstrom der ausgewählten Maschine ist, so erhält man eine Bemessungsgrundlage für die Auswahl der Maschine bei komplizierten Lastverläufen. Der Betrieb ist dann thermisch zulässig, wenn die ermittelte äquivalente Belastung der Maschine unter der Bemessungslast liegt. Bleibt noch zu prüfen, ob die elektrischen Überlastungseigenschaften der Maschine den Betrieb erlauben.

\[ I_{äq}=\sqrt{\frac{\int_0^{T}{i^2(t)\cdot dt}}{T}} \]

Auf ähnliche Art und Weise lassen sich ebenfalls äquivalente Drehmoment- bzw. Leistungswerte (\(M_{äq}\) bzw. \(P_{äq}\)) bestimmen, wobei man beim Drehmoment von Maschinen mit konstantem magnetischen Fluss (\(M\sim \Phi \cdot I\)) und von konstanter Winkelgeschwindigkeit (\(P=\omega \cdot M\)) ausgeht. Entsprechend erhält man das äquivalente Drehmoment aus:

\[ M_{äq}=\sqrt{\frac{\int_0^{T}{m^2(t)\cdot dt}}{T}} \]

Die äquivalente Leistung ergibt sich folglich aus:

\[ P_{äq}=\sqrt{\frac{\int_0^{T}{p^2(t)\cdot dt}}{T}} \]

3.15 Mechanische Übergangsvorgänge

Drehzahlveränderbare Antriebe laufen nur selten längere Zeit mit einer festen Drehzahl. Sie werden oft hochgefahren oder abgebremst, damit der Arbeitsmaschine optimaler Betrieb ermöglicht wird. Zur Beurteilung, ob eine Maschine im Motorbetrieb mit der Arbeitsmaschine hochlaufen, oder im Generatorbetrieb die Arbeitsmaschine abbremsen kann, gehört die Ermittlung der Anlauf- resp. Bremszeit. Wegen der üblichen regelungstechnischen Begrenzung der Drehmomente kann hierbei vereinfachend mit konstanten mittleren Maschinendrehmomenten \(M_{bMi}\) gerechnet werden. Mindestens für die Überschlagsrechnungen wird man auch die Lastmomente durch mittlere Momente ersetzen. Aus der Differenz der drehzahlabhängigen Drehmomente erhält man allgemein das beschleunigende Drehmoment \(M_{b} = konst\). Die Hochlaufzeit \(t_{Ho}\) bis zum Erreichen der Winkelgeschwindigkeit \(\omega_{e}\) errechnet sich aus:

\[ t_{Ho}=\frac{J\cdot \omega_{e}}{M_{bMi}}=\frac{J\cdot 2\pi \cdot n_{e}}{M_{bMi} \cdot 60} \]

Auf ähnliche Art und Weise erhält man die Bremszeit \(t_{b}\) sinngemäss mit der änfänglichen Winkelgeschwindigkeit \(\omega_{a}\):

\[ t_{b}=\frac{J\cdot \omega_{a}}{M_{bMi}}=\frac{J\cdot 2\pi \cdot n_{a}}{M_{bMi} \cdot 60} \]

3.15.1 Einfluss und Arten von Reibung in Antriebssystemen

Ganz allgemein betrachtet stellt die Reibung eine Kraft dar, die zwischen Körpern oder Teilchen wirkt, die sich gegenseitig berühren. Diese sog. Reibungskraft erschwert dann die Bewegung der Körper gegeneinander. Aufgrund dessen muss Arbeit verrichtet werden, um eine reibungsbehaftete Bewegung zu erzeugen. Im Falle von Antriebssystem muss diese Arbeit, bei Beschleunigungsvorgängen von der antreibenden Maschine aufgebracht werden. Grundsätzlich werden verschiedene Arten von Reibung unterschieden:

• Haftreibung
• Gleitreibung
• Rollreibung
• Wälzreibung
• Bohrreibung
• Seilreibung

Gewisse Reibungsarten, die in der Antriebstechnik häufiger anzutreffen sind, sollen näher vorgestellt werden.

3.15.1.1 Coulombsche oder trockene Reibung

Die Reibkraft bei der trockenen Reibung steigt mit der Normalkraft \(F_{N}\) mit der ein Körper auf seine Unterlage drückt. Desweiteren ist sie abhängig von der Materialpaarung, die durch die Gleitzahl \(\mu\) zum Ausdruck gebracht wird.

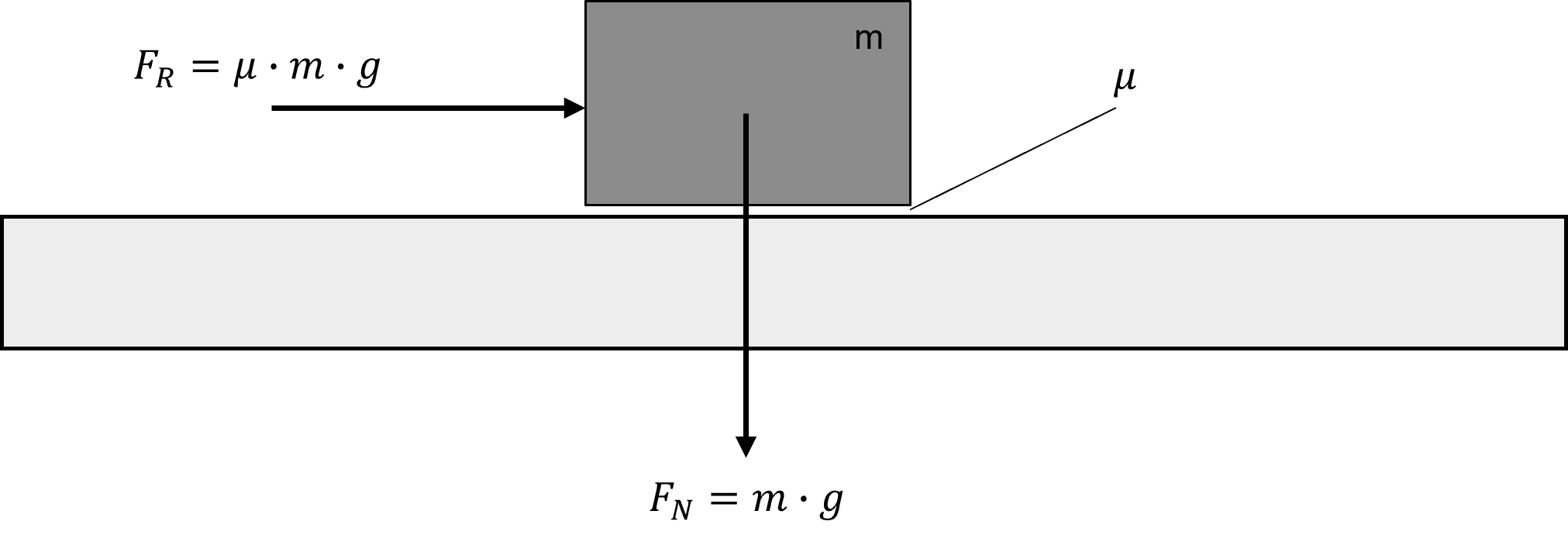
Abbildung 3.32: Darstellung eines horizontal bewegten Körpers und dessen Reibkraft

Die Reibkraft eine flach auf einer Unterlage positionierten Körpers kann anhand der folgenden Gleichung berechnet werden:

\[ F_{R} = \mu\cdot F_{N}=\mu\cdot m\cdot g \]

Wirken auf den Körper äussere Kräfte ein, dann kann die daraus entstehende Bewegung mit Hilfe der entsprechenden Gleichgewichtsbedingungen für die Translation

\[ \sum{F} -m\cdot a = 0 \Rightarrow \sum{F} = m\cdot a \]

bzw. für die Rotation

\[ \sum{M} -J\cdot \alpha = 0 \Rightarrow \sum{M} = J\cdot \alpha \]

bestimmt werden. Dabei muss jedoch die Wirkunsgrichtung der Kräfte berücksichtigt werden. Wird eine Masse beispielsweise horizontal beschleunigt, dann wirken der antreibenden Kraft \(F\) sowohl die Reib- als auch die Trägheitskraft entgegen (vgl. Abb. 3.33 links). Wird eine, sich horizontal bewegende Masse hingegen abgebremst, dann stimmt die Wirkrichtung der verzögernd wirkenden Kraft \(F\) mit der Wirkrichtung der Trägheitskraft \(F_{T}=m\cdot a\) überein (vgl. Abb. 3.33 rechts).

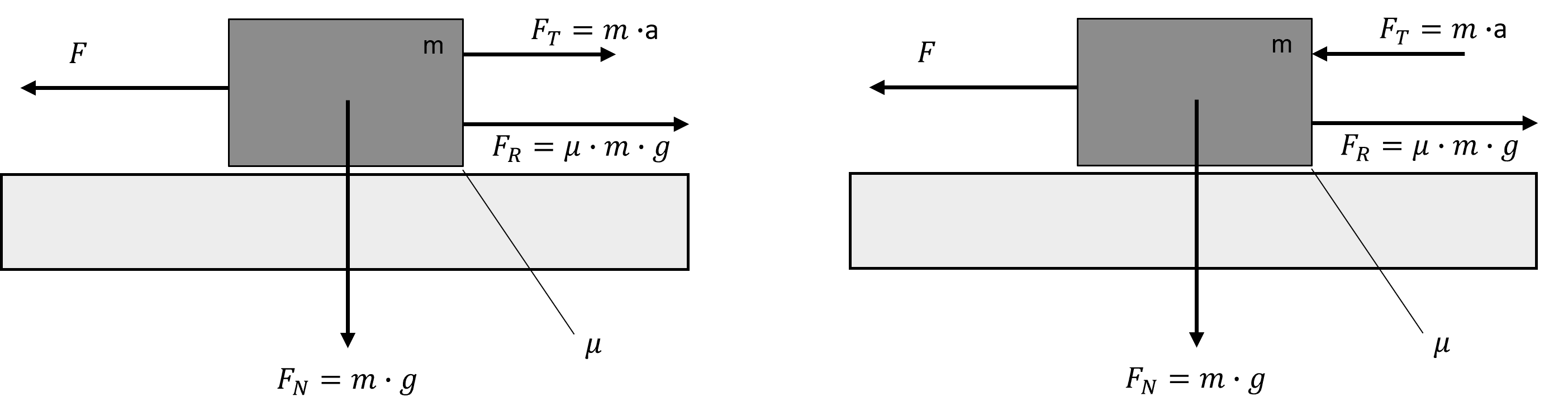
Abbildung 3.33: Kräfte an einer horizontal bewegten Masse (links: Beschleunigung, rechts: Verzögerung)

Dies muss bei der Bildung der Kräftesumme berücksichtigt werden. Da in der Antriebstechnik auch häufig Lasten gehoben oder abgesenkt werden müssen, kann dies mittels Modellvorstellung einer geneigten Ebene verallgemeinert werden.

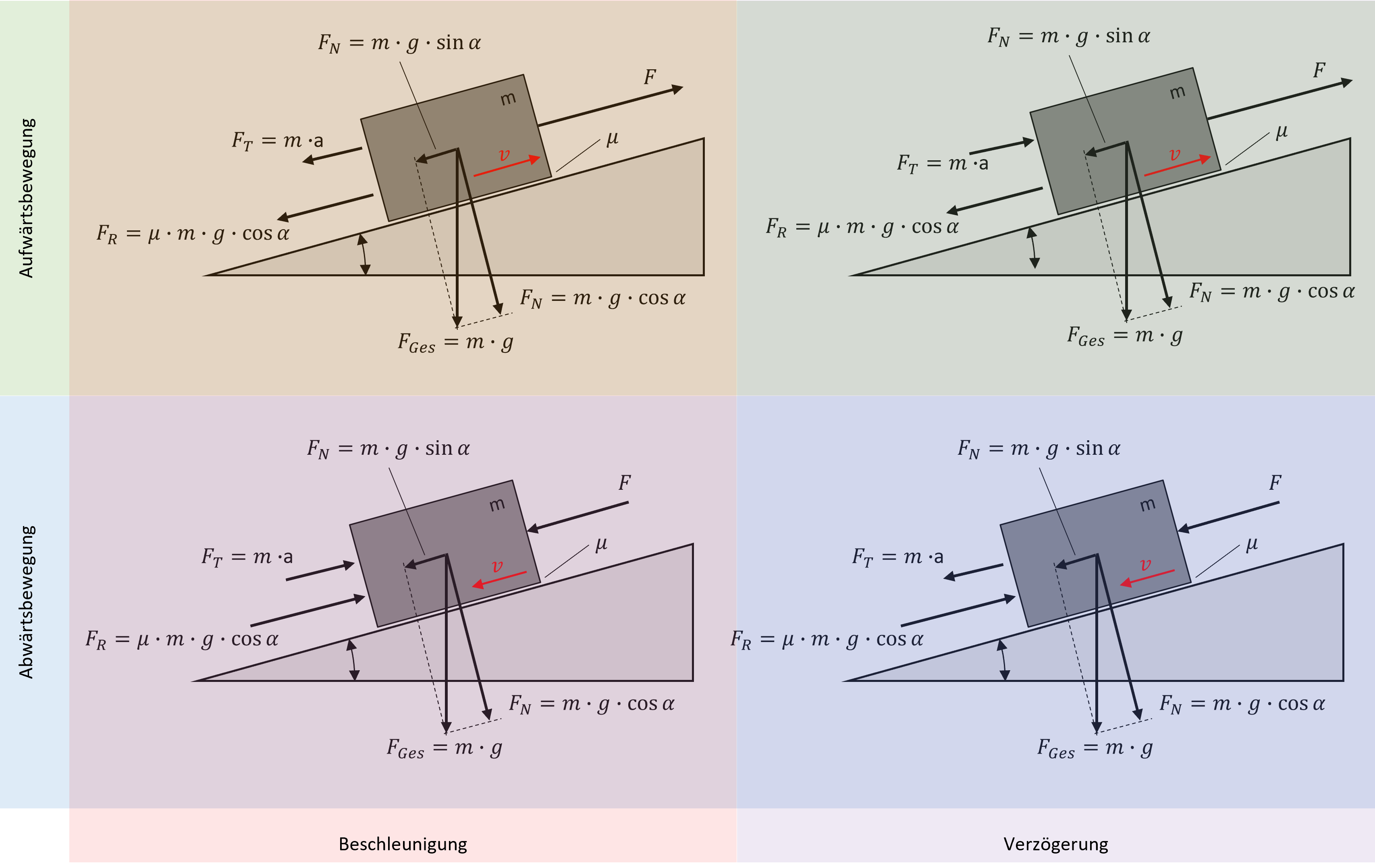
Abbildung 3.34: Kraftwirkungsrichtungen an der geneigten Ebene bei unterschiedlicher Bewegungsrichtung sowie Beschleunigung bzw. Verzögerung

Die Richtungen der sich einstellenden Kräftevektoren bei unterschiedlichen Bewegungsrichtungen sowie beschleunigten bzw. verzögerten Bewegungen ist in Abb. 3.34 dargestellt. Dieser Sachverhalt lässt sich mathemetisch folgendermassen zusammenfassen. Handelt es sich um einen Beschleunigungsvorgang gilt

\[ F=m\cdot g\left(\mu\cdot \cos (\alpha) \pm \sin(\alpha) +\frac{a}{g} \right) \]

Bei einem Verzögerungsvorgang hingegen gilt:

\[ F=m\cdot g\left(\mu\cdot \cos (\alpha) \pm \sin(\alpha) - \frac{a}{g} \right) \]

Dabei wird das positive Vorzeichen für die Aufwärts- und das negative Vorzeichen für die Abwärtsbewegung verwendet. Bei Auf- bzw. Abwärtsbewegungen mit konstanter Geschwindigkeit, fällt in beiden obigen Gleichungen die Trägheitskraft \(F_{T}=m\cdot a\) weg.

3.15.2 Getriebe

Nur in wenigen Fällen gelingt es Antriebe zu verwenden, deren zulässiger Drehmoment- und Drehzahlbereich ohne weitere Modifikationen den Anforderungen der Last genügen. Diese Antriebsart wird als Direktantrieb bezeichnet. Können die Drehmoment- und Drehzahlanforderungen der Last nicht erfüllt werden, werden Getriebe benötigt.

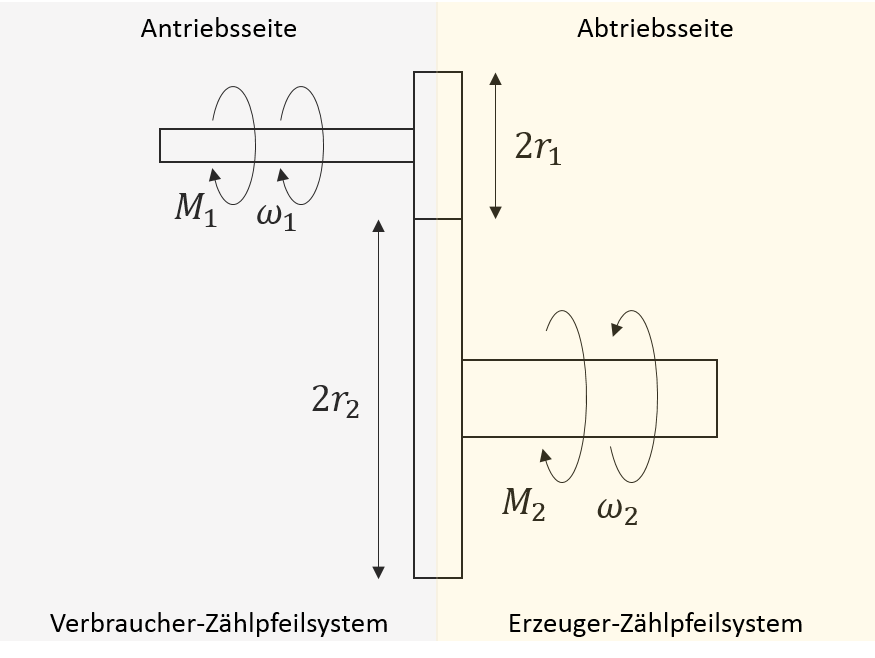
Abbildung 3.35: Darstellung eines Getriebes

Getriebe können auf vielfältige Arten ausgeführt werden (z.B. Zahn- bzw. Reibräder). Reibräder ermöglichen eine kraftschlüssige, Zahnräder hingegen eine formschlüssige Verbindung. Kraftschlüssige Verbindungen sind allgemein mit Schlupf verbunden, was für die folgenden Betrachtungen unberücksichtigt bleiben soll. Die Getriebeübersetzung berechnet sich folgendermassen:

\[ i_{G} = \frac{\omega_{1}}{\omega_{2}}=\frac{r_{2}}{r_{1}}=\frac{z_{2}}{z_{1}} \]

Dabei repräsentieren \(r_{1}\) bzw. \(r_{2}\) die effektiven Radien bzw. \(z_{1}\) und \(z_{2}\) die Zahnzahlen der Zahnräder auf Antriebs- bzw. Abtriebsseite. Werden sowohl Trägheit als auch die innere Reibung vernachlässigt, folgt somit für die Berechnung der Drehmomente

\[ i_{G} = \frac{M_{2}}{M_{1}} \]

bzw. für die Leistungen

\[ P_{1} = P_{2} \]

Insbesondere bei grösseren Leistungen ist eine Vernachlässigung der inneren Reibung bzw. des Trägheitsmomentes des Getriebes nicht mehr zulässig. Der Drehmomentbedarf erhöht sich wegen des Getriebewirkungsgrades \(\eta_{G}\).

\[ M_{1}=\frac{M_{2}\cdot \omega_{2}}{\eta_{G}\cdot \omega_{1}} \]

Richtwerte für Getriebewirkungsgrade zeigt die Abbildung 3.36.

Abbildung 3.36: Gegenüberstellung der typischen Wirkungsgrade von Getrieben

Aus der Tabelle kann man auch entnehmen, dass ausser bei Schneckengetrieben der Wirkungsgrad bei Überschlagsrechnungen unberücksichtigt bleiben darf, ohne dass grosse Fehler zu erwarten sind. Treibt die Arbeitsmaschine, z.B. beim Bremsen, die elektrische Maschine (Generator) an, so ist das treibende Moment an der elektrischen Maschine wegen des Wirkungsgrades des Getriebes kleiner.

\[ M_{1}=\eta_{G}\cdot M_{2} \]

3.15.2.1 Translatorisch-rotatorische Anpassung

Zur Umsetzung einer rotatorischen in eine translatorische Bewegung eignen sich Seilscheiben, Räder oder Zahnrad-Zahnstangen. Dabei gilt:

\[ v=\omega \cdot r \]

bzw.

\[ M=F\cdot r \]

3.15.3 Gewindespindeln

Bei Positionierantrieben müssen sehr häufig Dreh- in Längsbewegungen umgewandelt werden, wobei häufig Gewindespindeln zum Einsatz kommen. Dabei wird häufig zwischen Trapezgewindetriebe und Kugelgewindetrieben unterschieden. Bei Trapezgewindespindeln wird das Prinzip der Gleitreibung verwendet, was dazu führt, dass diese Spindelart einen geringen Wirkungsgrad aufweist. es handelt sich dabei allerdings um eine kostengünstige Lösung.

Abbildung 3.37: Trapezgewindespindel (Quelle: www.bornemann-gewindetechnik.de)

Kugelgewindespindeln werden auch als Kugelumlaufspindeln bezeichnet und zeichnen sich dadurch aus, dass, ähnlich wie bei einem Kugellager, Rollreibung zwischen Spindel und Mutter auftritt. Dies wird dadurch erreicht, dass Wälzkörper (Kugeln) zwischen der Spindel und der Spindelmutter aufgefädelt werden. Bei hochgenauen Kugelumlaufspindeln laufen diese Kugeln in einem geschlossenen System innerhalb der Spindelmutter um.

Abbildung 3.38: Kugelumlaufspindel (Quelle: www.bs-wiki.de)

Kugelumlaufspindeln erreichen damit einen relativ hohen Wirkungsgrad. Da sich die Last während einer Umdrehung der Spindel um die Steigung \(k\) vorwärts bewegt, kann somit die lineare Geschwindigkeit \(v\) aus der Winkelgeschwindigkeit \(\omega\) der Gewindestange berechnet werden:

\[\begin{equation} v= n\cdot \frac{k}{60} = \frac{k\cdot \omega}{2\pi} \tag{3.6} \end{equation}\]

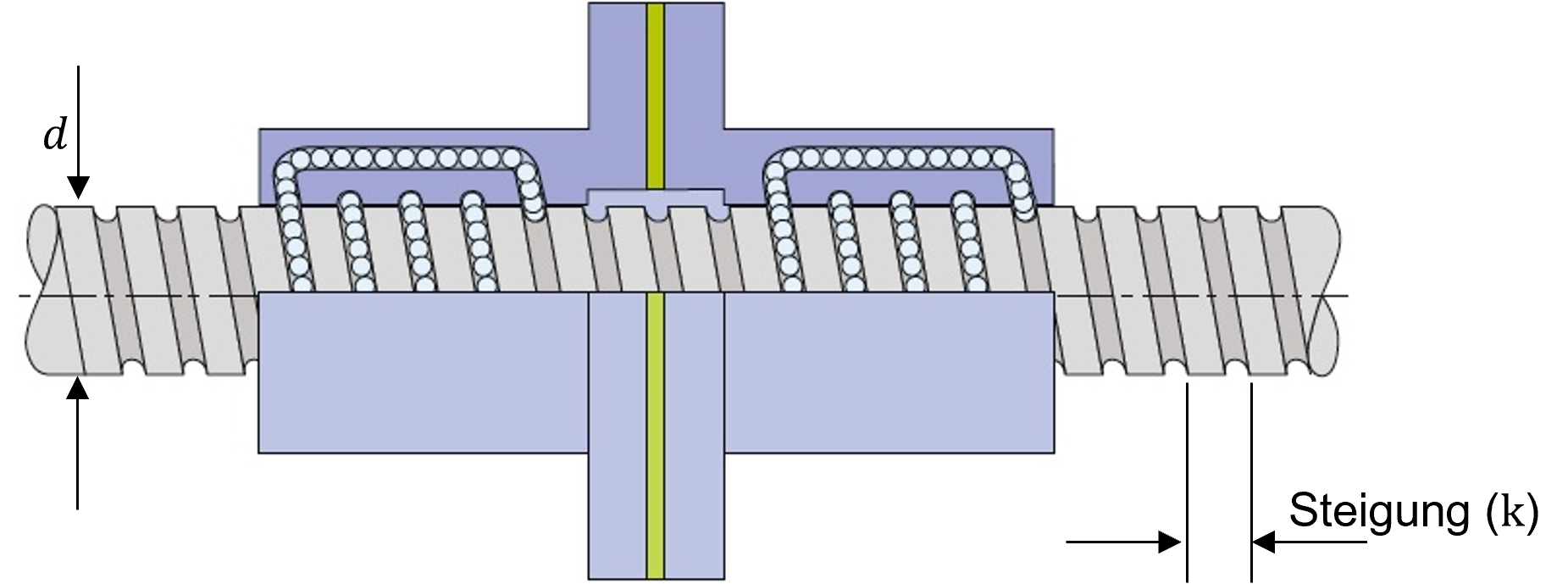
Abbildung 3.39: Wichtige Parameter am Beispiel der Kugelumlaufspindel (Quelle: www.ludwigmeister.de; modifiziert)

Die Umrechnung zwischen der auf die Last wirkenden Kraft und dem entsprechenden Drehmoment kann einerseits über die Leistungsbilanz erfolgen:

\[\begin{equation} P_{Rot} = M\cdot \omega = P_{Lin} = F\cdot v = F\cdot \frac{k\cdot \omega}{2\pi} \Rightarrow F=M\cdot \frac{2\pi}{k} \Longleftrightarrow M=F\frac{k}{2\pi} \tag{3.7} \end{equation}\]

Andererseits ergibt sich dieses Ergebnis auch, wenn man die geometrischen Verhältnisse der durch die Gewindesteigung entstehenden Kraftvektoren berücksichtigt. Um die notwendigen Antriebsmomente bestimmen zu können, muss die Kraft bestimmt werden, die notwendig ist, um einen Körper (Masse der zu bewegenden Last) eine schiefe Ebene nach oben zu bewegen. Diese schiefe Ebene entspricht dabei der Steigung, die durch die Steigung des Gewindes hervorgerufen wird (vgl. Abb. 3.40).

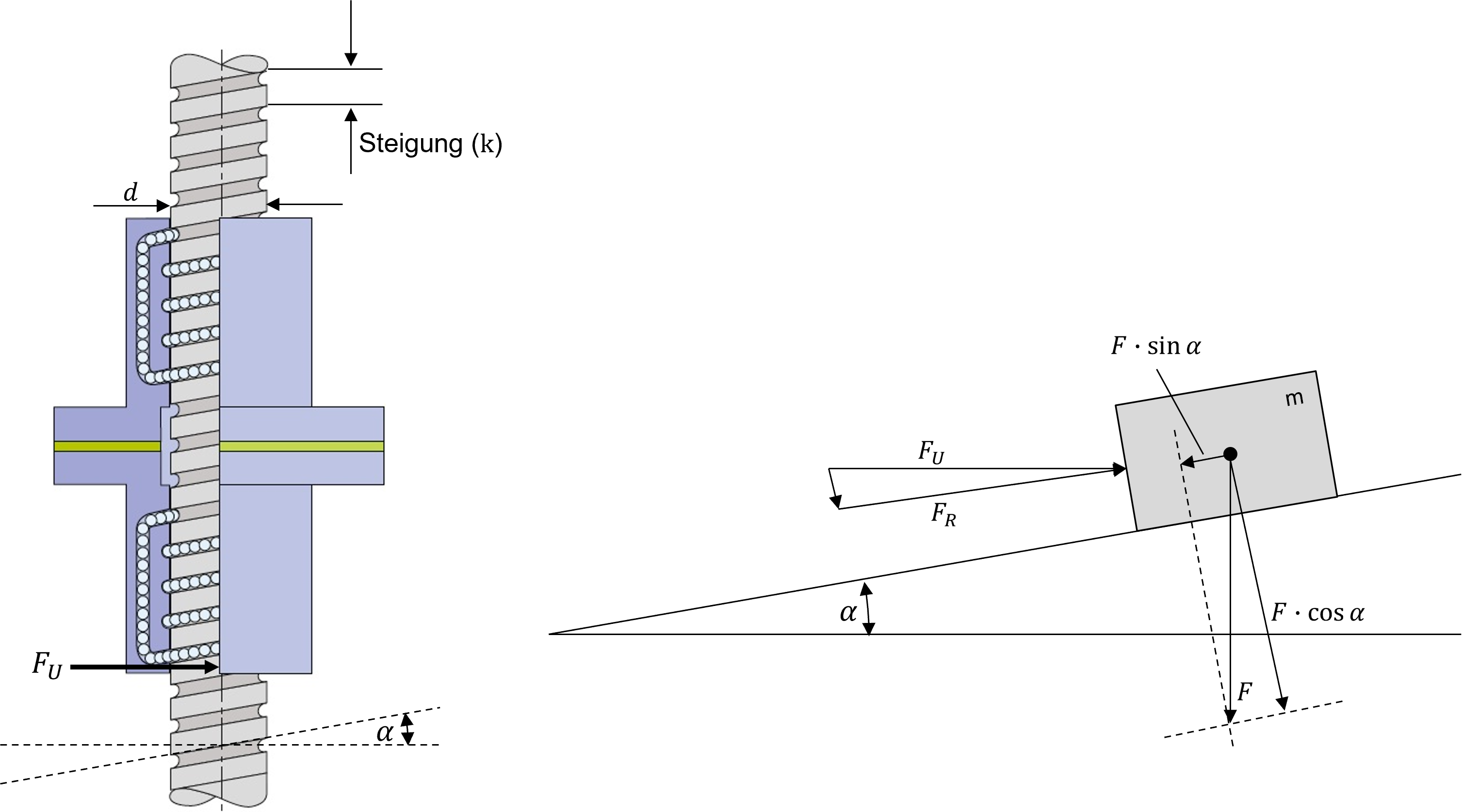
Abbildung 3.40: Kraftwirkungen an einer Gewindespindel ohne Reibung (Quelle: www.ludwigmeister.de; modifiziert)

Die Steigung \(k\) beschreibt dabei um wieviel das Gewinde über eine Umdrehung hinweg steigt und \(d\) stellt den Durchmesser der Gewindespindel dar. Für die resultierende Kraft (\(F_{R}\)), um einen Körper auf der schiefen Ebene nach oben zu bewegen, wenn dieser mit der Kraft F senkrecht nach unten wirkt, gilt [2]:

\[\begin{equation} F_{R}=F\cdot sin (\alpha) \tag{3.8} \end{equation}\]

Der Steigungswinkel der schiefen Ebene kann dabei mit Hilfe der Winkelverhältnisse am rechtwinkligen Dreieck bestimmt werden (vgl. Abb. 3.41).

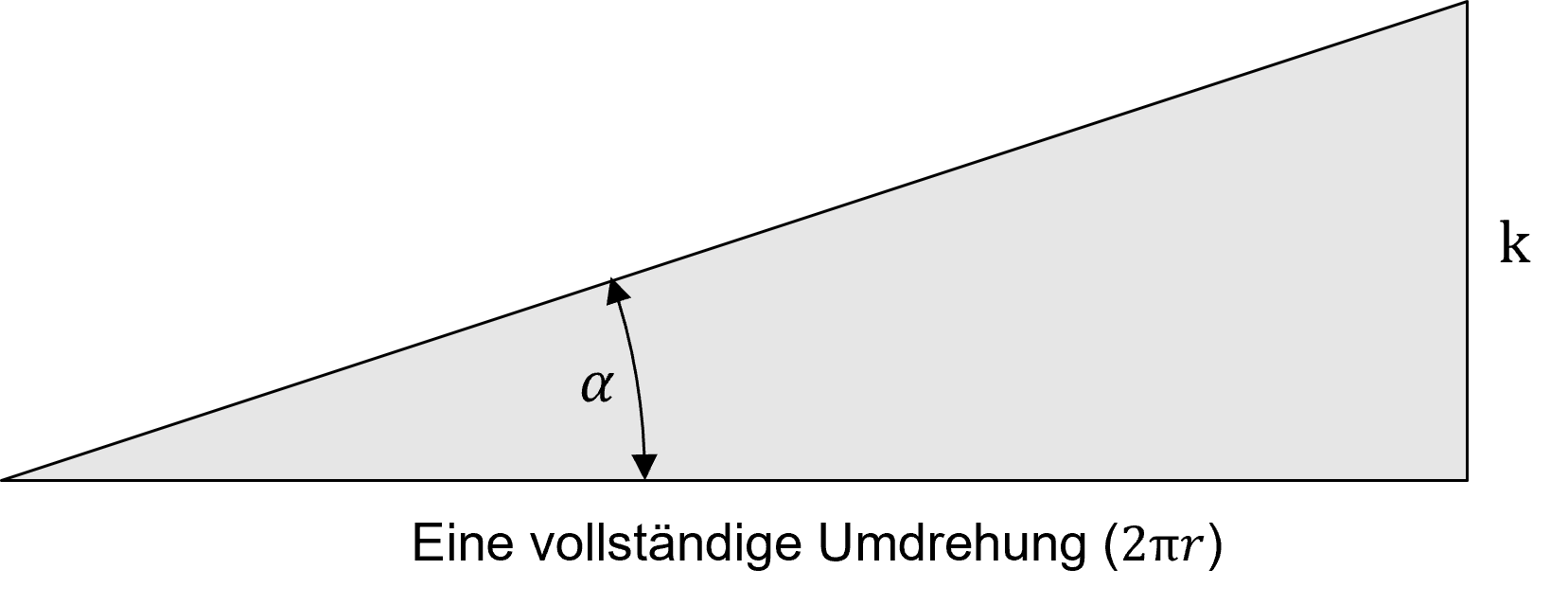
Abbildung 3.41: Winkelverhältnisse an einer schiefen Ebene

Da mit der Steigung und der auf der schiefen Ebene zurückgelegte Winkelweg bekannt sind, kommt der Tangens bei der Berechnung zur Anwendung:

\[\begin{equation} \alpha=\arctan \left(\frac{k}{2\pi\cdot r}\right) \tag{3.9} \end{equation}\]

Bei dem Paramter \(r\) handelt es sich dabei um den Radius der Gewindestange. Die Umfangskraft \(F_{U}\) (vgl. Abb. 3.40), ist die Kraft die vom Antrieb aufgebracht werden muss, da diese orthogonal zur Mittellinie der Spindel angreift. Die eigentlich zum Bewegen einer Masse \(m\) auf der schiefen Ebene resultierende Kraft \(F_{R}\) die parallel zur schiefen Ebene verläuft, ist somit kleiner als die orthogonal zur Mittellinie der Spindel angreifende Umfangskraft \(F_{U}\).

\[\begin{equation} F_{U}=\frac{F_{R}}{cos(\alpha)}=F\cdot \frac{\sin \alpha}{\cos \alpha} = F\cdot \tan \left(\alpha\right) \tag{3.10} \end{equation}\]

Setzt man die Formel zur Berechnung des Winkels \(\alpha\) (Formel (3.9)) in die Gleichung zur Berechnung der Umfangskraft ein, kann unter Berücksichtigung des Radius \(r\) der Gewindestange das entsprechende Drehmoment bestimmt werden:

\[\begin{equation} M=F\cdot r\cdot \tan \alpha = F\cdot r\cdot \tan \left(\arctan \left(\frac{k}{2\pi\cdot r}\right)\right) = F\cdot r\cdot\frac{k}{2\pi\cdot r} \tag{3.11} \end{equation}\]

Bei beiden obigen Gleichungen ((3.7) und (3.11)) zur Bestimmung des Drehmomentes gilt es zu beachten, dass dabei die Reibung nicht berücksichtigt wurde. Bei hochgenauen und hochdynamischen Antriebssystemen, wie sie häufig bei Positionierantrieben gefordert werden, wird die Reibung sehr häufig in der Antriebsdimensionierung und der Einstellung der Regelparameter berücksichtigt.

3.15.3.1 Berücksichtigung der Reibung

Gilt es die Reibung bei der Dimensionierung zu berücksichtigen, so wird die bereits erwähnte schiefe Ebene, die sich durch die Gewindesteigung ergibt, mit einem zusätzlichen Reibwert versehen (siehe Parameter \(\mu\) in Abbildung 3.42).

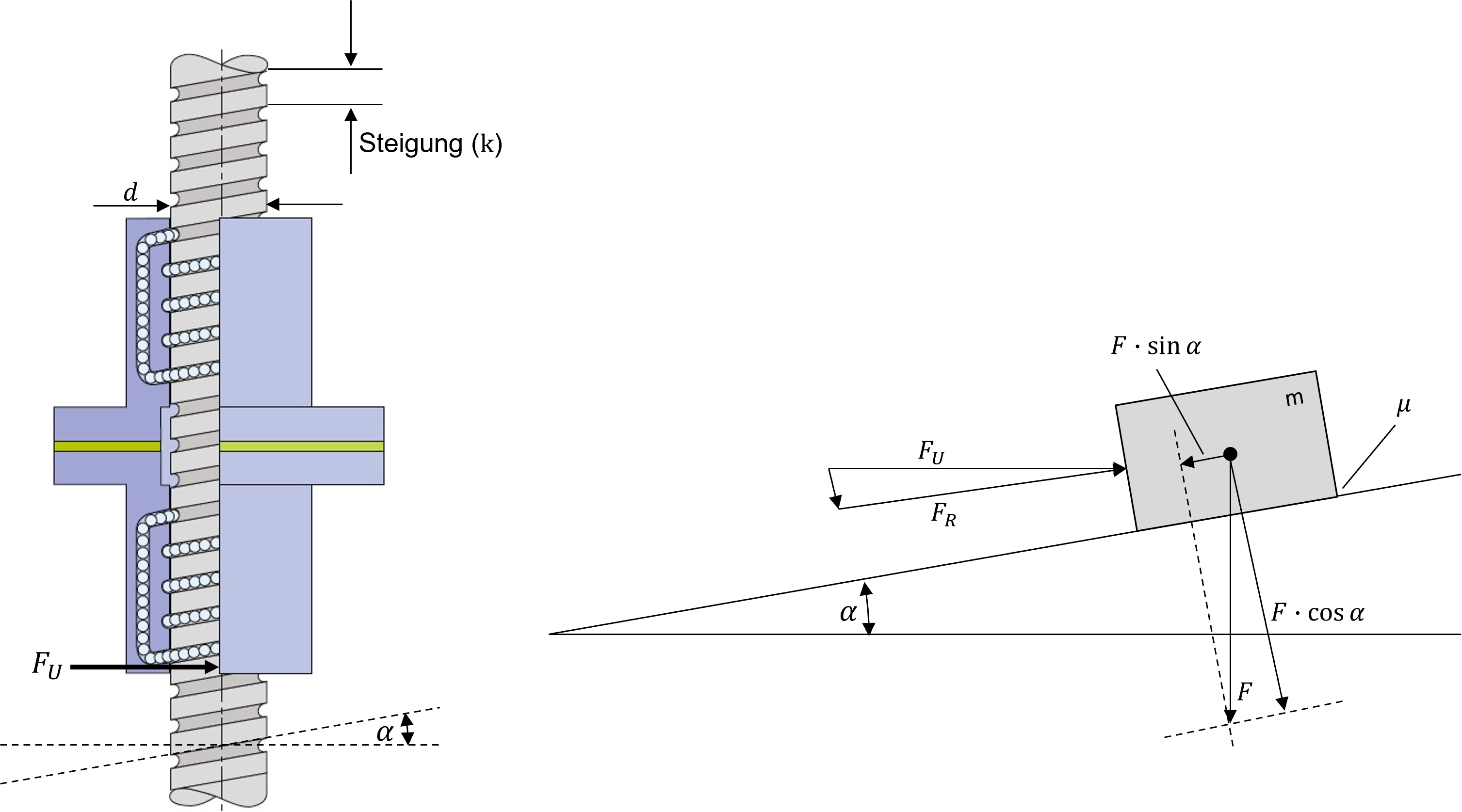
Abbildung 3.42: Kraftwirkungen an einer Gewindespindel (Quelle: www.ludwigmeister.de; modifiziert)

Die resultierende Kraft (\(F_{R}\)), um den Körper auf der schiefen Ebene nach oben zu bewegen, wird somit um eine zusätzliche, winkelabhängige Komponente erweitert [2]:

\[ F_{R}=F\cdot sin (\alpha) + F \cdot \mu \cdot cos (\alpha) \]

Der Reibwert \(\mu\) quantifiziert die Reibung zwischen Gewindebolzen und Spindelmutter. Auf diese Art und Weise wird es möglich zwischen Spindelantrieben mit Trapezgewinde und Kugelumlaufspindel zu unterscheiden. Wird auch hier der allgemeine Ansatz zur Berechnung der Umfangskraft verwendet (Teil 1 Formel (3.10)), ergibt sich für die Umfangskraft \(F_{U}\) unter Berücksichtigung der Spindelreibung:

\[ F_{U} = \frac{F_{R}}{\cos {\alpha}} = \frac{F\cdot sin (\alpha) + F \cdot \mu \cdot cos (\alpha)}{\cos \left(\alpha\right)} =F\cdot tan(\alpha) + \mu \cdot F \]

In [2] wird dabei für den Reibwert \(\mu\) ein fiktiver Reibungswinkel \(\rho\) eingeführt, der die zusätzliche Reibkraft zum Ausdruck bringt:

\[ \rho = arctan(\mu) \]

Diese Modifikation erlaubt es die Gleichung für die Umfangskraft weiter zu vereinfachen:

\[ F_{U} = F\cdot tan(\alpha \pm \rho) \]

Somit wird der eigentliche Steigungswinkel \(\alpha\) angepasst und berücksichtigt neben der Steigung auch die Reibung im Gewinde selbst. Da die Reibung beim Senken einer Last der Abwärtsbewegung hemmend entgegenwirkt, wird dies durch das negative Vorzeichen des Reibungswinkels berücksichtigt. Basierend auf der benötigten, reibungsbehafteten Umfangskraft lässt sich somit das notwendige Drehmoment bestimmen:

\[ M=F\cdot r\cdot \tan\left(\alpha \pm \rho\right) \]

3.15.3.2 Getriebebemessung

Die Auslegung des Getriebes richtet sich in starkem Masse nach der entsprechenden Applikation. Reine Positionier- bzw. Beschleunigungsantriebe beispielsweise werden lediglich dazu verwendet die beteiligten Massenträgheiten zu beschleunigen. Ein zusätzliches Last-Drehmoment tritt in diesem Fall nicht auf. Aufgrund dessen werden entsprechende Getriebe so bemessen, dass sich kürzeste Hochlaufzeiten ergeben, indem die Winkelbeschleunigung ihr Maximum erreicht.

3.15.3.2.1 Getriebebemessung für Positionierantriebe

Manche Antriebe laufen gegen ein sehr geringes, vernachlässigbares Lastmoment an. Dies sind die Beschleunigungsantriebe, wie z.B. beim Schleifstein oder einer Zentrifugen. Dort spricht man dann auch von einem Leeranlauf (\(M_{2}=0\)). Wird vereinfachend angenommen, dass keine weiteren Last-Drehmomente berücksichtigt werden, wird das Antriebsmoment dazu verwendet die beteiligten Massenträgheiten (\(J_{1}\) und \(J_{2}\)) zu beschleunigen. Um die maximale Winkelbeschleunigung bestimmen zu können, muss die Winkelbeschleunigung auf der Abtriebsseite (\(\dot{\omega}_{2}\)) bestimmt werden.

\[ M_{2} = i_{G}\cdot M_{1} \]

Dieses Drehmoment wird dazu verwendet die Gesamtträgheit zu beschleunigen.

\[ J_{Ges}\dot{\omega}_{2} = i_{G}\cdot M_{1} \]

Wird die Gesamtträgheit auf die Lastseite bezogen, gilt

\[ J_{Ges} = J_{2}+J^{'}_{1} \]

Wobei \(J^{'}_{1}\) das auf die Lastseite umgerechnete motorseitige Trägheitsmoment darstellt.

\[ J^{'}_{1} = i_{G}^{2}\cdot J_{1} \]

Damit ergibt sich folgende Gleichung:

\[ \bigl(i_{G}^{2}\cdot J_{1}+J_{2}\bigr) \dot{\omega}_{2}=i_{G}\cdot M_{1} \]

Die lastseitige Winkelbeschleunigung ergibt sich somit folgendermassen:

\[ \alpha_{2}=\dot{\omega}_{2}=\frac{i_{G}}{i_{G}^{2}\cdot J_{1}+J_{2}}M_{1} \]

Einen beispielhaften Verlauf der Winkelbeschleunigung in Abhängigkeit von der Getriebeübersetzung liefert Abbildung 3.43.

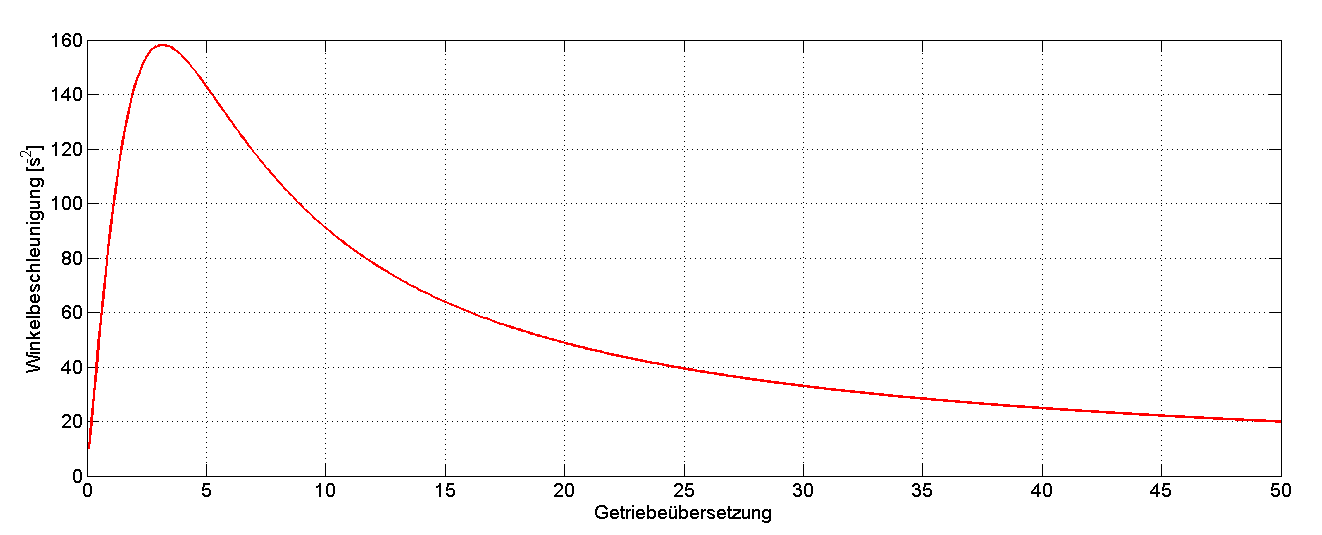
Abbildung 3.43: Typischer Verlauf der Winkelbeschleunigung

Die maximale Winkelbeschleunigung ergibt sich somit aus der Extremwertaufgabe

\[ 0=\frac{d\alpha_{2}}{i_{G}}=\frac{i_{G}^{2}J_{1}+J_{2}-2i_{G}^{2}J_{1}}{\bigl(i_{G}^{2}J_{1}+J_{2}\bigr)^{2}} \]

die folgendes Ergebnis liefert:

\[ i_{G}^{2}J_{1}=J_{2} \]

Geringste Hochlaufzeiten bei Beschleunigungsantrieben sind somit zu erwarten, wenn das Übersetzungsverhältnis \(i_{G}\) entsprechend der folgenden Formel gewählt wird:

\[ i_{G,opt}=\sqrt{\frac{J_{2}}{J_{1}}} \]

Die auf eine Seite umgerechneten Drehträgheiten sind in diesem speziellen Fall gleich gross.

\[ J^{'}_{1}=J_{2} \]

Aufrgund dessen lässt sich bei gegebenem Antriebsdrehmoment auch die maximale Lastbeschleunigung bestimmen.

\[ \alpha_{2,opt}=\frac{M_{1}}{2\sqrt{J_{1}J_{2}}} \]

3.15.3.3 Getriebebemessung für Positionierantriebe mit zusätzlichem Lastmoment

Für den Fall das das Lastmoment nicht vernachlässigt werden kann, ergibt sich durch ähnliche Überlegungen folgende Gleichung für die dynamische Grundgleichung auf der Lastseite.

\[ \bigl(i_{G}^{2}\cdot J_{1}+J_{2}\bigr) \dot{\omega}_{2}=i_{G}\cdot M_{1}-M_{2} \]

Die Winkelbeschleunigung ergibt sich somit zu:

\[ \alpha_{2}=\dot{\omega}_{2}=\frac{i_{G}M_{1}-M_{2}}{i_{G}^{2}\cdot J_{1}+J_{2}} \]

Auch in diesem Fall ermöglicht das Lösen der entsprechenden Extremwertaufgabe die Bestimmung der grösstmöglichen Lastbeschleunigung.

\[ 0=\frac{d\alpha_{2}}{i_{G}}=\frac{M_{1}\bigl(i^{2}_{G}J_{1}+J_{2}\bigr) - (i_{G}M_{1}-M_{2})2i_{G}J_{1}}{\bigl(i_{G}^{2}J_{1}+J_{2}\bigr)^{2}} \]

\[ 0=i^{2}_{G}J_{1}+J_{2}-\bigl(i_{G}-\frac{M_{2}}{M_{1}}\bigr)2i_{G}J_{1} \]

\[ 0=i^{2}_{G}-2\frac{M_{2}}{M_{1}}i_{G}-\frac{J_{2}}{J_{1}} \]

Bei dieser Gleichung handelt es sich um eine quadratische Gleichung, welche zwei Lösungen besitzt. Für die Bemessung der Getriebeübersetzung ist allerdings nur die positive Lösung relevant.

\[ i_{G,opt}=\frac{M_{2}}{M_{1}}+\sqrt{\bigl(\frac{M_{2}}{M_{1}}\bigr)^{2}+\frac{J_{2}}{J_{1}}} \]

Abbildung 3.44 zeigt den qualitativen Verlauf der Winkelbeschleunigung in Abhängigkeit der Getriebeübersetzung für unterschiedliche zusätzliche Lastmomente.

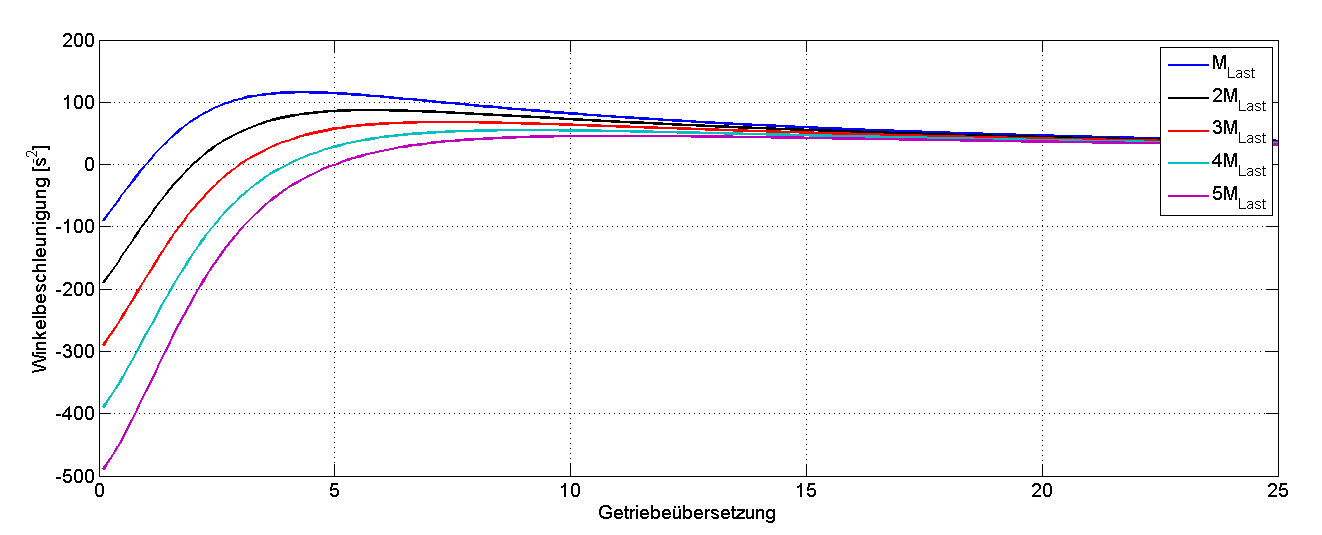
Abbildung 3.44: Typischer Verlauf der Winkelbeschleunigung für unterschiedliche zusätzliche Lastmomente

Das Diagramm zeigt, dass sich die optimale Getriebeübersetzung bei zusätzlichem Lastmoment im Vergleich zur unbelasteten Beschleunigung hin zu grösseren Werten verschiebt. Das Minimum der entsprechenden Kurven verläuft allerdings sehr flach, so dass bei kleinen Abweichungen keine grossen Fehler gemacht werden.

3.16 Wachstumsgesetze

Maschinen und mechanische Konstruktionen fallen allgemein sehr verschieden aus. Für den Entwickler ist es jedoch interessant zu wissen, wie sich bei unveränderten äusseren Daten die inneren Parameter einer Maschine oder Konstruktion mit der Baugrösse ändern. Untersucht man so, unter der Voraussetzung konstanter elektromagnetischer oder mechanischer Beanspruchungen, die Abhängigkeit der Parameter von wachsenden Abmessungen \(L\), so erhält man die sogenannten Wachstumsgesetze. Unter der Annahme konstanter Induktion \(B\) und konstanter Stromdichte \(S\) ergeben sich entsprechende Abhängigkeiten für die Dimensionen der Maschine. Eine Auswahl entsprechender Parameter sind in der folgenden Tabelle dargestellt.

Man erkennt dort z.B., dass der Wirkungsgrad \(\eta\) mit der Maschinengrösse wächst ebenso wie das Massenträgheitsmoment \(J\) und die Leerhochlaufzeit \(t_{Ho}\). Da die Verluste stärker steigen als die kühlende Oberfläche, sieht man ausserdem, dass grössere Maschinen stärker gekühlt werden müssen als kleinere Maschinen.

3.17 DIN-Normen und DIN VDE-Vorschriften

• DIN VDE 0530 Teil 1 bis 18, bzw. entsprechende Teile der DIN EN 60 034 oder IEC 34
• DIN ISO 1940-1 - Anforderungen an die Auswuchtgüte starrer Rotoren; Bestimmung der zulässigen Restunwucht
• DIN ISO 7919-… - Mechanische Schwingungen von Maschinen mit Ausnahme von Kolbenmaschinen - Messung und Bewertung von Wellenschwingungen
• DIN ISO 8821-… - Mechanische Schwingungen Vereinbarung über die Passfeder - Art beim Auswuchten von Wellen und Verbundteilen
• DIN ISO 10816-…- Mechanische Schwingungen - Bewertung von Schwingungen von Maschinen durch Messungen an nicht-rotierenden Teilen

Für explosionsgeschützte (ex-geschützte) Bereiche gelten ausserdem folgende gesonderte Normen:

• DIN VDE 0165 - Errichten elektrischer Anlagen in explosionsgefährdeten Bereichen
• DIN VDE 0166 - Errichten elektrischer Anlagen in durch explosionsgefährliche Stoffe gefährdeten Bereiche
• DIN EN 50014 - Elektrische Betriebsmittel für explosionsgefährdete Bereiche; Allgemeine Bestimmungen
• DIN EN 50016 - Elektrische Betriebsmittel für explosionsgefährdete Bereiche; Überdruck-Kapselung
• DIN EN 50019 - Elektrische Betriebsmittel für explosionsgefährdete Bereiche; Erhöhte Sicherheit

References

2.

Garbrecht FW (2019) Das 1x1 der Antriebsauslegung, 3rd Aufl. VDE Verlag GmbH, Berlin, Deutschland