Kapitel 7 Synchronmaschine

Drehstromsynchronmaschinen gehören zur Familie der Drehfeldmaschinen. In ihrer Form als Synchrongenerator stellen sie den wichtigsten Erzeuger elektrischer Energie dar. Mit Leistungen bis zu 1.7GVA werden sie in den Kraftwerken der Energieversorgungsunternehmen verwendet. Auch als Motoren finden sie in vielen Anwendungen und einem breiten Leistungsbereich (z.B. Kleinstmotoren im Milliwattbereich in der Uhrenindustrie) Verwendung. Neben einem tendenziell guten Wirkungsgrad besitzen den Vorteil, dass ihr Leistungsfaktor variabel einstellbar ist, wodurch sie beispielsweise den Blindstromanteil der grösstenteils induktiv belasteten Netze kompensieren können. Somit werden sie auch häufig in grossen Industrieanlagen als leerlaufende Maschine als Phasenschieber betrieben. Immer häufiger sind Synchronmaschinen heute auch als elektronisch kommutierte Maschinen, auch als Bürstenloser Gleichstrommotor (DC-brushless) bezeichnet, in vielen Bereichen anzutreffen. Die Bezeichnung als bürstenlose Gleichstrommaschine ist dem nahezu identischen Betriebsverhalten mit dem der Gleichstrommaschine geschuldet.

7.1 Aufbau und Wirkungsweise

7.1.1 Unterteilung nach Bauart

Eine grundsätzliche Unterteilung anhand der Bauart kann in sog. Aussenpol- bzw. Innenpolmaschine erfolgen. Die Aussenpolmaschine entspricht im Statoraufbau dem der Gleichstrommaschine. In diesem Fall sind die Gleichstrom führenden Magnetpole im Stator angeordnet und der Läufer trägt die eigentliche Drehstromwicklung. Über Schleifringe wird bei diesem Maschinentyp der Läuferwicklung der Strom zugeführt. Da die Drehstromleistung im Vergleich zur Erregerwicklung im Normalfall deutlich grösser ausfällt, führt dies inbesondere bei grossen Leistungen zu erheblichen Schwierigkeiten. Aufgrund dessen findet diese Bauart nur bei besonderen Anwendungen Bedeutung.

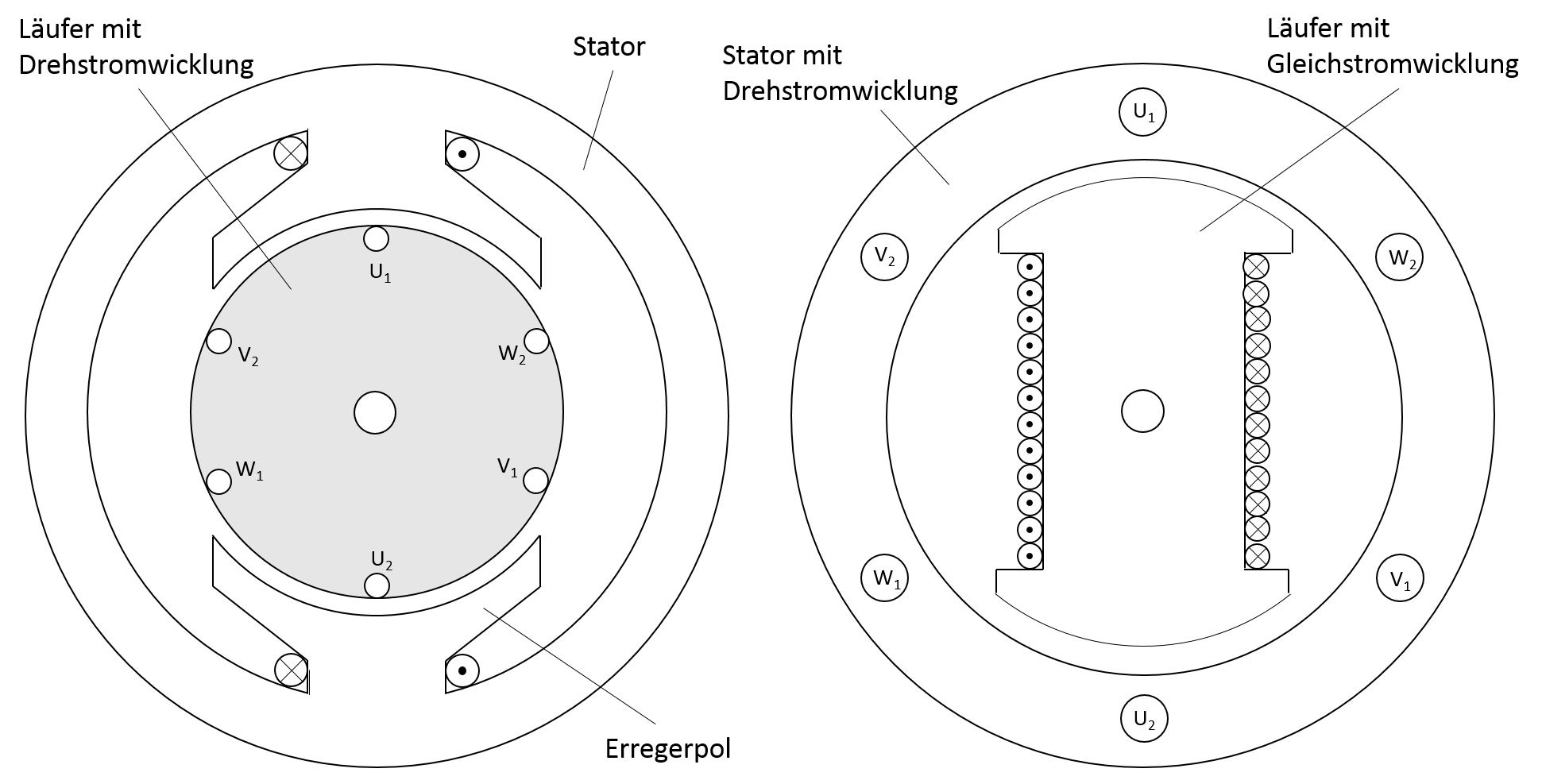
Abbildung 7.1: Synchronmaschine als Aussenpolmaschine (links) und Innenpolmaschine (rechts)

Insbesondere Maschinen grosser Leistung werden stets als Innenpolmaschine ausgeführt. In diesem Fall befindet sich die gleichstromführende Erregerwicklung auf dem Läufer. Der vergleichsweise geringe Erregerstrom wird ebenfalls über Schleifringe zugeführt. Die Drehstromwicklung hingegen ist auf dem Stator angeordnet. Bei Synchronmaschinen kleinerer Leistung, insbesondere bei Servoanwendungen, kann der Läufer (Polrad) auch mit Permanentmagneten ausgetattet werden, wodurch die Stromzufuhr zum Läufer gänzlich entfällt und der Wirkungsgrad weiter gesteigert werden kann. Der Leistungsbereich dieser Bauart wird kontinuierlich erweitert, wodurch bereits erste Motoren im Megawattbereich in Betrieb sind (Stand 2018). Nachteilig äussert sich bei diesen Maschinen ihre Temperatur- und Vibrationsanfälligkeit. In speziellen Anwendungen kommen auch bürstenlose Synchronmaschinen zum Einsatz, bei denen der Läufer mit einem rotierenden Diodengleichrichter ausgestattet ist und die Stromzufuhr über einen sog. rotierenden Transformator erfolgt.

7.1.2 Aufbau der Innenpolmaschine

Im Normalfall besteht der Stator der Innenpolmaschine aus geschichteten Dynamoblechen, die gleichmässig über den Umfang verteilte Nuten besitzen. In den Nuten befindet sich die dreisträngige Statorwicklung. Somit entspricht der Aufbau des Stators und der Statorwicklung dem der Asynchronmaschine. In Abhängigkeit vom Aufbau des Läufers der fremderregten Synchronmaschine unterscheidet man wiederum in:

• Vollpolmaschinen und
• Schenkelpolmaschinen

Im Gegensatz zur Asynchronmaschine, die als isotroper Maschinentyp gilt, weisen sogenannte anisotrope Maschinen (z.B. Schenkelpol-Synchronmaschine) unterschiedliche magnetische Eigenschaften längs und quer zur Rotorachse auf, wodurch sich diese Maschinen durch unterschiedliche Längs- \(X_{d}\) und Querreaktanzen \(X_{q}\) in Ihren Ersatzschaltbildern auszeichnen. Aufgrund der Abhängigkeit der Drehzahl von der Netzfrequenz und der Polpaarzahl der Maschine, werden Schenkelpolmaschinen, die tendenziell hohe Polpaarzahlen (4..60..) aufweisen, für niedrige Drehzahlen verwendet. Vollpolmaschinen hingegen besitzen eher kleinere Polpaarzahlen und weisen hohe Drehzahlen auf.

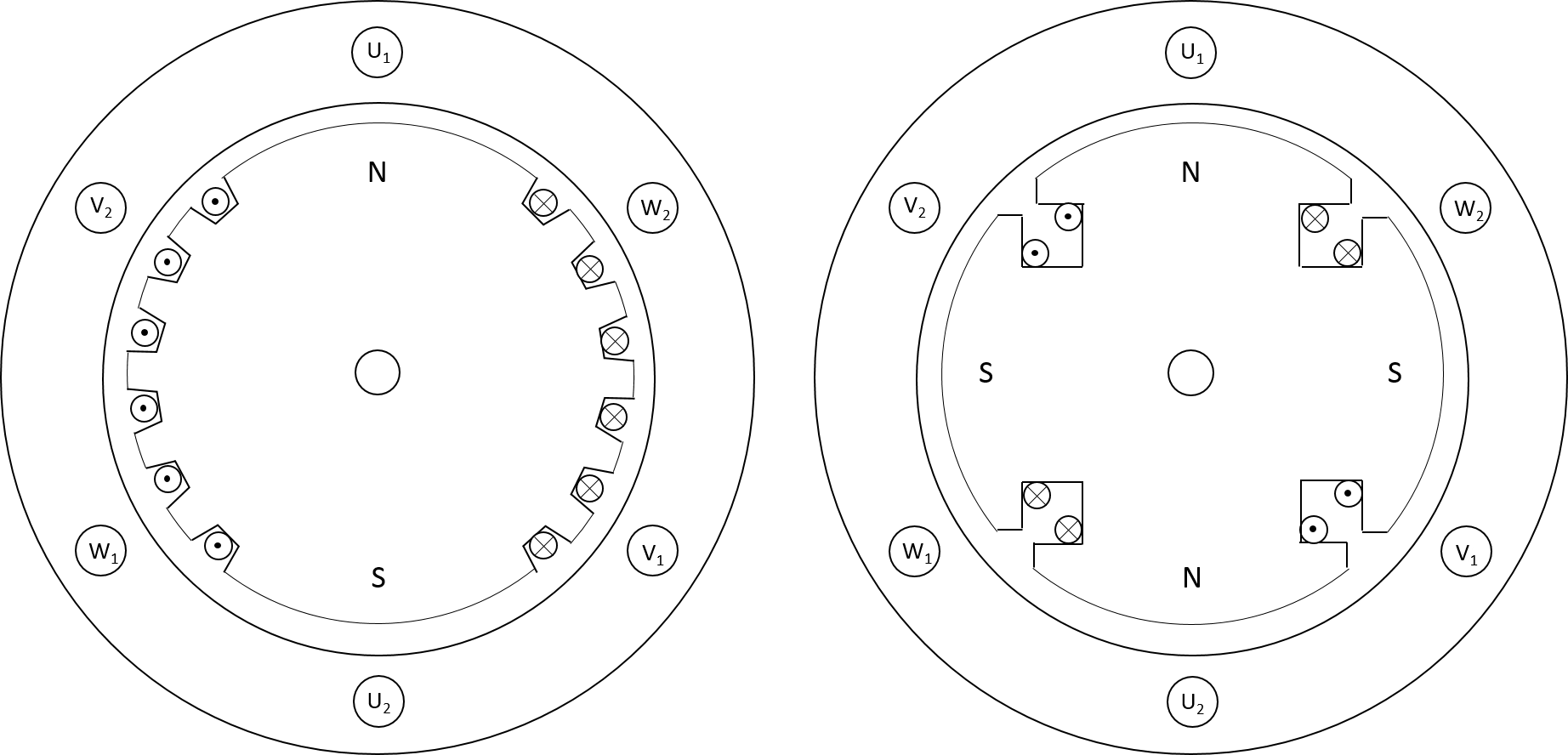
Abbildung 7.2: Querschnitt der Synchronmaschine (Vollpol = links, Schenkelpol = rechts)

Die Schenkelpolmaschine weist ausgeprägte Magentpole auf dem Läufer auf, die gleichmässig über den Umfang verteilt angeordnet sind. Die einzelnen Pole besitzen einen grossen Platzbedarf, wodurch der Durchmesser einer solchen Maschine recht gross ausfällt und sich somit bei grossen Drehzahlen grosse Fliehkräfte ergeben. Bei der Vollpolmaschine wird der Läufer häufig aus hochfestem, massiven Chrom-Nickel-Stahl gebaut, da eine Blechung aufgrund der Gleichstromzufuhr unnötig wird. Die Erregerwicklung wird in diesem Fall in den ausgefrästen Nuten untergebracht. Diese Bauart weist weniger Platzbedarf auf, wodurch der Aussendurchmesser geringer und die Baulänge häufig grösser ausfällt. Im Falle von Reluktanz- bzw. Permanentmagnet-Synchronmaschinen ist der Rotor von aussen nicht über Schleifringe zugänglich, wodurch im Rotor keine Ströme fliessen (Wirbelströme vernachlässigt). Aufgrund dessen weisen diese Maschinentypen geringere Kupferverluste auf und besitzen somit eine, der Asynchronmaschine gegenüber, höhere Effizienz auf. Ein Beispiel für eine Reluktanz-Synchronmaschine ist in Abbildung 7.3 dargestellt.

Abbildung 7.3: Geöffnete Reluktanz-Synchronmaschine (Bildquelle: ABB)

7.1.3 Wirkungsweise der Synchronmaschine

Wie im Kapitel 6 erläutert, erzeugt eine Drehstromwicklung ein Drehfeld, welches in Abhängigkeit von der Frequenz des speisenden Netzes sowie der Polpaarzahl den Luftspalt umläuft.

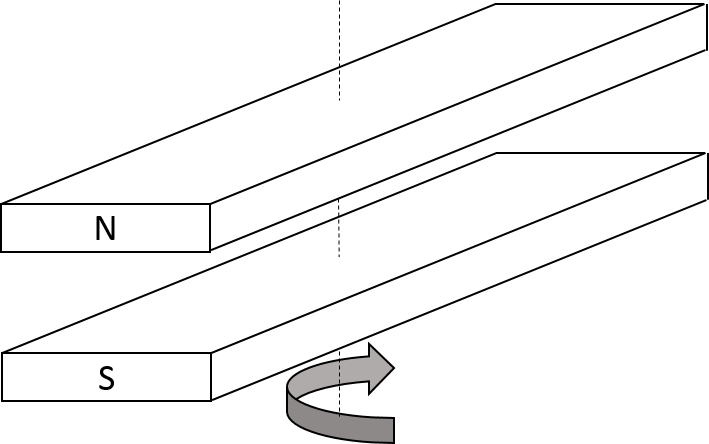
Abbildung 7.4: Vereinfachtes Wirkprinzip der Synchronmaschine

Ein im Luftspalt untergebrachter Stabmagnet (wie in Abbildung 7.4 dargestellt) würde in diesem Fall einen entsprechende Kraftwirkung erfahren. Rotiert der Stabmagnet mit der erforderlichen Drehzahl des Magnetfeldes, wird dieser mitgenommen und rotiert mit der identischen (synchronen) Drehzahl, wobei immer der Süpol des Drehfeldes einem Nordpol des Läufers gegenübersteht. Im Falle reiner Reluktanz-Synchronmaschinen ohne jegliche Permanentmagnete entsteht ein sogennantes Reluktanzmoment, welches vom anisotropen magnetischen Aufbau des Rotors, der den magnetischen Fluss entlang definierter Pfade führt, hervorgerufen wird. In vielen Fällen werden Permanentmagnet-synchronmaschinen gleichzeitig mit einem solchen Rotoraufbau, mit definierten Flusspfaden, kombiniert, wodurch sich Maschinen mit unterschiedlichen Anisotropieverhältnissen \(L_{s}^{d}/L_{s}^{q} \neq 1\) ergeben. Der fliessende Übergang von reinen Permanentmagnet-Synchronmaschinen hin zu reinen Reluktanz-Synchronmaschinen ist in Abbildung 7.5 dargestellt.

Abbildung 7.5: Rotorausführungen für SM mit steigender Anisotropie (Bild aus [5])

Synchronmaschinen, deren Rotor einen magnetischen Fluss hervorruft (z.B. fremderregte- bzw. Permanentmagnet-Synchronmaschinen) können gleichzeitig auch als Generator verwendet werden, da der mechanisch angetriebene Läufer ein rotierendes Magnetfeld erzeugt, welches die Statorwicklungen durchsetzt und somit in diesen zeitlich verzögerte Spannungen gleicher Amplitude und Frequenz erzeugt. Synchronmaschinen können nicht ohne weiteres am Drehstromnetzt betrieben werden, da beim Anlaufen der Maschine am Netz, aufgrund der Trägheit, kein ausreichend grosses und dauerhaft wirksames Beschleunigungsmoment hervorgerufen werden kann.

7.2 Systemtheoretische Beschreibung

Ein Modell zur Beschreibung isotroper Drehfeldmaschinen (sog. Grundwellenmodell) wurde in Kapitel 6.3 hergeleitet. Dieses Modell kann somit für Vollpol-Synchronmaschinen verwendet werden. Für Synchronmaschinen mit ausgeprägten Polen (Schenkelpolmaschinen), Reluktanzmaschinen oder Permanentmagneterregte Synchronmaschinen mit vergrabenen Magneten ist diese Modell jedoch nicht ohne weiteres anwendbar.

7.2.1 Einfluss der Anisotropie

Aufgrund des Aufbaus des Rotors eine anisotropen Drehfeldmaschine unterscheiden sich die Rotorinduktivitäten in a- und in q-Richtung, da die magnetischen Widerstände, aufgrund des unterschiedlichen Luftspaltes, unterschiedlich gross ausfallen. Dieser Zusammenhang wird in Abbildung 7.6 verdeutlicht.

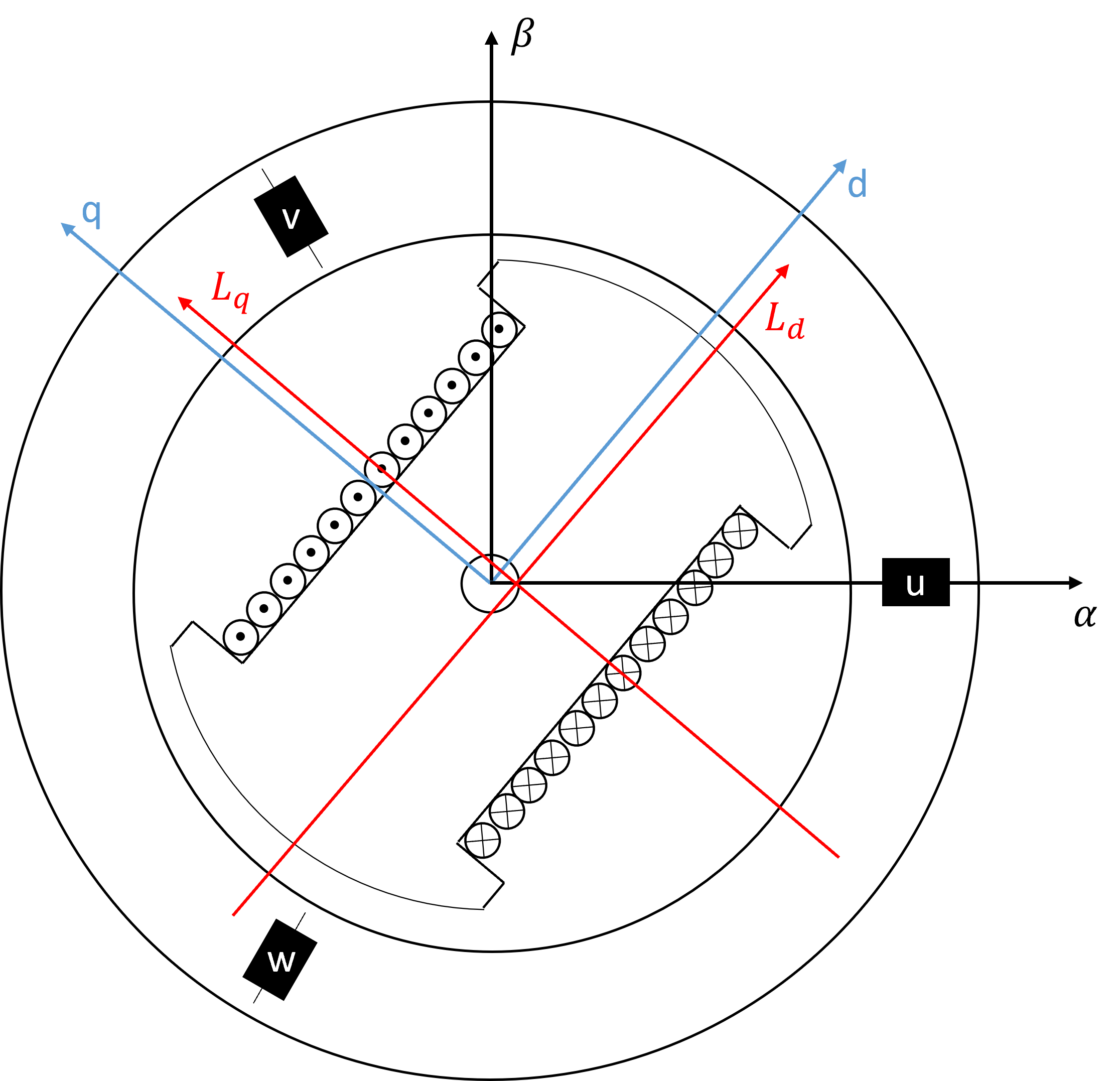
Abbildung 7.6: Unterschiedliche Rotorinduktivitäten einer anisotropen Synchronmaschine im rotorfesten k-KOS

Dieser Effekt führt dazu, dass die magnetische Kopplung in d- bzw- q-Richtung unterschiedlich stark ausfällt, weshalb dieser Zusammenhang bei der Bestimmung der Stator- bzw- Rotorflussraumzeiger berücksichtigt werden muss.

\[ \begin{matrix} \underline{\Psi}_{s}^{k} = \left(\begin{matrix} L_{s}^{d} & 0 \\ 0 & L_{s}^{q} \end{matrix}\right)\underline{i}_{s}^{k} + \left(\begin{matrix} L_{sr}^{d} & 0 \\ 0 & L_{sr}^{q} \end{matrix}\right)\underline{i}_{r}^{k} \\ \underline{\Psi}_{r}^{k} = \left(\begin{matrix} L_{r}^{d} & 0 \\ 0 & L_{r}^{q} \end{matrix}\right)\underline{i}_{r}^{k} + \left(\begin{matrix} L_{rs}^{d} & 0 \\ 0 & L_{rs}^{q} \end{matrix}\right)\underline{i}_{s}^{k} \end{matrix} \]

Der Grund dafür, dass es sich bei den Induktivitätsmatrizen um Diagonalmatrizen (nur Diagonalelemente unterscheiden sich von Null) liegt darin, dass aufgrund der Orthogonalität ein d-Strom keinen Einfluss auf den q-Fluss hat und umgekehrt.

7.2.2 Feldorientierte Regelung einer anisotropen PMSM

Das Vorgehen bei der Feldorientierten Regelung anisotroper Maschinen soll am Beispiel einer anisotropen Permanentmagnet-Synchronmaschine ausgeführt werden, deren Induktivitäten sich in d- und in q-Richtung unterscheiden. Die Statorspannungsgleichung, in rotorflussorienten k-Koordinaten, einer solchen Maschine lautet:

\[ \underline{u}_{s}^{k} = R_{s}\underline{i}_{s}^{k}+\omega_{k}\tilde J\underline{\Psi}_{s}^{k}+\frac{d\underline{\Psi}_{s}^{k}}{dt}, \quad \underline{\Psi}_{s}^{k}(t=0s)=\underline{\Psi}_{PM}^{k} \]

Eine Differentialgleichung die den Rotorkreis beschreibt entfällt, da es rotorseitig keinen elektrischen Kreis gibt. Bei dem verketteten Fluss \(\underline{\Psi}_{PM}^{k}\) handelt es sich um den Statorfluss, der in der unbestromten Maschine messbar ist. Der Statorfluss in rotorfesten k-Koordinaten lautet:

\[ \underline{\Psi}_{s}^{k} = \underbrace{\left(\begin{matrix}L_{s}^{d} & 0 \\ 0 & L_{s}^{q} \end{matrix}\right)}_{\tilde{L}_{s}^{k}}\underline{i}_{s}^{k} + \left(\begin{matrix} \underline{\Psi}_{PM}^{d} \\ 0\end{matrix}\right) \]

Da Sättigungserscheinungen des magnetischen Kreises ausgeschlossen wurden, kann der verkettete Fluss mit Hilfe der Statorinduktivität und des Statorstromraumzeigers ausgedrückt werden und ermöglich somit die zeitliche Ableitung der Statorflussverkettung umzuschreiben:

\[ \frac{d\underline{\Psi}_{s}^{k}}{dt}=\tilde{L}_{s}^{k}\frac{d\underline{i}_{s}^{k}}{dt} \ \]

Der Term \(\omega_{k}\tilde J\underline{\Psi}_{s}^{k}\) in der Statorspannungsgleichung kann ungeformt werden

\[\begin{equation} \begin{matrix} \tilde J\underline{\Psi}_{s}^{k}= \left(\begin{matrix}0 & -1\\1&0 \end{matrix}\right)\left[\left(\begin{matrix}L_{s}^{d} & 0 \\ 0 & L_{s}^{q} \end{matrix}\right)\underline{i}_{s}^{k}+\left(\begin{matrix} \underline{\Psi}_{PM}^{d} \\ 0\end{matrix}\right) \right] \\ =\left(\begin{matrix}0 & -1\\1&0 \end{matrix}\right)\left(\begin{matrix}L_{s}^{d}i_{s}^{d} +\Psi_{PM}^{d}\\ L_{s}^{q}i_{s}^{q} \end{matrix}\right)\\ =\left(\begin{matrix}-L_{s}^{q}i_{s}^{q}\\ L_{s}^{d}i_{s}^{d} +\Psi_{PM}^{d} \end{matrix}\right) \end{matrix} \tag{7.1} \end{equation}\]

und somit kann die Statorspannungsgleichung umgeschrieben werden.

\[ \begin{matrix} \left(\begin{matrix}u_{s}^{d}\\ u_{s}^{q} \end{matrix}\right) = R_{s}\left(\begin{matrix}i_{s}^{d}\\i_{s}^{q} \end{matrix}\right) + \omega_{k}\left(\begin{matrix}-L_{s}^{q}i_{s}^{q}\\ L_{s}^{d}i_{s}^{d} +\Psi_{PM}^{d} \end{matrix}\right)+\tilde{L}_{s}^{k}\frac{d}{dt} \left(\begin{matrix}i_{s}^{d}\\i_{s}^{q}\end{matrix}\right) \\ = \left(\begin{matrix}R_{s}i_{s}^{d}-\omega_{k}L_{s}^{q}i_{s}^{q}+L_{s}^{d}\frac{di_{s}^{d}}{dt} \\ R_{s}i_{s}^{q} + \omega_{k}L_{s}^{d}i_{s}^{d} +\omega_{k}\Psi_{PM}^{d} + L_{s}^{q}\frac{di_{s}^{q}}{dt}\end{matrix}\right) \end{matrix} \]

Wird diese Gleichung nach den zeitlichen Ableitungen der zwei Stromkomponenten umgestellt erhält man die Statorstromdynamiken.

\[ \frac{d}{dt} \left(\begin{matrix}i_{s}^{d}\\ i_{s}^{q} \end{matrix}\right) = \left(\begin{matrix} \frac{1}{L_{s}^{d}}\left(u_{s}^{d}-R_{S}i_{s}^{d}+\underbrace{\omega_{k}L_{s}^{q}i_{s}^{q}}_{Störterm} \right) \\ \frac{1}{L_{s}^{q}}\left(u_{s}^{q}-R_{S}i_{s}^{q}-\underbrace{\omega_{k}L_{s}^{d}i_{s}^{d} -\omega_{k}\Psi_{PM}^{d}}_{Störterm} \right) \end{matrix}\right) \]

Die Störterme repräsentieren den Einfluss der drehzahlabhängigen induzierten Spannung. Wie schon bei der Asynchronmaschine können diese Terme durch eine Störgrössenaufschaltung kompensiert werden und können somit für die Reglerauslegung vernachlässigt werden.

7.2.3 Statorstromregelung

Geht man davon aus, dass die Störterme der Statorstromdynamiken ideal kopmensiert werden, lassen sich aus den beiden Gleichungen, durch Laplacetransformation, die Übertragungsfunktionen des Statorkreises in permanentmagnetflussorientierten Koordinaten herleiten.

\[ \begin{matrix} \frac{di_{s}^{d}(t)}{dt}=\frac{1}{L_{s}^{d}}\left(u_{s}^{d}(t)-R_{s}i_{s}^{d}(t)\right) \Rightarrow \frac{i_{s}^{d}(s)}{u_{s}^{d}(s)}=\frac{\frac{1}{R_{s}}}{1+s\frac{L_{s}^{d}}{R_{s}}} \\ \frac{di_{s}^{q}(t)}{dt}=\frac{1}{L_{s}^{q}}\left(u_{s}^{q}(t)-R_{s}i_{s}^{q}(t)\right) \Rightarrow \frac{i_{s}^{q}(s)}{u_{s}^{q}(s)}=\frac{\frac{1}{R_{s}}}{1+s\frac{L_{s}^{q}}{R_{s}}} \end{matrix} \]

Wie bereits im Kapitel 10.1 dargelegt, gilt es das Verhalten (PT1-Glied mit der Zeitkonstante \(T_{SR}\)) des Stromrichters bei der Reglerauslegung zu berücksichtigen. Wird Führungsübertragungsfunktion des Stromrichters

\[ G_{SR}(s) = \frac{u_{s}(s)}{u_{s,ref}(s)} = \frac{1}{1+sT_{SR}} \]

berücksichtigt, können die Streckenübertragungsfunktionen des Statorstromes in rotorflussorientierten Koordinaten bestimmt werden.

\[ \begin{matrix} G_{s,i_{s}^{d}}(s) = \frac{i_{s}^{d}(s)}{u_{s,ref}^{d}(s)} = \frac{1}{1+sT_{SR}}\cdot \frac{\frac{1}{R_{s}}}{1+s\frac{L_{s}^{d}}{R_{s}}} \\ G_{s,i_{s}^{d}}(s) = \frac{i_{s}^{q}(s)}{u_{s,ref}^{q}(s)} = \frac{1}{1+sT_{SR}}\cdot \frac{\frac{1}{R_{s}}}{1+s\frac{L_{s}^{q}}{R_{s}}} \end{matrix} \]

Um ein gutes Führungsverhalten zu erreichen, werden die Statorstromregler nach dem Betragsoptimum ausgelegt. Die obigen Herleitungen machen deutlich, dass sich die Reglerparameter bei einer anisotropen Maschine \((L_{s}^{d}\neq L_{s}^{q})\) unterscheiden. Desweiteren gilt es zu berücksichtigen, dass bei Frequenzumrichtern Stellgrössenbeschränkungen aufgrund der begrenzten Zwischenkreisspannung existieren. Aufrgund dessen sollten die PI-Statorstromregler mit einem entsprechenden Anti-Windup umgesetzt werden.

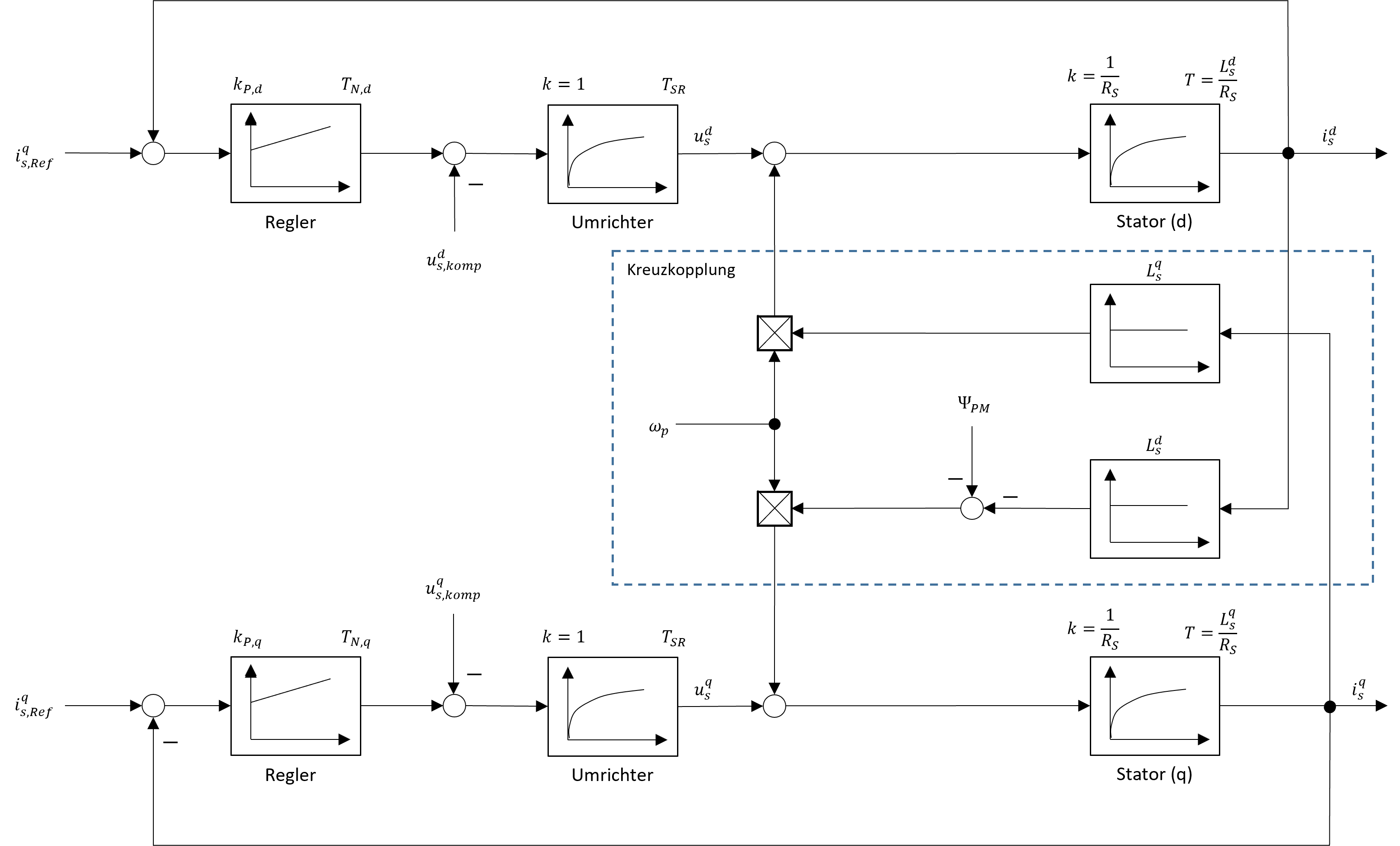
Abbildung 7.7: Stromregelkreise der anisotropen PMSM bei Permanentmagnetflussorientierung unter Berücksichtigung der Kreuzkopplungen

7.2.4 Drehzahlregelung

Für die Auslegung des Drehzahlreglers ist es zulässig die beiden unterlagerten Stromregelkreise (Führungsübertragungsfunktionen) als PT1-Glieder mit identischen Zeitkonstanten zu vereinfachen.

\[ G_{W,i_{s}^{d}}(s)=\frac{i_{s}^{d}}{i_{s,Ref}^{d}}\approx \frac{1}{1+sT_{T_{ers,i_{s}^{d}}}}= \frac{1}{1+sT_{T_{ers,i_{s}^{q}}}} \approx \frac{i_{s}^{q}}{i_{s,Ref}^{q}} = G_{W,i_{s}^{q}}(s) \]

Wie in Kapitel @ref{symmetrisches-optimum} beschrieben, kann diese Ersatzzeitkonstante mit

\[ T_{ers,i_{s}^{d}}=T_{ers,i_{s}^{q}}=2T_{SR} \]

approximiert werden. Unter dieser Voraussetzung kann der überlagerte Drehzahlregelkreis nach dem Symmetrischen Optimum ausgelegt werden. Das Drehmoment in permanentflussorientierten Koordinaten kann folgendermassen bestimmt werden:

\[ M=\frac{3p}{2}\cdot {\underline{i}_{s}^{k}}^{T} \cdot \tilde J\cdot \underline{\Psi}_{s}^{k} \]

Dabei kann der Ausdruck \(\tilde J\cdot \underline{\Psi}_{s}^{k}\) durch Gleichung (7.1) ersetzt werden.

\[ \begin{matrix} M=\frac{3p}{2}\cdot \left(\begin{matrix}i_{s}^{d} & i_{s}^{q} \end{matrix}\right)\cdot \left(\begin{matrix}-L_{s}^{q}i_{s}^{q}\\ L_{s}^{d}i_{s}^{d} +\Psi_{PM}^{d} \end{matrix}\right)\\ =\frac{3p}{2}\cdot \left(-L_{s}^{q}\cdot i_{s}^{d}\cdot i_{s}^{q} + L_{s}^{d}\cdot i_{s}^{d}\cdot i_{s}^{q} + i_{S}^{q}\cdot \Psi_{PM}^{d}\right) \\ = \underbrace{\frac{3p}{2}\cdot \left( L_{s}^{d}-L_{s}^{q}\right)\cdot i_{s}^{d}\cdot i_{s}^{q}}_{Reluktanzmoment} + \underbrace{\frac{3p}{2}\cdot \Psi_{PM}^{d}\cdot i_{s}^{q}}_{Lorentzmoment} \end{matrix} \]

7.3 Zeigerdiagramme

7.3.1 Zeigerdiagramm der Durchflutungen und Flüsse

Die dreisträngige Statorwicklung erzeugt bei Betrieb am Drehstromnetz ein rotierendes Stator Drehfeld \(\Phi_{S}\) bzw. die entsprechende Drehdurchflutung \(\Theta_{S}\). Da diese Grössen somit im Raum (im Luftspalt) rotieren, können diese als Raumzeiger dargestellt werden. Der vom rotierenden Läufer ausgehende Erregerfluss \(\Phi_{E}\) bzw. die entsprechende Durchflutung \(\Theta_{E}\) können somit ebenfalls als Raumzeiger dargestellt werden (siehe Bild 7.8.

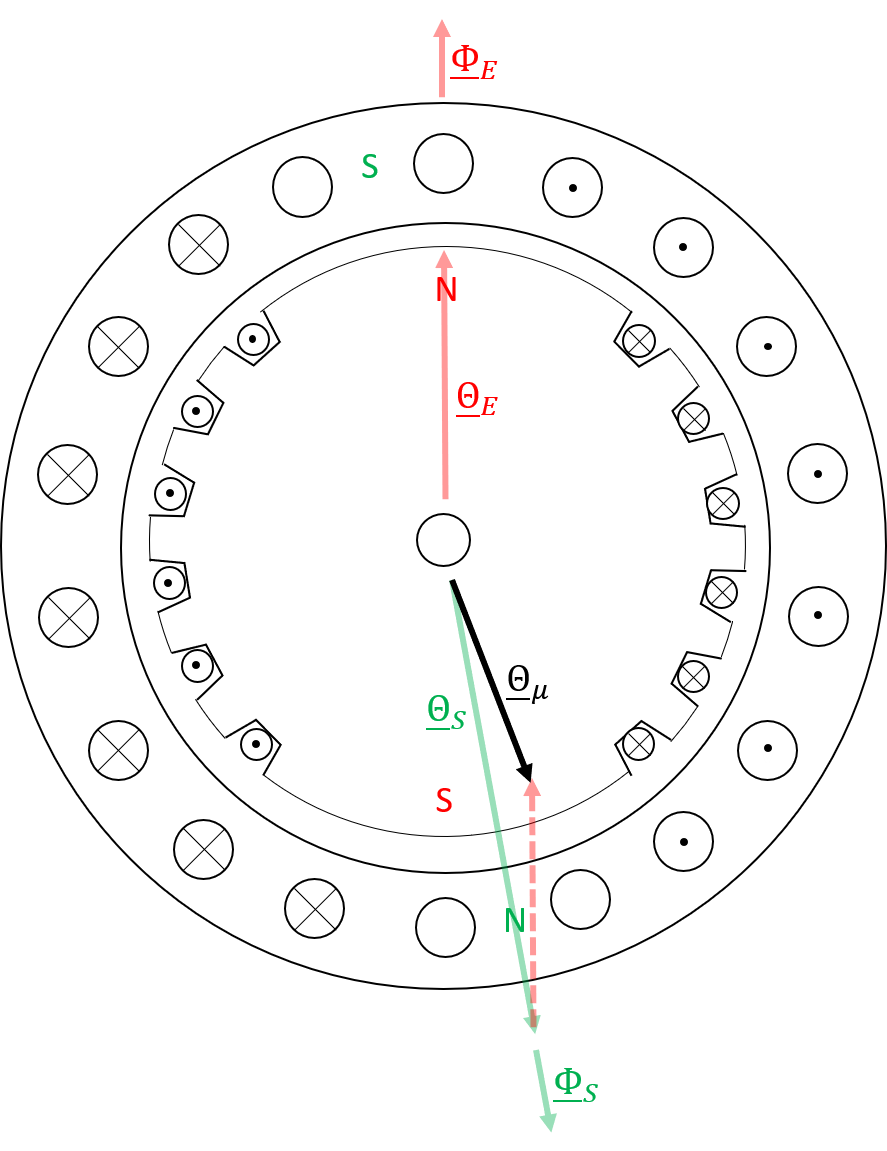
Abbildung 7.8: Vereinfachte Darstellung der Raumzeiger von Stator- und Rotordurchflutung

Schlussendlich kommt es im Luftspalt zu einer Überlagerung der Läufer- und der Statordurchflutung. Die Raumzeigerdarstellung ermöglicht somit eine einfache Bestimmung der resultierende Gesamtdurchflutung:

\[\begin{equation} \Theta_{\mu}=\Theta_{E}+\Theta_{S} \tag{7.2} \end{equation}\]

bzw. des magnetischen Flusses im Luftspalt, welcher auch als Hauptfluss bezeichnet wird:

\[\begin{equation} \Phi_{\mu}=\Phi_{E}+\Phi_{S} \tag{7.3} \end{equation}\]

7.3.2 Zeigerdiagramm der Spannungen

Mit Hilfe des Induktionsgesetzes lassen sich die Raumzeiger der Spannungen aus den Durchflutungs- und Fluss-Raumzeigern, die mit der Drehzahl \(n_{S}=\frac{f_{S}}{p}\) umlaufen, ermitteln. Auch hier ist es möglich die einzelnen Spannungskomponenten getrennt voneinander zu betrachten. Die durch den umlaufenden Läuferfluss in den einzelnen Wicklungen eines Statorstranges induzierte, ideelle Leerlaufspannung wird dabei als Polradspannung \(U_{p}\) bezeichnet:

\[\begin{equation} \underline{U_{P}}=j\omega\cdot \underline{\Phi_{E}} \tag{7.4} \end{equation}\]

References

5.

Morimoto S (2007) Trend of permanent magnet synchronous machines., 2. Aufl. IEEJ Transactions on Electrical; Electronic Engineering, 2(2):101-108