Kapitel 6 Allgemeines zu Drehfeldmaschinen
Im Gegensatz zur orstfesten, räumlichen Flussdichteverteilung des Hauptfeldes (Erregerfeldes) einer Gleichstrommaschine, die ihre Position in Bezug auf den Stator der Maschine nicht ändert, weisen Drehfeldmaschinen eine sich kontinuierlich ändernde Flussdichteverteilung im Luftspalt auf. In diesem Fall bewegt sich diese in Form einer Welle durch den Luftspalt.
Folgende Maschinen können der Gruppe der Drehfeldmaschinen zugeordnet werden:
- Asynchronmaschine
- Synchronmaschine
- Bürstenlose (elektronisch kommutierte) Gleichstrommaschine
6.1 Das Drehfeld und Raumzeiger
Drehfelder werden erzeugt, um die Wellen von Drehfeldmaschinen und selbstständig anlaufenden Wechselstrommotoren anzutreiben. Üblicherweise werden Drehfelder durch Dreiphasenwechselstrom erzeugt, da der zeitliche Versatz der drei Wechselströme in Kombination mit räumlich kreisförmig versetzt angeordneten Spulen ein Drehfeld hervorrufen. In der Antriebstechnik werden Drehfelder häufig mit Hilfe von Raumzeigern beschrieben, da diese betrachtungsweise die mathematische Handhabung massgeblich vereinfacht.
6.1.1 Erzeugung von Drehfeldern
Grundsätzlich ist es möglich ein Drehfeld auf folgende Art zu erzeugen:
- Rotation eines Polrades im Stator
- Bestromung einer Drehfeldwicklung mit Drehstrom
- Bestromung zweier um 90° räumlich versetzten Spulen mit Zweiphasenwechselstrom dessen zeitlicher Versatz ebenfalls 90° beträgt
Die Erzeugung von Drehfeldern durch Zweiphasenwechselstrom kommt selten zur Anwendung, da die Leiterquerschnitte schlecht ausgenutzt werden. Um die Entstehung eines Drehfeldes mit Hilfe einer Drehfeldwicklung zu begründen, kann anfänglich von einer einzelnen Wicklung, wie im Abbildung 6.1 dargestellt, ausgegangen werden (unter Vernachlässigung von Sättigungserscheinungen).
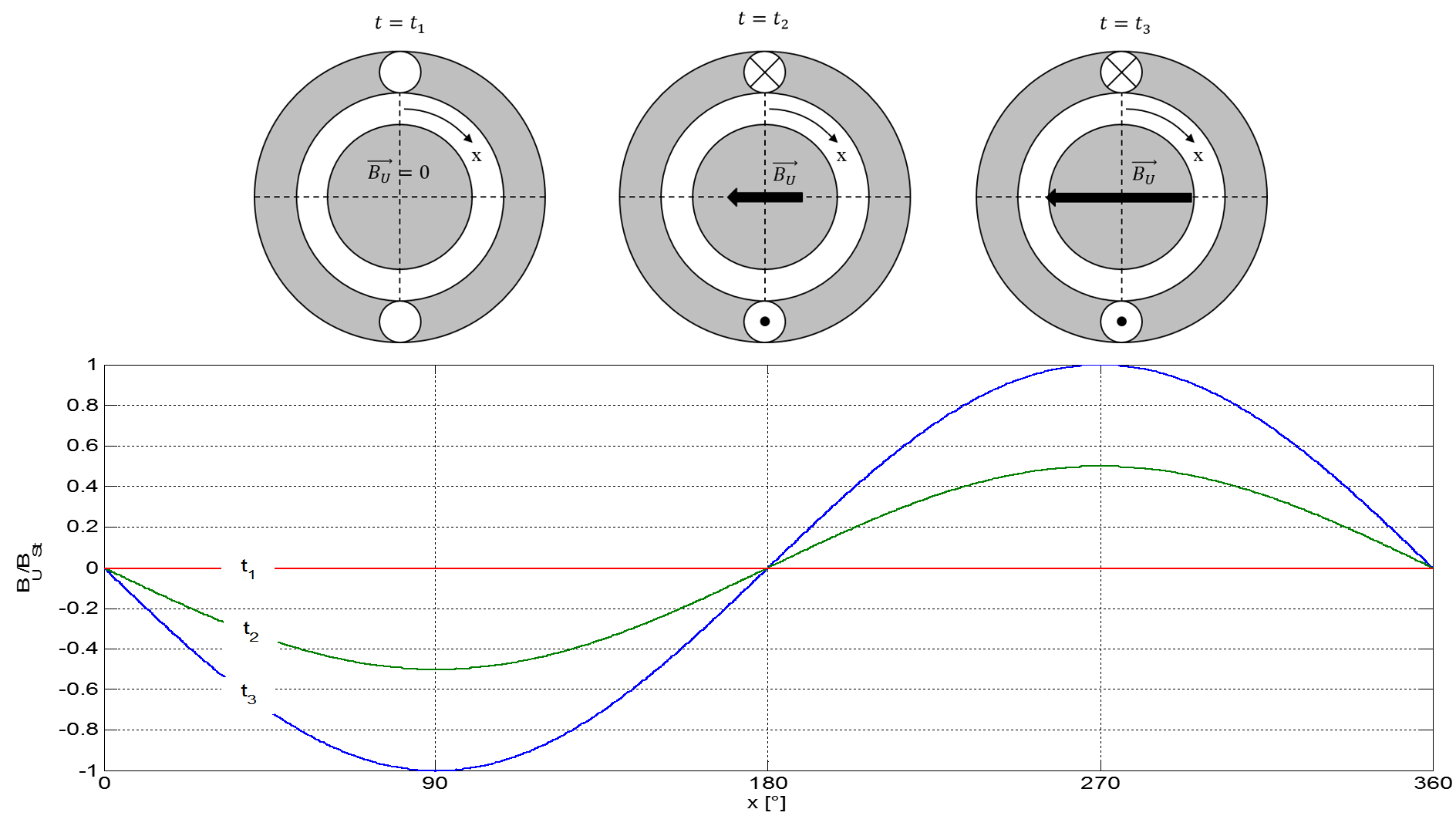
Abbildung 6.1: Flussdichteverteilung einer einzelnen Wicklung mit dem Strom als Parameter
Die Abbildung 6.1 zeigt die unterschiedlichen Flussdichteverteilungen einer einzelnen, unterschiedlich stark bestromten Wicklung im Stator einer elektrischen Maschine. Es zeigt sich eine direkte Proportionalität zwischen dem Wicklungsstrom und der Amplitude der Flussdichte, solange man sich im linearen Bereich der Magnetisierungskennlinie befindet. Die Nulldurchgänge sowie die Maxima sind von der Stromamplitude unabhängig. Die zugehörige Flussdichte dieses Stranges U kann anhand der folgenden Gleichung beschrieben werden.
\[ B_{U}(x,t)=-\hat{B}\cdot \sin{(x)}\cdot \sin{(\omega t)} \]
Da es sich bei einer dreisträngigen Drehstromwicklung um drei Strangwicklungen handelt, die um \(120^{\circ}\) zueinander versetzt am Umfang des Stators in Nuten untergebracht werden und diese gleichzeitig mit um \(120^{\circ}\) zeitlich verschobener Spannung versorgt werden, können die von diesen zwei zusätzlichen Wicklungen ausgehenden Flussdichteverteilungen anhand der Gleichungen:
\[ B_{V}(x,t)=-\hat{B}\cdot \sin{(x-\frac{2\pi}{3})}\cdot \sin{(\omega t-\frac{2\pi}{3})} \]
bzw.
\[ B_{W}(x,t)=-\hat{B}\cdot \sin{(x-\frac{4\pi}{3})}\cdot \sin{(\omega t-\frac{4\pi}{3})} \]
beschrieben werden. Somit lässt sich die räumliche Flussdichteverteilung im Luftspalt durch Addition aller drei Flussdichteverteilungen beschreiben:
\[\begin{equation} B_{Ges}(x,t)=B_{U}(x,t)+B_{V}(x,t)+B_{W}(x,t) \end{equation}\]
Stellt die Flussdichteverteilung \(B(x)\) innerhalb des Luftspaltes einer Maschine eine fortschreitende Welle dar, liegt ein Drehfeld vor. Der Parameter \(x\) stellt dabei die Weg-Koordinate entlang des Luftspaltes dar. Eine solche, sich im Luftspalt bewegende Welle ist in Abbildung 6.2 dargestellt, indem die räumliche Verteilung innerhalb des Luftspaltes zu zwei unterschiedlichen Zeitpunkten (\(t_{0}=0\) bzw. \(t_{1}>0\)) in einem Diagramm abgebildet wird (unter Vernachlässigung eventueller Oberwellendrehfelder).
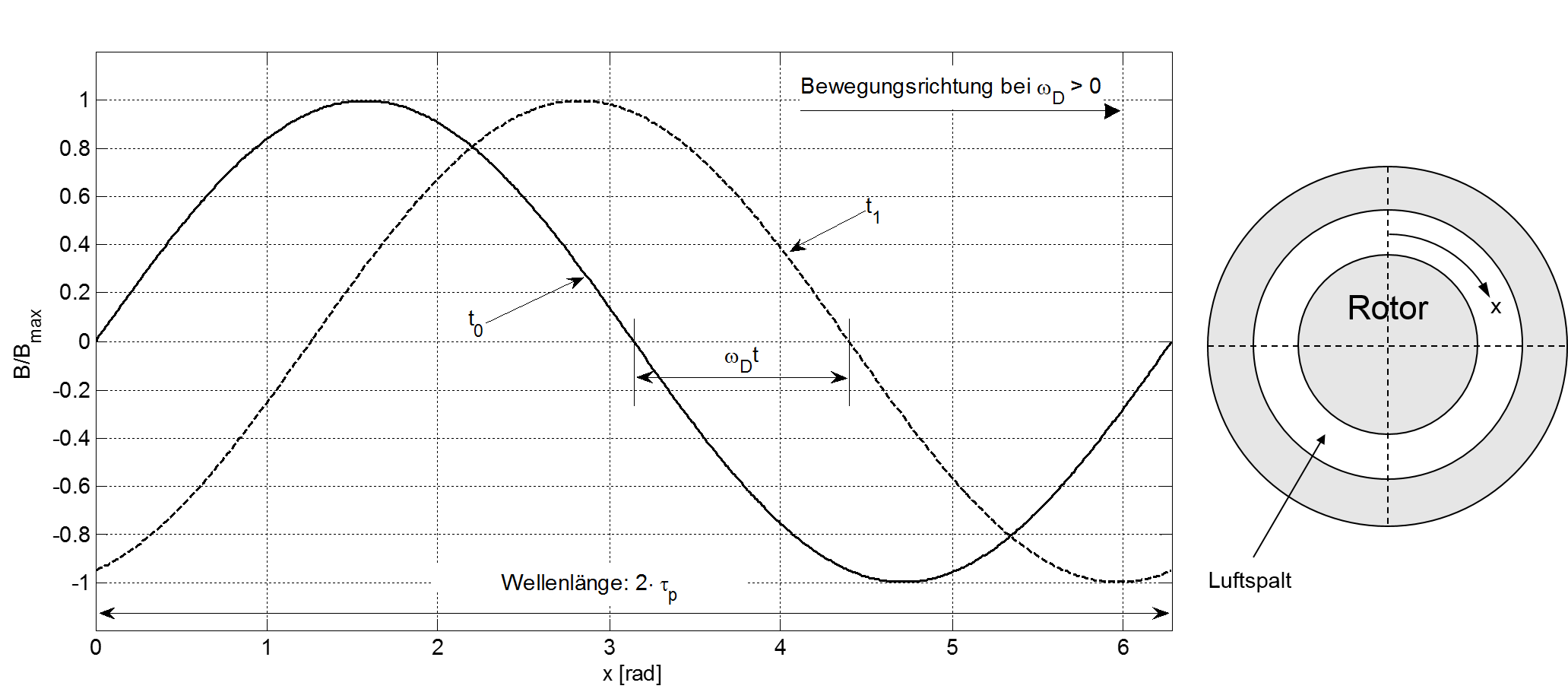
Abbildung 6.2: Flussdichteverteilung des Grundwellendrehfeldes (Polpaarzahl p=1)
Unter oben getroffener Annahme liesse sich somit der zurückgelegte Weg \(x\) zwischen den zwei Zeitpunkten \(t_{0}\) und \(t_{1}\) unter Berücksichtigung der Winkelgeschwindigkeit \(\omega\) anhand der Gleichung
\[ x = \omega_{D}\cdot \omega \]
bestimmen (bei konstanter Winkelgeschwindigkeit).
Der sinusförmige Verlauf der Flussdichteverteilung im Luftspalt besitzt eine Wellenlänge die durch die Polteilung bestimmt wird (\(T_{Welle}=2\cdot \tau_{p}\)). Eine charakteristische Eigenschaft des Drehfeldes ist die Bewegung mit konstanter Winkelgeschwindigkeit \(\omega_{D}\), wobei sowohl die Amplitude als auch die räumliche Ausdehnung (Wellenlänge \(T_{Welle}\)) unverändert bleiben. Somit besitzt das Grundwellendrehfeld eine Abhängigkeit von der Zeit und von der zu betrachtenden Position. Kommt der Nulldurchgang des Grundwellendrehfeldes zum Zeitpunkt \(t=0s\) zum liegen, berechnet sich die Flussdichteverteilung anhand folgender Gleichung:
\[\begin{equation} B(x,t)=\hat{B}\cdot \sin{\biggl(\frac{\pi}{\tau_{p}}(x-\omega_{D}\cdot t)\biggr)} \tag{6.1} \end{equation}\]
An jeder räumlichen Position \(x\) des Luftspaltes ändert sich die Flussdichte zeitlich sinusförmig mit der Frequenz \(f_{D}\):
\[ \omega_{D}=2\pi\cdot f_{D} = 2\pi\cdot p \cdot \mid n_{D} \mid \]
6.1.2 Symmetriebedingung des Dreiphasensystems
Voraussetzung für die Beschreibung eines symmetrischen Dreiphasensystems als Raumzeiger ist die Symmetriebedingung selbst. Dazu müssen die Amplituden aller Phasen gleich gross sein:
\[ \forall t \geq 0: \hat y(t):= \hat y_{a}(t)=\hat y_{b}(t)=\hat y_{c}(t) \]
Gleichzeitig müssen die Phasenwinkel aller Phasen um einen Winkel von \(\frac{2\pi}{3}\) zueinander versetzt sein:
\[ \forall t \geq 0: \phi(t):= \phi_{a}(t)=\phi_{b}(t)=\phi_{c}(t) \]
Sind diese Bedingungen erfüllt, beträgt die Summe aller drei Grössen zu jedem Zeitpunkt Null:
\[ y_{a}(t) + y_{b}(t) + y_{c}(t)=\hat y \bigg[cos\big(\phi(t)\big)+cos\bigg(\phi(t)-\frac{2\pi}{3}\bigg)+cos\bigg(\phi(t)-\frac{4\pi}{3}\bigg)\bigg] \]
Mit Hilfe des Additionstheorems \(cos(a)+cos(b)=2\cdot cos\bigg(\frac{a+b}{2}\bigg)cos\bigg(\frac{a-b}{2}\bigg)\) folgt daraus:
\[ y_{a}(t) + y_{b}(t) + y_{c}(t) = \hat y \bigg[2\cdot cos\bigg(\phi(t)-\frac{\pi}{3}\bigg)cos\bigg(\frac{\pi}{3}\bigg) + cos\bigg(\phi(t)-\frac{4\pi}{3}\bigg)\bigg] \]
Wird weiterhin berücksichtigt, dass \(cos\big(\frac{\pi}{3}\big)=\frac{1}{2}\) gilt, lässt sich dieser Ausdruck durch erneute Verwendung des Additionstheorems weiter vereinfachen:
\[ y_{a}(t) + y_{b}(t) + y_{c}(t) = \hat y \bigg[cos\big(\phi(t)\big)\cdot cos\bigg(\frac{\pi}{2}\bigg)\bigg] \]
Mit \(cos\big(\frac{\pi}{2}\big) = 0\) lässt sich diese Nullbedingung somit mathemtisch beweisen:
\[ y_{a}(t) + y_{b}(t) + y_{c}(t) = 0 \]
6.1.3 Raumzeigerdarstellung
Mit Hilfe eines Raumzeigers werden physikalische Grössen eines Dreiphasensystems als Zeiger in einer komplexen Ebene dargestellt, wobei eine Verwechslung mit der Zeigerdarstellung in der Wechselstromlehre vermieden werden sollte. Sie werden dazu verwendet Magnetfelder sowie Ströme und Spannungen von Drehfeldmaschinen zu beschreiben.
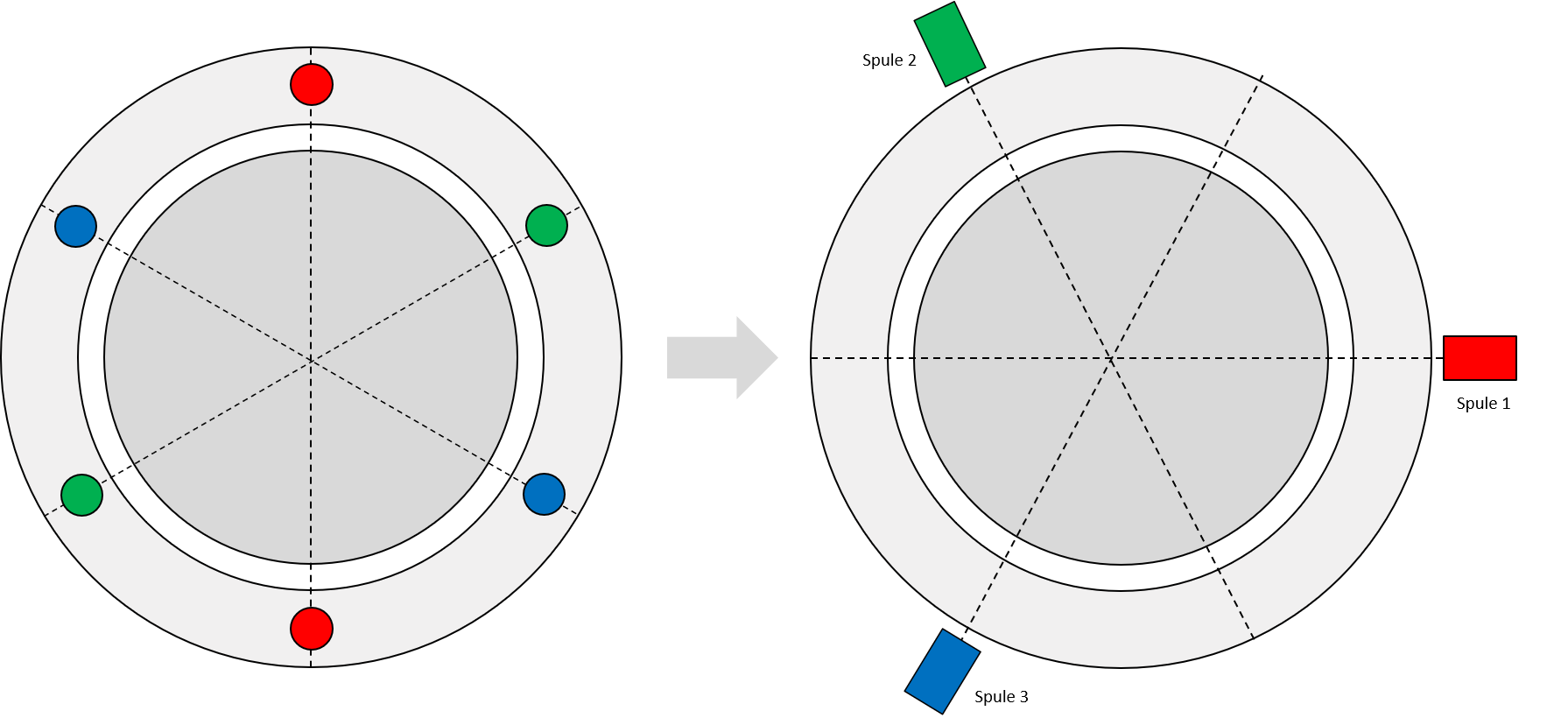
Abbildung 6.3: Modell einer Drehfeldmaschine (links: Darstellung mit örtlich konzentrierten Spulen; rechts: mit wirkungsorientierter Spulenanordnung)
Überträgt man die Erkenntnisse aus dem Kapitel 6.1 auf das in Abbildung 6.3 dargestellte Modell einer Drehfeldmaschine, lassen sich die physikalischen Grössen (Strom, Spannung, etc.) der einzelnen Wicklungen (Spule 1-3) mit Hilfe eines Vektors darstellen, dessen Betrag mit der Amplitude der physikalischen Grösse variiert. Hierbei gilt es zu berücksichtigen, dass die Flussdichteverteilung im Luftspalt einer Maschine, aufgrund der Verteilung der Wicklungen nicht ideal sinusförmig verläuft. Durch Überlagerung (Vektoraddition) der drei Vektoren, deren Betrag bei sinusförmiger Speisung variiert, kann der zugehörige Raumzeiger, wie in Abbildung 6.4 gezeigt, dargestellt werden.
Abbildung 6.4: Entstehung des rotierenden Spannungs-Raumzeigers (schwarz) einer symmetrischen Drehfeldmaschine
Der so enstandene Raumzeiger, der in der Schnittebene der Maschine verläuft (somit zweidimensional) kann mit Hilfe eines orthogonalen Koordinatensystems mathematisch dargestellt werden. Bei der Wahl der Lage des Koordinatensystems ist man grundsätzlich frei. Je nach Literatur bzw. betrachtetem Modell wird zwischen statorfestem, rotorfestem bzw. beliebigem Koordinatensystem unterschieden.
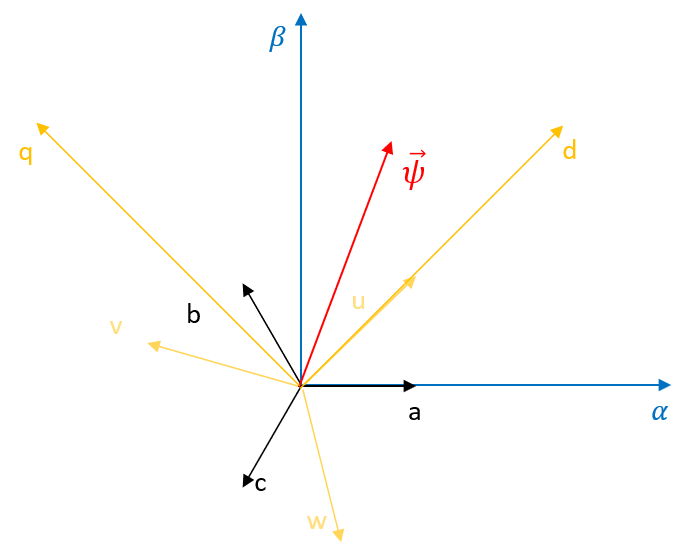
Abbildung 6.5: Darstellung eines Raumzeigers in unterschiedlichen Koordinatensystemen
Das statorfeste Koordinatensystem (Index \(S\)) wird dabei folgendermassen definiert:
\[ \vec{x}^{S}=(x_{\alpha},x_{\beta})^{T}=\begin{pmatrix}x_{\alpha}\\x_{\beta}\end{pmatrix} \]
Das statorfeste Koordinatensystem ist ein ortsfestes Koordinatensystem, welches üblicherweise so angeordnet wird, dass die \(\alpha\)-Achse mit einer der drei Wicklungsachsen des Stators (üblicherweise U) zusammenfällt. Beim rotorfesten Koordinatensystem (Index \(R\)) hingegen handelt es sich um ein rotierendes Koordinatensystem, welches so angeordnet wird, dass es mit einer Wicklungsachse des Rotors (welcher rotiert) zusammenfällt.
\[ \vec{x}^{R}=(x_{d},x_{q})^{T}=\begin{pmatrix}x_{d}\\x_{q}\end{pmatrix} \]
Folglich rotiert das rotorfeste Koordinatensystem mit der mechanischen Winkelgeschwindigkeit \(\Omega_{mech}\) um das statorfeste Koordinatensystem. Je nach Verwendung ist es ebenfalls möglich ein beliebig rotierendes Koordinatensystem zu definieren, welches beispielsweise mit dem Statorfluss, dem Rotorfluss bzw. dem Luftspaltfluss rotiert. Vor allem in der Vergangenheit wurden die Raumzeiger mit Hilfe der komplexen Zahlen dargestellt, wobei berücksichtigt werden muss, dass die reele Achse der komplexen Zahlenebene mit der \(\alpha\)-Achse (üblicherweise Spulenachse U) zusammenfällt. Die Berechnung des Raumzeigers basiert in diesem Fall auf der Gleichung:
\[ \vec{x}=\frac{2}{3}\big(x_{U}+a\cdot x_{V} + a^{2}\cdot x_{W} \big) \]
Wobei der komplexe Drehoperator \(a\) verwendet wird:
\[ a=e^{j\frac{2\pi}{3}}=-\frac{1}{2}+j\frac{\sqrt{3}}{2} \]
\[ a^{2}=e^{j\frac{4\pi}{3}}=-\frac{1}{2}-j\frac{\sqrt{3}}{2} \]
In moderneren Veröffentlichungen wird stattdessen immer öfter die oben dargestellte Vektornotation verwendet. Um Grössen des Dreiphasen-Systems \(\vec{x}^{a,b,c}\) in das statorfeste Koordinatensystem umwandeln zu können, wird die Allgemeine Clarke Transformation herangezogen:
\[ \begin{pmatrix}x_{\alpha}(t) \\ x_{\beta}(t) \\ x_{0}(t) \end{pmatrix} = c\cdot \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} \cdot \vec{x}^{a,b,c} = c \cdot T_{C}\cdot \vec{x}^{a,b,c} \]
Der Skalierungsfaktor \(c\) variiert, je nachdem ob eine amplitudenkorrekte \((c=\frac{2}{3})\) oder eine leistungskorrekte \((c=\sqrt{\frac{2}{3}})\) Transformation gewünscht ist. Bei der leistungskorrekten Transformation kann die Leistungberechnung durch Multiplikation des Strom- und Spannungsraumzeigers im statorfesten Koordinatensystem erfolgen. Bei der amplitudenkorrekten Transformation entspricht der Maximalwert des Raumzeigers der Maximalwert der jeweiligen Stranggrösse. Die Drehmatrix \(T_{C}\) kann bei symmetrischen Dreiphasensystemen noch weiter vereinfacht werden, da die Nullkomponente \(x_{0}(t)\) in diesem Fall entfällt:
\[ \begin{pmatrix}x_{\alpha}(t) \\ x_{\beta}(t)\end{pmatrix} = c\cdot \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \cdot \vec{x}^{a,b,c} = c \cdot T_{C}\cdot \vec{x}^{a,b,c} \]
Die inverse Clarke-Transformation wird verwendet, um eine Umrechnung vom statorfesten in das dreiphasige Koordinatensystem zu ermöglichen.
\[ \vec{x}^{a,b,c}=\frac{1}{c}\cdot \begin{bmatrix} \frac{2}{3} & 0 \\ -\frac{1}{3} & \frac{1}{\sqrt{3}} \\ -\frac{1}{3} & -\frac{1}{\sqrt{3}} \end{bmatrix} \cdot \begin{pmatrix}x_{\alpha}(t) \\ x_{\beta}(t)\end{pmatrix} = \frac{1}{c} \cdot T^{-1}_{C}\cdot \vec{x}^{S} \]
Da alle betrachteten Koordinatensystem den gleichen Ursprung besitzen, kann eine Drehung des Koordinatensystems durch eine entsprechende Drehmatrix \(T_{P}(\varphi_{k})\) in Abhängigkeit des unter Umständen zeitabhängigen Winkels \(\varphi_{k}\) vorgenommen werden. Durch eine solche Drehung ist der Raumzeiger somit in beliebig rotierten bzw. beliebig rotierenden Koordinaten darstellbar.
\[ T_{P}(\varphi_{k}) = \begin{bmatrix} cos\big(\varphi_{k}(t)\big) & -sin\big(\varphi_{k}(t)\big) \\ sin\big(\varphi_{k}(t)\big) & cos\big(\varphi_{k}(t)\big) \end{bmatrix} \]
Diese Umrechnung der physikalischen Grössen einer Drehfeldmaschine vom statorfesten Koordinatensystem in beliebige Koordinatensysteme \((\vec{x}^{k}\) wird in der Antriebstechnik als Park-Transformation bezeichnet (Index \(P\)). Die Anwendung der Drehmatrix \(T_{P}(\varphi_{k})\) ist gleichbedeutend mit einer Drehung des statorfesten Koordinatensystems um den Winkel \(\varphi_{k}\), wie es in Abbildung 6.6 dargstellt ist.
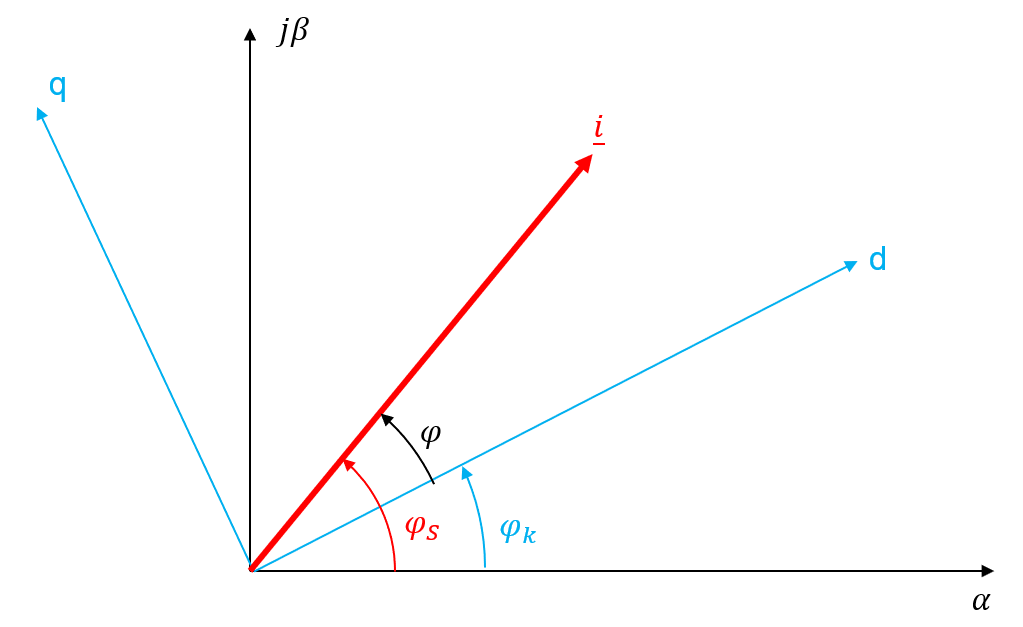
Abbildung 6.6: Darstellung eines Raumzeigers im statorfesten und k-Koordinatensystem
Der Winkel \(\varphi_{S}\) repräsentiert hierbei den Winkel des Strom-Raumzeigers \(\vec{i}\) im statorfesten Koorrdinatensystem. Der Winkel \(\varphi_{k}\) hingegen repräsentiert den Winkel, der notwendig ist, um das statorfeste KOS in die Position des beliebigen k-KOS zu drehen. Der eigentliche Winkel des Strom-Raumzeigers im k-KOS wird durch den Winkel \(\varphi\) zum Ausdruck gebracht. Für die Winkelbeziehungen in der Abbildung 6.6 ergibt sich somit folgender Zusammenhang.
\[ \varphi=\varphi_{S} - \varphi_{k} \]
Um einen beliebigen Raumzeiger \(\vec{x}^{S}\), gegeben im statorfesten KOS (Index \(S\)), in das beliebige k-KOS (Index \(k\)) zu überführen \(\vec{x}^{k}\) muss die inverse Park-Transformation angewandt werden, was gleichbedeutend ist mit der Park-Transformation mit negativem Winkel \(\varphi_{k}\).
\[ \vec{x}^{k}=T_{P}^{-1}(\varphi_{k})\cdot \vec{x}^{S}=T_{P}(-\varphi_{k})\cdot \vec{x}^{S}= \begin{bmatrix} cos\big(\varphi_{k}\big) & sin\big(\varphi_{k}\big) \\ -sin\big(\varphi_{k}\big) & cos\big(\varphi_{k}\big) \end{bmatrix}\cdot \vec{x}^{S} \]
Begründen lässt sich dies damit, dass ein beliebiger Raumzeiger, welcher im statorfesten KOS dargestellt wird, einen grösseren Winkel \(\varphi_{S}\) aufweist als der gleiche Raumzeiger im beliebigen k-KOS, nachdem dieses um den Winkel \(+\varphi_{k}\) gedreht wurde. Der gleiche Raumzeiger weist somit im beliebigen k-KOS einen, um den Wert \(\varphi_{k}\) kleineren, Winkel auf als im statorfesten KOS. Auch die Park-Transformation sowie deren Inverse lassen sich mit Hilfe von komplexen Zahlen äquivalent darstellen.
\[ \vec{x}^{k}=\vec{x}^{S}\cdot e^{-j\varphi_{k}} \]
\[ \vec{x}^{S}=\vec{x}^{k}\cdot e^{j\varphi_{k}} \]
6.2 Aufbau der Drehfeldmaschine
Um das Verhalten von Drehfeldmaschinen mathematisch beschreiben zu können, werden folgende Vereinfachungen getroffen:
- Keine axiale Ausbreitung des magnetischen Flusses in der Maschine (2 dimensionale Betrachtung)
- Der magnetische Fluss breitet sich sinusförmig im Luftspalt der Maschine aus (Grundwellenmodell)
- Sättigungserscheinungen im magnetischen Kreis werden vernachlässigt (lineares Verhalten \(L\neq f(I)\))
- Keine Wirbelströme (lediglich ohmsche Verluste)
- Keine Temperaturabhängigkeit (\(R, L \neq f(T)\))
- Die Eigenschaften der Wicklungsstränge sind identisch
Bei der allgemeinen Drehfeldmaschine geht man davon aus, dass sie ein dreiphasiges Wicklungssystem jeweils im Rotor (Index R) und im Stator (Index S) besitzt und von symmetrischen und unabhängigen Dreiphasen-Spannungssystemen gespeist werden. Ein solcher Aufbau ist beispielhaft in Abbildung 6.7 dargestellt, wobei die einzelnen Wicklungen simplifiziert gezeigt werden.
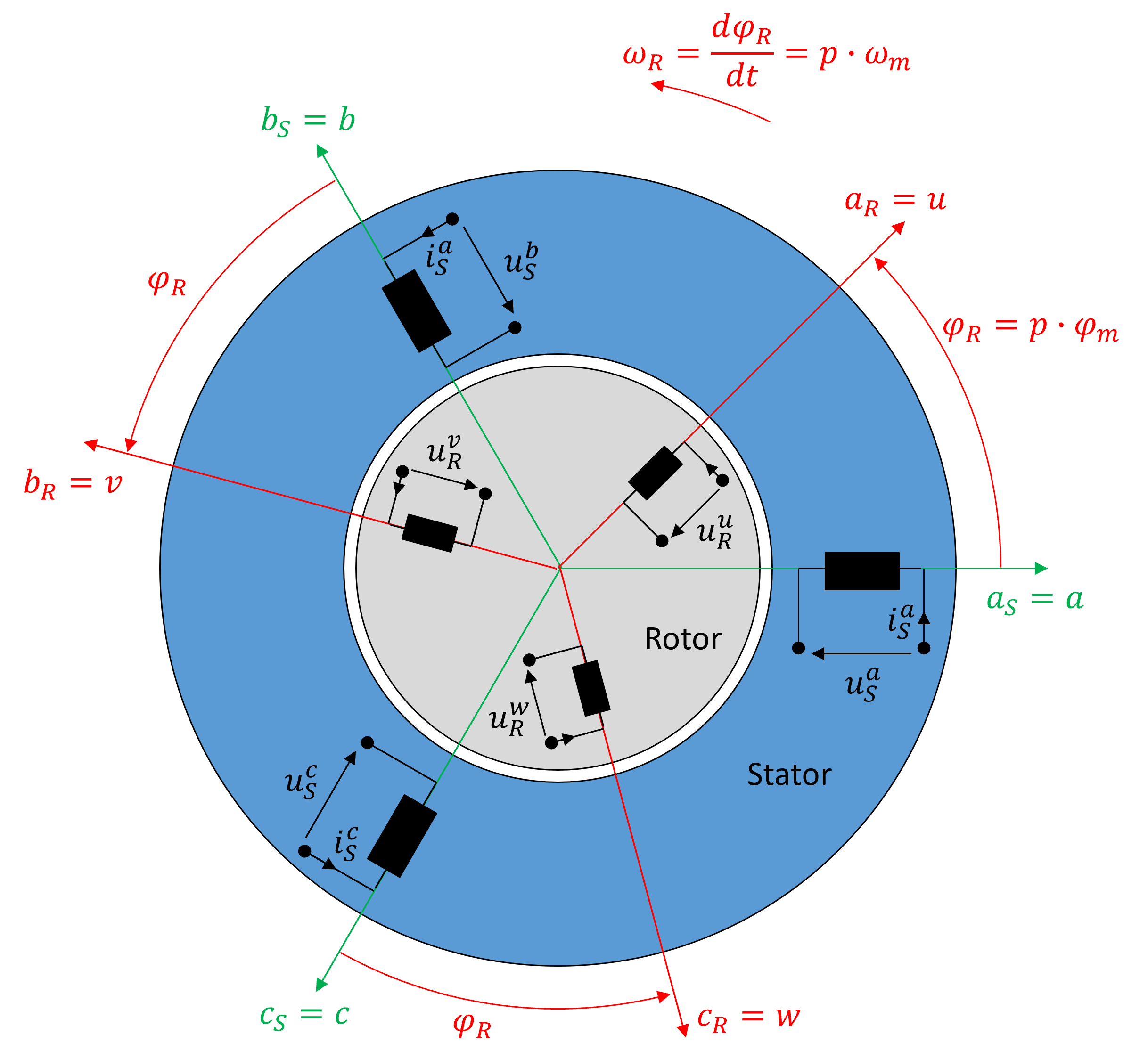
Abbildung 6.7: Prinzipbild einer allgemeinen Drehfeldmaschine
Zur mathematischen Beschreibung des Verhaltens einer Drehfeldmaschine existieren unterschiedliche Ansätze, die sich bezüglich Komplexität und zu beschreibendem Verhalten (z.B. stationärer oder dynamischer Betrieb bzw. elektromagnetische Zusammenhänge) unterscheiden.
6.2.1 Elektromagnetische Abhängigkeiten
Wie in Abbildung 6.8 dargestellt, können die magnetischen Zusammenhänge dargestellt werden, indem die magnetische Durchflutung und der magnetische Fluss berücksichtigt werden.
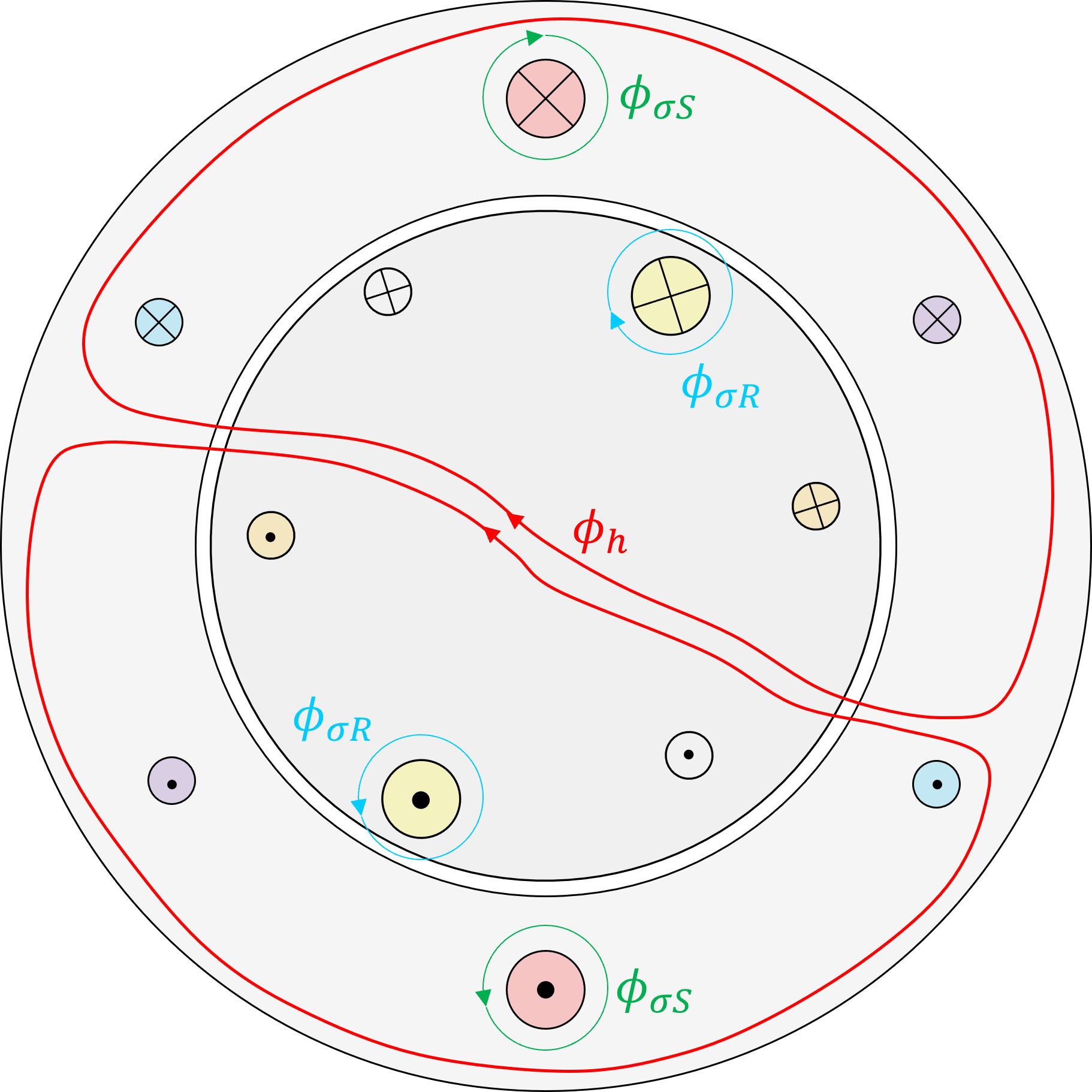
Abbildung 6.8: Simplifizierte Darstellung der magnetischen Flüsse einer Drehfeldmaschine
Die Abbildung zeigt dabei nicht die Raumzeiger sondern den simplifizierten verlauf der magnetischen Flüsse. Verwendet man die Raumzeigerdarstellung und berücksichtigt den allgemeinen Zusammenhang zwischen magnetischer Durchflutung (häufig auch magnetische Spannung bezeichnet) und magnetischem Fluss
\[ \underline{\Theta}=N\cdot \underline{i}=R_{m}\cdot \underline{\Phi} \rightarrow \underline{\Phi}=\frac{\underline{\Theta}}{R_{m}}=\frac{N\cdot \underline{i}}{R_{m}} \] lassen sich somit sowohl die Streuflüsse (\(\Phi_{\sigma S}\) bzw. \(\Phi_{\sigma R}\)) als auch der Hauptfluss \(\Phi_{h}\) bestimmen. Der Hauptfluss ergibt sich somit zu:
Im Statorkoordinatensystem:
\[ \underline{\Phi}_{h}^{s}=\frac{\underline{\Theta}_{h}^{s}}{R_{mh}}=\frac{\underline{\Theta}_{s}^{s}+\underline{\Theta}_{r}^{s}}{R_{mh}}=\frac{N_{s}\cdot \underline{i}_{s}^{s}+N_{r}\cdot \underline{i}_{r}^{s}}{R_{mh}} \]
Im Rotorkoordinatensystem:
\[ \underline{\Phi}_{h}^{r}=\frac{\underline{\Theta}_{h}^{r}}{R_{mh}}=\frac{\underline{\Theta}_{s}^{r}+\underline{\Theta}_{r}^{r}}{R_{mh}}=\frac{N_{s}\cdot \underline{i}_{s}^{r}+N_{r}\cdot \underline{i}_{r}^{r}}{R_{mh}} \]
Die Streuflüsse umfassen lediglich ein einzelnes Wicklungssystem, wodurch sich die Streuflüsse für Rotor und Stator jeweils in ihrem eignen Koordinatensystem dargestellt, bestimmen lassen:
Stator:
\[ \underline{\Phi}_{\sigma s}^{s} = \frac{\underline{\Theta}_{s}^{s}}{R_{m\sigma s}} = \frac{N_{s}\cdot \underline{i}_{s}^{s}}{R_{m\sigma s}} \]
Rotor:
\[ \underline{\Phi}_{\sigma r}^{r} = \frac{\underline{\Theta}_{r}^{r}}{R_{m\sigma r}} = \frac{N_{r}\cdot \underline{i}_{r}^{r}}{R_{m\sigma r}} \]
Da zur Beschreibung des Verhaltens der Drehfeldmaschine die Spannungsgleichungen verwendet werden, werden die verketteten Flüsse bzw. die entsprechenden Induktivitäten benötigt. Beim verketteten Fluss handelt es sich um um den gesamten Fluss, der von einer Spule (Wicklung) umfasst wird. Aufgrund dessen kann die folgende, allgemeine Gleichung zur Bestimmung des verketteten Flusses verwendet werden:
\[\begin{equation} \underline{\Psi}=N\cdot \underline{\Phi}=N\cdot \frac{\underline{\Theta}}{R_{m}}=N\cdot \frac{N\cdot \underline{i}}{R_{m}}=\frac{N^{2}\cdot \underline{i}}{R_{m}} \tag{6.2} \end{equation}\]
Da die Induktivität den Proportionalitätsfaktor zwischen Strom und verkettetem Fluss darstellt, lässt sich somit eine Gleichung zur Bestimmung der Induktivität aufstellen:
\[\begin{equation} L=\frac{d\underline{\Psi}}{d\underline{i}}=\frac{N^{2}}{R_{m}} \tag{6.3} \end{equation}\]
Unter Berücksichtigung der Gleichung (6.2) können somit die verketteten Streuflüsse des Stators und des Rotors bestimmt werden:
Stator:
\[ \underline{\Psi}_{\sigma s}^{s} = N_{s}\cdot \underline{\Phi_{\sigma s}^{s}} = \frac{\underline{\Theta}_{s}^{s}}{R_{m\sigma s}}=N_{s}\cdot \frac{N_{s}\cdot \underline{i}_{s}^{s}}{R_{m\sigma s}}=\frac{N_{s}^{2}\cdot \underline{i}_{s}^{s}}{R_{m\sigma s}} \]
Rotor:
\[ \underline{\Psi}_{\sigma r}^{r} = N_{r}\cdot \underline{\Phi_{\sigma r}^{r}} = \frac{\underline{\Theta}_{r}^{r}}{R_{m\sigma r}}=N_{r}\cdot \frac{N_{r}\cdot \underline{i}_{r}^{r}}{R_{m\sigma r}}=\frac{N_{r}^{2}\cdot \underline{i}_{r}^{r}}{R_{m\sigma r}} \]
Und unter Berücksichtigung der Gleichung (6.3) können die Streuinduktivitäten bestimmt werden:
Stator:
\[ L_{\sigma s}=\frac{d\underline{\Psi}_{\sigma s}^{s}}{d\underline{i}_{s}^{s}}=\frac{N_{s}^{2}}{R_{m\sigma s}} \]
Rotor:
\[ L_{\sigma r}=\frac{d\underline{\Psi}_{\sigma r}^{r}}{d\underline{i}_{r}^{r}}=\frac{N_{r}^{2}}{R_{m\sigma r}} \]
Der gleiche Ansatz liefert die Möglichkeit die verketteten Hauptflüsse in den jeweiligen Koordinatensystemen zu bestimmen:
Stator:
\[ \underline{\Psi}_{hs}^{s}=N_{s}\cdot \underline{\Phi}_{h}^{s}=N_{s}\cdot \frac{\underline{\Theta}_{h}^{s}}{R_{mh}}=N_{s}\cdot \frac{\underline{\Theta}_{s}^{s}+\underline{\Theta}_{r}^{s}}{R_{mh}}=N_{s}\cdot \frac{N_{s}\cdot \underline{i}_{s}^{s}+N_{r}\cdot \underline{i}_{r}^{s}}{R_{mh}} \]
Rotor:
\[ \underline{\Psi}_{hr}^{r}=N_{r}\cdot \underline{\Phi}_{h}^{r}=N_{r}\cdot \frac{\underline{\Theta}_{h}^{r}}{R_{mh}}=N_{r}\cdot \frac{\underline{\Theta}_{s}^{r}+\underline{\Theta}_{r}^{r}}{R_{mh}}=N_{r}\cdot \frac{N_{s}\cdot \underline{i}_{s}^{r}+N_{r}\cdot \underline{i}_{r}^{r}}{R_{mh}} \]
Werden auch hier die Induktivitäten als Proportionalitätskonstanten zwischen verkettetem Fluss und Strom des jeweiligen Wicklungssystems (Stator und Rotor) berücksichtigt, lassen sich die Hauptinduktivitäten für Stator und Rotor bestimmen:
Stator:
\[ L_{hs}=\frac{d\underline{\Psi}_{hs}^{s}}{d\underline{i}_{s}^{s}}=\frac{N_{s}^{2}}{R_{mh}} \]
Rotor:
\[ L_{hr}=\frac{d\underline{\Psi}_{hr}^{r}}{d\underline{i}_{r}^{r}}=\frac{N_{r}^{2}}{R_{mh}} \]
Die Hauptinduktivitäten von Stator und Rotor beschreiben somit den Fluss, der von den stromdurchflossenen Wicklungen des jeweiligen Wicklungssystems erzeugt und gleichzeitig von allen Wicklungen dieses Wicklungssystems umfasst wird. Da die Wicklungen beider Wicklungssysteme auch von einen Flussanteil durchsetzt werden, der vom benachbarten Wicklungssystem erzeugt wird, müssen auch entsprechende Koppelinduktivitäten berücksichtigt werden (vgl. Kapitel 3.2.4):
\[ L_{sr}=\frac{d\underline{\Psi}_{hs}^{s}}{d\underline{i}_{r}^{s}}=\frac{N_{s}\cdot N_{r}}{R_{mh}}=L_{rs}=\frac{d\underline{\Psi}_{hs}^{s}}{d\underline{i}_{s}^{r}}=\frac{N_{r}\cdot N_{s}}{R_{mh}}=L_{M} \]
Abbildung 6.8 macht deutlich, dass je nach Verdrehwinkel zwischen Stator und Rotor die magnetische Kopplung zwischen den zwei Wicklungssystemen unterschiedlich stark ausfällt. Die verketteten Flüsse im Stator als auch im Rotor lassen sich folglich immer aus der Summe der jeweiligen Streu- bzw. Hauptflüsse bestimmen, die vom betrachteten Wicklungssystem umfasst werden. Dieser Zusammenhang lässt sich mathematisch folgendermassen berücksichtigen:
Von der Statorwicklung umfasster magnetischer Fluss:
\[ \begin{matrix} \underline{\Psi}_{s}^{s}= N_{s}\left(\underline{\Phi}_{h}^{s}+\underline{\Phi}_{\sigma s}^{s}\right) = \underline{\Psi}_{hs}^{s}+\underline{\Psi}_{\sigma s}^{s}=N_{s}\cdot \frac{N_{s}\cdot \underline{i}_{s}^{s}+N_{r}\cdot \underline{i}_{r}^{s}}{R_{mh}}+\frac{N_{s}^{2}\cdot \underline{i}_{s}^{s}}{R_{m\sigma s}} \\ \underline{\Psi}_{s}^{s}= \frac{N_{s}^{2}}{R_{mh}}\cdot \underline{i}_{s}^{s}+\frac{N_{s}\cdot N_{r}}{R_{mh}}\cdot \underline{i}_{r}^{s}+\frac{N_{s}^{2}}{R_{m\sigma s}}\cdot \underline{i}_{s}^{s} \end{matrix} \]
Von der Rotorwicklung umfasster magnetischer Fluss:
\[ \begin{matrix} \underline{\Psi}_{r}^{r}= N_{r}\left(\underline{\Phi}_{h}^{r}+\underline{\Phi}_{\sigma r}^{r}\right) = \underline{\Psi}_{hr}^{r}+\underline{\Psi}_{\sigma r}^{r}=N_{r}\cdot \frac{N_{s}\cdot \underline{i}_{s}^{r}+N_{r}\cdot \underline{i}_{r}^{r}}{R_{mh}}+\frac{N_{r}^{2}\cdot \underline{i}_{r}^{r}}{R_{m\sigma r}} \\ \underline{\Psi}_{r}^{r}= \frac{N_{r}^{2}}{R_{mh}}\cdot \underline{i}_{r}^{r}+\frac{N_{r}\cdot N_{s}}{R_{mh}}\cdot \underline{i}_{s}^{r}+\frac{N_{r}^{2}}{R_{m\sigma r}}\cdot \underline{i}_{r}^{r} \end{matrix} \]
Werden die konstanten Faktoren vor den Strömen in den obigen zwei Gleichungen durch die bekannten Induktivitäten ersetzt, ergeben sich die in der Literatur häufig verwendeten Stator- bzw. Rotorflussverkettungen:
Statorflussverkettung im Statorkoordinatensystem:
\[\begin{equation} \underline{\Psi}_{s}^{s}=\left(L_{hs}+L_{\sigma s}\right)\cdot \underline{i}_{s}^{s}+L_{M}\cdot \underline{i}_{r}^{s} = L_{s}\cdot \underline{i}_{s}^{s}+L_{M}\cdot \underline{i}_{r}^{s} \tag{6.4} \end{equation}\]
Rotorflussverkettung im Rotorkoordinatensystem:
\[\begin{equation} \underline{\Psi}_{r}^{r}=\left(L_{hr}+L_{\sigma r}\right)\cdot \underline{i}_{r}^{r}+L_{M}\cdot \underline{i}_{s}^{r} = L_{r}\cdot \underline{i}_{r}^{r}+L_{M}\cdot \underline{i}_{s}^{r} \tag{6.5} \end{equation}\]
In beiden Gleichungen wurde die Summe aus den Streu- und Hauptinduktivitäten durch die sogenannte Stator- (\(L_{s}\)) bzw. Rotorinduktivität (\(L_{r}\)) ersetzt.
6.3 Systemtheoretische Beschreibung der Drehfeldmaschine
6.3.1 Spannungsgleichungen
Wie bereits bei der Gleichstrommachine dargestellt, kann die Ersatzschaltung einer Wicklung einer elektrischen Maschine ganz allgemein durch eine Reihenschaltung aus einem Widerstand und einer Spule gebildet werden.
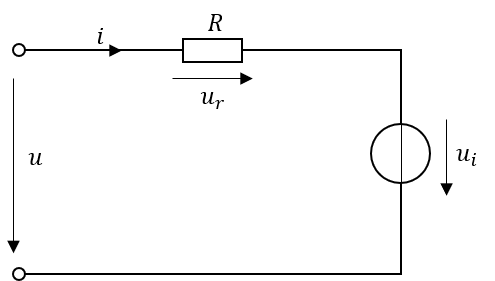
Abbildung 6.9: Ersatzschaltbild einer einzelnen Wicklung
Dieses in Abbildung 6.9 dargestellte Ersatzschaltbild beinhaltet die von aussen angelegte Versorgungsspannung \(u\), den Spannungsabfall über dem Wicklungswiderstand \(u_{r}\) sowie die induzierte Spannung \(u_{i}\). Die induzierte Spannung kann dabei durch Selbst- oder Fremdinduktion bzw. eine Kombination von beiden erzeugt werden. Die zugehörige Maschengleichung
\[ u=R\cdot i+u_{i}=R\cdot i+\frac{d\Psi}{dt} \]
kann somit auch für die allgemeine Drehfeldmaschine, unter Verwendung von Raumzeigern, angewandt werden:
\[\begin{equation} \underline{u}_{s}^{s}=R_{s}\cdot \underline{i}_{s}^{s}+\frac{d\underline{\Psi}_{s}^{s}}{dt} \tag{6.6} \end{equation}\]
\[\begin{equation} \underline{u}_{r}^{r}=R_{r}\cdot \underline{i}_{r}^{r}+\frac{d\underline{\Psi}_{r}^{r}}{dt} \tag{6.7} \end{equation}\]
Die verketteten Flüsse in obigen Gleichungen können dabei jeweils durch die Angaben in den Gleichungen (6.4) bzw. (6.5) ersetzt werden.
6.3.2 Elektromagnetisches Drehmoment
In [mueller] wird die allgemeine Gleichung für das Drehmoment aus dem Energieansatz hergeleitet.
\[ \underline{M}=\frac{3}{2}\cdot p\cdot\left(\underline{\Psi} \times \underline{i} \right) \]
Der Faktor \(\frac{3}{2}\) ergibt sich aus dem um den Faktor \(\frac{2}{3}\) verkürzten Stromraumzeiger und der Faktor \(p\) berücksichtigt eine beliebige Anzahl von Polpaaren. Obige Gleichung gilt für Raumzeiger in beliebigen Koordinatensystemen (Stator-, Rotor- oder belibiebiges k-KOS) solange alle Grössen im gleichen Koordinatensystem zur Verfügung stehen. In Vektor-Matrix Notation der Raumzeiger in Statorkoordinaten ergibt sich folgende Gleichung:
\[ \begin{matrix}\underline{M}=\left(\begin{array}{c}M_{\alpha}\\ M_{\beta}\\ M_{\gamma}\end{array}\right)=\frac{3}{2}\cdot p\cdot \left(\underline{\Psi}_{s}^{s}\times\underline{i}_{s}^{s} \right)= \frac{3}{2}\cdot p\cdot \left[\left(\begin{array}{c}\Psi_{s\alpha}^{s}\\ \Psi_{s\beta}^{s}\\ 0\end{array}\right)\times \left(\begin{array}{c}i_{s\alpha}^{s}\\ i_{s\beta}^{s}\\ 0\end{array}\right) \right]\\= \frac{3}{2}\cdot p\cdot\left(\begin{array}{c}0\\ 0\\ \Psi_{s\alpha}^{s}\cdot i_{s\beta}^{s}- \Psi_{s\beta}^{s}\cdot i_{s\alpha}^{s}\end{array}\right)\end{matrix} \]
In obiger Gleichung wird deutlich, dass das Drehmoment lediglich eine \(\gamma\)-Komponente besitzt, was sich aus dem geometrischen Zusammenhang des Kreuzproduktes ergibt (siehe Abb. 6.10).
Abbildung 6.10: Grafische Repräsentation des Kreuzproduktes (Bildquelle: www.elsenjau.info)
Da sowohl die Flussverkettungen als auch die Ströme jedoch nur aus \(\alpha\)- und \(\beta\)-Komponenten bestehen, ist diese Berechnungsvorschrift zur weiteren Verwendung in Blockschaltbildern eher hinderlich, weshalb sich folgende Berechnungsvorschrift bei der Darstellung von Raumzeigern in Vektor-Matrix-Notation durchgesetzt hat:
In Statorkoordinaten:
\[ M=\frac{3}{2}\cdot p\cdot \underline{i}_{s}^{T}\cdot J\cdot \underline{\Psi}_{s} \]
In Rotorkoordinaten:
\[ M=-\frac{3}{2}\cdot p\cdot \underline{i}_{r}^{T}\cdot J\cdot \underline{\Psi}_{r} \]
Der Superskript \(^{T}\) bezieht sich auf einen transponierten Vektor und die Drehmatrix \(J\)
\[ J=\left(\begin{matrix} 0 & -1 \\ 1 & 0 \end{matrix}\right) \]
sorgt für eine Drehung um 90° im Uhrzeigersinn. Sind sowohl der Fluss- als auch der Stromraumzeiger in komplexen Grössen gegeben, lässt sich das Drehmoment folgendermassen bestimmen:
Raumzeiger im Statorkoordinatensystem:
\[ M=\frac{3}{2}\cdot p\cdot \Im(\underline{\Psi}_{s}^{s^{*}}\cdot \underline{i}_{s}^{s}) = \frac{3}{2}\cdot p\cdot L_{M}\cdot \Im(\underline{i}_{r}^{s^{*}}\cdot \underline{i}_{s}^{s}) \]
Raumzeiger im Rotorkoordinatensystem:
\[ M=-\frac{3}{2}\cdot p\cdot \Im(\underline{\Psi}_{r}^{r^{*}}\cdot \underline{i}_{r}^{r}) \]
Der Superskript \(^{*}\) stellt hierbei eine konjugiert komplexe Zahl dar und das negative Vorzeichen bei gegebenen Rotorgrössen berücksichtigt das “Wegdrücken” vom Stator. Der zweite Teil der obigen Gleichung zur Berechnung des Drehmomentes, basierend auf Raumzeigern im Stator-KOS, ergibt sich dadurch, dass der verkettete Statorfluss \(\underline{\Psi}_{s}^{s}\) durch die Gleichung (6.4) ersetzt und anschliessend das Produkt gebildet wird. Es sei ausserdem darauf explizit hingewiesen, dass die obigen Gleichungen, basierend auf der Darstellung mittels komplexer Zahlen, nur der Imaginärteil des Produktes berücksichtigt wird.
6.3.3 Mechanik
Die Zusammenhänge, die die Mechanik betreffen, können von der Gleichstrommaschine in Kapitel 5.8.2 übernommen werden. Um die Polpaarzahl berücksichtigen zu können, muss zwischen mechanischer (Index \(m\)) und elektrischer (Index \(e\)) Winkelgeschwindigkeit bzw. Winkelposition unterschieden werden:
\[ \begin{matrix} \omega_{e}=p\cdot \omega_{m} \\ \varphi_{e}=p\cdot \varphi_{m} \end{matrix} \]
6.3.4 Gesamtsystem der allgemeinen Drehfeldmaschine
Ausgangspunkt für die Erstellung eines Blockschaltbildes für die allgemeine Drehfeldmaschine bilden die Spannungsgleichungen (6.6) bzw.(6.7). Bei diesen Gleichungen handelt es sich um Differentialgleichungen erster Ordnung, die jeweils die zeitlichen Ableitungen der Flussverkettungen beinhalten. Da es in der Realität keine reinen Differenzierer gibt, werden die Spannungsgleichungen, zur Herleitung eines Blockschaltbildes, allerdings nach den zeitlichen Ableitungen umgestellt und über die Zeit integriert.
\[\begin{equation} \begin{matrix} \underline{u}_{s}^{s}=R_{s}\cdot \underline{i}_{s}^{s}+\frac{d\underline{\Psi}_{s}^{s}}{dt} \iff \underline{\Psi}_{s}^{s}=\int{\left(\underline{u}_{s}^{s}-R_{s}\cdot \underline{i}_{s}^{s} \right)}dt+ \underline{\Psi}_{s0}^{s} \\ \underline{u}_{r}^{r}=R_{r}\cdot \underline{i}_{r}^{r}+\frac{d\underline{\Psi}_{r}^{r}}{dt} \iff \underline{\Psi}_{r}^{r}=\int{\left(\underline{u}_{r}^{r}-R_{r}\cdot \underline{i}_{r}^{r}\right)}dt + \underline{\Psi}_{r0}^{s} \end{matrix} \tag{6.8} \end{equation}\]
Die Gleichungen (6.8) lassen sich bereits in ein Blockschaltbild umformen (siehe Abb. 6.11).
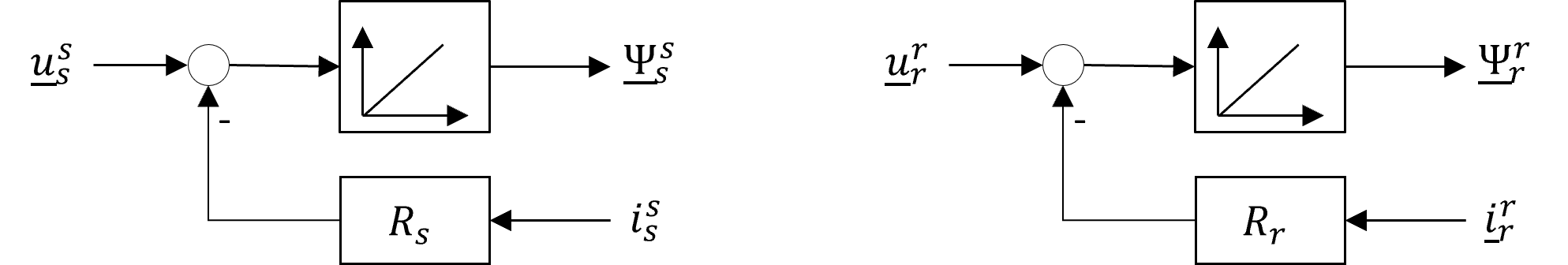
Abbildung 6.11: Blockschaltbild der Spannungsintegralgleichungen (links: Stator, rechts: Rotor)
Die beiden Blockschaltbilder für den Stator und den Rotor der allgemeinen Drehfeldmaschine (Abb. 6.11) können vervollständigt werden, indem eine Möglichkeit gefunden wird die, als Eingänge vorhandenen, Ströme mit Hilfe der Stator- bzw. Rotorflussverklettungen zum Ausdruck zu bringen. Dies wird möglich, indem die Gleichung (6.4) der Statorflussverkettung sowohl nach dem Rotor- als auch nach dem Statorstrom umgestellt wird.
\[ \underline{\Psi}_{s}^{s}=L_{s}\cdot \underline{i}_{s}^{s} + L_{M}\cdot \underline{i}_{r}^{s} \iff \frac{\underline{\Psi}_{s}^{s}-L_{M}\cdot \underline{i}_{r}^{s}}{L_{s}} = \underline{i}_{s}^{s} \iff \frac{\underline{\Psi}_{s}^{s}-L_{s}\cdot \underline{i}_{s}^{s}}{L_{M}} = \underline{i}_{r}^{s} \]
Die so gewonnenen Gleichungen können in die Gleichung (6.5) der Rotorflussverkettung eingesetzt werden, nachdem beide Ströme, mit Hilfe der inversen Park-Transformation in das Rotorkoordinatensystem transformiert wurden.
\[ \begin{matrix} \underline{i}_{s}^{r} = T_{P}(-\varphi_{e})\cdot \underline{i}_{s}^{s} = T_{P}(-\varphi_{e})\cdot \frac{\underline{\Psi}_{s}^{s}-L_{M}\cdot \underline{i}_{r}^{s}}{L_{s}} \\ \underline{i}_{r}^{r} = T_{P}(-\varphi_{e})\cdot \underline{i}_{r}^{s} = T_{P}(-\varphi_{e})\cdot \frac{\underline{\Psi}_{s}^{s}-L_{s}\cdot \underline{i}_{s}^{s}}{L_{M}} \end{matrix} \]
Wird obige Gleichung für den Statorraumzeiger in Rotorkoordinaten in die Gleichung (6.5) für die Rotorflussverkettung eingesetzt
\[ \begin{matrix} \underline{\Psi}_{r}^{r}= L_{r}\cdot \underline{i}_{r}^{r} + L_{M}\cdot \underline{i}_{s}^{r}= L_{r}\cdot \underline{i}_{r}^{r}+L_{M}\cdot T_{P}(-\varphi_{e})\cdot \frac{\underline{\Psi}_{s}^{s}-L_{M}\cdot \underline{i}_{r}^{s}}{L_{s}} \iff \\ L_{s}\cdot \underline{\Psi}_{r}^{r}= L_{s}\cdot L_{r}\cdot \underline{i}_{r}^{r}+L_{M}\cdot \underbrace{T_{P}(-\varphi_{e})\cdot \underline{\Psi}_{s}^{s}}_{\underline{\Psi_{s}^{r}}}-L_{M}^{2} \cdot \underbrace{T_{P}(-\varphi_{e})\cdot \underline{i}_{r}^{s}}_{\underline{i}_{r}^{r}}= \\ L_{s}\cdot L_{r}\cdot \underline{i}_{r}^{r}+L_{M}\cdot \underline{\Psi}_{s}^{r}-L_{M}^{2} \cdot \underline{i}_{r}^{r} \end{matrix} \]
kann diese Gleichung nach dem Rotorstromraumzeiger in Rotorkoordinaten umgestellt werden.
\[ \begin{matrix} L_{s}\cdot \underline{\Psi}_{r}^{r}= L_{s}\cdot L_{r}\cdot \underline{i}_{r}^{r}+L_{M}\cdot \underline{\Psi}_{s}^{r}-L_{M}^{2} \cdot \underline{i}_{r}^{r} \iff \\ \underline{i}_{r}^{r} = \frac{\underline{\Psi}_{r}^{r}\cdot L_{s}-L_{M}\cdot \underline{\Psi}_{s}^{r}}{L_{s}\cdot L_{r}-L_{M}^{2}} \end{matrix} \]
Um eine Gleichung für den Statorstromraumzeiger zu erhalten, wird gleich verfahren, indem die Gleichung für den Rotorstromraumzeiger in Rotorkoordinaten in die Gleichung (6.5) für die Rotorflussverkettung eingesetzt wird.
\[ \begin{matrix} \underline{\Psi}_{r}^{r}= L_{r}\cdot \underline{i}_{r}^{r} + L_{M}\cdot \underline{i}_{s}^{r}= L_{r}\cdot T_{P}(-\varphi_{e})\cdot \frac{\underline{\Psi}_{s}^{s}-L_{s}\cdot \underline{i}_{s}^{s}}{L_{M}}+L_{M}\cdot \underline{i}_{s}^{r} \iff \\ L_{M}\cdot \underline{\Psi}_{r}^{r}= L_{r}\cdot \underbrace{T_{P}(-\varphi_{e})\cdot \underline{\Psi}_{s}^{s}}_{\underline{\Psi}_{s}^{r}}-L_{r}\cdot L_{s}\cdot \underbrace{T_{P}(-\varphi_{e})\cdot \underline{i}_{s}^{s}}_{\underline{i}_{s}^{r}}+L_{M}^{2}\cdot \underline{i}_{s}^{r}= \\ L_{r}\cdot \underline{\Psi}_{s}^{r} + \underline{i}_{s}^{r}\cdot \left(L_{M}^{2}-L_{r}\cdot L_{{s}} \right) \end{matrix} \]
Somit kann auch diese Gleichung nach dem Statorraumzeiger umgestellt werden.
\[ \begin{matrix} L_{M}\cdot \underline{\Psi}_{r}^{r}= L_{r}\cdot \underline{\Psi}_{s}^{r} + \underline{i}_{s}^{r}\cdot \left(L_{M}^{2}-L_{r}\cdot L_{{s}} \right) \iff \\ \underline{i}_{s}^{r} = \frac{L_{M}\cdot \underline{\Psi}_{r}^{r}-L_{r}\cdot \underline{\Psi}_{s}^{r}}{L_{M}^{2}-L_{r}\cdot L_{s}} \end{matrix} \]
Die Gleichung beschreibt das Verhalten des Statorstromes in Rotorkoordinaten in Abhängigkeit des Rotor- und des Statorflusses. Da die Statorspannungsleichung ((6.6)) jedoch den Statorstrom in Statorkoordinaten verwendet, wird obige Gleichung mit Hilfe der Park-Transformation in das Stator-Koordinatensystem transformiert.
\[ \begin{matrix} \underline{i}_{s}^{s} = T_{P}(\varphi_{e})\cdot \underline{i}_{s}^{r} = \frac{L_{M}\cdot \overbrace{T_{P}(\varphi_{e})\cdot\underline{\Psi}_{r}^{r}}^{\underline{\Psi}_{r}^{s}}-L_{r}\cdot \overbrace{T_{P}(\varphi_{e})\cdot\underline{\Psi}_{s}^{r}}^{\underline{\Psi}_{s}^{s}}}{L_{M}^{2}-L_{r}\cdot L_{s}} \\ \underline{i}_{s}^{s} = \frac{L_{M}\cdot \underline{\Psi}_{r}^{s}-L_{r}\cdot \underline{\Psi}_{s}^{s}}{L_{M}^{2}-L_{r}\cdot L_{s}} \end{matrix} \]
Diese beiden Gleichungen, die das Verhalten der Ströme in Abhängigkeiten der Flussverkettungen beschreiben, können mit Hilfe eines entsprechenden Blockschaltbildes visualisiert werden (vgl. Abb. 6.12).
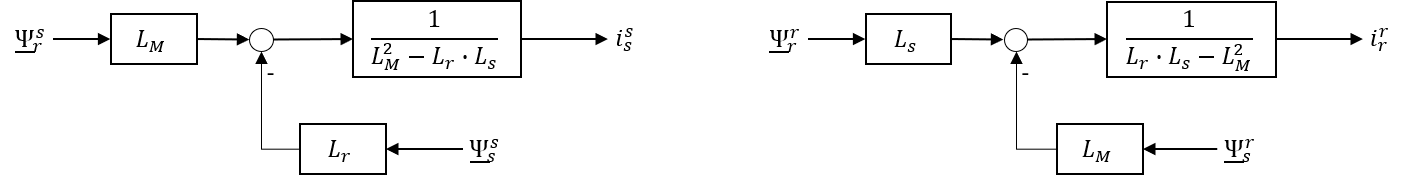
Abbildung 6.12: Blockschaltbild der Stator- und Rotorströme (links: Stator, rechts: Rotor)
Die Blockschaltbilder 6.11 und 6.12 können, unter Berücksichtigung der jeweiligen Koordinatentransformationen, kombiniert werden und liefern das vollständige Blockschaltbild der allgemeinen Drehfeldmaschine (vgl. Abb. 6.13).
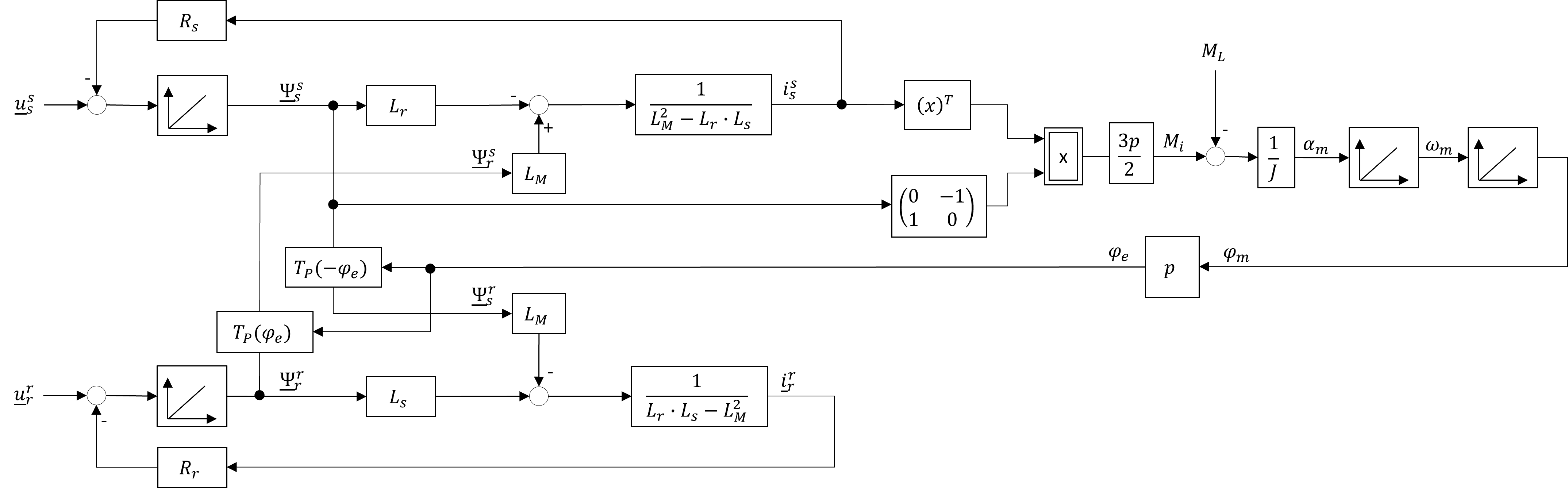
Abbildung 6.13: Blockschaltbild der allgemeinen Drehfeldmaschine in Stator und Rotorkoordinaten
Die erarbeiteten Gleichungen zur allgemeinen Drehfeldmaschine können direkt verwendet werden, um folgende Drehfeldmaschinen darstellen zu können:
- Käfigläuferasynchronmaschine indem der Rotorspannungsraumzeiger null gesetzt wird (\(\underline{u}_{r}^{r}=\underline{0}\))
- Fremderregte Vollpolsynchronmaschine durch \(\underline{u}_{r}^{r}=\left(\begin{array}{c}u_{r}^{d}\\ 0\end{array}\right)\)
- Permanentmagneterregte Synchronmaschine mit oberflächenmontierten Magneten durch \(\underline{\Psi}_{r}^{r}=\left(\begin{array}{c}\Psi_{PM}\\ 0\end{array}\right)\) und \(\underline{i}_{r}^{r}=\left(\begin{array}{c}\frac{\Psi_{PM}}{L_{s}}\\ 0\end{array}\right)\)
- doppelt gespeiste Asynchronmaschien indem ein beliebiger Rotorspannungsraumzeiger \(\underline{u}_{r}^{r}\) gewählt wird.
Das hergeleitete Modell ist somit für sogenannte isotrope Maschinen verwendbar. Isotrope Maschinen zeichnen sich dadurch aus, dass sich die magnetischen Eigenschaften längs und quer zur Rotorflussachse nicht unterscheiden \((L_{d}=L_{q})\). Andere Maschinentypen mit anisotropen Rotoren (z.B. Schenkelpolsynchronmaschinen, Permanentmagnetsynchronmaschine mit vergrabenen Magneten bzw. Reluktanz-Synchronmaschinen) benötigen Anpassungen des Modells.